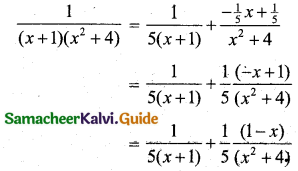Prasanna

Students can download 11th Business Maths Chapter 2 Algebra Ex 2.1 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 2 Algebra Ex 2.1

Samacheer Kalvi 11th Business Maths Algebra Ex 2.1 Text Book Back Questions and Answers

Resolve into partial fractions for the following:

Question 1.
\(\frac{3 x+7}{x^{2}-3 x+2}\)
Solution:
Here the denominator x² – 3x + 2 is not a linear factor.
So if possible we have to factorise it then only we can split up into partial fraction.
x² – 3x + 2 = (x – 1) (x – 2)
\(\frac{3 x+7}{(x-1)(x-2)}=\frac{A}{x-1}+\frac{B}{x-2}\) …….. (1)
Multiply both side by (x – 1) (x – 2)
3x + 7 = A(x – 2) + B(x – 1) …….. (2)
Put x = 2 in (2) we get
3(2) + 7 = A(2 – 2) + B(2 – 1)
6 + 7 = 0 + B(1)
∴ B = 13
Put x = 1 in (2) we get
3(1) + 7 = A(1 – 2) + B(1 – 1)
3 + 7 = A (-1) + 0
10 = A(-1)
∴ A = -10
Using A = -10 and B = 13 in (1) we get

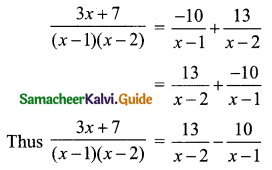
Note: When the denominator is only two linear factors we can adopt the following method.

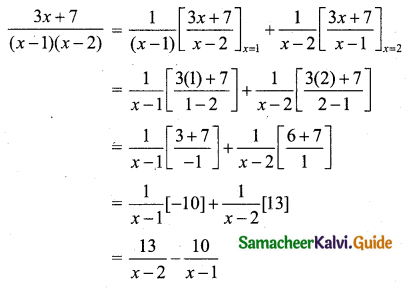
Question 2.
\(\frac{4 x+1}{(x-2)(x+1)}\)
Solution:
Let \(\frac{4 x+1}{(x-2)(x+1)}=\frac{A}{x-2}+\frac{B}{x+1}\) ……… (1)
Multiply both sides by (x – 2) (x + 1) we get
4x + 1 = A(x + 1) + B(x – 2) ……. (2)
Put x = -1 in (2) we get
4(-1) + 1 = A(-1 + 1) + B(-1 – 2)
-4 + 1 = A(0) + B(-3)
-3 = B(-3)
B = \(\frac{-3}{-3}\) = 1
Put x = 2 in (2) we get
4(2) + 1 = A(2 + 1) + B(2 – 2)
8 + 1 = A(3) + B(0)
9 = 3A
A = 3
Using A = 3, B = 1 in (1) we get
\(\frac{4 x+1}{(x-2)(x+1)}=\frac{3}{x-2}+\frac{1}{x+1}\)

Question 3.
\(\frac{1}{(x-1)(x+2)^{2}}\)
Solution:
Here the denominator has repeated factors. So we write
\(\frac{1}{(x-1)(x+2)^{2}}=\frac{A}{x-1}+\frac{B}{(x+2)}+\frac{C}{(x+2)^{2}}\) …… (1)
Multiply both sides by (x – 1) (x + 2)² we get
1 = A(x + 2)² + B(x – 1) (x + 2) + C(x – 1) …… (2)
Put x = 1 in (2) we get
1 = A(1 + 2)² + B(1 – 1) (1 + 2) + C(1 – 1)
1 = A(3²) + 0 + 0
1 = 9A
A = \(\frac{1}{9}\)
Put x = -2 in (2) we get
1 = A(-2 + 2)² + B(-2 – 1) (-2 + 2) + C(-2 – 1)
1 = 0 + 0 + C(-3)
C = \(\frac{-1}{3}\)
From (2) we have
1 = A(x + 2)² + B(x – 1) (x + 2) + C(x – 1)
0x² + 1 = A(x² + 4x + 4) + B(x² + x – 2) + C(x – 1)
Equating coefficient of x² on both sides we get
0 = A + B
0 = \(\frac{1}{9}\) (∴ A = \(\frac{1}{9}\))
B = \(-\frac{1}{9}\)
Using A = \(\frac{1}{9}\), B = \(-\frac{1}{9}\), C = \(-\frac{1}{3}\) in (1) we get,

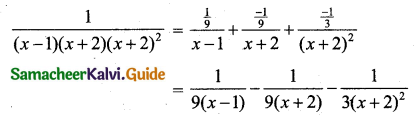
Question 4.
\(\frac{1}{x^{2}-1}\)
Solution:

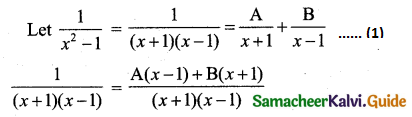
1 = A(x – 1) + B(x + 1) ……. (2)
Put x = 1 in (2) we get
1 = 0 + B(1 + 1)
1 = B(2)
B = \(\frac{1}{2}\)
Put x = -1 in (2) we get
1 = A(-1 – 1) + B(-1 + 1)
1 = -2A + 0
A = \(\frac{-1}{2}\)
Using A = \(\frac{-1}{2}\), B = \(\frac{1}{2}\) in (1) we get

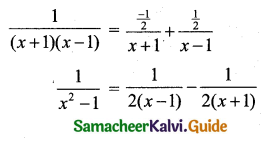
Question 5.
\(\frac{x-2}{(x+2)(x-1)^{2}}\)
Solution:

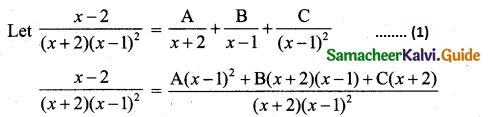
x – 2 = A(x – 1)² + B(x + 2) (x – 1) + C(x + 2) ……(2)
Put x = 1 in (2) we get
1 – 2 = A(1 – 1)² + B(1 + 2) (1 – 1) + C(1 + 2)
-1 = 0 + 0 + 3C
C = \(-\frac{1}{3}\)
Put x = -2 in (2) we get
-2 – 2 = A(-2 – 1)² + B(-2 + 2) (-2 – 1) + C(-2 + 2)
-4 = A(-3)² + 0 + 0
-4 = 9A
A = \(\frac{-4}{9}\)
From (2) we have,
0x² + x – 2 = A(x – 1)² + B(x + 2) (x – 1) + C(x + 2)
Equating coefficients of x² on both sides we get
0 = A + B
0 = \(\frac{-4}{9}\) + B (∵ A = \(\frac{-4}{9}\))
B = \(\frac{4}{9}\)
Using A = \(\frac{-4}{9}\), B = \(\frac{4}{9}\), C = \(-\frac{1}{3}\) in (1) we get

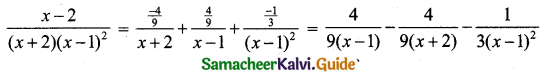
Question 6.
\(\frac{2 x^{2}-5 x-7}{(x-2)^{3}}\)
Solution:

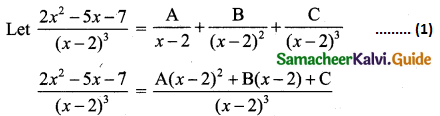
2x² – 5x – 7 = A(x – 2)² + B(x – 2) + C
2x² – 5x – 7 = A(x² – 4x + 4) + B(x – 2) + C …….. (2)
Put x = 2 in (2) we get
2(2²) – 5(2) – 7 = A(0) + B(0) + C
8 – 10 – 7 = 0 + 0 + C
-9 = C
C = -9
Equating coefficient of x2 on both sides of (2) we get
2 = A
A = 2
Equating coefficient of x on both sides of (2) we get
-5 = A(-4) + B(1)
-5 = 2(-4) + B(∵ A = 2)
-5 = -8 + B
B = 8 – 5 = 3
Using A = 2, B = 3, C = -9 in (1) we get

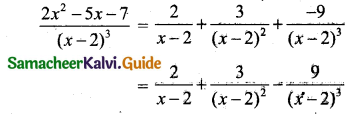
Question 7.
\(\frac{x^{2}-6 x+2}{x^{2}(x+2)}\)
Solution:
Here the denominator has three factors. So given fraction can be expressed as a sum of three simple fractions.
Let \(\frac{x^{2}-6 x+2}{x^{2}(x+2)}=\frac{A}{x}+\frac{B}{x^{2}}+\frac{C}{x+2}\) …… (1)
Multiply both sides by x² (x + 2) we get

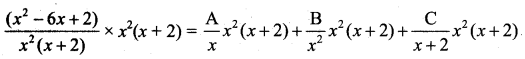
x² – 6x + 2 = Ax(x + 2) + B(x + 2) + C(x²) ……… (2)
Put x = 0 in (2) we get
0 – 0 + 2 = 0 + B(0 + 2) + 0
2 = B(2)
B = 1
Put x = -2 in (2) we get
(-2)² – 6(-2) + 2 = 0 + 0 + C(-2)²
4 + 12 + 2 = C(4)
18 = 4C
C = \(\frac{9}{2}\)
Comparing coefficient of x² on both sides of (2) we get,
1 = A + C
1 = A + \(\frac{9}{2}\)
A = 1 – \(\frac{9}{2}\) = \(\frac{2-9}{2}=\frac{-7}{2}\)
Using A = \(\frac{-7}{2}\), B = 1, C = \(\frac{9}{2}\) in (1) we get,
\(\frac{\left(x^{2}-6 x+2\right)}{x^{2}(x+2)}=\frac{-7}{2 x}+\frac{1}{x^{2}}+\frac{9}{2(x+2)}\)

Question 8.
\(\frac{x^{2}-3}{(x+2)\left(x^{2}+1\right)}\)
Solution:
Here the quadratic factor x² + 1 is not factorisable.
Let \(\frac{x^{2}-3}{(x+2)\left(x^{2}+1\right)}=\frac{A}{x+2}+\frac{(B x+C)}{x^{2}+1}\) ….. (1)
Multiply both sides by (x + 2) (x² + 1) we get,
x² – 3 = A(x² + 1) + (Bx + C) (x + 2)
Put x = -2 we get
(-2)² – 3 = [A(-2)² + 1] + 0
4 – 3 = A(4 + 1)
1 = 5A
A = \(\frac{1}{5}\)
Equating coefficient of x² on both sides of (2) we get
1 = A + B
1 = \(\frac{1}{5}\) + B
B = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
Equating coefficients of x on both sides of (2) we get
0 = 2B + C
0 = 2(\(\frac{4}{5}\)) + C
C = \(\frac{-8}{5}\)
Using A, B, C’s values in (1) we get

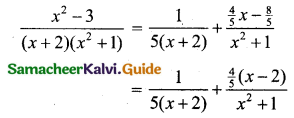
Question 9.
\(\frac{x+2}{(x-1)(x+3)^{2}}\)
Solution:
Here the denominator has three factors. So given fraction can be expressed as a sum of three simple fractions.
Let \(\frac{x+2}{(x-1)(x+3)^{2}}=\frac{A}{x-1}+\frac{B}{x+3}+\frac{C}{(x+3)^{2}}\) ……. (1)
Multiply both sides by (x – 1) (x + 3)² we get
\(\frac{x+2}{(x-1)(x+3)^{2}}\) (x – 1) (x + 3)² = \(\frac{A}{x-1}\) (x – 1) (x + 3)² +
\(\frac{B}{x+3}\) (x – 1) (x + 3)² + \(\frac{C}{(x+3)^{2}}\) (x – 1) (x + 3)²
x + 2 = A(x + 3)² + B(x – 1) (x + 3) + C(x – 1) ……. (2)
Put x = 1 in (2) we get
1 + 2 = A(1 + 3)² + 0 + 0
3 = A(4)²
A = \(\frac{3}{16}\)
Put x = -3 in (2) we get
-3 + 2 = 0 + 0 + C(-3 – 1)
-1 = C(-4)
C = \(\frac{1}{4}\)
Comparing coefficient of x² on both sides of (2) we get,
0 = A + B
0 = \(\frac{3}{16}\) + B
B = \(-\frac{3}{16}\)
Using A = \(\frac{3}{16}\), B = \(-\frac{3}{16}\), C = \(\frac{1}{4}\) in (1) we get,
\(\frac{x+2}{(x-1)(x+3)^{2}}=\frac{3}{16(x-1)}-\frac{3}{16(x+3)}+\frac{1}{4(x+3)^{2}}\)

Question 10.
\(\frac{1}{\left(x^{2}+4\right)(x+1)}\)
Solution:
Here the quadratic factor x² + 4 is not factorisable.
Let \(\frac{1}{(x+1)\left(x^{2}+4\right)}=\frac{A}{x+1}+\frac{B x+C}{x^{2}+4}\) ……. (1)
Multiply both sides by (x + 1) (x² + 4) we get
1 = A(x² + 4) + (Bx + C) (x + 1) ……. (2)
Put x = -1 in (2) we get
1 = A((-1)² + 4) + 0
1 = A(1 + 4)
A = \(\frac{1}{5}\)
Equating coefficient of x² on both sides of (2) we get,
0 = A + B
0 = \(\frac{1}{5}\) + B
B = \(\frac{-1}{5}\)
Equating coefficient of x on both sides of (2) we get,
{∵ (Bx + C) (x + 1) = Bx² + Cx = Bx + C}
0 = B + C
0 = \(\frac{-1}{5}\) + C
C = \(\frac{1}{5}\)
Using A = \(\frac{1}{5}\), B = \(\frac{-1}{5}\), C = \(\frac{1}{5}\) we get,

Students can download 11th Business Maths Chapter 1 Matrices and Determinants Ex 1.5 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 1 Matrices and Determinants Ex 1.5

Samacheer Kalvi 11th Business Maths Matrices and Determinants Ex 1.5 Text Book Back Questions and Answers

Choose the Correct Answer.

Question 1.
The value of x if \(\left|\begin{array}{lll}
0 & 1 & 0 \\
x & 2 & x \\
1 & 3 & x
\end{array}\right|=0\) is
(a) 0, -1
(b) 0, 1
(c) -1, 1
(d) -1, -1
Answer:
(b) 0, 1
Hint:
0 – 1[x² – x] + 0 = 0
⇒ x² – x = 0
⇒ x(x – 1) = 0
⇒ x = 0 (or) x = 1

Question 2.
The value of \(\left|\begin{array}{lll}
2 x+y & x & y \\
2 y+z & y & z \\
2 z+x & z & x
\end{array}\right|\) is
(a) xyz
(b) x + y + z
(c) 2x + 2y + 2z
(d) 0
Answer:
(d) 0
Hint:
= \(\left|\begin{array}{lll}
2 x & x & y \\
2 y & y & z \\
2 z & z & x
\end{array}\right|\) C₁ → C₁ – C₃
= 0 (C₁ and C₂ are proportional)

Question 3.
The cofactor of -7 in the determinant \(\left|\begin{array}{rrr}
2 & -3 & 5 \\
6 & 0 & 4 \\
1 & 5 & -7
\end{array}\right|\) is
(a) -18
(b) 18
(c) -7
(d) 7
Answer:
(b) 18
Hint:
A cofactor of -7 = \(\left|\begin{array}{rr}
2 & -3 \\
6 & 0
\end{array}\right|\)
= 0 + 18
= 18

Question 4.
If Δ = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
3 & 1 & 2 \\
2 & 3 & 1
\end{array}\right|\) then \(\left|\begin{array}{lll}
3 & 1 & 2 \\
1 & 2 & 3 \\
2 & 3 & 1
\end{array}\right|\) is
(a) Δ
(b) -Δ
(c) 3Δ
(d) -3Δ
Answer:
(b) -Δ
Hint:
\(\left|\begin{array}{lll}
3 & 1 & 2 \\
1 & 2 & 3 \\
2 & 3 & 1
\end{array}\right|=-\left|\begin{array}{lll}
1 & 2 & 3 \\
3 & 1 & 2 \\
2 & 3 & 1
\end{array}\right|\) R₁ ↔ R₂
= -Δ

Question 5.
The value of the determinant \(\left|\begin{array}{lll}
a & 0 & 0 \\
0 & b & 0 \\
0 & 0 & c
\end{array}\right|^{2}\) is
(a) abc
(b) 0
(c) a²b²c²
(d) -abc
Answer:
(c) a²b²c²
Hint:
\(a^{2} b^{2} c^{2}\left|\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right|\)
= a²b²c² × 1²
= a²b²c²

Question 6.
If A is square matrix of order 3 then |kA| is:
(a) k|A|
(b) -k|A|
(c) k³|A|
(d) -k³|A|
Answer:
(c) k³|A|

Question 7.
adj (AB) is equal to:
(a) adj A adj B
(b) adj A^T adj B^T
(c) adj B adj A
(d) adj B^T adj A^T
Answer:
(c) adj B adj A

Question 8.
The inverse matrix of \(\left(\begin{array}{cc}
\frac{4}{5} & \frac{5}{12} \\
\frac{2}{5} & \frac{1}{2}
\end{array}\right)\) is
(a) \(\frac{7}{30}\left(\begin{array}{cc}
\frac{1}{2} & \frac{5}{12} \\
\frac{2}{5} & \frac{4}{5}
\end{array}\right)\)
(b) \(\frac{7}{30}\left(\begin{array}{cc}
\frac{1}{2} & \frac{-5}{12} \\
\frac{-2}{5} & \frac{1}{5}
\end{array}\right)\)
(c) \(\frac{30}{7}\left(\begin{array}{rr}
\frac{1}{2} & \frac{5}{12} \\
\frac{2}{5} & \frac{4}{5}
\end{array}\right)\)
(d) \(\frac{30}{7}\left(\begin{array}{rr}
\frac{1}{2} & \frac{-5}{12} \\
\frac{-2}{5} & \frac{4}{5}
\end{array}\right)\)
Answer:
(c) \(\frac{30}{7}\left(\begin{array}{rr}
\frac{1}{2} & \frac{5}{12} \\
\frac{2}{5} & \frac{4}{5}
\end{array}\right)\)

Question 9.
If A = \(\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\) such that ad – bc ≠ 0 then A^-1 is:
(a) \(\frac{1}{a d-b c}\left[\begin{array}{cc}
d & b \\
-c & a
\end{array}\right]\)
(b) \(\frac{1}{a d-b c}\left[\begin{array}{ll}
d & b \\
c & a
\end{array}\right]\)
(c) \(\frac{1}{a d-b c}\left[\begin{array}{cc}
d & -b \\
-c & a
\end{array}\right]\)
(d) \(\frac{1}{a d-b c}\left[\begin{array}{ll}
d & -b \\
c & a
\end{array}\right]\)
Answer:
(c) \(\frac{1}{a d-b c}\left[\begin{array}{cc}
d & -b \\
-c & a
\end{array}\right]\)
Hint:

Question 10.
The number of Hawkins-Simon conditions for the viability of input-output analysis is:
(a) 1
(b) 3
(c) 4
(d) 2
Answer:
(d) 2

Question 11.
The inventor of input-output analysis is:
(a) Sir Francis Galton
(b) Fisher
(c) Prof. Wassily W. Leontief
(d) Arthur Cayley
Answer:
(c) Prof. Wassily W. Leontief

Question 12.
Which of the following matrix has no inverse?
(a) \(\left(\begin{array}{rr}
-1 & 1 \\
1 & -4
\end{array}\right)\)
(b) \(\left(\begin{array}{rr}
2 & -1 \\
-4 & 2
\end{array}\right)\)
(c) \(\left(\begin{array}{cc}
\cos a & \sin a \\
-\sin a & \cos a
\end{array}\right)\)
(d) \(\left(\begin{array}{rr}
\sin a & \sin a \\
-\cos a & \cos a
\end{array}\right)\)
Answer:
(b) \(\left(\begin{array}{rr}
2 & -1 \\
-4 & 2
\end{array}\right)\)
Hint:
So \(\left(\begin{array}{rr}
2 & -1 \\
-4 & 2
\end{array}\right)\) has no inverse.

Question 13.
Inverse of \(\left(\begin{array}{ll}
3 & 1 \\
5 & 2
\end{array}\right)\) is:
(a) \(\left(\begin{array}{rr}
2 & -1 \\
-5 & 3
\end{array}\right)\)
(b) \(\left(\begin{array}{rr}
-2 & 5 \\
1 & -3
\end{array}\right)\)
(c) \(\left(\begin{array}{rr}
3 & -1 \\
-5 & -3
\end{array}\right)\)
(d) \(\left(\begin{array}{rr}
-3 & 5 \\
1 & -2
\end{array}\right)\)
Answer:
(a) \(\left(\begin{array}{rr}
2 & -1 \\
-5 & 3
\end{array}\right)\)
Hint:
Let A = \(\left(\begin{array}{ll}
3 & 1 \\
5 & 2
\end{array}\right)\)
|A| = [6 – 5] = 1
adj A = \(\left[\begin{array}{rr}
2 & -1 \\
-5 & 3
\end{array}\right]\)
∴ A^-1 = \(\left[\begin{array}{rr}
2 & -1 \\
-5 & 3
\end{array}\right]\)

Question 14.
If A = \(\left(\begin{array}{rr}
-1 & 2 \\
1 & -4
\end{array}\right)\) then A (adj A) is:
(a) \(\left(\begin{array}{ll}
-4 & -2 \\
-1 & -1
\end{array}\right)\)
(b) \(\left(\begin{array}{rr}
4 & -2 \\
-1 & 1
\end{array}\right)\)
(c) \(\left(\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right)\)
(d) \(\left(\begin{array}{ll}
0 & 2 \\
2 & 0
\end{array}\right)\)
Answer:
(c) \(\left(\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right)\)
Hint:
A = \(\left(\begin{array}{rr}
-1 & 2 \\
1 & -4
\end{array}\right)\)
|A| = 4 – 2 = 2
We know that A (adj A) = |A| I
⇒ 2 \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)=\left(\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right)\)

Question 15.
If A and B non-singular matrix then, which of the following is incorrect?
(a) A² = I implies A^-1 = A
(b) I^-1 = I
(c) If AX = B then X = B^-1A
(d) If A is square matrix of order 3 then |adj A| = |A|²
Answer:
(c) If AX = B then X = B^-1A
Hint:
If AX = B then X = A^-1B so, X = B^-1A is incorrect.

Question 16.
The value of \(\left|\begin{array}{rrr}
5 & 5 & 5 \\
4 x & 4 y & 4 z \\
-3 x & -3 y & -3 z
\end{array}\right|\) is:
(a) 5
(b) 4
(c) 0
(d) -3
Answer:
(c) 0
Hint:
= 4 × (-3) \(\left|\begin{array}{lll}
5 & 5 & 5 \\
x & y & z \\
x & y & z
\end{array}\right|\)
[Take out 4 from R₂ and -3 from R₃]
= 0 (∵ R₂ ≡ R₃)

Question 17.
If A is an invertible matrix of order 2 then det (A^-1) be equal
(a) det (A)
(b) \(\frac{1}{{det}(A)}\)
(c) 1
(d) 0
Answer:
(b) \(\frac{1}{{det}(A)}\)
Hint:
AA^-1 = I
|AA^-1| = |I|
|A| |A^-1| = 1
|A^-1| = \(\frac{1}{|\mathrm{A}|}\)
det A^-1 = \(\frac{1}{\det (A)}\)

Question 18.
If A is 3 × 3 matrix and |A| = 4 then |A^-1| is equal to:
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{16}\)
(c) 2
(d) 4
Answer:
(a) \(\frac{1}{4}\)
Hint:
|A^-1| = \(\frac{1}{|A|}=\frac{1}{4}\)

Question 19.
If A is a square matrix of order 3 and |A| = 3 then |adj A| is equal to:
(a) 81
(b) 27
(c) 3
(d) 9
Answer:
(d) 9
Hint:
|adj A| = |A|² = 3² = 9

Question 20.
The value of \(\left|\begin{array}{ccc}
x & x^{2}-y z & 1 \\
y & y^{2}-z x & 1 \\
z & z^{2}-x y & 1
\end{array}\right|\) is:
(a) 1
(b) 0
(c) -1
(d) -xyz
Answer:
(b) 0
Hint:

Question 21.
If A = \(\left[\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\), then |2A| is equal to:
(a) 4 cos 2θ
(b) 4
(c) 2
(d) 1
Answer:
(b) 4
Hint:
|2A| = 2² |A|
= 4 \(\left|\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right|\)
= 4 [cos²θ + sin²θ]
= 4 × 1
= 4

Question 22.
If Δ = \(\left|\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right|\) and A_ij is cofactor of a_ij, then value of Δ is given by:
(a) a₁₁A₃₁ + a₁₂A₃₂ + a₁₃A₃₃
(b) a₁₁A₁₁ + a₁₂A₂₁ + a₁₃A₃₁
(c) a₂₁A₁₁ + a₂₂A₁₂ + a₂₃A₁₃
(d) a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁
Answer:
(d) a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁

Question 23.
If \(\left|\begin{array}{ll}
x & 2 \\
8 & 5
\end{array}\right|=0\) then the value of x is:
(a) \(\frac{-5}{6}\)
(b) \(\frac{5}{6}\)
(c) \(\frac{-16}{5}\)
(d) \(\frac{16}{5}\)
Answer:
(d) \(\frac{16}{5}\)
Hint:
\(\left|\begin{array}{ll}
x & 2 \\
8 & 5
\end{array}\right|=0\)
5x – 16 = 0
⇒ x = \(\frac{16}{5}\)

Question 24.
If \(\left|\begin{array}{ll}
4 & 3 \\
3 & 1
\end{array}\right|\) = -5 then the value of \(\left|\begin{array}{rr}
20 & 15 \\
15 & 5
\end{array}\right|\) is:
(a) -5
(b) -125
(c) -25
(4) 0
Answer:
(b) -125
Hint:
\(\left|\begin{array}{rr}
20 & 15 \\
15 & 5
\end{array}\right|\)
= 5 × 5 \(\left|\begin{array}{ll}
4 & 3 \\
3 & 1
\end{array}\right|\)
= 5 × 5 × (-5)
= -125

Question 25.
If any three rows or columns of a determinant are identical then the value of the determinant is:
(a) 0
(b) 2
(c) 1
(d) 3
Answer:
(a) 0

Subject Matter Experts at SamacheerKalvi.Guide have created Tamil Nadu State Board Samacheer Kalvi 11th Business Maths and Statistics Book Answers Solutions Guide Pdf Free Download of Volume 1 and Volume 2 in English Medium and Tamil Medium are part of Samacheer Kalvi 11th Books Solutions.

Let us look at these TN State Board New Syllabus Samacheer Kalvi 11th Std Business Maths Guide Pdf of Text Book Back Questions and Answers, Notes, Chapter Wise Important Questions, Model Question Papers with Answers, Study Material, Question Bank and revise our understanding of the subject.

Samacheer Kalvi 11th Business Maths Guide Book Back Answers

Tamilnadu State Board Samacheer Kalvi 11th Business Maths Book Back Answers Solutions Guide Volume 1 and Volume 2.

Samacheer Kalvi 11th Business Maths Book Back Answers

Tamilnadu State Board Samacheer Kalvi 11th Business Maths Book Volume 1 Solutions

Samacheer Kalvi 11th Business Maths Guide Chapter 1 Matrices and Determinants

• Chapter 1 Matrices and Determinants Ex 1.1
• Chapter 1 Matrices and Determinants Ex 1.2
• Chapter 1 Matrices and Determinants Ex 1.3
• Chapter 1 Matrices and Determinants Ex 1.4
• Chapter 1 Matrices and Determinants Ex 1.5

11th Business Maths Book Back Answers Chapter 2 Algebra

• Chapter 2 Algebra Ex 2.1
• Chapter 2 Algebra Ex 2.2
• Chapter 2 Algebra Ex 2.3
• Chapter 2 Algebra Ex 2.4
• Chapter 2 Algebra Ex 2.5
• Chapter 2 Algebra Ex 2.6
• Chapter 2 Algebra Ex 2.7

11th Business Maths Solution Book Chapter 3 Analytical Geometry

• Chapter 3 Analytical Geometry Ex 3.1
• Chapter 3 Analytical Geometry Ex 3.2
• Chapter 3 Analytical Geometry Ex 3.3
• Chapter 3 Analytical Geometry Ex 3.4
• Chapter 3 Analytical Geometry Ex 3.5
• Chapter 3 Analytical Geometry Ex 3.6
• Chapter 3 Analytical Geometry Ex 3.7

11th Samacheer Business Maths Book Chapter 4 Trigonometry

• Chapter 4 Trigonometry Ex 4.1
• Chapter 4 Trigonometry Ex 4.2
• Chapter 4 Trigonometry Ex 4.3
• Chapter 4 Trigonometry Ex 4.4
• Chapter 4 Trigonometry Ex 4.5

11th Business Maths Guide Volume 1 Chapter 5 Differential Calculus

• Chapter 5 Differential Calculus Ex 5.1
• Chapter 5 Differential Calculus Ex 5.2
• Chapter 5 Differential Calculus Ex 5.3
• Chapter 5 Differential Calculus Ex 5.4
• Chapter 5 Differential Calculus Ex 5.5
• Chapter 5 Differential Calculus Ex 5.6
• Chapter 5 Differential Calculus Ex 5.7
• Chapter 5 Differential Calculus Ex 5.8
• Chapter 5 Differential Calculus Ex 5.9
• Chapter 5 Differential Calculus Ex 5.10

Tamilnadu State Board Samacheer Kalvi 11th Business Maths Book Volume 2 Solutions

11th Business Maths Guide Volume 2 Chapter 6 Applications of Differentiation

• Chapter 6 Applications of Differentiation Ex 6.1
• Chapter 6 Applications of Differentiation Ex 6.2
• Chapter 6 Applications of Differentiation Ex 6.3
• Chapter 6 Applications of Differentiation Ex 6.4
• Chapter 6 Applications of Differentiation Ex 6.5
• Chapter 6 Applications of Differentiation Ex 6.6

TN 11th Business Maths Solution Book Chapter 7 Financial Mathematics

• Chapter 7 Financial Mathematics Ex 7.1
• Chapter 7 Financial Mathematics Ex 7.2
• Chapter 7 Financial Mathematics Ex 7.3

11th Std Business Maths Guide Pdf Chapter 8 Descriptive Statistics and Probability

• Chapter 8 Descriptive Statistics and Probability Ex 8.1
• Chapter 8 Descriptive Statistics and Probability Ex 8.2
• Chapter 8 Descriptive Statistics and Probability Ex 8.3

11th Business Maths Book Answer Key Chapter 9 Correlation and Regression Analysis

• Chapter 9 Correlation and Regression Analysis Ex 9.1
• Chapter 9 Correlation and Regression Analysis Ex 9.2
• Chapter 9 Correlation and Regression Analysis Ex 9.3

11th Business Maths Book Pdf Chapter 10 Operations Research

• Chapter 10 Operations Research Ex 10.1
• Chapter 10 Operations Research Ex 10.2
• Chapter 10 Operations Research Ex 10.3

We hope these Tamilnadu State Board Samacheer Kalvi Class 11th Business Maths Book Solutions Answers Guide Volume 1 and Volume 2 Pdf Free Download in English Medium and Tamil Medium will help you get through your subjective questions in the exam.

Let us know if you have any concerns regarding TN State Board New Syllabus Samacheer Kalvi 11th Standard Business Maths Guide Pdf of Text Book Back Questions and Answers, Notes, Chapter Wise Important Questions, Model Question Papers with Answers, Study Material, Question Bank, drop a comment below and we will get back to you as soon as possible.

Students can Download 9th Tamil Chapter 4.2 ஓ, என் சமகாலத் தோழர்களே Questions and Answers, Summary, Notes, Samacheer Kalvi 9th Tamil Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Tamil Solutions Chapter 4.2 ஓ, என் சமகாலத் தோழர்களே

கற்பவை கற்றபின்

Question 1.
அறிவியல் செய்திகளை வெளிப்படுத்தும் கவிதைகளைத் தொகுத்து வகுப்பறையில் படித்துக் காட்டுக.
Answer:
அ) நீர்நின் றிளகிற் றிதுவேண்டா
– சீவகசிந்தாமணி (காந்தருவதத்தை இலம்பகம்)

அறிவியல் செய்தி:
மரத்தில் செய்யப்படும் வீணையே இன்னிசை எழுப்ப ஏற்றது. மரத்தின் ஈரத்தன்மைக்கு ஏற்ப அதில் மோதும் ஒலி அலைகளின் அதிர்வெண்ணும் வேறுபடும். சீவகன், தத்தை கொடுத்த யாழினை ஆராயும் போது, நீரில் இருந்து ஊறிய மரத்தால் செய்யப்பட்ட யாழில், அதிர்வெண் வேறுபட்டு சமச்சீரற்று காணப்படும் என்பதால் “நீர்நின் றிளகிற் றிதுவேண்டா” என்றான்.

ஆ) “அணுவைத் துளைத்து ஏழ்கடலைப் புகட்டி” – ஔவையார்
“ஓர் அணுவினைச் சதகூறிட்ட கோணினும் உளன்” – கம்பர்
அறிவியல் செய்தி:
அணுவைப் பிளக்கவும், சேர்க்கவும் முடியும் என்ற இன்றைய அறிவியலை நம் கவிஞர்கள் அன்றே தம் கவிதைகளில் கூறியுள்ளனர். அணுசேர்ப்பும், அணுப்பிரிப்பும் பற்றிய கருத்துகள் அன்றே அரும்பியுள்ளன.

இ) “அகல்வயல் பொழிந்தும்…….
உறுமிடத் துதவா உவர்நிலம்…….” – புறநானூறு பரணர்
“பயவாக் களரணையர் கல்லாதவர்” – திருவள்ளுவர்
அறிவியல் செய்தி:
எவ்வளவு மழை பொழிந்தாலும் “களர்நிலம்” என அழைக்கப்படும் உவர்நிலம் எதற்கும் உதவாது என்ற மண்ணியல் அறிவியலைக் கூறுகிறது.
இவ்வாறு நம் தமிழ்ப் புலவர்கள் இயற்றிய கவிதைகள் பல, நமக்கு அறிவியல் செய்திகளைக் கூறுவதாக உள்ளன என்பதை மறுக்க இயலாது.

Question 2.
விமானமும் ஏவுகணையும் பேசிக்கொள்வது போல ஓர் உரையாடலைக் குழுவாகச் சேர்ந்து உருவாக்குக.
Answer:
விமானமும் – ஏவுகணையும் பேசுவதுபோல உரையாடல்
விமானம் : வணக்கம்! ஏவுகணை அவர்களே!
ஏவுகணை : வணக்கம்! வணக்கம்!
விமானம் : ஐயா உங்களை சந்திப்பதில் மிக்க மகிழ்ச்சி
ஏவுகணை : எனக்கும் மகிழ்ச்சி
விமானம் : என் பெயர் விமானம். நான், மக்களை நாடுவிட்டு நாடு செல்ல உதவும் பொருட்டு
வானில் பறப்பேன். அதனால் என்னை வானூர்தி என்றும் அழைப்பர்.
ஏவுகணை : அப்படியா! நான் அதற்கும் மேலே பல்லாயிரக்கணக்கான கிலோமீட்டர் தூரம் மேலே சென்று செயற்கைகோள்களை அதனதன் பாதையில் நிறுத்துவேன்.
விமானம் : அப்படியா கேட்கவே ஆச்சரியமாக இருக்கிறதே. என்னை இயக்க விமானி துணை விமானி எல்லாம் இருப்பார்கள். உங்களை இயக்க……
ஏவுகணை : ஆளெல்லாம் இருக்கமாட்டார்கள். ஏவு ஊர்தியில் என்னை நிறுத்தி, இரண்டு மூன்று நாள்களுக்கு முன்னதாகவே எண்நிலை (count down) தொடங்கி கண்காணித்து, குறிப்பிட்ட நேரம் வந்தவுடனே என்னை மிக வேகமாக ஏவி விடுவார்கள். நானே குறிப்பிட்ட இடத்திற்கு சென்று விடுவேன்.
விமானம் : என்னை பூமியில் இருந்து கண்காணிப்பது போல் உங்களையும் கண்காணிப்பார்களா!
ஏவுகணை : ஆம்! என்னையும் கண்காணித்துக் கொண்டேதான் இருப்பார்கள்.
விமானம் : நன்றி!!
ஏவுகணை : நன்றி!!

Question 3.
பாடலில் அமைந்துள்ள தொடைநயங்களை எழுதுக:
கிளிக்கு றெக்கை இருக்கும் வரைக்கும்
கிழக்கு வானம் தூரமில்லை
முளைக்கும் விதைகள் முளைக்கத் துடித்தால்
பூமி ஒன்றும் பாரமில்லை .
Answer:
தொடைநயங்கள் :

1. கிளிக்கு, கிழக்கு – முதல் எழுத்து ஒன்றிவந்து “ மோனை நயம்” உள்ளது.
2. முளைக்கும் – முளைக்கத்
   இதில், முதல் எழுத்து ஒன்றிவந்து “சீர் மோனை” நயமும்
   இரண்டாம் எழுத்து ஒன்றி வந்து “சீர் எதுகை” நயமும் இடம் பெற்றுள்ளது.
3. தூரமில்லை – பாரமில்லை
   இதில் “மில்லை” என்னும் இறுதி சீர் ஒன்றி வந்து “இயைபுத் தொடை” நயம் அமைந்துள்ளது.

பாடநூல் வினாக்கள்

பலவுள் தெரிக

Question 1.
பின்வரும் தொடர்களைப் படித்து ‘நான் யார் என்று கண்டுபிடிக்க.
அறிவியல் வாகனத்தில் நிறுத்தப்படுவேன்.
எல்லாக் கோளிலும் ஏற்றப்படுவேன்.
இளையவர் கூட்டம் என்னை ஏந்தி நடப்பர்.
அ) இணையம்
ஆ) தமிழ்
இ) கணிணி
ஈ) ஏவுகணை
Answer:
ஆ) தமிழ்

குறுவினா

Question 1.
கூட்டுப் புழுவை எடுத்துக்காட்டிக் கவிஞர் உணர்த்தும் கருத்துக்களை எழுதுக.
Answer:
பொறுமை, அடக்கம் என்னும் கட்டுப்பாடுகளைக் கடைப்பிடித்து ஒழுக வேண்டும். கூட்டுப்புழுவாக இருந்து தான் பின்னாளில் பட்டுப்பூச்சியாய்க் கோலம் கொள்ளும் எனக் கவிஞர் குறிப்பிடுகிறார்.

சிறுவினா

Question 1.
‘என் சமகாலத் தோழர்களே“ கவிதையில் கவிஞர் விடுக்கும் வேண்டுகோள் யாது?
Answer:
அறிவியல் என்னும் வாகனத்தின் மீது நம்மை ஆளும் தமிழ்மொழியை நிறுத்துங்கள். பழங்கால மன்னர்களுள் ஒருவன் கரிகாலன். அவனது பெருமைகளையும் சிறப்புகளையும் கணிப்பொறிக்குள்ளே பதிவு செய்து வையுங்கள்.

அடுத்தவர் ஏவுகின்ற திசையில் நோக்கமில்லாமல் செல்லும் அம்பைப்போல் இருந்த மக்கள் இனத்தை மாற்றுங்கள். ஏவுகணை செலுத்துவதிலும் தமிழை எழுதி எல்லாக் கோளிகளிலும் ஏற்றிச் செலுத்துங்கள் என்று கவிஞர் வைரமுத்து வேண்டுகோள் விடுக்கிறார்.

கூடுதல் வினாக்கள்

பலவுள் தெரிக

Question 1.
பட்டுப் பூச்சியாய் உருப்பெறுவது
அ) தேனீ
ஆ) வண்டு
இ) கூட்டுப்புழு
ஈ) ஈசல்
விடை:
இ) கூட்டுப்புழு

Question 2.
அறிவை மறந்ததாக …… இருக்கக் கூடாது.
அ) உணர்ச்சி
ஆ) வேகம்
இ) செயல்
ஈ) பண்பாடு
விடை:
அ) உணர்ச்சி

Question 3.
கழனிகள் சுமக்க வேண்டியது ……
அ) கதிர்கள்
ஆ) வெம்பிய பழங்கள்
இ) வறண்ட தாவரம்
ஈ) அழுகிய பொருள்கள்
விடை:
அ) கதிர்கள்

Question 4.
காட்டும் பொறுமை அடக்கம் என்னும் கட்டுப்பாட்டைக் கடவாதீர் – இவ்வடியில் “பொறுமை அடக்கம்” என்பதன் இலக்கணக் குறிப்பு தருக.
விடை:
உம்மைத் தொகை

Question 5.
2003-ம் ஆண்டு சாகித்ய அகாடமி விருது பெற்ற வைரமுத்துவின் நூல் எது?
விடை :
கள்ளிக்காட்டு இதிகாசம்

Students can download 5th Maths Term 1 Chapter 4 Measurements InText Questions and Answers, Notes, Samacheer Kalvi 5th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 5th Maths Solutions Term 1 Chapter 4 Measurements InText Questions

Try These (Text Book Page No. 65)

Convert into millimeters

Question 1.
90 cm
Answer:
90 cm = 90 × 10
= 900 mm

Question 2.
5 cm 8 mm
Answer:
5 cm 8 mm = 5 × 10 + 8 mm
= 50 + 8 = 58 mm

Question 3.
5 m 9 mm
Answer:
5 m 9 mm = 5 × 1000 + 9 mm
= 5009 mm

Try These (Text Book Page No. 66)

Convert into centimeter

Question 1.
8 m
Answer:
8 m = 8 × 100
= 800 cm

Question 2.
6 m 4 cm
Answer:
6m4cm = 6 × 10 + 4 = 600 + 4
= 604 cm

Question 3.
80 mm
Answer:
80mm = 80 × 10
= 8 cm

Try These (Text Book Page No. 66)

Convert into meter

Question 1.
8 km 400 m
Answer:
8 km 400 m = (8 × 1000) + 400 m = 8000 + 400 = 8400 m

Question 2.
900 cm
Answer:
900 cm = 900 + 100 = 9 m

Question 3.
3500 mm
Answer:
3500 mm = 3500 + 1000 = 3 m 500

Try These (Text Book Page No. 67)

Convert into kilometers.

Question 1.
5430 m
Answer:
5430 m = 5430 + 1000 = 5 km 430 m

Question 2.
7500 m
Answer:
7500 m = 7500 + 1000 = 7 km 500 m

Question 3.
8000 m
Answer:
8000 m = 8000 + 1000 = 8 km

Try These (Text Book Page No. 68)

Subtract the following

Question 1.
1075 km 400 m – 27 km 350 m
Answer:
Difference = 1075 km 400 m – 27 km 350 m
= 1048 km 50 m

Question 2.
250 m 25 cm – 127 m 18 cm
Answer:
Difference = 250 m 25 cm – 127 m 18 cm
= 123 m 7 cm

Question 3.
27 km 900 m – 18 km 850 m
Answer:
Difference = 27 km 900 m – 18 km 850 m
= 9 km 50 m

Try These (Text Book Page No. 69)

a. 7 m 20 cm × 6
Answer:
20 cm × 6 = 120 cm
= 1m 20 cm

7 m 20 cm × 6 = 43 m 20 cm

b. 15 m 75 cm × 5
Answer:
75 cm × 5 = 375 cm
= 3m 75 cm

15 m 75 cm × 5 = 78 m 75 cm

c. 15 km 200 m × 4
Answer:

15 km 200 m × 4 = 60 km 800 m

d. 35 km 500 m × 5
Answer:
500 m × 5 = 2500 m
= 2 km 500 m

35 km 500 m × 5 = 177 km 500 m

Try These (Text Book Page No. 70)

a. 750 m 45 cm ÷ 5
b. 49 km 630 m ÷ 7
c. 770 km 550 m ÷ 11
Answer:
a. 750 m 45 cm ÷ 5

750 m 45 cm ÷ 5 = 150 m 9 cm

b. 49 km 630 m ÷ 7

49 km 630 m ÷ 7 = 7 km 90 m

c. 770 km 550 m ÷ 11

770 km 550 m ÷ 11 = 70 km 50 m

Students can Download 9th Tamil Chapter 4.1 இயந்திரங்களும் இணையவழிப் பயன்பாடும் Questions and Answers, Summary, Notes, Samacheer Kalvi 9th Tamil Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Tamil Solutions Chapter 4.1 இயந்திரங்களும் இணையவழிப் பயன்பாடும்

கற்பவை கற்றபின்

Question 1.
வங்கியில் இணையவழிச் சேமிப்புக் கணக்குத் தொடங்கும் நடைமுறையை எழுதுக:
Answer:
நாம் வங்கியில் சேமிப்புக் கணக்கு வைத்திருந்தால் வங்கிக்கு நேரில் சென்று தான் நம்முடைய பணப் பரிவர்த்தனைகளை மேற்கொள்ள இயலும். இணையவழி சேமிப்புக் கணக்கு இருந்தால் மற்ற பணிகளைச் செய்து கொண்டிருக்கும் போதே வங்கிப் பணிகளையும் செய்து கொள்ளலாம். இணையவழி சேமிப்புக் கணக்கு:

முதலில் நாம் எந்த வங்கியில் சேமிப்புக் கணக்கு வைத்திருக்கிறோமோ? அந்த வங்கிக்குரிய செயலியை (APP) முதலில் நம் கணினியிலோ அல்லது அலைபேசியிலோ பதிவிறக்கம் செய்துகொள்ள வேண்டும், பின்னர் மின் அஞ்சல் முகவரி (E-Mail ID) ஒன்றும், கடவு வார்த்தை (Password) ஒன்றும் உருவாக்குதல் வேண்டும்.

பெயர்
வங்கிக் கணக்கு எண் :
வங்கிக் கிளை :
வங்கி குறியீட்டு எண் :

என மேற்கூறிய அனைத்தையும் குறிப்பிட்டு, இணையவழி (Net Banking) மூலம் வங்கி சேமிப்புக் கணக்கைத் தொடங்கிக் கொள்ளலாம்.

Question 2.
உங்கள் குடும்பத்தினருடன் வெளியூர் சென்ற தொடர்வண்டிப் பயணத்திற்கு இணையத்தில்
எவ்வாறு முன்பதிவு செய்தீர்கள்? அதன் வழிமுறைகளை அனுபவத்தில் (அ) கேட்டறிந்து வகுப்பறையில் வழங்குக.
Answer:
நாங்கள் கடந்தவாரத்தில் கோவையில் இருந்து சென்னைக்கு நீலகிரி விரைவு தொடர்வண்டியில் (வண்டி எண் 12672) இரவு 20.30 மணிக்கு முன்பதிவு செய்தோம். இரண்டாம் வகுப்பு (S – 6, 45, 46, 47, 48) தூங்கும் வசதி உள்ள பெட்டியில் இரண்டு நடுப்படுக்கை, இரண்டு கீழ்படுக்கை முன்பதிவு செய்து தானியக்கப் பண இயந்திர அட்டை மூலம் பணம் செலுத்தி கைபேசியில் வந்த குறுஞ்செய்தியை பயணச்சீட்டு பரிசோதகரிடம் காண்பித்து சுகமான பயணம் மேற்கொண்டோம்.

இணையத்தில் தொடர்வண்டிப் பயணத்திற்கு முன்பதிவு செய்தல்:

• மாணவர்களே! நாம் பயணம் செய்ய திட்டமிடும் பொழுதே, பயணத்திற்கான சீட்டை இணையவழியில் பதிவு செய்து கொள்ளலாம்.
• இன்றைய காலக்கட்டத்தில் இணையதளத்தில் பயணச் சீட்டை பதிவு செய்வது மிகவும் எளிது. நம் நேரமும், பெருமளவு மிச்சமாகும்.
• பயணம் மேற்கொள்ள வேண்டிய ஊருக்கு உங்கள் ஊரில் இருந்து செல்லும் தொடர் வண்டிகளை அறிந்து கொண்டு, அவற்றின் நேரங்களையும் தெளிவாகத் தெரிந்து கொள்ள வேண்டும்.
• பயணம் செய்ய விரும்பும் நாளில் எந்த தொடர்வண்டியில், எந்த பெட்டியில் இருக்கை வசதி மற்றும் படுக்கை வசதியுடன் இருக்கும் காலியிடங்களை அறிந்து கொள்ள வேண்டும். அவற்றை அறிய முனையும் போதே பயணச் சீட்டுக்கான தொகையும் அறிந்து கொள்ளலாம்.
• பின்னர் வங்கி அட்டைகளின் உதவியுடன், பயணச் சீட்டிற்கான தொகையைச் செலுத்தி முன்பதிவு செய்து கொண்டோம் எனில், சற்று நேரத்தில் நமது அலைபேசிக்கு குறுஞ்செய்தியும், அச்செய்தியில் நமக்கான இருக்கை எண், புறப்படும் நேரம் போன்றவை வந்துவிடும்.
• மின் அஞ்சலில் பயணச்சீட்டும் வந்துவிடுகிறது. நாம் பயணம் செய்யும் பொழுது, குறுஞ்செய்தியையும், நம்முடைய அடையாள அட்டை ஏதேனும் ஒன்றைக் காட்டி சுகமான பயணத்தை மேற்கொள்ளலாம்.
• களைப்பின்றி பயணம் செய்ய இணையவழி பதிவு முறையே சிறந்ததாகும்.

Question 3.
விரலியில் (Pendrive) உள்ள பாடல்களையும், எழுத்துக் கோப்புகளையும் (Document) கணினியில் நுழைந்து உறைகளில் (Folder) இட்டுச் சேமிப்பதைச் செய்து பார்த்துத் தெரிந்து கொள்க.
Answer:
‘விரலி’ என்ற வார்த்தை Pendrive என்ற ஆங்கில வார்த்தையின் தமிழாக்கம் ஆகும்.
விரலியில் உள்ள பாடல்கள் எழுத்துக் கோப்புகளை கணினியில் சேமிக்கும் முறை:

• முதலில் விரலியை அதன் பகுதியில் நுழைத்தல் வேண்டும்.
• கணினித் திரையில் குறியீடு ஒன்று தோன்றும்.
• அந்தக் குறியீட்டை இயக்கும் போது, விரலியில் உள்ள செய்திகளை எந்தப் பகுதியில் சேமிக்க வேண்டும், தனி உறை வேண்டுமா என்று திரையில் தோன்றும்.
• கோப்புகள் உள்ள பகுதியில் சேமிக்க வேண்டுமென்றாலும் குறிப்பிட்ட கோப்புப் பகுதியை இயக்கி அதனுடன் சேமித்துக கொள்ளலாம்.
• தனியாக ஒரு உறையை உருவாக்கியும் சேமித்துக் கொள்ளலாம்.
• திரையின் முகப்புப் பகுதியில் உறையை உருவாக்கி வைத்துக் கொண்டோம் என்றால் விரலி மூலம் நாம் சேமித்த செய்திகள் பாடல்கள், எழுத்துக் கோப்புகளை உடனடியாக இயக்கி பயன்படுத்திக் கொள்ளலாம்.
• இதுவே விரலியில் உள்ளனவற்றை கணினியில் சேமிக்கும் முறையாகும்.

பாடநூல் வினாக்கள்

பலவுள் தெரிக

Question 1.
கீழ்க்காணும் மூன்று தொடர்களுள்
அ) இருந்த இடத்திலிருந்தே பயணச்சீட்டு எடுப்பதை எளிதாக்கிய மிகப் பெரிய இந்திய நிறுவனம் இந்தியத் தொடர்வண்டி உணவு வழங்கல் மற்றும் சுற்றுலாக் கழகம் ஆகும்.
ஆ) வங்கி அட்டை இல்லை என்றால் அலைபேசி எண், வங்கிக் கணக்கு எண் ஆகியவற்றைக் கொண்டு பணம் செலுத்துதல் இயலாது.
இ) திறன் அட்டைகள் என்பவை குடும்ப அட்டைகளுக்கு மாற்றாக வழங்கப்பட்டவைகும்.
i) அ, ஆ ஆகியன சரி; இ தவறு
ii) அ, இ ஆகியன சரி; ஆ தவறு
iii) அதவறு; ஆ, இ ஆகியன சரி
iv) மூன்றும் சரி
Asnwer:
ii) அ, இ ஆகியன சரி; ஆ தவறு

Question 2.
தமிழ்நாடு அரசு கிராமப்புற மாணவர்களுக்கு நடத்தும் திறனாய்வுத் தேர்வு எது?
அ) தேசியத் திறனாய்வுத் தேர்வு
ஆ) ஊரகத் திறனாய்வுத் தேர்வு
இ) தேசியத் திறனாய்வுத் தேர்வ
ஈ) மூன்றும் சரி
Asnwer:
ஆ) ஊரகத் திறனாய்வுத் தேர்வு

குறுவினா

Question 1.
இணைய வழியில் இயங்கும் மின்னணு இயந்திரங்கள் எவையேனும் ஐந்தினைக் குறிப்பிடுக.
Answer:
இணையவழியில் இயங்கும் மின்னணு இயந்திரங்கள்

1. தொலைநகல் இயந்திரம் (Fax)
2. தானியக்கப் பண இயந்திரம் (Automated Teller Machine)
3. அட்டை பயன்படுத்துதல் இயந்திரம் (Swiping Machione)
4. தமிழக அரசின் நியாய விலைக் கடை திறனட்டைக் கருவி (TNePDS)
5. இந்தியத் தொடர்வண்டி உணவு வழங்கல் மற்றும் சுற்றுலாக் கழக இணைய வழி பதிவு (Indian Railway Catering and Tourism Corporation)

சிறுவினா

Question 1.
பள்ளி மாணவர்களுக்கான தமிழக அரசின் இணையவழிச் சேவைகளை எழுதுக.
Answer:

• தமிழக அரசு ஆண்டு தோறும் பல கல்வி உதவி தொகை தேர்வுகளை நடத்துகின்றன.
• 8ம் வகுப்பு மாணவர்களுக்கு – தேசியத்திறனாய்வு மற்றும் கல்வி உதவித் தொகைத் தேர்வு (NMMS)
• 9ம் வகுப்பு கிராம பள்ளி மாணவர்களுக்கு – ஊரகத் திறனாய்வுத் தேர்வு (TRUST)
• 10ம் வகுப்பு மாணவர்களுக்கு – தேசியத்திறனாய்வு தேர்வு (NTSE) நடத்தப்படுகின்றது. அவற்றில் கலந்து கொள்ள விரும்பும் மாணவர்கள் தாங்கள் படிக்கும் பள்ளிகளிலேயே இணையத்தின் சேவையைப் பெறலாம் ஹ
• 10 மற்றும் 12 ம் வகுப்பு முடித்த மாணவர்களுக்கு, அரசின் வேலைவாய்ப்பு அலுவலகத்தில் செய்யப்பட வேண்டிய பதிவு, ஆண்டுதோறும் அவர்கள் படித்த பள்ளிகளிலேயே இணையத்தின் வழியாகச் செய்யப்பட்டு வருகிறது.
  அரசின் விலையில்லா மிதிவண்டி, மடிக்கணினி ஆகியவற்றைப் பெற
• மாணவர்களின் விவரங்கள் இணையத்தின் மூலம் பதிவு செய்யப்பட்டு வருகின்றன.

நெடுவினா

Question 1.
அன்றாட வாழ்வில் நீங்கள் பயன்படுத்தும் இரண்டு இணையவழிச் சேவைகள் பற்றி விரிவாகத் தொகுத்து எழுதுக.
Answer:
தற்காலத்தில் பேருந்து முன்பதிவு, விமான முன்பதிவு தங்கும் விடுதிகள் முன்பதிவு ஆகியவற்றை இணையம் மூலமாக மேற்கொள்ளப் பலமுகமைகள் உள்ளன. இது பலருக்கு வேலைவாய்ப்பையும் தருகிறது. பெரு நகரங்களில் திரைப்படங்களுக்கு இருக்கைகள் முன்பதிவு செய்வதுகூட இணையம் மூலம் நடைபெறுகின்றது. அரசுக்குச் செலுத்த வேண்டிய சொத்துவரி, தண்ணீர் வரி, ஆகியன இணைய வழியில் செலுத்தப்படுகின்றன. இச்சேவைகளில் ஒன்று பயணச்சீட்டு வழங்குவதையும் சுற்றுலாவுக்கு ஏற்பாடு செய்வதையும் பயனுள்ள வகையில் செய்து வருகிறது. இந்தியத் தொடர்வண்டி உணவு வழங்கல் மற்றும் சுற்றுலாக்கழகம். மற்றொன்று தானியக்கப் பண இயந்திரம்.

இந்தியத் தொடர்வண்டி உணவு வழங்கல் மற்றும் சுற்றுலாக் கழக இணைய வழிப் பதிவு (IRCTC – INDIAN RAILWAY CATERING AND TOURISM CORPORATION) :
மக்கள் தொகை மிகுந்த இந்தியா போன்ற நாடுகளில் வரிசையில் நிற்பது நேரவிரயம். இதனைக் குறைப்பதுடன் இருந்த இடத்திலிருந்தே பயணச் சீட்டு எடுப்பதை எளிதாக்கிய மிகப்பெரிய அமைப்பு இந்நிறுவனம் ஆகும். பயணம் செய்ய வேண்டிய நாளில் ஊர்களுக்குச் செல்லும் தொடர்வண்டிகளையும் அவற்றின் நேரங்களையும் பயணம் செய்ய விரும்பும் பெட்டி வகைகளையும் அதற்குரிய தொகையையும் காண்பிக்கிறது. வங்கி அட்டைகளின் உதவியுடன் தெகையைச் செலுத்தி முன்பதிவு செய்து கொள்ளலாம். மின்னஞ்சலில் பயணச்சீட்டு வந்து விடுகிறது. நமது அலைபேசிக்குக் குறுஞ்செய்தியும் வந்து விடுகிறது. 2002 ஆம் ஆண்டு இந்த வசதி அறிமுகப்படுத்தப்பட்டது. தற்போது ஒரு நிமிடத்திற்கு 1500 பயணச் சீட்டுகள் பதிவு செய்யவும் ஒரே நேரத்தில் மூன்று இலட்சம் பயனர்கள் இணைய வழிச் சேவையைப் பயன்படுத்தவும் வழிவகை செய்யப்பட்டுள்ளது.

தானியக்கப் பண இயந்திரம் (Automated Teller Machine) :
இங்கிலாந்தைச் சேர்ந்த பொறியாளரான ஜான் ஷெப்பர்டு பாரன் (John Sheperd Barron) என்பவர் தலைமையிலான குழுவொன்று பார்க்லேஸ் வங்கிக்காக இலண்டனில் 1967 ஜுன் 27 இல் தானியக்கப் பண இயந்திரத்தை நிறுவியது.

வங்கியில் வழங்கப்பட்ட காசோலையைக் கொண்டு தான் அப்போது பணம் எடுக்கப்பட்டது. அந்தக் காசோலையில் உள்ள குறியீடுகளை இயந்திரம் படித்துப் புரிந்து கொண்டு பணத்தைத் தள்ளும். அதற்குப்பின் வாடிக்கையாளரின் ஆறிலக்கக் கடவுச்சொல் (Password) தருமாறு மேம்படுத்தப்பட்டது. வங்கிகளின் அட்டைகளில் தனிப்பட்ட அடையாள எண்ணை உருவாக்கித் தானியக்கப் பண இயந்திரத்தில் பயன்படுத்தத் தொடங்கினர்.

கூடுதல் வினாக்கள்

பலவுள் தெரிக

Question 1.
முதன்முதலில் ஒளிப்படியை எடுத்தவர் …………………
அ) அலெக்சாண்டர் பெயின்
ஆ) கிரகாம்பெல்
இ) செஸ்டர் கார்ல்சன்
ஈ) சாமுவேல் மோர்சு
Answer:
இ) செஸ்டர் கார்ல்சன்

Question 2.
கணினி மூலம் தொலைநகல் எடுக்கும் தொழில்நுட்பத்தைக் கண்டறிந்தவர் …………
அ) ஹாங்க் மாக்னஸ்கி
ஆ) ஈஸ்ட்ம ன்
இ) தாமஸ் ஆல்வா எடிசன்
ஈ) சென்கின்சு
Answer:
அ) ஹாங்க் மாக்னஸ்கி

Question 3.
தானியக்கப் பண இயந்திரத்தை நிறுவியவர் ……..
அ) செஸ்டர் கார்ல்சன்
ஆ) ஸ்டீபன் ஹாக்கின்ஸ்
இ) ஸ்டீவ் ஜாப்ஸ்
ஈ) ஜான் ஷெப்பர்டு பாரன்
Answer:
ஈ) ஜான் ஷெப்பர்டு பாரன்

Question 4.
பொருந்தாத இணையைத் தேர்ந்தெடு.
அ) நியாய விலைக் கடை – திறனட்டைக் கருவி
ஆ) வருகைப் பதிவு – ஆளறி சோதனைக் கருவி
இ) பொருள் வாங்க – கட்டை தேய்ப்பி இயந்திரம்
ஈ) போக்குவரத்து முன்பதிவு – எழுதுபொருள்கள்
Answer:
ஈ) போக்குவரத்து முன்பதிவு – எழுதுபொருள்கள்

Question 5.
பொருந்தாத இணையைத் தேர்ந்தெடு.
அ) டிம் பெர்னெர்ஸ் லீ – வையக விரிவு வலை
ஆ) ஆட்ரியன் ஆஷ்ஃபீல்டு – கடவுச்சொல் அட்டை
இ) மைக்கேல் ஆல்ட்ரிச் – இணைய வணிகம்
ஈ) ஜியோவான்னி காசில்லி – சீரோகிராபி
Answer:
ஈ) ஜியோவான்னி காசில்லி – சீரோகிராபி

Question 6.
தொலைநகல் சேவை முதன்முதலில் எந்த இரு நகரங்களுக்கு இடையில் அறிமுகமானது?
அ) பெர்லின் – ஆம்ஸ்டர்டாம்
ஆ) ஸ்டாக்ஹோம் – வியன்னா
இ) பாரிஸ் – லியான்
ஈ) இலண்டன் – பாரிஸ்
Answer:
இ) பாரிஸ் – லியான்

நிரப்புக

Question 1.
குறுஞ்செய்தியின் வருகைக்குப் பின் தந்தி விடைபெற்றுக்கொண்டது. (சரியா, தவறா)
Answer:
சரி

Question 2.
தானியக்கப் பண இயந்திரத்தை முதன்முதலில் நிறுவிய நாடு எது? எந்த ஆண்டு நிறுவியது?
Answer:
இலண்டன் நகரில் (இங்கிலாந்து) 1967 ஜுன் 27ல்.

Question 3.
இணைய வணிகத்தை கண்டுபிடித்தவர் யார்? எந்த ஆண்டு கண்டுபிடிக்கப்பட்டது?
Answer:
மைக்கேல் ஆல்ட்ரிச், 1979.

குறுவினா

Question 1.
ஒளிப்படி இயந்திரம் – குறிப்பு எழுதுக.
Answer:

• நியூயார்க்கைச் சேர்ந்த செஸ்டர் கார்ல்சன் கந்தகம் தடவிய துத்தநாகத் தட்டைக் கொண்டு 1938-ல் உலகின் முதல் ஒளிப்படியை எடுத்தார்.
• சீரோகிராஃபி என்னும் உலர் எழுத்து முறை இயந்திரம் இவரால் உலகிற்கு அறிமுகப்படுத்தப் பட்டது.
• இதுவே ஜெராக்ஸ் என்ற பெயரில் நிலைத்துவிட்டது.

சிறுவினா

Question 1.
தானியக்கப் பண இயந்திரம் – குறிப்புத் தருக.
Answer:
இங்கிலாந்தைச் சேர்ந்த பொறியாளரான ஜான் ஷெப்பர்டு பாரன் (John Sheperd Barron) என்பவர் தலைமையிலான குழுவொன்று பார்க்லேஸ் வங்கிக்காக இலண்டனில் 1967 ஜுன் 27 இல் தானியக்கப் பண இயந்திரத்தை நிறுவியது.

வங்கியில் வழங்கப்பட்ட காசோலையைக் கொண்டு தான் அப்போது பணம் எடுக்கப்பட்டது. அந்தக் காசோலையில் உள்ள குறியீடுகளை இயந்திரம் படித்துப் புரிந்து கொண்டு பணத்தைத் தள்ளும். அதற்குப்பின் வாடிக்கையாளரின் ஆறிலக்கக் கடவுச்சொல் (Password) தருமாறு மேம்படுத்தப்பட்டது.

வங்கிகளின் அட்டைகளில் தனிப்பட்ட அடையாள எண்ணை உருவாக்கித் தானியக்கப் பண இயந்திரத்தில் பயன்படுத்தத் தொடங்கினர்.

Question 2.
இந்தியத் தொடர் வண்டி இணைய வழிப் பதிவு – விளக்குக.
Answer:
மக்கள் தொகை மிகுந்த இந்தியா போன்ற நாடுகளில் வரிசையில் நிற்பது நேரவிரயம். இதனைக் குறைப்பதுடன் இருந்த இடத்திலிருந்தே பயணச் சீட்டு எடுப்பதை எளிதாக்கிய மிகப்பெரிய அமைப்பு இந்நிறுவனம் ஆகும்.

பயணம் செய்ய வேண்டிய நாளில் ஊர்களுக்குச் செல்லும் தொடர்வண்டிகளையும் அவற்றின் நேரங்களையும் பயணம் செய்ய விரும்பும் பெட்டி வகைகளையும் அதற்குரிய தொகையையும் காண்பிக்கிறது.

வங்கி அட்டைகளின் உதவியுடன் தொகையைச் செலுத்தி முன்பதிவு செய்து கொள்ளலாம்.

மின்னஞ்சலில் பயணச்சீட்டு வந்து விடுகிறது. நமது அலைபேசிக்குக் குறுஞ்செய்தியும் வந்து விடுகிறது.

2002 ஆம் ஆண்டு இந்த வசதி அறிமுகப்படுத்தப்பட்டது. தற்போது ஒரு நிமிடத்திற்கு 1500 பயணச் சீட்டுகள் பதிவு செய்யவும் ஒரே நேரத்தில் மூன்று இலட்சம் பயனர்கள் இணைய வழிச் சேவையைப் பயன்படுத்தவும் வழிவகை செய்யப்பட்டுள்ளது.

Students can download 11th Business Maths Chapter 1 Matrices and Determinants Ex 1.3 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 1 Matrices and Determinants Ex 1.3

Samacheer Kalvi 11th Business Maths Matrices and Determinants Ex 1.3 Text Book Back Questions and Answers

Question 1.
Solve by matrix inversion method: 2x + 3y – 5 = 0; x – 2y + 1 = 0.
Solution:
2x + 3y = 5
x – 2y = -1
The given system can be written as
\(\left[\begin{array}{rr}
2 & 3 \\
1 & -2
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{r}
5 \\
-1
\end{array}\right]\)
AX = B
where A = \(\left[\begin{array}{rr}
2 & 3 \\
1 & -2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{r}
5 \\
-1
\end{array}\right]\)
|A| = \(\left|\begin{array}{rr}
2 & 3 \\
1 & -2
\end{array}\right|\) = -4 – 3 = -7 ≠ 0
∴ A^-1 Exists.

∴ x = 1, y = 1

Question 2.
Solve by matrix inversion method:
(i) 3x – y + 2z = 13; 2x + y – z = 3; x + 3y – 5z = -8
(ii) x – y + 2z = 3; 2x + z = 1; 3x + 2y + z = 4
(iii) 2x – z = 0; 5x + y = 4; y + 3z = 5
Solution:
(i) The given system can be written as
\(\left[\begin{array}{rrr}
3 & -1 & 2 \\
2 & 1 & -1 \\
1 & 3 & -5
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{r}
13 \\
3 \\
-8
\end{array}\right]\)
AX = B
Where A = \(\left[\begin{array}{rrr}
3 & -1 & 2 \\
2 & 1 & -1 \\
1 & 3 & -5
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{r}
13 \\
3 \\
-8
\end{array}\right]\)
|A| = \(\left|\begin{array}{rrr}
3 & -1 & 2 \\
2 & 1 & -1 \\
1 & 3 & -5
\end{array}\right|\)
= 3(-5 + 3) – (-1) (-10 + 1) + 2 (6 – 1)
= 3(-2) + 1(-9) + 2(5)
= -6 – 9 + 10
= -5




\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{r}
3 \\
-2 \\
1
\end{array}\right]\)
∴ x = 3, y = -2, z = 1.

(ii) The given system can be written as
\(\left[\begin{array}{rrr}
1 & -1 & 2 \\
2 & 0 & 1 \\
3 & 2 & 1
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
3 \\
1 \\
4
\end{array}\right]\)
AX = B
where A = \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
2 & 0 & 1 \\
3 & 2 & 1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
3 \\
1 \\
4
\end{array}\right]\)
|A| = \(\left|\begin{array}{rrr}
1 & -1 & 2 \\
2 & 0 & 1 \\
3 & 2 & 1
\end{array}\right|\)
= 1(0 – 2) – (-1)(2 – 3) + 2(4 – 0)
= -2 – (-1)(-1) + 2(4)
= -2 – 1 + 8
= 5



\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{r}
-1 \\
2 \\
3
\end{array}\right]\)
x = -1, y = 2, z = 3.

(iii) The given system can be written as
\(\left[\begin{array}{rrr}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
0 \\
4 \\
5
\end{array}\right]\)
AX = B
Where A = \(\left[\begin{array}{rrr}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
0 \\
4 \\
5
\end{array}\right]\)
|A| = \(\left|\begin{array}{rrr}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right|\)
= 2(3 – 0) – 0(15 – 0) – 1(5 – 0)
= 2(3) – 0(15) – 1(5)
= 6 – 0 – 5
= 1


∴ x = 1, y = -1, z = 2.

Question 3.
A salesperson Ravi has the following record of sales for the month of January, February, and March 2009 for three products A, B, and C. He has been paid a commission at a fixed rate per unit but at varying rates for products A, B and C.

Find the rate of commission payable on A, B and C per unit sold using matrix inversion method.
Solution:
Let x, y and z be the rate of commission for the three products A, B and C respectively.
9x + 10y + 2z = 800
15x + 5y + 4z = 900
6x + 10y + 3z = 850
The given system can be written as
\(\left[\begin{array}{rrr}
9 & 10 & 2 \\
15 & 5 & 4 \\
6 & 10 & 3
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
800 \\
900 \\
850
\end{array}\right]\)
AX = B
Where A = \(\left[\begin{array}{rrr}
9 & 10 & 2 \\
15 & 5 & 4 \\
6 & 10 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
800 \\
900 \\
850
\end{array}\right]\)
Now, |A| = \(\left|\begin{array}{rrr}
9 & 10 & 2 \\
15 & 5 & 4 \\
6 & 10 & 3
\end{array}\right|\)
= \(9\left|\begin{array}{rr}
5 & 4 \\
10 & 3
\end{array}\right|-10\left|\begin{array}{rr}
15 & 4 \\
6 & 3
\end{array}\right|+2\left|\begin{array}{rr}
15 & 5 \\
6 & 10
\end{array}\right|\)
= 9[15 – 40] – 10(45 – 24) + 2(150 – 30)
= 9[-25] – 10[21] + 2[120]
= -225 – 210 + 240
= -195


\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{r}
17.948 \\
43.0769 \\
103.846
\end{array}\right]\)
\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{r}
17.95 \\
43.08 \\
103.85
\end{array}\right]\)
∴ x = 17.95, y = 43.08, z = 103.85
The rate of commission of A, B and C are 17.95, 43.08 and 103.85 respectively.

Question 4.
The prices of three commodities A, B, and C are ₹ x, y, and z per unit respectively. P purchases 4 units of C and sells 3 units of A and 5 units of B. Q purchases 3 units of B and sells 2 units of A and 1 unit of C. R purchases 1 unit of A and sells 4 units of B and 6 units of C. In the process P, Q and R earn ₹ 6,000, ₹ 5,000 and ₹ 13,000 respectively. By using the matrix inversion method, find the prices per unit of A, B, and C.
Solution:
Take selling the units js positive earning and buying the units is negative earning.
Given that
3x + 5y – 4z = 6000
2x – 3y + z = 5000
-1x + 4y + 6z = 13000

The given statement can be written as
\(\left(\begin{array}{rrr}
3 & 5 & -4 \\
2 & -3 & 1 \\
-1 & 4 & 6
\end{array}\right)\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)=\left(\begin{array}{r}
6000 \\
5000 \\
13000
\end{array}\right)\)
AX = B
Where A = \(\left(\begin{array}{rrr}
3 & 5 & -4 \\
2 & -3 & 1 \\
-1 & 4 & 6
\end{array}\right)\), X = \(\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)\) and B = \(\left(\begin{array}{r}
6000 \\
5000 \\
13000
\end{array}\right)\)
X = A^-1B
|A| = \(\left|\begin{array}{rrr}
3 & 5 & -4 \\
2 & -3 & 1 \\
-1 & 4 & 6
\end{array}\right|\)
= 3(-18 – 4) – 5(12 + 1) – 4(8 – 3)
= 3(-22) – 5(13) – 4(5)
= -66 – 65 – 20
= -151


\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
3000 \\
1000 \\
2000
\end{array}\right]\)
The prices per unit of A, B and C are ₹ 3000, ₹ 1000 and ₹ 2000.

Question 5.
The sum of three numbers is 20. If we multiply the first by 2 and add the second number and subtract the third we get 23. If we multiply the first by 3 and add second and third to it, we get 46. By using the matrix inversion method find the numbers.
Solution:
Let the three numbers be x, y, and z.
x + y + z = 20
2x + y – z = 23
3x + y + z = 46
The given system can be written as




The numbers are 13, 2, and 5.

Question 6.
Weekly expenditure in an office for three weeks is given as follows. Assuming that the salary in all three weeks of different categories of staff did not vary, calculate the salary for each type of staff, using the matrix inversion method.

Solution:
Let ₹ x, ₹ y, ₹ z be the salary for each type of staff A, B and C.
4x + 2y + 3z = 4900
3x + 3y + 2z = 4500
4x + 3y + 4z = 5800
The given system can be written as
\(\left[\begin{array}{lll}
4 & 2 & 3 \\
3 & 3 & 2 \\
4 & 3 & 4
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
4900 \\
4500 \\
5800
\end{array}\right]\)
AX = B
where A = \(\left[\begin{array}{lll}
4 & 2 & 3 \\
3 & 3 & 2 \\
4 & 3 & 4
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{c}
4900 \\
4500 \\
5800
\end{array}\right]\)
|A| = \(\left|\begin{array}{lll}
4 & 2 & 3 \\
3 & 3 & 2 \\
4 & 3 & 4
\end{array}\right|\)
= 4(12 – 6) – 2(12 – 8) + 3(9 – 12)
= 4(6) – 2(4) + 3(-3)
= 24 – 8 – 9
= 7




\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
700 \\
600 \\
300
\end{array}\right]\)
∴ Salary for each type of staff A, B and C are ₹ 700, ₹ 600 and ₹ 300.

Students can Download 9th Tamil Chapter 3.5 திருக்குறள் Questions and Answers, Summary, Notes, Samacheer Kalvi 9th Tamil Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Tamil Solutions Chapter 3.5 திருக்குறள்

கற்பவை கற்றபின்

Question 1.
படத்திற்கேற்ற குறளைத் தேர்வு செய்க.

அ) நாணாமை நாடாமை நாரின்மை யாதொன்றும்
பேணாமை பேதை தொழில்.
ஆ) விழைதகையான் வேண்டி இருப்பர் கெழுதகையாற்
கேளாது நட்டார் செயின்
இ) செல்வத்துள் செல்வம் செவிச்செல்வம் அச்செல்வம்
செல்வத்துள் எல்லாந் தலை.
Answer:
இ) செல்வத்துள் செல்வம் செவிச்செல்வம் அச்செல்வம்
செல்வத்துள் எல்லாந் தலை.

Question 2.
பாடலின் பொருளுக்குப் பொருத்தமான திருக்குறளைக் கண்டறிக.
பாடல்
ஆண்டில் இளையவனென்று அந்தோ அகந்தையினால்
ஈண்டிங்கு இகழ்ந்தென்னை ஏளனம்செய் – மாண்பற்ற
காரிருள்போல் உள்ளத்தான் காந்திமதி நாதனைப்
பாரதி சின்னப் பயல்.
(1893ல் பாரதியாரின் பதினோராவது வயதில் எட்டையபுரம் மன்னர் சமஸ்தானப் புலவர்கள் அவையில், அவரது கவித்திறனைப் புகழ்ந்து ‘பாரதி’ என்ற பட்டத்தைச் சூட்டினார்.)

குறள்
அ) செவியிற் சுவையுணரா வாயுணர்வின் மாக்கள்
அவியினும் வாழினும் என்.
ஆ) மிகுதியான் மிக்கவை செய்தாரைத் தாம்தம்
தகுதியான் வென்று விடல்.
இ) குணம்நாடிக் குற்றமும் நாடி அவற்றுள்
மிகைநாடி மிக்க கொளல்.
Answer:
ஆ) மிகுதியான் மிக்கவை செய்தாரைத் தாம்தம்
தகுதியான் வென்று விடல்.

குறளுக்குப் பொருள்:
நமக்கு நல்ல வசதியும் வாய்ப்பும் இருக்கிறது என்றெண்ணி “இவர்க்கு இத்தீங்கை செய்தால் எவர் நம்மை என்ன செய்ய முடியும்?” என்ற இறுமாப்புக் கொண்டு தீங்கிழைத்தவர்களையும் பொறுமைப் பண்பால் வெற்றி காண வேண்டும். (பொறையுடைமை : 8 வது குறள்)

Question 3.
பொருளுக்கேற்ற அடியைக் கண்டுபிடித்துப் பொருத்துக.
Answer:

Question 4.
தீரா இடும்பை தருவது எது?
அ) ஆராயாமை, ஐயப்படுதல்
ஆ) குணம், குற்றம்
இ) பெருமை, சிறுமை
ஈ) நாடாமை, பேணாமை
Answer:
அ) ஆராயாமை, ஐயப்படுதல்

குறள்: தேரான் தெளிவும் தெளிந்தான்கண் ஐயுறவும்
தீரா இடும்பை தரும்.

Question 5.
சொல்லுக்கான பொருளைத் தொடரில் அமைத்து எழுதுக.

Answer:
அ) நுணங்கிய கேள்வியர் – நுட்பமான கேள்வியறிவு உடையவர்.
முகிலன் நுட்பமான கேள்வியறிவு உடையவனாக இருந்தான். அதனால் பெரியோரிடத்துப் பணிவான சொற்களில் பேசுகிறான்.

ஆ) பேணாமை – பாதுகாக்காமை.
அப்பாவின் நூலைப் பாதுகாக்காமையால் இனியன் பழைய பேப்பர் வியாபாரியிடம் போட்டுவிட்டான்.

இ) செவிச் செல்வம் – கேட்பதால் பெறும் அறிவு.
அறிஞர்களின் அறிவுரைகளைக் கேட்பதால் பெறும் அறிவு தக்க சமயத்தில் பேச்சுப் போட்டியில் பேசுவதற்கு பயன்பட்டது.

ஈ) அறனல்ல செய்யாமை – அறம் அல்லாத செயல்களைச் செய்யாதிருத்தல்.
மலரவன் இளமையிலிருந்தே அறம் அல்லாத செயல்களைச் செய்யாதிருந்ததனால் தான், அமைதிக்கான விருது கிடைத்தது.

குறுவினா

Question 1.
நிலம் போல யாரிடம் பொறுமை காக்கவேண்டும்?
Answer:
தன்னைத் தோண்டுபவரைத் தாங்கும் நிலம்போலத் தன்னை இகழ்பவரிடத்தும் பொறுமை காக்க வேண்டும்.

Question 2.
தீயவை தீய பயத்தலால் தீயவை
தீயினும் அஞ்சப் படும் – இக்குறட்பாவின் கருத்தை விளக்குக.
Answer:
தான் இன்பம் அடைய வேண்டுமென எண்ணி இன்னொருவருக்குச் செய்யும் தீய செயல்களே பின்னர் அந்த இன்பத்தை நீக்கும். தீச்செயலை எவர் செய்தாரோ அவருக்கே துன்பத்தைத் தரும். தீ தொட்டால் தான் சுடும். தீயசெயல்கள் நினைத்த அளவிலே சுட்டெரிக்கும் ஆற்றல் உள்ளன. அதனால் தான் ‘தீயினும் அஞ்சப்படும்’ என்றார்.

Question 3.
ஒற்றொற்றித் தந்த பொருளையும் மற்றுமோர்
ஒற்றினால் ஒற்றிக் கொளல் – இக்குறட்பாவில் அமைந்துள்ள நயங்களை எழுதுக.
Answer:
ஒற்றன் ஒருவன் மறைந்திருந்து கேட்டுத் தெரிந்த செய்தியை மற்றோர் ஒற்றனை அனுப்பி அறிந்து வரச் செய்ய வேண்டும் நம்ப வேண்டும் மன்னன், அவற்றை ஒப்புநோக்கிய பின்பே, அதனை உண்மையென நம்பவேண்டும்.

Question 4.
கனவிலும் இனிக்காதது எவர் நட்பு?
Answer:
சொல் ஒன்று, செயல் வேறு என ஒன்றுக்கொன்று தொடர்பில்லாமல் நடந்து கொள்பவரின் நட்பு கனவிலும் துன்பம் தருவதாகும்.

கதைக்குப் பொருத்தமான குறளைத் தேர்வு செய்து காரணத்தை எழுதுக.
மௌனவிரதம் என்னும் தலைப்பில் நான்கு நண்பர்கள் ஒரு சொற்பொழிவைக் கேட்டனர். தாங்களும் ஒரு வாரத்துக்கு மௌனவிரதம் இருப்பதாகத் தீர்மானம் செய்தனர். மௌனவிரதம் ஆரம்பமாகி விட்டது! கொஞ்ச நேரம் போனதும் ஒருவன் சொன்னான். “எங்கள் வீட்டு அடுப்பை அணைத்துவிட்டேனா தெரியவில்லையே!”

பக்கத்திலிருந்தவன் “அடப்பாவி! பேசிட்டியே!” என்றான். உடனே மூன்றாவது ஆள், “நீ மட்டும் என்ன? நீயும்தான் பேசிவிட்டாய்!” என்றான். நான்காவது ஆள், “நல்லவேளை! நான் மட்டும் பேசவில்லை !” என்றான். இப்படியாக அவர்களின் மௌனவிரதம் முடிந்துபோனது.

1. மறந்தும் பிறன்கேடு சூழற்க சூழின்
அறஞ்சூழும் சூழ்ந்தவன் கேடு.
2. திறனல்ல தற்பிறர் செய்யினும் நோநொந்து
அறனல்ல செய்யாமை நன்று.
3. ஓதி உணர்ந்தும் பிறர்க்குரைத்தும் தானடங்காப்
பேதையின் பேதையார் இல்.
Answer:
கதைக்குப் பொருத்தமான குறள்

3. ஓதி உணர்ந்தும் பிறர்க்குரைத்தும் தானடங்காப்
பேதையின் பேதையார் இல்.
விளக்கம்:
கற்க வேண்டிய அறநூல்களைக் கற்றறிந்தும் அதன் உண்மைகளை மற்றவர்களுக்கு எடுத்துக் கூறியும் வாழ்கின்ற ஒருவன், தான் கற்றறிந்த ஒழுக்க நெறியில் வாழத் தவறினால் அவனைப் போன்ற அறிவிலிகள் உலகில் இல்லை
எனவே “சொல்வதைப் போல செய்ய வேண்டும் செய்வதையே சொல்ல வேண்டும்”.

திருக்குறள் பற்றிய சில ஆராய்ச்சி செய்திகள்

திருக்குறள் முதன்முதலில் அச்சிடப்பட்ட ஆண்டு – 1812
திருக்குறள் அகரத்தில் தொடங்கி னகரத்தில் முடிகிறது.
திருக்குறளில் இடம்பெறும் இருமலர்கள் – அனிச்சம், குவளை
திருக்குறளில் இடம்பெறும் ஒரே பழம் – நெருஞ்சிப்பழம்
திருக்குறளில் இடம்பெறும் ஒரே விதை – குன்றிமணி
திருக்குறளில் இருமுறை வரும் ஒரே அதிகாரம் – குறிப்பறிதல்
திருக்குறளில் இடம்பெற்ற இரண்டு மரங்கள் – பனை, மூங்கில்
திருக்குறள் மூலத்தை முதன் முதலில் அச்சிட்டவர் – தஞ்சை ஞானப்பிரகாசர்
திருக்குறளுக்கு முதன் முதலில் உரை எழுதியவர் – மணக்குடவர்
திருக்குறளை ஆங்கிலத்தில் மொழிபெயர்த்தவர் – ஜி.யு.போப்
திருக்குறளில் கோடி என்ற சொல் ஏழு இடங்களில் இடம்பெற்றுள்ளது.
ஏழு என்ற சொல் எட்டுக் குறட்பாக்களில் எடுத்தாளப்பட்டுள்ளது.
திருக்குறள் இதுவரை நூற்றுக்கும் மேற்பட்ட மொழிகளில் வெளிவந்துள்ளது.

கலைச்சொல் அறிவோம்

அகழாய்வு – ……………………
நடுகல் – ……………………
புடைப்புச் சிற்பம் – ……………………
கல்வெட்டியல் – ……………………
பொறிப்பு – ……………………
Answer:
அகழாய்வு – Excavation
நடுகல் – Hero Stone
புடைப்புச் சிற்பம் – Embossed sculpture
கல்வெட்டியல் – Epigraphy
பண்பாட்டுக் குறியீடு – Cultural Symbol
பொறிப்பு – Inscription

Students can Download 6th Tamil Chapter 1.1 இன்பத்தமிழ் Questions and Answers, Summary, Notes, Samacheer Kalvi 6th Tamil Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Tamil Solutions Chapter 1.1 இன்பத்தமிழ்

கற்பவை கற்றபின்

Question 1.
இன்பத்தமிழ் என்ற பாடலை இனிய ஓசையுடன் பாடுக.
Answer:
கீழ்க்காணும் பாடலைக் குரலேற்ற இறக்கத்துடன் இனிமையாகப் பாடச் செய்தல்.
தமிழுக்கும் அமுதென்றுபேர்! – அந்தத்
தமிழ் இன்பத் தமிழ் எங்கள் உயிருக்கு நேர்!
தமிழுக்கு நிலவென்று பேர்! – இன்பத்
தமிழ் எங்கள் சமூகத்தின் விளைவுக்கு நீர்!
தமிழுக்கு மணமென்று பேர்! – இன்பத் தமிழ்
எங்கள் வாழ்வுக்கு நிருமித்த ஊர்!
தமிழ் எங்கள் இளமைக்குப் பால்! – இன்பத்
தமிழ் நல்ல புகழ்மிக்க புலவர்க்கு வேல்!
தமிழ் எங்கள் உயர்வுக்கு வான்! – இன்பத்
தமிழ் எங்கள் அசதிக்குச் சுடர்தந்த தேன்!
தமிழ் எங்கள் அறிவுக்குத் தோள்! – இன்பத்
தமிழ் எங்கள் கவிதைக்கு வயிரத்தின் வாள் !

Question 2.
தமிழை அமுது, நிலவு, மணம் என்று பெயரிட்டு அழைப்பது பற்றி வகுப்பறையில் கலந்துரையாடுக.
Answer:
தமிழை அமுது, நிலவு, மணம் என்று பெயரிட்டு அழைப்பது ஏன் என்பது குறித்து
கலத்துரையாடுதல்.
மாணவன் 1 : வணக்கம் ! கவிஞர்கள் தமிழை அமுது, நிலவு, மணம் என்று அழைக்கிறார்கள். அதைப் பற்றி உனக்குத் தெரியுமா?

மாணவன் 2 : தெரியும். அமுதம் என்பது வானுலகில் வாழும் தேவர்கள் உண்ணும் உணவுப் பொருள் ஆகும். அது மிகவும் சுவை உடையது என்றும் அதனை உண்பதினால் தேவர்கள் சாகா வரம் பெற்றுள்ளார்கள் என்றும் ஒரு நம்பிக்கை உண்டு. நல்ல சுவையுள்ள உணவை நாம் உண்ணும்போது தேவாமிர்தமாக இனிக்கிறது என்றும் நாம் கூறுவோம். அதைப்போல் கவிஞர்களும் தமிழ் இனிமையானது என்ற பொருளிலும், இறவாநிலையில் உள்ளது என்ற பொருளிலும் தமிழை அமுது எனக் கூறுகிறார்கள்.

மாணவன் 3 : ஆமாம், ஆமாம் அதேபோல்தான் நிலவு என்று அழைப்பதற்கும் ஒரு காரணம் உண்டு. நிலவானது குளிர்ச்சி பொருந்தியது. அதுமட்டுமின்றி உலகின் இருளைப் போக்கி வெளிச்சத்தைத் தருகிறது. தமிழ் தண்மையானது குளிர்ச்சி) என்பதாலும் மக்களின் அறியாமை என்ற இருளைப் போக்கி ஒளியைத் தருவதாலும் தமிழை நிலவு என்று அழைக்கிறார்கள்.

மாணவன் 4 : சரியாகச் சொன்னாய். மணம் என்று கூறுவதற்கும் ஒரு காரணம். உண்டு. அது என்னவெனில் பூக்களின் மணம், காற்றில் கலந்து எல்லாவிடங்களிலும் பரவுகிறது. அதேபோல் நம் தமிழ்மொழியும் – மாநிலம் கடந்து, நாடு கடந்து ஏன் உலகமெங்கும் தன் நறுமணத்தைப் பரப்பியுள்ளது. எனவேதான் தமிழை மணம் என்ற பெயரிட்டு அழைத்துள்ளனர்.

Question 3.
தமிழுக்கு நீங்கள் சூட்ட விரும்பும் பெயர்களைப் பட்டியலிடுக.
Answer:
மாணவர்கள் தமிழுக்குச் சூட்டப்படும் பெயர்களை அறிந்து எழுதுதல்.
தேன்தமிழ், செந்தமிழ், இனிமைத் தமிழ், இளமைத் தமிழ், முத்தமிழ்…
முதல் பருவம்

Question 4.
தமிழ்க் கவிதைகள், பாடல்களைப் படித்து மகிழ்க.
Answer:
கீழ்க்காணும் பாடலைக் குரலேற்ற இரக்கத்துடன் இனிமையாகப் பாடச் செய்தல். தென்றலுக்கு நன்றி!
கழுகொடு நெடிய தென்னை
கமழ்கின்ற சந்தனங்கள்
சமைக்கின்ற பொதிகை அன்னை
உனைத் தந்தாள்; தமிழைத் தந்தாள்!
தமிழ் எனக் ககத்தும், தக்க
தென்றல் நீ புறத்தும் இன்பம்
அமைவுறச் செய்வதை நான்
கனவிலும் மறவேன் அன்றோ ?

மதிப்பீடு

சரியான விடையைத் தேர்ந்தெடுத்து எழுதுக.
Question 1.
ஏற்றத் தாழ்வற்ற …………….. அமைய வேண்டும்.
அ) சமூகம்
ஆ) நாடு
இ) வீடு
ஈ) தெரு
Answer:
(விடை: அ) சமூகம்)

Question 2.
நாள் முழுவதும் வேலை செய்து களைத்தவர்க்கு ………….. ஆக இருக்கும்.
அ) மகிழ்ச்சி
ஆ) கோபம்
இ) வருத்தம்
ஈ) அசதி
Answer:
(விடை : ஈ) அசதி)

Question 3.
நிலவு + என்று என்பதனைச் சேர்த்து எழுதக் கிடைக்கும் சொல் …………
அ) நிலயென்று
ஆ) நிலவென்று
இ) நிலவன்று
ஈ) நிலவுஎன்று
Answer:
(விடை: ஆ) நிலவென்று)

Question 4.
தமிழ் + எங்கள் என்பதனைச் சேர்த்து எழுதக் கிடைக்கும் சொல் …….
அ) தமிழங்கள்
ஆ) தமிழெங்கள்
இ) தமிழுங்கள்
ஈ) தமிழ் எங்கள்
Answer:
[விடை: ஆ) தமிழெங்கள்)

Question 5.
‘அமுதென்று’ என்னும் சொல்லைப் பிரித்து எழுதக் கிடைப்பது ……………
அ) அமுது + தென்று
ஆ) அமுது + என்று
இ) அமுது + ஒன்று
ஈ) அமு + தென்று
Answer:
(விடை: ஆ) அமுது + என்ற)

Question 6.
‘செம்பயிர்’ என்னும் சொல்லைப் பிரித்து எழுதக் கிடைப்பது ………….
அ) செம்மை + பயிர்
ஆ) செம் + பயிர்
இ) செமை + பயிர்
ஈ) செம்பு + பயிர்
Answer:
(விடை: அ) செம்மை + பயிர்)

இன்பத்தமிழ் பாடலின் கருத்துக்கு ஏற்றபடி பொருத்துக
அ) விளைவுக்கு – பால்
ஆ) அறிவுக்கு – வேல்
இ) இளமைக்கு – நீர்
ஈ) புலவர்க்கு – தோள்
விடை:
அ) விளைவுக்கு – நீர்
ஆ) வாழ்வுக்கு – ஊர்
இ) இளமைக்கு – பால்
ஈ) புலவர்க்கு – வேல்

ஒத்த ஓசையில் முடியும் (இயைபு) சொற்களை எடுத்து எழுதுக
(எ.கா.) பேர் –நேர்
விடை :
பேர் – நேர் அமுதென்று – நிலவென்று
பேர் – நீர் உயிருக்கு – விளைவுக்கு
பேர் – ஊர் இளமைக்கு – புலவர்க்கு
பால் – வேல் தமிழுக்கு – வாழ்வுக்கு
வான் – தேன் உயர்வுக்கு – அசதிக்கு
தோள்- வாள் அறிவுக்கு – கவிதைக்கு

குறுவினா 

Question 1.
பாரதிதாசன் தமிழுக்குச் சூட்டியுள்ள பெயர்கள் யாவை?
Answer:
அமுதம், நிலவு, மணம்.

Question 2.
நீங்கள் தமிழை எதனோடு ஒப்பிடுவீர்கள்?
Answer:
தேன், தங்கம், கரும்பு, சந்தனம், அமுதசுரபி, நவமணிகள் போன்றவற்றோடு தமிழை ஒப்பிடுவேன்.

சிறுவினா

Question 1.
இன்பத் தமிழ் – பாடலில் உங்களுக்குப் பிடித்த அடிகள் இரண்டனை எழுதுக.
Answer:
தமிழ் எங்கள் உயர்வுக்கு வான்! – இன்பத்
தமிழ் எங்கள் அசதிக்குச் சுடர்தந்த தேன்!

Question 2.
விளைவுக்கும் நீருக்கும் உள்ள தொடர்பு யாது?
Answer:
(விளைவு – விளைச்சல்)
(i) நீரின்றி வேளாண்தொழில் (விளைச்சல்) நிகழாது.
(ii) நீர் இவ்வுலகில் உள்ள அனைத்து உயிரினங்களுக்கும் உயிர் போன்றது.
(iii) நீரினால் விளையும் விளைச்சலினால் மக்கள் பயன் பெறுவர்.

சிந்தனை வினா

Question 1.
வேல் என்பது ஓர் ஆயுதம். தமிழ் ஏன் வேலுடன் ஒப்பிடப்படுகிறது?
Answer:
(i) வேல் கூர்மையான ஆயுதம் அதைப்போல தமிழ்மொழியிலுள்ள இலக்கியங்கள், பாடல்கள், கவிதைகள் கூர்மையான கருத்துகளைக் கொண்டு மக்களை நல்வழிப்படுத்துகிறது.
(ii) ஆகவே தமிழ், வேலுடன் ஒப்பிடப்படுகிறது. அதேபோல் கத்தியின் முனையைவிட பேனாவின் முனை கூர்மையானது என்ற பழமொழியும் இதனையே விளக்கும்.

கூடுதல் வினாக்கள்

பொருள் தருக :

வான் – வானம்
இணை – சமம்
சுடர் – ஒளி

எதிர்சொல் தருக:

இளமை × முதுமை
புகழ் × இகழ்
அசதி × சுறுசுறுப்பு
ஒளி × இருள்
இன்பம் × துன்பம்
அமுதம் × விடம்

வினாக்கள் :

Question 1.
பாரதிதாசனின் இயற்பெயர் யாது?
Answer:
பாரதிதாசனின் இயற்பெயர் சுப்புரத்தினம்

Question 2.
பாரதிதாசனின் பெற்றோர் யாவர்?
Answer:
பாரதிதாசனின் பெற்றோர்
தந்தையார் – கனகசபை
தாயார் – இலக்குமி.

Question 3.
பாரதிதாசனார் புரட்சிக்கவி ‘ என்று போற்றப்படக் காரணம் யாது?
Answer:
பாரதிதாசனார் தம் கவிதைகளில் பெண்கல்வி, கைம்பெண் மறுமணம், பொதுவுடைமை, பகுத்தறிவு ஆகியவை குறித்த புரட்சிகரமான கருத்துகளைப் பாடியுள்ளமையால் ‘புரட்சிக்கவி’ என்று போற்றப்படுகிறார்.

Question 4.
பாரதிதாசனாரின் சிறப்புப் பெயர்கள் யாவை?
Answer:
பாரதிதாசனாரின் சிறப்புப் பெயர்கள் : புரட்சிக் கவி, பாவேந்தர்.

Question 5.
பாரதிதாசன் பற்றி சிறுகுறிப்பு எழுதுக.
Answer:
பெயர் : பாரதிதாசன்
இயற்பெயர் : சுப்புரத்தினம்
பிறந்த ஊர் : புதுச்சேரி
பெற்றோர் : கனகசபை – இலக்குமி அம்மையார்
பணி : தமிழாசிரியர்
சிறப்புப்பெயர் : பாவேந்தர்,புரட்சிக் கவிஞர்
காலம் : 29-04-1891 முதல் 21-04-1964 வரை
இயற்றிய நூல்கள் : குடும்ப விளக்கு, பாண்டியன் பரிசு, பிசிராந்தையார், அழகின் சிரிப்பு

நூல் வெளி
இப்பாடல் “பாரதிதாசன் கவிதைகள்’ தொகுப்பில் “இன்பத்தமிழ்” என்னும் தலைப்பில் இடம் பெற்றுள்ளது.

பொருளுரை
இனிக்கும் அமுதத்தை ஒத்திருப்பதால் தமிழுக்கு அமுது என்று பெயர். இன்பம் தரும் தமிழ் எங்கள் உயிருக்கு இணையானது. தமிழுக்கு நிலவென்றும் பெயர். இன்பத்தமிழ் எங்கள் சமூகத்தின் வளர்ச்சிக்கு அடிப்படையான நீர் போன்றதாகும்.
தமிழுக்கு மணம் என்று பெயர். இன்பத்தமிழ் எங்கள் வாழ்க்கைக்கெனவே உருவாக்கப்பட்ட ஊராகும். தமிழ் எங்கள் இளமைக்குக் காரணமான பால் போன்றது. சிறந்த புகழ்மிக்க புலவர்களுக்கு இன்பத்தமிழே கூர்மையான வேல் போன்ற கருவியாகும்.
தமிழ் எங்கள் உயர்வின் எல்லையாகிய வான் போன்றது. இன்பத்தமிழ் எங்கள் சோர்வை நீக்கி ஒளிர்விடச் செய்யும் தேனாகும். தமிழ் எங்கள் அறிவுக்குத் துணையாகும் தோள் போன்றது. தமிழ் எங்கள் கவிதைக்கு வைரம் போன்ற உறுதி மிக்க வாள் ஆகும்.

விளக்கவுரை
தமிழ், அமுதம் எவ்வாறு இனிமையாக இருக்குமோ அதைப்போல இனிமையான மொழியாக இருப்பதால் தமிழைஅமுதம் என்கிறார். மேலும் தமிழைமனித உயிருக்கு நிகராக ஒப்புமைப்படுத்துகின்றார். சமூகம் (சமுதாயம்) சிறப்புடன் வளர்வதற்குத் தமிழ்மொழி நீராகப் பயன்படுகிறது. தமிழ்மொழி நறுமணம் உடையது என்றும் கூறுகிறார். இன்பத்தமிழானது மக்கள் நல்வாழ்வு வாழ்வதற்கெனவே உருவாக்கப்பட்ட ஊராகும்.
மனிதர்கள் பொலிவுடனும் இளமையுடனும் இருப்பதற்குப் பால் எப்படிப் பயன்படுகிறதோ! அதனைப் போன்று வளமும் சுவையும் நிறைந்தது தமிழ்மொழி. இந்தத்தமிழ் சிறந்த புகழ்மிக்க தமிழ்ப்புலவர்களின் புலமையை அறிவிக்கின்ற கூர்மையான வேலாகும். தமிழ்மொழி எங்கள் உயர்வுக்கு வானமாகும். தமிழ்மொழி எங்கள் அறிவுக்குத் தோள்கொடுக்கும். தமிழ்மொழி எங்கள் கவிதையின் கவித்துவத்திற்கு வாளாகும்.

சொல்லும் பொருளும்

1. நிருமித்த – உருவாக்கிய
2. விளைவு – விளைச்சல்
3. சமூகம் – மக்கள் குழு
4. அசதி – சோர்வு

Students can download 11th Business Maths Chapter 1 Matrices and Determinants Ex 1.2 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 1 Matrices and Determinants Ex 1.2

Samacheer Kalvi 11th Business Maths Matrices and Determinants Ex 1.2 Text Book Back Questions and Answers

Question 1.
Find the adjoint of the matrix A = \(\left[\begin{array}{ll}
2 & 3 \\
1 & 4
\end{array}\right]\)
Solution:
A = \(\left[\begin{array}{ll}
2 & 3 \\
1 & 4
\end{array}\right]\)
Adj A = \(\left[\begin{array}{rr}
4 & -3 \\
-1 & 2
\end{array}\right]\)

Question 2.
If A = \(\left[\begin{array}{lll}
1 & 3 & 3 \\
1 & 4 & 3 \\
1 & 3 & 4
\end{array}\right]\) then verify that A(adj A) = |A| I and also find A^-1.
Solution:
Given A = \(\left[\begin{array}{lll}
1 & 3 & 3 \\
1 & 4 & 3 \\
1 & 3 & 4
\end{array}\right]\)
|A| = \(\left|\begin{array}{lll}
1 & 3 & 3 \\
1 & 4 & 3 \\
1 & 3 & 4
\end{array}\right|\)
= \(1\left|\begin{array}{ll}
4 & 3 \\
3 & 4
\end{array}\right|-3\left|\begin{array}{ll}
1 & 3 \\
1 & 4
\end{array}\right|+3\left|\begin{array}{ll}
1 & 4 \\
1 & 3
\end{array}\right|\)
= 1[16 – 9] – 3[4 – 3] + 3[3 – 4]
= 1(7) – 3(1) + 3(-1)
= 7 – 3 – 3
= 1



From (1) and (2), A(Adj A) = |A| I

Question 3.
Find the inverse of each of the following matrices:
(i) \(\left[\begin{array}{rr}
1 & -1 \\
2 & 3
\end{array}\right]\)
(ii) \(\left[\begin{array}{rr}
3 & 1 \\
-1 & 3
\end{array}\right]\)
(iii) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
(iv) \(\left[\begin{array}{rrr}
-3 & -5 & 4 \\
-2 & 3 & -1 \\
1 & -4 & -6
\end{array}\right]\)
Solution:
(i) \(\left[\begin{array}{rr}
1 & -1 \\
2 & 3
\end{array}\right]\)

(ii) \(\left[\begin{array}{rr}
3 & 1 \\
-1 & 3
\end{array}\right]\)

(iii) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)

(iv) \(\left[\begin{array}{rrr}
-3 & -5 & 4 \\
-2 & 3 & -1 \\
1 & -4 & -6
\end{array}\right]\)

Question 4.
If A = \(\left[\begin{array}{rr}
2 & 3 \\
1 & -6
\end{array}\right]\) and B = \(\left[\begin{array}{rr}
-1 & 4 \\
1 & -2
\end{array}\right]\), then verify adj(AB) = (adj B) (adj A).
Solution:


From (1) and (2), adj (AB) = (adj B) (adj A)

Question 5.
If A = \(\left[\begin{array}{rrr}
2 & -2 & 2 \\
2 & 3 & 0 \\
9 & 1 & 5
\end{array}\right]\) then, show that (adj A) A = O.
Solution:

Question 6.
If A = \(\left[\begin{array}{rrr}
-1 & 2 & -2 \\
4 & -3 & 4 \\
4 & -4 & 5
\end{array}\right]\) then, show that the inverse of A is A itself.
Solution:


∴ A^-1 = A
Hence proved.

Question 7.
If A^-1 = \(\left[\begin{array}{rrr}
1 & 0 & 3 \\
2 & 1 & -1 \\
1 & -1 & 1
\end{array}\right]\) then, find A.
Solution:
Given A^-1 = \(\left[\begin{array}{rrr}
1 & 0 & 3 \\
2 & 1 & -1 \\
1 & -1 & 1
\end{array}\right]\)
We know that (A^-1)^-1 = A
So we have to find inverse of A^-1

Question 8.
Show that the matrices A = \(\left[\begin{array}{lll}
2 & 2 & 1 \\
1 & 3 & 1 \\
1 & 2 & 2
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
\frac{4}{5} & \frac{-2}{5} & \frac{-1}{5} \\
\frac{-1}{5} & \frac{3}{5} & \frac{-1}{5} \\
\frac{-1}{5} & \frac{-2}{5} & \frac{4}{5}
\end{array}\right]\) are inverses of each other.
Solution:
To prove that A and B are inverses of each other.
We have to prove that AB = BA = I.


Thus AB = BA = I
Hence A and B are inverses of each other.

Question 9.
If A = \(\left[\begin{array}{ll}
3 & 7 \\
2 & 5
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
6 & 8 \\
7 & 9
\end{array}\right]\), then verify that (AB)^-1 = B^-1A^-1
Solution:

Now we will find B^-1A^-1


From (1) and (2), (AB)^-1 = B^-1A^-1

Question 10.
Find λ if the matrix \(\left[\begin{array}{rrr}
1 & 1 & 3 \\
2 & \lambda & 4 \\
9 & 7 & 11
\end{array}\right]\) has no inverse.
Solution:

1[11λ – 28] – 1[22 – 36] + 3[14 – 9λ] = 0
11λ – 28 + 14 + 42 – 27λ = 0
-16λ + 28 = 0
-16λ = -28
λ = \(\frac{-28}{-16}=\frac{7}{4}\)

Question 11.
If X = \(\left[\begin{array}{rrr}
8 & -1 & -3 \\
-5 & 1 & 2 \\
10 & -1 & -4
\end{array}\right]\) and Y = \(\left[\begin{array}{rrr}
2 & 1 & -1 \\
0 & 2 & 1 \\
5 & p & q
\end{array}\right]\) then, find p, q if Y = X^-1
Solution:
Given that Y is the inverse of X.
∴ XY = I

6 – 3p = 0 and -9 – 3q = 0
6 = 3p and -9 = 3q
∴ p = 2; q = -3