Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 7 Financial Mathematics Ex 7.2 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 7 Financial Mathematics Ex 7.2
Samacheer Kalvi 11th Business Maths Financial Mathematics Ex 7.2 Text Book Back Questions and Answers
Question 1.
Find the market value of 62 shares available at ₹ 132 having the par value of ₹ 100.
Solution:
Market value = ₹ Number of shares × Market value of a share
= ₹ 132 × 62
= ₹ 8,184
![]()
Question 2.
How much will be required to buy 125 of ₹ 25 shares at a discount of ₹ 7.
Solution:
Face value of a share = ₹ 25
Market value of a share = ₹ 25 – 7 = ₹ 18
Amount of money required to buy 125 shares = Number of shares × Market value of a share
= ₹ 125 × 18
= ₹ 2,250
Question 3.
If the dividend received from 9% of ₹ 20 shares is ₹ 1,620, find the number of shares.
Solution:
Income = Number of shares × Face value of a share × Rate of dividend
1620 = Number of shares × 20 × \(\frac{9}{100}\)
Number of shares = \(\frac{1620 \times 100}{20 \times 9}\) = 900 shares
![]()
Question 4.
Mohan invested ₹ 29,040 in 15% of ₹ 100 shares of a company quoted at a premium of 20%. Calculate
(i) the number of shares bought by Mohan
(ii) his annual income from shares
(iii) the percentage return on his investment
Solution:
Investment = ₹ 29,040
Rate of dividend = 15%
Number of shares = 100
Premium = 20%
(i) Number of shares
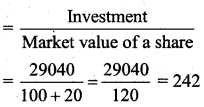
(ii) Annual income from shares = (Number of shares) × (Face value of a share) × (Rate of dividend)
= 242 × 100 × \(\frac{15}{100}\)
= ₹ 3630
(iii) The percentage return on his investment
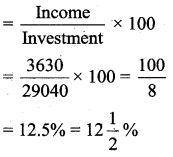
Question 5.
A man buys 400 of ₹ 10 shares at a premium of ₹ 2.50 on each share. If the rate of dividend is 12% find
(i) his investment
(ii) annual dividend received by him
(iii) rate of interest received by him on his money
Solution:
(i) Given Number of shares = 400
Face value of a share ₹ 10 market values of a share = 10 + 2.50 = ₹ 12.50
Investment = Number of shares × Market value of a share = ₹ 400 × 12.50 = ₹ 5000
(ii) Annual dividend = Number of shares × Face value × Rate of dividend
= 400 × 10 × \(\frac{12}{100}\)
= ₹ 480
(iii) Rate of dividend = \(\frac{\text { Dividend }}{\text { Investment }}\) × 100
= \(\frac{480}{5000}\) × 100
= \(\frac{48}{5}\)
= 9.6%
![]()
Question 6.
Sundar bought 4,500 of ₹ 10 shares, paying 2% per annum. He sold them when the price rose to ₹ 23 and invested the proceeds in ₹ 25 shares paying 10% per annum at ₹ 18. Find the change in his income.
Solution:
Number of shares = \(\frac{4500}{10}\) = 450
Income from 2% stock = Number of shares × face value × Rate of dividend
= 450 × 10 × \(\frac{2}{100}\)
= ₹ 90
Selling price of450 shares = 450 × 23 = ₹ 10,350
Number of shares bought in 10% stock = \(\frac{\text { Selling price of } 450 \text { shares at } ₹ 23}{\text { Market value }}\)
= \(\frac{10350}{18}\)
= ₹ 575
Income, from 10% stock = No of shares × face value × Rate of dividend
= 575 × 25 × \(\frac{10}{100}\)
= 575 × \(\frac{10}{4}\)
= ₹ 1437.5
= ₹ 1437.50
Charge in his income = ₹ 1437.50 – ₹ 90 = ₹ 1347.50
Question 7.
A man invests ₹ 13,500 partly in 6% of ₹ 100 shares at ₹ 140 and partly in 5% of ₹ 100 shares at ₹ 125. If his total income is ₹ 560, how much has he invested in each?
Solution:
Let the amount invested in 6% of ₹ 100 shares at ₹ 140 be x.
Then the amount invested in 5% of ₹ 100 shares at ₹ 125 is ₹ 13500 – x.
Income from 6% shares = Number of shares × Face value of a share × Rate of dividend
= \(\frac{x}{140} \times 100 \times \frac{6}{100}\)
= \(\frac{3 x}{70}\)
Income from 5% shares = Number of shares × Face value of a share × Rate of dividend
= \(\frac{13500-x}{125} \times 100 \times \frac{5}{100}\)
= \(\frac{13500-x}{25}\)
Given that the total income = ₹ 560
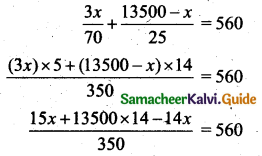
x + 13500 × 14 = 560 × 350
x = 196000 – 189000 = 7000
Amount invested at 6% stock = ₹ 7,000
Amount invested at 5% stock = ₹ 13500 – ₹ 7000 = ₹ 6500
![]()
Question 8.
Babu sold some ₹ 100 Shares at a 10% discount and invested his sales proceeds in 15% of ₹ 50 shares at ₹ 33. Had he sold his shares at a 10% premium instead of a 10% discount, he would have earned ₹ 450 more. Find the number of shares sold by him.
Solution:
Let the number of shares sold by Babu be x.
The face value of a share is ₹ 100.
He sold a 10% discount; the selling price of one share ₹ 90.
The selling price of x shares = ₹ 90x
He bought a share of face value ₹ 50 and the number of shares 33.
∴ Number of shares bought for the amount ₹ 90x i.e., \(\frac{90 x}{33}\)
∴ Face value of 50 shares = Cost of one share × Number of share
= 50 × \(\frac{90 x}{33}\)
The dividend is 15%.
∴ Income = \(\frac{15}{100}\) × Face value of 50 shares
= \(\frac{15}{100} \times 50 \times \frac{90 x}{33}\)
= \(\frac{225 x}{11}\)
Suppose he sold his shares at 10% premium instead of 10% discount, the market value of one share is ₹ 110.
Selling price of x shares = 110 × x = 110x
Number of shares bought for ₹ 33 = \(\frac{110 x}{33}\)
Face value of 50 shares = \(\frac{110 x}{33}\) × 50
Income = \(\frac{15}{100} \times \frac{110 x}{33}\) × 50 = 25x
Change Income = ₹ 450

x = \(\frac{450}{50}\) × 11 = 9 × 11 = 99 shares
Question 9.
Which is better investment? 7% of ₹ 100 shares at ₹ 120 (or) 8% of ₹ 100 shares at ₹ 135.
Solution:
Let the investment in each case be ₹ (120 × 135)
Case (i): Income from 7% of ₹ 100 shares at ₹ 120 = \(\frac{7}{120}\) × 120 × 135
= 7 × 135
= ₹ 945
Case (ii): Income from 8% of ₹ 100 shares at ₹ 135 = \(\frac{8}{135}\) × (120 × 135)
= 8 × 120
= ₹ 960
∴ 8% of 100 shares at ₹ 135 is better investment.
![]()
Question 10.
Which is better investment? 20% stock at 140 (or) 10% stock at 70.
Solution:
Let the investment in case be ₹ 140 × 70
Income from 20% stock at ₹ 140 is = \(\frac{20}{140}\) × 140 × 70
= 20 × 70
= ₹ 1400
Income from 10% stock at 70 = \(\frac{10}{70}\) × 140 × 70 = ₹ 1400
For the same investtnent both stocks fetch the same income. Therefore they are equivalent shares.