Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.9 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.9
Evaluate the following using properties of definite integrals:
Question 1.
\(\int_{-π/4}^{π/4}\) x³ cos³ x dx
Solution:
Let f(x) = x³cos³x
f(-x) = (-x)³ cos³(-x)
= -x³ cos³x
f(-x) = -f(x)
⇒ f(x) is an odd function
∴ \(\int_{-π/4}^{π/4}\) x³ cos³ x dx = 0
![]()
Question 2.
\(\int_{-π/2}^{π/2}\) sin² θ dθ
Solution:
Let f(θ)= sin² θ
f(-θ) = sin² (-θ) = [sin (-θ)]²
= [-sin θ]² = sin² θ
f(-θ) = f(θ)
∴ f(θ) is an even function
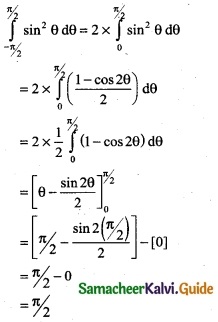
![]()
Question 3.
\(\int_{-1}^{1}\) log(\(\frac { 2-x }{2+x}\)) dx
Solution:

![]()
Question 4.
\(\int_{0}^{π/2}\) \(\frac { sin^7x }{sin^7x+cos^7x}\) dx
Solution:
Using the property
\(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – x) dx
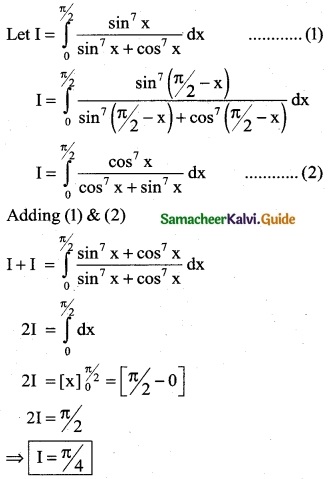
Question 5.
\(\int_{0}^{1}\) log (\(\frac { 1 }{x}\) – 1) dx
Solution:

![]()
Question 6.
\(\int_{0}^{1}\) \(\frac { x }{(1-x)^{3/4}}\) dx
Solution:
Let I = \(\int_{0}^{1}\) log \(\frac { x }{(1-x)^{3/4}}\) dx
Using the property
\(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – x) dx

![]()
Read More: