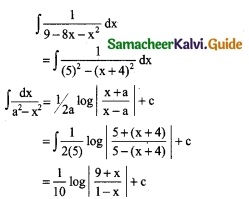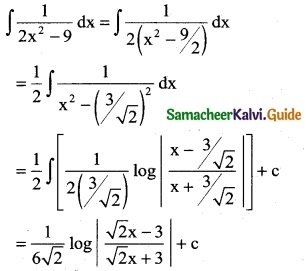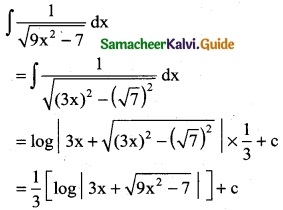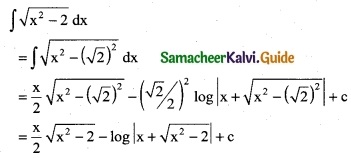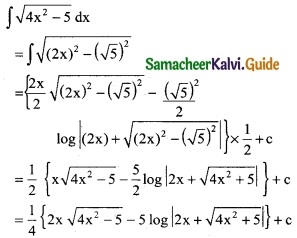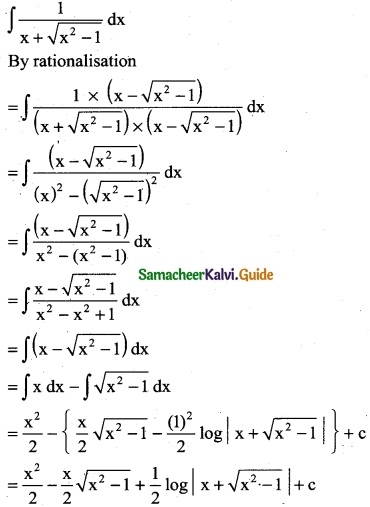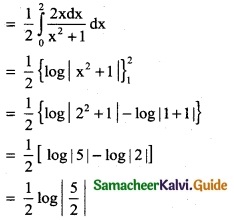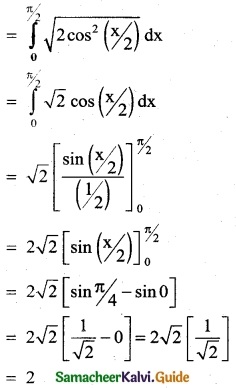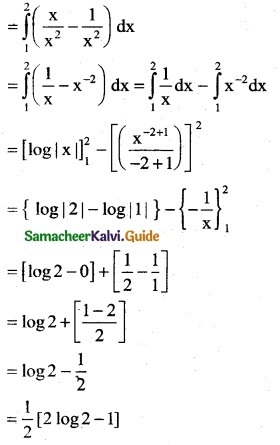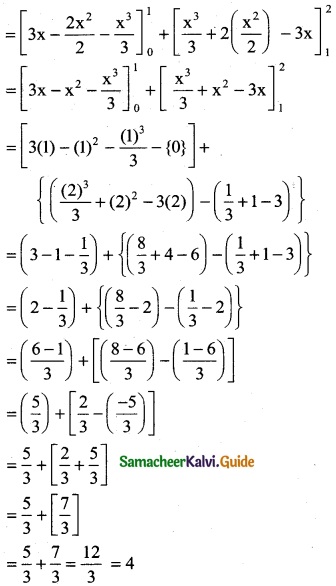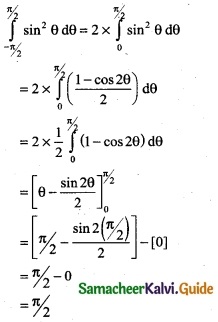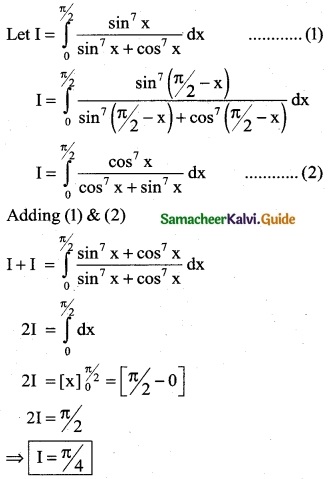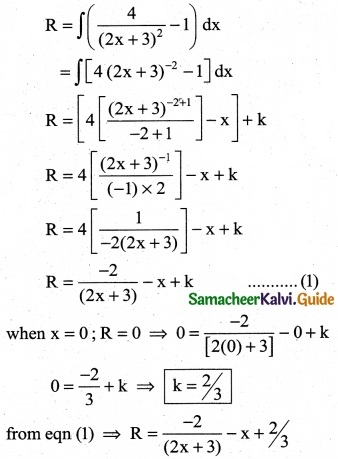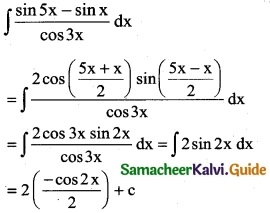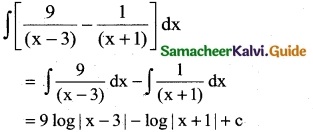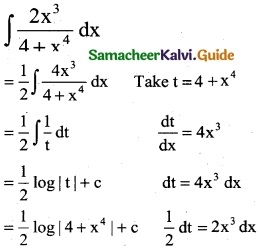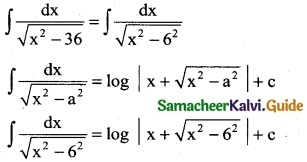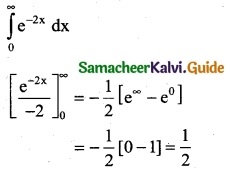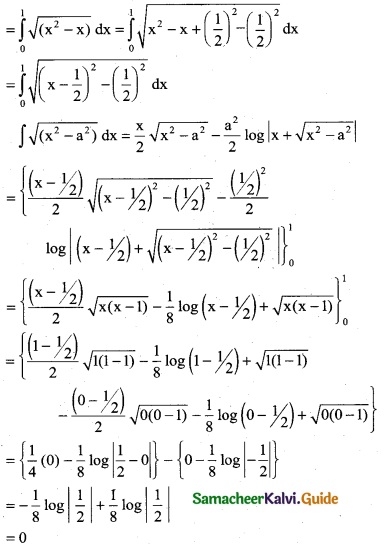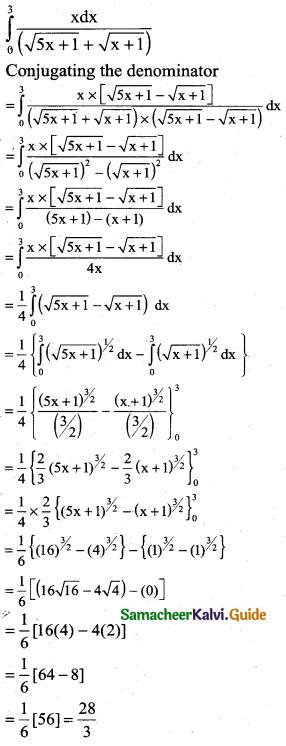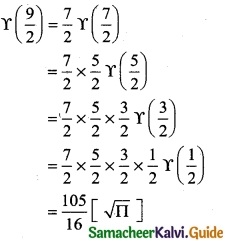Category: Class 12

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.6 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.6

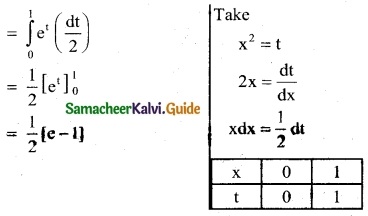
Question 1.
Integrate the following with respect to x.
\(\frac { 2x+5 }{x^2+5x-7}\)
Solution:
∫\(\frac { 2x+5 }{x^2+5x-7}\) dx
∫\(\frac { 1 }{z}\) dz
= log |z| + c
= log |x² + 5x – 7| + c
Take z = x² + 5x – 7
\(\frac { dz }{dx}\) = 2x + 5
dz = (2x + 5)dx

Question 2.
\(\frac { e^{3logx} }{x^4+1}\)
Solution:

Question 3.
\(\frac { e^{2x} }{e^{2x}-2}\)
Solution:

Question 4.
\(\frac { (logx)^3 }{x}\)
Solution:

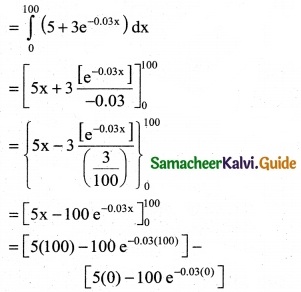
Question 5.
\(\frac { 6x+7 }{\sqrt{3x^2+7x-1}}\)
Solution:

Question 6.
(4x + 2) \(\sqrt {x^2+x+1}\)
Solution:

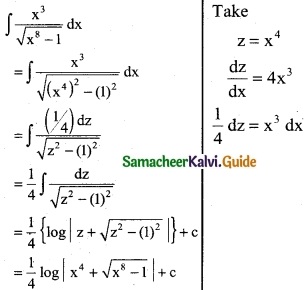
Question 7.
x⁸ (1 + x⁹)⁵
Solution:

Question 8.
\(\frac { x^{e-1}+e^{x-1} }{x^e+e^x}\)
Solution:

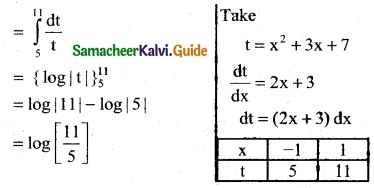
Question 9.
\(\frac { 1 }{x log x}\)
Solution:
∫\(\frac { 1 }{x log x}\) dx
∫\(\frac { 1 }{z}\) dz
= log |z| + c
= log |log x| + c
Take z = log x
\(\frac { 1 }{z}\) = \(\frac { 1 }{x}\)
dz = \(\frac { 1 }{x}\) dx

Question 10.
\(\frac { x }{2x^4-3x^2-2}\)
Solution:

Question 11.
e^x (1 + x) log (xe^x)
Solution:
e^x (1 + x) log(x e^x) = (e^x + x e^x) log (x e^x)
Let z = x e^x, Then dz = d(x e^x)
dz = (x e^x + e^x) dx (Using product rule)
So ∫ e^x (1 + x) log (x e^x) dx
= ∫ log (x e^x) (e^x + x e^x) dx
= ∫ log z dz
= z (log z – 1) + c
= x e^x [log (x e^x) – 1] + c

Question 12.
\(\frac { 1 }{x(x^2+1)}\)
Solution:

Put x = 0
1 = A(1)
A = 1
Put x = 1
1 = A(2) + 1(B + C)
1 = (1)2 + B + C
B + C = -1 …….. (1)
Put x = -1
1 = A[(-1)² + 1] + (-1)[B(-1) + C]
1 = A(2) – (-B + C)
1 = 2A + B – C
1 = 2(1) + B – C
B – C = -1 ………. (2)
Adding (1) & (2)
2B = -2
B = -1
C = 0

Question 13.
e^x [ \(\frac { 1 }{x^2}\) – \(\frac { 2 }{x^3}\) ]
Solution:
∫e^x [ \(\frac { 1 }{x^2}\) – \(\frac { 2 }{x^3}\) ] dx
= ∫e^x [f(x) + f'(x)] dx
= e^x f(x) + c
= e^x [ \(\frac { 1 }{x^2}\) ] + c
Take
f(x) = \(\frac { 1 }{x^2}\)
f'(x) = \(\frac { -2 }{x^3}\)

Question 14.
e^x [ \(\frac { x-1 }{(x+1)^3}\) ]
Solution:

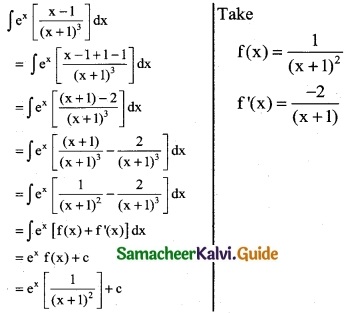
Question 15.
e^3x [ \(\frac { 3x-1 }{9x^2}\) ]
Solution:

Read More:

MARUTI Pivot Point Calculator

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.7 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.7

Question 1.
Integrate the following with respect to x.
\(\frac { 1 }{9-16x^2}\)
Solution:

Question 2.
\(\frac { 1} {9-8x-x^2}\)
Solution:

By Completing the squares
9 – 8x – x²
= -(x² + 8x – 9)
= – [x² + 8x + (4)² – (4)² – 9]
= – [(x + 4)² – 25]
= [25 – (x + 4)²]
= (5)² – (x + 4)²

Question 3.
\(\frac { 1 }{2x^2-9}\)
Solution:

Question 4.
\(\frac { 1 }{x^2-x-2}\)
Solution:

Question 5.
\(\frac { 1 }{x^2+3x+2}\)
Solution:

Question 6.
\(\frac { 1 }{2x^2+6x-8}\)
Solution:

Question 7.
\(\frac { e^x }{e^2x-9}\)
Solution:

Question 8.
\(\frac { 1 }{\sqrt {9x^2-7}} \)
Solution:

Question 9.
\(\frac { 1 }{\sqrt {x^2+16x+13}} \)
Solution:
∫\(\frac { 1 }{\sqrt {x^2+16x+13}} \) dx
= ∫\(\frac { 1 }{\sqrt {(x+3)^2+(2)^2}} \) dx
= log |(x + 3) + \(\sqrt {(x+3)^2+(2)^2}\)| + c
= log |(x + 3) + \(\sqrt {x^2+16x+13}\)| + c
By Completing the squares
x² + 6x + 3 = x² + 6x + (3)² – (3)² + 13
= (x + 3)² – 9 + 13
= (x + 3)² + 4
= (x + 3)² + (2)²

Question 10.
\(\frac { 1 }{ \sqrt x^2-3x+2 }\)
Solution:

Question 11.
\(\frac { x^3 }{ \sqrt x^8-1 }\)
Solution:

Question 12.
\(\sqrt { 1 + x + x^2}\)
Solution:

Question 13.
\(\sqrt { x^2 -2}\)
Solution:

Question 14.
\(\sqrt { 4x^2 -5}\)
Solution:

Question 15.
\(\sqrt { 2x^2 +4x+1}\)
Solution:

Question 16.
\(\frac { 1 }{ x + \sqrt x^2-1 }\)
Solution:

Must Read:

L&TFH Pivot Point Calculator

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.8 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.8

Using second fundamental theorem, evaluate the following:

Question 1.
\(\int_{0}^{1}\) e^2x dx
Solution:

Question 2.
\(\int_{0}^{1/4}\) \(\sqrt { 1 -4x}\) dx
Solution:

Question 3.
\(\int_{0}^{1}\) \(\frac { xdx }{x^2+1}\)
Solution:

Question 4.
\(\int_{0}^{3}\) \(\frac { e^xdx }{1+e^x}\)
Solution:
\(\int_{0}^{3}\) \(\frac { e^xdx }{1+e^x}\)
= {log |1 + ex|}\(_{0}^{3}\)
= log |1 + e³| – log |1 + e°|
= log |1 + e³| – log |1 + 1|
= log |1 + e³| – log |2|
= log |\(\frac { 1+e^3 }{2}\)|

Question 5.
\(\int_{0}^{1}\) xe^x² dx
Solution:

Question 6.
\(\int_{1}^{e}\) \(\frac { dx }{x(1+logx)^3}\)
Solution:

Question 7.
\(\int_{-1}^{1}\) \(\frac { 2x+3 }{x^2+3x+7}\) dx
Solution:

Question 8.
\(\int_{0}^{π/2}\) \(\sqrt { 1 +cosx} \) dx
Solution:

Question 9.
\(\int_{1}^{2}\) \(\frac { x-1 }{x^2}\) dx
Solution:

Evaluate the following

Question 10.
\(\int_{1}^{4}\) f(x) dx where f(x) = \(\left\{\begin{array}{l}
4 x+3,1 \leq x \leq 2 \\
3 x+5,2 \end{array}\right.\)
Solution:
\(\int_{1}^{4}\) f(x) dx
= \(\int_{1}^{2}\) f(x) dx + \(\int_{2}^{4}\) f(x) dx
= \(\int_{1}^{2}\) (4x + 3) dx + \(\int_{2}^{4}\) (3x + 5) dx

(8 + 6) – [5] + [24 + 20] – [6 + 10]
= 14 – 5 + 44 – 16
= 58 – 21
= 37

Question 11.
\(\int_{0}^{2}\) f(x) dx where f(x) = \(\left\{\begin{array}{ll}
3-2 x-x^{2}, & x \leq 1 \\
x^{2}+2 x-3, & 1<x \leq 2
\end{array}\right.\)
Solution:
\(\int_{0}^{2}\) f(x) dx
= \(\int_{0}^{1}\) f(x) dx + \(\int_{1}^{2}\) f(x) dx
= \(\int_{0}^{1}\) (3 – 2x – x²) dx + \(\int_{1}^{2}\) (x² + 2x – 3) dx

Question 12.
\(\int_{-1}^{1}\) f(x) dx where f(x) = \(\left\{\begin{array}{ll}
x, & x \geq 0 \\
-x, & x<0
\end{array}\right.\)
Solution:
\(\int_{-1}^{1}\) f(x) dx
\(\int_{-1}^{0}\) f(x) dx + \(\int_{0}^{1}\) f(x) dx
= \(\int_{-1}^{0}\) (-x) dx + \(\int_{0}^{1}\) x dx

Question 13.
f(x) = \(\left\{\begin{array}{l}
c x, \quad 0<x<1 \\
0, \text { otherwise }
\end{array}\right.\) find ‘c’ if \(\int_{0}^{1}\) f(x) dx = 2
Solution:
Given
f(x) = \(\left\{\begin{array}{l}
c x, \quad 0<x<1 \\
0, \text { otherwise }
\end{array}\right.\)
⇒ \(\int_{0}^{1}\) f(x) dx = 2
⇒ \(\int_{0}^{1}\) cx dx = 2
c[ \(\frac { x^2 }{ 2 }\) ]\(_{0}^{1}\) = 2
c[ \(\frac { 1 }{ 2 }\) – 0 ] = 2
\(\frac { 1 }{ 2 }\) = 2
⇒ c = 4

Read More:

CUMMINSIND Pivot Point Calculator

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.9 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.9

Evaluate the following using properties of definite integrals:

Question 1.
\(\int_{-π/4}^{π/4}\) x³ cos³ x dx
Solution:
Let f(x) = x³cos³x
f(-x) = (-x)³ cos³(-x)
= -x³ cos³x
f(-x) = -f(x)
⇒ f(x) is an odd function
∴ \(\int_{-π/4}^{π/4}\) x³ cos³ x dx = 0

Question 2.
\(\int_{-π/2}^{π/2}\) sin² θ dθ
Solution:
Let f(θ)= sin² θ
f(-θ) = sin² (-θ) = [sin (-θ)]²
= [-sin θ]² = sin² θ
f(-θ) = f(θ)
∴ f(θ) is an even function

Question 3.
\(\int_{-1}^{1}\) log(\(\frac { 2-x }{2+x}\)) dx
Solution:

Question 4.
\(\int_{0}^{π/2}\) \(\frac { sin^7x }{sin^7x+cos^7x}\) dx
Solution:
Using the property
\(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – x) dx

Question 5.
\(\int_{0}^{1}\) log (\(\frac { 1 }{x}\) – 1) dx
Solution:

Question 6.
\(\int_{0}^{1}\) \(\frac { x }{(1-x)^{3/4}}\) dx
Solution:
Let I = \(\int_{0}^{1}\) log \(\frac { x }{(1-x)^{3/4}}\) dx
Using the property
\(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – x) dx

Read More:

BOSCHLTD Pivot Point Calculator

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 3 Integral Calculus II Ex 3.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 3 Integral Calculus II Ex 3.2

Question 1.
The cost of an overhaul of an engine is Rs 10,000 The Operating cost per hour is at the rate of 2x-240 where the engine has run x km. find out the total cost of the engine run for 300 hours after overhaul.
Solution:
Given that the overhaul cost is Rs. 10,000.
The marginal cost is 2x – 240
MC = 2x – 240
C = ∫ MC dx + k
C = x² – 240x + k
k is the overhaul cost
⇒ k = 10,000
So C = x² – 240x + 10,000
When x = 300 hours, total cost is
C = (300)² – 240(300) + 10,000
⇒ C = 90,000 – 72000 + 10,000
⇒ C = 28,000
So the total cost of the engine run for 300 hours after the overhaul is ₹ 28,000.

Question 2.
Elasticity of a function \(\frac { Ey }{Ex}\) is given by \(\frac { Ey }{Ex}\) = \(\frac { -7x }{(1-2x)(2+3x)}\). Find the function when x = 2, y = \(\frac { 3 }{8}\)
Solution:

Put x = 0
7 = A (3(0) + 2) + B (2(0) – 1)
7 = A (2) + B (-1)
7 = (2) (2) – B
B = 4 – 7
B = -3

Question 3.
The Elasticity of demand with respect to price for a commodity is given by where \(\frac { (4-x)}{x}\) p is the price when demand is x. find the demand function when the price is 4 and the demand is 2. Also, find the revenue function
Solution:
The elasticity at the demand

Integrating on both sides
∫\(\frac { 1}{(x-4)}\) = ∫\(\frac { 1}{p}\) dp
log |x – 4| = log |p| + log k
log |x – 4| = log |pk| ⇒ (x – 4) = pk ……… (1)
when p = 4 and x = 2
(2 – 4) = 4k ⇒ -2 = 4k
k = -1/2
Eqn (1) ⇒ (x – 4) = p(-1/2)
-2 (x – 4) = p ⇒ p = 8 – 2x
Revenue function R = px = (8 – 2x)x
R = 8x – 2x²

Question 4.
A company receives a shipment of 500 scooters every 30 days. From experience it is known that the inventory on hand is related to the number of days x. Since the shipment, I (x) = 500 – 0.03 x², the daily holding cost per scooter is Rs 0.3. Determine the total cost for maintaining inventory for 30 days
Solution:
Here I (x) = 500 – 0.03 x²
C¹ = Rs 0.3
T = 30
Total inventory carrying cost
= C¹ \(\int _{0}^{T}\) I(x) dx
= 0.3 \(\int _{0}^{30}\) (500 – 0.03 x²)dx
= 0.3 [500 x – 0.03(\(\frac { x^3 }{3}\))]\( _{0}^{30}\)
= 0.3 [ 500 x – 0.01 x³]\( _{0}^{30}\)
= 0.3 [500(30) – 0.01 (30)³] – [0]
= 0.3 [15000 – 0.01 (27000)]
= 0.3 [15000 – 270] = 0.3 [14730]
= Rs 4,419

Question 5.
An account fetches interest at the rate of 5% per annum compounded continuously an individual deposits Rs 1000 each year in his account. how much will be in the account after 5 years (e^0.25 = 1.284)
Solution:
P = 1000
r = \(\frac { 5 }{1000}\) = 0.05
N = 5
Annuity = \(\int _{0}^{5}\) 1000 e^0.05t dt
= 1000 [ \(\frac { e^{0.05t} }{0.05}\) ] \(_{0}^{5}\)
= \(\frac { 1000 }{0.05}\) [e^0.05(5) – e⁰]
= 20000 [e^0.25 – 1]
= 20000 [1.284 – 1]
= 20000 [0.284]
= Rs 5680

Question 6.
The marginal cost function of a product is given by \(\frac { dc }{dx}\) = 100 – 10x + 0.1 x² where x is the output. Obtain the total and average cost function of the firm under the assumption, that its fixed cost is t 500
Solution:
\(\frac { dc }{dx}\) = 100 – 10x + 0.1 x² and k = Rs 500
dc = (100 – 10x + 0.1 x²) dx
Integrating on both sides,

Question 7.
The marginal cost function is M.C = 300 x^2/5 and the fixed cost is zero. Find the total cost as a function of x
Solution:
M.C = 300 x^2/5 and fixed cost K = 0
Total cos t = ∫M.C dx

Question 8.
If the marginal cost function of x units of output is \(\frac { a }{\sqrt {ax+b}}\) and if the cost of output is zero. Find the total cost as a function of x.
Solution:

∴ C(x) = 2(ax + b)^1/2 + k …….. (1)
When x = 0
eqn (1) ⇒ 0 = 2 [a(0) + b]^1/2 + k
k = -2(b)^1/2 ⇒ k = -2√b
Required cost function
C(x) = 2(ax + b)^1/2 – 2√b
∴ C = 2\(\sqrt { ax + b}\) – 2√b

Question 9.
Determine the cost of producing 200 air conditioners if the marginal cost (is per unit) is C'(x) = \(\frac { x^2 }{200}\) + 4
Solution:

= 13333.33 + 800
∴ Cost of producing 200 air conditioners
= Rs 14133.33

Question 10.
The marginal revenue (in thousands of Rupees) function for a particular commodity is 5 + 3 e^-0.03x where x denotes the number of units sold. Determine the total revenue from the sale of 100 units (given e^-3 = approximately)
Solution:
The marginal Revenue (in thousands of Rupees) function
M.R = 5 + 3^-0.03x
Total Revenue from sale of 100 units is
Total Revenue T.R = \(\int _{0}^{ 100}\) M.R dx

= [500 – 100 e^-3] – [0 – 100 e°]
= [500 -100 (0.05)] – [-100 (1)]
= [500 – 5]+ 100
= 495 + 100 = 595 thousands
= 595 × 1000
∴ Revenue R = Rs 595000

Question 11.
If the marginal revenue function for a commodity is MR = 9 – 4x². Find the demand function.
Solution:
Marginal Revenue function MR = 9 – 4x²
Revenue function R = ∫MR dx

Question 12.
Given marginal revenue function \(\frac { 4 }{(2x+3)^2}\) -1, show that the average revenue function is P = \(\frac { 4 }{6x+9}\) -1
Solution:
M.R = \(\frac { 4 }{(2x+3)^2}\) -1
Total Revenue R = ∫M.R dx

Question 13.
A firms marginal revenue functions is M.R = 20 e^-x/10 Find the corresponding demand function.
Solution:

Question 14.
The marginal cost of production of a firm is given by C’ (x) = 5 + 0.13 x, the marginal revenue is given by R’ (x) = 18 and the fixed cost is Rs 120. Find the profit function.
Solution:
MC = C'(x) = 5 + 0.13x
C(x) = ∫C'(x) dx + k₁
= ∫(5 + 0.13x) dx + k₁
= 5x + \(\frac{0.13}{2} x^{2}\) + k₁
When quantity produced is zero, fixed cost is 120
(i.e) When x = 0, C = 120 ⇒ k₁ = 120
Cost function is 5x + 0.065x² + 120
Now given MR = R'(x) = 18
R(x) = ∫18 dx + k₂ = 18x + k₂
When x = 0, R = 0 ⇒ k₂ = 0
Revenue = 18x
Profit P = Total Revenue – Total cost = 18x – (5x + 0.065x² + 120)
Profit function = 13x – 0.065x² – 120

Question 15.
If the marginal revenue function is R'(x) = 1500 – 4x – 3x². Find the revenue function and average revenue function.
Solution:
Given marginal revenue function
MR = R’(x)= 1500 – 4x – 3x²
Revenue function R(x) = ∫R'(x) dx + c
R = ∫(1500 – 4x – 3x²) dx + c
R = 1500x – 2x² – x³ + c
When x = 0, R = 0 ⇒ c = 0
So R = 1500x – 2x² – x³
Average revenue function P = \(\frac{R}{x}\) ⇒ 1500 – 2x – x²

Question 16.
Find the revenue function and the demand function if the marginal revenue for x units MR = 10 + 3x – x
Solution:
The marginal revenue function
MR = 10 + 3x – x²
The Revenue function
R = ∫(MR) dx
= ∫(10 + 3x – x²)dx

Question 17.
The marginal cost function of a commodity is given by M_c = \(\frac { 14000 }{\sqrt{7x+4}}\) and the fixed cost is Rs 18,000. Find the total cost average cost.
Solution:
The marginal cost function of a commodity
M_c = \(\frac { 14000 }{\sqrt{7x+4}}\) = 14000 (7x + 4)^-1/2
Fixed cost k = Rs 18,000
Total cost function C = ∫(M.C) dx
= ∫14000 (7x + 4)^-1/2 dx

Question 18.
If the marginal cost (MC) of production of the company is directly proportional to the number of units (x) produced, then find the total cost function, when the fixed cost is Rs 5,000 and the cost of producing 50 units is Rs 5,625.
Solution:
M.C αx
M.C = λx
fixed cost k = Rs 5000
Cost function C = ∫(M.C) dx
= ∫λx dx

Question 19.
If MR = 20 – 5x + 3x², Find total revenue function
Solution:
MR = 20 – 5x + 3x²
Total Revenue function
R = ∫(MR) dx = ∫(20 – 5x + 3x²) dx
R = 20x – \(\frac { 5x^2 }{2}\) + \(\frac {3x^3 }{3}\) + k
when x = 0; R = 0 ⇒ k = 0
∴ R = 20x – \(\frac { 5 }{2}\) x² + x³

Question 20.
If MR = 14 – 6x + 9x², Find the demand function.
Solution:
MR = 14 – 6x + 9x²
R = ∫(14 – 6x + 9x²) dx + k
= 14x – 3x² + 3x³ + k
Since R = 0, when x = 0, k = 0
So revenue function R = 14x – 3x² + 3x³
Demand function P = \(\frac{R}{x}\) = 14 – 3x + 3x²

Read More:

• ABFRL Pivot Point Calculator

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 3 Integral Calculus II Ex 3.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 3 Integral Calculus II Ex 3.1

Question 1.
Using Interation, find the area of the region bounded the line given is 2y + x = 8, the x axis and the lines x = 2, x = 4.
Solution:
The equation of the line given is 2y + x = 8
⇒ 2y = 8 – x ⇒ y = \(\frac { 8-x }{2}\)
y = 4 – \(\frac { x }{2}\)
Also x varies from 2 to 4
The required Area

= (16 – 4) – (8 – 1)
= 12 – 7 = 5 sq.units

Question 2.
Find the area bounded by the lines y – 2x – 4 = 0, y = 0, y = 3 and the y-axis.
Solution:
The equation of the line given is y – 2x – 4 = 0
⇒ 2x = y – 4 ⇒ x = \(\frac { y-4 }{2}\)
∴ x = \(\frac { y }{2}\) – 2
Also y varies from 1 to 3
Required Area

= 2 – 4 = -2
Area can’t be in negative.
∴ Area = 2 sq.units

Question 3.
Calculate the area bounded by the parabola y² = 4ax and its latus rectum.
Solution:
Given parabola is y² = 4ax
Its focus is (a, 0)
Equation of latus rectum is x = a
The parabola is symmetrical about the x-axis

Question 4.
Find the area bounded by the line y = x and x-axis and the ordinates x = 1, x = 2
Solution:
The equation of the given line is y = x and x varies from 1 to 2

Question 5.
Using integration, find the area of the region bounded by the line y – 1 = x, the x-axis and the ordinates x = -2, x = 3.
Solution :
The equation of given line is y – 1 = x
y = x + 1

The line y = x + 1 meets the x-axis at x = -1
Since x varies from -2 to 3
Hence a part of lies below the x-axis and the other part lies above the x-axis.

Question 6.
Find the area of the region lying in the first quadrant bounded by the region y = 4x², x = 0, y = 0 and y = 4
Solution:
The equation of a parabola given is y = 4x²

Area of the region lying in the first quadrant

Question 7.
Find the area bounded by the curve y = x² and the line y = 4
Solution:
Equation of the curve y = x² ………. (1)
Equation of the line y = 4 ………. (2)
Solving equation (1) & (2)
x² = 4 ⇒ x = ± 2

Must Read:

Gift Nifty Timings

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.12 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.12

Choose the most suitable answer from the given four alternatives:

Question 1.
∫\(\frac { 1 }{x^3}\) dx is
(a) \(\frac { -3 }{x^2}\) + c
(b) \(\frac { -1 }{2x^2}\) + c
(c) \(\frac { -1 }{3x^2}\) + c
(d) \(\frac { -2 }{x^2}\) + c
Solution:
(b) \(\frac { -1 }{2x^2}\) + c
Hint:
∫\(\frac { 1 }{x^3}\) dx = ∫x^-3 dx = [ \(\frac { x^{-3+1} }{-3+1}\) ] + c
= (\(\frac { x^{-2} }{-2}\)) + c = \(\frac { -1 }{2x^2}\) + c

Question 2.
∫2^x dx is
(a) 2^x log 2 + c
(b) 2^x + c
(c) \(\frac { 2^x }{log 2}\) + c
(d) \(\frac { log 2 }{2^x}\) + c
Solution:
(c) \(\frac { 2^x }{log 2}\) + c
Hint:
∫2^x dx = ∫a^x dx = \(\frac { a^x }{log a}\) + c

Question 3.
∫\(\frac { sin 2x }{2 sin x}\) dx is
(a) sin x + c
(b) \(\frac { 1 }{2}\) sin x + c
(c) cos x + c
(d) \(\frac { 1 }{2}\) cos x + c
Solution:
(a) sin x + c
Hint:
∫\(\frac { sin 2x }{2 sin x}\) dx = ∫\(\frac { 2sin x cos x }{2 sin x}\) dx
= ∫cos x dx
= sin x + c

Question 4.
∫\(\frac { sin 5x-sin x }{cos 3x}\) dx is
(a) -cos 2x + c
(b) -cos 2x – c
(c) –\(\frac { 1 }{4}\) cos 2x + c
(d) -4 cos 2x + c
Solution:
(a) -cos 2x + c
Hint:

Question 5.
∫\(\frac { log x}{x}\) dx, x > 0 is
(a) \(\frac { 1 }{2}\) (log x)² + c
(b) –\(\frac { 1 }{2}\) (log x)²
(c) \(\frac { 2 }{x^2}\) + c
(d) \(\frac { 2 }{x^2}\) – c
Solution:
(a) \(\frac { 1 }{2}\) (log x)² + c
Hint:
∫\(\frac { log x}{x}\) dx, x > 0
∫ tdt = [ \(\frac { t^2 }{2}\) ] + c
= \(\frac { (log x)^2 }{2}\) + c
let t = log x
\(\frac { dt }{dx}\) = \(\frac { 1 }{x}\)
dt = \(\frac { 1 }{x}\) dx

Question 6.
∫\(\frac { e^x }{\sqrt{1+e^x}}\) dx is
(a) \(\frac { e^x }{\sqrt{1+e^x}}\) + c
(b) 2\(\sqrt{1+e^x}\) + c
(c) \(\sqrt{1+e^x}\) + c
(d) e^x\(\sqrt{1+e^x}\) + c
Solution:
(b) 2\(\sqrt{1+e^x}\) + c
Hint:

Question 7.
∫\(\sqrt { e^x}\) dx is
(a) \(\sqrt { e^x}\) + c
(b) 2\(\sqrt { e^x}\) + c
(c) \(\frac { 1 }{2}\) \(\sqrt { e^x}\) + c
(d) \(\frac { 1 }{2\sqrt { e^x}}\) + c
Solution:
(b) 2\(\sqrt { e^x}\) + c
Hint:
∫\(\sqrt { e^x}\) dx
= ∫\(\sqrt { e^x}\) dx = ∫(e^x)^1/2 dx = ∫ e^x/2 dx
= \(\frac { e^{x/2} }{1/2}\) + c = 2e^x/2 + c
= 2(e^x)^1/2 + c = 2\(\sqrt { e^x}\) + c

Question 8.
∫e^2x [2x² + 2x] dx
(a) e^2x x² + c
(b) xe^2x + c
(c) 2x²e² + c
(d) \(\frac { x^2e^x }{2}\) + c
Solution:
(a) e^2x x² + c
Hint:
∫e^2x (2x² + 2x) dx
Let f(x) = x²; f'(x) = 2x and a = 2
= ∫e^ax [af(x),+ f ’(x)] = e^ax f(x) + c
= ∫e^2x (2x² + 2x) dx = e^2x (x²) + c

Question 9.
\(\frac { e^x }{e^x+1}\) dx is
(a) log |\(\frac { e^x }{e^x+1}\)| + c
(b) log |\(\frac { e^x+1 }{e^x}\)| + c
(c) log |e^x| + c
(d) log |e^x + 1| + c
Solution:
(d) log |e^x + 1| + c
Hint:
∫\(\frac { e^x }{e^x+1}\) dx
= ∫\(\frac { dt }{t}\)
= log |t| + c
= log |e^x + 1| + c
take t = e^x + 1
\(\frac { dt }{dx}\) = e^x
dt = e^x dx

Question 10.
∫\(\frac { 9 }{x-3}-\frac { 1 }{x+1}\) dx is
(a) log |x – 3| – log|x + 1| + c
(b) log|x – 3| + log|x + 1| + c
(c) 9 log |x – 3| – log |x + 1| + c
(d) 9 log |x – 3| + log |x + 1| + c
Solution:
(c) 9 log |x – 3| – log |x + 1| + c
Hint:

Question 11.
∫\(\frac { 2x^3 }{4+x^4}\) dx is
(a) log |4 + x⁴| + c
(b) \(\frac { 1 }{2}\) log |4 + x⁴| + c
(c) \(\frac { 1 }{2}\) log |4 + x⁴| + c
(d) log |\(\frac { 2x^3 }{4+x^4}\) + c
Solution:
(b) \(\frac { 1 }{2}\) log |4 + x⁴| + c
Hint:

Question 12.
∫\(\frac { dx }{\sqrt{x^2-36}}\) is
(a) \(\sqrt{x^2-36}\) + c
(b) log |x + \(\sqrt{x^2-36}\)| + c
(c) log |x – \(\sqrt{x^2-36}\)| + c
(d) log |x² + \(\sqrt{x^2-36}\)| + c
Solution:
(b) log |x + \(\sqrt{x^2-36}\)| + c
Hint:

Question 13.
∫\(\frac { 2x+3 }{\sqrt{x^2+3x+2}}\) dx is
(a) \(\sqrt{x^2+3x+2}\) + c
(b) 2\(\sqrt{x^2+3x+2}\) + c
(c) \(\sqrt{x^2+3x+2}\) + c
(d) \(\frac { 2 }{3}\) (x² + 3x + 2) + c
Solution:
(b) 2\(\sqrt{x^2+3x+2}\) + c
Hint:

Question 14.
\(\int_{0}^{4}\) (2x + 1) dx is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b) 2
Hint:
\(\int_{0}^{4}\) (2x + 1) dx
= [2(\(\frac { x^2 }{2}\)) + x]\(_{0}^{1}\) = [x² + x]\(_{0}^{1}\)
= [(1)² + (1)] – [0] = 2

Question 15.
\(\int_{2}^{4}\) \(\frac { dx }{x}\) is
(a) log 4
(b) 0
(c) log 2
(d) log 8
Solution:
(c) log 2
Hint:
\(\int_{2}^{4}\) \(\frac { dx }{x}\)
\(\int_{2}^{4}\) \(\frac { dx }{x}\) = [log |x|]\(_{0}^{1}\) = log |4| – log |2|
= log[ \(\frac { 4}{2}\) ] = log 2

Question 16.
\(\int_{0}^{∞}\) e^-2x dx is
(a) 0
(b) 1
(c) 2
(d) \(\frac { 1 }{2}\)
Solution:
(d) \(\frac { 1 }{2}\)
Hint:

Question 17.
\(\int_{-1}^{1}\) x³ e^x4 dx is
(a) 1
(b) 2\(\int_{0}^{1}\) x³ e^x4
(c) 0
(d) e^x4
Solution:
(c) 0
Hint:
\(\int_{-1}^{1}\) x³ e^x4 dx
Let f (x) = x³e^x4
f(-x) = (-x)² e^(-x)4
= -x² e^x4
f(-x) = -f(x)
⇒ f(x) is an odd function
∴ \(\int_{-1}^{1}\) x³ e^x4 dx = 0

Question 18.
If f(x) is a continuous function and a < c < b, then \(\int_{a}^{c}\) f(x) dx + \(\int_{c}^{b}\) f(x) dx is
(a) \(\int_{a}^{b}\) f(x) dx – \(\int_{a}^{c}\) f(x) dx
(b) \(\int_{a}^{c}\) f(x) dx – \(\int_{a}^{b}\) f(x) dx
(c) \(\int_{a}^{b}\) f(x) dx
(d) 0
Solution:
(c) \(\int_{a}^{b}\) f(x) dx

Question 19.
The value of \(\int_{-π/2}^{π/2}\) cos x dx is
(a) 0
(b) 2
(c) 1
(d) 4
Solution:
(b) 2
Hint:
\(\int_{-π/2}^{π/2}\) cos x dx
Let f(x) = cos x
f(-x) = cos (-x) = cos (x) = f(x)
∴ f(x) is an even function
\(\int_{-π/2}^{π/2}\) cos x dx = 2 × \(\int_{0}^{π/2}\) cos x dx
= 2 × [sin x]\(_{0}^{-π/2}\) = 2 [sin π/2 – sin 0]
= 2 [1 – 0] = 2

Question 20.
\(\int_{-π/2}^{π/2}\) \(\sqrt {x^4(1-x)^2}\) dx
(a) \(\frac { 1 }{12}\)
(b) \(\frac { -7 }{12}\)
(c) \(\frac { 7 }{12}\)
(d) \(\frac { -1 }{12}\)
Solution:
(a) \(\frac { 1 }{12}\)
Hint:

Question 21.
If \(\int_{0}^{1}\) f(x) dx = 1, \(\int_{0}^{1}\) x f(x) dx = a and \(\int_{0}^{1}\) x² f(x) dx = a², then \(\int_{0}^{1}\) (a – x)² f(x) dx is
(a) 4a²
(b) 0
(c) a²
(d) 1
Solution:
(b) 0
Hint:
\(\int_{0}^{1}\) (a – x)² f(x) dx
= \(\int_{0}^{1}\) [a² +x² – 2ax] f(x) dx
= \(\int_{0}^{1}\) a² + f (x) dx + \(\int_{0}^{1}\) x² f (x) dx – 2a\(\int_{0}^{1}\) x f(x) dx
= a²(1) + a² – 2a(a) – 2a² – 2a² = 0

Question 22.
The value of \(\int_{2}^{3}\) f(5 – x) dx – \(\int_{2}^{3}\) f(x) dx is
(a) 1
(b) 0
(c) -1
(d) 5
Solution:
(b) 0
Hint:
\(\int_{2}^{3}\) f(5 – x) dx – \(\int_{2}^{3}\) f(x) dx
Using the property
= \(\int_{2}^{3}\) f(x) dx = \(\int_{a}^{b}\) f(a + b – x) dx
= \(\int_{2}^{3}\) f (5 – x) – \(\int_{2}^{3}\) f (5 – x) dx
= 0

Question 23.
\(\int_{0}^{4}\) (√x + \(\frac { 1 }{√x}\)), dx is
(a) \(\frac { 20 }{3}\)
(b) \(\frac { 21 }{3}\)
(c) \(\frac { 28 }{3}\)
(d) \(\frac { 1 }{3}\)
Solution:
(c) \(\frac { 28 }{3}\)
Hint:

Question 24.
\(\int_{0}^{π/3}\) tan x dx is
(a) log 2
(b) 0
(c) log √2
(d) 2 log 2
Solution:
(a) log 2
Hint:
\(\int_{0}^{π/3}\) tan x dx
= ∫tan x dx
= ∫\(\frac { sin x }{cos x}\) dx
= -∫\(\frac { -sin x }{cos x}\) dx
= -log |cos x| + c
= log sec x + c
= [log (sec x)]\(_{0}^{π/3}\)
= log [(sec π/3) – log (sec 0)]
= log (2) – log (1)
= log 2 – (0) = log 2

Question 25.
Using the factorial representation of the gamma function, which of the following is the solution for the gamma function Γ(n) when n = 8
(a) 5040
(b) 5400
(c) 4500
(d) 5540
Solution:
(a) 5040
Hint:
\(\Upsilon\) (8) = 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040

Question 26.
Γ(n) is
(a) (n – 1)!
(b) n!
(c) n Γ (n)
(d) (n – 1) Γ(n)
Solution:
(a) (n – 1)!
Hint:
Γ(n) = Γ(n – 1) + 1 = (n – 1)!

Question 27.
Γ(1) is
(a) 0
(b) 1
(c) n
(d) n!
Solution:
(b) 1
Hint:
\(\Upsilon\) (1) = 0! = 1

Question 28.
If n > 0, then Γ(n) is
(a) \(\int_{0}^{1}\) e^-x x^n-1 dx
(b) \(\int_{0}^{1}\) e^-x xⁿ dx
(c) \(\int_{0}^{∞}\) e^x x^-n dx
(d) \(\int_{0}^{∞}\) e^-x x^n-1 dx
Solution:
(d) \(\int_{0}^{∞}\) e^-x x^n-1 dx

Question 29.
Γ(\(\frac { 3 }{2}\))
(a) √π
(b) \(\frac { √π }{2}\)
(c) 2√π
(d) \(\frac { 3 }{2}\)
Solution:
(b) \(\frac { √π }{2}\)
Hint:
\(\Upsilon\) (3/2) = \(\frac { 2 }{2}\) \(\Upsilon\) [ \(\frac { 3 }{2}\) ]
= \(\frac { 3 }{2}\) √π

Question 30.
\(\int_{0}^{∞}\) x⁴ e^-x dx is
(a) 12
(b) 4
(c) 4!
(d) 64
Solution:
(b) \(\frac { √π }{2}\)
Hint:
\(\int_{0}^{∞}\) x⁴ e^-x dx
= ∫xⁿ e^-ax dx = \(\frac { n! }{a{n+1}}\)
= \(\frac { 4! }{(1)^{n+1}}\)
= \(\frac { 4! }{(1)^5}\)
= 4!

Try More:

Moving Average Crossover Scanner

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Miscellaneous Problems Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Miscellaneous Problems

Question 1.
∫\(\frac { 1 }{\sqrt{x-1}-\sqrt{x+3}}\) dx
Solution:
∫\(\frac { 1 }{\sqrt{x+2}-\sqrt{x+3}}\) dx
Conjugating the Denominator

Question 2.
∫\(\frac { dx }{2-3x-2x^2}\)
Solution:

Question 3.
∫\(\frac { dx }{e^x+6+5e^{-x}}\)
Solution:

Question 4.
∫\(\sqrt { 2x^2-3}\) dx
Solution:

Question 5.
∫\(\sqrt { 9x^2+12x+3}\) dx
Solution:

Question 6.
∫(x + 1)² log x dx
Solution:
∫udv = uv – ∫vdu
∫(x + 1)² log x dx

Question 7.
∫log (x – \(\sqrt { x^2-1}\)) dx
Solution:

Question 8.
\(\int_{0}^{1}\) \(\sqrt { x(x-1)}\) dx
Solution:

Question 9.
\(\int_{-1}^{1}\) x² e^-2x dx
Solution:

Question 10.
\(\int_{0}^{3}\) \(\frac { xdx }{\sqrt {x+1} + \sqrt{5x+1}}\)
Solution:

Must Try:

Nr7 stocks

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.10 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.10

Evaluate the following:

Question 1.
(i) \(\Upsilon\) (4)
Solution:
Γ(4) = Γ(3 + 1) = 3! = 6

(ii) \(\Upsilon\) (\(\frac { 9 }{2}\))
Solution:

(iii) \(\int_{0}^{∞}\) e^-mx x⁶ dx
Solution:
W.K.T \(\int_{0}^{∞}\) xⁿ e^-ax dx = \(\frac { n! }{a^{n+1}}\)
∴ \(\int_{0}^{∞}\) e^-mx x⁶ dx = \(\frac { 6! }{3^{6+1}}\) = \(\frac { 6! }{m^7}\)

(iv) \(\int_{0}^{∞}\) e^-4x x⁴ dx
Solution:

(v) \(\int_{0}^{∞}\) e^-x/2 x⁵ dx
Solution:

Question 2.
If f(x) = \(\left\{\begin{array}{l}
x^{2} e^{-2 x}, x \geq 0 \\
0, \text { otherwise }
\end{array}\right.\), then evaluate \(\int_{0}^{∞}\) f(x) dx
Solution:
Given

Must Read:

Finnifty Pivot Point

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.11 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.11

Evaluate the following integrals as the limit of the sum:

Question 1.
\(\int_{0}^{1}\) (x + 4) dx
Solution:

Question 2.
\(\int_{1}^{3}\) x dx
Solution:

Question 3.
\(\int_{1}^{3}\) (2x + 3) dx
Solution:

Question 4.
\(\int_{0}^{1}\) x² dx
Solution:

Must Try:

Nifty Pivot Point Calculator