Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Chemistry Guide Pdf Chapter 1 Basic Concepts of Chemistry and Chemical Calculations Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Chemistry Solutions Chapter 1 Basic Concepts of Chemistry and Chemical Calculations
11th Chemistry Guide Basic Concepts of Chemistry and Chemical Calculations Text Book Back Questions and Answers
Textual Questions:
I. Choose the best answer:
Question 1.
40 ml of methane is completely burnt using 80 ml of oxygen at room temperature. The volume of gas left after cooling to room temperature
(a) 40 ml CO2
(b) 40 ml CO2 gas and 80 ml H2o gas
(c) 60 ml CO2 gas and 60 ml H2o gas
(d) 120 ml CO2 gas
Answer:
(a) 40 ml CO2
Solution:
CH4(g) + 2O2 → CO2(g) + 2H2O (1)
| Content | CH4 | O2 | CO2 |
| Stoichiometric coefficient | 1 | 2 | 1 |
| Volume of reactants allowed to react | 40 mL | 80 mL | – |
| Volume of reactant reacted and product formed | 40 mL | 80 mL | 40 mL |
| Volume of gas after cooling to the room temperature | – | – | – |
Since the product was cooled to room temperature, water exists mostly as liquid. Hence, option (a) is correct.
Question 2.
An element X has the following isotopic composition 200X = 90%, 199X = 8% and 202X = 2%. The weighted average atomic mass of the element X is closest to
(a) 201 u
(b) 202 u
(c) 199 u
(d) 200 u
Answer:
(d) 200 u
Solution:
X = \(\frac{(200 \times 90)+(199 \times 8)+(202 \times 2)}{100}\) = 199.96 = 200 u
Question 3.
Assertion:
Two mole of glucose contains 12.044 × 1023 molecules of glucose
Reason:
Total number of entities present in one mole of any substance is equal to 6.02 × 1022
(a) both assertion and reason are true and the reason is the correct explanation of assertion
(b) both assertion and reason are true but reason is not the correct explanation of assertion
(c) assertion is true but reason is false
(d) both assertion and reason are false
Answer:
(c) assertion is true but reason is false
Solution:
Correct reason:
Total number of entities present in one mole of any substance is equal to 6.022 × 1023.
Question 4.
Carbon forms two oxides, namely carbon monoxide and carbon dioxide. The equivalent mass of which element remains constant?
(a) Carbon
(b) Oxygen
(c) both carbon and oxygen
(d) neither carbon nor oxygen
Answer:
(b) Oxygen
Solution:
Reaction 1:
2C + O2 → 2CO
2 × 12g carbon combines with 32g of oxygen. Hence, Equivalent mass of carbon
\(\frac{2 \times 12}{32}\) × 8 = 6
Reaction 2:
C + O2 → CO2
12 g carbon combines with 32 g of oxygen. Hence, Equivalent mass of carbon
= \(\frac{12}{32}\) × 8 = 6
![]()
Question 5.
The equivalent mass of a trivalent metal element is 9 g eq-1 the molar mass of its anhydrous oxide is
(a) 102 g
(b) 27 g
(c) 270 g
(d) 78 g
Answer:
(a) 102 g
Solution:
Let the trivalent metal be M3
Equivalent mass = mass of the metal / 3 eq
9 g eq-1 = mass of the metal / 3 eq
Mass of the metal = 27 g
Oxide formed M2O3 ;
Mass of the oxide = (2 × 27) + (3 × 16) = 102 g
Question 6.
The number of water molecules in a drop of water weighing 0.018 g is
(a) 6.022 × 1026
(b) 6.022 × 1023
(c) 6.022 × 1020
(d) 9.9 × 1022
Answer:
(c) 6.022 × 1020
Solution:
Weight of the water drop 0.018 g
No. of moles of water in the drop = Mass of water / molar mass = 0.018/18 = 10-3 mole
No of water molecules present in 1 mole of water = 6.022 × 1023
No. water molecules in one drop of water(10-3 mole)
= 6.022 × 1023 × 10-3
= 6.022 × 1020
Question 7.
1 g of an impure sample of magnesium carbonate (containing no thermally decomposable impurities) on complete thermal decomposition gave 0.44 g of carbon dioxide gas. The percentage of impurity in the sample is
(a) 0 %
(b) 4.4 %
(c) 16 %
(d) 8.4 %
Answer:
(c) 16 %
Solution:
MgCO3 → MgO + CO2↑
MgCO3:
(1 × 24) + (1 × 12) + (3 × 16) = 84 g
CO2: (1 × 12) + (2 × 16) = 44g
100 % pure 84 g MgCO3 on heating gives 44 g CO2
Given that 1 g of MgCO3 on heating gives 44 g of CO2
Therefore, 84 g MgCO3 sample on heating gives 36.96 g CO2
Percentage of purity of the sample = \(\frac{100 \%}{44 \mathrm{~g} \mathrm{CO}_{2}}\) × 36.96 g of CO2 = 84 %
Percentage of impurity = 16 %
Question Question 8.
When 6.3 g of sodium bicarbonate is added to 30 g of acetic acid solution, the residual solution is found to weigh 33 g. The number of moles of carbon dioxide released in the reaction is
(a) 3
(b) 0.75
(c) 0.075
(d) 0.3
Answer:
(c) 0.075
solution:
NaHCO3 + CH3COOH → CH3OONa + H2O + CO2
6.3 g + 30 g → 33 g + x
The amount of CO2 released, x = 3.3 g
No. of moles of CO2 released = 3.3/44 = 0.075 mol.
![]()
Question 9.
When 22.4 litres of H2 (g) is mixed with 11.2 litres of Cl2 (g), each at 273 K at 1 atm the moles of HCl (g), formed is equal to
(a) 2 moles of HCl (g)
(b) 0.5 moles of HCl (g)
(c) 1.5 moles of HCl (g)
(d) 1 moles of HCl (g)
Answer:
(d) 1 moles of HCl (g)
Solution:
H2(g) + Cl2(g) → 2HCl(g)
| Content | CH4 | 02 | CO2 |
| Stoichiometric coefficient | 1 | 1 | 2 |
| No. of moles of reactants allowed to react at 273 K and 1 atm pressure |
22.4 L (1 mol) |
11.2 L (0.5 mol) | _ |
| No. of moles of a reactant reacted and product formed | 0.5 | 0.5 | _ |
Amount of HCl formed = 1 mol
Question 10.
Hot concentrated sulphuric acid is a moderately strong oxidising agent. Which of the following reactions does not show oxidising behaviour?
(a) Cu + 2H2 → CuSO4 + SO2 +2 H2O
(b) C + 2 H2SO4 → CO2 + 2 SO2 +2 H2O
(c) BaCl2 + H2SO4 → BaSO4 + 2HCl
(d) none of the above
Answer:
(c) BaCl2 + H2SO4 → BaSO4 + 2HCl
Solution:
![]()
Question 11.
Choose the disproportionation reaction among the following redox reactions.
(a) 3Mg(s) + N2(g) → Mg3N2(s)
(b) P4(s) + 3NaOH + 3H2O → PH3(g) + 3NaH2PO2(aq)
(c) Cl2(g) + 2KI(aq) → 2KCl(aq) + I2(s)
(d) Cr2O3(s) + 2Al(s) → Al2O3(s) + 2Cr(s)
Answer:
b) P4(s) + 3NaOH + 3H2O → PH3(g) + 3NaH2PO2(aq)
Solution:
![]()
Question 12.
The equivalent mass of potassium permanganate in an alkaline medium is
MnO4 + 2H2O + 3e → MnO2 + 4OH–
(a) 31.6
(b) 52.7
(c) 79
(d) None of these
Answer:
(b) 52.7
Solution:
The reduction reaction of the oxidising agent (Mn04) involves the gain of 3 electrons.
Hence the equivalent mass = (Molar mass of KMnO4)/3 = 158.1/3 = 52.7
![]()
Question 13.
Which one of the following represents 180g of water?
(a) 5 Moles of water
(b) 90 moles of water
(c) \(\frac{6.022 \times 10^{23}}{180}\)
(d) \(\frac{6.022 \times 10^{23}}{1.7}\)
Answer:
(d) \(\frac{6.022 \times 10^{23}}{1.7}\)
Solution:
No. of moles of water present in 180 g = Mass of water / Molar mass of water = 180 g/18 gmol-1 = 10 moles
One mole of water contains = 6.022 × 1023 water molecules
10 mole of water contains = 6.022 × 1023 × 10 × 6.022 × 1024 water molecules
Question 14.
7.5 g of a gas occupies a volume of 5.6 litres at 0° C and 1 atm pressure. The gas is
(a) NO
(b ) N2O
(c) CO
(d) CO2
Answer:
(a) NO
Solution:
7.5 g of gas occupies a volume of 5.6 liters at 273 K and 1 atm pressure Therefore, the mass of gas that occupies a volume of 22.4 liters
= \(\frac{7.5 g}{5.61}\) × 22.41 = 30 g
Molar mass of NO (14 + 16) = 30 g
Question 15.
Total number of electrons present in 1.7 g of ammonia is
(a) 6.022 × 1023
(b) \(\frac{6.022 \times 10^{22}}{1.7}\)
(c) \(\frac{6.022 \times 10^{24}}{1.7}\)
(d) \(\frac{6.022 \times 10^{23}}{1.7}\)
Answer:
(a) 6.022 × 1023
Solution:
No. of electrons present in one ammonia (NH3) molecule (7 + 3) = 10
No. of moles of ammonia = \(\frac{\text { Mass }}{\text { Molar mass }}\)
= \(\frac{1.7 \mathrm{~g}}{17 \mathrm{~mol}^{-1}}\) = 0.1 mol
= 0.1 × 6.022 × 1023 = 6.022 × 1022
= No. of electrons present in 0.1 mol of ammonia
Question 16.
The correct increasing order of the oxidation state of sulphur in the anions
SO42-, SO32-, S2O42-, S2O62- is
(a) SO32- < SO42- < S2O42- < S2O62-
(b) SO42- < S2O42- < S2O62- < SO32-
(c) S2O42- < SO32- < S2O62- < SO42-
(d) S2O62- < S2O42- < SO42- < SO32-
Answer:
(c) S2O42- < SO32- < S2O62- < SO42-
Solution:
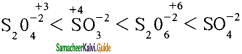
![]()
Question 17.
The equivalent mass of ferrous oxalate is
(a) \(\frac{\text { molar mass of ferrous oxalate }}{1}\)
(b) \(\frac{\text { molar mass of ferrous oxalate }}{2}\)
(c) \(\frac{\text { molar mass of ferrous oxalate }}{3}\)
(d) none of these
Answer:
(c) \(\frac{\text { molar mass of ferrous oxalate }}{3}\)
Solution:
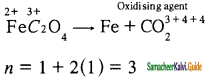
Question 18.
If Avogadro number were changed from 6.022 × 1023 to 6.022 × 1020, this would change
(a) the ratio of chemical species to each other in a balanced equation
(b) the ratio of elements to each other in a compound
(c) the definition of mass in units of grams
(d) the mass of one mole of carbon
Answer:
(d) the mass of one mole of carbon
Question 19.
Two 22.4 liter containers A and B contains 8 g of O2 and 8 g of SO2 respectively at 273 K and 1 atm pressure, then
(a) Number of molecules in A and B are the same
(b) Number of molecules in B is more than that in A.
(c) The ratio between the number of molecules in A to number of molecules in B is 2 : 1
(d) Number of molecules in B is three times greater than the number of molecules in A.
Answer:
(c) The ratio between the number of molecules in A to number of molecules in B is 2 : 1
Solution:
No. of moles of oxygen = 8 g/32 g = 0.25 moles of oxygen
No. of moles of sulphur dioxide = 8 g/64 g
= 0.125 moles of sulphur dioxide
Ratio between the no. of molecules = 0.25 : 0.125 = 2 : 1
Question 20.
What is the mass of precipitate formed when 50 ml of 8.5 % solution of AgNO3 is mixed with 100 ml of 1.865 % potassium chloride solution?
(a) 3.59 g
(b) 7 g
(c) 14 g
(d) 28 g
Answer:
(a) 3.59 g
Solution:
AgNO3 + KCl → KNO3 + AgCl
50 mL of 8.5 % solution contains 4.25 g of AgNO3
No. of moles of AgNO3 present in 50 mL of 8.5 % AgNO3 solution
= Mass / Molar mass = 4.25 / 170 = 0.025 moles
Similarly, No of moles of KCl present in 100 mL of 1.865 % KCl solution = 1.865 / 74.5 = 0.025 moles
So total amount of AgCl formed is 0.025 moles (based on the stoichiometry)
Amount of AgCl present in 0.025 moles of AgCl
= No. of moles × molar mass = 0.025 × 143.5 = 3.59 g
![]()
Question 21.
The mass of a gas that occupies a volume of 612.5 ml at room temperature and pressure (25°C and 1 atm pressure) is 1.1 g. The molar mass of the gas is
(a) 66.25 g mol-1
(b) 44 g mol-1
(c) 24.5 g mol-1
(d) 662.5 g mol-1
Answer:
(b) 44 g mol-1
Solution:
No. of moles of a gas that occupies a volume of 612.5 mL at room temperature and pressure (25° C and 1 atm pressure)
= 612.5 × 10-3 L/24.5 L mol-1
= 0.025 moles
We know that,
Molar mass = Mass / no. of moles
= 1.1 g / 0.025 mol
= 44 g mol-1
Question 22.
Which of the following contain the same number of carbon atoms as in 6 g of carbon -12.
(a) 7.5 g ethane
(b) 8 g methane
(c) both (a) and (b)
(d) none of these
Answer:
(c) both (a) and (b)
Solution:
No. of moles of carbon present in 6 g of C – 12 = Mass/Molar mass
= 6/12 = 0.5 moles
= 0.5 × 6.022 × 1023 carbon atoms.
No. of moles in 8 g of methane
= 8/16 = 0.5 moles
= 0.5 × 6.022 × 1023 carbon atoms.
No. of moles in 7.5 g of ethane = 7.5 / 16 = 0.25 moles
= 2 × 0.25 × 6.022 × 1023 carbon atoms.
Question 23.
Which of the following compound(s) has/have a percentage of carbon same as that in ethylene (C2H4)
(a) Propene
(b) ethyne
(c) benzene
(d) ethane
Answer:
(a) Propene
Solution:
Percentage of carbon in ethylene (C2H4) = \(\frac{\text { mass of carbon }}{\times 100 \text { Molar mass }}\)
= \(\frac{24}{28}\) × 100 = 85.71 %
Percentage of carbon in propene (C3H6) = \(\frac{24}{28}\) × 100 = 85.71 %
Question 24.
Which of the following is/are true with respect to carbon -12.
(a) relative atomic mass is 12 u
(b) oxidation number of carbon is +4 in all its compounds.
(c) 1 mole of carbon-12 contains 6.022 × 1022 carbon atoms.
(d) all of these
Answer:
(a) relative atomic mass is 12 u
Question 25.
Which one of the following is used as a standard for atomic mass.
(a) 6C12
(b) 7C12
(c) 6C13
(d) 6C14
Answer:
(a) 6C12
![]()
II. Write brief answer to the following questions:
Question 26.
Define relative atomic mass.
Answer:
Relative atomic mass is defined as the ratio of the average atomic mass factor to the unified atomic mass unit.
Relative atomic mass (Ar) = \(\frac{\text { Average mass of the atom }}{\text { Unified atomic mass }}\)
Question 27.
What do you understand by the term mole?
Answer:
The mole is defined as the amount of a substance which contains 6.023 x 1023 particles such as atoms, molecules, or ions. It is represented by the symbol.
Question 28.
Define equivalent mass.
Answer:
Gram equivalent mass of an element, compound or ion is the mass that combines or displaces 1.008 g hydrogen or 8 g oxygen or 35.5 g chlorine. Equivalent mass has no unit but gram equivalent mass has the unit g eq-1.
Gram equivalent mass = \(\frac{\text { Molar mass }\left(\mathrm{g} \mathrm{mol}^{-1}\right)}{\text {Equivalence factor }\left(\mathrm{eq} \mathrm{mol}^{-1}\right)}\)
Question 29.
Distinguish between oxidation and reduction.
Answer:
| Oxidation | Reduction |
| 1. Reactions involving the addition of oxygen | Reactions involving removal of hydrogen |
| 2. Reactions involving loss of an electron | Reactions involving gain of electron |
| 3. Reaction in which oxidation number of the element increases. | Reaction in which oxidation number of the element decreases. |
Question 30.
What do you understand by the term oxidation number.
Answer:
Oxidation:
According to the classical concept, oxidation is a process of addition of oxygen or removal of hydrogen.
Removal of hydrogen
2H2S + O2 → H2O + 2S
Addition of oxygen
C + O2 → CO2
According to the electronic concept, loss of electrons is called oxidation reaction.
Ca → Ca2+ + 2e–
During oxidation, oxidation number increases.
Dining oxidation, reducing agent gets oxidised.
Reduction:
Reduction is a process of removal of oxygen or addition of hydrogen.
Addition of hydrogen
Ca + H2 → CaH2
Removal of oxygen
Zn O + C → Zn + CO
According to the electronic concept, gain of electrons is called a reduction reaction.
Zn2+ + 2e– → Zn
During reduction, oxidation number decreases.
During reduction, oxidising agent gets reduced.
![]()
Question 31.
Calculate the molar mass of the following compounds.
Answer:
(i) urea [CO(NH2)2]:
Molar mass of urea = (4 × Atomic mass of hydrogen) + ( 1 × Atomic mass of carbon) + ( 2 × Atomic mass of nitrogen) + ( 1 × Atomic mass of oxygen)
= (4 × 1.008) +(1 × 12) + (2 × 14)+ ( 1 × 16)
= 4.032 + 12 + 28 + 16 = 60.032 g mol-1
(ii) acetone[CH3COCH3]
Molar mass of Acetone = (6 × Atomic mass of hydrogen) + ( 3 × Atomic mass of carbon) + (1 × Atomic mass of oxygen) = (6 × 1.008) + (3 × 12) + ( 1 × 16)
= 6.048 + 36 + 16 = 52.024 g mol-1.
(iii) boric acid [H3BO3]:
Molar mass of Boric acid = (3 × Atomic mass of hydrogen) + ( 1 × Atomic mass of boron) + ( 3 × Atomic mass of oxygen)
= (3 × 1.008) + (3 × 11) + ( 1 × 16)
= 3.024 + 33 + 16 = 52.024 g mol-1.
(iv) sulphuric acid [H2SO4] = (2 × Atomic mass of hydrogen) + ( 1 × Atomic mass of sulphur) + ( 4 × Atomic mass of oxygen)
= (2 × 1.008) +(1 × 32) + (4 × 16)
= 2.016 + 32 +64 = 98.016 g mol-1.
Question 32.
The density of carbon dioxide is equal to 1.965 kgm-3 at 273 K and 1 atm pressure. Calculate the molar mass of CO2.
Answer:
Given:
The density of C02 at 273 K and 1 atm pressure = 1.965 kgm-3
Molar mass of CO2 =?
At 273 K and 1 atm pressure, 1 mole of CO2 occupies a volume of 22.4 L
Mass of 1 mole of CO2 = \(\frac{1.965 \mathrm{Kg}}{1 \mathrm{~m}^{3}}\) × 22.4 L
= \(\frac{1.965 \times 10^{3} \mathrm{~g} \times 22.4 \times 10^{-3} \mathrm{~m}^{3}}{1 \mathrm{~m}^{3}}\)
= 44.01 g
Molar mass of CO2 = 44 gmol-1
Question 33.
Which contains the greatest number of moles of oxygen atoms.
1 mol of ethanol
1 mol of formic acid
1 mol of H2O
Answer:
|
Compound |
Given no. of moles |
No. of oxygen atoms |
|
Ethanol – C2H5OH |
1 | 1 × 6.022 × 1023 |
|
Formic acid -HCOOH |
1 |
2 × 6.022 × 1023 |
| Water – H2O | 1 |
1 × 6.022 × 1023 |
Answer: Formic acid
Question 34.
Calculate the average atomic mass of naturally occurring magnesium using the following data:
| Isotope | Isotopic atomic mass | Abundance (%) |
| Mg24 | 23.99 | 78.99 |
| Mg26 | 24.99 | 10.00 |
| Mg25 | 25.98 | 11.01 |
Answer:
Average atomic mass
= \(\frac{(78.9923 .99)(1024.99)(11.0125 .98)}{100}\)
= \(\frac{2430.9}{100}\)
= 24.31 u
Question 35.
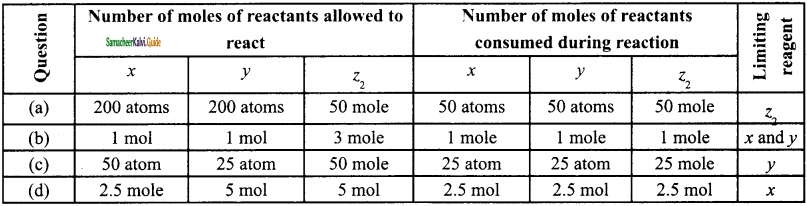
In a reaction x + y + xyz. identify the Limiting reagent if any, in the following reaction mixtures.
(a) 200 atoms of x + 200 atoms of y + 50 molecules of z2.
(b) 1 mol of x + 1 mol ofy + 3 mol of z2.
(c) 50 atoms of x + 25 atoms of y + 50 molecules of z2.
(d) 2.5 mol ofx + 5 mol ofy + 5 mol of z2.
Reaction:
x + y + z2 → xyz2
(a) 200 atoms of x + 200 atoms of y + 50 molecules of z2 According to the reaction, 1 atom of x reacts with one atom of y and one molecule of z to give product. In the case (a) 200 atoms of x, 200 atoms of y react with 50 molecules of z2 (4 part) i.e. 50 molecules of z2 react with 50 atoms of x and 50 atoms of y. Hence z is the limiting reagent.
(b) 1 mol of x + 1 mol of y + 3 mol of z2
According to the equation 1 mole of z2 only react with one mole of x and one mole of y. If 3 moles of z2 are there, z is limiting reagent.
(c) 50 atoms of x + 25 atoms of y + 50 molecules of z2
25 atoms of y react with 25 atoms of x and 25 molecules of z2. So y is the limiting reagent.
(d) 2.5 mol of x + 5 mol of y + 5 mol of z2
2.5 mol of x react with 2.5 mole of y and 2.5 mole of z2. So x is the limiting reagent.
![]()
Question 36.
Mass of one atom of an element is 6.645 × 1023 g How many moles of element are there in 0.320 kg.
Answer:
there in 0.320 kg
Given:
mass of 1 atom = 6.645 × 10-23 g
∴ mass of 1 mole of atom = 6.645 × 10-2323 g × 6.022 × 1023 = 40 g
∴ Number of moles of element in 0.320 kg = \(\frac{1 \mathrm{~mol}}{40 \mathrm{~g}}\) × 0.320 kg
= \(\frac{1 \mathrm{~mol} \times 320 \mathrm{~g}}{40 \mathrm{~g}}\) = 8 mol
Question 37.
What is the difference between molecular mass and molar mass? Calculate the molecular mass and molar mass for carbon monoxide.
Answer:
Molecular mass:
- Relative molecular mass is defined as the ratio of the mass of the molecule to the unified atomic mass unit.
- It can be calculated by adding the relative atomic masses of its constituent atoms.
- For carbon monoxide (CO) Molecular mass = Atomic mass of carbon + Atomic mass of oxygen 12 + 16 = 28 u.
Molar mass:
- It is defined as the mass of one mole of a substance.
- The molar mass of a compound is equal to the sum of the relative atomic masses of its constituent expressed in g mol-1.
- For carbon monoxide (CO) 12 + 16 = 28 g mol-1 Both molecular mass and molar mass are numerically the same but the units are different.
Question 38.
What is the empirical formula of the following?
(i) Fructose (C6H12O6) found in honey
(ii) Caffeine (C8H10N4O2 )a substance found in tea and coffee.
Answer:
| Compound | Molecular formula | Empirical formula |
| Fructose | C6H12O6 | CH2O |
| Caffeine | C8H10N4O2 | C4H5N2O |
Question 39.
The reaction between aluminium and ferric oxide can generate temperatures up to 3273 K and is used in welding metals. (Atomic mass of AC = 27 u Atomic mass of O = 16 u)
2Al + Fe2O3 → Al2O3 + 2Fe; If, in this process, 324 g of aluminium is allowed to react with 1.12 kg of ferric oxide
(i) Calculate the mass of Al2O3 formed.
(ii) How much of the excess reagent is left at the end of the reaction?
Answer:
Given:
2Al + Fe2O3 → Al2O3 + 2Fe
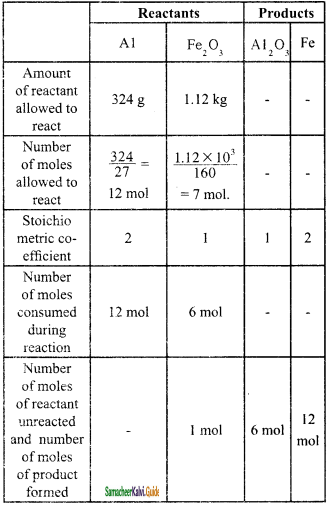
Molar mass of Al2O3 formed = 6mol × 102 g mol-1 = 612 g
[Al2O3 = (2 × 27) + (3 × 16) = 54 + 48 = 102]
Excess reagent = Fe2O3.
Amount of excess reagent left at the end of the reaction = 1 mol × 160 g mol-1 = 160 g
[Fe2O3 = (2 × 56) + (3 × 16) = 112 + 48 = 160 g] = 160 g
Question 40.
How many moles of ethane is requircd to produce 44 g of CO2 (g) after combustion. Balanced equation for the combustion of ethane.
Answer:
C2H6 + \(\frac{7}{2}\)O2 → 2CO2 + 3H2O
⇒ 2C2H6 + 7O2 → 4CO2 + 6H2O
∴ To produce 4 moles of CO2, 2 moles of ethane is required
To produce 1 mole (44g) of CO2 required number of moles of ethane
= \(\frac{1}{2}\) mole of ethane
= 0.5 mole of ethane
![]()
Question 41.
Hydrogen peroxide is an oxidising agent. It oxidises ferrous ion to ferric ion and reduced itself to water. Write a balanced equation.
Answer:

Question 42.
Calculate the empirical and molecular formula of a compound containing 76.6% carbon, 6.38 % hydrogen and rest oxygen its vapour density is 47.
Answer:
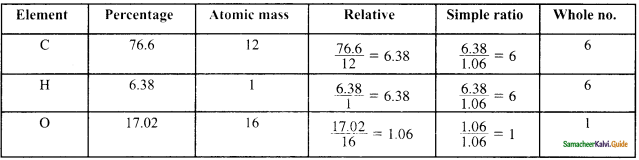
Empirical formula = C6H6O
η = Molar mass / Calculated empirical formula mass = \(\frac{2 \times \text { vapour density }}{94}\)
= \(\frac{2 \times 47}{94}\) = 1
∴ Molecular formula(C6H6O) × 1 = C6H6O
Question 43.
A Compound on analysis gave Na = 14.31% S = 9.97% H= 6.22% and 0= 69.5% calculate the molecular formula of the compound if all the hydrogen in the compound is present in combination with oxygen as water of crystallization, (molecular mass of the compound is 322).
Answer:
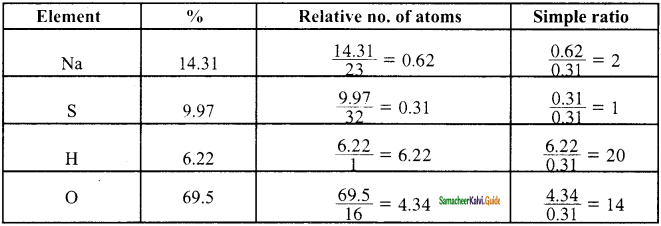
∴ Empirical formula = Na2SH20O14
η = Molar mass / Calculated empirical formula mass
= \(\frac{322}{322}\) = 1
[Na2SH20O14 = (2 × 23) + (1 × 32) + (20 × 1) + (14 × 16)
= 46 + 32 + 20 + 224 = 322]
Molecular formula = Na2SH20O14
Since all the hydrogen in the compound present as water
∴ Molecular formula is Na2SH20O14
Question 44.
Balance the following equations by oxidation number method
(i) K2Cr2O7 + KI + H2SO4 → K2SO4 + Cr2(SO4)3 + I2 + H2O
Answer:

K2Cr2O7 + 6KI + H2SO4 → K2SO4 + Cr2(SO4)3 + I2 + H2O
K2Cr2O7 + 6KI + H2SO4 → K2SO4 + Cr2(SO4)3 + 3I2 + H2O
K2Cr2O7 + 6KI + 7H2SO4 → 4K2SO4 + Cr2(SO4) + I2 + 7H2O
(ii) KMnO4 + Na2SO3 → MnO2 + Na2SO4 + KOH
Answer:
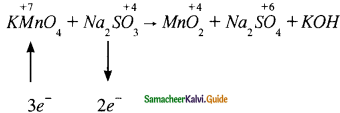
⇒ 2KMnO4 + 3Na2SO3 → MnO2 + Na2SO4 + KOH
⇒ 2KMnO4 + 3Na2SO3 → 2MnO2 + 3Na2SO4 + KOH
⇒ 2KMnO4 + 3Na2SO3 → MnO2 + Na2SO4 + 2KOH
(iii) Cu + HNO3 → Cu(NO3)2 + NO2 + H2O
Answer:
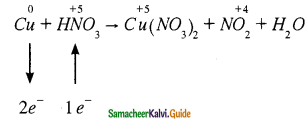
Cu + 2HNO3 → Cu(NO3)2 + NO2 + H2O
Cu + 2HNO3 + 2HNO3 → Cu(NO3)2 + 2NO2 + 2H2O
Cu + 4HNO3 → Cu(NO3)2 + 2NO2 + 2H2O
(iv) KMnO4 + H2C2O4 + H2SO4 → K2SO + MnSO4 + CO2 + H2O
Answer:
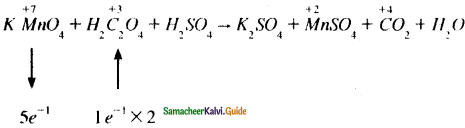
KMnO4 + 5H2C2O4 + H2SO4 → K2SO + MnSO4 + CO2 + H2O
2KMnO4 + 5H2C2O4 + H2SO4 → 2MnSO4 + 10CO2 + H2O
2KMnO4 + 5H2C2O4 + 3H2SO4 → K2SO + 2MnSO4 + 10CO2 + 8H2O
![]()
Question 45.
Balance the following equations by ion electron method.
(i) KMnO4 + SnCl2 + HCl → MnCl2 SnCl4 + H2O + KCl
Answer:
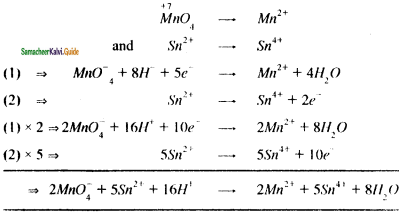
(ii) C2O42- + Cr2O72- →
Cr3+ + CO2 (in acid medium)
Answer:

(iii) Na2S2O3 + I2 → Na2S4O6 + NaI 2 (in acid medium)
Answer:
S2O32- → S4O62- ………….(1)
Half reaction ⇒ I2 → I– …………….(2)
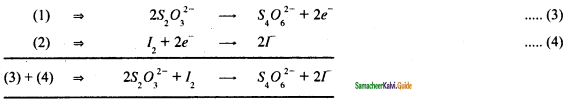
(iv) Zn + NO3– → Zn+2 + NO
Half reactions are

![]()
11th Chemistry Guide Basic Concepts of Chemistry and Chemical Calculations Additional Questions and Answers
I. Choose the best answer:
Question 1.
_____ consists of more than one chemical entity present without any chemical interactions.
(a) Mixtures
(b) Pure substances
(c) Compounds
(d) Elements
Answer:
(a) Mixtures
Question 2.
_______ are made up of molecules which contain two or more atoms of different elements.
(a) Mixtures
(b) Compounds
(c) Pure substances
(d) Elements
Answer:
(b) Compounds
Question 3.
Match the correct pair:
| A. Compound | (i) S8 |
| B. Mixture | (ii) Glucose |
| C. Element | (iii) Air |
(a) A – ii, B – i, C – iii
(b) A – i, B – ii, C – iii
(c) A – ii, B – iii, C – i
(d) A – iii, B – ii, C – i
Answer:
(c) A – ii, B – iii, C – i
Question 4.
_______ atom is considered as standard by the IUPAC for calculating atomic masses.
(a) C – 13
(b) C – 15
(c) C – 14
(d) C – 12
Answer:
(d) C – 12
Question 5.
The value of unified mass is equal to
(a) 1.6605 × 10-27 kg
(b) 1.6736 × 10-27 kg
(c) 1.6605 × 1027 kg
(d) 1.6736 × 10-29 kg
Answer:
(a) 1.6605 × 10-27 kg
![]()
Question 6.
Chlorine consists of two naturally occurring isotopes 17Cl35 and 17Cl37 in the ratio 77 : 23. The average relative atomic mass of chlorine is
(a) 36.45 u
(b) 35.56 u
(c) 35.46 u
(d) 35.65 u
Answer:
(c) 35.46 u
Question 7.
The relative atomic masses of hydrogen, oxygen, and carbon are 1.008 u, 16 u, and 12 u respectively. The relative molecular mass of glucose (C6 H12 O6 ) is
(a) 170.096 u
(b) 189.096 u
(c) 180.096 u
(d) 190.086 u
Answer:
(c) 180.096 u
Question 8.
The specific amount of a substance is represented in SI unit is
(a) amu
(b) mole
(c) atomic mass
(d) equivalent mass
Answer:
(b) mole
Question 9.
Commonly used medicines for treating heart bum and acidity are called
(a) antipyretics
(b) analgesics
(c) antiseptics
(d) antacids
Answer:
(d) antacids
Question 10.
The typical concentration of hydrochloric acid in gastric acid is
(a) 0.1 M
(b) 0.01 M
(c) 0.082 M
(d) 0.82 M
Answer:
(c) 0.082 M
![]()
Question 11.
Antacids used to treat acidity contain mostly
(a) Al(OH)3
(b) Mg(OH)2
(c) (a) or (b)
(d) Ca(OH)2
Answer:
(c) (a) or (b)
Question 12.
The value of Avogadro number is
(a) 6.022 × 1023
(b) 6.022 × 1022
(e) 6.022 × 10-25
(d) 6.022 × 10-23
Answer:
(a) 6.022 × 1023
Question 13.
The volume occupied by one mole of any substance in the gaseous state st 273 K and 1 atm pressure is _______ (in litres)
(a) 24.5
(b) 22.4
(e) 22.71
(d) 21.18
Answer:
(b) 22.4
Question 14.
The equivalent mass of KMnO4(Molar mass 158 g mol -1 based on the equation
MnO4 + 8H+ + 5e → Mn2+ + 4H2O
(a) 158
(b) 52.66
(c) 31.6
(d) 40
Answer:
(c) 31.6
Question 15.
The molecular formula of acetic acid is C2H4O2 Its empirical formula is
(a) C2H4O2
(b) C2H2O
(c) CH2O2
(d) CH2O
Answer:
(d) CH2O
![]()
Question 16.
The number of moles of hydrogen required to produce 20 moles of ammonia is
(a) 10
(b) 15
(c) 30
(d) 20
Answer:
(c) 30
Question 17.
Which of the following is/are redox reactions?
(i) 4Fe + 3O2 → 2Fe2O3
(ii) H2S + Cl2 → 2HCl + S
(iii) CuO + C → Cu + CO
(iv) S +H2 → H2S
(a) (i) and (ii)
(b) (i) and (iii)
(c) (ii) and (iv)
(d) (iii) and (iv)
Answer:
(d) (iii) and (iv)
Question 18.
The oxidation number of sulphur on H2SO4 is
(a) -2
(b) -6
(c) +2
(d) +6
Answer:
(d) +6
Question 19.
Choose the correct pair:
| Compound | Oxidation number |
| A. Cr in Cr2O7 | (i) +4 |
| B. C in CO2 | (ii) +2 |
| C. C in CH2F2 | (iii) +6 |
| D. Mn in MnSO4 | (iv) 0 |
(a) A – i, B – iv, C- iii, D – ii
(b) A – iii, B – i, C – iv, D – ii
(c) A – i, B – ii, C – iv, D – iii
(d) A – iii, B – iv, C – i, D – ii
Answer:
(b) A – iii, B – i, C – iv, D – ii
Question 20.
The change in the oxidation number of Manganese in the following reaction 2 KMnO4 + 10 FeSO4 + 8 H2SO4 → K2SO4 + 5 Fe2(SO4)3 + 8 H2O
(a) +2 to +7
(b) +2 to +5
(c) +7 to +2
(d) +5 to +2
Answer:
(c) +7 to +2
![]()
Question 21.
Which of the following statements are correct about oxidation?
(i) Removal of oxygen
(ii) Addition of hydrogen
(iii) Loss of electron
(iv) Gain of electron
(v) Addition of oxygen
(vi) Removal of hydrogen
(a) i, ii, iv
(b) iii, v, vi
(c) i, iii, v
(d) iii, iv, v
Answer:
(b) iii, v, vi
Question 22.
Choose the correct oxidation number of oxygen in the following compounds.
| (A) KO2 | (i) -2 |
| (B) H2O | (ii) +2 |
| (C) H2O2 | (iii) -1/2 |
| (D) OF2 | (iv) -1 |
(a) A -iii, B- iv, C – i, D – ii.
(b) A – iv, B – i, C – iii, D – ii
(c) A – iii, B – i, C – iv, D – ii
(d) A – iv, B – iii, C – i, D – ii
Answer:
(c) A – iii, B – i, C – iv, D – ii
Question 23.
The correct order of electron releasing tendency of the following elements is
(a) Zn > Cu > Ag
(b) Cu > Zn > Ag
(c) Ag > Zn > Cu
(d) Ag > Cu > Zn
Answer:
(a) Zn > Cu > Ag
Question 24.
H2O2 → 2 H2O + O2 is a
(a) Displacement reaction
(b) Combinationreaction
(c) Decomposition reaction
(d) Disproportionate reaction
Answer:
(d) Disproportionate reaction
Question 25.
The molar mass and empirical formula mass of a compound are 78 and 13 respectively. The molecular formula of the compound is (Empirical formula is CH)
(a) C2H2O2
(b) C2H4
(c) C6H6
(d) C3H8
Answer:
(c) C6H6
![]()
II. Very Short Question and Answers (2 Marks):
Question 1.
State Avogadro’s Hypothesis.
Answer:
It states that ‘Equal volume of all gases under the same conditions of temperature and pressure contain the same number of molecules’.
Question 2.
How is matter classified physically?
Answer:
Matter can be classified as solids, liquids, and gases based on their physical state. The physical state of matter can be converted into one another by modifying the temperature and pressure suitably.
Question 3.
How is matter classified chemically?
Answer:
Matter can be classified into mixtures and pure substances based on chemical compositions.
Question 4.
Calculate a number of moles of carbon atoms ¡n three moles of ethane.
Answer:
Ethane – Molecular formula = C2H6
1 mole of ethane contains 2 atoms of carbon (6.023 x 1023 C)
∴ 3 moles of ethane contains 6 atoms of Carbon.
∴ No. of moles of Carbon atoms = 3 x 6.023 x 1023 Carbon atoms.
= 18.069 x 1023 Carbon atoms.
Question 5.
What are pure substances? How are they classified?
Answer:
Pure substances are composed of simple atoms or molecules. They are further classified as elements and compounds.
![]()
Question 6.
Mass of one atom of an element ¡s 6.66 x 1023 g. How many moles of the element are there in 0.320 kg?
Answer:
Mass of one atom of an element = 6.66 x 1023g
No. of moles = \(\frac {Mass}{Molecular mass}\) 3
Molecular mass = Mass of 1 atom x Avogadro number
6.66 x 1023 x 6.023 x 1023
= 6.66 x 6.023 = 40.11318
Number of moles = \(\frac {Mass}{Molecular mass}\) = \(\frac{0.320 \mathrm{kg} \times 10^{3}}{40}\) = 8 moles.
Question 7.
What are compounds? Give examples.
Answer:
Compounds are made up of molecules which contain two or more atoms of different elements.
Example: Carbon dioxide (CO2), Sodium Chloride (NaCl).
Question 8.
Calculate the weight of 0.2 moles of sodium carbonate.
Answer:
Sodium carbonate = Na2CO3
Molecular mass of Na2CO3 = (23 x 2)+(12 x 1)+(16 x 3)
= 46 + 12 + 48 = 106 g
Mass of 1 mole of Na2CO3 = \(\frac{106 \times 0.2}{1}\) = 21.2 g
Question 9.
Define relative atomic mass.
Answer:
The relative atomic mass is defined as the ratio of the average atomic mass factor to the unified atomic mass unit.
Relative atomic mass
(Ar) = Average mass of the atom / Unified atomic mass
Question 10.
What is the average atomic mass?
Answer:
Average atomic mass is defined as the average of the atomic masses of all atoms in their naturally occurring isotopes.
![]()
Question 11.
Calculate the equivalent mass of barium hydroxide.
Answer:
Barium hydroxide = Ba(OH)2
Molecular mass of Ba(OH)2 = 137 + (16 x 2) + (1 x 2) = 171.0 g / mol.
Acidity = 2
Equivalent mass of Ba(OH)2 = \(\frac {17 1.0}{2}\) = 85.5
Question 12.
What is a mole?
Answer:
One mole is the amount of substance of a system, which contains as many elementary particles as there are atoms in 12 g of carbon – 12 isotope. The elementary particles can be molecules, atoms, ions, electrons or any other specified particles.
Question 13.
What do you understand by the terms empirical formula and molecular formula?
Answer:
Empirical Formula:
- It is the simplest formula.
- It shows the ratio of the number of atoms of different elements in one molecule of the compound.
Molecular Formula:
- It is the actual formula.
- It shows the actual number of different types of atoms present in one molecule of the compound.
Question 14.
What is Avogadro’s number?
Answer:
The total number of entities present in one mole of any substance is equal to 6.022 × 1023. This number is called the Avogadro number.
Question 15.
State Avogadro hypothesis.
Answer:
Equal volume of all gases under the same conditions of temperature and pressure contain equal number of molecules.
![]()
Question 16.
Calculate the mass of sodium (in kg) present in 95 kg of a crude sample of sodium nitrate whose percentage purity is 70%.
Answer:
Sodium Nitrate = NaNO3
Molecular mass of Sodium Nitrate = 23 + 14 + 48 = 85
100% pure 85 g of NaNO3 contains 23 g of Sodium.
100% pure 95 x 103 g of NaNO3 will contains \(\frac {23}{85}\) x 95 x 103
= 25.70 x 103 g of Sodium.
100% pure NaNO3 contains 25.70 x 103 g of Sodium.
∴ 70% pure NaNO3 will contains = 17990 g (or) 17.99 Kg of Na.
Question 17.
Define molar volume.
Answer:
The volume occupied by one mole of any substance in the gaseous state at a given temperature and pressure is called molar volume.
Question 18.
What is gram equivalent mass?
Answer:
Gram equivalent mass of an element, compound or ion is the mass that combines or displaces 1.008 g hydrogen or 8 g oxygen or 35.5 g chlorine.
Gram equivalent mass = (Molar mass(g mol-1)) / Equivalence factor (eq mol-1)
Question 19.
What is meant by Plasma state? Give an example.
Answer:
The gaseous state of matter at a very high temperature containing gaseous ions and free-electron is referred to as the Plasma state. e.g. Lightning.
Question 20.
What is the acidity of a base? Give an example.
Answer:
The acidity of a base is the number of moles of ionizable OH- ions present in 1 mole of the base. The acidity of potassium hydroxide (KOH) is 1.
![]()
Question 21.
What is empirical formula ola compound?
Answer:
The empirical formula of a compound is the formula written with the simplest ratio of the number of different atoms present in one molecule of the compound as a subscript to the atomic symbol.
Question 22.
Chlorine has a fractional average atomic mass. Justify this statement.
Answer:
Chlorine molecule has two isotopes as in 17Cl35, 17 Cl37 in the ratio of 77 : 23, so when we are calculating the average atomic mass, it becomes fractional.
The average relative atomic mass of Chlorine = \(\frac {(35 x 77) + (37 x 23)}{100}\) = 35.46 amu
Question 23.
What is meant by Stoichiometry?
Answer:
Stoichiometry is the quantitative relationship between reactants and products in a balanced chemical equation in moles. The quantity of reactants and products can be expressed in moles or in terms of mass unit or as volume.
Question 24.
What are limiting and excess reagents?
Answer:
When a reaction is carried out using non-stoichiometric quantifies of the reactants, the product yield will be determined by the reactant that is completely consumed and is called the limiting reagent. It limits the further reaction to take place. The other reagent which is in excess is called the excess reagent.
Question 25.
Define Avogadro Number.
Answer:
Avogadro number is the number of atoms present in one mole of an element or number of molecules present in one mole of a compound. The value of Avogadro number (N) = 6.023 x 1023
![]()
Question 26.
Define oxidation number.
Answer:
The oxidation number is defined as the imaginary charge left on the atom when all other atoms of the compound have been removed in their usual oxidation states that are assigned according to a set of rules.
Question 27.
Calculate the equivalent mass of Copper. (Atomic mass of copper = 63.5)
Answer:
Equivalent mass = \(\frac {Atomic mass}{Valency}\)
Equivalent mass of Copper = \(\frac {63.5}{2}\) = 31.75 g eq-1.
Question 28.
Mention the types of redox reactions?
Answer:
The types of redox reactions are combination reaction, decomposition reaction, displacement reaction, disproportionate reaction and competitive electron transfer reactions.
![]()
III. Short Question and Answers (3 Marks):
Question 1.
Describe the chemical classification of matter.
Answer:
Matter can be classified into mixtures and pure substances based on chemical compositions. Mixtures consists of more than one chemical entity present without any chemical interactions. They can be further classified as homogeneous or heterogeneous mixtures based on their physical appearance. Pure substances are composed of simple atoms or molecules. They are further classified as elements and compounds.
Question 2.
Distinguish between element and compound.
Answer:
An element consists of only one type of atom. Element can exists as monoatomic or polyatomic units. The polyatomic elements are called molecules.
Example: Monoatomic unit – Gold (Au), Copper (Cu);
Polyatomic unit: Hydrogen (H2), Phosphorous (P4).
Compounds are made up of molecules which contain two or more atoms of different elements.
Example: Carbon dioxide (CO2), Glucose (C6 H12 O6)
Properties of compounds are different from those of their constituent elements. For example, sodium is a shiny metal, and chlorine is an irritating gas. But the compound formed from these two elements, sodium chloride shows different characteristics as it is crystalline solid, vital for biological functions.
Question 3.
What is average atomic mass? How is average atomic mass of chlorine calculated?
Answer:
Average atomic mass is defined as the average of the atomic masses of all atoms in their naturally occurring isotopes. Chlorine consists of two naturally occurring isotopes 17Cl37 and 17Cl35 in the ratio 77 : 23, the average relative atomic mass of chlorine is
= ((35 × 77) + (37 × 23)) / 100
= 35.46 u
Question 4.
What will be the mass of one 12C atom in g?
Answer:
Molar mass of 12C = 12.00 g mol-1.
∴ Mass of 6.023 x 1023 carbon atom = 12.0 g
∴ Mass of 1 carbon atom = \(\frac{12}{6.023 \times 10^{23}}\) = 1.992 x 10 g.
![]()
Question 5.
Discuss the role of antacids.
Answer:
Gastric acid is a digestive fluid formed in the stomach and it contains hydrochloric acid. The typical concentration of the acid in gastric acid is 0.082 M. When the concentration exceeds 0.1M it causes heartburn and acidity. Antacids used to treat acidity contain mostly magnesium hydroxide or aluminium hydroxide that neutralizes the excess acid. The chemical reactions are as follows.
3 HCl + Al(OH)3 → AlCl3 + 3H2O
2HCl + Mg(OH)2 → MgCl2 + 2H2O.
From the above reactions, we know that 1 mole of aluminium hydroxide neutralizes 3 moles of HCl while 1 mole of magnesium hydroxide neutralizes 2 moles of HCl.
Question 6.
Explain gram equivalent mass.
Answer:
Gram equivalent mass of an element, compound, or ion is the mass that combines or displaces 1.008 g hydrogen or 8 g oxygen or 35.5 g chlorine.
Consider the following reaction:
Zn + H2 SO4 → ZnSO4 + H2
In this reaction, 1 mole of zinc (65.38 g) displaces one mole of hydrogen molecule (2.016 g). Mass of zinc required to displace 1.008 g hydrogen is
= \(\frac{65.38}{2.016}\) × 1.008
= \(\frac{65.38}{2}\)
= 32.69
The equivalent mass of zinc = 32.69
The gram equivalent mass of zinc = 32.69 g eq-1.
The expression used to calculate gram equivalent mass is
Gram equivalent mass = Molar mass(g mol-1) / Equivalence factor (eq mol-1)
Question 7.
Calculate the gram equivalent mass of sulphuric acid.
Answer:
Basicity of sulphuric acid (H2SO4) = 2eq mol-1
Molar mass of H2SO4 = (2 × 1) +(1 × 32) +(4 × 16) = 56 g mol-1
Gram equivalent mass of H2SO4 = \(\frac{98}{2}\)
= 49 g eq-1
Question 8.
Calculate the gram equivalent mass of potassium hydroxide.
Answer:
Acidity of potassium hydroxide (KOH) = 1 eq mol-1
Molar mass of KOH = (1 × 39) + (1 × 16) + (1 × 1) = 56 g mol-1
Gram equivalent mass of KOH = \(\frac{56}{1}\) = 56 g eq-1.
![]()
Question 9.
Calculate the gram equivalent mass of Potassium permanganate.
Answer:
Potassium permanganate is an oxidizing agent. Molar mass of
KMnO4 = (1 × 39)+ (1 × 55)+ (4 × 16)
= 158 g mol-1
In an acidic medium, permanganate is reduced during oxidation and is given by the following equation,
MnO4– + 8H+ + 5e → Mn2 + 4H2O
Therefore, n = 5.
Gram equivalent mass of KMnO4 = \(\frac{158}{5}\) = 31.6 g mol-1
Question 10.
An acid found in tamarind on analysis shows the following percentage composition: 32 % Carbon; 4 % Hydrogen; 64 % Oxygen. Find the empirical formula of the compound.
Answer:

The ratio of C : H : O is 2 : 3 : 3 and hence, the empirical formula of the compound is CH2O
Question 11.
An organic compound present in vinegar has 40 % Carbon, 6.6 % Hydrogen: and 53.4 % Oxygen. Find the empirical formula of the compound.
Answer:
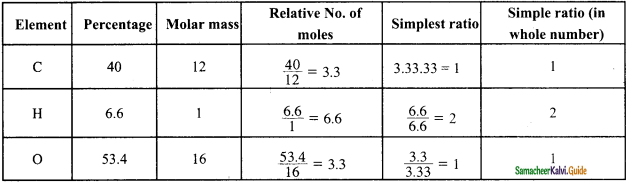
The ratio of C: H : O is 1 : 2 : 1 and hence, the empirical formula of the compound is CH2O.
Question 12.
How much copper can be obtained from 100 g of anhydrous copper sulphate?
Answer:
Anhydrous copper sulphate = CuSO4
Molecular mass of CuSO4 = 63.5 + 32 + (16 x 4)
= 63.5 + 32 + 64
= 159.5 g
159.5 g of CuSO4 contains 63.5 g of copper.
∴ 100 g of CuSO4 contains \(\frac{6.35}{159.5}\) x 100 = 0.39811 x 100 = 39.81 g of Copper.
![]()
Question 13.
Explain the classical concept of oxidation and reduction.
Answer:
According to classical concept, the addition of oxygen or removal of hydrogen is called oxidation.
Consider the following reactions,
4Fe + 3O2 → 2Fe2O3
H2S +Cl2 → 2 HCl + S
In the first reaction, which is responsible for the rusting of iron, the oxygen adds on to the metal, iron. In the second reaction, hydrogen is removed from Hydrogen sulphide.
According to classical concept, addition of hydrogen or removal of oxygen is called reduction.
Consider the following reactions,
CuO + C → Cu + CO
S + H2 → H2S
In the first reaction, oxygen is removed from cupric oxide and in the second reaction, hydrogen is added to sulphur.
Question 14.
Describe the electron concept of oxidation and reduction.
Answer:
The reaction involving loss of electron is termed as oxidation and gain of electron is termed as reduction.
Fe2+ → Fe3+ + e– (loss of electron – oxidation)
Cu2+ + 2e– → Cu ( gain of electron – reduction)
Question 15.
Describe the oxidation number concept of oxidation and reduction.
Answer:
During redox reactions, the oxidation number of elements changes. A reaction in which oxidation number of the element increases is called oxidation whereas the oxidation number of the element 3 decreases is called reduction.

In this reaction, manganese in potassium permanganate favours the oxidation of ferrous sulphate into ferric sulphate by gets reduced.
Question 16.
Write notes on displacement reaction.
Answer:
Redox reactions in which an ion or an atom in a compound is replaced by an ion or an atom of another element are called displacement reactions. They are further classified into
(i) metal displacement reactions
(ii) non-metal displacement reactions.
(i) Metal displacement reactions:
Place a zinc metal strip in an aqueous copper sulfate solution taken in a beaker. The intensity of blue colour of the solution slowly reduced and finally disappeared. The zinc metal strip became coated with brownish metallic copper. This is due to the following metal displacement reaction.
CuSO4(aq)+ Zn(s) → Cu + ZnSO4.
(ii) Non-metal displacement reaction:
Zn + 2HCl → ZnCl2 + H2
![]()
IV. Long Question and Answers:
Question 1.
What is a matter? Explain its classification.
Answer:
Matter is defined as anything that has mass and occupies space. All matter is composed of atoms.
Physical Classification:
Matter can be classified as solids, liquids and gases based on their physical state. The physical state of matter can be converted into one another by modifying the temperature and pressure suitably.
Chemical Classification:
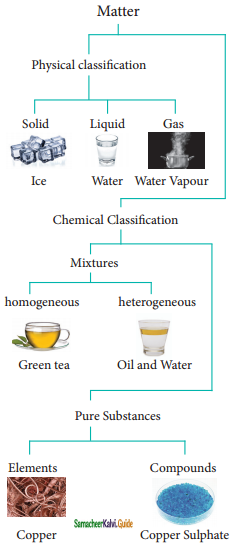
Classification of Matter
Matter can be classified into mixtures and pure substances based on chemical compositions. Mixtures consists of more than one chemical entity present without any chemical interactions. They can be further classified as homogeneous or heterogeneous mixtures based on their physical appearance. Pure substances are composed of simple atoms or molecules. They are further classified as elements and compounds.
An element consists of only one type of atom. Element can exists as monoatomic or polyatomic units. The polyatomic elements are called molecules.
Example: Monoatomic unit – Gold (Au), Copper (Cu);
Polyatomic unit: Hydrogen (H2), Phosphorous (P4).
Compounds are made up of molecules which contain two or more atoms of different elements.
Example: Carbon dioxide (CO2), Glucose (C6H12O6)
Properties of compounds are different from those of their constituent elements. For example, sodium is a shiny metal, and chlorine is an irritating gas. But the compound formed from these two elements, sodium chloride shows different characteristics as it is a crystalline solid, vital for biological function.
Question 2.
How is empirical formula of a compound determined from the elemental analysis?
Answer:
The empirical formula of a compound determined from the elemental analysis by the following steps.
(i) Since the composition is expressed in percentage, we can consider the total mass of the compound as 100 g and the percentage values of individual elements as a mass in grams.
(ii) Divide the mass of each element by its atomic mass. This gives the relative number of moles of various elements in the compound.
(iii) Divide the value of a relative number of moles obtained in the step – (ii) by the smallest number of them to get the simplest ratio.
(iv) In case the simplest ratios obtained in step – (iii) are not whole numbers then they may be converted into the whole numbers by multiplying a suitable smallest number.
![]()
Question 3.
An organic compound present in vinegar has 40% carbon, 6.6 % hydrogen, and 53.4 % oxygen, Find the empirical formula and molecular formula of the compound. (Given, Molar mass: 60 g mol-1).
Answer:
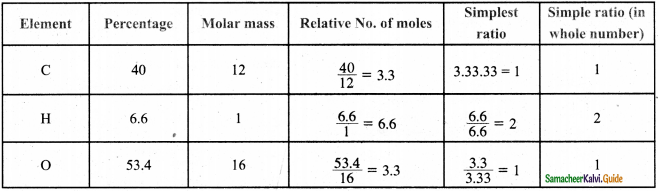
The ratio of C: H : O is 1 : 2 : 1 and hence, the empirical formula of the compound is CH2O.
Empirical Formula mass = (1 × 12 + 1 × 2 + 1 × 16) = 12 + 2 + 16 = 30.
Whole number η = Molar mass / Empirical formula mas = \(\frac{60}{30}\) = 2
Therefore, Molecular formula = (CH2O)2 = C2H4O2
Question 4.
An organic compound present in vinegar has 40% carbon, 6.6 % hydrogen, and 53.4 % oxygen, Find the empirical formula and molecular formula of the compound. (Given, Molar mass: 90 g mol-1).
Answer:

The ratio of C : H : O is 1 : 2 : 1 and hence, the empirical formula of the compound is CH2O.
Empirical Formula mass = (1 × 12 + 1 × 2 × 16) = 12 + 2 + 16 = 30.
Whole number, n = \(\frac{\text { Molar mass }}{\text { Empirical formula mass }}\)
= \(\frac{90}{30}\) = 3
Therefore, Molecular formula = (CH2O)3 = C3H6O3
Question 5.
What is a redox reaction? Explain the different concepts of redox reaction.
Answer:
The reaction involving loss of electron is oxidation and gain of electron is reduction. Both these reactions take place simultaneously and are called as redox reactions.
Classical concept of oxidation and reduction:
According to classical concept, addition of oxygen or removal of hydrogen is called oxidation.
Consider the following reactions,
4Fe + 3O2 → 2Fe2O3
H2S + Cl2 → 2HCl + S
In the first reaction, which is responsible for the rusting of iron, the oxygen adds on to the metal, iron. In the second reaction, hydrogen is removed from Hydrogen sulphide.
According to classical concept, addition of hydrogen or removal of oxygen is called reduction.
Consider the following reactions,
CuO + C → Cu + CO
S + H2 → H2S
In the first reaction, oxygen is removed from cupric oxide, and in the second reaction, hydrogen is added to sulphur.
Electron concept of oxidation and reduction.
The reaction involving loss of electron is termed as oxidation and gain of an electron is termed as reduction.
Fe2+ → Fe3+ + e– (loss of electron – oxidation)
Cu2+ + 2e– → Cu (gain of electron – reduction)
Oxidation number concept of oxidation and reduction:
During redox reactions, the oxidation number of elements changes. A reaction in which oxidation number of the element increases is called oxidation whereas the oxidation number of the element decreases is called reduction.

In this reaction, manganese in potassium permanganate favours the oxidation of ferrous sulphate into ferric sulphate by gets reduced.
![]()
Question 6.
What is an oxidation number? State the rules to find the oxidation number.
Answer:
Oxidation number is defined as the imaginary charge left on the atom when all other atoms of the compound have been removed in their usual oxidation states that are assigned according to set of rules. A term that is often used interchangeably with oxidation number is oxidation state.
- The oxidation state of a free element (i.e., uncombined state) is zero.
Example: H2 Cl2, Na, and S8 have the oxidation number of zero. - For a monoatomic ion, the oxidation state is equal to the net charge on the ion.
Example: The oxidation number of sodium in Na+ is +1.
The oxidation number of chlorine in Cl– is -1. - The algebraic sum of oxidation states of all atoms in a molecule is equal to zero, while in ions, it is equal to the net charge on the ion.
Example: In H2SO4, 2 × (oxidation number of hydrogen) + 1 × (oxidation number of sulphur) + 4 × (oxidation number of oxygen) = 0. - Hydrogen has an oxidation number of +1 in all its compounds except in metal hydrides where it has -1 value.
Example: Oxidation number of hydrogen in hydrogen chloride (HCl) is + 1.
Oxidation number of hydrogen in sodium hydride (NaH) is -1. - Fluorine has an oxidation state of -1 in all its compounds.
- The oxidation state of oxygen in most compounds is -2. Exceptions are peroxides, superoxides, and compounds with fluorine.
Example: Oxidation number of oxygen
(i) in water is -2,
(ii) in hydrogen peroxide is -1,
(iii) in superoxides such as KO2 is 4, and
(iv) in oxygen difluoride (OF2) is +2. - Alkali metals have an oxidation state of +1 and alkaline earth metals have an oxidation state of +2 in all their compounds.
Question 7.
Balance the following chemical equation by oxidation number method.
KMnO4 + FeSO4 + H2SO4 → K2SO4 + Fe(SO4)3 + 8H2O
Answer:
Using oxidation number concept, the reactants which undergoes oxidation and reduction are as follows:

The oxidation number of Mn in KMnO4 changes from +7 to +2 by gaining five electrons and the oxidation number of Fe FeSO4 changes from +2 to +3 by loosing one electron.
Since the total number of electrons lost is equal to the total number of electrons gained, the number of electrons, by cross multiplication of the respective formula with suitable integers on reactant side.
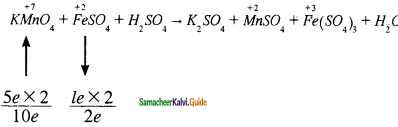
Based on the reactant side, the products are balanced.
2KMnO4 + 10 FeSO4 + H2SO4 → K2SO4 + MnSO4 + Fe( SO4)3 + H2O
Balance the other elements except H and O atoms. K and S are balanced as follows
2KMnO4 + 10 FeSO4 + H2SO4 → K2SO4 + MnSO4 + Fe( SO4)3 + H2O
The difference of 8 – S atoms in reactant side, has to be balanced by multiplying H2SO4 by ‘8’. The equation now becomes,
2KMnO4 + 10 FeSO4 + 8 H2SO4 → K2SO4 + MnSO4 + Fe( SO4)3 + H2O
‘H’ and ‘O’ atoms are balanced by multiplying H2O molecules in the product side by ‘8’.
2KMnO4 + 10 FeSO4 + 8 H2SO4 → K2SO4 + 2 MnSO4 + 5 Fe( SO4)3 + 8 H2O
The above equation is a balanced equation.
Question 8.
How is the following equation ¡s balanced by Ion electron method?
MnO4– + Fe2+ + H+ → Mn2+ + Fe3+ + H2O.
Answer:
Using the oxidation number concept, the reactants which undergoes oxidation and reduction are as follows;

The two half reactions are,
Fe2+ → Fe3+ + 1e ……….(1)
MnO4– + 5e + 8H+ → Mn2+ + 4H2O ……….(2)
Balancing the atoms and charges on both sides of the half reactions.
There is no change in the equation (1) whereas in equation (2), there are four ‘O’ atoms on the reractant side .
Therefore, four H2 is added on the product side, to balance ‘H’ – add, 8 H+ in the reactant side.
MnO4– + 5e + 8H+ → Mn2+ + 4H2O ………..(3)
The two half reactions are equated in such a way that the number of electrons lost is equal to number of electrons gained.
Adding the two half reactions as follows:
(1) × 5 5 Fe2+ → 5 Fe3+ + 5e ……………(4)
(3) × 1 MnO4– + 5e + 8H+ → Mn2+ + 4H2O ………(5)
(4) + (5)
MnO4– + 5Fe2+ + 8H+ → Mn2+ + 5 Fe3+ + 4H2O ………..(6)
The equation (6) is a balanced equation.
![]()
Question 9.
Calculate the percentage composition of the elements present in lead nitrate. How many Kg of 02 can be obtained from 50 kg of 70% pure lead nitrate?
Answer:
Lead nitrate = Pb (NO3)2
Molecular mass of lead nitrate = 207 + (14 x 2) + (16 x 6)
= 207 + 28 + 96 = 331 g / mol.
331 g of lead nitrate contains 96 g of oxygen.
∴ 50 x 103 g of lead nitrate will contain \(\frac {96}{331}\) x 50 x 103
= 14501.5 g
= 14.501 Kg of oxygen.
100 % pure lead nitrate contains 14.501 Kg of oxygen.
70 % pure lead nitrate will contain = \(\frac {14.501}{100}\) x 70 = 10.15 Kg of oxygen.
.’. 70 % pure lead nitrate will contain 10.15 Kg of oxygen.
Must Read: