Students can download 11th Business Maths Chapter 5 Differential Calculus Ex 5.1 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 5 Differential Calculus Ex 5.1
Samacheer Kalvi 11th Business Maths Differential Calculus Ex 5.1 Text Book Back Questions and Answers
Question 1.
Determine whether the following functions are odd or even?
(i) f(x) = \(\left(\frac{a^{x}-1}{a^{x}+1}\right)\)
(ii) f(x) = log(x2 + \(\sqrt{x^{2}+1}\))
(iii) f(x) = sin x + cos x
(iv) f(x) = x2 – |x|
(v) f(x) = x + x2
Solution:
(i) f(x) = \(\left(\frac{a^{x}-1}{a^{x}+1}\right)\)

Thus f(-x) = -f(x)
∴ f(x) is an odd function.
(ii) f(x) = log(x2 + \(\sqrt{x^{2}+1}\))
f(-x) = log((-x)2 + \(\sqrt{(-x)^{2}+1}\))
= log(x2 + \(\sqrt{x^{2}+1}\))
Thus f(-x) = f(x)
∴ f(x) is an even function.
(iii) f(x) = sin x + cos x
f(-x) = sin(-x) + cos(-x)
= -sin x + cos x
= -[sin x – cos x]
Since f(-x) ≠ -f(x) (or) f(x) ≠ -f(x)
∴ f(x) is neither odd nor even function.
(iv) Given f(x) = x2 – |x|
f(-x) = (-x)2 – |-x|
= x2 – |x|
= f(x)
∴ f(x) is an even function.
(v) f(x) = x + x2
f(-x) = (-x) + (-x)2 = -x + x2
Since f(-x) ≠ f(x), f(-x) ≠ -f(x).
∴ f(x) is neither odd nor even function.
Question 2.
Let f be defined by f(x) = x3 – kx2 + 2x, x ∈ R. Find k, if ‘f’ is an odd function.
Solution:
For a polynomial function to be an odd function each term should have odd powers pf x. Therefore there should not be an even power of x term.
∴ k = 0.
![]()
Question 3.
If f(x) = \(x^{3}-\frac{1}{x^{3}}\), then show that f(x) + f(\(\frac{1}{x}\)) = 0
Solution:
f(x) = \(x^{3}-\frac{1}{x^{3}}\) …….. (1)
\(f\left(\frac{1}{x}\right)=\left(\frac{1}{x}\right)^{3}-\frac{1}{\left(\frac{1}{x}\right)^{3}}\) = \(\frac{1}{x^{3}}-x^{3}\) …….. (2)
(1) + (2) gives \(f(x)+f\left(\frac{1}{x}\right)=x^{3}-\frac{1}{x^{3}}+\frac{1}{x^{3}}-x^{3}=0\)
Hence Proved.
Question 4.
If f(x) = \(\frac{x+1}{x-1}\), then prove that f(f(x)) = x.
Solution:
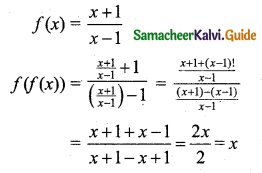
Hence proved.
![]()
Question 5.
For f(x) = \(\frac{x-1}{3 x+1}\), write the expressions of f(\(\frac{1}{x}\)) and \(\frac{1}{f(x)}\).
Solution:
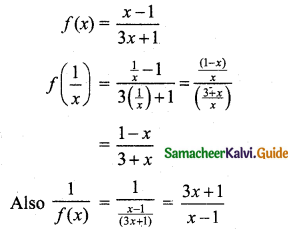
Question 6.
If f(x) = ex and g(x) = loge x then find
(i) (f + g) (1)
(ii) (fg) (1)
(iii) (3f) (1)
(iv) (5g) (1)
Solution:
(i) (f+g) (1) = e1 + loge 1 = e + 0 = e
(ii) (fg) (1) = f(1) g(1) = e1 \(\log _{e}^{1}\) = e × 0 = 0
(iii) (3f) (1) = 3 f(1) = 3 e1 = 3e
(iv) (5g) (1) = 5 (g) (1) = 5 \(\log _{e}^{1}\) = 5 × 0 = 0
Question 7.
Draw the graph of the following functions:
(i) f(x) = 16 – x2
(ii) f(x) = |x – 2|
(iii) f(x) = x|x|
(iv) f(x) = e2x
(v) f(x) = e-2x
(vi) f(x) = \(\frac{|x|}{x}\)
Solution:
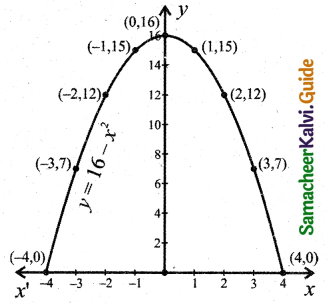
(i) f(x) = 16 – x2
Let y = f(x) = 16 – x2
Choose suitable values for x and determine y. Thus we get the following table.

Plot the points (-4, 0), (-3, 7), (-2, 12), (-1, 15), (0, 16), (1, 15), (2, 12), (3, 7), (4, 0).
The graph is as shown in the figure.
(ii) Let y = f(x) = |x – 2|
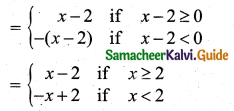
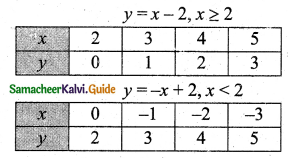
Plot the points (2, 0), (3, 1) (4, 2), (5, 3), (0, 2), (-1, 3), (-2, 4), (-3, 5) and draw a line.
The graph is as shown in the figure.
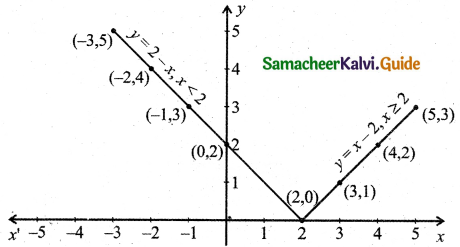
![]()
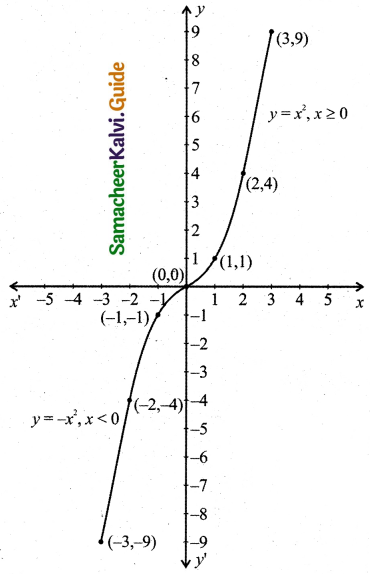
(iii) Let y = f(x) = x|x|
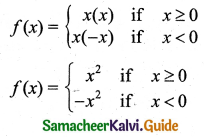
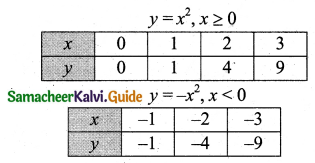
Plot the points (0, 0), (1, 1) (2, 4), (3, 9), (-1, -1), (-2, -4), (-3, -9) and draw a smooth curve.
The graph is as shown in the figure.
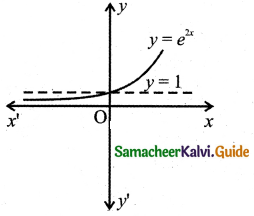
(iv) For x = 0, f(x) becomes 1 i.e., the curve cuts the y-axis at y = 1.
For no real value of x, f(x) equals to 0. Thus it does not meet the x-axis for real values of x.
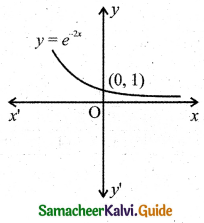
(v) For x = 0, f(x) becomes 1 i.e., the curve cuts the y-axis at y = 1.
For no real value of x, f(x) equal to 0. Thus it does not meet the x-axis for real values of x.
![]()
(vi) If f: R → R is defined by
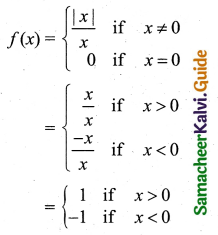
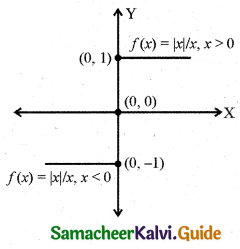
The domain of the function is R and the range is {-1, 0, 1}.