Students can download 11th Business Maths Chapter 1 Matrices and Determinants Ex 1.4 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 1 Matrices and Determinants Ex 1.4
Samacheer Kalvi 11th Business Maths Matrices and Determinants Ex 1.4 Text Book Back Questions and Answers
Question 1.
The technology matrix of an economic system of two industries is \(\left[\begin{array}{cc}
0.50 & 0.30 \\
0.41 & 0.33
\end{array}\right]\). Test whether the system is viable as per Hawkins Simon conditions.
Solution:
Technology matrix B = \(\left[\begin{array}{cc}
0.50 & 0.30 \\
0.41 & 0.33
\end{array}\right]\)
I – B = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]-\left[\begin{array}{ll}
0.50 & 0.30 \\
0.41 & 0.33
\end{array}\right]\)
= \(\left[\begin{array}{rr}
0.50 & -0.30 \\
-0.41 & 0.67
\end{array}\right]\), the main diagonal elements are positive.
|I – B| = \(\left[\begin{array}{rr}
0.50 & -0.30 \\
-0.41 & 0.67
\end{array}\right]\)
= 0.335 – 0.123
= 0.212, positive
Since the main diagonal elements of I – B are positive and |I – B| is positive, Hawkins-Simon conditions are satisfied. Therefore, the given system is viable.
![]()
Question 2.
The technology matrix of ah economic system of two industries is \(\left[\begin{array}{rr}
0.6 & 0.9 \\
0.20 & 0.80
\end{array}\right]\). Test whether the system is viable as per Hawkins-Simon conditions.
Solution:
Technology matrix B = \(\left[\begin{array}{cc}
0.60 & 0.9 \\
0.20 & 0.80
\end{array}\right]\)
I – B = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]-\left[\begin{array}{cc}
0.60 & 0.9 \\
0.20 & 0.80
\end{array}\right]\)
= \(\left[\begin{array}{rr}
0.4 & -0.9 \\
-0.20 & 0.20
\end{array}\right]\), the main diagonal elements are positive.
|I – B| = \(\left|\begin{array}{rr}
0.4 & -0.9 \\
-0.20 & 0.20
\end{array}\right|\)
= 0.4 × 0.20 – (-0.20) × (-0.9)
= 0.08 – 0.18
= -0.1, negative
Since |I – B| is negative one of the Hawkins-Simon condition is not satisfied. Therefore, the given system is not viable.
Question 3.
The technology matrix of an economic system of two industries is \(\left[\begin{array}{ll}
0.50 & 0.25 \\
0.40 & 0.67
\end{array}\right]\). Test whether the system is viable as per Hawkins-Simon conditions.
Solution:
Technology matrix B = \(\left[\begin{array}{ll}
0.50 & 0.25 \\
0.40 & 0.67
\end{array}\right]\)
I – B = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]-\left[\begin{array}{cc}
0.50 & 0.25 \\
0.40 & 0.67
\end{array}\right]\)
= \(\left[\begin{array}{rr}
0.50 & -0.25 \\
-0.40 & 0.33
\end{array}\right]\), the main diagonal elements are positive.
|I – B| = \(\left|\begin{array}{rr}
0.50 & -0.25 \\
-0.40 & 0.33
\end{array}\right|\)
= (0.50) (0.33) – (-0.40) (-0.25)
= 0.165 – 0.1
= 0.065 (positive)
Since the main diagonal elements of I – B are positive and |I – B| is positive, Hawkins-Simon conditions are satisfied. Therefore, the given system is viable.
![]()
Question 4.
Two commodities A and B are produced such that 0.4 tonne of A and 0.7 tonnes of B are required to produce a tonnes of A. Similarly 0.1 tonne of A and 0.7 tonne of B are needed to produce a tonnes of B. Write down the technology matrix. If 6.8 tonnes of A and 10.2 tones of B are required, find the gross production of both of them.
Solution:
Here the technology matrix is given under
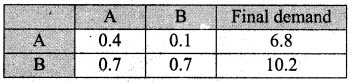
The technology matrix is B = \(\left[\begin{array}{cc}
0.4 & 0.1 \\
0.7 & 0.7
\end{array}\right]\)
I – B = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]-\left[\begin{array}{ll}
0.4 & 0.1 \\
0.7 & 0.7
\end{array}\right]\) = \(\left[\begin{array}{rr}
0.6 & -0.1 \\
-0.7 & 0.3
\end{array}\right]\)
|I – B| = \(\left|\begin{array}{rr}
0.6 & -0.1 \\
-0.7 & 0.3
\end{array}\right|\)
= (0.6) (0.3) – (-0.1) (-0.7)
= 0.18 – 0.07
= 0.11
Since the main diagonal elements of I – B are positive and the value of |I – B| is positive, the system is viable.

Production of A is 27.82 tonnes and the production of B is 98.91 tonnes.
Question 5.
Suppose the inter-industry flow of the product of two industries is given as under.
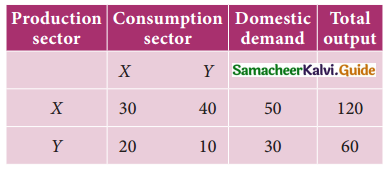
Determine the technology matrix and test Hawkin’s-Simon conditions for the viability of the system. If the domestic changes to 80 and 40 units respectively, what should be the gross output of each sector in order to meet the new demands.
Solution:
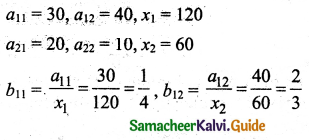
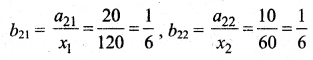
The technology matrix B = \(\left[\begin{array}{ll}
\frac{1}{4} & \frac{2}{3} \\
\frac{1}{6} & \frac{1}{6}
\end{array}\right]\)
I – B = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]-\left[\begin{array}{ll}
\frac{1}{4} & \frac{2}{3} \\
\frac{1}{6} & \frac{1}{6}
\end{array}\right]\)
= \(\left[\begin{array}{rr}
\frac{3}{4} & -\frac{2}{3} \\
-\frac{1}{6} & \frac{5}{6}
\end{array}\right]\), elements of main diagonal are positive.
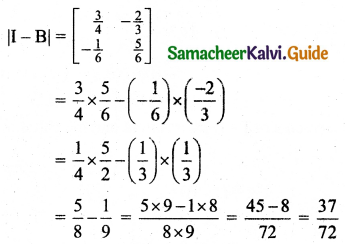
The main diagonal elements of I – B are positive and |I – B| is positive. Therefore the system is viable.

The output of industry X should be 181.62 and Y should be 84.32.
![]()
Question 6.
You are given the following transaction matrix for a two-sector economy.
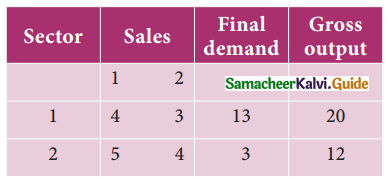
(i) Write the technology matrix?
(ii) Determine the output when the final demand for the output sector 1 alone increases to 23 units.
Solution:


The main diagonal elements are positive and |I – B| is positive. Therefore the system is viable.
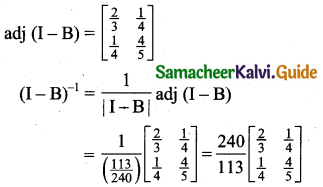
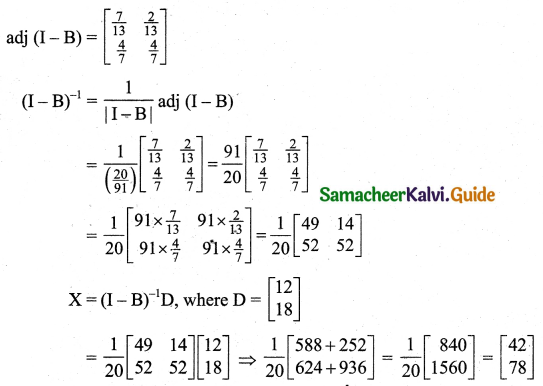
X = (I – B)-1D, where

The output of sector 1 should be 34.16 and sector 2 should be 17.31.
![]()
Question 7.
Suppose the inter-industry flow of the product of two Sectors X and Y are given as under.
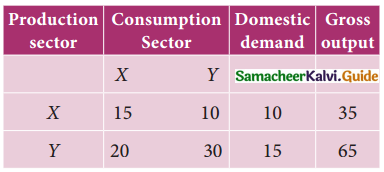
Find the gross output when the domestic demand changes to 12 for X and 18 for Y.
Solution:


Since the main diagonal elements of I – B are positive and |I – B| is positive the problem has a solution.