Samacheer Kalvi 11th Business Maths Guide Chapter 9 Correlation and Regression Analysis Ex 9.3

Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 9 Correlation and Regression Analysis Ex 9.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 9 Correlation and Regression Analysis Ex 9.3

Samacheer Kalvi 11th Business Maths Correlation and Regression Analysis Ex 9.3 Text Book Back Questions and Answers

Choose the correct answer.

Question 1.
An example of a positive correlation is:
(a) Income and expenditure
(b) Price and demand
(c) Repayment period and EMI
(d) Weight and Income
Answer:
(a) Income and expenditure

Question 2.
If the values of two variables move in the same direction then the correlation is said to be:
(a) Negative
(b) Positive
(c) Perfect positive
(d) No correlation
Answer:
(b) Positive

Question 3.
If the values of two variables move in the opposite direction then the correlation is said to be:
(a) Negative
(b) Positive
(c) Perfect positive
(d) No correlation
Answer:
(a) Negative

Question 4.
Correlation co-efficient lies between:
(a) 0 to ∞
(b) -1 to +1
(c) -1 to 0
(d) -1 to ∞
Answer:
(b) -1 to +1

Question 5.
If r(X, Y) = 0 the variables X and Y are said to be:
(a) Positive correlation
(b) Negative correlation
(c) No correlation
(d) Perfect positive correlation
Answer:
(c) No correlation

Question 6.
The correlation coefficient from the following data N = 25, ΣX = 125, ΣY = 100, ΣX² = 650, ΣY²= 436, ΣXY = 520:
(a) 0.667
(b) -0.006
(c) -0.667
(d) 0.70
Answer:
(a) 0.667
Hint:

Question 7.
From the following data, N = 11, ΣX = 117, ΣY = 260, ΣX² = 1313, ΣY² = 6580, ΣXY = 2827. the correlation coefficient is:
(a) 0.3566
(b) -0.3566
(c) 0
(d) 0.4566
Answer:
(a) 0.3566
Hint:

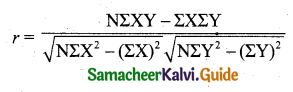
Question 8.
The correlation coefficient is:

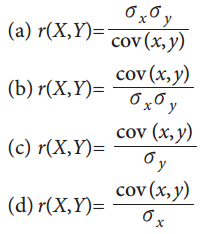
Answer:
(b) r(X, Y) = \(\frac{cov(x, y)}{\sigma_{x} \sigma_{y}}\)

Question 9.
The variable whose value is influenced or is to be predicted is called:
(a) dependent variable
(b) independent variable
(c) regressor
(d) explanatory variable
Answer:
(a) dependent variable

Question 10.
The variable which influences the values or is used for prediction is called:
(a) Dependent variable
(b) Independent variable
(c) Explained variable
(d) Regressed
Answer:
(b) Independent variable

Question 11.
The correlation coefficient:

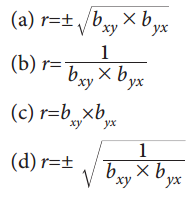
Answer:
(a) \(r=\pm \sqrt{b_{x y} \times b_{y x}}\)

Question 12.
The regression coefficient of X on Y:

Answer:
(a) \(b_{x y}=\frac{\mathrm{N} \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{\mathrm{N} \Sigma d y^{2}-(\Sigma d y)^{2}}\)

Question 13.
The regression coefficient of Y on X:

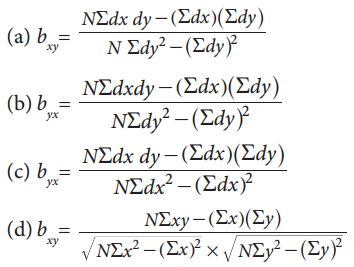
Answer:
(c) \(b_{y x}=\frac{\mathrm{N\Sigma} d x d y-(\Sigma d x)(\Sigma d y)}{\mathrm{N} \Sigma d x^{2}-(\Sigma d x)^{2}}\)

Question 14.
When one regression coefficient is negative, the other would be:
(a) Negative
(b) Positive
(c) Zero
(d) None of these
Answer:
(a) Negative

Question 15.
If X and Y are two variates, there can be at most:
(a) one regression line
(b) two regression lines
(c) three regression lines
(d) more regression lines
Answer:
(b) two regression lines

Question 16.
The lines of regression of X on Y estimates:
(a) X for a given value of Y
(b) Y for a given value of X
(c) X from Y and Y from X
(d) none of these
Answer:
(a) X for a given value of Y

Question 17.
Scatter diagram of the variate values (X, Y) give the idea about:
(a) functional relationship
(b) regression model
(c) distribution of errors
(d) no relation
Answer:
(a) functional relationship

Question 18.
If regression co-efficient of Y on X is 2, then the regression co-efficient of X on Y is:
(a) ≤ \(\frac{1}{2}\)
(b) 2
(c) > \(\frac{1}{2}\)
(d) 1
Answer:
(a) ≤ \(\frac{1}{2}\)

Question 19.
If two variables move in a decreasing direction then the correlation is:
(a) positive
(b) negative
(c) perfect negative
(d) no correlation
Answer:
(a) positive

Question 20.
The person suggested a mathematical method for measuring the magnitude of the linear relationship between two variables say X and Y is:
(a) Karl Pearson
(b) Spearman
(c) Croxton and Cowden
(d) Ya Lun Chou
Answer:
(a) Karl Pearson

Question 21.
The lines of regression intersect at the point:
(a) (X, Y)
(b) \((\overline{\mathrm{X}}, \overline{\mathrm{Y}})\)
(c) (0, 0)
(d) (σ_x, σ_y)
Answer:
(b) \((\overline{\mathrm{X}}, \overline{\mathrm{Y}})\)

Question 22.
The term regression was introduced by:
(a) R.A Fisher
(b) Sir Francis Galton
(c) Karl Pearson
(d) Croxton and Cowden
Answer:
(b) Sir Francis Galton

Question 23.
If r = -1, then correlation between the variables:
(a) perfect positive
(b) perfect negative
(c) negative
(d) no correlation
Answer:
(b) perfect negative

Question 24.
The coefficient of correlation describes:
(a) the magnitude and direction
(b) only magnitude
(c) only direction
(d) no magnitude and no direction
Answer:
(a) the magnitude and direction

Question 25.
If Cov(x, y) = -16.5, \(\sigma_{x}^{2}\) = 2.89, \(\sigma_{y}^{2}\) = 100. Find correlation coeffient.
(a) -0.12
(b) 0.001
(c) -1
(d) -0.97
Answer:
(d) -0.97