Students can download 11th Business Maths Chapter 2 Algebra Ex 2.4 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 2 Algebra Ex 2.4
Samacheer Kalvi 11th Business Maths Algebra Ex 2.4 Text Book Back Questions and Answers
Question 1.
If nPr = 1680 and nCr = 70, find n and r.
Solution:
Given that nPr = 1680, nCr = 70
We know that nCr = \(\frac{n \mathrm{P}_{r}}{r !}\)
70 = \(\frac{1680}{r !}\)
r! = \(\frac{1680}{70}\) = 24
r! = 4 × 3 × 2 × 1 = 4!
∴ r = 4
![]()
Question 2.
Verify that 8C4 + 8C3 = 9C4.
Solution:
LHS = 8C4 + 8C3
= \(\frac{8 \cdot 7 \cdot 6 \cdot 5}{4 \cdot 3 \cdot 2 \cdot 1}+\frac{8 \cdot 7 \cdot 6}{3 \cdot 2 \cdot 1}\)
= 7 × 2 × 5 + 8 × 7
= 70 + 56
= 126
RHS = 9C4
= \(\frac{9 \times 8 \times 7 \times 6}{4 \times 3 \times 2 \times 1}\)
= 9 × 7 × 2
= 126
∴ LHS = RHS
Hence verified.
Question 3.
How many chords can be drawn through 21 points on a circle?
Solution:
To draw a chord we need two points on a circle.
∴ Number chords through 21 points on a circle = 21C2 = \(\frac{21 \times 20}{2 \times 1}\) = 210.
![]()
Question 4.
How many triangles can be formed by joining the vertices of a hexagon?
Solution:
A hexagon has six vertices. By joining any three vertices of a hexagon we get a triangle.
∴ Number of triangles formed by joining the vertices of a hexagon = 6C3 = \(\frac{6 \times 5 \times 4}{3 \times 2 \times 1}\) = 20.
Question 5.
Out of 7 consonants and 4 vowels, how many words of 3 consonants and 2 vowels can be formed?
Solution:
In this problem first, we have to select consonants and vowels.
Then we arrange a five-letter word using 3 consonants and 2 vowels.
Therefore here both combination and permutation involved.
The number of ways of selecting 3 consonants from 7 is 7C3.
The number of ways of selecting 2 vowels from 4 is 4C3.
The number of ways selecting 3 consonants from 7 and 2 vowels from 4 is 7C3 × 4C2.
Now with every selection number of ways of arranging 5 letter word
= 5! × 7C3 × 4C2
= 120 × \(\frac{7 \times 6 \times 5}{3 \times 2 \times 1} \times \frac{4 \times 3}{2 \times 1}\)
= 25200
![]()
Question 6.
If four dice are rolled, find the number of possible outcomes in which atleast one die shows 2.
Solution:
When a die is rolled number of possible outcomes is selecting an event from 6 events = 6C1
When four dice are rolled number of possible outcomes = 6C1 × 6C1 × 6C1 × 6C1
When a die is rolled number of possible outcomes in which ‘2’ does not appear is selecting an event from 5 events = 5C1
When four dice are rolled number of possible outcomes in which 2 does not appear = 5C1 × 5C1 × 5C1 × 5C1
Therefore the number of possible outcomes in which atleast one die shows 2
= 6C1 × 6C1 × 6C1 × 6C1 – 5C1 × 5C1 × 5C1 × 5C1
= 6 × 6 × 6 × 6 – 5 × 5 × 5 × 5
= 1296 – 625
= 671
Note: when two dice are rolled number of possible outcomes is 36 and the number of possible outcomes in which 2 doesn’t appear = 25. When two dice are rolled the number of possible outcomes in which atleast one die shows 2 = 36 – 25 = 11. Use the sample space, S = {(1, 1), (1, 2),… (6, 6)}.
Question 7.
There are 18 guests at a dinner party. They have to sit 9 guests on either side of a long table, three particular persons decide to sit on one side and two others on the other side. In how many ways can the guests to be seated?
Solution:
Let A and B be two sides of the table 9 guests sit on either side of the table in 9! × 9! ways.
Out of 18 guests, three particular persons decide to sit namely inside A and two on the other side B. remaining guest = 18 – 3 – 2 = 13.
From 13 guests we can select 6 more guests for side A and 7 for the side.
Selecting 6 guests from 13 can be done in 13C6 ways.
Therefore total number of ways the guest to be seated = 13C6 × 9! × 9!
= \(\frac{13 !}{6 !(13-6) !} \times 9 ! \times 9 !\)
= \(\frac{13 !}{6 ! \times 7 !} \times 9 ! \times 9 !\)
![]()
Question 8.
If a polygon has 44 diagonals, find the number of its sides.
Solution:
A polygon of n sides has n vertices. By joining any two vertices of a polygon, we obtain either a side or a diagonal of the polygon.
A number of line segments obtained by joining the vertices of a n sided polygon taken two at a time = Number of ways of selecting 2 out of n.
= nC2
= \(\frac{n(n-1)}{2}\)
Out of these lines, n lines are the sides of the polygon, Sides can’t be diagonals.
∴ Number of diagonals of the polygon = \(\frac{n(n-1)}{2}\) – n = \(\frac{n(n-3)}{2}\)
Given that a polygon has 44 diagonals.
Let n be the number of sides of the polygon.
\(\frac{n(n-3)}{2}\) = 44
⇒ n(n – 3) = 88
⇒ n2 – 3n – 88 = 0
⇒ (n + 8) (n – 11)
⇒ n = -8 (or) n = 11
n cannot be negative.
∴ n = 11 is number of sides of polygon is 11.
Question 9.
In how many ways can a cricket team of 11 players be chosen out of a batch of 15 players?
(i) There is no restriction on the selection.
(ii) A particular player is always chosen.
(iii) A particular player is never chosen.
Solution:
(i) Number of ways choosing 11 players from 15 is 15C11 = 15C4
= \(\frac{15 \times 14 \times 13 \times 12}{4 \times 3 \times 2 \times 1}\)
= 15 × 7 × 13
= 1365.
(ii) If a particular is always chosen there will be only 14 players left put, in which 10 are to selected in 14C10 ways.
14C10 = 14C4
= \(\frac{14 \times 13 \times 12 \times 11}{4 \times 3 \times 2 \times 1}\)
= \(\frac{14 \times 13 \times 11}{2}\)
= 91 × 11
= 1001 ways
(iii) If a particular player is never chosen we have to select 11 players out of remaining 14 players in 14C11 ways.
i.e., 14C3 ways = \(\frac{14 \times 13 \times 12}{3 \times 2 \times 1}\) = 364 ways.
![]()
Question 10.
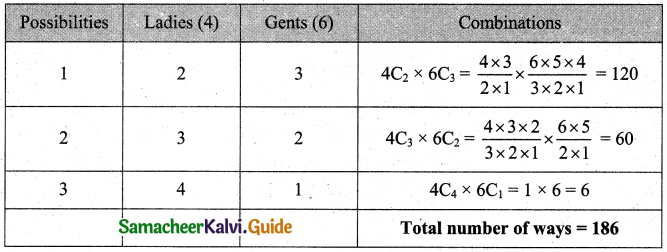
A committee of 5 is to be formed out of 6 gents and 4 ladies. In how many ways this can be done when
(i) atleast two ladies are included.
(ii) atmost two ladies are included.
Solution:
(i) A committee of 5 is to be formed.
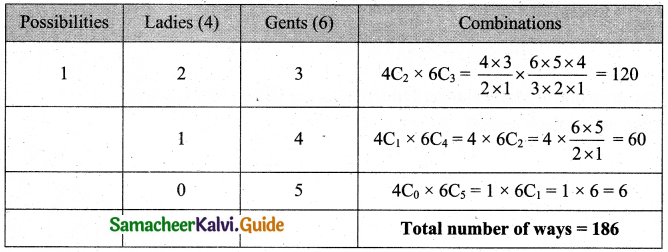
(ii) Almost two ladies are included means maximum of two ladies are included.