Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.2 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.2
Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.2 Text Book Back Questions and Answers
Question 1.
Find the angle between the lines whose slopes are \(\frac{1}{2}\) and 3.
Solution:
Given that m1 = \(\frac{1}{2}\) and m2 = 3.
Let θ be the angle between the lines then
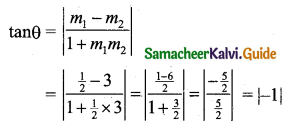
tan θ = 1
tan θ = tan 45°
∴ θ = 45°
![]()
Question 2.
Find the distance of the point (4, 1) from the line 3x – 4y + 12 = 0.
Solution:
The length of perpendicular from a point (x1, y1) to the line ax + by + c = 0 is d = \(\left|\frac{a x_{1}+b y_{1}+c}{\sqrt{a^{2}+b^{2}}}\right|\)
∴ The distance of the point (4, 1) to the line 3x – 4y + 12 = 0 is
[Here (x1, y1) = (4, 1), a = 3, b = -4, c = 12]
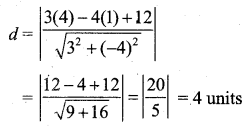
Question 3.
Show that the straight lines x + y – 4 = 0, 3x + 2 = 0 and 3x – 3y + 16 = 0 are concurrent.
Solution:
The lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0, a3x + b3y + c3 = 0 are concurrent if
\(\left|\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|=0\)
The given lines x + y – 4 = 0, 3x + 0y + 2 = 0, 3x – 3y + 16 = 0
\(\left|\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|=\left|\begin{array}{rrr}
1 & 1 & -4 \\
3 & 0 & 2 \\
3 & -3 & 16
\end{array}\right|\)
= 1(0 + 6) – 1(48 – 6) – 4(-9 – 0)
= 6 – (42) + 36
= 42 – 42
= 0
The given lines are concurrent.
![]()
Question 4.
Find the value of ‘a’ for which the straight lines 3x + 4y = 13; 2x – 7y = -1 and ax – y – 14 = 0 are concurrent.
Solution:
The lines 3x + 4y = 13, 2x – 7y = -1 and ax – y – 14 = 0 are concurrent.
\(\left|\begin{array}{rrr}
3 & 4 & -13 \\
2 & -7 & 1 \\
a & -1 & -14
\end{array}\right|=0\)
⇒ 3(98 + 1) – 4(-28 – a) – 13(-2 + 7a) = 0
⇒ 3(99) + 112 + 4a + 26 – 91a = 0
⇒ 297 + 112 + 26 + 4a – 91a = 0
⇒ 435 – 87a = 0
⇒ -87a = -435
⇒ a = \(\frac{-435}{-87}\) = 5
Question 5.
A manufacturer produces 80 TV sets at a cost of ₹ 2,20,000 and 125 TV sets at a cost of ₹ 2,87,500. Assuming the cost curve to be linear, find the linear expression of the given information. Also, estimate the cost of 95 TV sets.
Solution:
Let x represent the TV sets, andy represent the cost.
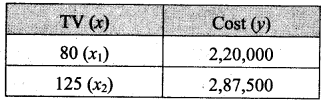
The equation of straight line expressing the given information as a linear equation in x and y is
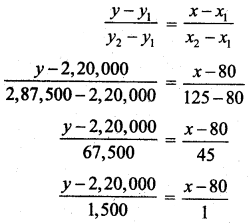
1(y – 2,20,000) = (x – 80)1500
y – 2,20,000 = 1500x – 80 × 1500
y = 1500x – 1,20,000 + 2,20,000
y = 1500x + 1,00,000 which is the required linear expression.
When x = 95,
y = 1,500 × 95 + 1,00,000
= 1,42,500 + 1,00,000
= 2,42,500
∴ The cost of 95 TV sets is ₹ 2,42,500.