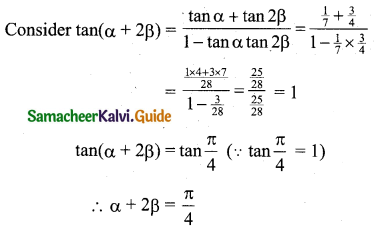Students can download 11th Business Maths Chapter 4 Trigonometry Ex 4.2 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 4 Trigonometry Ex 4.2
Samacheer Kalvi 11th Business Maths Trigonometry Ex 4.2 Text Book Back Questions and Answers
Question 1.
Find the values of the following:
(i) cosec 15°
(ii) sin (-105°)
(iii) cot 75°
Solution:
(i) cosec 15° = \(\frac{1}{\sin 15^{\circ}}\)
Consider sin 15° = sin(45° – 30°)
= sin 45° cos 30° – cos 45° sin 30°
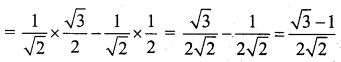
cosec 15° = \(\frac{1}{\sin 15^{\circ}}\) = \(\frac{2 \sqrt{2}}{\sqrt{3}-1}\)
(ii) sin (-105°) = -sin (105°) (∵ sin (-θ) = – sin θ)
= -[sin(60° + 45°)]
= -[sin 60° cos 45° + cos 60° sin 45°]
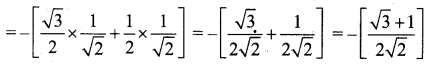
(iii) cot 75° = \(\frac{1}{\tan 75^{\circ}}\)
Consider tan 75° = tan (30° + 45°)
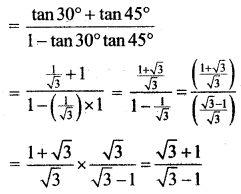
cot 75° = \(\frac{1}{\tan 75^{\circ}}=\frac{\sqrt{3}-1}{\sqrt{3}+1}\)
![]()
Question 2.
Find the values of the following:
(i) sin 76° cos 16° – cos 76° sin 16°
(ii) \(\sin \frac{\pi}{4} \cos \frac{\pi}{12}+\cos \frac{\pi}{4} \sin \frac{\pi}{12}\)
(iii) cos 70° cos 10° – sin 70° sin 10°
(iv) cos2 15° – sin2 15°
Solution:
(i) Given that, sin 76° cos 16° – cos 76° sin 16° (∴ This is of the form sin(A – B))
= sin(76° – 16°)
= sin 60°
= \(\frac{\sqrt{3}}{2}\)
(ii) This is of the form sin(A + B) = \(\sin \left(\frac{\pi}{4}+\frac{\pi}{12}\right)\)
= \(\sin \left(\frac{3 \pi+\pi}{12}\right)\)
= \(\sin \frac{4 \pi}{12}\)
= \(\sin \frac{\pi}{3}\)
= \(\frac{\sqrt{3}}{2}\) (∵ sin 60° = \(\frac{\sqrt{3}}{2}\))
(iii) Given that cos 70° cos 10° – sin 70° sin 10°
(This is of the form of cos (A + B), A = 70°, B = 10°)
= cos (70° + 10°)
= cos 80°
(iv) cos2 15° – sin2 15°
[∵ cos 2A = cos2 A – sin2 A, Here A = 15°]
= cos (2 × 15°)
= cos 30°
= \(\frac{\sqrt{3}}{2}\)
![]()
Question 3.
If sin A = \(\frac{3}{5}\), 0 < A < \(\frac{\pi}{2}\) and cos B = \(\frac{-12}{13}\), π < B < \(\frac{3 \pi}{2}\), find the values of the following:
(i) cos(A + B)
(ii) sin(A – B)
(iii) tan(A – B)
Solution:
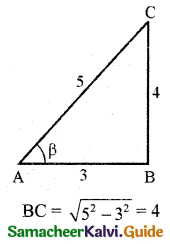
Given that sin A = \(\frac{3}{5}\), 0 < A < \(\frac{\pi}{2}\) (i.e., A lies in first quadrant)
Since A lies in first quadrant cos A is positive.
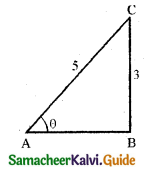
cos A = \(\frac{\text { Adjacent side }}{\text { Hypotenuse }}=\frac{4}{5}\)
tan A = \(\frac{3}{4}\)
AB = \(\sqrt{5^{2}-3^{2}}\) = 4
Also given that cos B = \(\frac{-12}{13}\), π < B < \(\frac{3 \pi}{2}\) (i.e., B lies in third quadrant)
Now sin B lies in third quadrant. sin B is negative.
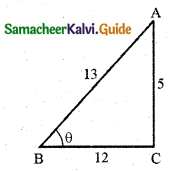
CA = \(\sqrt{13^{2}-12^{2}}\) = 5
sin B = \(\frac{-\text { Opposite side }}{\text { Hypotenuse }}=\frac{-5}{13}\)
tan B = \(\frac{-\text { Opposite side }}{\text { Adjacent }}=\frac{5}{12}\) [B lies in 3rd quadrant. tan B is positive.]
(i) cos(A + B) = cos A cos B – sin A sin B
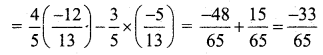
(ii) sin(A – B) = sin A cos B – cos A sin B
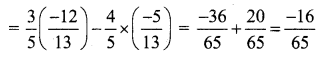
(iii) tan(A – B)
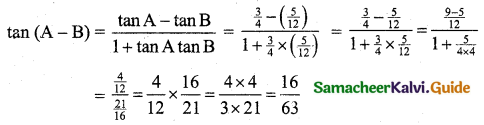
Question 4.
If cos A = \(\frac{13}{14}\) and cos B = \(\frac{1}{7}\) where A, B are acute angles prove that A – B = \(\frac{\pi}{3}\)
Solution:
cos A = \(\frac{13}{14}\), cos B = \(\frac{1}{7}\)
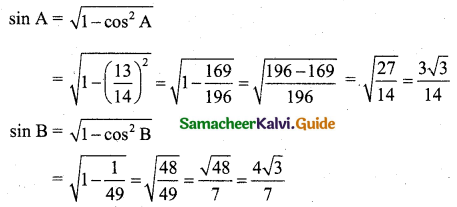
cos(A – B) = cos A cos B + sin A sin B
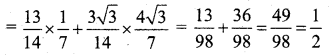
cos(A – B) = cos 60°
A – B = 60° = \(\frac{\pi}{3}\)
![]()
Question 5.
Prove that 2 tan 80° = tan 85° – tan 5°.
Solution:
Consider tan 80° = tan(85° – 5°)
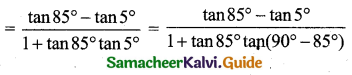
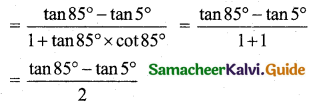
∴ 2 tan 80° = tan 85° – tan 5°
Hence Proved.
Question 6.
If cot α = \(\frac{1}{2}\), sec β = \(\frac{-5}{3}\), where π < α < \(\frac{3 \pi}{2}\) and \(\frac{\pi}{2}\) < β < π, find the value of tan(α + β). State the quadrant in which α + β terminates.
Solution:
Given that cot α = \(\frac{1}{2}\) where π < α < \(\frac{3 \pi}{2}\) (i.e,. α lies in third quadrant)
tan α = \(\frac{1}{\frac{1}{2}}\) = 2 [∵ In 3rd quadrant tan α is positive]
Also given that sec β = \(\frac{-5}{3}\) where \(\frac{\pi}{2}\) < β < π (i.e., β lies in second quadrant cos β and tan β are negative)

tan (α + β) = \(\frac{2}{11}\) which is positive.
α + β terminates in first quandrant.
![]()
Question 7.
If A + B = 45°, prove that (1 + tan A) (1 + tan B) = 2 and hence deduce the value of tan 22\(\frac{1}{2}\).
Solution:
Given A + B = 45°
tan (A + B) = tan 45°
\(\frac{\tan A+\tan B}{1-\tan A \tan B}=1\)
tan A + tan B = 1 – tan A . tan B
tan A + tan B + tan A tan B = 1
Add 1 on both sides we get,
(1 + tan A) + tan B + tan A tan B = 2
1(1+ tan A) + tan B (1 + tan A) = 2
(1 + tan A) (1 + tan B) = 2 ……. (1)
Put A = B = 22\(\frac{1}{2}\) in (1) we get
(1 + tan 22\(\frac{1}{2}\)) (1 + tan 22\(\frac{1}{2}\)) = 2
⇒ (1 + tan22\(\frac{1}{2}\))2 = 2
⇒ 1 + tan 22\(\frac{1}{2}\) = ±√2
⇒ tan 22\(\frac{1}{2}\) = ±√2 – 1
Since 22\(\frac{1}{2}\) is acute, tan 22\(\frac{1}{2}\) is positive and therefore tan 22\(\frac{1}{2}\) = √2 – 1
Question 8.
Prove that
(i) sin(A + 60°) + sin(A – 60°) = sin A.
(ii) tan 4A tan 3A tan A + tan 3A + tan A – tan 4A = 0
Solution:
(i) LHS = sin (A + 60°) + sin (A – 60°)
= sin A cos 60° + cos A sin 60° + sin A cos 60° – cos A sin 60°
= 2 sin A cos 60°
= 2 sin A \(\left(\frac{1}{2}\right)\)
= sin A
= RHS
(ii) 4A = 3A + A
tan 4A = tan (3A + A)
tan 4A = \(\frac{\tan 3 \mathrm{A}+\tan \mathrm{A}}{1-\tan 3 \mathrm{A} \tan \mathrm{A}}\)
on cross multiplication we get,
tan 3A + tan A = tan 4A (1 – tan 3A tan A) = tan 4A – tan 4A tan 3A tanA
i.e., tan 4A tan 3A tan A + tan 3A + tan A = tan 4A
(or) tan 4A tan 3A tan A + tan 3A + tan A – tan 4A = 0
![]()
Question 9.
(i) If tan θ = 3 find tan 3θ
(ii) If sin A = \(\frac{12}{13}\), find sin 3A.
Solution:
(i) tan θ = 3
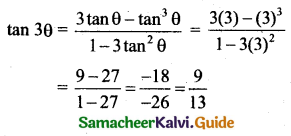
(ii) If sin A = \(\frac{12}{13}\)
We know that sin 3A = 3 sin A – 4 sin3 A
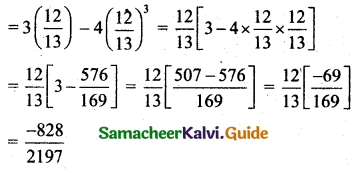
Question 10.
If sin A = \(\frac{3}{5}\), find the values of cos 3A and tan 3A.
Solution:
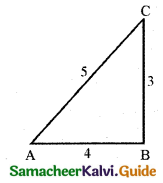
Given sin A = \(\frac{3}{5}\)
cos A = \(\frac{\text { Adjacent side }}{\text { Hypotenuse }}=\frac{4}{5}\)
and tan A = \(\frac{\text { Opposite side }}{\text { Adjacent side }}=\frac{3}{4}\)
We know that cos 3A = 4 cos3 A – 3 cos A
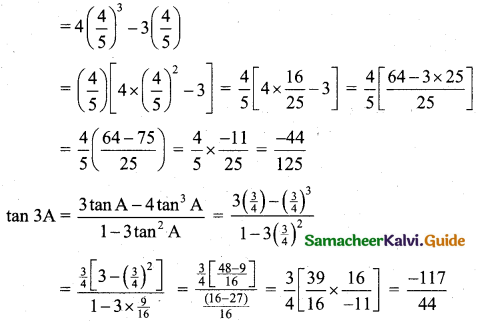
![]()
Question 11.
Prove that \(\frac{\sin (B-C)}{\cos B \cos C}+\frac{\sin (C-A)}{\cos C \cos A}+\frac{\sin (A-B)}{\cos A \cos B}=0\)
Solution:
Consider \(\frac{\sin (B-C)}{\cos B \cos C}\)
= \(\frac{\sin \mathrm{B} \cos \mathrm{C}-\cos \mathrm{B} \sin \mathrm{C}}{\cos \mathrm{B} \cos \mathrm{C}}\)
= \(\frac{\sin B \cos C}{\cos B \cos C}-\frac{\cos B \sin C}{\cos B \cos C}\)
= tan B – tan C ……… (1)
Similarly we can prove \(\frac{\sin (C-A)}{\cos C \cos A}\) = tan C – tan A …….(2)
and \(\frac{\sin (A-B)}{\cos A \cos B}\) = tan A – tan B …….. (3)
Add (1), (2) and (3) we get
\(\frac{\sin (B-C)}{\cos B \cos C}+\frac{\sin (C-A)}{\cos C \cos A}+\frac{\sin (A-B)}{\cos A \cos B}=0\)
Question 12.
If tan A – tan B = x and cot B – cot A = y prove that cot(A – B) = \(\frac{1}{x}+\frac{1}{y}\).
Solution:
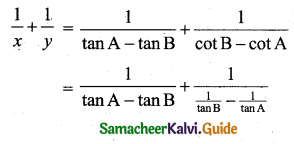

Hence proved.
Question 13.
If sin α + sin β = a and cos α + cos β = b, then prove that cos(α – β) = \(\frac{a^{2}+b^{2}-2}{2}\)
Solution:
Consider a2 + b2 = sin2α + sin2β + 2 sin α sin β + cos2α + cos2β + 2 cos α cos β
a2 + b2 = (sin2α + cos2α) + (sin2β + cos2β) + 2[cos α cos β + sin α sin β]
a2 + b2 = 1 + 1 + 2 cos(α – β)
∴ cos(α – β) = \(\frac{a^{2}+b^{2}-2}{2}\)
![]()
Question 14.
Find the value of tan\(\frac{\pi}{8}\).
Solution:
Method 1:
\(\frac{\pi}{8}=\frac{180^{\circ}}{8}=\frac{45^{\circ}}{2}=22 \frac{1}{2}\)
We know that tan 2A = \(\frac{2 \tan A}{1-\tan ^{2} A}\)
Put A = 22\(\frac{1}{2}\) in the above formula

On cross multiplication we get
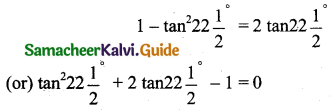
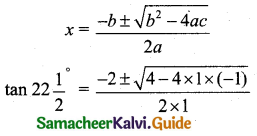
Here a = 1, b = 2, c = -1
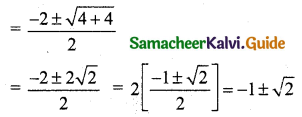
Since 22\(\frac{1}{2}\) is acute tan 22\(\frac{1}{2}\) is positive tan 22\(\frac{1}{2}\) = tan \(\frac{\pi}{8}\)
= -1 + √2
= √2 – 1
Method 2:
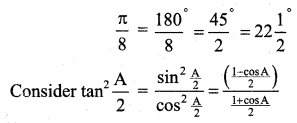
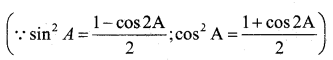
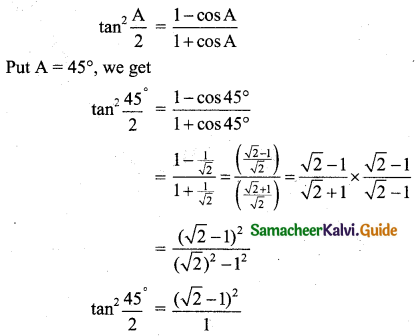
∴ \(\tan ^{2} 22 \frac{1}{2}=(\sqrt{2}-1)^{2}\)
Taking square root, \(\tan ^{2} 22 \frac{1}{2}\) = ±(√2 – 1)
But \(22 \frac{1}{2}\) lies in first quadrant, tan \(22 \frac{1}{2}\) is positive.
∴ tan 22\(\frac{1}{2}\) = √2 – 1
Method 3:
consider tan A = \(\frac{\sin 2 A}{1+\cos 2 A}\)
Put A = \(22 \frac{1}{2}\)
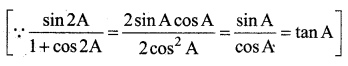
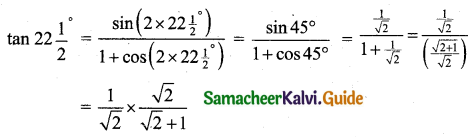
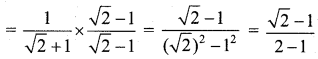
tan 22\(\frac{1}{2}\) = √2 – 1
![]()
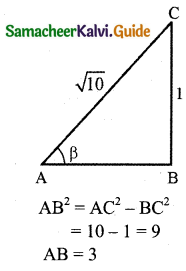
Question 15.
If tan α = \(\frac{1}{7}\), sin β = \(\frac{1}{\sqrt{10}}\). Prove that α + 2β = \(\frac{\pi}{4}\) where 0 < α < \(\frac{\pi}{2}\) and 0 < β < \(\frac{\pi}{2}\).
Solution:
Given that tan α = \(\frac{1}{7}\)
We wish to find tan(α + 2β)