Students can download 11th Business Maths Chapter 5 Differential Calculus Ex 5.2 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 5 Differential Calculus Ex 5.2
Samacheer Kalvi 11th Business Maths Differential Calculus Ex 5.2 Text Book Back Questions and Answers
Question 1.
Evaluate the following:
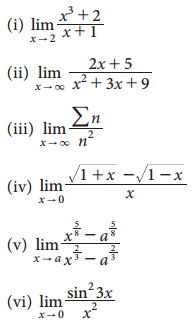
Solution:
(i) \(\lim _{x \rightarrow 2} \frac{x^{3}+2}{x+1}\)
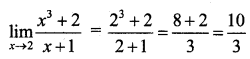
(ii) \(\lim _{x \rightarrow \infty} \frac{2 x+5}{x^{2}+3 x+9}\)
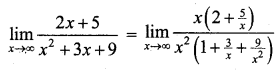
[Takeout x from numerator and take x2 from the denominator]
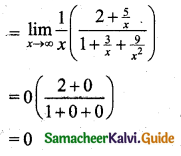
(iii) \(\lim _{x \rightarrow \infty} \frac{\Sigma n}{n^{2}}\)
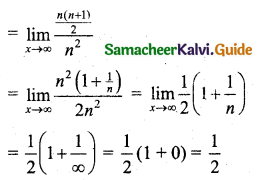
(iv) \(\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-\sqrt{1-x}}{5 x}\)

(v) \(\lim _{x \rightarrow a} \frac{x^{\frac{5}{8}}-a^{\frac{5}{8}}}{x^{\frac{2}{3}}-a^{\frac{2}{3}}}\)
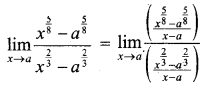
[Divide both numerator and denominator by x – a; \(\lim _{x \rightarrow a} \frac{x^{n}-a^{n}}{x-a}=n a^{n}\)]
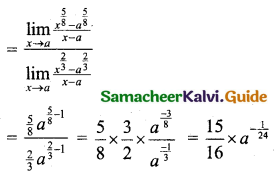
(vi) \(\lim _{x \rightarrow 0} \frac{\sin ^{2} 3 x}{x^{2}}\)
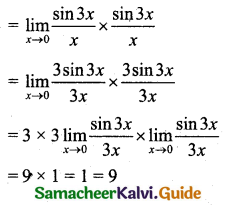
![]()
Question 2.
If \(\lim _{x \rightarrow a} \frac{x^{9}-a^{9}}{x-a}=\lim _{x \rightarrow 3}(x+6)\), find the value of a.
Solution:
\(\lim _{x \rightarrow a} \frac{x^{9}-a^{9}}{x-a}=\lim _{x \rightarrow 3}(x+6)\)
9 . a9-1 = 3 + 6
9 . a8 = 9
a8 = 1
Taking squareroot on bothsides, we get
\(\left(a^{8}\right)^{\frac{1}{2}}\) = ±1
a4 = ±1
But a4 = -1 is imposssible.
∴ a4 = 1
Again taking squareroot, we get
\(\left(a^{4}\right)^{\frac{1}{2}}\) = ±1
a2 = ±1
a2 = -1 is imposssible
∴ a2 = 1
Again taking positive squareroot, a = ±1
![]()
Question 3.
If \(\lim _{x \rightarrow 2} \frac{x^{n}-2^{n}}{x-2}=448\), then find the least positive integer n.
Solution:


Question 4.
If f(x) = \(\frac{x^{7}-128}{x^{5}-32}\), then find \(\lim _{x \rightarrow 2} f(x)\)
Solution:
\(\lim _{x \rightarrow 2} f(x)\)

![]()
Question 5.
Let f(x) = \(\frac{a x+b}{x+1}\), if \(\lim _{x \rightarrow 0} f(x)=2\) and \(\lim _{x \rightarrow \infty} f(x)=1\), then show that f(-2) = 0
Solution:
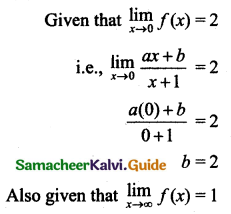

Hence Proved.