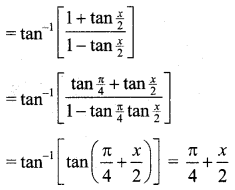Students can download 11th Business Maths Chapter 4 Trigonometry Ex 4.4 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 4 Trigonometry Ex 4.4
Samacheer Kalvi 11th Business Maths Trigonometry Ex 4.4 Text Book Back Questions and Answers
Question 1.
Find the principal value of the following:
(i) sin-1 (\(-\frac{1}{2}\))
(ii) tan-1 (-1)
(iii) cosec-1 (2)
(iv) sec-1 (-√2)
Solution:
(i) sin-1 (\(-\frac{1}{2}\))
Let sin-1 (\(-\frac{1}{2}\)) = y
[where \(\frac{-\pi}{2} \leq y \leq \frac{\pi}{2}\)]
\(-\frac{1}{2}\) = sin y
sin y = \(-\frac{1}{2}\) (∵ \(\sin \frac{\pi}{6}=\frac{1}{2}\))
sin y = sin(\(-\frac{\pi}{6}\)) [∵ \(\sin \left(-\frac{\pi}{6}\right)=-\sin \left(\frac{\pi}{6}\right)\)]
∴ y = \(-\frac{\pi}{6}\)
∴ The principal value of sin-1 (\(-\frac{1}{2}\)) is \(-\frac{\pi}{6}\)
(ii) tan-1 (-1) = y
(-1) = tan y where \(\frac{-\pi}{2} \leq y \leq \frac{\pi}{2}\)
(or) tan y = – 1
tan y = tan(\(-\frac{\pi}{4}\)) (∵ \(\tan \frac{\pi}{4}\) = 1)
∴ y = \(-\frac{\pi}{4}\) [∵ \(\tan \left(-\frac{\pi}{4}\right)=-\tan \left(\frac{\pi}{4}\right)=-1\)]
∴ The principal value of tan-1 (-1) is \(-\frac{\pi}{4}\).
(iii) Let cosec-1 (2) = y
2 = cosec y
(or) cosec y = 2
⇒ \(\frac{1}{\sin y}\) = 2
⇒ sin y = \(\frac{1}{2}\) (Take reciprocal)
⇒ sin y = \(\sin \left(\frac{\pi}{6}\right)\)
⇒ y = \(\frac{\pi}{6}\)
The principal value of cosec-1 (-1) is \(\frac{\pi}{6}\).
(iv) Let sec-1 (-√2 ) = y
-√2 = sec y
sec y = -√2
\(\frac{1}{\cos y}\) = -√2
Taking reciprocal cos y = \(\frac{-1}{\sqrt{2}}\) [where 0 ≤ y ≤ π]

∴ The principal value of sec-1 (-√2) is \(\frac{3 \pi}{4}\)
![]()
Question 2.
Prove that
(i) 2 tan-1 (x) = \(\sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)\)
(ii) \(\tan ^{-1}\left(\frac{4}{3}\right)+\tan ^{-1}\left(\frac{1}{7}\right)=\frac{\pi}{4}\)
Solution:
(i) Let tan-1 x = θ
x = tan θ
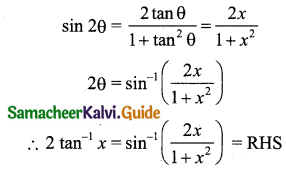
(ii) \(\tan ^{-1}\left(\frac{4}{3}\right)+\tan ^{-1}\left(\frac{1}{7}\right)=\frac{\pi}{4}\)

Question 3.
Show that \(\tan ^{-1}\left(\frac{1}{2}\right)+\tan ^{-1}\left(\frac{2}{11}\right)=\tan ^{-1}\left(\frac{3}{4}\right)\)
Solution:
We know that tan-1 x + tan-1 y = \(\tan ^{-1}\left(\frac{x+y}{1-x y}\right)\)
Now LHS = \(\tan ^{-1}\left(\frac{1}{2}\right)+\tan ^{-1}\left(\frac{2}{11}\right)\)
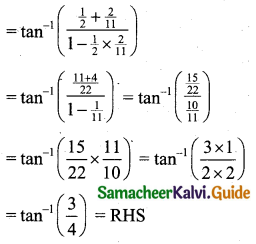
![]()
Question 4.
Solve: tan-1 2x + tan-1 3x = \(\frac{\pi}{4}\).
Solution:
Given tan-1 (2x) + tan-1 (3x) = \(\frac{\pi}{4}\)
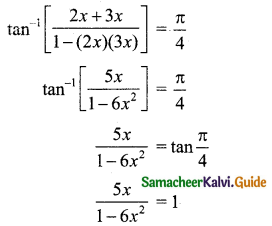
⇒ 5x = 1(1 – 6x2)
⇒ 6x2 + 5x – 1 = 0
⇒ (x + 1) (6x – 1) = 0
⇒ x + 1 = 0 (or) 6x – 1 = 0
⇒ x = -1 (or) x = \(\frac{1}{6}\)
x = -1 is rejected. It doesn’t satisfies the question.
Note: Put x = -1 in the given question.
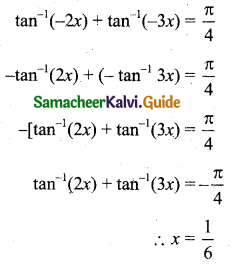
So the question changes.
Question 5.
Solve: tan-1 (x + 1) + tan-1 (x – 1) = \(\tan ^{-1}\left(\frac{4}{7}\right)\)
Solution:

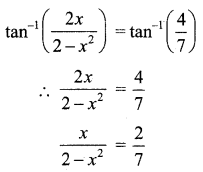
⇒ 7x = 2(2 – x2)
⇒ 7x = 4 – 2x2
⇒ 2x2 + 7x – 4 = 0
⇒ (x + 4) (2x – 1) = 0
⇒ x + 4 = 0 (or) 2x – 1 = 0
⇒ x = -4 (or) x = \(\frac{1}{2}\)
x = -4 is rejected, since does not satisfies the question.
∴ x = \(\frac{1}{2}\)
![]()
Question 6.
Evaluate
(i) cos[tan-1(\(\frac{3}{4}\))]
(ii) \(\sin \left[\frac{1}{2} \cos ^{-1}\left(\frac{4}{5}\right)\right]\)
Solution:
(i) Let \(\tan ^{-1}\left(\frac{3}{4}\right)\) = θ
\(\frac{3}{4}\) = tan θ
tan θ = \(\frac{3}{4}\)
∴ cos θ = \(\frac{4}{5}\)
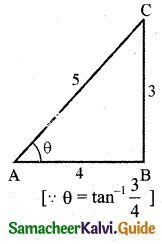
Now \(\cos \left(\tan ^{-1} \frac{3}{4}\right)\) = cos θ = \(\frac{4}{5}\)
(ii) Let \(\cos ^{-1}\left(\frac{4}{5}\right)\) = A
Then \(\frac{4}{5}\) = cos A
cos A = \(\frac{4}{5}\)
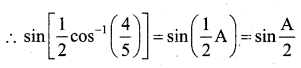
We know that

Question 7.
Evaluate: \(\cos \left(\sin ^{-1}\left(\frac{4}{5}\right)+\sin ^{-1}\left(\frac{12}{13}\right)\right)\)
Solution:
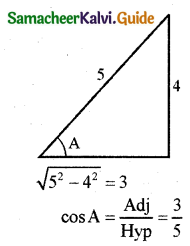
Let \(\sin ^{-1}\left(\frac{4}{5}\right)\) = A
sin A = \(\frac{4}{5}\)
∴ cos A = \(\frac{3}{5}\)
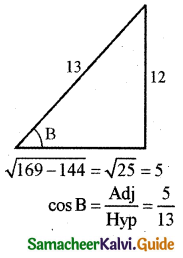
Let \(\sin ^{-1}\left(\frac{12}{13}\right)\) = B
\(\frac{12}{13}\) = sin B
sin B = \(\frac{12}{13}\)
∴ cos B = \(\frac{5}{13}\)
Now \(\cos \left(\sin ^{-1}\left(\frac{4}{5}\right)+\sin ^{-1}\left(\frac{12}{13}\right)\right)\) = cos (A + B)
= cos A cos B – sin A sin B
= \(\frac{3}{5} \times \frac{5}{13}-\frac{4}{5} \times \frac{12}{13}\)
= \(\frac{15}{65}-\frac{48}{65}\)
= \(-\frac{33}{65}\)
![]()
Question 8.
Prove that \(\tan ^{-1}\left(\frac{m}{n}\right)-\tan ^{-1}\left(\frac{m-n}{m+n}\right)=\frac{\pi}{4}\)
Solution:
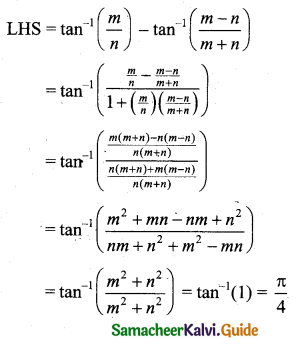
Question 9.
Show that \(\sin ^{-1}\left(-\frac{3}{5}\right)-\sin ^{-1}\left(-\frac{8}{17}\right)=\cos ^{-1}\left(\frac{84}{85}\right)\)
Solution:
\(\sin ^{-1}\left(-\frac{3}{5}\right)-\sin ^{-1}\left(-\frac{8}{17}\right)=-\sin ^{-1}\left(\frac{3}{5}\right)+\sin ^{-1}\left(\frac{8}{17}\right)\)
= \(\sin ^{-1}\left(\frac{8}{17}\right)-\sin ^{-1}\left(\frac{3}{5}\right)\)
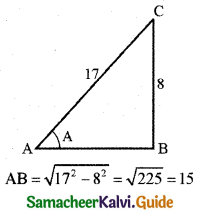
Let \(\sin ^{-1}\left(\frac{8}{17}\right)\) = A
\(\frac{8}{17}\) = sin A
sin A = \(\frac{8}{17}\)
∴ cos A = \(\frac{15}{17}\)
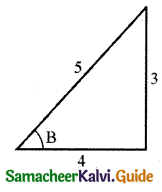
Let \(\sin ^{-1}\left(\frac{3}{5}\right)\) = B
sin B = \(\frac{3}{5}\)
∴ cos B = \(\frac{4}{5}\)
Consider cos(A – B) = cos A cos B + sin A sin B
= \(\frac{15}{17} \times \frac{4}{5}+\frac{8}{17} \times \frac{3}{5}\)
= \(\frac{60}{85}+\frac{24}{85}\)
cos (A – B) = \(\frac{84}{85}\)
∴ A – B = \(\cos ^{-1}\left(\frac{84}{85}\right)\)
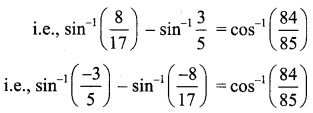
![]()
Question 10.
Express \(\tan ^{-1}\left[\frac{\cos x}{1-\sin x}\right]\), \(-\frac{\pi}{2}<x<\frac{3 \pi}{2}\) in the simplest form.
Solution:
\(\tan ^{-1}\left[\frac{\cos x}{1-\sin x}\right]\)
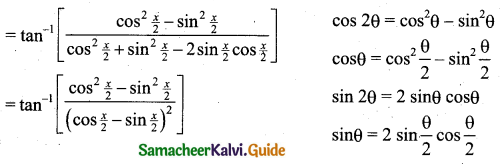
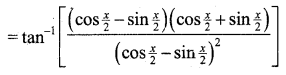
[∵ a2 – b2 = (a + b) (a – b)]
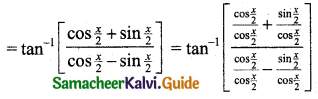
[∵ Divide each term by cos \(\frac{x}{2}\)]