Samacheer Kalvi 11th Business Maths Guide Chapter 5 Differential Calculus Ex 5.10

Students can download 11th Business Maths Chapter 5 Differential Calculus Ex 5.10 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 5 Differential Calculus Ex 5.10

Samacheer Kalvi 11th Business Maths Differential Calculus Ex 5.10 Text Book Back Questions and Answers

Question 1.
If f(x) = x² – x + 1 then f(x + 1) is:
(a) x²
(b) x
(c) 1
(d) x² + x + 1
Answer:
(d) x² + x + 1
Hint:
f(x) = x² – x + 1
f(x + 1) = (x + 1)² – (x + 1) + 1
= x² + 2x + 1 – x – 1 + 1
= x² + x + 1

Question 2.

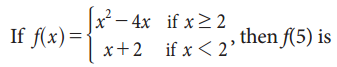
(a) -1
(b) 2
(c) 5
(d) 7
Answer:
(c) 5
Hint:

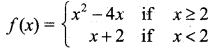
f(5) = 5² – 4(5) = 25 – 20 = 5
[For x = 5 take f(x) = x² – 4x]

Question 3.

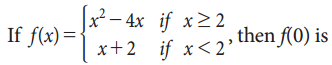
(a) 2
(b) 5
(c) -1
(d) 0
Answer:
(a) 2
Hint:

f(0) = 0 + 2 = 2
[For x = 0 take f(x) = x + 2]

Question 4.
If f(x) = \(\frac{1-x}{1+x}\) then f(-x) is equal to:
(a) -f(x)
(b) \(\frac{1}{f(x)}\)
(c) \(-\frac{1}{f(x)}\)
(d) f(x)
Answer:
(b) \(\frac{1}{f(x)}\)
Hint:
f(x) = \(\frac{1-x}{1+x}\)

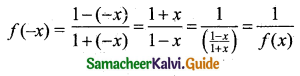
Question 5.
The graph of the line y = 3 is:
(a) Parallel to x-axis
(b) Parallel to the y-axis
(c) Passing through the origin
(d) Perpendicular to the x-axis
Answer:
(a) Parallel to x-axis
Hint:

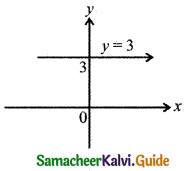
Question 6.
The graph of y = 2x² is passing through:
(a) (0, 0)
(b) (2, 1)
(c) (2, 0)
(d) (0, 2)
Answer:
(a) (0, 0)
Hint:

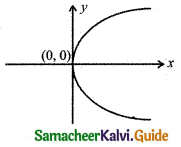
y = 2x²
Put x = 0, y = 0 the equation is satisfied.

Question 7.
The graph of y = e^x intersect the y-axis at:
(a) (0, 0)
(b) (1, 0)
(c) (0, 1)
(d) (1, 1)
Answer:
(c) (0, 1)
Hint:
y = e^x
Put x = 0, we get y = e⁰ = 1.
∴ The graph intersects the y-axis at (0, 1)

Question 8.
The minimum value of the function f(x) = |x| is:
(a) 0
(b) -1
(c) +1
(d) ∞
Answer:
(a) 0
Hint:

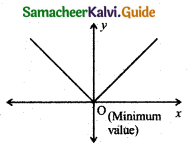
f(x) = |x|
f(0) = |0| = 0

Question 9.
Which one of the following functions has the property f(x) = f(\(\frac{1}{x}\))?
(a) f(x) = \(\frac{x^{2}-1}{x}\)
(b) f(x) = \(\frac{1-x^{2}}{x}\)
(c) f(x) = x
(d) f(x) = \(\frac{x^{2}+1}{x}\)
Answer:
(d) f(x) = \(\frac{x^{2}+1}{x}\)
Hint:
f(x) = f(\(\frac{1}{x}\))
take f(x) = \(\frac{x^{2}+1}{x}\)

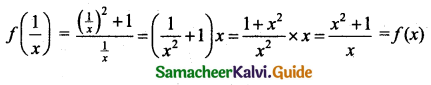
Question 10.
If f(x) = 2^x and g(x) = \(\frac{1}{2^{x}}\) then (fg)(x) is:
(a) 1
(b) 0
(c) 4^x
(d) \(\frac{1}{4^{x}}\)
Answer:
(a) 1
Hint:
(fg) x = f(x) g(x) = \(2^{x} \times \frac{1}{2^{x}}\) = 1

Question 11.
Which of the following function is neither even nor odd?
(a) f(x) = x³ + 5
(b) f(x) = x⁵
(c) f(x) = x¹⁰
(d) f(x) = x²
Answer:
(a) f(x) = x³ + 5
Hint:
Since it has a constant term 5.
f(x) = x³ + 5
f(-x) = (-x)³ + 5 = -x³ + 5.
It is not either f(x) or -f(x).

Question 12.
f(x) = -5, for all x ∈ R is a:
(a) an identity function
(b) modulus function
(c) exponential function
(d) constant function
Answer:
(d) constant function

Question 13.
The range of f(x) = |x|, for all x ∈ R is:
(a) (0, ∞)
(b) [0, ∞)
(c) (-∞, ∞)
(d) [1, ∞)
Answer:
(b) [0, ∞)
Hint:
[0, ∞) since in this interval 0 is included and f(0) = 0.

Question 14.
The graph of f(x) = e^x is identical to that of:
(a) f(x) = a^x, a > 1
(b) f(x) = a^x, a < 1
(c) f(x) = a^x, 0 < a < 1
(d) y = ax + b, a ≠ 0
Answer:
(a) f(x) = a^x, a > 1

Question 15.
If f(x) = x² and g(x) = 2x + 1 then (fg)(0) is:
(a) 0
(b) 2
(c) 1
(d) 4
Answer:
(a) 0
Hint:
(fg)(0) = f(o) g(o)
= 0² (2(0) + 1)
= 0(1)
= 0

Question 16.
\(\lim _{\theta \rightarrow 0} \frac{\tan \theta}{\theta}=\)
(a) 1
(b) ∞
(c) -∞
(d) θ
Answer:
(a) 1 (By formula)

Question 17.
\(\lim _{x \rightarrow 0} \frac{e^{x}-1}{x}=\)
(a) e
(b) nx^n-1
(c) 1
(d) 0
Answer:
(c) 1 (By formula)

Question 18.
For what value of x, f(x) = \(\frac{x+2}{x-1}\) is not continuous?
(a) -2
(b) 1
(c) 2
(d) -1
Answer:
(b) 1
Hint:
When x = 1, \(\frac{x+2}{x-1}\) is not defined.

Question 19.
A function f(x) is continuous at x = a \(\lim _{x \rightarrow a} f(x)\) is equal to:
(a) f(-a)
(b) f(\(\frac{1}{a}\))
(c) 2f(a)
(d) f(a)

Question 20.
\(\frac{d}{d x}\left(\frac{1}{x}\right)\) is equal to:
(a) \(-\frac{1}{x^{2}}\)
(b) \(-\frac{1}{x}\)
(c) log x
(d) \(\frac{1}{x^{2}}\)
Answer:
(a) \(-\frac{1}{x^{2}}\)

Question 21.
\(\frac{d}{d x}\) (5e^x – 2 log x) is equal to:
(a) 5e^x – \(\frac{2}{x}\)
(b) 5e^x – 2x
(c) 5e^x – \(\frac{1}{x}\)
(d) 2 log x
Answer:
(a) 5e^x – \(\frac{2}{x}\)
Hint:

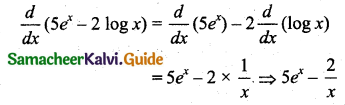
Question 22.
If y = x and z = \(\frac{1}{x}\) then \(\frac{d y}{d z}\) =
(a) x²
(b) 1
(c) -x²
(d) \(\frac{-1}{x^{2}}\)
Answer:
(c) -x²
Hint:

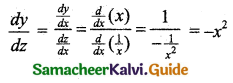
Question 23.
If y = e^2x then \(\frac{d^{2} y}{d x^{2}}\) at x = 0 is:
(a) 4
(b) 9
(c) 2
(d) 0
Answer:
(a) 4
Hint:

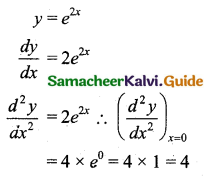
Question 24.
If y = log x then y₂ =
(a) \(\frac{1}{x}\)
(b) \(-\frac{1}{x^{2}}\)
(c) \(-\frac{2}{x^{2}}\)
(d) e2
Answer:
(b) \(-\frac{1}{x^{2}}\)
Hint:
y = log x
∴ y₁ = \(\frac{1}{x}\)
∴ y₂ = \(\frac{-1}{x^{2}}\)

Question 25.
\(\frac{d}{d x}\left(a^{x}\right)=\)
(a) \(\frac{1}{x \log _{e} a}\)
(b) a^a
(c) x log_ea
(d) a^x log_ea
Answer:
(d) a^x log_ea (by formula)