Students can download 11th Business Maths Chapter 6 Applications of Differentiation Ex 6.2 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 6 Applications of Differentiation Ex 6.2
Samacheer Kalvi 11th Business Maths Applications of Differentiation Ex 6.2 Text Book Back Questions and Answers
Question 1.
The average cost function associated with producing and marketing x units of an item is given by AC = 2x – 11 + \(\frac{50}{x}\). Find the range of values of the output x, for which AC is increasing.
Solution:
AC increases when \(\frac{d}{d x}\) (AC) > 0
C = 2x – 11 + \(\frac{50}{x}\)
\(\frac{d \mathrm{C}}{d x}\) = 2 – 0 + 50(\(\frac{-1}{x^{2}}\)) = 2 – \(\frac{50}{x^{2}}\)
\(\frac{d}{d x}\) (AC) > 0
2 – \(\frac{50}{x^{2}}\) > 0
2 > \(\frac{50}{x^{2}}\)
2x2 > 50
x2 > 25
x > 5
![]()
Question 2.
A television manufacturer finds that the total cost for the production and marketing of x number of television sets is C(x) = 300x2 + 4200x + 13500. If each product is sold for ₹ 8,400. show that the profit of the company is increasing.
Solution:
C(x) = 300x2 + 4200x + 13,500
Selling price of one product = ₹ 8,400
Selling price of x numbers of products = 8400x
Profit, P = Selling price – Cost price
= 8400x – (300x2 + 4200x + 13500)
= 8400x – 300x2 – 4200x – 13500
P = -300x2 + 4200x – 13500
Differentiating with respect to x we get
P'(x)= \(\frac{d \mathrm{P}}{d x}\) = -600x + 4200
\(\frac{d \mathrm{P}}{d x}\) = 0 gives -600x + 4200 = 0
-600x = -4200
x = 7
The point x = 7 divide the real numbers into the intervals (0, 7), (7, ∞). Here x cannot be negative.
![]()
Now P'(x) = – 600x + 4200
Take x = 2 in (0, 7)
P'(2) = -600 × 2 + 4200
= -1200 + 4200
= 3000, positive
∴ P'(x) is increasing in (0, 7) the profit of the company increasing when each product is sold for ₹ 8,400.
Question 3.
A monopolist has a demand curve x = 106 – 2p and average cost curve AC = 5 + \(\frac{x}{50}\), where p is the price per unit output and x is the number of units of output. If the total revenue is R = px, determine the most profitable output and the maximum profit.
Solution:
x = 106 – 2p
(or) 2p = 106 – x
p = \(\frac{1}{2}\) (106 – x)
Revenue, R = px
= \(\frac{1}{2}\)(106 – x) x
= 53x – \(\frac{x^{2}}{2}\)
Average Cost, AC = 5 + \(\frac{x}{50}\)
Cost C = (AC)x
= \(\left(5+\frac{x}{50}\right) x\)
= 5x + \(\frac{x^{2}}{50}\)
Profit (P) = Revenue – Cost
\(\frac{d \mathrm{P}}{d x}=48-\frac{13(2 x)}{25}\)
\(\frac{d \mathbf{P}}{d x}\) = 0 gives
48 – \(\frac{13(2 x)}{25}\) = 0
48 = \(\frac{13 \times 2 x}{25}\)
x = \(\frac{48 \times 25}{13 \times 2}\) = 46.1538 = 46 (approximately)
Also \(\frac{d^{2} P}{d x^{2}}=0-\frac{(13)^{2}}{25}\), negative since \(\frac{d^{2} \mathrm{P}}{d x^{2}}\) is negative, profit is maximum at x = 46 units.
Profit = 48x – \(\frac{13}{25}\) x2
When x = 46,
Profit = 48 × 46 – \(\frac{13}{25}\) × 46 × 46
= 2208 – \(\frac{27508}{25}\)
= 2208 – 1100.32
= ₹ 1107.68
![]()
Question 4.
A tour operator charges ₹ 136 per passenger with a discount of 40 paise for each passenger in excess of 100. The operator requires at least 100 passengers to operate the tour. Determine the number of passengers that will maximize the amount of money the tour operator receives.
Solution:
Let x be the required number of passengers
Tour operator charges

Amount of money, A = (Number of passengers) × (Tour operator charges)

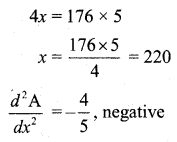
∴ The amount of money is maximum when the number of passengers is 220.
Question 5.
Find the local minimum and local maximum of y = 2x3 – 3x2 – 36x + 10.
Solution:
y = 2x3 – 3x2 – 36x + 10
\(\frac{d y}{d x}\) = 6x2 – 6x – 36 = 6(x2 – x – 6)
\(\frac{d y}{d x}\) = 0 gives 6(x2 – x – 6) = 0
6(x – 3) (x + 2) = 0
x = 3 (or) x = -2
\(\frac{d^{2} y}{d x^{2}}\) = 6(2x – 1)
Case (i): when x = 3,
\(\left(\frac{d^{2} y}{d x^{2}}\right)_{x=3}\) = 6(2 × 3 – 1)
= 6 × 5
= 30, positive
Since \(\frac{d^{2} y}{d x^{2}}\) is positive y is minimum when x = 3.
The local minimum value is obtained by substituting x = 3 in y.
Local minimum value = 2(33) – 3(32) – 36(3) + 10
= 2(27) – (27) – 108 + 10
= 27 – 98
= -71
Case (ii): when x = -2,
\(\left(\frac{d^{2} y}{d x^{2}}\right)_{x=-2}\) = 6(-2 × 2 – 1)
= 6 × -5
= -30, negative
Since \(\frac{d^{2} y}{d x^{2}}\) is negative, y is maximum when x = -2.
Local maximum value = 2(-2)3 – 3(-2)2 – 36(-2) + 10
= 2(-8) – 3(4) + 72 + 10
= -16 – 12 + 82
= -28 + 82
= 54
![]()
Question 6.
The total revenue function for a commodity is R = 15x + \(\frac{x^{2}}{3}-\frac{1}{36} x^{4}\). Show that at the highest point average revenue is equal to the marginal revenue.
Solution:
R = 15x + \(\frac{x^{2}}{3}-\frac{1}{36} x^{4}\)
Average Revenue = AR = \(\frac{\mathrm{R}}{x}\)
= \(\frac{15 x+\frac{x^{2}}{3}-\frac{1}{36} x^{4}}{x}\)
= \(15+\frac{x}{3}-\frac{1}{36} x^{3}\)
To test maxima or minima for AR = \(\frac{d(\mathrm{AR})}{d x}\)
= 0 + \(\frac{1}{3}-\frac{3 x^{2}}{36}\)
= \(\frac{1}{3}-\frac{x^{2}}{12}\)
\(\frac{d(\mathrm{AR})}{d x}\) = 0
\(\frac{1}{3}-\frac{x^{2}}{12}\) = 0
\(\frac{1}{3}=\frac{x^{2}}{12}\)
x2 = \(\frac{12}{3}\)
x2 = 4
x = 2
\(\frac{d^{2}(\mathrm{AR})}{d x^{2}}=0-\frac{2 x}{12}=-\frac{x}{6}\)
When x = 2, \(\frac{d^{2}(\mathrm{AR})}{d x^{2}}=-\frac{2}{6}=-\frac{1}{3}\), negative
∴ AR is maximum when x = 2
Now, AR = 15 + \(\frac{x}{3}-\frac{1}{36} x^{3}\)
When x = 2, AR = \(15+\frac{2}{3}-\frac{2^{3}}{36}\)
= \(15+\frac{2}{3}-\frac{8}{36}\)
= \(15+\frac{24-8}{36}\)
= 15 + \(\frac{16}{36}\)
= 15 + \(\frac{4}{9}\) ……… (1)
R = \(15 x+\frac{x^{2}}{3}-\frac{1}{36} x^{4}\)
Marginal Revenue (MR) = \(\frac{d \mathrm{R}}{d x}\)
= \(15+\frac{2 x}{3}-\frac{4 x^{3}}{36}\)
= \(15+\frac{2}{3} x-\frac{x^{3}}{9}\)
When x = 2, MR = 15 + \(\frac{2}{3} \times 2-\frac{2^{3}}{9}\)
= 15 + \(\frac{4}{3}-\frac{8}{9}\)
= 15 + \(\frac{12-8}{9}\)
= 15 + \(\frac{4}{9}\) ……… (2)
From (1) and (2) at the highest point average revenue is equal to the marginal revenue.