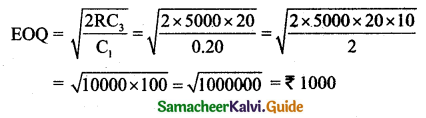Samacheer Kalvi 11th Business Maths Guide Chapter 6 Applications of Differentiation Ex 6.6

Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 6 Applications of Differentiation Ex 6.6 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 6 Applications of Differentiation Ex 6.6

Samacheer Kalvi 11th Business Maths Applications of Differentiation Ex 6.6 Text Book Back Questions and Answers

Choose the correct answer.

Question 1.
Average fixed cost of the cost function C(x) = 2x³ + 5x² – 14x + 21 is:
(a) \(\frac{2}{3}\)
(b) \(\frac{5}{x}\)
(c) \(-\frac{14}{x}\)
(d) \(\frac{21}{x}\)
Answer:
(d) \(\frac{21}{x}\)
Hint:
Average fixed cost \(\frac{k}{x}=\frac{21}{x}\)

Question 2.
Marginal revenue of the demand function p = 20 – 3x is:
(a) 20 – 6x
(b) 20 – 3x
(c) 20 + 6x
(d) 20 + 3x
Answer:
(a) 20 – 6x
Hint:
p = 20 – 3x
Revenue, R = px = (20 – 3x)x = 20x – 3x²
Marginal revenue = \(\frac{d \mathrm{R}}{d x}\) = 20 – 6x

Question 3.
If demand and the cost function of a firm are p = 2 – x and C = -2x² + 2x + 7 then its profit function is:
(a) x² + 7
(b) x² – 7
(c) -x² + 7
(d) -x² – 7
Answer:
(b) x² – 7
Hint:
Profit = Revenue – Cost
= (2 – x)x – (-2x² + 2x + 7)
= 2x – x² + 2x² – 2x – 7
= x² – 7

Question 4.
If the demand function is said to be inelastic, then:
(a) |η_d| > 1
(b) |η_d| = 1
(c) |η_d| < 1
(d) |η_d| = 0
Answer:
(a) |η_d| > 1

Question 5.
The elasticity of demand for the demand function x = \(\frac{1}{p}\) is:
(a) 0
(b) 1
(c) \(-\frac{1}{p}\)
(d) ∞
Answer:
(b) 1
Hint:

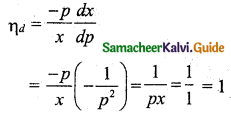
Question 6.
Relationship among MR, AR and ηd is:
(a) \(\eta_{d}=\frac{\mathrm{AR}}{\mathrm{AR}-\mathrm{MR}}\)
(b) η_d = AR – MR
(c) MR = AR = η_d
(d) AR = \(\frac{\mathrm{MR}}{\eta_{d}}\)
Answer:
(a) \(\eta_{d}=\frac{\mathrm{AR}}{\mathrm{AR}-\mathrm{MR}}\)

Question 7.
For the cost function C = \(\frac{1}{25} e^{5x}\), the marginal cost is:
(a) \(\frac{1}{25}\)
(b) \(\frac{1}{5} e^{5 x}\)
(c) \(\frac{1}{125} e^{5 x}\)
(d) 25e^5x
Answer:
(b) \(\frac{1}{5} e^{5 x}\)
Hint:
C = \(\frac{1}{25} e^{5x}\)
Marginal cost \(\frac{d c}{d x}=\frac{1}{25}\left(5 e^{5 x}\right)=\frac{1}{5} e^{5 x}\)

Question 8.
Instantaneous rate of change of y = 2x² + 5x with respect to x at x = 2 is:
(a) 4
(b) 5
(c) 13
(d) 9
Answer:
(c) 13
Hint:
y = 2x² + 5x
\(\frac{d y}{d x}\) = 4x + 5
\(\left(\frac{d y}{d x}\right)_{x=2}\) = 4 × 2 + 5 = 13

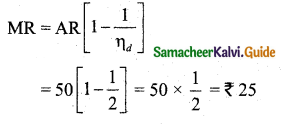
Question 9.
If the average revenue of a certain firm is ₹ 50 and its elasticity of demand is 2, then their marginal revenue is:
(a) ₹ 50
(b) ₹ 25
(c) ₹ 100
(d) ₹ 75
Answer:
(b) ₹ 25
Hint:

Question 10.
Profit P(x) is maximum when:
(a) MR = MC
(b) MR = 0
(c) MC = AC
(d) TR = AC
Answer:
(a) MR = MC

Question 11.
The maximum value of f(x) = sin x is:
(a) 1
(b) \(\frac{\sqrt{3}}{2}\)
(c) \(\frac{1}{\sqrt{2}}\)
(d) \(-\frac{1}{\sqrt{2}}\)
Answer:
(a) 1
Hint:
When x = \(\frac{\pi}{2}\), sin x is maximum.
Maximum value is sin\(\frac{\pi}{2}\) = 1

Question 12.
If f(x, y) is a homogeneous function of degree n, then \(x \frac{\partial f}{\partial x}+y \frac{\partial f}{\partial y}\) is equal to:
(a) (n – 1)f
(b) n(n – 1)f
(c) nf
(d) f
Answers:
(c) nf

Question 13.
If u = 4x² + 4xy + y² + 4x + 32y + 16, then \(\frac{\partial^{2} u}{\partial y \partial x}\) is equal to:
(a) 8x + 4y + 4
(b) 4
(c) 2y + 32
(d) 0
Answer:
(b) 4
Hint:
u = 4x² + 4xy + y² + 4x + 32y + 16

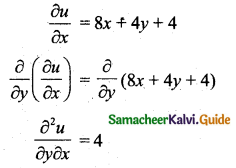
Question 14.
If u = x³ + 3xy² + y³ then \(\frac{\partial^{2} u}{\partial y \partial x}\) is:
(a) 3
(b) 6y
(c) 6x
(d) 2
Answer:
(b) 6y
Hint:
u = x³ + 3xy² + y³

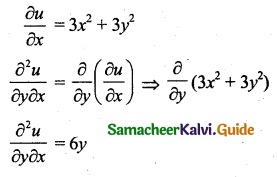
Question 15.
If u = \(e^{x^{2}}\) then \(\frac{\partial u}{\partial x}\) is equal to:
(a) \(2 x e^{x^{2}}\)
(b) \(e^{x^{2}}\)
(c) \(2 e^{x^{2}}\)
(d) 0
Answer:
(a) \(2 x e^{x^{2}}\)
Hint:
u = \(e^{x^{2}}\)
\(\frac{\partial u}{\partial x}=2 x e^{x^{2}}\)

Question 16.
Average cost is minimum when:
(a) Marginal cost = marginal revenue
(b) Average cost = marginal cost
(c) Average cost = Marginal revenue
(d) Average Revenue = Marginal cost
Answer:
(b) Average cost = marginal cost

Question 17.
A company begins to earn profit at:
(a) Maximum point
(b) Breakeven point
(c) Stationary point
(d) Even point
Answer:
(b) Breakeven point

Question 18.
The demand function is always:
(a) Increasing function
(b) Decreasing function
(c) Non-decreasing function
(d) Undefined function
Answer:
(b) Decreasing function

Question 19.
If q = 1000 + 8p₁ – p₂ then, \(\frac{\partial q}{\partial p_{1}}\) is:
(a) -1
(b) 8
(c) 1000
(d) 1000 – p₂
Answer:
(b) 8
Hint:
q = 1000 + 8p₁ – p₂
\(\frac{8 q}{\partial p_{1}}\) = 8

Question 20.
If R = 5000 units/year, C₁ = 20 paise, C₃ = ₹ 20 then EOQ is:
(a) 5000
(b) 100
(c) 1000
(d) 200
Answer:
(c) 1000
Hint: