Students can download 11th Business Maths Chapter 1 Matrices and Determinants Ex 1.3 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 1 Matrices and Determinants Ex 1.3
Samacheer Kalvi 11th Business Maths Matrices and Determinants Ex 1.3 Text Book Back Questions and Answers
Question 1.
Solve by matrix inversion method: 2x + 3y – 5 = 0; x – 2y + 1 = 0.
Solution:
2x + 3y = 5
x – 2y = -1
The given system can be written as
\(\left[\begin{array}{rr}
2 & 3 \\
1 & -2
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{r}
5 \\
-1
\end{array}\right]\)
AX = B
where A = \(\left[\begin{array}{rr}
2 & 3 \\
1 & -2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{r}
5 \\
-1
\end{array}\right]\)
|A| = \(\left|\begin{array}{rr}
2 & 3 \\
1 & -2
\end{array}\right|\) = -4 – 3 = -7 ≠ 0
∴ A-1 Exists.

∴ x = 1, y = 1
![]()
Question 2.
Solve by matrix inversion method:
(i) 3x – y + 2z = 13; 2x + y – z = 3; x + 3y – 5z = -8
(ii) x – y + 2z = 3; 2x + z = 1; 3x + 2y + z = 4
(iii) 2x – z = 0; 5x + y = 4; y + 3z = 5
Solution:
(i) The given system can be written as
\(\left[\begin{array}{rrr}
3 & -1 & 2 \\
2 & 1 & -1 \\
1 & 3 & -5
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{r}
13 \\
3 \\
-8
\end{array}\right]\)
AX = B
Where A = \(\left[\begin{array}{rrr}
3 & -1 & 2 \\
2 & 1 & -1 \\
1 & 3 & -5
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{r}
13 \\
3 \\
-8
\end{array}\right]\)
|A| = \(\left|\begin{array}{rrr}
3 & -1 & 2 \\
2 & 1 & -1 \\
1 & 3 & -5
\end{array}\right|\)
= 3(-5 + 3) – (-1) (-10 + 1) + 2 (6 – 1)
= 3(-2) + 1(-9) + 2(5)
= -6 – 9 + 10
= -5
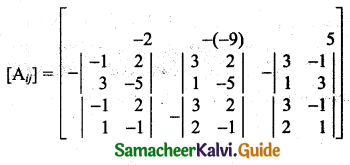
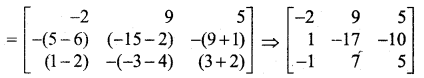
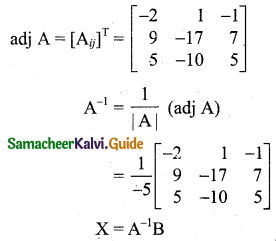
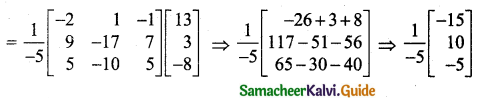
\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{r}
3 \\
-2 \\
1
\end{array}\right]\)
∴ x = 3, y = -2, z = 1.
(ii) The given system can be written as
\(\left[\begin{array}{rrr}
1 & -1 & 2 \\
2 & 0 & 1 \\
3 & 2 & 1
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
3 \\
1 \\
4
\end{array}\right]\)
AX = B
where A = \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
2 & 0 & 1 \\
3 & 2 & 1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
3 \\
1 \\
4
\end{array}\right]\)
|A| = \(\left|\begin{array}{rrr}
1 & -1 & 2 \\
2 & 0 & 1 \\
3 & 2 & 1
\end{array}\right|\)
= 1(0 – 2) – (-1)(2 – 3) + 2(4 – 0)
= -2 – (-1)(-1) + 2(4)
= -2 – 1 + 8
= 5


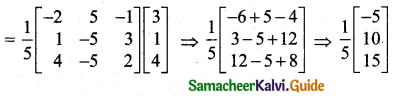
\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{r}
-1 \\
2 \\
3
\end{array}\right]\)
x = -1, y = 2, z = 3.
![]()
(iii) The given system can be written as
\(\left[\begin{array}{rrr}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
0 \\
4 \\
5
\end{array}\right]\)
AX = B
Where A = \(\left[\begin{array}{rrr}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
0 \\
4 \\
5
\end{array}\right]\)
|A| = \(\left|\begin{array}{rrr}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right|\)
= 2(3 – 0) – 0(15 – 0) – 1(5 – 0)
= 2(3) – 0(15) – 1(5)
= 6 – 0 – 5
= 1
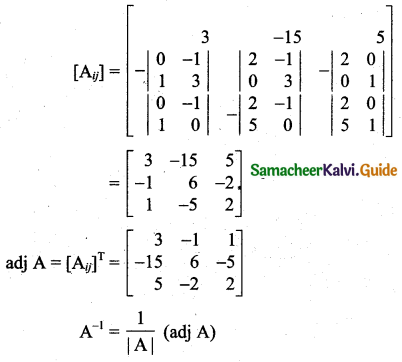

∴ x = 1, y = -1, z = 2.
Question 3.
A salesperson Ravi has the following record of sales for the month of January, February, and March 2009 for three products A, B, and C. He has been paid a commission at a fixed rate per unit but at varying rates for products A, B and C.
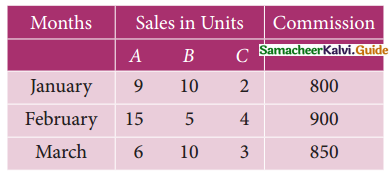
Find the rate of commission payable on A, B and C per unit sold using matrix inversion method.
Solution:
Let x, y and z be the rate of commission for the three products A, B and C respectively.
9x + 10y + 2z = 800
15x + 5y + 4z = 900
6x + 10y + 3z = 850
The given system can be written as
\(\left[\begin{array}{rrr}
9 & 10 & 2 \\
15 & 5 & 4 \\
6 & 10 & 3
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
800 \\
900 \\
850
\end{array}\right]\)
AX = B
Where A = \(\left[\begin{array}{rrr}
9 & 10 & 2 \\
15 & 5 & 4 \\
6 & 10 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
800 \\
900 \\
850
\end{array}\right]\)
Now, |A| = \(\left|\begin{array}{rrr}
9 & 10 & 2 \\
15 & 5 & 4 \\
6 & 10 & 3
\end{array}\right|\)
= \(9\left|\begin{array}{rr}
5 & 4 \\
10 & 3
\end{array}\right|-10\left|\begin{array}{rr}
15 & 4 \\
6 & 3
\end{array}\right|+2\left|\begin{array}{rr}
15 & 5 \\
6 & 10
\end{array}\right|\)
= 9[15 – 40] – 10(45 – 24) + 2(150 – 30)
= 9[-25] – 10[21] + 2[120]
= -225 – 210 + 240
= -195


\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{r}
17.948 \\
43.0769 \\
103.846
\end{array}\right]\)
\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{r}
17.95 \\
43.08 \\
103.85
\end{array}\right]\)
∴ x = 17.95, y = 43.08, z = 103.85
The rate of commission of A, B and C are 17.95, 43.08 and 103.85 respectively.
![]()
Question 4.
The prices of three commodities A, B, and C are ₹ x, y, and z per unit respectively. P purchases 4 units of C and sells 3 units of A and 5 units of B. Q purchases 3 units of B and sells 2 units of A and 1 unit of C. R purchases 1 unit of A and sells 4 units of B and 6 units of C. In the process P, Q and R earn ₹ 6,000, ₹ 5,000 and ₹ 13,000 respectively. By using the matrix inversion method, find the prices per unit of A, B, and C.
Solution:
Take selling the units js positive earning and buying the units is negative earning.
Given that
3x + 5y – 4z = 6000
2x – 3y + z = 5000
-1x + 4y + 6z = 13000
The given statement can be written as
\(\left(\begin{array}{rrr}
3 & 5 & -4 \\
2 & -3 & 1 \\
-1 & 4 & 6
\end{array}\right)\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)=\left(\begin{array}{r}
6000 \\
5000 \\
13000
\end{array}\right)\)
AX = B
Where A = \(\left(\begin{array}{rrr}
3 & 5 & -4 \\
2 & -3 & 1 \\
-1 & 4 & 6
\end{array}\right)\), X = \(\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)\) and B = \(\left(\begin{array}{r}
6000 \\
5000 \\
13000
\end{array}\right)\)
X = A-1B
|A| = \(\left|\begin{array}{rrr}
3 & 5 & -4 \\
2 & -3 & 1 \\
-1 & 4 & 6
\end{array}\right|\)
= 3(-18 – 4) – 5(12 + 1) – 4(8 – 3)
= 3(-22) – 5(13) – 4(5)
= -66 – 65 – 20
= -151


\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
3000 \\
1000 \\
2000
\end{array}\right]\)
The prices per unit of A, B and C are ₹ 3000, ₹ 1000 and ₹ 2000.
![]()
Question 5.
The sum of three numbers is 20. If we multiply the first by 2 and add the second number and subtract the third we get 23. If we multiply the first by 3 and add second and third to it, we get 46. By using the matrix inversion method find the numbers.
Solution:
Let the three numbers be x, y, and z.
x + y + z = 20
2x + y – z = 23
3x + y + z = 46
The given system can be written as
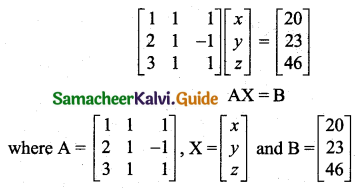

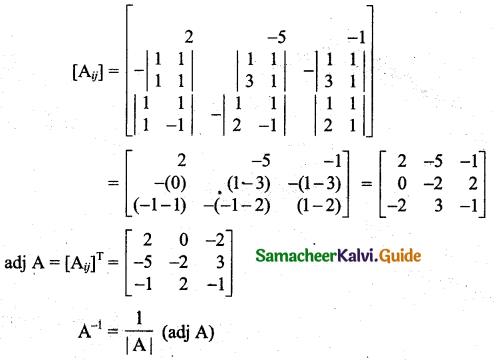
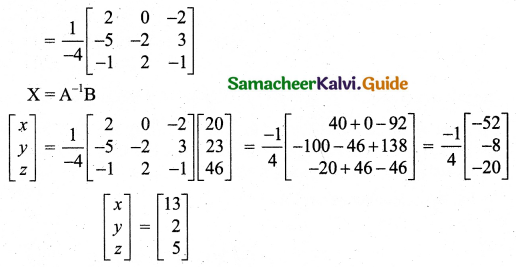
The numbers are 13, 2, and 5.
![]()
Question 6.
Weekly expenditure in an office for three weeks is given as follows. Assuming that the salary in all three weeks of different categories of staff did not vary, calculate the salary for each type of staff, using the matrix inversion method.
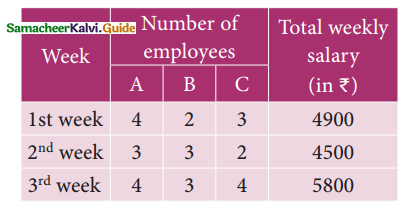
Solution:
Let ₹ x, ₹ y, ₹ z be the salary for each type of staff A, B and C.
4x + 2y + 3z = 4900
3x + 3y + 2z = 4500
4x + 3y + 4z = 5800
The given system can be written as
\(\left[\begin{array}{lll}
4 & 2 & 3 \\
3 & 3 & 2 \\
4 & 3 & 4
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
4900 \\
4500 \\
5800
\end{array}\right]\)
AX = B
where A = \(\left[\begin{array}{lll}
4 & 2 & 3 \\
3 & 3 & 2 \\
4 & 3 & 4
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{c}
4900 \\
4500 \\
5800
\end{array}\right]\)
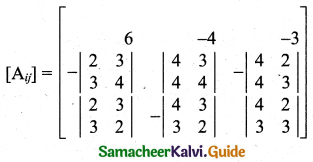
|A| = \(\left|\begin{array}{lll}
4 & 2 & 3 \\
3 & 3 & 2 \\
4 & 3 & 4
\end{array}\right|\)
= 4(12 – 6) – 2(12 – 8) + 3(9 – 12)
= 4(6) – 2(4) + 3(-3)
= 24 – 8 – 9
= 7



\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
700 \\
600 \\
300
\end{array}\right]\)
∴ Salary for each type of staff A, B and C are ₹ 700, ₹ 600 and ₹ 300.