Bhagya

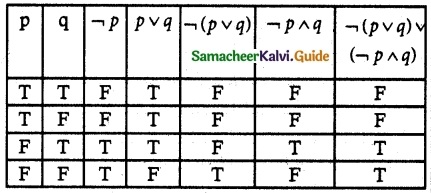
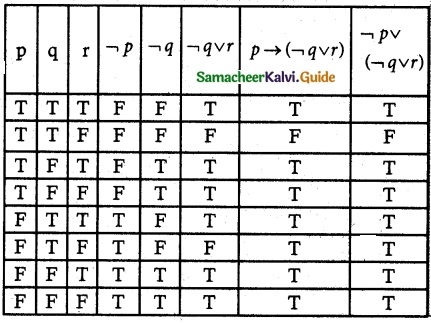
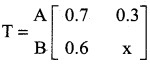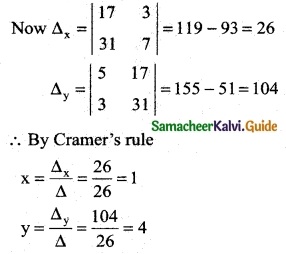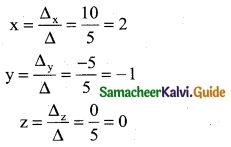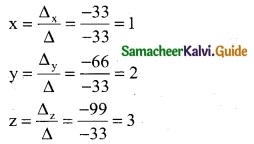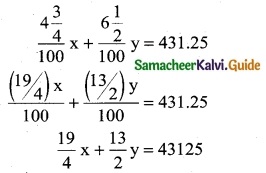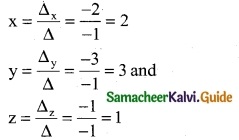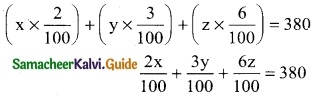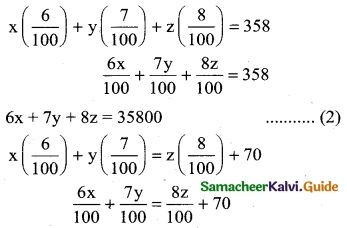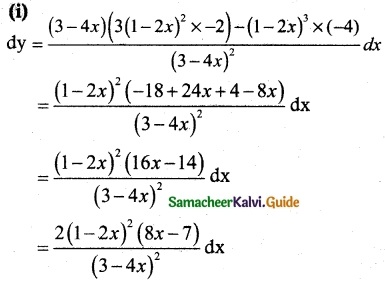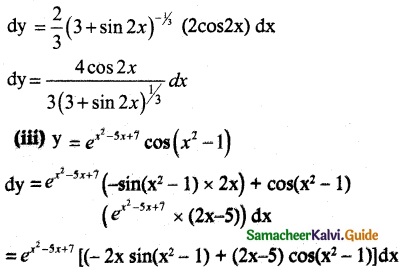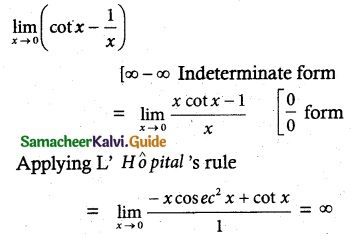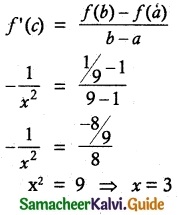Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Miscellaneous Problems Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Miscellaneous Problems

Question 1.
Find the rank of the matrix
A = \(\left(\begin{array}{cccc}
1 & -3 & 4 & 7 \\
9 & 1 & 2 & 0
\end{array}\right)\)
Solution:
\(\left(\begin{array}{cccc}
1 & -3 & 4 & 7 \\
9 & 1 & 2 & 0
\end{array}\right)\)
The order of A is 2 × 4
∴ P(A) ≤ 2
Let us transform the matrix A to an echelon form

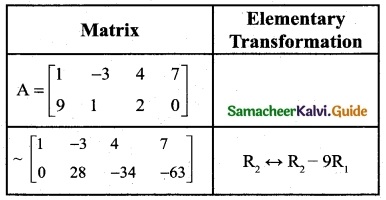
The number of non-zero rows is 2
∴ P(A) = 2

Question 2.
Find the rank of the matrix
A = \( \left[\begin{array}{cccc}
-2 & 1 & 3 & 4 \\
0 & 1 & 1 & 2 \\
1 & 3 & 4 & 7
\end{array}\right]\)
Solution:
A = \( \left[\begin{array}{cccc}
-2 & 1 & 3 & 4 \\
0 & 1 & 1 & 2 \\
1 & 3 & 4 & 7
\end{array}\right]\)
The order of A is 3 × 4
∴ P(A) < 3
Let us transform the matrix A to an echelon form

The number of non-zero rows = 3
∴ P(A) = 3

Question 3.
Find the rank of the matrix
A = \(\left[\begin{array}{llll}
4 & 5 & 2 & 2 \\
3 & 2 & 1 & 6 \\
4 & 4 & 8 & 0
\end{array}\right]\)
Solution:
A = \(\left[\begin{array}{llll}
4 & 5 & 2 & 2 \\
3 & 2 & 1 & 6 \\
4 & 4 & 8 & 0
\end{array}\right]\)
The order of A is 3 × 4
∴ p(A) < 3
Let us transform the matrix A to an echelon form


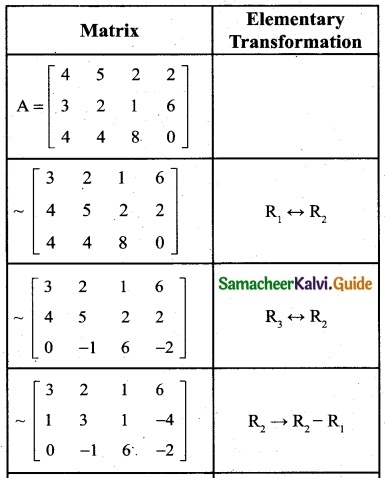
The last equivalent matrix is in the echelon form.
Number of non-zero rows = 3
∴ P(A) = 3

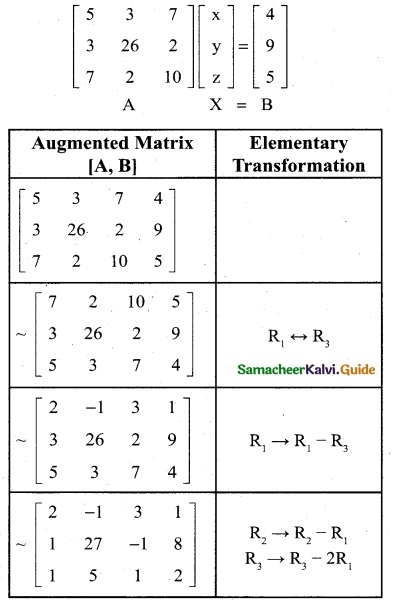
Question 4.
Examine the consistency of the system of equations;
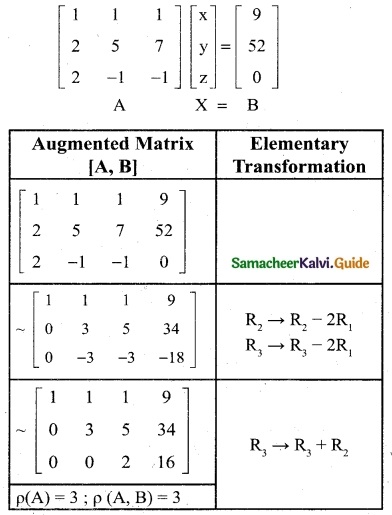
x + y + z = 7, x + 2y + 3z = 18, y + 2z = 6
Solution:
x + y + z = 7
x + 2y + 3z = 18
y + 2z = 6
The matrix form of the equations

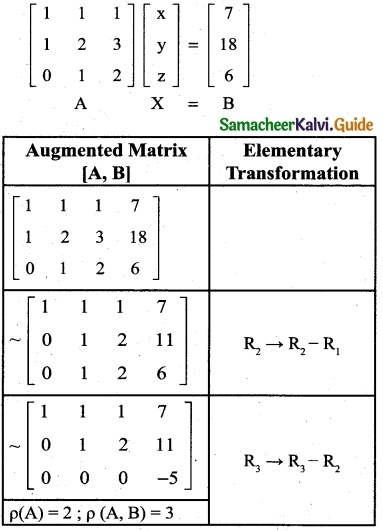
Here p(A) ≠ p(A, B)
∴ The given system is inconsistent and has no solution.

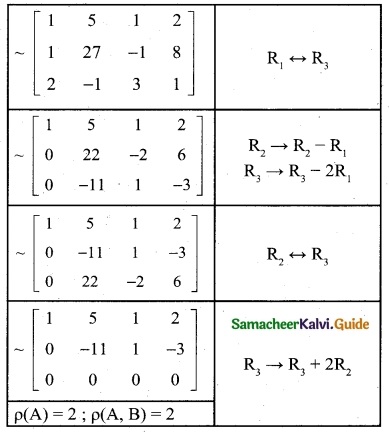
Question 5.
Find k if the equations 2x + 3y – z = 5, 3x – y + 4z = 2, x + 7y – 6z = k are consistent.
Solution:
2x + 3y – z = 5
3x – y + 4z = 2
x + 7y – 6z = k
The matrix form of these equations

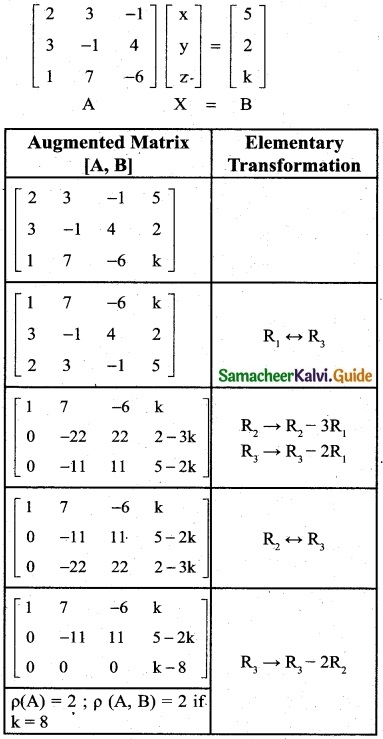
Obviously, the last equivalent matrix is in the ech-elon form.
Since the equations are consistent
P(-A) = p(A, B)
p(A) = 2 and p (A, B) = 2 then
k = 8

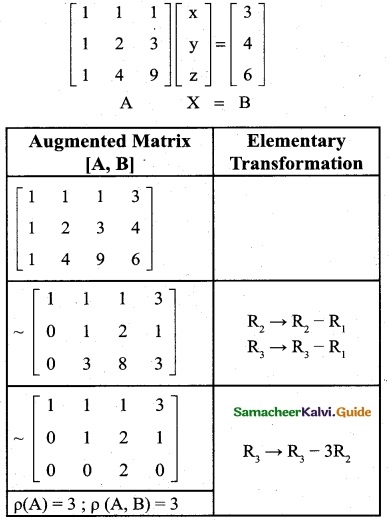
Question 6.
Find k if the equations x + y + z = 1, 3x – y – z = 4, x + 5y + 5z = k are inconsistent.
Solution:
x + y + z = 1
3x – y – z = 4
x + 5y + 5z = k
The matrix equation corresponding to the given system is

Obviously, the last equivalent matrix is in the ech-elon form.
Since the equations are inconsistent
p(A) ≠ p (A, B)
Here p(A) = 2 but p(A, B) should not equal to 2
∴ k ≠ 0
The equations are inconsistent when k assume any real value other than 0.

Question 7.
Solve the equations x + 2y + z = 7, 2x – y + 2z = 4, x + y – 2z = -1 by using Cramer’s rule.
Solution:
x + 2y + z = 7
2x – y + 2z = 4
x + y – 2z = -1
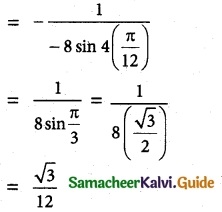
Here Δ = \(\left|\begin{array}{ccc}
1 & 2 & 1 \\
2 & -1 & 2 \\
1 & 1 & -2
\end{array}\right|\)
= 1(2 – 2)-2 (-4 – 2) + 1(2 + 1)
= 1(0) -2 (-6) + 1(3)
= 12 + 3 = 15 ≠ 0
∴ We can apply Cramer’s Rule and the system is consistent and it has unique solution.
Δ_x = \(\left|\begin{array}{ccc}
7 & 2 & 1 \\
4 & -1 & 2 \\
-1 & 1 & -2
\end{array}\right|\)
= 7 (2 – 2) -2 (-8 + 2) + 1(4 – 1)
= 7(0)-2 (-6) + 1(3)
= 12 + 3
= 15
Δ_y = \(\left|\begin{array}{ccc}
1 & 7 & 1 \\
2 & 4 & 2 \\
1 & -1 & -2
\end{array}\right|\)
= 1(-8 + 2) -7 (-4 – 2) + 1(-2 – 4)
= 1 (-6) – 7 (-6) + 1 (-6)
= -6 + 42 – 6 = 30
Δ_z = \(\left|\begin{array}{ccc}
1 & 2 & 7 \\
2 & -1 & 4 \\
1 & 1 & -1
\end{array}\right|\)
= 1(1 – 4) -2 (-2 – 4) + 7 (2 + 1)
= 1 (-3) -2 (-6) + 7 (3)
= -3 + 12 + 21 = 30
∴ By cramer’s rule

∴ The Solution is (x, y, z) = (1, 2, 2)

Question 8.
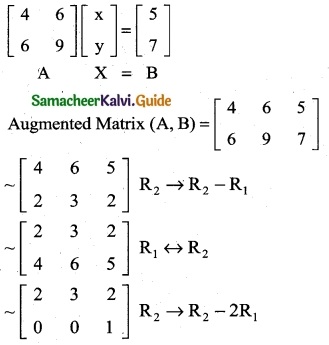
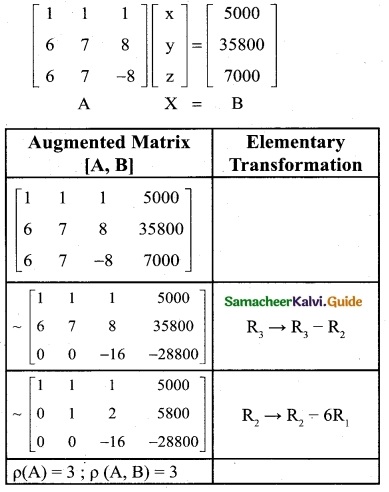
The cost of 2kg. of wheat and 1kg. of sugar is Rs 100. The cost of 3kg. of wheat, 2kg. of sugar and 1kg of rice is Rs 220. Find the cost of each per kg. using Cramer’s rule.
Solution:
Let cost of 1 kg of wheat be x; cost of 1kg of sugar be y and cost of 1 kg of rice be z.
2x + y = 100
x + z = 80
3x + 2y + z = 220
Here Δ = \(\left|\begin{array}{ccc}
2 & 1 & 0 \\
1 & 0 & 1 \\
3 & 2 & 1
\end{array}\right|\)
= 2 (0 – 2) -1 (1 – 3)
= – 4 + 2 = -2
≠ 0
∴ We can apply Cramer’s Rule and the system is consistent and it has unique solution.
Δ_x = \(\left|\begin{array}{ccc}
100 & 1 & 0 \\
80 & 0 & 1 \\
220 & 2 & 1
\end{array}\right|\)
= 100 (0 – 2) -1 (80 – 220)
= – 200 -1 (-140)
= – 200 +140
= -60
Δ_y = \(\left|\begin{array}{ccc}
2 & 100 & 0 \\
1 & 80 & 0 \\
3 & 220 & 1
\end{array}\right|\)
= 2 (80 – 220) -100 (1 – 3)
= 2 (-140) – 100 (-2)
= – 280 + 200
= -80
Δ_x = \(\left|\begin{array}{ccc}
2 & 1 & 100 \\
1 & 0 & 80 \\
3 & 2 & 220
\end{array}\right|\)
= 2 (0 -160) -1 (220 – 240) + 100 (2 – 0)
= 2 (-160) -1 (-20) + 100 (2)
= -320 + 20 + 200
= -100
∴ By cramer’s rule

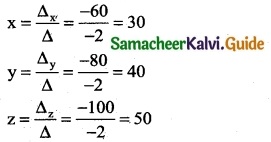
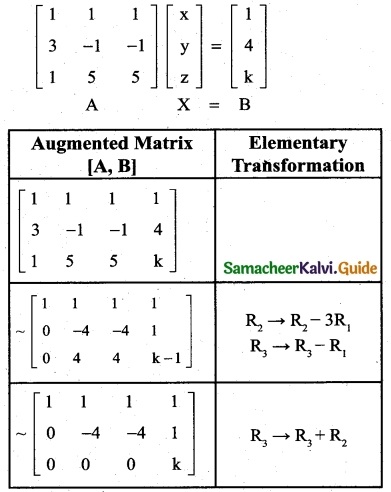
The solution is (x, y, z) = (30, 40, 50)
∴ The cost of 1 kg of wheat is Rs 30; the cost of 1 kg of sugar is Rs 40 and the cost of 1 kg of rice is Rs 50.

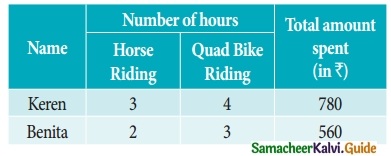
Question 9.
A salesman has the following record of sales during three items A, B, and C, which has different rates of commission.

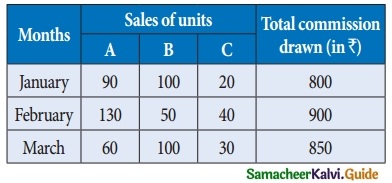
Find out the rate of commission on items A, B, and C by using Cramer’s rule.
Solution:
Let x, y, and z be the commission on items A, B, and C respectively.
90x + 100y + 20z = 800 ⇒ 9x + 10y + 2z = 80 ……… (1)
130x + 50y + 40z = 900 ⇒ 13x + 5y + 4z = 90 ………. (2)
60x + 100y + 30z = 850 ⇒ 6x + 10y + 3z = 85 ………. (3)
Here Δ = \(\left|\begin{array}{ccc}
9 & 10 & 2 \\
13 & 5 & 4 \\
6 & 10 & 3
\end{array}\right|\)
= 9 (15 – 40) -10 (39 – 24) + 2 (130 – 30)
= 9 (-25) – 10 (15) + 2 (100)
= -225 – 150 + 200
= -175
≠ 0
∴ We can apply Cramer’s Rule and the system is consistent and it has unique solution.
Δ_x = \(\left|\begin{array}{ccc}
80 & 10 & 2 \\
90 & 5 & 4 \\
85 & 10 & 3
\end{array}\right|\)
= 80 (15 – 40) -10 (270 – 340) + 2 (900 – 425)
= 80 (-25) -10 (-70) + 2 (475)
= -2000 + 700 + 950
= -350
Δ_y = \(\left|\begin{array}{ccc}
9 & 80 & 2 \\
13 & 90 & 4 \\
6 & 85 & 3
\end{array}\right|\)
= 9 (270 – 340) – 80 (39 – 24) + 2 (1105 – 540)
= 9 (-70)-80 (15) + 2 (565)
= -630 – 1200 + 1130
= -700
Δ_z = \(\left|\begin{array}{ccc}
9 & 10 & 80 \\
13 & 5 & 90 \\
6 & 10 & 85
\end{array}\right|\)
= 9 (425 – 900) -10 (1105 – 540) + 80 (130 – 30)
= 9 (-475) -10 (565) + 80 (100)
= – 4275 – 5650 + 8000
= -1925
∴ By cramer’s rule

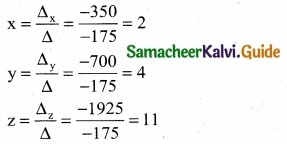
The solution is (x, y, z) = (2, 4, 11)
∴ The rates of commission for A, B and C are Rs 2, Rs 4 and Rs 11 respectively.

Question 10.
The subscription department of a magazine sends out a letter to a large mailing list inviting subscriptions for the magazine. Some of the people receiving this letter already subscribe to the magazine while others do not. From this mailing list, 60% of those who already subscribe will subscribe again while 25% of those who do not now subscribe will subscribe. In the last letter, it was found that 40% of those receiving it ordered a subscription. What percent of those receiving the current letter can be expected to order a subscription?
Solution:
The transition probability matrix is S

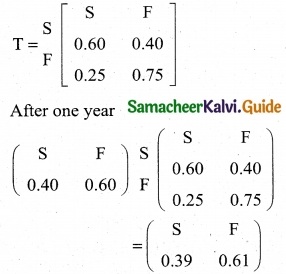
∴ 39% of those receiving the current letter can be expected to order a subscription.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.4

Choose the most suitable answer from the given four alternatives:

Question 1.
A = (1, 2, 3), then the rank of AA^T is
(a) 0
(b) 2
(c) 3
(d) 1
Solution:
(d) 1
Hint:
A = (1, 2, 3) then
A^T = \(\left(\begin{array}{l}
1 \\
2 \\
3
\end{array}\right)\)
AA^T = (1, 2, 3) \(\left(\begin{array}{l}
1 \\
2 \\
3
\end{array}\right)\) = (1 + 4 + 9) = (14)
Number of non-zero rows = 1
∴ P (AA^T) = 1

Question 2.
The rank of m × n matrix whose elements are unity is
(a) 0
(b) 1
(c) m
(d) n
Solution:
(b) 1

Question 3.
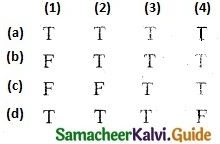
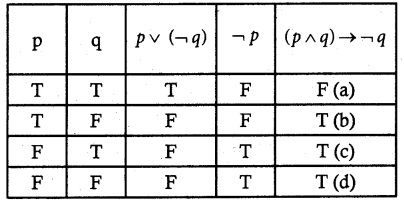
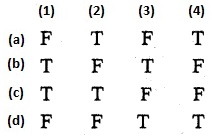
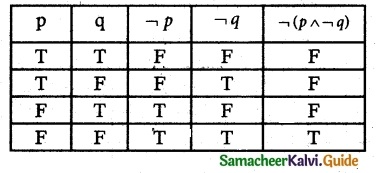
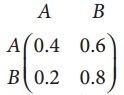If T = is a transition probability matrix, then at equilibriuium A is equal to
(a) \(\frac { 1 }{ 4 }\)
(b) \(\frac { 1 }{ 5 }\)
(c) \(\frac { 1 }{ 6 }\)
(d) \(\frac { 1 }{ 8 }\)
Solution:
(a) \(\frac { 1 }{ 4 }\)
Hint:

At equilibrium (A B) \(\left(\begin{array}{ll}
0.4 & 0.6 \\
0.2 & 0.8
\end{array}\right)\)
0.4 A + 0.2 B = A
0.4 A + 0.2(1 – A) = A
0.4 A + 0.2 – 0.2 A = A
0.2 A + 0.2 = A
0.2 = A – 0.2 A
0.2 = 0.8 A
A = \(\frac { 0.2 }{ 0.8 }\) = \(\frac { 1 }{ 4 }\)

Question 4.
If A = \(\left(\begin{array}{ll}
2 & 0 \\
0 & 8
\end{array}\right)\), then p(A) is
(a) 0
(b) 1
(c) 2
(d) n
Solution:
(c) 2
Hint:
A = \(\left(\begin{array}{ll}
2 & 0 \\
0 & 8
\end{array}\right)\)
No. of Non-zero rows = 2
∴ p(A) = 2

Question 5.
The rank of the matrix \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 2 & 3 \\
1 & 4 & 9
\end{array}\right]\) is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(d) 3
Hint:

No. of Non-zero rows = 3
∴ p(A) = 3

Question 6.
The rank of the unit matrix of order n is
(a) n – 1
(b) n
(c) n + 1
(d) n²
Solution:
(b) n

Question 7.
If p(A) = r then which of the following is correct?
(a) all the minors of order r which does not vanish
(b) A has at least one minor of order r which does not vanish
(c) A has at least one (r + 1) order minor which vanishes
(d) all (r + 1) and higher order minors should not vanish
Solution:
(b) A has at least one minor of order r which does not vanish.

Question 8.
If A = \(\left(\begin{array}{l}
1 \\
2 \\
3
\end{array}\right)\) then the rank of AA^T is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(b) 1
Hint:

No. of non-zero rows = 1
p (AA^T) = 1

Question 9.
If the rank of the matrix \(\left[\begin{array}{ccc}
\lambda & -1 & 0 \\
0 & \lambda & -1 \\
-1 & 0 & \lambda
\end{array}\right]\) is 2. then λ is
(a) 1
(b) 2
(c) 3
(d) only real number
Solution:
(a) 1
Hint:
A = \(\left[\begin{array}{ccc}
\lambda & -1 & 0 \\
0 & \lambda & -1 \\
-1 & 0 & \lambda
\end{array}\right]\)
Since the Rank is 2, third order matrix vanishes
∴ |A| = 0
\(\left[\begin{array}{ccc}
\lambda & -1 & 0 \\
0 & \lambda & -1 \\
-1 & 0 & \lambda
\end{array}\right]\) = 0
λ(λ² – 0) + 1 (0 – 1) = 0
λ³ – 1 = 0 ⇒ λ³ = 1
∴ λ = 1

Question 10.

(a) 0
(b) 2
(c) 3
(d) 5
Solution:
(c) 3
Hint:
Number of non-zero rows = 3
∴ Rank = 3

Question 11.
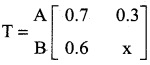If is a transition probability matrix, then the value of x is
(a) 0.2
(b) 0.3
(c) 0.4
(d) 0.7
Solution:
(c) 0.4
Hint:

is a transition probability matrix then 0.6 + x = 1
x = 1 – 0.6
x = 0.4

Question 12.
Which of the following is not an elementary transformation?
(a) R_i ↔ Rj
(b) R_i → 2R_i + 2Cj
(c) R_i → 2R_i + 4Rj
(d) C_i → C_i + 5Cj
Solution:
(b) R_i → 2R_i + 2Cj

Question 13.
If p(A) = p(A,B)= then the system is
(a) Consistent and has infinitely many solutions
(b) Consistent and has a unique solution
(c) inconsistent
(d) consistent
Solution:
(d) Consistent

Question 14.
If p(A) = p(A,B)= the number of unknowns, then the system is
(a) Consistent and has infinitely many solutions
(b) Consistent and has a unique solution
(c) inconsistent
(d) consistent
Solution:
(b) Consistent and has a unique solution

Question 15.
If p(A) ≠ p(A, B) =, then the system is
(a) Consistent and has infinitely many solutions
(b) Consistent and has a unique solution
(c) inconsistent
(d) consistent
Solution:
(c) inconsistent

Question 16.
In a transition probability matrix, all the entries are greater than or equal to
(a) 2
(b) 1
(c) 0
(d) 3
Solution:
(c) 0

Question 17.
If the number of variables in a non-homogeneous system AX = B is n, then the system possesses a unique solution only when
(a) p(A) = p(A, B) > n
(b) p(A) = p(A, B) = n
(c) p(A) = p(A, B) < n
(d) none of these
Solution:
(b) p(A) = p(A, B) = n

Question 18.
The system of equations 4x + 6y = 5, 6x + 9y = 7 has
(a) a unique solution
(b) no solution
(c) infinitely many solutions
(d) none of these
Solution:
(b) no solution
Hint:
The matrix form of the equations

p(A) ≠ p(A, B)
∴ The system is inconsistent.

Question 19.
For the system of equations x + 2y + 3z = 1, 2x + y – z = 3, 3x + 2y + k = 4
(a) there is only one solution
(b) there exists infinitely many solution
(c) there is no solution
(d) none of these
Solution:
(a) there is only one solution
Hint:
The matrix form of the equations

The last equivalent matrix in the echelon form
p(A) = p (A, B) = no. of unknowns
∴ The system is consistent.

Question 20.
If |A| ≠ 0, then A is
(a) non – singular matrix
(b) singular matrix
(c) zero matrix
(d) none of these
Solution:
(a) non-singular matrix

Question 21.
The system of linear equations x = y + z = 2, 2x + y – z = 3, 3x + 2y + k = 4 has unique solution, if k is not equal to
(a) 1
(b) 0
(c) 3
(d) 7
Solution:
(b) 0
Hint:
The matrix form of the equations

Since the system has unique solution.
P(A) = p(A, B) ≠ n
∴ K ≠ 0

Question 22.
Cramer’s rule is applicable only to get an unique solution when
(a) Δ_z ≠ 0
(b) Δ_x ≠ 0
(c) Δ ≠ 0
(d) Δ_y ≠ 0
Solution:
(c) Δ ≠ 0

Question 23.

Then (x, y) is

Solution:
(d) (\(\frac { -Δ_1 }{ Δ_2 }\), \(\frac { -Δ_1 }{ Δ_3 }\))

Question 24.
|A_{n × n}| = 3 |adj A| = 243 = (3)5 then the value n is
(a) 4
(b) 5
(c) 6
(d) 7
Solution:
(c) 6

Question 25.
Rank of a null matrix is
(a) 0
(b) -1
(c) ∞
(d) 1
Solution:
(a) 0

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.3

Question 1.
The subscription of a magazine sends out a letter to a large mailing list inviting subscriptions for the magazine. Some of the people receiving this letter already subscribe to the magazine while others do not. From this mailing list, 45% of those who already subscribe will subscribe again while 30% of those who do not now subscribe will subscribe. On the last letter, it was found that 40% of those receiving it ordered a subscription. What percent of those receiving the current letter can be expected to order a subscription?
Solution:
Transition Probability Matrix

S = 36%; F = 64%
∴ 36% of those receiving the current letter can be expected to order a subscription

Question 2.
Anew transit system has just gone into operation in Chennai. Of those who use the transit system this year, 30% will switch over to using metro train next year and 70% will continue to use he transit system. Of those who use metro train this year and 70% will continue to use metro train next year and 30% will switch over to transit system. Suppose the population of Chennai city remains constant and that 60% of the commuters use the transit system and 40% of the commuters use metro train this year.
(i) What percent of commuters will be using the transit system after one year?
(ii) What percent of commuters will be using the transit system in the one run?
Solution:
Transition Probability Matrix

S = 54%; C = 46%
Equilibrium will be reached in the long run
At equilibrium we must have
(S C) T = (S C) where S + C = 1
(S C) = \(\left(\begin{array}{ll}
0.7 & 0.3 \\
0.3 & 0.7
\end{array}\right)\) = (S C)
0.7S + 0.3C = S
0.7S + 0.3 (1 – S) = S
0.7S + 0.3 – 0.3S = S
0.4S + 0.3 = S
0.3 = S – 0.4S ⇒ 0.6S = 0.3
S = \(\frac { 0.3 }{ 0.6 }\) = 0.50
∴ 50% of the commuters will be transit system the long run.

Question 3.
Two types of soaps A and B are in the market. Their present market shares are 15% for A and 85% for B. Of those who bought A the previous year, 65% contionues to buy it again while 35% switch over to B. Of those who bought B the previous year, 55% buy it again and 45% switch over to A. Find their market shares after one year and when is the equilibrium reached?
Solution:
Transition Probability Matrix

Equilibrium will be reached in the long run
At equilibrium we must have
(A B) T = (A, B) where A + B = 1
(A B) = \(\left(\begin{array}{ll}
0.65 & 0.35 \\
0.45 & 0.55
\end{array}\right)\) = (A B)
0.65 A + 0.45 B = A
0.65 A + 0.45 (1 – A) = A
0.65 A + 0.45 – 0.45 A = A
0.20 A + 0.45 = A
A – 0.20 A = 0.45
0.80 A = 0.45
A = \(\frac { 0.45 }{ 0.80 }\) = 0.5625 and B = 04375
In the long sum {∴ B = 1 – A}
∴ A = 56.25 % and B = 43.75%

Question 4.
Two products A and B currently share the market with shares of 50% and 50% each respectively. Each week some brand switching takes place. Of those who bought A the previous week, 60% buy it again whereas 40% switch over to B. Of those who bought B the previous week, 80% buy it again whereas 20% switch over to A. Find their shares after one week and after two weeks. If the price war continues, when is the equilibrium reached?
Solution:
Transition Probability Matrix

Equilibrium will be reached in the long run.
At equilibrium, we must have
(A B) T = (A B) where A + B = 1
(A B) = \(\left(\begin{array}{ll}
0.60 & 0.40 \\
0.20 & 0.80
\end{array}\right)\) = (A B)
0.60 A + 0.20 B = A
0.60 A+ 0.20 (1 – A) = A
0.60 A + 0.20 – 0.20 A = A
0.40 A + 0.20 = A
0.20 = A – 0.40 A
0.60 A = 0.20
A = \(\frac { 0.20 }{ 0.60 }\) = 0.33 and B = 0.67
{∴ B = 1 – A}
In the long run
∴ A = 33% and B = 67%

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.2

Question 1.
Solve the following . equations by using Cramer’s rule
(i) 2x + 3y = 7; 3x + 5y = 9
(ii) 5x + 3v = 17; 3x + 7y = 31
(iii) 2x + y – z = 3; x + y + z – 1; x – 2y – 3z = 4
(iv) x + y + z = 6; 2x + 3y – z = 56; x – 2y – 3z = -7
Solution:
The equations are
2x + 3y = 7
3x + 5y = 9
Here Δ = \(\left|\begin{array}{ll}
2 & 3 \\
3 & 5
\end{array}\right|\) = 10 – 9 = 1
≠ 0
∴ We can apply Cramer’s Rule

∴ x = 8; y = -3

(ii) The equations are
5x + 3y = 17
3x + 7y = 31
Here Δ = \(\left|\begin{array}{ll}
5 & 3 \\
3 & 7
\end{array}\right|\) = 35 – 9 = 26
≠ 0
We can apply Cramer’s Rule

∴ x = 1; y = 4

(iii) The equations are
2x + y – z = 3
x + y + z = 1
x – 2y – 3z = 4
Here Δ = \(\left|\begin{array}{ccc}
2 & 1 & -1 \\
1 & 1 & 1 \\
1 & -2 & -3
\end{array}\right|\)
= 2 (-3 + 2) – 1 (-3 – 1) – 1 (-2 – 1)
= 2 (-1) -1 (-4) -1 (-3)
= -2 + 4 + 3
Δ = 5 ≠ 0
∴ We can apply Cramer’s Rule and the system is consistant and it has unique solution.
Δ_x = \(\left|\begin{array}{ccc}
3 & 1 & -1 \\
1 & 1 & 1 \\
4 & -2 & -3
\end{array}\right|\)
= 3 (-3 + 2) – 1 (-3 – 4) – 1 (-2 – 4)
= 3 (-1) -1 (-7) -1 ( 6)
= -3 + 7 + 6 = 10
Δ_y = \(\left|\begin{array}{ccc}
2 & 3 & -1 \\
1 & 1 & 1 \\
1 & 4 & -3
\end{array}\right|\)
= 2 (- 3 – 4) -3 (-3 – 1) -1 (4 – 1)
= 2 (-7) – 3 (-4) – 1 (3)
= -14 + 12 – 3
= -5
Δ_z = \(\left|\begin{array}{ccc}
2 & 1 & 3 \\
1 & 1 & 1 \\
1 & -2 & 4
\end{array}\right|\)
= 2 (4 + 2) – 1 (4 – 1) + 3 (- 2 – 1)
= 2 (6) – 1(3) + 3 (-3)
= 12 – 3 – 9 = 0
∴ By Cramer’s rule

∴ (x, y, z) = (2, -1, 0)

(iv) The equations are
x + y + z = 6
2x + 3y – z = 5
6x – 2y – 3z = -7
Here Δ = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
2 & 3 & -1 \\
6 & -2 & -3
\end{array}\right|\)
= 1 (-9 – 2) -1 (-6 + 6) + 1 (-4 – 18)
= 1 (-11) – 1 (0) +1 (-22)
= -11 – 22
= -33 ≠ 0
∴ We can apply Cramer’s Rule and the system is consistent and it has unique solution.
Now,
Δ_x = \(\left|\begin{array}{ccc}
6 & 1 & 1 \\
5 & 3 & -1 \\
-7 & -2 & -3
\end{array}\right|\)
= 6 (- 9 – 2) – 1 (- 15 – 7) + 1 (- 10 + 21)
= 6 (-11) – 1 (-22)+ 1 (11)
= -66 + 22 + 11
= -33
Δ_y = \(\left|\begin{array}{ccc}
1 & 6 & 1 \\
2 & 5 & -1 \\
6 & -7 & -3
\end{array}\right|\)
= 1 (-15 – 7) – 6 (- 6 + 6) + 1 (- 14 – 30)
= 1 (-22) – 6 (0) + 1 (-44)
= -66
Δ_z = \(\left|\begin{array}{ccc}
1 & 1 & 6 \\
2 & 3 & 5 \\
6 & -2 & -7
\end{array}\right|\)
= 1 (- 21 + 10) – 1 (- 14 – 30) + 6 (- 4 – 18)
= 1 (-11) – 1 (-44) + 6 (-22)
= -11 + 44 – 132
= -99
∴ By Cramer’s rule

(x, y, z) = (1, 2, 3)

(v) The equations are
x + 4y + 3z = 2
2x – 6y + 6z = -3
5x – 2y + 3z = -5
Here Δ = \(\left|\begin{array}{ccc}
1 & 4 & 3 \\
2 & -6 & 6 \\
5 & -2 & 3
\end{array}\right|\)
= 1 (-18 + 12) -4 (6 -30) + 3 (-4 + 30)
= 1 (-6) – 4 (-24) + 3 (26)
= -6 + 96 + 78
= 168 ≠ 0
We can apply Cramer’s Rule and the system is consistent and it has unique solution.
Δ_x = \(\left|\begin{array}{ccc}
2 & 4 & 3 \\
-3 & -6 & 6 \\
-5 & -2 & 3
\end{array}\right|\)
= 2 (-18 + 12) – 4 (-9 + 30) + 3 (6 – 30)
= 2 (-6) -4 (21) + 3 (-24)
= -12 – 84 – 72
= -168
Δ_y = \(\left|\begin{array}{ccc}
1 & 2 & 3 \\
2 & -3 & 6 \\
5 & -5 & 3
\end{array}\right|\)
= 1 (-9 + 30) – 2 (6 – 30) + 3 (-10 + 15)
= 1(21) – 2 (-24) + 3 (5)
= 21 + 48 + 15
= 84
Δ_z = \(\left|\begin{array}{ccc}
1 & 4 & 2 \\
2 & -6 & -3 \\
5 & -2 & -5
\end{array}\right|\)
= 1 (30 – 6) – 4 (-10 +15) + 2 (-4 + 30)
= 1 (24) – 4 (5) + 2 (26)
= 24 – 20 + 52
= 56
∴ By Cramer’s rule

(x, y, z) = (-1, \(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 3 }\))

Question 2.
A commodity was produced by using 3 units of labour and 2 units of capital, the total cost is Rs 62. If the commodity had been produced by using 4 units of labour and one unit of capital, the cost is Rs 56. What is the cost per unit of labour and capital? (Use determinant method).
Solution:
Let ‘x’ be the cost per unit of labour
Let ‘y’ be the capital
∴ 3x + 2y = 62
4x + y = 56

∴ The cost per unit of labour is Rs 10 and Cost per unit of capital is Rs 16

Question 3.
A total of Rs 8,600 was invested in two accounts. One account earned 4\(\frac { 3 }{ 4 }\)% annual interest and the other earned 6\(\frac { 1 }{ 2 }\)% annual interest. If the total interest for one year was Rs 431.25, how much was invested in each accout? (Use determinant method)
Solution:
Let the two investments be x and y
Given that
x + y = 8600 ……. (1)

Multiply by 4 (both sides)
19x + 26y = 172500 ……….. (2)
Here Δ = \(\left|\begin{array}{ll}
1 & 1 \\
19 & 26
\end{array}\right|\) = 26 – 19 = 7 ≠ 0
∴ We can apply Cramer’s Rule
Δ_x = \(\left|\begin{array}{ll}
8600 & 1 \\
172500 & 26
\end{array}\right|\)
= 223600 – 172500
= 51100
Δ_y = \(\left|\begin{array}{ll}
1 & 8600 \\
19 & 172500
\end{array}\right|\)
= 172500 – 163400
= 9100
By Cramer’s Rule
x = \(\frac { Δ_x }{ Δ }\) = \(\frac { 51100 }{ 7 }\) = 7300
y = \(\frac { Δ_y }{ Δ }\) = \(\frac { 9100 }{ 7 }\) = 1300
∴ Amount invested at 4\(\frac { 3 }{ 4 }\)% is Rs 7,300 and
Amount invested at 6\(\frac { 1 }{2 }\)% is Rs 1,300

Question 4.
At marina two types of games viz., Horse riding and Quad Bikes riding are available on hourly rent. Keren and Bentia spent Rs 780 and Rs 560 during the month of May

Find the hourly charges for the two games (rides). (Use determinant method).
Solution:
let the hourly charges for horse riding be x and let the hourly charges for Quad Bikes riding be y.
For Keren
3x + 4y = 780 ……… (1)
For Benita
2x + 3y = 560 ……… (2)
Here Δ = \(\left|\begin{array}{ll}
3 & 4 \\
2 & 3
\end{array}\right|\) = 9 – 8 = 1 ≠ 0
∴ We can apply Cramer’s Rule

∴ The hourly charges for horse riding is Rs 100 and Quad Bikes riding is Rs 120

Question 5.
In a market survey three commodities A, B and C were considered. In finding out the index number some fixed weights were assigned to the three varieties in each of the commodities. The table below provides the information regarding the consumption of three commodities according to the three varieties and also the total weight received by the commodity.

Find the weights assigned to the three varieties by using Cramer’s Rule.
Solution:
Let x, y and z be are consumption of three commodities A, B and C respectively.
Given that
x + 2y + 3z = 11 ……… (1)
2x + 4y + 5z = 21 ……… (2)
3x + 5y + 6z = 27 ……… (2)
Here Δ = \(\left|\begin{array}{ccc}
1 & 2 & 3 \\
2 & 4 & 5 \\
3 & 5 & 6
\end{array}\right|\)
= 1 (24 – 25) – 2 (12 – 15) + 3 (10- 12)
= 1 ( 1) 2 ( 3) + 3 (- 2)
= -1 + 6 – 6 = -1 ≠ 0
∴ We can apply Cramer’s Rule
Now Δ_x = \(\left|\begin{array}{ccc}
11 & 2 & 3 \\
21 & 4 & 5 \\
27 & 5 & 6
\end{array}\right|\)
= 11 (24 – 25) -2 (126 – 135) + 3 (105 – 108)
= 11(-1) -2 (-9)+ 3 (-3)
= -11 + 18 – 9
= -2
Δ_y = \(\left|\begin{array}{ccc}
1 & 11 & 3 \\
2 & 21 & 5 \\
3 & 27 & 6
\end{array}\right|\)
= 1 (126 – 135) -11 (12 – 15) + 3 (54 – 63)
= 1 (-9) -11 (-3) + 3 (-9)
= -9 + 33 – 27
= -3
Δ_z = \(\left|\begin{array}{ccc}
1 & 2 & 11 \\
2 & 4 & 21 \\
3 & 5 & 27
\end{array}\right|\)
= 1 (108 – 105) – 2 (54 – 63) + 11 (10 – 12)
= 1(3) – 2 (-9) + 11 (-2)
= 3 + 18 – 22 = -1
By Cramer’s Rule

∴ (x, y, z) = (2, 3, 1)

Question 6.
A total of Rs 8,500 was invested in three interest-earning accounts. The interest rates were 2%, 3%, and 6%, if the total simple interest for one year was Rs 380 and the amount invested at 6% was equal to the sum of the amounts in the other two accounts, then how much was invested in each account? (use Cramer’s rule)
Solution:
Let the amount invested at 2%, 3%, and 6% are x, y, and z respectively.
x + y + z = 8500 ………. (1)

2x + 3y + 6z = 38000 ………. (2)
x + y = z
x + y – z = 0 ……… (3)
Here Δ = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
2 & 3 & 6 \\
1 & 1 & -1
\end{array}\right|\)
= 1 (-3 – 6) -1 (-2 – 6) + 1 (2 – 3)
= 1 (-9) -1 (-8) + 1 (-1)
= -9 + 8 – 1 = -2
≠ 0
∴ We can apply Cramer’s Rule
Δ_x = \(\left|\begin{array}{ccc}
8500 & 1 & 1 \\
38000 & 3 & 6 \\
0 & 1 & -1
\end{array}\right|\)
= 8500 (-3 – 6) -1 (-38000 – 0) + 1 (38000 – 0)
= 8500 (-9) + 38000 + 38000
= -76500 + 76000
= -500
Δ_y = \(\left|\begin{array}{ccc}
1 & 8500 & 1 \\
2 & 38000 & 6 \\
1 & 0 & -1
\end{array}\right|\)
= 1(-38000 – 0) – 8500 (-2 – 6) + 1 (0 – 38000)
= -38000 + 68000-38000
= 68000 – 76000
= -8000
Δ_z = \(\left|\begin{array}{ccc}
1 & 1 & 8500 \\
2 & 3 & 38000 \\
1 & 1 & 0
\end{array}\right|\)
= (0 – 38000) -1 (0 – 38000) + 8500 (2 – 3)
= -38000 + 38000 – 8500
= -8500
By Cramer’s Rule

∴ Amount invested at 2% is Rs 250; Amount invested at 3% is Rs 4,000 and Amount invested at 6% is Rs 4,250

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.1

Question 1.
Find the rank of each of the following matrices
(i) \(\left(\begin{array}{ll}
5 & 6 \\
7 & 8
\end{array}\right)\)
Solution:
Let A = \(\left|\begin{array}{ll}
5 & 6 \\
7 & 8
\end{array}\right|\)
Order of A is 2 × 2 [∴ P(A) ≤ 2]
Consider the second order minor = \(\left|\begin{array}{ll}
5 & 6 \\
7 & 8
\end{array}\right|\)
= 40 – 42
|A| = -2 ≠ 0
There is a minor of order 2, which is not zero
ρ(A) = 2

(ii) \(\left(\begin{array}{ll}
1 & -1 \\
3 & -6
\end{array}\right)\)
Solution:
Let A = \(\left(\begin{array}{ll}
1 & -1 \\
3 & -6
\end{array}\right)\)
Order of A is 2 × 2 [∴ ρ(A) ≤ 2]
Consider the second order minor = \(\left|\begin{array}{ll}
1 & -1 \\
3 & -6
\end{array}\right|\)
= -6 – (-3)
= -6 + 3 = -3
|A| ≠ 0
There is a minor of order 2, which is not zero
∴ ρ(A) = 2

(iii) \(\left(\begin{array}{ll}
1 & 4 \\
2 & 8
\end{array}\right)\)
Solution:
Let A = \(\left(\begin{array}{ll}
1 & 4 \\
2 & 8
\end{array}\right)\)
Order of A is 2 × 2 [∴ ρ(A) ≤ 2]
Consider the second order minor = \(\left|\begin{array}{ll}
1 & 4 \\
2 & 8
\end{array}\right|\)
= 8 – 8 = 0
Since the second are minor vanishes, ρ(A) ≠ 2
Consider a first order minor |1| ≠ 0
There is a minor of order 1, which is not zero
∴ ρ(A) = 1

(iv) \(\left[\begin{array}{ccc}
2 & -1 & 1 \\
3 & 1 & -5 \\
1 & 1 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
2 & -1 & 1 \\
3 & 1 & -5 \\
1 & 1 & 1
\end{array}\right]\)
Order of A is 3 × 3
∴ ρ(A) ≤ 2
Consider the third order minor \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
3 & 1 & -5 \\
1 & 1 & 1
\end{array}\right|\)
= 2(1 + 5) – (-1) (3 + 5) + 1 (3 – 1)
= 2 (6) + 1(8) + 1(2)
= 12 + 8 + 2
= 22 ≠ 0
There is a minor of order 3, which is not zero
∴ ρ(A) = 3

(v) \(\left[\begin{array}{ccc}
-1 & 2 & -2 \\
4 & -3 & 4 \\
-2 & 4 & -4
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
-1 & 2 & -2 \\
4 & -3 & 4 \\
-2 & 4 & -4
\end{array}\right]\)
Order of A is 3 × 3
∴ ρ(A) ≤ 3
Consider the third order minor \(\left|\begin{array}{ccc}
-1 & 2 & -2 \\
4 & -3 & 4 \\
-2 & 4 & -4
\end{array}\right|\)
= -1(12 – 16) – 2 (-16 + 8) – 2 (16 – 6)
= -1(-4) – 2 (-8) – 2 (10)
= 4 + 16 – 20
= 0
Since the third order minor vanishes, therefore
∴ ρ(A) ≠ 3
Consider a second order minor \(\left|\begin{array}{ll}
-1 & 2 \\
4 & -3
\end{array}\right|\)
= 3 – 8
= -5 ≠ 0
There is a minor of order 2, which is not zero.
∴ ρ(A) = 2

The order of A is 3 × 4
∴ ρ(A) ≤ 3

The number of non zero rows is 2
∴ ρ(A) = 2

The order of A is 3 × 4
∴ ρ(A) ≤ 3
Consider the third order minor \(\left|\begin{array}{ccc}
3 & 1 & -5 \\
1 & -2 & 1 \\
1 & 5 & -7
\end{array}\right|\)
= 3 (14 – 5) – 1 (- 7 – 1) – 5 (5 + 2)
= 3 (9) – 1 (-8) – 5 (7)
= 27 + 8 – 35
= 0
\(\left|\begin{array}{ccc}
1 & -5 & 1 \\
-2 & 1 & -5 \\
5 & -7 & 2
\end{array}\right|\)
= 1 (2 – 35) + 5 (-4 + 25) – 1 (14 – 5)
= 1 (-33) + 5(21) – 1 (9)
= -33 + 105 – 9
= 63 ≠ 0
There is a minor of order 3, which is not zero.
∴ ρ(A) = 3

Order of A is 3 × 4
∴ ρ(A) ≤ 3
Consider the third order minor \(\left|\begin{array}{ccc}
1 & -2 & 3 \\
-2 & 4 & -1 \\
-1 & 2 & 7
\end{array}\right|\)
= 1 (28 + 2)+ 2 (-14 – 1) + 3 (-4 + 4)
= 1 (30) + 2 (- 15) + 3 (0)
= 0
\(\left|\begin{array}{ccc}
-2 & 3 & 4 \\
4 & -1 & -3 \\
2 & 7 & 6
\end{array}\right|\)
= -2 (-6 + 21) – 3 (24 + 6) + 4 (28 + 2)
= -2(15) – 3 (30)+ 4 (30)
= 0
\(\left|\begin{array}{ccc}
1 & 3 & 4 \\
-2 & -1 & -3 \\
-1 & 7 & 6
\end{array}\right|\)
= 1 (-6 + 21) – 3 (-12 – 3) + 4 (-14 – 1)
= 1 (15) -3 (-15) + 4 (-15)
= 15 + 45 – 60
= 0
\(\left|\begin{array}{ccc}
1 & -2 & 4 \\
-2 & 4 & -3 \\
-1 & 2 & 6
\end{array}\right|\)
= 1 (24 + 6) + 2 (-12 – 3) + 4 (-4 + 4)
= 1 (30) + 2 (-15) + 4(0)
= 30 – 30
= 0
Since all third order minors vanishes, ρ(A) ≠ 3
Now, let us consider the second order minors.
Consider one of the second order minors
\(\left|\begin{array}{ll}
-2 & 3 \\
4 & -1
\end{array}\right|\) = 2 – 12 = -10 ≠ 0
There is a minor of order 2 which is not zero
∴ ρ(A) = 2

Question 2.
If A = \(\left(\begin{array}{ccc}
1 & 1 & -1 \\
2 & -3 & 4 \\
3 & -2 & 3
\end{array}\right)\) and B = \(\left(\begin{array}{ccc}
1 & -2 & 3 \\
-2 & 4 & -6 \\
5 & 1 & -1
\end{array}\right)\)
find the rank of A B and the rank of B A.
Solution:

To find the rank of AB
Order of AB is 3 × 3
∴ ρ(AB) ≤ 3
Consider the third order minor |AB| = \(\left|\begin{array}{ccc}
-6 & 3 & -2 \\
28 & -12 & 20 \\
22 & -11 & 18
\end{array}\right|\)
= -6(-216 + 220) -3(504 – 440) – 2(-308 + 264)
= – 6(4) – 3(64) – 2(-44)
= -24 – 192 + 88
= 128 ≠ 0
There is a minor of order 3, which is not zero.
∴ ρ(AB) = 3
To find the rank of BA
Order of BA is 3 × 3
∴ ρ(BA) ≤ 3
Consider the third order minor |BA| = \(\left|\begin{array}{ccc}
6 & 1 & 0 \\
-12 & -2 & 0 \\
4 & 4 & -4
\end{array}\right|\)
= 6(8 – 0) – 1(48 – 0) + 0(-48 + 8)
= 6(8) – 1(48) + 0(-40)
= 48 – 48 + 0
= 0
Since the third order minor vanishes, therefore P(BA) ≠ 3
Consider a second order minor \(\left|\begin{array}{ll}
-12 & -2 \\
4 & 4
\end{array}\right|\) = -48 + 8 = -40 ≠ 0
There is a minor of order 2 which is not zero
∴ ρ(BA) = 2

Question 3.
Solve the following system of equations by rank method
x + y + z = 9, 2x + 5y + 7z = 52, 2x – y – z = 0
Solution:
x + y + z = 9
2x + 5y + 7z = 52
2x – y – z = 0
The matrix equation corresponding to the given system is

Obviously the last equivalent matrix is in the echelon form. It has three non-zero rows.
P(A) = P (A, B) = 3 = Number of unknowns
The given system is consistent and has unique solution.
To find the solution, let us rewrite the above ech-elon form into the matrix form.
\(\left[\begin{array}{lll}
1 & 1 & 1 \\
0 & 3 & 5 \\
0 & 0 & 2
\end{array}\right]\) \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right] =\left[\begin{array}{c}
9 \\
34 \\
16
\end{array}\right]\)
x + y + z = 9 ……..(1)
3y + 5z = 34 ……… (2)
2z = 16 ……… (3)
z = \(\frac { 16 }{ 2 }\) = 8
z = 8
Substitute z = 8 in eqn (2)
3y + 5 (8) = 34
3y + 40 = 34
3y = 34 – 40
3y = -6
y = -2
Substitute y = -2 and z = 8 in eqn (1)
x = (-2) + 8 = 9
x + 6 = 9
x = 9 – 6
x = 3
∴ x = 3, y = -2, z = 8

Question 4.
Show that the equations 5x + 3y + 7z = 4, 3x + 26y + 2z = 9, 7x + 2y + 10z = 5 are consistent and solve them by rank method.
Solution:
5x + 3y + 7z = 4
3x + 26y + 2z = 9
7x + 2y + 10z = 5
The matrix equation corresponding to the given systematic


Obviously, the last equivalent matrix is in the echelon form. It has two non-zero rows.
P([A, B]) = 2 ; P(A) = 2
P(A) = P ([A, B]) = 2 < Number of unknowns
The given system is consistent and has infinitely many solutions.
The given system is equivalent to the matrix equation
\(\left[\begin{array}{lll}
1 & 5 & 1 \\
0 & -11 & 1 \\
0 & 0 & 0
\end{array}\right]\) \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right] =\left[\begin{array}{c}
2 \\
-3 \\
0
\end{array}\right]\)
x + 5y + z = 2 ……. (1)
-11y + z = -3 ……… (2)
let z = k

Where K ε R

Question 5.
Show that the following system of equations have unique solutions:
x + y + z = 3, x + 2y + 3z = 4, x + 4y + 9z = 6 by rank method.
Solution:
x + y + z = 3
x + 2y + 3z = 4
x + 4y + 9z = 6
The matrix equation corresponding to the given system is

The last equivalent matrix is in the echelon form [A, B] has 3 non-zero rows and [A] has 3 non-zero rows.
p([A,B]) = 3; ρ(A) = 3
ρ([A, B]) = ρ(A) = No. of unknowns
∴ The system of equations have unique solution.

Question 6.
For what values of the parameter λ, will the following equations fail to have unique solution:
3x – y + λz = 1, 2x + y + z = 2, x + 2y – λz = -1
Solution:
3x – y + λz = 1
2x + y + z = 2
x + 2y – λz = -1
The matrix equation corresponding to the given system is

If the equations fail to have unique solution.
ρ(A) ≠ ρ(A, B)
ρ(A, B) = 3
ρ(A) ≠ 3
Therefore 7 + 2λ = 0
2λ = -7 and λ = -7/2

Question 7.
The price of three commodities. X, Y, and Z are x,y, and z respectively Mr. Anand purchases 6 units of Z and sells 2 units of Y. Mr. Amar purchases a unit of Y and sells 3 units of X and 2 units of Z. Mr. Amit purchases a unit of X and sells 3 units of Y and a unit of Z. In the process they earn Rs 5,000/-, Rs 2,000/- and Rs 5,500/- respectively. Find the prices per unit of three commodities by the rank method.
Solution:
Let the equations for Mr. Anand, Mr. Amar, and Mr. Amit are
2x + 3y – 6z = 5000
3x – y + 2z = 2000
-x + 3y + z = 5500 respectively
The matrix equation corresponding to the given system is

∴ The given system is equivalent to the matrix equation
\(\left[\begin{array}{lll}
-1 & 4 & -8 \\
0 & 1 & -2 \\
0 & 0 & 7
\end{array}\right]\) \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right] =\left[\begin{array}{c}
3000 \\
1000 \\
3500
\end{array}\right]\)
-x + 4y – 8z = 3000 …….. (1)
y – 2z = 1000 ………. (2)
7z = 3500 ……….. (3)
Eqn (3) ⇒ z = \(\frac { 3500 }{ 7 }\)
∴ z = 500
Eqn (2) ⇒ y – 2(500) = 1000
y = 1000 + 1000
∴ y = 2000
Eqn (1) ⇒ -x + 4 (2000) – 8 (500) = 3000
-x + 8000 – 4000 = 3000
-x + 4000 = 3000
-x = 3000 – 4000
-x = – 1000
∴ x = 1000
The price of three commodities, x, y and z are Rs. 1000; Rs. 2000 and Rs. 500 respectively.

Question 8.
An amount of Rs 5,000/- is to be deposited in three different bonds bearing 6%, 7%, and 8% per year respectively. Total annual income is Rs 358/-, If the income from the first two investments is Rs 70/- more than the income from the third, then find the amount of investment in each bond by the rank method.
Solution:
Let the three different bonds be x, y, and z
x + y + z = 5000 …….. (1)

6x + 7y = 8z + 7000
6x + 7y – 8z = 7000 ……… (3)
The matrix equation corresponding to the given system is

∴ The given system is equivalent to the matrix equation
\(\left[\begin{array}{lll}
1 & 1 & 1 \\
0 & 1 & 2 \\
0 & 0 & -16
\end{array}\right]\) \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right] =\left[\begin{array}{c}
5000 \\
5800 \\
-28800
\end{array}\right]\)
x + y + z = 5000 ……… (1)
y + 2z = 5800 …….. (2)
-16z = -28800 ……… (3)
eqn (3) ⇒ z = \(\frac { -28800 }{ -16 }\)
∴ z = 1800
eqn (2) ⇒ y + 2(1800) = 5800
y + 3600 = 5800
y = 5800 – 3600
∴ y = 2200
eqn (1) ⇒ x + 2200 + 1800 = 5000
x + 4000 = 5000
x = 5000 – 4000
∴ x = 1000
The amount of investment in each bond is Rs 1000, Rs 2200 and Rs 1800.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 12 Discrete Mathematics Ex 12.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 12 Discrete Mathematics Ex 12.3

Choose the most suitable answer from the given four alternatives:

Question 1.
A binary operation on a set Sis a function from
(a) S → S
(b) (S × S) → S
(c) S → (S × S)
(d) (S × S) → (S × S)
Solution:
(b) (S × S) → S

Question 2.
Subtraction is not a binary operation in
(a) R
(b) Z
(c) N
(d) Q
Solution:
(c) N
Hint:
Let 1, 2 ∈ N
1 * 2 = 1 – 2 = -1 ∉ N

Question 3.
Which one of the following is a binary operation on N?
(a) Subtraction
(b) Multiplication
(c) Division
(d) All the above
Solution:
(b) Multiplication

Question 4.
In the set R of real numbers ‘*’ is defined as follows. Which one of the following is not a binary operation on R ?
(a) a * b = min (a.b)
(b) a * b = max (a, b)
(c) a * b = a
(d) a * b = a^b
Solution:
(d) a * b = a^b
Hint:
Since -2, 1/2 ∈ R , but (-2)^1/2 ∉ R.

Question 5.
The operation * defined by a * b = \(\frac { ab }{ 7 }\) is not a binary operation on
(a) Q⁺
(b) Z
(c) R
(d) C
Solution:
(b) Z
Hint:
a * b = \(\frac { ab }{ 7 }\) ∉ Z
as Z is set of all integers.

Question 6.
In the set Q define a \(\bigodot\) b = a + b + ab. For what value of y, 3 \(\bigodot\) (y \(\bigodot\) 5) = 7?
(a) y = \(\frac { 2 }{ 3 }\)
(b) y = \(\frac { -2 }{ 3 }\)
(c) y = \(\frac { -3 }{ 2 }\)
(d) y = 4
Solution:
(b) y = \(\frac { -2 }{ 3 }\)
Hint:
a \(\bigodot\) b = a + b + ab
Given 3 \(\bigodot\) (y \(\bigodot\) 5) = 7
3 \(\bigodot\) (y + 5 + 5y) = 7
3 \(\bigodot\) (6y + 5) = 7
3 + 6y + 5 + 3 (6y + 5) = 7
8 + 6y + 18y + 15 = 7
24 y = 7 – 23 = -16
y = \(\frac { -16 }{ 24 }\) = \(\frac { -2 }{ 3 }\)

Question 7.
If a * b = \(\sqrt { a^2+b^2 }\) on the real numbers then * is
(a) Commutative but not associative
(b) Associative but not commutative
(c) Both commutative and associative
(d) Neither commutative nor associative
Solution:
(c) Both commutative and associative
Hint:

∴ (a * b) * c = a * (b * c)
* is associative

Question 8.
Which one of the following statements has the truth value T?
(a) sin x is an even function.
(b) Every square matrix is non-singular
(c) The product of complex number and its conjugate is purely imaginary
(d) \(\sqrt{5}\) is an irrational number
Solution:
(d) \(\sqrt{5}\) is an irrational number

Question 9.
Which one of the following statements has truth value F?
(a) Chennai is in India or √2 is an integer.
(b) Chennai is in India or √2 is an irrational number.
(c) Chennai is in China or √2 is an integer.
(d) Chennai is in China or √2 is an irrational number.
Solution:
(c) Chennai is in China or √2 is an integer.

Question 10.
If a compound statement involves 3 simple statements, then the number of rows in the truth table is ……….
(a) 9
(b) 8
(c) 6
(d) 3
Solution:
(b) 8
Hint:
(i.e.) 2³ = 8

Question 11.
Which one is the inverse of the statement (p v q) → (p ∧ q)?
(a) (p ∧ q) → (p v q)
(b) ¬(p v q) → (p ∧ q)
(c) (¬P v ¬q) → (¬p ∧ ¬q)
(d) (¬p ∧ ¬q) → (¬p v ¬q)
Solution:
(d) (¬p ∧ ¬q) → (¬p v ¬q)
Hint:
(p v q) → (p ∧ q)
¬(p v q) → ¬(p ∧ q)
(¬P ∧ ¬q) → (¬p v ¬q)

Question 12.
Which one is the contrapositive of the statement (p v q) → r?
(a) ¬r → (¬p ∧ ¬q)
(b) ¬r → (p v q)
(c) r → (p ∧ q)
(d) p → (q v r)
Solution:
(a) ¬r → (¬p ∧ ¬q)
Hint:
(p v q) → r
Contrapositive is ¬r → ¬(p v q)
¬r → (¬p ∧ ¬q)

Question 13.
The truth table for (p ∧ q) v ¬q is given below

Solution:
(c) (1) T, (2) T, (3) F, (4) T
Hint:

1 = T, 2 = T, 3 = F, 4 = T

Question 14.
In the last column of the truth table for ¬(p v ¬q) the number of final outcomes of the truth value ‘F’ is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(c) 3
Hint:

Number of ‘F’ in last column is 3

Question 15.
Which one of the following is incorrect? For any two propositions p and q, we have
(a) ¬(p v q) ≡ ¬p ∧ ¬q
(b) ¬(p ∧ q) ≡ ¬p v ¬q
(c) ¬(p v q) ≡ ¬p v ¬q
(d) ¬(¬p) ≡ p
Solution:
(c) ¬(p v q) ≡ ¬p v ¬q

Question 16.

Which one of the following is correct for the truth value of (p ∧ q) → ¬p

Solution:
(b) (1) F, (2) T, (3) T, (4) T
Hint:

Question 17.
The dual of ¬(p v q) v [p v(p ∧ ¬r)] is
(a) ¬(p ∧ q) ∧ [p v(p ∧ ¬r)]
(b) (p ∧ q) ∧ [p v(p v ¬r)]
(c) ¬(p ∧ q) ∧ [p ∧ (p ∧ r)]
(d) ¬(p ∧ q) ∧ [p ∧ (p v ¬r)]
Solution:
(d) ¬(p ∧ q) ∧ [p ∧ (p v ¬r)]
Hint:
Dual is obtained by changing ∧ into v and vice versa.

Question 18.
The proposition \(p \wedge(\neg p \vee q)]\) is ……..
(a) a tautology
(b) a contradiction
(c) logically equivalent to \(p \wedge q\)
(d) logically equivalent to \(p \vee q\)
Solution:
(c) logically equivalent to \(p \wedge q\)

Question 19.
Determine the truth value of each of the following statements:
(a) 4 + 2 = 5 and 6 + 3 = 9
(b) 3 + 2 = 5 and 6 + 1 = 7
(c) 4 + 5 = 9 and 1 + 2 = 4
(d) 3 + 2 = 5 and 4 + 7 = 11

Solution:
(a) (1) F, (2) T, (3) F, (4) T
Hint:
(1) F and T = F
(2) T and T =T
(3) T and F = F
(4) T and T = T

Question 20.
Which one of the following is not true?
(a) Negation of a statement is the statement itself.
(b) If the last column of the truth table contains only T then it is a tautology.
(c) If the last column of its truth table contains only F then it is a contradiction
(d) If p and q are any two statements then p ⟷ q is a tautology.
Solution:
(d) If p and q are any two statements then p ⟷ q is a tautology.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 12 Discrete Mathematics Ex 12.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 12 Discrete Mathematics Ex 12.2

Question 1.
Let p : Jupiter is a planet and q: India is an island be any two simple statements. Give verbal sentence describing each of the following statements.
(i) ¬P
(ii) P ∧ ¬q
(iii) ¬p v q
(iv) p → ¬q
(v) p ↔ q
Solution:
p: Jupiter is a planet
q: India is an island
(i) ¬P : Jupiter is not a planet
(ii) P ∧ ¬q : Jupiter is a planet and India is not an island.
(iii) ¬p v q : Jupiter is not a planet or India is an island
(iv) p → ¬q : Jupiter is a planet then India is not an island
(v) p ↔ q : Jupiter is a planet if and only if India is an island

Question 2.
Write each of the following sentences in symbolic form using statement variables p and q.
(i) 19 is not a prime number and all the angles of a triangle are equal.
(ii) 19 is a prime number or all the angles of a triangle are not equal.
(iii) 19 is a prime number and all the angles of a triangle are equal.
(iv) 19 is not a prime number.
Solution:
Let p : 19 is a prime number
q : All the angles of a triangle are equal
(i) 19 is not a prime number and all the angles of a triangle are equal ⇒ ¬p ∧ q
(ii) 19 is a prime number or all the angles of a triangle are not equal ⇒ p v ¬q
(iii) 19 is a prime number and all the angles of a triangle are equal ⇒ p ∧ q
(iv) 19 is not a prime number ⇒ ¬p

Question 3.
Determine the truth value of each of the following statements
(i) If 6 + 2 = 5, then the milk is white.
(ii) China is in Europe dr √3 is art integer
(iii) It is not true that 5 + 5 = 9 or Earth is a planet.
(iv) 11 is a prime number and all the sides of a rectangle are equal.
Solution:
(i) If 6 + 2 = 5, then milk is white,
p: 6 + 2 = 5(F)
q: Milk is white (T)
∴ p → q is having the truth value T

(ii) China is in Europe or √3 is an integer
p: China is in Europe (F)
q: √3 is an integer (F)
∴ p v q is having the truth value F

(iii) It is not true that 5 + 5 = 9 or Earth is a planet
p: 5 + 5 = 9 (F)
q: Earth is a planet (T)
∴ ¬p v q is having the truth value T

(iv) 11 is a prime number and all the sides of a rectangle are equal.
p : 11 is a prime number (T)
q: All the sides of a rectangle are equal (F)
∴ p ∧ q is having the truth value F

Question 4.
Which one of the following sentences is a proposition?

1. 4 + 7 = 12
2. What are you doing?
3. 3ⁿ ≤ 81, n ∈ N
4. Peacock is our national bird.
5. How tall this mountain is!

Solution:

1. is a proposition
2. not a proposition
3. is a proposition
4. is a proposition
5. not a proposition

Question 5.
Write the converse, inverse, and contrapositive of each of the following implication.
(i) If x and y are numbers such that x = y, then x² = y²
(ii) If a quadrilateral is a square then it is a rectangle.
Solution:
(i) Converse: If x and y are numbers such that x² = y² then x = y.
Inverse: If x and y are numbers such that x ≠ y then x² ≠ y².
Contrapositive: If x and v are numbers such that x² ≠ y² then x ≠ y.

(ii) Converse: If a quadrilateral is a rectangle then it is a square.
Inverse: If a quadrilateral is not a square then it is not a rectangle.
Contrapositive: If a quadrilateral is not a rectangle then it is not a square.

Question 6.
Construct the truth table for the following statements.
(i) ¬P ∧ ¬q
(ii) ¬(P ∧ ¬q)
(iii) (p v q) v ¬q
(iv) (¬p → r) ∧ (p ↔ q)
Solution:
(i) ¬P ∧ ¬q

(ii) ¬(P ∧ ¬q)

(iii) (p v q) v ¬q

(iv) (¬p → r) ∧ (p ↔ q)

Question 7.
Verify whether the following compound propositions are tautologies or contradictions or contingency.
(i) (P ∧ q) ∧¬ (p v q)
(ii) ((P v q) ∧¬p) → q
(iii) (p → q) ↔ (¬p → q)
(iv) ((p → q) ∧ (q → r)) → (p → r)
Solution:
(i) (P ∧ q) ∧¬ (p v q)

The entries in the last column are only F.
∴ The given statement is a contradiction

(ii) ((P v q) ∧¬p) → q

The entries in the last column are only T.
∴ The given statement is a Tautology

(iii) (p → q) ↔ (¬p → q)

The entries in the last column are a combination of T and F.
∴ The given statement is a contingency.

(iv) ((p → q) ∧ (q → r)) → (p → r)

All the entries in the last column are only T.
∴ The given statement is a tautology.

Question 8.
Show that (i) ¬(p ∧ q) ≡ ¬P v ¬q
(ii) ¬(p → q) ≡ p ∧¬q
Solution:
(i) ¬(p ∧ q) ≡ ¬P v ¬q

The entries in the columns corresponding to ¬(p ∧ q) and ¬P v ¬q are identical and hence they are equivalent.

(ii) ¬(p → q) ≡ p ∧ ¬q

The entries in the columns corresponding to ¬(p → q) and p ∧ ¬q are identical and hence they are equivalent.

Question 9.
Prove that q → p ≡ ¬p → ¬q
Solution:
q → p ≡ ¬p → ¬q

The entries in the columns corresponding to q → p and ¬p → ¬q are identical and hence they are equivalent.
∴ q → q = ¬p → ¬q
Hence proved.

Question 10.
Show that p → q and q → p are not equivalent
Solution:

From the table, it is clear that
p → q ≠ q → P

Question 11.
Show that ¬(p ↔ q) ≡ p ↔ ¬q
Solution:

From the table, it is clear that
¬(p ↔ q) ≡ p ↔ ¬q

Question 12.
Check whether the statement p → (q → p) is a tautology or a contradiction without using the truth table.
Solution:
P → (q → p)
≡ P → (¬q v p) [∵ implication law]
≡ ¬p v (¬q v p) [∵ implication law]
≡ ¬p v (p v ¬q) [∵ Commutative law]
≡ (¬p V p) v (¬p v ¬q) [∵ Distribution law]
≡ T v ¬(p ∧ q) ≡ T [Tautology]
Hence p → (q → p) is a Tautology.

Question 13.
Using the truth table check whether the statements ¬(p v q) v (¬p ∧ q) and ¬P are logically equivalent.
Solution:

From the table, it is clear that ¬P and
¬(p v q) v (¬p ∧ q) are logically equivalent
i.e. ¬(p v q) v (¬p ∧ q) ≡ ¬p

Question 14.
Prove p → (q → r) ≡ (p ∧ q) → r without using the truth table.
Solution:
P → (q → r)
≡ P → (¬q v r) [∵ implication law]
≡ ¬p v (¬q v r) [∵ implication law]
≡ (¬p v ¬q) v r [∵ Associative law]
≡ ¬(p ∧ p) v r [∵ DeMorgan’s law]
≡ (p ∧ q) → r ≡ T [∵ implication law]
Hence Proved.

Question 15.
Prove that p → (¬q v r) ≡ ¬p v (¬q v r) using truth table.
Solution:

From the table, it is clear that the column of p → (¬q v r) and ¬p v (¬q v r) are identical.
∴ p → (¬q v r) ≡ ¬p v (¬q v r)
Hence proved.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 8 Differentials and Partial Derivatives Ex 8.2 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.2

Question 1.
Find the differential dy for each of the following functions.
(i) y = \(\frac { (1-2x)^3 }{ 3-4x }\)
(ii) y = (3 + sin2x)^2/3
(iii) y = e^{x2 – 5x +7} cos(x² – 1)
Solution:

(ii) y = (3 + sin2x)^2/3

Question 2.
Find df for f(x) = x² + 3x and evaluate it for
(i) x = 2 and dx = 0.1
(ii) x = 3 and dx = 0.02
Solution:
y = f(x) = x² + 3x
dy = (2x + 3) dx
(i) dy {when x = 2 and ate = 0.1} = [2(2) + 3] (0.1)
= 7(0.1) = 0.7

(ii) dy {when x = 3 and dx = 0.02} = [2(3) + 3] (0.0.2)
= 9(0.02) = 0.18

Question 3.
Find Δf and df for the function f for the indicated values of x, Δx and compare:
(i) f(x) = x³ – 2x², x = 2, Δx = dx = 0.5
(ii) f(x) = x² + 2x + 3, x = -0.5, Δx = dx = 0.1
Solution:
(i) y = f(x) = x³ – 2x²
dy = (3x² – 4x) dx
dy (when x = 2 and dx = 0.5) = [3(2²) – 4(2)] (0.5)
= (12 – 8)(0.5) = 4(0.5) = 2
(i.e.,) df = 2
Now ∆f = f(x + ∆x) – f(x)
Here x = 2 and ∆x = 0.5
f(x) = x³ – 2x²
So f(x + ∆x) = f(2 + 0.5) = f(2.5) = (2.5)³ – 2 (2.5)² = (2.5)² [2.5 – 2] = 6.25 (0.5) = 3.125
f(x) = f(2) = 2³ – 2(2²) = 8 – 8 = 0
So ∆f = 3.125 – 0 = 3.125

(ii) y = f(x) = x² + 2x + 3
dy = (2x + 2) dx
dy (when x = – 0.5 and dx = 0.1)
= [2(-0.5) + 2] (0.1)
= (-1 + 2) (0.1) = (1) (0.1) = 0.1
(i.e.,) df = 0.1
Now ∆f = f(x + ∆x) – f(x)
Here x = -0.5 and ∆x = 0.1
x² + 2x + 3
f(x + ∆x) = f(-0.5 + 0.1) = f(-0.4)
= (-0.4)² + 2(-0.4) + 3
= 0.16 – 0.8 + 3 = 3.16 – 0.8 = 2.36
f(x) = f(-0.5) = (-0.5)² + 2(-0.5) + 3
= 0.25 – 1 + 3 = 3.25 – 1 = 2.25
So ∆ f = f(x + ∆x) – f(x) = 2.36 – 2.25 = 0.11

Question 4.
Assuming log₁₀ e = 0.4343, find an approximate value of Iog₁₀ 1003.
Solution:
Let f(x) = log ₁₀ x then
f ‘(x) = \(\frac { 1 }{ x }\) log₁₀ e (log₁₀ x = log₁₀ e log_e x)
f(x + Δx) – f(x) = f ‘(x) Δx
f(1003) – f(1000) = \(\frac { 0.4344 }{ 1000 }\) × 3
log₁₀ 1003 – log₁₀ 1000 = 0.0013029
log₁₀ 1003 = log₁₀ 10³ + 0.0013029
= 3 + 0.0013029
= 3.0013029
Approximate value of log₁₀ 1003 = 3.0013029

Question 5.
The trunk of a tree has a diameter of 30 cm. During the following year, the circumference grew 6 cm.
(i) Approximately how much did the tree diameter grow?
(ii) What is the percentage increase in the area of the cross-section of the tree?
Solution:
(i) Diameter of the trunk of the tree
D = 30 cm
Rate of change of circumference
ds = 6 cm per year
Circumference S = πD
dS = πdD
6 = πdD
\(\frac { 6 }{ π }\) = dD
Rate of increasing diameter = \(\frac { 6 }{ π }\) cm

Question 6.
An egg of a particular bird is very nearly spherical. If the radius to the inside of the shell is 5 mm and the radius to the outside of the shell is 5.3 mm, find the volume of the shell approximately.
Solution:
Radius of the inside shell = 5 mm
Radius of the outside shell = 5.3 mm
Volume V = \(\frac { 4 }{ 3 }\) πr³
dV = \(\frac { 4 }{ 3 }\) π3r²dr
= 4 π 5 × 5 × 0.3
= 100 π × 0.3
= 30 π
Approximate volume of the shell = 30 mm³

Question 7.
Assume that the cross-section of the artery of human is circular. A drug is given to a patient to dilate his arteries. If the radius of an artery is increased from 2 mm to 2.1 mm, how much is the cross-sectional area increased approximately?
Solution:
The radius of an artery section = 2 mm
dr = 2.1 – 2
= 0.1
Area A = πr²
dA = 2πrdr
= 2 × π × 2 × 0.1
= 0.4 π
Increased area = 0.4 π mm²

Question 8.
In a newly developed city, it is estimated that the voting population (in thousands) will increase according to V(t) =30 + 12t² – t³, 0 ≤ t ≤ 8 where t is the time in years. Find the approximate change in voters for the time change from 4 to 4 1/6 years.
Solution:
V(t) = 30 + 12t² – t³; dt = 4 \(\frac { 1 }{ 6 }\) – 4 = \(\frac { 1 }{ 6 }\)
V’(t) = (24t – 3t²)dt
= (24(4)-3 (4)²) × \(\frac { 1 }{ 6 }\)
= (96 – 48) × \(\frac { 1 }{ 6 }\)
= 48 × \(\frac { 1 }{ 6 }\)
= 8
Voters in thousands
∴ Approximate change of voters = 8 × 1000 = 8000

Question 9.
The relation between the number of words y a person learns in x hours is given by y = 52√x, 0 ≤ x ≤ 9. What is the approximate number of words learned when x changes from
(i) 1 to 1.1 hours?
(ii) 4 to 4.1 hours?
Solution:
y = 52 √x
dy = 52 × \(\frac { 1 }{ 2 }\) × x^-1/2 dx
x = 1, dx = 0.1
\(\frac { 26 }{ √x }\) × 0.1 = 26 × 0.1
= 2.6
≅ 3 words

(ii) y = 52 √y
dy = 52 × \(\frac { 1 }{ 2 }\) × x^-1/2 dx
x = 4, dx = 0.1
\(\frac { 26 }{ √4 }\) × 0.1 = 13 × 0.1
= 1.3
≅ 1 word

Question 10.
A circular plate expands uniformly under the influence of heat. If its radius increases from 10.5 cm to 10.75 cm, then find an approximate change in the area and the approximate percentage change in the area.
Solution:
Area of the circular plate A = πr²
= π × 10.5 × 105
= 110.25 π
dA = 2πrdr
= 2π × 10.5 × 0.251
= 5.25 π
Approximate percentage change in the area
= \(\frac { dA }{ A }\) × 100
= \(\frac { 5.25π }{ 110.25π }\) × 100
= 0.04761 × 100
= 4.76%

Question 11.
A coat of paint of thickness 0.2 cm is applied to the faces of cube whose edge is 10 cm. Use the differentials to find approximately how many cubic centimeters of paint is used to paint this cube. Also calculate the exact amount of paint used to paint this cube.
Solution:
v = a³
so dv = a² da
dv (when) a = 10 cm and da = 0.20 cm
= 3(10²) (0.2)
300 × 0.2 = 60 cm³

Actual paint used = v at x + ∆x = 10.2 and x = 10 cm
= a³ at x + ∆x = 10.2 and x = 10
= (10.2)³ – (10) = 61.2 cm³

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 8 Differentials and Partial Derivatives Ex 8.1 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.1

Question 1.
Let f(x) = \(\sqrt[3] { x }\). Find the linear approximation at x = 27. Use the linear approximation to approximate \(\sqrt[3] { 27.2 }\)
Solution:
x = 27
f(x) = \(\sqrt[3] { 27 }\) = 3
We need to find the value of \(\sqrt[3] { 27.2 }\)
We know that
f(x₀ + Δx) = f(x₀) + f'(x₀) Δx

∴ Approximate value of \(\sqrt[3] { 27.2 }\) = 3.0074

Question 2.
Use the linear approximation to find approximate value of
(i) (123)^2/3
(ii) \(\sqrt[4] { 15 }\)
(iii) \(\sqrt[4] { 26 }\)
Solution:
(i) (123)^2/3
Let x₀ = 125, Δx = -2
f(x) = x^2/3, f(x₀) = 25
We know that
f(x₀ + Δx) = f(x₀) + f'(x₀) Δx

= 25 – 0.2666
(123)^2/3 = 24.7334

(ii) \(\sqrt[4] { 15 }\) = (15)^1/4
f(x) = x^1/4, f(x₀) = (16)^1/4 = 2
We know that
f(x₀ + Δx) = f(x₀) + f’(x₀) Δx

= 2 – 0.03125
(15)^1/4 = 1.96875

(iii) (26)^1/3
f(x) = x^1/3, f(x₀) = (27)^1/3 = 2, Δx = -1
We know that
f(x₀ + Δx) = f(x₀) + f’(x₀) Δx

= 3 – 0.370
(26)^1/3 = 2.963

Question 3.
Find a linear approximation for the following functions at the indicated points
(i) f(x) = x³ – 5x + 12, x₀ = 2
(ii) g(x) = \(\sqrt { x^2+9 }\), x₀ = -4
(iii) h(x) = \(\frac { x }{ x+1 }\), x₀ = 1
Solution:
(i) We know that the linear approximation
L(x) = f(x₀) + f’(x₀)(x – x₀)
f(x) = x³ – 5x + 12
f'(x) = 3x² – 5
f'(x₀) = f'(2) = 12 – 5 = 7
f(x₀) = f(2) = 8 – 10 + 12 = 10
L(x) = 10 + 7 (x – 2)
= 10 + 7x – 14
= 7x – 4

(ii) g(x) = \(\sqrt { x^2+9 }\), x₀ = -4
g(x₀) = g(14) = \(\sqrt {16+9 }\) = 5

(iii) h(x) = \(\frac { x }{ x+1 }\), x₀ = 1

Question 4.
The radius of a circular plate is measured as 12.65. cm instead of the actual length 12.5 cm find the following in calculating the area of the circular plate:
(i) Absolute error
(ii) Relative error
(iii) Percentage error
Solution:
Actual radius of the circular plate = 12.5 cm
Measured radius of the circular plate = 12.65
dr = 12.65 – 12.5
= 0.15
A = π r²
dA = 2π r dv
Change in Area
A(12.65) – A(12.5) = dA
= 2π × 12.5 × 0.15
= 3.75 π
Exact calculation of the Area changes gives
A(12.65) – A(12.5) = π(12.65)² – π(12.5)²
= 160.0225 π – 156.25 π
= 3.7725 π
Absolute error = 3.7725 π – 3.75 π
= 0.0225 π cm²
Relative error
= \(\frac { 3.7725π-3.75π }{ 3.7725π }\)
= \(\frac { 0.0225π }{ 3.7725π }\)
= 0.00596
= 0.006 cm²
Percentage error = Relative error × 100
= 0.006 × 100
= 0.6% .

Question 5.
A sphere is made of ice having radius 10 cm. Its radius decreases from 10 cm to 9.8 cm. Find approximations for the following:
(i) Change in the volume.
(ii) Change in the surface area
Solution:
(i) Given r = 10
dr = 10 – 9.8 = 0.2
Volume v = \(\frac { 4 }{ 3 }\)πr³
dv = \(\frac { 4 }{ 3 }\).3πr²dv
Change in volume
v(10) – v(9.8) = 4π(10)²(0.2)
= 80π cm³

(ii) Surface area of the sphere
S(r) = 4πr²
S'(r) = 8πr
Change in surface area at r = 10 is
= S'(r) [10 – 9.8]
= 8π (10) (0.2) = 16π cm²
∴ Surface Area decreases by 16π cm²

Question 6.
The time T, taken for a complete oscillation of a single pendulum with length l, is given by the equation T = 2π\(\sqrt{\frac { l }{ g }}\) where g is a constant. Find the approximate percentage error in the calculated value of T corresponding to an error of 2 percent in the value of l.
Solution:
Given T = 2π\(\sqrt{\frac { l }{ g }}\)
On taking log both sides, we get
log T = log 2 + log π + \(\frac { 1 }{ 2 }\) log l – \(\frac { 1 }{ 2 }\) log g
On differentiating both sides w. r. to l, we get

So, the percentage error in T is 1%

Question 7.
Show that the percentage error in the nth root of a number is approximately \(\frac { 1 }{ n }\) times the percentage error in the number.
Solution:
Let x be the number
Let y = x^1/n
log y = \(\frac { 1 }{ n }\) log x
Taking differentiate on both sides, we have

= \(\frac { 1 }{ n }\) times the percentage error in the number.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 Applications of Differential Calculus Ex 7.10 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.10

Choose the most suitable answer from the given four alternatives:

Question 1.
The volume of a sphere is increasing in volume at the rate of 3π cm³/ sec. The rate of change of its radius when radius is \(\frac { 1 }{ 2 }\) cm
(a) 3 cm/s
(b) 2 cm/s
(c) 1 cm/s
(d) \(\frac { 1 }{ 2 }\) cm/s
Solution:
(a) 3 cm/s
Hint:
Volume V = \(\frac { 4 }{ 3 }\) πr³
Given \(\frac { dV }{ dt }\) = 3π cm³/sec
Differentiating w.r.t. ‘t’ r = \(\frac { 1 }{ 2 }\) cm

Rate of change of radius is 3 cm/sec.

Question 2.
A balloon rises straight up at 10 m/s. An observer is 40 m away from the spot where the balloon left the ground. Find the rate of change of the balloon’s angle of elevation in radian per second when the balloon is 30 metres above the ground.
(a) \(\frac { 3 }{ 25 }\) radan/sec
(b) \(\frac { 4 }{ 25 }\) radian/sec
(c) \(\frac { 1 }{ 5 }\) radian/sec
(d) \(\frac { 1 }{ 3 }\) radian/sec
Solution:
(b) \(\frac { 4 }{ 25 }\) radian/sec
Hint:

Question 3.
The position of a particle moving along a horizontal line of any time t is given by s(t) = 3t² – 2t – 8. The time at which the particle is at rest is
(a) t = 0
(b) t = \(\frac { 1 }{ 3 }\)
(c) t = 1
(d) t = 3
Solution:
(b) t = \(\frac { 1 }{ 3 }\)
Hint:
s(t) = 3t² – 2t – 8
Velocity V = \(\frac { ds }{ dt }\) = 6t – 2
When the particle comes to rest,
velocity V = 0
6t – 2 = 0
t = \(\frac { 1 }{ 3 }\)

Question 4.
A stone is thrown, up vertically. The height reaches at time t seconds is given by x = 80t – 16t². The stone reaches the maximum! height in time t seconds is given by
(a) 2
(b) 2.5
(c) 3
(d) 3.5
Solution:
(b) 2.5
Hint:
x = 80t – 16t²
Velocity V = \(\frac { ds }{ dt }\) = 80 – 32t
When it reaches the maximum height
V = 0 ⇒ 80 – 32t = 0
t = \(\frac { 80 }{ 32 }\) = 2.5

Question 5.
Find the point on the curve 6y = x³ + 2 at which y-coordinate changes 8 times as fast as x-coordinate is
(a) (4, 11)
(b) (4, -11)
(c) (-4, 11)
(d) (-4, -11)
Solution:
(a) (4, 11)
Hint:

x = ±4
When x = 4, y = 11
∴ Point on the curve is (4, 11).

Question 6.
The abscissa of the point on the curve f(x) = \(\sqrt { 8-2x }\) at which the slope of the tangent is -0.25?
(a) -8
(b) -4
(c) -2
(d) 0
Solution:
(b) -4
Hint:
f(x) = \(\sqrt { 8-2x }\)
f'(x) = –\(\frac { 2 }{ 2\sqrt { 8-2x } }\) = –\(\frac { 1 }{ \sqrt { 8-2x } }\)
Slope of the tangent is – 0.25
ie„ f'(x) = -0.25
–\(\frac { 1 }{ \sqrt { 8-2x } }\) = -0.25 = \(\frac { -1 }{ 4 }\)
\(\sqrt { 8-2x }\) = 4
8 – 2x = 16
x = –\(\frac { 8 }{ 2 }\) = -4
Abscissa x = -4

Question 7.
The slope of the line normal to the curve f(x) = 2 cos 4x at x = \(\frac { π }{ 12 }\) is
(a) -4√3
(b) -4
(c) –\(\frac { √3 }{ 12 }\)
(d) 4√3
Solution:
(c) –\(\frac { √3 }{ 12 }\)
Hint:
f(x) = 2 cos 4x
f'(x) = -8 sin 4x
Slope of the normal at x = \(\frac { π }{ 12 }\) is

Question 8.
The tangent to the curve y² – xy + 9 = 0 is vertical when
(a) y = 0
(b) y = ±√3
(c) –\(\frac { 1 }{ 2 }\)
(d) y = ±3
Solution:
(d) y = ±3
Hint:
y² – xy + 9 = 0 ……… (1)
2y\(\frac { dy }{ dx }\) – (x\(\frac { dy }{ dx }\) + y) = 0
\(\frac { dy }{ dx }\) (2y – x) = y
\(\frac { dy }{ dx }\) = \(\frac { y }{ 2y-x }\)
When the tangent is vertical \(\frac { dy }{ dx }\) = ∞
i.e., \(\frac { y }{ 2y-x }\) = \(\frac { 0 }{ 1 }\)
⇒ 2y – x = 0
2y = x
sub in (1)
y² – 2y² + 9 = 0
⇒ y² = 9
y = ±3

Question 9.
The angle between y² = x and x² = y at the origin is
(a) tan^-1 \(\frac { 3 }{ 4 }\)
(b) tan^-1 (\(\frac { 4 }{ 3 }\))
(c) \(\frac { π }{ 2 }\)
(d) \(\frac { π }{ 4 }\)
Solution:
(c) \(\frac { π }{ 2 }\)
Hint:
y² = x and x² = y are the standard forms of parabolas for which y-axis and x-axis are the two tangents respectively.
Angle between x-axis and y-axis is \(\frac { π }{ 2 }\)

Question 10.
The value of the limit \(\lim _{x \rightarrow 0}\) (cot x – \(\frac { 1 }{ x }\)) is
(a) 0
(b) 1
(c) 2
(d) ∞
Solution:
(d) ∞
Hint:

Question 11.
The function sin⁴ x + cos⁴ x is increasing in the interval
(a) [ \(\frac { 5π }{ 8 }\), \(\frac { 3π }{ 4 }\) ]
(b) [ \(\frac { π }{ 2 }\), \(\frac { 5π }{ 8 }\) ]
(c) [ \(\frac { π }{ 4 }\), \(\frac { π }{ 2 }\) ]
(d) [ 0, \(\frac { π }{ 4 }\) ]
Solution:
(c) [ \(\frac { π }{ 4 }\), \(\frac { π }{ 2 }\) ]
Hint:
f(x) = sin⁴x + cos⁴x
f'(x) = 4 sin³ x cos x – 4 cos³ x sin x
f'(x) = 0 ⇒ 4 sin x cos x (sin²x – cos²x) = 0
sin x = 0; cos x = 0; sin² – cos² x = 0
x = 0; x = \(\frac { π }{ 2 }\); sin² x = cos² x
x = \(\frac { π }{ 4 }\)

In [0, \(\frac { π }{ 2 }\) ], f'(x) = -ve ⇒ f(x) is decreasing
In [ \(\frac { π }{ 2 }\), \(\frac { π }{ 2 }\) ], f'(x) = +ve ⇒ f(x) is increasing

Question 12.
The number is given by Rolle’s theorem for the function x³ – 3x², x ∈ [0, 3] is
(a) 1
(b) √2
(c) \(\frac { 3 }{ 2 }\)
(d) 2
Solution:
(d) 2
Hint:
f(x) = x³ – 3x²
f'(x) = 3x² – 6x
f'(x) = 0
⇒ 3x (x – 2) = 0
x = 0, 2

Question 13.
The number given by the Mean value theorem for the function \(\frac { 1 }{ x }\), x ∈ [1, 9] is
(a) 2
(b) 2.5
(c) 3
(d) 3.5
Solution:
(c) 3
Hint:

Question 14.
The minimum value of the function |3 – x| + 9 is
(a) 0
(b) 3
(c) 6
(d) 9
Solution:
(d) 9
Hint:
f(x) = |3 – x | + 9
Minimum value of |3 – x | = 0
Minimum value of |3 – x| + 9 = 0 + 9 = 9 and No Maximum value.

Question 15.
The maximum slope of the tangent to the curve y = e^x sin x, x ∈ [0, 2π] is at
(a) x = \(\frac { π }{ 4 }\)
(b) x = \(\frac { π }{ 2 }\)
(c) x = π
(d) x = \(\frac { 3π }{ 2 }\)
Solution:
(b) x = \(\frac { π }{ 2 }\)
Hint:
y = e^x sin x, x ∈ [0, 2π] dy
Slope ‘S’ = \(\frac { dy }{ dx }\) = e^x cos x + e^x sin x
S = e^x (cos x + sin x)
\(\frac { dS }{ dx }\) = e^x (-sin x + cos x) + (cos x + sin x)e^x
= e^x (2 cos x)
For maximum or minimum,
\(\frac { dS }{ dx }\) = 0 ⇒ 2e^x cos x = 0
e^x = 0 is not possible
∴ cos x = 0
x = \(\frac { π }{ 2 }\)

Question 16.
The maximum value of the function x² e^-2x, x > 0 is
(a) \(\frac { 1 }{ e }\)
(b) \(\frac { 1 }{ 2e }\)
(c) \(\frac { 1 }{ e^2 }\)
(d) \(\frac { 4 }{ e^4 }\)
Solution:
(c) \(\frac { 1 }{ e^2 }\)
Hint:
Let f(x) = x²e^-2x, x > 0
f'(x) = -2x² e^-2x + e^-2x (2x)
f'(x) = 0 ⇒ -2xe^-2x(x – 1) = 0
x = 0 and x = 1
f(x) attains maximum at x = 1 as f”(x) < 0
when x = 1
∴ Maximum value f(1) = (1)² e^-2 = \(\frac { 1 }{ e^2 }\)

Question 17.
One of the closest points on the curve x² – y² = 4 to the point (6, 0) is
(a) (2, 0)
(b) (√5, 1)
(c) (3, √5)
(d) (\(\sqrt { 13 }\), -√3)
Solution:
(c) (3, √5)
Hint:
x² – y² = 4
y² = x² – 4
y = ±\(\sqrt { x^2-4 }\)
Any point on the curve is (x, ± \(\sqrt { x^2-4 }\))
Distance between (6, 0) and (x, ± \(\sqrt { x^2-4 }\)) is \(\sqrt { (x-6)^2+x^2-4 }\)
Substituting all’ the given options, we get minimum distance.
∴ Required point is (3, √5)

Question 18.
The maximum value of the product of two positive numbers’, when their sum of the squares is 200, is
(a) 100
(b) 25√7
(c) 28
(d) 24\(\sqrt { 14 }\)
Solution:
(a) 100
Hint:
Given x² + y² = 200
y² = 200 – x²
y = \(\sqrt { 200-x^2 }\)
Product P = xy = x\(\sqrt { 200-x^2 }\)
\(\frac { dP }{ dx }\) = \(\frac { x(-2x) }{ 2\sqrt{200-x^2} }\) + \(\sqrt{200-x^2}\) …. (1)
\(\frac { dP }{ dx }\) = 0 ⇒ -2x² + 200 = 0
x² = 100
x = 10
∴ y = \(\sqrt{200-100}\) = 10
∴ Maximum product is P = xy
= (10) (10)
= 100

Question 19.
The curve y = ax⁴ + bx² with ab > 0
(a) has no horizontal tangent
(b) is concave up
(c) is concave down
(d) has no points of inflection
Solution:
(d) has no points of inflection
Hint:
y = ax⁴ + bx²
\(\frac { dy }{ dx }\) = 4ax³ + 2bx
\(\frac { d^2y }{ dx^2 }\) = 12ax² + 2b
\(\frac { d^2y }{ dx^2 }\) = 0 ⇒ 12ax² + 2b = 0
x² = –\(\frac { b }{ 6a }\)
x is unreal.
Hence no points of inflection.

Question 20.
The point of inflection of the curve y = (x – 1)³ is
(a) (0, 0)
(b) (0, 1)
(c) (1, 0)
(d) (1, 1)
Solution:
(c) (1, 0)
Hint:
y = (x – 1)³
\(\frac { dy }{ dx }\) = 3(x – 1)²
\(\frac { d^2y }{ dx^2 }\) = 6(x – 1)
\(\frac { d^2y }{ dx^2 }\) = 0 ⇒ 6(x – 1) = 0
x = 1
y = f(x)
\(\frac { dy }{ dx }\) = f'(x)
\(\frac { d^2y }{ dx^2 }\) = f”(x)
In (-∞, 1), f”(x) < 0, curve is concave down In (1, ∞), f”(x) > 0, curve is concave up
f”(x) changes its sign when passing through x = 1
when x = 1, y = 0
∴ (1, 0) is the point of inflection.