Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.4 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.4
Choose the most suitable answer from the given four alternatives:
Question 1.
A = (1, 2, 3), then the rank of AAT is
(a) 0
(b) 2
(c) 3
(d) 1
Solution:
(d) 1
Hint:
A = (1, 2, 3) then
AT = \(\left(\begin{array}{l}
1 \\
2 \\
3
\end{array}\right)\)
AAT = (1, 2, 3) \(\left(\begin{array}{l}
1 \\
2 \\
3
\end{array}\right)\) = (1 + 4 + 9) = (14)
Number of non-zero rows = 1
∴ P (AAT) = 1
![]()
Question 2.
The rank of m × n matrix whose elements are unity is
(a) 0
(b) 1
(c) m
(d) n
Solution:
(b) 1
Question 3.
If T = 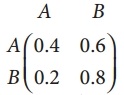 is a transition probability matrix, then at equilibriuium A is equal to
is a transition probability matrix, then at equilibriuium A is equal to
(a) \(\frac { 1 }{ 4 }\)
(b) \(\frac { 1 }{ 5 }\)
(c) \(\frac { 1 }{ 6 }\)
(d) \(\frac { 1 }{ 8 }\)
Solution:
(a) \(\frac { 1 }{ 4 }\)
Hint:

At equilibrium (A B) \(\left(\begin{array}{ll}
0.4 & 0.6 \\
0.2 & 0.8
\end{array}\right)\)
0.4 A + 0.2 B = A
0.4 A + 0.2(1 – A) = A
0.4 A + 0.2 – 0.2 A = A
0.2 A + 0.2 = A
0.2 = A – 0.2 A
0.2 = 0.8 A
A = \(\frac { 0.2 }{ 0.8 }\) = \(\frac { 1 }{ 4 }\)
Question 4.
If A = \(\left(\begin{array}{ll}
2 & 0 \\
0 & 8
\end{array}\right)\), then p(A) is
(a) 0
(b) 1
(c) 2
(d) n
Solution:
(c) 2
Hint:
A = \(\left(\begin{array}{ll}
2 & 0 \\
0 & 8
\end{array}\right)\)
No. of Non-zero rows = 2
∴ p(A) = 2
![]()
Question 5.
The rank of the matrix \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 2 & 3 \\
1 & 4 & 9
\end{array}\right]\) is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(d) 3
Hint:
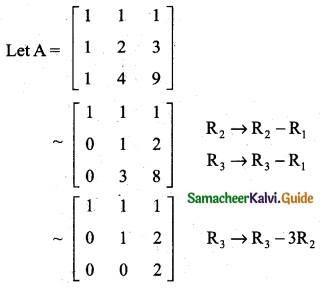
No. of Non-zero rows = 3
∴ p(A) = 3
Question 6.
The rank of the unit matrix of order n is
(a) n – 1
(b) n
(c) n + 1
(d) n²
Solution:
(b) n
Question 7.
If p(A) = r then which of the following is correct?
(a) all the minors of order r which does not vanish
(b) A has at least one minor of order r which does not vanish
(c) A has at least one (r + 1) order minor which vanishes
(d) all (r + 1) and higher order minors should not vanish
Solution:
(b) A has at least one minor of order r which does not vanish.
![]()
Question 8.
If A = \(\left(\begin{array}{l}
1 \\
2 \\
3
\end{array}\right)\) then the rank of AAT is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(b) 1
Hint:

No. of non-zero rows = 1
p (AAT) = 1
Question 9.
If the rank of the matrix \(\left[\begin{array}{ccc}
\lambda & -1 & 0 \\
0 & \lambda & -1 \\
-1 & 0 & \lambda
\end{array}\right]\) is 2. then λ is
(a) 1
(b) 2
(c) 3
(d) only real number
Solution:
(a) 1
Hint:
A = \(\left[\begin{array}{ccc}
\lambda & -1 & 0 \\
0 & \lambda & -1 \\
-1 & 0 & \lambda
\end{array}\right]\)
Since the Rank is 2, third order matrix vanishes
∴ |A| = 0
\(\left[\begin{array}{ccc}
\lambda & -1 & 0 \\
0 & \lambda & -1 \\
-1 & 0 & \lambda
\end{array}\right]\) = 0
λ(λ² – 0) + 1 (0 – 1) = 0
λ³ – 1 = 0 ⇒ λ³ = 1
∴ λ = 1
Question 10.

(a) 0
(b) 2
(c) 3
(d) 5
Solution:
(c) 3
Hint:
Number of non-zero rows = 3
∴ Rank = 3
![]()
Question 11.
If 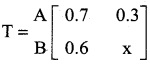 is a transition probability matrix, then the value of x is
is a transition probability matrix, then the value of x is
(a) 0.2
(b) 0.3
(c) 0.4
(d) 0.7
Solution:
(c) 0.4
Hint:
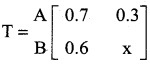
is a transition probability matrix then 0.6 + x = 1
x = 1 – 0.6
x = 0.4
Question 12.
Which of the following is not an elementary transformation?
(a) Ri ↔ Rj
(b) Ri → 2Ri + 2Cj
(c) Ri → 2Ri + 4Rj
(d) Ci → Ci + 5Cj
Solution:
(b) Ri → 2Ri + 2Cj
Question 13.
If p(A) = p(A,B)= then the system is
(a) Consistent and has infinitely many solutions
(b) Consistent and has a unique solution
(c) inconsistent
(d) consistent
Solution:
(d) Consistent
![]()
Question 14.
If p(A) = p(A,B)= the number of unknowns, then the system is
(a) Consistent and has infinitely many solutions
(b) Consistent and has a unique solution
(c) inconsistent
(d) consistent
Solution:
(b) Consistent and has a unique solution
Question 15.
If p(A) ≠ p(A, B) =, then the system is
(a) Consistent and has infinitely many solutions
(b) Consistent and has a unique solution
(c) inconsistent
(d) consistent
Solution:
(c) inconsistent
Question 16.
In a transition probability matrix, all the entries are greater than or equal to
(a) 2
(b) 1
(c) 0
(d) 3
Solution:
(c) 0
![]()
Question 17.
If the number of variables in a non-homogeneous system AX = B is n, then the system possesses a unique solution only when
(a) p(A) = p(A, B) > n
(b) p(A) = p(A, B) = n
(c) p(A) = p(A, B) < n
(d) none of these
Solution:
(b) p(A) = p(A, B) = n
Question 18.
The system of equations 4x + 6y = 5, 6x + 9y = 7 has
(a) a unique solution
(b) no solution
(c) infinitely many solutions
(d) none of these
Solution:
(b) no solution
Hint:
The matrix form of the equations
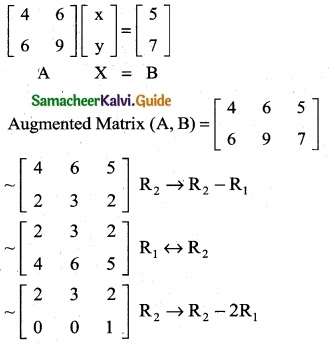
p(A) ≠ p(A, B)
∴ The system is inconsistent.
Question 19.
For the system of equations x + 2y + 3z = 1, 2x + y – z = 3, 3x + 2y + k = 4
(a) there is only one solution
(b) there exists infinitely many solution
(c) there is no solution
(d) none of these
Solution:
(a) there is only one solution
Hint:
The matrix form of the equations

The last equivalent matrix in the echelon form
p(A) = p (A, B) = no. of unknowns
∴ The system is consistent.
![]()
Question 20.
If |A| ≠ 0, then A is
(a) non – singular matrix
(b) singular matrix
(c) zero matrix
(d) none of these
Solution:
(a) non-singular matrix
Question 21.
The system of linear equations x = y + z = 2, 2x + y – z = 3, 3x + 2y + k = 4 has unique solution, if k is not equal to
(a) 1
(b) 0
(c) 3
(d) 7
Solution:
(b) 0
Hint:
The matrix form of the equations

Since the system has unique solution.
P(A) = p(A, B) ≠ n
∴ K ≠ 0
Question 22.
Cramer’s rule is applicable only to get an unique solution when
(a) Δz ≠ 0
(b) Δx ≠ 0
(c) Δ ≠ 0
(d) Δy ≠ 0
Solution:
(c) Δ ≠ 0
![]()
Question 23.
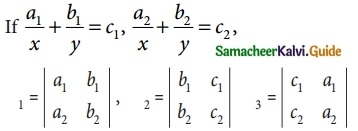
Then (x, y) is
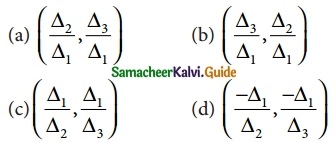
Solution:
(d) (\(\frac { -Δ_1 }{ Δ_2 }\), \(\frac { -Δ_1 }{ Δ_3 }\))
Question 24.
|An × n| = 3 |adj A| = 243 = (3)5 then the value n is
(a) 4
(b) 5
(c) 6
(d) 7
Solution:
(c) 6
Question 25.
Rank of a null matrix is
(a) 0
(b) -1
(c) ∞
(d) 1
Solution:
(a) 0
![]()