Samacheer Kalvi 12th Maths Guide Chapter 8 Differentials and Partial Derivatives Ex 8.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 8 Differentials and Partial Derivatives Ex 8.1 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.1

Question 1.
Let f(x) = \(\sqrt[3] { x }\). Find the linear approximation at x = 27. Use the linear approximation to approximate \(\sqrt[3] { 27.2 }\)
Solution:
x = 27
f(x) = \(\sqrt[3] { 27 }\) = 3
We need to find the value of \(\sqrt[3] { 27.2 }\)
We know that
f(x₀ + Δx) = f(x₀) + f'(x₀) Δx

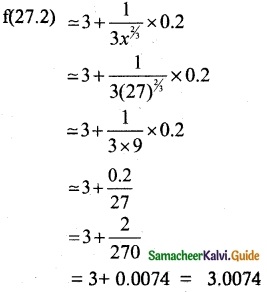
∴ Approximate value of \(\sqrt[3] { 27.2 }\) = 3.0074

Question 2.
Use the linear approximation to find approximate value of
(i) (123)^2/3
(ii) \(\sqrt[4] { 15 }\)
(iii) \(\sqrt[4] { 26 }\)
Solution:
(i) (123)^2/3
Let x₀ = 125, Δx = -2
f(x) = x^2/3, f(x₀) = 25
We know that
f(x₀ + Δx) = f(x₀) + f'(x₀) Δx

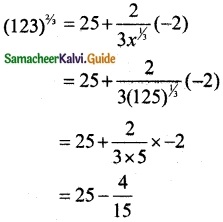
= 25 – 0.2666
(123)^2/3 = 24.7334

(ii) \(\sqrt[4] { 15 }\) = (15)^1/4
f(x) = x^1/4, f(x₀) = (16)^1/4 = 2
We know that
f(x₀ + Δx) = f(x₀) + f’(x₀) Δx

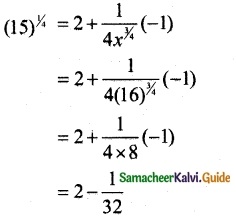
= 2 – 0.03125
(15)^1/4 = 1.96875

(iii) (26)^1/3
f(x) = x^1/3, f(x₀) = (27)^1/3 = 2, Δx = -1
We know that
f(x₀ + Δx) = f(x₀) + f’(x₀) Δx

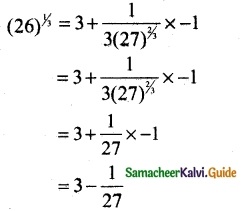
= 3 – 0.370
(26)^1/3 = 2.963

Question 3.
Find a linear approximation for the following functions at the indicated points
(i) f(x) = x³ – 5x + 12, x₀ = 2
(ii) g(x) = \(\sqrt { x^2+9 }\), x₀ = -4
(iii) h(x) = \(\frac { x }{ x+1 }\), x₀ = 1
Solution:
(i) We know that the linear approximation
L(x) = f(x₀) + f’(x₀)(x – x₀)
f(x) = x³ – 5x + 12
f'(x) = 3x² – 5
f'(x₀) = f'(2) = 12 – 5 = 7
f(x₀) = f(2) = 8 – 10 + 12 = 10
L(x) = 10 + 7 (x – 2)
= 10 + 7x – 14
= 7x – 4

(ii) g(x) = \(\sqrt { x^2+9 }\), x₀ = -4
g(x₀) = g(14) = \(\sqrt {16+9 }\) = 5

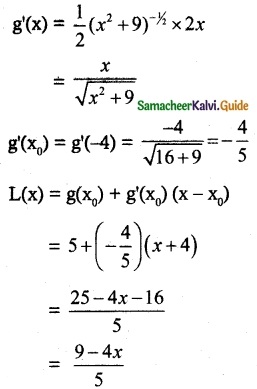
(iii) h(x) = \(\frac { x }{ x+1 }\), x₀ = 1

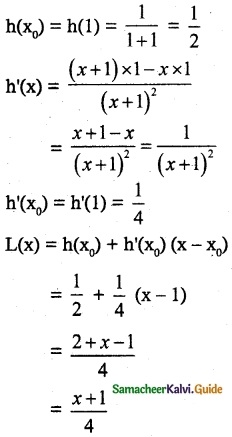
Question 4.
The radius of a circular plate is measured as 12.65. cm instead of the actual length 12.5 cm find the following in calculating the area of the circular plate:
(i) Absolute error
(ii) Relative error
(iii) Percentage error
Solution:
Actual radius of the circular plate = 12.5 cm
Measured radius of the circular plate = 12.65
dr = 12.65 – 12.5
= 0.15
A = π r²
dA = 2π r dv
Change in Area
A(12.65) – A(12.5) = dA
= 2π × 12.5 × 0.15
= 3.75 π
Exact calculation of the Area changes gives
A(12.65) – A(12.5) = π(12.65)² – π(12.5)²
= 160.0225 π – 156.25 π
= 3.7725 π
Absolute error = 3.7725 π – 3.75 π
= 0.0225 π cm²
Relative error
= \(\frac { 3.7725π-3.75π }{ 3.7725π }\)
= \(\frac { 0.0225π }{ 3.7725π }\)
= 0.00596
= 0.006 cm²
Percentage error = Relative error × 100
= 0.006 × 100
= 0.6% .

Question 5.
A sphere is made of ice having radius 10 cm. Its radius decreases from 10 cm to 9.8 cm. Find approximations for the following:
(i) Change in the volume.
(ii) Change in the surface area
Solution:
(i) Given r = 10
dr = 10 – 9.8 = 0.2
Volume v = \(\frac { 4 }{ 3 }\)πr³
dv = \(\frac { 4 }{ 3 }\).3πr²dv
Change in volume
v(10) – v(9.8) = 4π(10)²(0.2)
= 80π cm³

(ii) Surface area of the sphere
S(r) = 4πr²
S'(r) = 8πr
Change in surface area at r = 10 is
= S'(r) [10 – 9.8]
= 8π (10) (0.2) = 16π cm²
∴ Surface Area decreases by 16π cm²

Question 6.
The time T, taken for a complete oscillation of a single pendulum with length l, is given by the equation T = 2π\(\sqrt{\frac { l }{ g }}\) where g is a constant. Find the approximate percentage error in the calculated value of T corresponding to an error of 2 percent in the value of l.
Solution:
Given T = 2π\(\sqrt{\frac { l }{ g }}\)
On taking log both sides, we get
log T = log 2 + log π + \(\frac { 1 }{ 2 }\) log l – \(\frac { 1 }{ 2 }\) log g
On differentiating both sides w. r. to l, we get

So, the percentage error in T is 1%

Question 7.
Show that the percentage error in the nth root of a number is approximately \(\frac { 1 }{ n }\) times the percentage error in the number.
Solution:
Let x be the number
Let y = x^1/n
log y = \(\frac { 1 }{ n }\) log x
Taking differentiate on both sides, we have

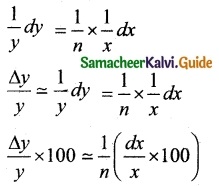
= \(\frac { 1 }{ n }\) times the percentage error in the number.