Prasanna

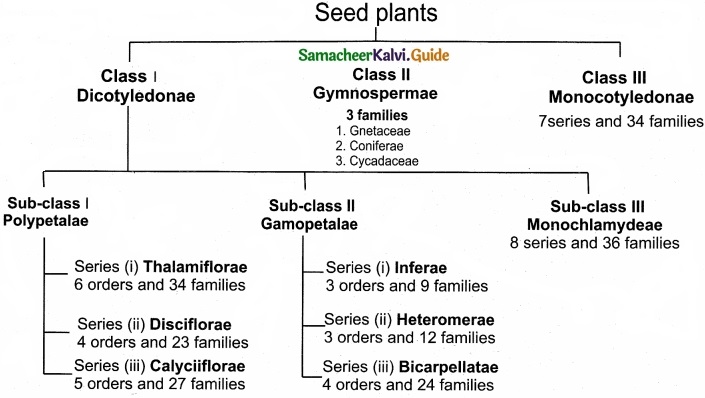
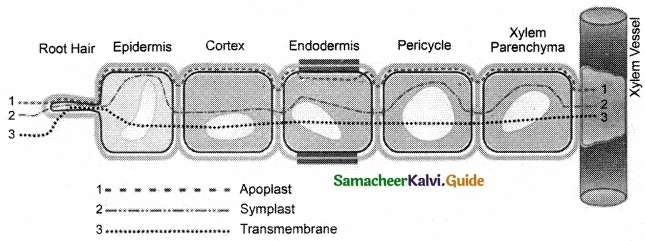
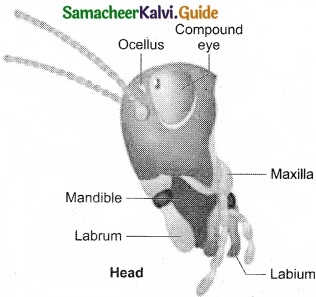
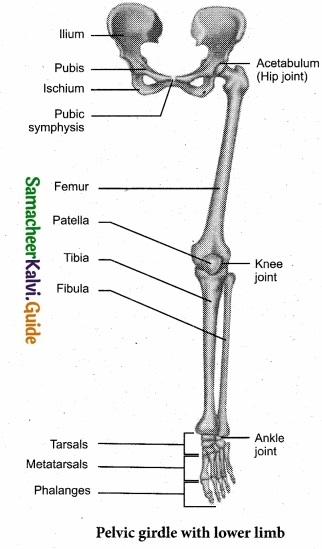
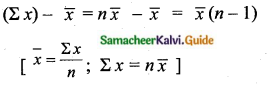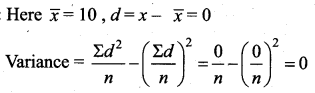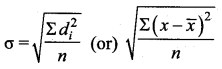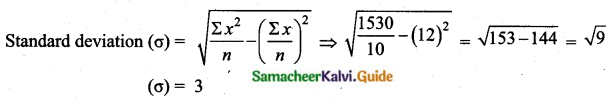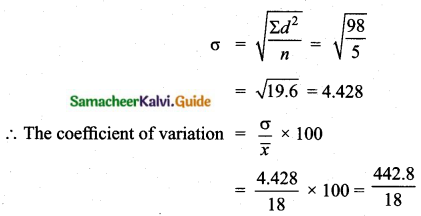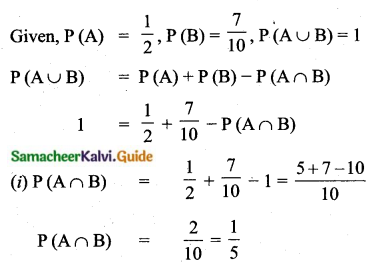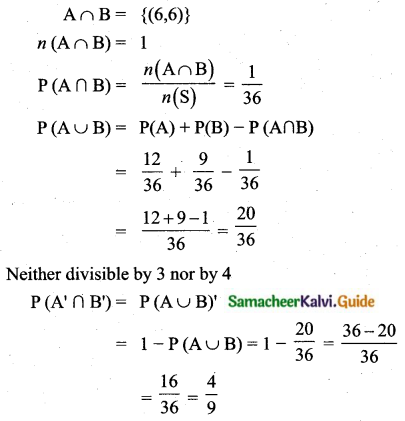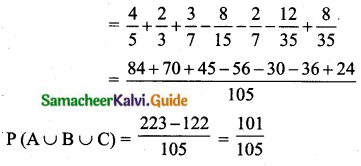Students can Download Tamil Nadu 11th Chemistry Model Question Paper 5 English Medium Pdf, Tamil Nadu 11th Chemistry Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

TN State Board 11th Chemistry Model Question Paper 5 English Medium

General Instructions:

1. The question paper comprises of four parts.
2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. All questions of Part I, II, III and IV are to be attempted separately.
4. Question numbers 1 to 15 in Part I are Multiple Choice Questions of one mark each.
   These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 16 to 24 in Part II are two-mark questions. These are to be answered in about one or two sentences.
6. Question numbers 25 to 33 in Part III are three-mark questions. These are to be answered in about three to five short sentences.
7. Question numbers 34 to 38 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.

Time: 2:30 Hours
Maximum Marks: 70

PART – 1

Answer all the Questions: [15 × 1 = 15]
Choose the most suitable answer from the given four alternatives.

Question 1.
The equivalent mass of ferrous oxalate is …………………….
(a)
(b)
(c)
(d) None of these
Solution:

n = 1 + 2(1) = 3
Answer:
(c)

Question 2.
Time independent Schnodinger wave equation is ………………….
(a) \(\widehat{\mathrm{H}} \psi=\mathrm{E} \psi\)
(b) \(\nabla^{2} \psi+\frac{8 \pi^{2} m}{h^{2}}(E+V) \psi=0\)
(c) \(\frac{\partial^{2} \Psi}{\partial x^{2}}+\frac{\partial^{2} \Psi}{\partial y^{2}}+\frac{\partial^{2} \Psi}{\partial z^{2}}+\frac{2 m}{h^{2}}(E-V) \psi=0\)
(d) All of these
Answer:
(a) \(\widehat{\mathrm{H}} \psi=\mathrm{E} \psi\)

Question 3.
Choose the incorrect statement.
(а) The chemical symbol of nickel is Ni.
(b) An element is a material made up of different kind of atoms.
(c) The physical state of bromine is liquid.
(d) The physical and chemical properties of the elements are periodic functions of their atomic numbers.
Answer:
(b) An element is a material made up of different kind of atoms.

Question 4.
Assertion: Permanent hardness of water is removed by treatment with washing soda.
Reason: Washing soda reacts with soluble calcium and magnesium chlorides and sulphates in hard water to form insoluble carbonates.
(a) Both assertion and reason are true and reason is the correct explanation of assertion.
(b) Both assertion and reason are true but reason is not the correct explanation of assertion.
(c) Assertion is true but reason is false
(d) Both assertion and reason are false
Solution:
Ca²⁺ + Na₂CO₃ → CaCO₃↓+ 2Na⁺
Answer:
(a) Both assertion and reason are true and reason is the correct explanation of assertion.

Question 5.
Match the following:

Answer:

Question 6.
Compressibility factor for CO₂ at 400 K and 71.0 bar is 0.8697. The molar volume of CO₂under these conditions is …………………………
(a) 22.04 dm³
(b) 2.24 dm³
(c) 0.41 dm³
(d) 19.5 dm³
Solution:
Compressibility factor (z) = \(\frac{PV}{nRT}\)
V = \(\frac{z × nRT}{p}\) = \(\frac{0.8697 \times 1 \times 8.314 \times 10^{-2} \mathrm{bar} \mathrm{dm}^{3} \mathrm{K}^{-1} \mathrm{mol}^{-1} \times 400 \mathrm{K}}{71 \mathrm{bar}}\)
V = 0.41 dm³
Answer:
(c) 0.41 dm³

Question 7.
Thermodynamics is applicable to …………………….
(a) Macroscopic system only
(b) Microscopic system only
(c) Homogenous system only
(d) Heterogeneous system only
Answer:
(a) Macroscopic system only

Question 8.
In the reaction, Fe(OH)₃ (s) ⇄ Fe³⁺ (aq) + 3OH^–(aq), if the concentration of OH^– ions is decreased by \(\frac{1}{4}\) times, then the equilibrium concentration of Fe³⁺ will …………………….
(a) Not changed
(b) Also decreased by \(\frac{1}{4}\) times
(c) Increase by 4 times
(d) Increase by 64 times
Solution:

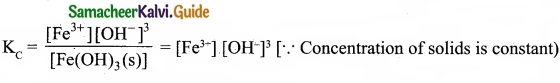
When concentration of OH^– ions declared by \(\frac{1}{4}\) times, then

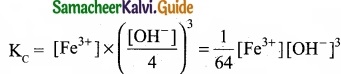
To maintain K_C as constant, concentration of Fe³⁺ will increase by 64 times.
Answer:
(d) Increase by 64 times

Question 9.
The degree of dissociation a is equal to ……………………
(a) \(\frac{i-1}{n-1}\)
(b) \(\frac{(1-i)n}{n-1}\)
(c) \(\frac{i+1}{n+1}\)
(d) \(\frac{(1+i)n}{n+1}\)
Answer:
(a) \(\frac{i-1}{n-1}\)

Question 10.
The molecules having same hybridisation, shape and number of lone pair of electrons are ………………………..
(a) SeF₄, XeO₂F₂
(b) SF₄, XeF₂
(c) XeOF₄, TeF₄
(d) SeCl₄, XeF₄
Solution:
SeF₄, XeO₂F₂ – sp³d hybridisation
T-shaped, one lone pair on central atom.
Answer:
(a) SeF₄, XeO₂F₂

Question 11.
Connect pair of compounds which give blue colouration/precipitate and white precipitate respectively, when their Lassaigne’s test is separately done.
(a) NH₂NH₂HCl and ClCH₂ – CHO
(b) NH₂CS NH₂ and CH₃ – CH₂Cl
(c) NH₂CH₂ COOH and NH₂ CONH₂
(d) C₆H₅NH₂ and ClCH₂ – CHO
Answer:
(d) C₆H₅NH₂ and ClCH₂ – CHO

Question 12.
4-hydroxy phenol oxidised in the presence of K₂Cr₂O₇?H⁺ to give, …………………….
(a) Quinol
(b) Quinone
(c) Diol
(d) Alkane
Answer:
(b) Quinone

Question 13.
Methane gas is also called as ……………………
(a) Marsh gas
(b) Mass gas
(c) Molecular gas
(d) Model gas
Answer:
(a) Marsh gas

Question 14.
The catalyst used in Darzen halogenation of alcohol is ……………………..
(a) CCl₄
(b) Acetone
(c) Pyridine
(d) Ethene
Answer:
(c) Pyridine

Question 15.
Identify the wrong statement in the following.
(a) The clean water would have a BOD value of more than 5 ppm
(b) Greenhouse effect is also called as Global warming
(c) Minute solid particles in air is known as particulate pollutants
(d) Biosphere is the protective blanket of gases surrounding the earth
Answer:
(a) The clean water would have a BOD value of more than 5 ppm

PART – II

Answer any six questions in which question No. 20 is compulsory. [6 × 2 = 12]

Question 16.
First ionization potential of C-atom is greater than that of B-atom, where as the reverse is true for second ionization potential?
Answer:
G (Z = 6) 1s² 2s² 2p_x‘ 2p_y‘. The electron removal from p orbital is very difficult. So carbon has highest first ionization potential.
B (Z = 5) 1s² 2s² 2p¹. In boron nuclear charge is less than that of carbon, so boron has lowest first ionization potential.
I.E₁ C > I.E₁B

But it is reverse in the case of second ionization energy. Because in case of B⁺ the electronic configuration is 1s² 2s², which is completely filled and it has high ionization energy. But in C⁺ the electronic configuration is 1s² 2s² 2p¹, one electron removal is easy so it has low ionization energy.

Question 17.
Why H₂O₂ is used as mild antiseptic?
Answer:
The oxidising property of hydrogen peroxide and harmless nature of its products such as water and oxygen, leads to oxidation of pollutants in water and act as a mild antiseptic.

Question 18.
An alkali metal (x) forms a hydrated sulphate, X₂SO₄.10H₂O. Is the metal more likely to be sodium (or) potassium?
Answer:
X forms X₂SO₄. 10H₂O. The metal is more likely be sodium. So X is Na₂SO₄. 10H₂O. It is otherwise called as Glauber’s salt.

Question 19.
Define Zeroth law of thermodynamics (or) Law of thermal equilibrium?
Answer:
Zeroth law of thermodynamics states that ‘If two systems at different temperatures are separately in thermal equilibrium with a third one, then they tend to be in thermal equilibrium with themselves’.

Question 20.
2.82 g of glucose is dissolved in 30 g of water. Calculate the mole fraction of glucose and water?
Solution:
Mass of glucose = 2.82 g
No. of moles of glucose = \(\frac{2.82}{180}\) = 0.016
Mass of water = 30g = \(\frac{20}{18}\) = 1.67
x_H2O = \(\frac{1.67}{1.67+0.016}\) = \(\frac{1.67}{1.686}\) = 0.99
∴x_H2O + xx_glucose = 1
0.99 + x_glucose = 1
x_glucose = 1 – 0.99 = 0.01

Question 21.
Considering x-axis as molecular axis, which out of the following will form a sigma bond.

1. 1s and 2p_y
2. 2p_x and 2p_x
3. 2p_x and 2p_y
4. 1s and 2p_z

Answer:
Along X-axis as molecular axis, only 2p_x and 2p_y can form a sigma bond

2p_x + 2p_y and 1s and 2p₂ also cannot form σ bond.

Question 22.
What happen when nitrile undergoes acid hydrolysis?
Answer:
When alkyl nitrile undergoes acid hydrolysis to give amide, which on further hydrolysis to give carboxylic acid.

Question 23.
How ozone reacts with 2-methyl propene?
Answer:

Question 24.
What are Freons? Discuss their uses and environmental effects?
Answer:
Freons are the chlorofluoro derivatives of methane and ethane.
Freon is represented as Freon – cba
Where, c – number of carbon atoms, b = number of hydrogen atoms,
a = total number of fluorine atoms.

Uses of Freons:

1. Freons are used as refrigerants in refrigerators and air conditioners.
2. It is used as a propellant for aerosols and foams.
3. It is used as propellant for foams, to spray out deodorants, shaving creams and insecticides.

Environmental effects of Freons:

1. Freon gas is a very powerful greenhouse gas which means that it traps the heat normally radiated from the earth out into the space. This causes the earth’s temperature to increase, resulting in rising sea levels, droughts, stronger storms, flash floods and a host of other very unpleasant effect. ,

2. As freon moves throughout the air, its chemical ingredients causes depletion of ozone layer. Depletion of ozone increases the amount of ultraviolet radiations that reaches the earths surface, resulting in serious risk to human health. High levels of ozone, in turn, causes respiratory problems and can also kill plants.

PART – III

Answer any six questions in which question No. 26 is compulsory. [6 × 3 = 18]

Question 25.
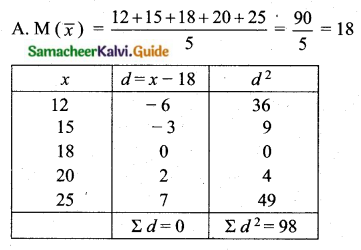
The first ionisation energy (IE₁) and second ionisation energy (IE₂) of elements X, Y and Z are given below.

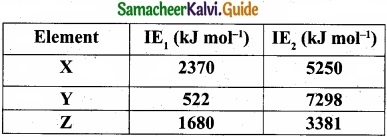
Which one of the above elements is the most reactive metal, the least reactive metal and a noble gas?
Answer:
Noble gases: Ioniation energy ranging from 2372 KJ mol^-1 to 1037 kJ mol^-1.
For element X, the IE₁, value is in the range of noble gas, moreover for this element both IE₁ and IE₂ are higher and hence X is the noble gas.

For Y, the first ionisation energy is low and second ionisation energy is very high and hence Y is most reactive metal.
For Z, both IE₁ and IE₂ are higher and hence it is least reactive.

Question 26.
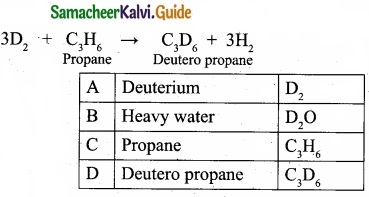
An isotope of hydrogen (A) reacts with diatomic molecule of element which occupies group number 16 and period number 2 to give compound (B) is used as a modulator in nuclear reaction. (A) adds on to a compound (C), which has the molecular formula C₃H₆ to give (D). Identify A, B, C and D?
Answer:
(I) An isotope of hydrogen Deuterium (A) reacts with diatomic molecule of element belongs to group number 16 and period number 2 oxygen O₂ to give a compound (B) which is heavy water D₂O. D₂O is used as a moderator in nuclear reaction:

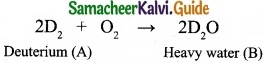
(II) Deuterium reacts with C₃H₆ propane (C) to give Deutero propane C₂D₆ (D).

Question 27.
Give the uses of gypsum?
Answer:

1. The Alabaster variety qf gypsum was used by the sculptors.
2. Gypsum is used in making drywalls or plaster boards.
3. Gypsum is used in the production of Plaster of Paris, which is used as a sculpting material.
4. Gypsum is used in making surgical and orthopedic casts.
5. It plays an important role in agriculture as a soil additive, conditioner and fertilizer.
6. Gypsum is used in toothpaste, shampoo and hair products.
7. Calcium sulphate acts as a coagulator in making tofu.
8. It is also used in baking as a dough conditioner.
9. Gypsum is a component of Portland cement, where it acts as a hardening retarder to control the speed at which concrete sets.
10. Gypsum is used to give colour to cosmetics and drugs.
11. Gypsum plays a very important role in wine making.

Question 28.
Define inversion temperature?
Answer:
The temperature below which a gas obey Joule-Thomson effect is called inversion temperature (T_i).
T_i = \(\frac{2a}{2Rb}\)

Question 29.
The vapour pressure of pure benzene (C₆H₆) at a given temperature is 640 mm Hg. 2.2g , of non-volatile solute is added to 40 g of benzene. The vapour pressure of the solution is 600 mm Hg. Calculate the molar mass of the solute?
Answer:

Question 30.
In CH₄, NH₃ and H₂O, the central atom undergoes sp³ hybridisation-yet their bond angles are different, why?
Answer:

1. In CH₄, NH₃ and H₂O the central atom undergoes sp³ hybridisation. But their bond angles are different due to .the presence of lone pair of electrons.
2. It can be explained by VSEPR theory. According to this theory, even though the hybridisation is same, the repulsive force between the bond pairs and lone pairs are not same.
3. Bond pair – Bond pair < Bond pair – Lone pair < Lone pair -Lone pair
   So due to the varying repulsive force the bond pairs and lone pairs are distorted from regular geometry and organise themselves in such a way that repulsion will be minimum and stability will be maximum.
4. In case of CH₄, there are 4 bond pairs and no lone pair of electrons. So it remains in its regular geometry, i.e., tetrahedral with bond angle = 109° 28’.
5. H₂O has 2 bond pairs and 2 lone pairs. There is large repulsion between lp – lp. Again repulsion between lp – bp is more than that of 2 bond pairs. So 2 bonds are more restricted to form inverted V shape (eg;) bent shape molecule with a bond angle of 104° 35.
6. NH₃ has 3 bond pairs and 1 lone pair. There is repulsion between lp – bp. So 3 bonds are. more restricted to form pyramidal shape with bond angle equal to 107° 18’.

Question 31.
How does hyper conjugation effect explain the stability of alkenes?
Answer:

1. The relative stability of various classes of carbonium ions may be explained by the number of no bond resonance structures that can be written for them.
2. Such structures are arrived by shifting the bonding electrons from an adjacent C – H bond to the electron deficient carbon.
3. In this way, the positive charge originally on carbon is dispersed to the hydrogen. This manner of electron release by assuming no bond character in the adjacent C – H bond is called hyper conjugation or Baker – Nathan effect.
4. The greater the hyper conjugation, the greater will be the stability of the compound.
   The increasing order of stability can be shown as:

5. Alkyl group increases in the C = C double bond carbon, hyper conjugation increases and stability of that organic compound also increases.

Question 32.
What is BHC? How will you prepare BHC? Mention its uses?
Answer:

1. BHC is Benzene hexachloride.

2. Benzene reacts with three molecule of Cl₂ in the presence of sunlight or UV light to yield BHC. This is also called as gammaxane or Lindane.

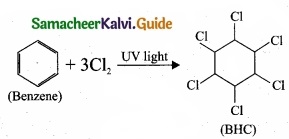
3. BHC is a powerful insecticide.

Question 33.
Write a chemical reaction useful to prepare the following:

1. Freon-12 from carbon tetrachloride.
2. Carbon tetrachloride from carbon disulphide.

Answer:
1. Freon – 12 from carbon tetrachloride:
Freon – 12 is prepared by the action of hydrogen fluoride on carbon tetrachloride in the presence of catalytic amount of antimony pentachloride. This reaction is called “Swarts reaction.”

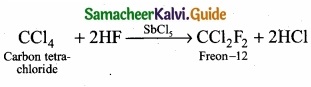
2. Carbon tetrachloride from carbon disulphide:
Carbon disulphide reacts with chlorine gas in the presence of anhydrous AlCl₃ as catalyst to give carbon tetrachloride.

PART – IV

Answer all the questions. [5 × 5 = 25]

Question 34 (a).
(I) What is the difference between molecular mass and molar mass? Calculate the molecular mass and molar mass for carbon monoxide.
(II) What are competitive electron transfer reaction? Give example.

[OR]

(b) (I) State the trends in the variation of electronegativity in period and group.
(II) The electron gain enthalpy of chlorine is 348 kJ mol^-1. How much energy in kJ is released when 17.5 g of chlorine is completely converted into Cl^– ions in the gaseous state?
Answer:
(a) (I) Molecular mass:

1. Relative molecular mass is defined as the ratio of the mass of the molecule to the unified atomic mass unit.
2. It can be calculated by adding the relative atomic masses of its constituent atoms.
3. For carbon monoxide (CO)

Molecular mass = Atomic mass of carbon + Atomic mass of oxygen 12 + 16 = 28 u.

Molar mass:

1. It is defined as the mass of one mole of a substance.
2. The molar mass of a compound is equal to the sum of the relative atomic masses of its constituent expressed in g mol^-1.
3. For carbon monoxide (CO)

12 + 16 = 28 g mol^-1.

Both molecular mass and molar mass are numerically same but the units are different.

(II) These are the reactions in which redox reactions take place in different vessels and it is an indirect redox reaction. There is a competition for the release of electrons among different metals.

Example:
Zn releases electrons to Cu and Cu releases electrons to Silver and so on.
Zn_(s) + Cu²⁺ → Zn²⁺_(aq) + Cu_(s) (Here Zn – oxidised; Cu²⁺ – reduced)
Cu_(s) + 2Ag⁺ → Cu²⁺_(aq) + 2Ag_(s) (Here Cu – oxidised; Ag⁺ – reduced)

[OR]

(b)
(I) Variation of electronegativity in a period:
The electronegativity increases across a period from left to right. Since the atomic radius decreases in a period, the attraction between the valence electron and the nucleus increases. Hence the tendency to attract shared pair of electrons increases, ‘therefore, electronegativity increases in a period.

(II) Water is amphoteric in nature and it behaves both as an acid as well as base. With acids stronger than itself (e.g., H₂S) it behaves as a base and with bases stronger than itself (e.g., NH, ) it acts as an acid.

Question 35 (a).
(I) Discuss the three types of Covalent hydrides?
(II) Write the chemical reactions to show the amphoteric nature of water?

[OR]

(b)
(I) Lithium forms monoxide with oxygen whereas sodium forms peroxide with oxygen. Why?
(II) Write about the uses of strontium?
Answer:
(a) (I)

1. They are the compounds in which hydrogen is attached to another element by sharing of electrons.
2. The most common examples of covalent hydrides are methane, ammonia, waterand hydrogen chloride.
3. Molecular hydrides of hydrogen are further classified into three categories as,
   • Electron precise (CH₄, C₂H₆, SiH₄, GeH₄)
   • Electron-deficient (B₂H₆) and
   • Electron-rich hydrides (NH₃, H₂O)
4. Since most of the covalent hydrides consist of discrete, small molecules that have relatively weak intermolecular forces, they are generally gases or volatile liquids.

(II) Water is amphotenc in nature and it behaves both as an acid as well as base. With acids stronger than itself (e.g., H₂S) it behaves as a base and with bases stronger than itself
(e.g., NH₃) it acts as an acid.

1. As a base: H₂O_(l) + H₂S_(aq) → H₃O_(aq) – HS^–_(aq)
2. As a acid: H₂O_(l) + NH_3(aq) → OH^–_(aq) + NH⁺_(aq)

[OR]

(b) (I)

1. The fact that a small cation can stabilize a small anion and a large cation can stabilize a large anion explains the formation and stability of the oxides.
2. The size of Li⁺ ion is very small and it has a strong positive field around it. It can combine . with only small anion, O^2- ion, resulting in the formation of monoxide Li₂O.
3. The Na⁺ ion is a larger cation and has a weak positive field around it and can stabilize a bigger peroxide ion, \(\mathrm{O}_{2}^{2-} \text { or }[-\mathrm{O}-\mathrm{O}-]^{2-}\) resulting in the formation of peroxide Na₂O₂.

(II)

1. 90Sr is used in cancer therapy.
2. \(^{87} \mathrm{Sr} /^{86} \mathrm{Sr}\) ratio is used in marine investigators as well as in teeth, tracking animal migrations or in criminal forensics.
3. Dating of rocks.
4. Strontium is used as a radioactive tracer in determining the ‘source of archaeological materials ’ such as timbers and coins.

Question 36 (a).
(I) When the driver of an automobile applies brake, the passengers are pushed toward the front of the car but a helium balloon is pushed toward back of the car. Upon forward acceleration the passengers are pushed toward the front of the car. Why?
(II) Critical temperature of H₂O, NH₃ and CO₂ are 647.4, 405.5 and 304.2 K, respectively. When we start cooling from a temperature of 700 K which will liquefy first and which will liquefy finally?

[OR]

(b)
(I) The following water gas shift reaction is an important industrial process for the production of hydrogen gas.
C0(g) + H₂O(g) ⇄ CO₂(g) + H₂(g)
At a given temperature K_p = 2.7. If 0.13 mol of CO, 0.56 mol of water, 0.78 mol of CO₂ and 0.28 mol of H₂ are introduced into a 2L flask, find out in which direction must the reaction proceed to reach equilibrium.

(II)
2H₂O(g) ⇄ 2H₂(g) + O₂(g) K_C = 4.1 × 10^-48 At 599 K
N₂(g) + O₂(g) ⇄ 2NO(g) K_C = 1 × 10^-30 at 1000 K
Predict the extent of the above two reactions.
Answer:
(a) (I)
1. When the driver of an automobile applies brake, the passengers are pushed toward the front of the car due to inertia of the body, but a helium balloon pushed toward back of the car. Helium balloon responds to the air around it. Helium molecules are lighter than air of our atmosphere, and so they move toward back by gravity as a result of the accelerating frame.

2. Upon forward acceleration, the passengers are pushed toward the front of the car,because the body in motion tends to stay in motion until acted upon by an outside force. Helium balloon is going to move opposite to this pseudo gravitational force.

(II) Critical temperature of a gas is defined as the temperature above which it cannot be liquefied even at high pressures.
∴ When cooling starts from 700 K, H₂O will liquefied first, then followed by ammonia and finally carbon dioxide will liquefied.

[OR]

(b) (I)
CO(g) + H₂O(g) ⇄ CO₂(g) + H₂(g)
Give K_P = 2.7
[CO] = 0.13 mol, [H₂O] = 0.56 mol
[CO₂] = 0.78 mol; [H₂] = 0.28 mol
V = 2L
K_P = K_C (RT)^∆ng
2.7 = K_C (RT)⁰
K_C = 2.7
_QC = \(\frac{\left[\mathrm{CO}_{2}\right]\left[\mathrm{H}_{2}\right]}{[\mathrm{CO}]\left[\mathrm{H}_{2} \mathrm{O}\right]}\) = \(\frac{\left(\frac{0.78}{2}\right)\left(\frac{0.28}{2}\right)}{\left(\frac{0.13}{2}\right)\left(\frac{0.56}{2}\right)}\)
Q = 3
Q > K_C, Hence the reaction proceed in the reverse direction.

(II) In the reactions, decomposition of water at 500 K and oxidation of nitrogen at 1000 K, the value of K_C is very less K_C < 10^-3. So reverse reaction is favoured.
∴ Products << reactants

Question 37 (a).
(I) CuCl is more covalent than NaCl. Give reason?
(II) Draw and explain the molecular orbital diagram of Boron molecule?

[OR]

(b)
(I) 0.30 g of a substance gives 0.88 g of carbon dioxide and 0.54 g of water.
Calculate the percentage of carbon and hydrogen in it.

(II) Draw the fisher projection formula for tartaric acid.
Answer:
(a) (I)
1. Cations having ns² np⁶ nd¹⁰ configuration show greater polarising power than the cations with ns² np⁶ configuration. Hence they show greater covalent character.
2. CuCl is more covalent than NaCl. As compared to Na⁺ (1.13\(\overset { \circ }{ A } \)), Cu⁺ (0.6\(\overset { \circ }{ A } \)) is small and has 3s23p63d10 configuration.
3. Electronic configuration of Cu⁺: [Ar] 3s²3p⁶3d¹⁰
Electronic configuration of Na+: [He] 2s²2p⁶
So CuCl is more covalent than NaCl.

(II)

1. Electronic configuration of B = 1s² 2s² 2p³
2. Electronic configuration of B₂ = \(\sigma 1 s^{2} \sigma^{*} 1 s^{2} \sigma 2 s^{2} \sigma^{*} 2 s^{2} \pi 2 p_{x}^{1} \pi 2 p_{z}^{1}\)
3. Bond order = \(\frac { N_{ b }-N_{ a } }{ 2 } \) = \(\frac{6-4}{2}\) = 1
4. B₂ molecule has two unpaired electrons hence it is paramagnetic.

[OR]

(b) (I) Weight of organic compound = 0.30 g
Weight of carbon-dioxide = 0.88 g
Weight of water = 0.54 g

Percentage of hydrogen:
18 g of water contains 2 g of hydrogen
∴ 0.54 g of water contain = \(\frac{2}{18}\) × 0.54g of hydrogen
∴% of hydrogen = \(\frac{2}{18}\) × \(\frac{0.54}{0.30}\) × 100 = \(\frac{2}{18}\) × \(\frac{54}{0.3}\)
% of H = 0.111 × 180 = 19.888 ~ 20%

Percentage of carbon:
44 g of water contains 12 g of hydrogen
0.88 g of water contain CO₂ contains = \(\frac{12}{44}\) × 0.88g of hydrogen
∴ % of carbon = \(\frac{12}{44}\) × \(\frac{0.88}{0.30}\) × 100 = \(\frac{12}{44}\) × \(\frac{88}{0.3}\) = \(\frac{24}{0.3}\)
% of carbon = 80%

(II)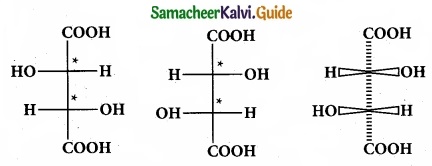

Question 38 (a).
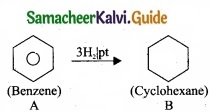
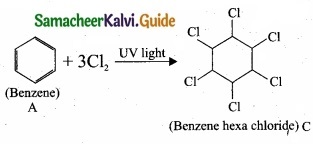
An organic compound (A) of a molecular formula C₆H₆ which is a simple aromatic hydrocarbon. A undergoes hydrogenation to give a cyclic compound (B). A reacts with chlorine in the presence of UV – light to give C which is used as insecticide. Identify A, B and C. Explain the reactions with equation.

[OR]

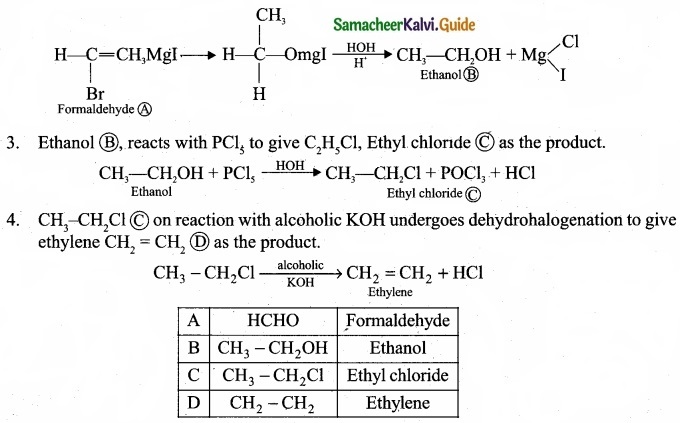
(b) An organic compound (A) of molecular formula CH₂ reacts with methyl magnesium iodide followed by acid hydrolysis to give (B) of molecular formula C₂H₆O. (B) on reaction with PCl gives (C).(C) on reaction with alcoholic KOH gives (D) an alkene as the product. Identify (A), (B), (C), (D) and explain the reactions involved.
Answer:

1. Simple aromatic hydrocarbon, C₆H₆ is benzene.
2. Benzene (A) reacts with H₂ in the presence of Pt to give cyclohexane (B).

3. Benzene (A) reacts with Cl₂ in presence of UV-light to give benzene hexachloride (C).

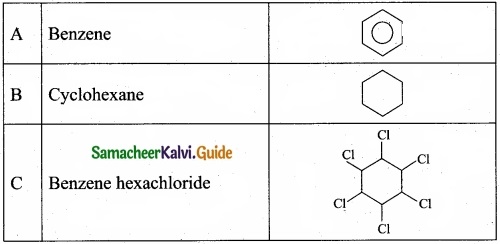
[OR]

(b) (I)
1. (A) Of molecular formula CH₂O is identified as HCHO, formaldehyde.
2. Formaldehyde reacts with CH₃MgI followed by hydrolysis to give ethanol, CH₃-CH₂OH B as the product.

Students can download Maths Chapter 8 Statistics and Probability Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 8 Statistics and Probability Additional Questions

I. Multiple Choice Questions

Question 1.
The range of the first 10 prime numbers 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 is ______
(1) 28
(2) 26
(3) 29
(4) 27
Answer:
(4) 27
Hint:
Range = Largest value – Smallest value = 29 – 2 = 27

Question 2.
The least value in a collection of data is 14.1. If the range of the collection is 28.4, then the greatest value of the collection is _______
(1) 42.5
(2) 43.5
(3) 42.4
(4) 42.1
Answer:
(1) 42.5
Hint:
Given, S = 14.1; R = 28.4,
L = S + R = 28.4 + 14.1 = 42.5

Question 3.
The greatest value of a collection of data is 72 and the least value is 28. Then the coefficient of range is ______
(1) 44
(2) 0.72
(3) 0.44
(4) 0.28
Answer:
(3) 0.44
Hint:
Coefficient of range = \(\frac{L-S}{L+S}\)
= \(\frac{72-28}{72+28}=\frac{44}{100}\)
= 0.44

Question 4.
For a collection of 11 items, Σx = 132, then the arithmetic mean is _______
(1) 11
(2) 12
(3) 14
(4) 13
Answer:
(2) 12
Hint:
\(\bar{x}=\frac{\Sigma x}{n}=\frac{132}{11}=12\)

Question 5.
For any collection of n items, Σ(x – \(\bar{x}\)) = _____
(1) Σx
(2) \(\bar{x}\)
(3) n\(\bar{x}\)
(4) 0
Answer:
(4) 0
Hint:
We know that, For all collection of n items,
Σ(x – \(\bar{x}\)) = 0

Question 6.
For any collection of n items, (Σx) – \(\bar{x}\) = ________
(1) n\(\bar{x}\)
(2) (n – 2)\(\bar{x}\)
(3) (n – 1)\(\bar{x}\)
(4) 0
Answer:
(3) (n – 1)\(\bar{x}\)
Hint:

Question 7.
If t is the standard deviation of x, y, z, then the standard deviation of x + 5, y + 5, z + 5 is _______
(1) \(\frac{t}{3}\)
(2) t + 5
(3) t
(4) xyz
Answer:
(3) t
Hint:
The S.D. of distribution remains unchanged when each value is added or subtracted by the same quantity.

Question 8.
If the standard deviation of a set of data is 1.6, then the variance is _______
(1) 0.4
(2) 2.56
(3) 1.96
(4) 0.04
Answer:
(2) 2.56
Hint:
Variance = (S.D.)² = (1.6)² = 2.56

Question 9.
If the variance of a data is 12.25, then the S.D is _______
(1) 3.5
(2) 3
(3) 2.5
(4) 3.25
Answer:
(1) 3.5
Hint:
S.D = √Variance = √12.25 = 3.5

Question 10.
Variance of the first 11 natural numbers is ______
(1) √5
(2) √10
(3) 5√2
(4) 10
Answer:
(4) 10
Hint:
Variance = \(\frac{n^{2}-1}{12}=\frac{11^{2}-1}{12}=\frac{120}{12}=10\)

Question 11.
The variance of 10, 10, 10, 10, 10 is _______
(1) 10
(2) √10
(3) 5
(4) 0
Answer:
(4) 0
Hint:

Question 12.
If the variance of 14, 18, 22, 26, 30 is 32, then the variance of 28, 36, 44, 52, 60 is _______
(1) 64
(2) 128
(3) 32√2
(4) 32
Answer:
(2) 128
Hint:
Variance of the given numbers = 32;
S.D. = √32 = 4√2
Each data is multiplied by 2.
New S.D.= 4√2 × 2 = 8√2
Variance = (8√2)² = 128

Question 13.
The standard deviation of a collection of data is 2√2. If each value is multiplied by 3, then the standard deviation of the new data is ______
(1) √12
(2) 4√2
(3) 6√2
(4) 9√2
Answer:
(3) 6√2
Hint:
Given, S.D. = 2√2
Each value is multiplied by 3
New S.D. = 2√2 × 3 = 6√2

Question 14.
Given Σ(x – \(\bar{x}\))2 = 48, \(\bar{x}\) = 20 and n = 12. The coefficient of variation is ______
(1) 25
(2) 20
(3) 30
(4) 10
Answer:
(4) 10
Hint:

Question 15.
Mean and standard deviation of a data are 48 and 12 respectively. The coefficient of variation is _______
(1) 42
(2) 25
(3) 28
(4) 48
Answer:
(2) 25
Hint:
Coefficient of variation
C.V = \(\frac{\sigma}{\bar{x}} \times 100\) = \(\frac{12}{48} \times 100\) = 25

Question 16.
If Φ is an impossible event, then P(Φ) = ______
(1) 1
(2) \(\frac{1}{4}\)
(3) 0
(4) \(\frac{1}{2}\)
Answer:
(3) 0
Hint:
Probability of an impossible event is 0.

Question 17.
If S is the sample space of a random experiment, then P(S) = _______
(1) 0
(2) \(\frac{1}{8}\)
(3) \(\frac{1}{2}\)
(4) 1
Answer:
(4) 1
Hint:
Every event is a subset of S. Sample space contain all the possible element.
P(S) = 1

Question 18.
If p is the probability of an event A, then p satisfies _______
(1) 0 < p < 1
(2) 0 < p < 1
(3) 0 < p < 1
(4) 0 < p < 1
Answer:
(2) 0 < p < 1
Hint:
The Probability of an event is always greater than 0 and less than or equal to 1.

Question 19.
Let A and B be any two events and S be the corresponding sample space. Then P (\(\bar{A}\) ∩ B) = ______

(1) P(B) – P(A ∩ B)
(2) P(A ∩ B) – P(B)
(3) P(S)
(4) P[(A ∪ B)’]
Answer:
(1) P(B) – P(A ∩ B)
Hint:
P(\(\bar{A}\) ∩ B) means only B and not A

Question 20.
The probability that a student will score centum in mathematics is \(\frac{4}{5}\). The probability that he will not score centum is ______
(1) \(\frac{1}{5}\)
(2) \(\frac{2}{5}\)
(3) \(\frac{3}{5}\)
(4) \(\frac{4}{5}\)
Answer:
(1) \(\frac{1}{5}\)
Hint:
P(\(\bar{A}\)) = 1 – P(A) = 1 – \(\frac{4}{5}\) = \(\frac{1}{5}\)

Question 21.
If A and B are two events such that P(A) = 0.25, P(B) = 0.05 and P(A ∩ B) = 0.14, then P(A ∪ B) = _____
(1) 0.61
(2) 0.16
(3) 0.14
(4) 0.6
Answer:
(2) 0.16
Hint:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 0.25 + 0.05 – 0.14 = 0.16

Question 22.
There are 6 defective items in a sample of 20 items. One item is drawn at random. The that it is probability a non-defective item is ________
(1) \(\frac{1}{10}\)
(2) 0
(3) \(\frac{3}{10}\)
(4) \(\frac{2}{3}\)
Answer:
(1) \(\frac{1}{10}\)
Hint:
Non-defective item = 20 – 6 = 14
Probability of non-defective items = \(\frac{14}{20}\) = \(\frac{7}{10}\)

Question 23.
If A and B are mutually exclusive events and S is the sample space such that P(A) = \(\frac{1}{3}\) P(B) and S = A ∪ B, then P(A) = _____
(1) \(\frac{1}{4}\)
(2) \(\frac{1}{2}\)
(3) \(\frac{3}{4}\)
(4) \(\frac{3}{8}\)
Answer:
(1) \(\frac{1}{4}\)
Hint:
P(A) = \(\frac{1}{3}\) P(B)
P(B) = 3 P(A)
P(A ∪ B) = P(A) + P(B)
[A and B are mutually exclusive]
P(A ∪ B) = P(A) + 3 P(A)
1 = 4P(A) [But P(A ∪ B) = 1]
P(A) = \(\frac{1}{4}\)

Question 24.
The probabilities of three mutually exclusive events A, B and C are given by \(\frac{1}{3}\), \(\frac{1}{4}\) and \(\frac{5}{12}\). Then P(A ∪ B ∪ C) is _______
(1) \(\frac{19}{12}\)
(2) \(\frac{11}{12}\)
(3) \(\frac{7}{12}\)
(4) 1
Answer:
(4) 1
Hint:
P (A ∪ B ∪ C) = P(A) + P(B) + P(C)
\(\frac{1}{3}+\frac{1}{4}=\frac{5}{12}=\frac{4+3+5}{12}=\frac{12}{12}=1\)

Question 25.
If P(A) = 0.25, P(B) = 0.50, P(A ∩ B) = 0.14 then P(neither A nor B) = ______
(1) 0.39
(2) 0.25
(3) 0.11
(4) 0.24
Answer:
(1) 0.39
Hint:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.25 + 0.50 – 0.14
= 0.61
P (neither A nor B) = P(\(\bar{A}\) ∩ \(\bar{B}\))
= 1 – P(A ∪ B)
= 1 – 0.61
= 0.39

Question 26.
A bag contains 5 black balls, 4 white balls and 3 red balls. If a ball is selected at random, the probability that it is not red is _______
(1) \(\frac{5}{12}\)
(2) \(\frac{4}{12}\)
(3) \(\frac{3}{12}\)
(4) \(\frac{3}{4}\)
Answer:
(4) \(\frac{3}{4}\)
Hint:
P(\(\bar{R}\)) = 1 – P(R)
\(=1-\frac{3}{12}=\frac{9}{12}=\frac{3}{4}\)

Question 27.
Two dice are thrown simultaneously. The probability of getting a doublet is ________
(1) \(\frac{1}{36}\)
(2) \(\frac{1}{3}\)
(3) \(\frac{1}{6}\)
(4) \(\frac{2}{3}\)
Answer:
(3) \(\frac{1}{6}\)
Hint:
n(S) = 36
Let A be the event of getting a doublet
A = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
n(A) = 6
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{6}{36}=\frac{1}{6}\)

Question 28.
A fair die is thrown once. The probability of getting a prime or composite number is _______
(1) 1
(2) 0
(3) \(\frac{5}{6}\)
(4) \(\frac{1}{6}\)
Answer:
(3) \(\frac{5}{6}\)
Hint:
S = {1, 2, 3, 4, 5, 6}
n(S) = 6
The required probability = \(\frac{5}{6}\)
[Science is neither prime not a composite number]

Question 29.
Probability of getting 3 heads or 3 tails in tossing a coin 3 times is _______
(1) \(\frac{1}{8}\)
(2) \(\frac{1}{4}\)
(3) \(\frac{3}{8}\)
(4) \(\frac{1}{2}\)
Answer:
(2) \(\frac{1}{4}\)
Hint:
S= {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
n(S) = 8
A = {HHH, TTT}; n(A) = 2
The required probability = \(\frac{2}{8}\) = \(\frac{1}{4}\)

Question 30.
A card is drawn from a pack of 52 cards at random. The probability of getting neither an ace nor a king card is _____
(1) \(\frac{2}{13}\)
(2) \(\frac{11}{13}\)
(3) \(\frac{4}{13}\)
(4) \(\frac{8}{13}\)
Answer:
(2) \(\frac{11}{13}\)
Hint:
n(S) = 52
Number of ace cards = 4
number of king cards = 4
n(non-ace and non-king cards) = 52 – 8 = 44
P(neither an ace nor a king) = \(\frac{44}{52}\) = \(\frac{11}{13}\)

Question 31.
The probability that a leap year will have 53 Fridays or 53 Saturdays is ______
(1) \(\frac{2}{7}\)
(2) \(\frac{1}{7}\)
(3) \(\frac{4}{7}\)
(4) \(\frac{3}{7}\)
Answer:
(4) \(\frac{3}{7}\)
Hint:
Leap year contains 52 weeks and 2 days
Sample space = {(sun, mon), (mon, tue), (tue, wed), (wed, thu), (thu, fri), (fri, sat), (sat, sun)}
n(S) = 7
The required probability = \(\frac{2}{7}+\frac{2}{7}-\frac{1}{7}=\frac{3}{7}\)

Question 32.
The probability that a non-leap year will have 53 Sundays and 53 Mondays is ________
(1) \(\frac{1}{7}\)
(2) \(\frac{2}{7}\)
(3) \(\frac{3}{7}\)
(4) 0
Answer:
(4) 0
Hint:
Non leap year contains 52 weeks and one day
Sample space (S) = {Sun, Mon, Tue, Wed, Thu, Fri, Sat}
n(S) = 7
The required probability = \(\frac{1}{7}+\frac{1}{7}-\frac{2}{7}\)
= \(\frac{2}{7}-\frac{2}{7}\)
= 0

Question 33.
The probability of selecting a queen of hearts when a card is drawn from a pack of 52 playing cards is ______
(1) \(\frac{1}{52}\)
(2) \(\frac{16}{52}\)
(3) \(\frac{1}{13}\)
(4) \(\frac{1}{26}\)
Answer:
(1) \(\frac{1}{52}\)
Hint:
n(S) = 52 [1 queen of hearts in 52 cards]
n(A) = 1
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{1}{52}\)

Question 34.
Probability of sure event is ______
(1) 1
(2) 0
(3) 100
(4) 0.1
Answer:
(1) 1

Question 35.
The outcome of a random experiment result in either success or failure. If the probability of success is twice the probability of failure, then the probability of success is ______
(1) \(\frac{1}{3}\)
(2) \(\frac{2}{3}\)
(3) 1
(4) 0
Answer:
(2) \(\frac{2}{3}\)
Hint:
n(A ∪ B) = 1; P(\(\bar{A}\)) = 1 – P(A)
Given P(A) = 2P(\(\bar{A}\))
P(A) = 2 [1 – P(A)] = 2 – 2 P(A)
3 P(A) = 2
P(A) = \(\frac{2}{3}\)

II. Answer the following questions.

Question 1.
Find the range and the coefficient of range of the following data.

Answer:
Largest value (L) = 690
Smallest value (S) = 610
Range R = L – S = 690 – 610 = 80
Coefficient of range = \(\frac{L-S}{L+S}=\frac{690-610}{690+610}=\frac{80}{1300}\) = 0. 06

Question 2.
Two dice are thrown simultaneously. What is the probability that
(i) 5 will not come up on either of them
(ii) 5 will come up at both dice
Answer:
S = {(1, 1)(1, 2)(1, 3)(1, 4)(1, 5)(1, 6), (2, 1)(2, 2)(2, 3)(2, 4)(2, 5)(2, 6), (3, 1)(3, 2)(3, 3)(3, 4)(3, 5)(3, 6), (4, 1)(4, 2)(4, 3)(4, 4)(4, 5)(4, 6), (5, 1)(5, 2)(5, 3)(5, 4)(5, 5)(5, 6), (6, 1)(6, 2)(6, 3)(6, 4)(6, 5)(6, 6)}
n(S) = 36
(i) Let A be the event of getting 5 on either of them.
A = {(1, 5) (2, 5) (3, 5) (4, 5) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) (6, 5)}
n(A) = 11
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{11}{36}\)
Probability that 5 will not come up on either of them = 1 – P (A)
\(=1-\frac{11}{36}=\frac{36-11}{36}=\frac{25}{36}\)
(ii) Let B be the event of getting 5 will come up at both dice
B = {(5, 5)}
n(B) = 1
P(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{1}{36}\)

Question 3.
The king, Queen and Jack of clubs are removed from a deck of 52 playing cards and the remaining cards are shuffled. A card is drawn from the remaining cards, find the probability of getting
(i) a card of clubs
(ii) a queen of diamond
Answer:
Sample space (S) = (52 – 3) = 49
n (S) = 49
(i) Let A be the event of getting a card of clubs.
n(A) = (13 – 3) = 10
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{10}{49}\)
(ii) Let B be the event of getting a queen of diamond
n(B) = 1
P(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{1}{49}\)

Question 4.
The standard deviation of 20 observations is √5. If each observation is multiplied by 2, find the standard deviation and variance of the resulting observations.
Answer:
Given a standard deviation of 20 observations = √5
Each observation is multiplied by 2 then,
New standard deviation = 2 × √5 = 2√5
New variance = (2√5)² = 20

Question 5.
Calculate the variance standard deviation of the following data 38, 40, 34, 31, 28, 26, 34.
Answer:
Arrange the given data in ascending order we get, 26, 28, 31, 34, 38, 40
Assumed mean = 34


Variance = 22
Standard deviation(σ) = √Variance = √22 = 4.69

Question 6.
Mean of 100 items is 48 and their standard deviation is 10. Find the sum of all the times and the sum of the squares of all items.
Answer:
The mean of 100 items = 48
The sum of 100 items (Σx) = 100 × 48 = 4800
standard deviation (σ²) = 10

Sum of the squares of all items (Σx²) = 240400

Question 7.
If n = 10, \(\bar{x}\) = 12 and Σx² = 1530, then calculate the coefficient of variation.
Answer:

Coefficient of variation = \(\frac{\sigma}{\bar{x}} \times 100 \Rightarrow \frac{3}{12} \times 100=25\)

Question 8.
If the coefficient of variation of a collection of data is 57 and its standard deviation is 6, 84, then find the mean.
Answer:
Given the coefficient of variation = 57
Standard deviation (σ) = 6.84

Arithmetic mean = \(\bar{x}\) = 12

Question 9.
Find the standard deviation and the variance of first 23 natural numbers?
Answer:
Standard deviation of first “n” natural numbers = \(\sqrt{\frac{n^{2}-1}{12}}\)
Standard deviation of first “23” natural numbers = \(\sqrt{\frac{23^{2}-1}{12}}\)
\(=\sqrt{\frac{529-1}{12}}=\sqrt{\frac{528}{12}}=\sqrt{44}\)
= 6.63

Question 10.
Find the coefficient of variation of the following data: 18, 20, 15, 12, 25.
Answer:
Let us calculate the A.M of the given data.


The coefficient of variation is 24.6

Question 11.
Three rotten eggs are mixed with 12 good ones. One egg is chosen at random. What is the probability of choosing a rotten egg?
Answer:
Number of good eggs = 12
Number of rotton eggs = 3
Total number of eggs = 12 + 3 = 15
Sample space n(S) = 15
Let A be the event of choosing a rotten egg
n(A) = 3
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{3}{15}=\frac{1}{5}\)
The Probability is \(\frac{1}{5}\)

Question 12.
Two coins are tossed together. What is the probability of getting at most one head?
Answer:
Sample space (S) = {(H, H), (H, T), (T, H), (T, T)}
n(S) = 4
Let A be the event of getting atmost one head
A = {HT, TH, TT}
n(A) = 3
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{3}{4}\)
The probability is \(\frac{3}{4}\)

Question 13.
A number is selected at random from integers 1 to 100. Find the probability that it is
(i) a perfect square
(ii) not a perfect cube.
Answer:
Sample space (S) = {1, 2, 3, …,100}
n(S) = 100
(i) Let A be the event of getting a perfect square.
A = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}
n(A) = 10
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{10}{100}=\frac{1}{10}\)
(ii) Let B be the event of getting a perfect cube.
B = {1, 8, 27, 64}
n(B) = 4
P(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{4}{100}=\frac{1}{25}\)
The Probability that the selected number is not a perfect cube is
P(\(\bar{B}\)) = 1 – P(B)
P(\(\bar{B}\)) = 1 – \(\frac{1}{25}\) = \(\frac{24}{25}\)

Question 14.
Three dice are thrown simultaneously. Find the probability of getting the same number on all the three dice.
Answer:
Sample space (S) = {(1, 1, 1) (1, 1, 2) (1, 1, 3) ….(6, 6, 6)}
n(S) = 63 = 216
Let A be the event of getting the same number on all the three dice.
A = {(1, 1, 1) (2, 2, 2) (3, 3, 3) (4, 4, 4) (5, 5, 5) (6, 6, 6)}
n(A) = 6
P(A) = \(\frac{n(A)}{n(S)}=\frac{6}{216}=\frac{1}{36}\)
The probability is \(\frac{1}{36}\)

Question 15.
If P(A) = \(\frac{1}{2}\), P(B) = \(\frac{7}{10}\), P(A∪B) = 1, Find
(i) P(A ∩ B)
(ii) P(A’ ∪ B’)
Answer:

III. Answer the following questions.

Question 1.
The mean of the following frequency distribution is 53 and the sum of all frequencies is 100. compute the missing frequencies f₁ and f₂.

Answer:


f₂ = 29
Substitute the value of f₂ = 29 in (1)
f₁ + 29 = 47
⇒ f₁ = 47 – 29 = 18
The value of f₁ = 18 and f₂ = 29

Question 2.
Calculate the standard deviation of the following data.

Answer:
Assumed mean (A) = 13

Standard deviation = 6.32

Question 3.
The time (in seconds) taken by a group to walk across a pedestrian crossing is given in the table below.

Calculate the variance and standard deviation of the data.
Answer:
Assumed mean (A) = 17.5, c = 5


Standard deviation (σ) = √36.76 = 6.063
Variance 36. 76, Standard deviation = 6.06

Question 4.
The mean and standard deviation of 20 items are found to be 10 and 2 respectively. At the time of checking it was found that an item 12 was wrongly entered as 8. Calculate the correct mean and standard deviation.
Answer:
Given, mean of 20 items (\(\bar{x}\)) = 10
and standard deviation (σ) = 2



(i) Corrected mean = 10. 2
(ii) Corrected Standard deviaton = 1.99

Question 5.
Calculate the coefficient of variation of the following data: 20, 18, 32, 24, 26.
Answer:
Arrange in ascending order, we get 18, 20, 24, 26, 32
Assumed mean = 24

Question 6.
The marks scored by two students A, B in a class are given below.

Who is more consistent?
Answer:
Student = A
\(\bar{x}\) = 60




From student A and B the coefficient of variation for A is less than the coefficient of variation for B.
Student A is more Consistent.

Question 7.
If for distribution Σ(x – 7) = 3, Σ(x – 7)² = 57 and total number of item is 20. find the mean and standard deviation.
Answer:


(i) Arithmetic mean = 7. 15
(ii) Standard deviation = 1.68

Question 8.
Two unbiased dice are rolled once. Find the probability of getting
(i) a sum 8
(ii) a doublet
(iii) a sum greater than 8
Answer:
When two dice are thrown, the sample space is
Sample space = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 6 × 6 = 36
(i) Let A be the event of getting a sum 8
A= {(2, 6) (3, 5) (4, 4) (5, 3) (6, 2)}
n(A) = 5
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{5}{36}\)
(ii) Let B be the event of getting a doublet.
B = {(1, 1) (2, 2) (3, 3) (4, 4) (5, 5) (6, 6)}
n(B) = 6
P(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{6}{36}=\frac{1}{6}\)
(iii) Let C be the event of getting a sum greater than 8
C = {(3, 6) (4, 5) (4, 6) (5, 4) (5, 5) (5, 6) (6, 3) (6, 4) (6, 5) (6, 6)}
n(C) = 10
P(C) = \(\frac{n(\mathrm{C})}{n(\mathrm{S})}=\frac{10}{36}=\frac{5}{18}\)

Question 9.
A die is thrown twice. Find the probability that atleast one of the two throws conies up with the number 5 (use addition theorem).
Answer:
In rolling a die twice, the size of the sample space, n(S) = 36
Let A be the event of getting 5 in the first throw.
A = {(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)}
Thus, n(A) = 6, and P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{6}{36}\)
Let B be the event of getting 5 in the second throw.
B = {(1, 5) (2, 5) (3, 5) (4, 5) (5, 5) (6, 5)}
Thus, n(B) = 6, and P(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{6}{36}\)
A and B are not mutually exclusive events, since A ∩ B = {(5, 5)}
n(A ∩ B) = 1 and P(A ∩ B) = \(\frac{1}{36}\)
By addition theorem,
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
\(=\frac{6}{36}+\frac{6}{36}-\frac{1}{36}=\frac{11}{36}\)

Question 10.
Let A, B, C be any three mutually exclusive and exhaustive events such that P(B) = \(\frac{3}{2}\) P(A) and P(C) = \(\frac{1}{2}\) P(B). Find P(A).
Answer:
Let P(A) = p
Now, P(B) = \(\frac{3}{2}\), P(A) = \(\frac{3}{2}\) p
Also, P(C) = \(\frac{1}{2}\) P(B)
= \(\frac{1}{2}\) (\(\frac{3}{2}\) p) = (\(\frac{3}{4}\) p)
Given that A, B and C are mutually exclusive and exhaustive events.
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) and S = A ∪ B ∪ C
Now, P(S) = 1
That is, P(A) + P(B) + P(C) = 1
p + \(\frac{3}{2}\) p + \(\frac{3}{4}\) p = 1
⇒ 4p + 6p + 3p = 4
Thus, p = \(\frac{4}{13}\)
Hence, P(A) = \(\frac{4}{13}\)

Question 11.
A bag contains 50 bolts and 150 nuts. Half of the bolts and half of the nuts are rusted. If an item is chosen at random, find the probability that it is rusted or that it is a bolt.
Answer:
Sample space (S) = (50 + 150) = 200
n(S) = 200
Number of rusted bolts = \(\frac{1}{2}\) (50) = 25
Number of rusted nuts = \(\frac{1}{2}\) (150) = 75
Let A be the event of getting rusted bolts and nuts.
n (A) = 25 + 75 = 100
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{100}{200}\)
Let B be the event of getting a bolt.
n(B) = 50
P(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{50}{200}\)
Number of bolts which are rusted n(A ∩ B) = 25

Question 12.
Two dice are rolled simultaneously. Find the probability that that sum of the numbers on the faces is neither divisible by 3 nor by 4.
Answer:
Sample space = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36
Let A be the event of getting the sum is divisible by 3
A = {(1, 2) (2, 1) (1, 5) (5, 1) (2, 4) (4, 2) (3, 3) (3, 6) (6, 3) (4, 5) (5, 4) (6, 6)}
n(A) = 12
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{12}{36}\)
Let B be the event of getting a sum is divisible by 4.
B = {(1, 3) (2, 2) (2, 6) (3, 1) (3, 5) (4, 4) (5, 3) (6, 2) (6, 6)}
n(B) = 9
P(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{9}{36}\)

Question 13.
In a class, 40% of the students participated in Mathematics-quiz, 30% in Science -quiz and 10% in both the quiz programmes. If a students is selected at random from the class, find the probability that the students participated in Mathematics or science or both quiz programmes.
Answer:
Sample space (S) = 100
n(S) = 100
Let A be the event of getting a number of students participated in mathematics-quiz programme
n(A) = 40
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{40}{100}\)
Let B be the event getting a number of students participated in science-quiz programme
n(B) = 30

\(=\frac{40+30-10}{100}=\frac{60}{100}=\frac{3}{5}\)
The required probability = \(\frac{3}{5}\)

Question 14.
A two digit number is formed with the digits 2, 5, 9 (repetition is allowed). Find the probability that the number is divisible by 2 or 5.
Answer:
Sample space (S) = {22, 25, 29, 55, 52, 59, 99, 92, 95}
n(S) = 9
Let A be the event of getting number is divisible by 2.
A = {22, 52, 92}
n(A) = 3
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{3}{9}\)
Let B be the event of getting number is divisible by 5.
B = {25, 95, 55}
n(B) = 3
P(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{3}{9}\)
If A and B are mutually exclusive.
P(A ∪ B) = P(A) + P(B)
P(A ∪ B) = \(\frac{3}{9}+\frac{3}{9}=\frac{6}{9}=\frac{2}{3}\)
The required probability is \(\frac{2}{3}\)

Question 15.
The probability that A, B and C can solve a problem are \(\frac{4}{5}\), \(\frac{2}{3}\) and \(\frac{3}{7}\) respectively. The probability of the problem being solved by A and B is \(\frac{8}{15}\), B and C is \(\frac{2}{7}\), A and C is \(\frac{12}{35}\). The probability of the problem being solved by all the three is \(\frac{8}{35}\). Find the probability that the problem can be solved by atleast one of them.
Answer:
Given P(A) = \(\frac{4}{5}\)
P(B) = \(\frac{2}{3}\)
P(C) = \(\frac{3}{7}\)
P(A ∩ B) = \(\frac{8}{15}\)
P(B ∩ C) = \(\frac{2}{7}\)
P(A ∩ C) = \(\frac{12}{35}\)
P(A ∩ B ∩ c) = \(\frac{8}{35}\)
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(A ∩ C) + P(A ∩ B ∩ C)

The probability of the problem can be solved by at least one of them = \(\frac{101}{105}\)

Students can Download Tamil Nadu 11th Biology Model Question Paper 2 English Medium Pdf, Tamil Nadu 11th Biology Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

TN State Board 11th Biology Model Question Paper 2 English Medium

General Instructions:

1. 1. The question paper comprises of four parts. Questions for Botany and Zoology are asked separately.
   2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
   3. All questions of Part I, II, III and IV are to be attempted separately.
   4. Question numbers 1 to 8 in Part I are Multiple Choice Questions of one mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer.
   5. Question numbers 9 to 14 in Part II are two-marks questions. These are to be answered in about one or two sentences.
   6. Question numbers 15 to 19 in Part III are three-marks questions. These are to be answered in about three to five short sentences.
   7. Question numbers 20 and 21 in Part IV are five-marks questions. These are to be answered in detail. Draw diagrams wherever necessary.

Time: 3:00 Hours
Maximum Marks: 70

Bio – Botany [Maximum Marks: 35]

PART – I

Answer all the questions. Choose the correct answer. [8 × 1 = 8]

Question 1.
Red sea is red colour due to ……………………
(a) Dermacarpa sps
(b) Trichodesmium sps
(c) Scytonema sps
(d) Gloeocapsa sps.
Answer:
(b) Trichodesmium sps

Question 2.
Sago is obtained from …………………..
(a) Cycas revoluta
(b) Pinus roxburghil
(c) Pinus insularis
(d) Cedrus deodara
Answer:
(a) Cycas revoluta

Question 3.
Plants growing on the water surface are called as …………………… type of aquatic plants.
(a) Emergent
(b) Submerged
(c) Free floating
(d) Mangroves
Answer:
(c) Free floating

Question 4.
Synapsis occur between
(a) mRNA and ribosomes
(b) Spindle fibres and centromeres
(c) Two homologous chromosomes
(d) A male and a female gamete
Answer:
(c) Two homologous chromosomes

Question 5.
An example of feedback inhibition is ………………………
(a) Cyanide action on cytochrome
(b) Sulpha drug on folic acid synthesiser bacteria
(c) Allosteric inhibition of hexokinase by glucose-6-phosphate
(d) The inhibition of succinic dehydrogenase by malonate
Answer:
(c) Allosteric inhibition of hexokinase by glucose-6-phosphate

Question 6.
Rubber is a …………………..
(a) Latex
(b) Resin
(c) Alkaloid
(d) Drug
Answer:
(a) Latex

Question 7.
Identify the correct statement:
(I) Sulphur is essential for amino acids Cystine and Methionine
(II) Low level of N, K, S and Mo affect the cell division
(III) Non-leguminous plant Aims which contain bacterium Frankia
(IV) Denitrification carried out by Nitrosomonas and Nitrobacter
(a) (I), (II) are correct
(b) (I), (II), (III) are correct
(c) (I) only correct
(d) All are correct
Answer:
(b) (I), (II), (III) are correct

Question 8.
Which step is irrelevant with respect to aerobic respiration?
(a) Glycolysis
(b) Pyruvate oxidate
(c) Fermentation
(d) TCA cycle
Answer:
(c) Fermentation

PART – II

Answer any four of the following questions. [4 × 2 = 8]

Question 9.
How milk is changed into curd, if a few drops of curd is added to it? What is the reason for its sourness?
Answer:
The change is brought by Lactobacillus lactis, a bacterium present in the curd. The sourness is due to the formation of lactic acid.

Question 10.
What are pyrenoids? Mention its role?
Answer:
Pyrenoids are proteinaceous bodies found in chromatophores of algae and assist in the synthesis and storage of starch.

Question 11.
From which type of flowers does the aggregate fruit develops?
Answer:
Aggregate fruits develop from a single flower having an apocarpous pistil. Each of the free carpel is develops into a simple fruitlet. A collection of simple fruitlets makes an aggregate fruit.

Question 12.
Define magnification. How will you calculate it?
Answer:
The optical increase in the size of an image is called magnification. It is calculated by the following formula;
Magnification =

Question 13.
Define Diffusion Pressure Deficit (DPD)?
Answer:
The difference between the diffusion pressure of the solution and its solvent at a particular . temperature and atmospheric pressure is called as Diffusion Pressure Deficit (DPD).

Question 14.
Name the two forms of phycobilins and also give an example?
Answer:
Phycobilins exists in two form. They are:

1. Phycocyanin found in Cyanobacteria.
2. Phycoerythrin found in red algae.

PART – III

Answer any three questions in which question number 19 is compulsory. [3 × 3 = 9]

Question 15.
Do you think shape of chloroplast is unique for algae? Justify your answer?
Answer:
Variation among the shape of the chloroplast is found in members of algae. It is Cup shaped (Chlartiydomonas), Discoid (Chara), Girdle shaped (Ulothrix), reticulate (Oedogonium), spiral (Spirogyra), stellate (Zygnema) and plate like (Mougeoutia).

Question 16.
Name few molecular markers used in molecular taxonomy?
Answer:
Allozymes, mitochondrial DNA, micro satellites, RFLP (Restriction Fragment Length Polymorphism), RAPD (Random amplified polymorphic DNA), AFLPs (Amplified Fragment Length Polymorphism), Single nucleotide Polymorphism – SNP, microchips or arrays.

Question 17.
List out the criteria for being as essential minerals?
Answer:
Amon and Stout (1939) gave criteria required for essential minerals:

1. Elements necessary for growth and development.
2. They should have direct role in the metabolism of the plant.
3. It cannot be replaced by other elements.
4. Deficiency makes the plants impossible to complete their vegetative and reproductive phase.

Question 18.
Draw a simplified diagram showing the various regions of root?
Answer:

Question 19.
What do you mean by the term – Basipetal transport and Acropetal transport?
Answer:
Basipetal means transport through phloem from shoot to root and acropetal means transport through xylem from root to shoot.

PART – IV

Answer all the questions. [2 × 5 = 10]

Question 20.
Describe in detail about the lytic cycle of phages with diagram?
Answer:
Lytic cycle:
During lytic cycle of phage, disintegration of host bacterial cell occurs and the progeny virions are released. The steps involved in the lytic cycle are as follows:

(I) Adsorption:
Phage (T₄) particles interact with cell wall of host (E coli). The phage tail makes contact between the two, and tail fibres recognize the specific receptor sites present on bacterial cell surface. The lipopolysaccharides of tail fibres act as receptor in phages.

The process involving the recognition of phage to bacterium is called landing. Once the contact is established between tail fibres of phage and bacterial cell, tail fibres bend to anchor the pins and base plate to the cell surface. This step is called pinning.

(II) Penetration:
The penetration process involves mechanical and enzymatic digestion of the cell wall of the host. At the recognition site phage digests certain cell wall structure by viral enzyme (lysozyme). After pinning the tail sheath contracts (using ATP) and appears shorter and thicker.

After contraction of the base plate enlarges through which DNA is injected into the cell wall without using metabolic energy. The step involving injection of DNA particle alone into the bacterial cell is called Transfection. The empty protein coat leaving outside the cell is known as ‘ghost’.

(III) Synthesis:
This step involves the degradation of bacterial chromosome, protein synthesis and DNA replication. The phage nucleic acid takes over the host biosynthetic machinery. Host DNA gets inactivated and breaks down.

Phage DNA suppresses the synthesis of bacterial protein and directs the metabolism of the cell to synthesis the proteins of the phage particles and simultaneously replication of phage DNA also takes place.

(IV) Assembly and Maturation:
The DNA of the phage and protein coat are synthesized separately and are assembled to form phage particles. The process of assembling the phage particles is known as maturation. After 20 minutes of infection about 300 new phages are assembled.

(V) Release:
The phage particle gets accumulated inside the host cell and are released by the lysis of the host cell wall.

[OR]

Draw a flow chart depicting the Bentham and Hooker Classification?
Answer:

Question 21.
With the help of diagram explain the possible route of water across root cells?
Answer:
There are three possible routes of water.
They are:-

1. Apoplast
2. Symplast and
3. Transmembrane route.

1. Apoplast:
The apoplast (Greek: apo = away; plast = cell) consists of everything external to the plasma membrane of the living cell. The apoplast includes cell walls, extra cellular spaces and the interior of dead cells such as vessel elements and tracheids.

In the apoplast pathway, water moves exclusively through the cell wall or the non-living part of the plant without crossing any membrane. The apoplast is a continuous system.

2. Symplast:
The symplast (Greek: sym = within; plast = cell) consists of the entire mass of cytosol of all the living cells in a plant, as well as the plasmodesmata, the cytoplasmic channel that interconnects them.

In the symplastic route, water has to cross plasma membrane to enter the cytoplasm of outer root cell; then it will move within adjoining cytoplasm through plasmodesmata around the vacuoles without the necessity to cross more membrane, till it reaches xylem.

3. Transmembrane route:
In transmembrane pathway water sequentially enters a cell on one side and exits from the cell on the other side. In this pathway, water crosses at least two membranes for each cell. Transport across the tonoplast is also involved.

Mechanism of Water Absorption Kramer (1949) recognized two distinct mechanisms which independently operate in the absorption of water in plants. They are,

1. Active absorption
2. Passive absorption.

[OR]

Explain the types of parasitic mode of nutrition in angiosperms?
Parasitic mode of nutrition in angiosperms:
Answer:
Organisms deriving their nutrient from another organism (host) and causing disease to the host are called parasites.

a. Obligate or Total parasite – Completely depends on host for their survival and produces haustoria.

(I) Total stem parasite:
The leafless stem twine around the host and produce haustoria. Example: Cuscuta (Dodder), a rootless plant growing on Zizyphns, Citrus and so on.

(II) Total root parasite:
They do not have stem axis and grow in the roots of host plants produce haustoria. Example: Rajflesia, Orobanche and Balanophora.

b. Partial parasite – Plants of this group contain chlorophyll and synthesize carbohydrates. Water and mineral requirements are dependent on host plant.

(I) Partial Stem Parasite:
Example: Loranthus and Viscum (Mistletoe) Loranthus grows on fig and mango trees and absorb water and minerals from xylem.

(II) Partial root parasite:
Example: Santalum album (Sandal wood tree) in its juvenile stage produces haustoria which grows on roots of many plants.

Bio – Zoology [Maximum marks: 35]

PART – I

Answer all the questions. Choose the correct answer. [8 × 1 = 8]

Question 1.
Which is not a unit of taxonomic category?
(a) Series
(b) Glumaceae
(c) Class
(d) Phylum
Answer:
(b) Glumaceae

Question 2.
Study of ticks and mites is ……………………
(a) Acarology
(b) Entomology
(c) Malacology
(d) Carcinology
Answer:
(a) Acarology

Question 3.
Match the List – I and List – II.

Answer:
(a) 1 – (iv), 2 – (i), 3 – (iii), 4 – (ii)
(b) 1 – (iv), 2 – (i), 3 – (ii), 4 – (iii)
(c) 1 – (i), 2 – (iii), 3 – (iv), 4 – (ii)
(d) 1 – (i), 2 – (iv), 3 – (iii), 4 – (ii)

Question 4.
MSH stands for ……………………
(a) Melanocyte stimulating hormone
(b) Malic stimulating hormone
(c) Myosin stimulating hormone
(d) Metabolic stimulating hormone
Answer:
(a) Melanocyte stimulating hormone

Question 5.
Which of the following is an correct statement?
(a) Ehler’s – Danlos syndrome – Affects collagen and results in facial abnormalities.
(b) Rhabdomyosarconca – Life threatening soft tissue tumour of head, neck and urinogenital tract.
(c) Rheumatoid arthritis – Progressive inability to secrete saliva and tears.
(d) Alzheiner’s disease – A degenerative disorder of the nervous system that affects movement often including tremors.
Answer:
(b) Rhabdomyosarconca – Life threatening soft tissue tumour of head, neck and urinogenital tract.

Question 6.
Which of the following is an incorrect statement?
(a) The functions of frontal region are Behaviour, intelligence, memory and movement.
(b) The functions of parietal region is intelligence and memory.
(c) The functions of temporal region are speech, hearing and memory.
(d) The functions of occipital region is visual processing.
Answer:
(b) The functions of parietal region is intelligence and memory.

Question 7.
Synovial fluid is present in …………………….
(a) Spinal cavity
(b) Cranial activity
(c) Freely movable joints
(d) Fixed joints
Answer:
(c) Freely movable joints

Question 8.
Glands responsible for secreting tears are ………………………….
(a) Glands of moll
(b) Lacrimal glands
(c) Meibomian glands
(d) Glands of Zeis
Answer:
(b) Lacrimal glands

PART – II

Answer any four of the following questions. [4 × 2 = 8]

Question 9.
Why are spongin and spicules important to a sponge?
Answer:
Spongin and spicules provide support and supports the soft body parts of the sponges. The spicules give the sponges rigidity and form to the sponges.

Question 10.
What is water vascular system?
Answer:
The system which helps in nutrition and respiration in echinoderms is called water vascular system. Water enters into the body through special organs.

Question 11.
Difference between chordates and non-chordates?
Answer:

Question 12.
Draw the diagram of head region of Periplaneta americana?
Answer:

Question 13.
Name the different types of movement?
Answer:

1. Amoeboid movement.
2. Ciliary movement.
3. Flagellar movement.
4. Muscular movement.

Question 14.
What is endomysium?
Answer:
The connective tissue surrounding the muscle fibre is called the endomysium.

PART – III

Answer any three questions in which question number 19 is compulsory. [3 × 3 = 9]

Question 15.
What are the classical taxonomical tools?
Answer:
Taxonomical tools are the tools for the study of classification of organisms.
They include:-

Taxonomical keys:
Keys are based on comparative analysis of the similarities and dissimilarities of organisms. There are separate keys for different taxonomic categories.

Museum:
Biological Museums have collection of preserved plants and animals for study and ready reference. Specimens of both extinct and living organisms can be studied.

Zoological parks:
These are places where wild animals are kept in protected environments under human care. It enables us to study their food habits and behavior.

Marine parks:
Marine organisms are maintained in protected environments.

Printed taxonomical tools:
It consist of identification cards, description, field guides and manuals.

Question 16.
Differentiate Ehler’s – Danlos syndrome and stickler syndrome?
Answer:
Ehler’s – Danlos syndrome is the defect in the synthesis of collagen in the joints, heart valves, organ walls and arterial walls:
Stickler syndrome is a group of hereditary conditions affecting collagen and results in facial abnormalities.

Question 17.
Define Purkinje fibres?
Answer:
Two special cardiac muscle fibres originate from the auriculo ventricular node and are called the bundle of his which runs down into the interventricular septum and the fibres spread into the ventricles. These fibres are called the Purkinje fibres.

Question 18.
Draw the diagram of pelvic girdle with lower limb?
Answer:

Question 19.
What are the symptoms of acromegaly?
Answer:
Acromegaly is caused due to excessive secretion of growth hormone in adults. The symptoms of acromegaly are:

1. Overgrowth of hand bones, feet bones, jaw bones.
2. Malfunctioning of gonads.
3. Enlargement of viscera, tongue, lungs, heart, liver, splean and endocrine glands like thyroid, or adrenal glands.

PART – IV

Answer all the questions. [2 × 5 = 10]

Question 20.
Describe the digestive system of Lamipto mauritii?
Answer:
The digestive system of the earthworm consists of the alimentary canal and the digestive glands. The alimentary canal runs as a straight tube throughout the length of the body from the mouth to anus.

The mouth opens into the buccal cavity which occupies the 1s^stand 2^2nd segments. The buccal cavity leads into a thick muscular pharynx,which occupies the 3^rd and 4^th segments and is surrounded by the pharyngeal glands.

A small narrow tube, oesophagus lies in the 5^th segment and continues into a muscular gizzard in the 6^th segment. The gizzard helps in the grinding of soil particles and decaying leaves. Intestine starts from the 7^th segment and continues till the last segment.

The dorsal wall of the intestine is folded into the cavity as the typhlosole. This fold contains blood vessels and increases the absorptive area of the intestine. The imier epithelium consists of columnar cells and glandular cells. The alimentary canal opens to the exterior through the anus.

The ingested organic rich soil passes through the digestive tract where digestive enzymes breakdown complex food into smaller absorbable units. The simpler molecules are absorbed through the intestinal membrane and are utilized.

The undigested particles along with earth are passed out through the anus, as worm castings or vermicasts. The pharyngeal or salivary gland cells and the glandular cells of the intestine are supposed to be the digestive glands which secrete digestive enzymes for digestion of food.

[OR]

What are the effects of smoking?
Answer:
Today due to curiosity, excitement or adventure youngsters start to smoke and later get addicted to smoking. Research says about 80% of the lung cancer is due to cigarette smoking. Smoking is inhaling the smoke from burning tobacco. There are thousands of known chemicals which includes nicotine, tar, carbon monoxide, ammonia, sulphur-dioxide and even small quantities of arsenic.

Carbon monoxide and nicotine damage the cardiovascular system and tar damages the gaseous exchange system. Nicotine is the chemical that causes addiction and is a stimulant which makes the heart beat faster and the narrowing of blood vessels results in raised blood pressure and coronary heart diseases.

Presence of carbon monoxide reduces oxygen supply. Lung cancer, mouth cancer and larynx is more common in smokers than non – smokers. Smoking also causes cancer of the stomach, pancreas and bladder and lowers sperm count in men.

Smoking can cause lunb diseases by damaging the airways and alveoli and results in emphysema and chronic bronchitis. These two diseases along with asthma are often referred as Chronic Obstructive Pulmonary Disease (COPD).

When a person smokes, nearly 85% of the smoke released is inhaled by the smoker himself and others in the vicinity, called passive smokers, are also affected. Guidance or counselling should be done in such users to withdraw this habit.

Question 21.
Explain the structure of spinal cord?
Answer:
The spinal cord is a long, slender, cylindrical nervous tissue. It is protected by the vertebral column and surrounded by the three membranes as in the brain. The spinal cord that extends from the brain stem into the vertebral canal of the vertebral column up to the level of 1^st or 2^2nd lumbar vertebra.

So the nerve roots of the remaining nerves are greatly elongated to exit the vertebral column at their appropriate space. The thick bundle of elongated nerve . roots within the lower vertebral canal is called the cauda equina (horse’s tail) because of its appearance.

In the cross section of spinal cord, there are two indentations: the posterior median sulcus and the anterior median fissure. Although there might be slight variations, the cross section of spinal cord is generally the same throughout its length. In contrast to the brain, the grey matter in the spinal cord forms an inner butterfly shaped region surrounded by the outer white matter.

The grey matter consists of neuronal cell bodies and their dendrites, intemeurons and glial cells. White matter consists of bundles of nerve fibres. In the center of the grey matter there is a central canal which is filled with CSF. Each half of the grey matter is divided into a dorsal horn, a ventral hom and a lateral horn.

The dorsal horn contains cell bodies of interneurons on which afferent neurons terminate. The ventral hom contains cell bodies of the efferent motor neurons supplying the skeletal muscle. Autonomic nerve fibres, supplying cardiac and smooth muscles and exocrine glands, originate from the cell bodies found in the lateral horn.

In the white matter, the bundles of nerve fibres form two types of tracts namely ascending tracts which carry’ sensory impulses to the brain and descending tracts which carry motor impulses from the brain to the spinal nerves at various levels of the spinal cord. The spinal cord shows two enlargements,one in the cervical region and another one in the lumbosacral region. The cervical enlargement serves the upper limb and lumbar enlargement serves the lower limbs.

[OR]

What are the stages involved in rearing of chicken?
Answer:
Stages involved in rearing:
There are some steps involved in rearing of chicken.

1. Selection of the best layer:
An active intelligent looking bird, with a bright comb, not obese should be selected.

2. Selection of eggs for hatching:
Eggs should be selected very carefully. Eggs should be fertile, medium sized, dark brown shelled and freshly laid eggs are preferred for rearing. Eggs should be washed, cleaned and dried.

3. Incubation and hatching:
The maintenance of newly laid eggs in optimum condition till hatching is called incubation. The fully developed chick emerges out of egg after an incubation period of 21 – 22 days.

There are two types of incubation namely natural incubation and artificial incubation. In the natural incubation method, only a limited number of eggs can be incubated by a mother hen. In artificial incubation, more number of eggs can be incubated in a chamber (Incubator).

4. Brooding:
Caring and management of young chicks for 4 – 6 weeks immediately after hatching is called brooding. It can also be categorized into two types namely natural and artificial brooding.

5. Housing of Poultry:
To protect the poultry from sun, rain and predators it is necessary to provide housing to poultry. Poultry house should be moisture proof, rat proof and it should be easily cleanable and durable.

6. Poultry feeding:
The diet of chicks should contain adequate amount of water,carbohydrates, proteins, fats, vitamins and minerals.

Students can download 5th Maths Term 1 Chapter 2 Numbers Ex 2.3 Questions and Answers, Notes, Samacheer Kalvi 5th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 5th Maths Solutions Term 1 Chapter 2 Numbers Ex 2.3

Question 1.
Read the following numbers by placing the commas at appropriate periods and write their number names.
a. 15731997
b. 341964
c. 29121972
d. 347810
Answer:
a. 15731997
15731997 = 1,57,31,997
Number Name: One crore fifty seven lakhs thirty one thousands nine hundred and ninety seven.

b. 341964
341964 = 3,41,964
Number Name: Three lakhs forty one thousands nine hundred and sixty four.

c. 21921972
21921972 = 2,19,21,972
Number Name; Two crores nineteen lakhs twenty one thousands nine hundred and seventy two.

d. 347810
347810 = 3,47,810
Number Name: Three lakhs forty seven thousands eight hundred and ten.

Question 2.
Write the place value of 5 in the following numbers.
a. 287500
b. 586012
c. 5869732
d. 5467859
Answer:
a. 287500
The place value of 5 is 5 × 100 = 500

b. 586012
The place value of 5 is 5 × 1,00,000 = 5,00,000

c. 5869732
The place value of 5 is 5 × 10,00,000 = 50,00,000

d. 5467859
The place value of first 5 is 5 × 10 = 50
The place value of Second 5 is 5 × 10,00,000 = 50 00,000

Question 3.
Write the following in standard notation.
a. 30000 + 3000 + 300 + 30 + 3
b. 200000 + 7000 + 7
c. 8000000 + 70000 + 3000 + 30 + 5
d. 4000000 + 400 + 4
Answer:
a. 30000 + 3000 + 300 + 30 + 3
= 33333 = 33,333

b. 200000 + 7000 + 7
= 207007 = 2,07,007

c. 8000000 + 70000 + 3000 + 30 + 5
= 8073035 = 80,73,035

d. 4000000 + 400 + 4
= 4000404 = 40,00,404

Question 4.
Write the following numbers in expanded form.
a. 63,570
b. 36,01,478
c. 1,45,70,004
d. 28,48,387
Answer:
a. 63,570
= 60000 + 3000 + 500 + 70 + 0

b. 36,01,478
= 3000000 + 600000 + 1000 + 400 + 70 + 8

c. 1,45,70,004
= 10000000 + 4000000 + 500000 + 70000 + 4

d. 28,48,387
= 2000000 + 800000 + 40000 + 8000 + 300 + 80 + 7

Students can Download Tamil Nadu 11th Physics Model Question Paper 4 English Medium Pdf, Tamil Nadu 11th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

TN State Board 11th Physics Model Question Paper 4 English Medium

General Instructions:

1. The question paper comprises of four parts.
2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. All questions of Part I, II, III and IV are to be attempted separately.
4. Question numbers 1 to 15 in Part I are Multiple Choice Questions of one mark each.
   These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 16 to 24 in Part II are two-mark questions. These are to be answered in about one or two sentences.
6. Question numbers 25 to 33 in Part III are three-mark questions. These are to be answered in about three to five short sentences.
7. Question numbers 34 to 38 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.

Time: 3 Hours
Maximum Marks: 70

PART – 1

Answer all the questions: [15 × 1 = 15]

Question 1.
In some region, the gravitational field is zero. The gravitational potential in this region is …………………….
(a) A variable
(b) A constant
(c) Zero
(d) Can’t be zero
Answer:
(b) A constant

Question 2.
The angle between two vectors 2\(\hat { i } \) + 3\(\hat { j } \) + \(\hat { k } \) and -3\(\hat { j } \) + 6k is …………………..
(a) 0°
(b) 30°
(c) 60°
(d) 90°
Hint:
The angle between the two vector is 90°.
[cos θ = \(\frac{\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}}{\mathrm{AB}}\)]
Answer:
(d) 90°

Question 3.
A stretched rubber has
(a) Increased kinetic energy
(b) Increased potential energy
(c) Decreased kinetic energy
(d) The axis of rotation
Answer:
(b) Increased potential energy

Question 4.
The direction of the angular velocity vector is along ……………………..
(a) The tangent to the circular path
(b) The inward radius
(c) The outward radius
(d) The axis of rotation
Answer:
(d) The axis of rotation

Question 5.
For a satellite moving in an orbit around the earth, the ratio of kinetic energy to potential energy is …………………….
(a) \(\frac{1}{2}\)
(b) \(\frac { 1 }{ \sqrt { 2 } } \)
(c) 2
(d) \(\sqrt{2}\)
Hint:

Answer:
(a) \(\frac{1}{2}\)

Question 6.
If the linear momentum of the object is increased by 0.1 %, then the kinetic energy is increased by ………………………..
(a) 0.1%
(b) 0.2%
(c) 0.4%
(d) 0.01%
Hint:
The relation b/w linear momentum and kinetic energy
P = \(\sqrt{2 \mathrm{mE}_{\mathrm{K}}} \Rightarrow \mathrm{E}_{\mathrm{K}}=\frac{\mathrm{P}^{2}}{2 \mathrm{m}}\)
If L is increased by 0.1% 1′ = P + \(\frac{0.1}{100}\)P

Answer:
(c) 0.4%

Question 7.
A block of mass 4 kg is suspended through two light spring balances A and B. Then A and B will read respectively ………………………
(a) 4 kg and 0 kg
(b) 0 kg and 4 kg
(c) 4 kg and 4 kg
(d) 2kg and 2 kg
Hint:
Tension is uniformly transmitted if the springs are massless.
Answer:
(c) 4 kg and 4 kg

Question 8.
At the same temperature, the mean kinetic energies of molecules of hydrogen and oxygen are in the ratio of ………………………
(a) 1 : 1
(b) 1 : 16
(c) 8 : 1
(d) 16 : 1
Hint:
Average kinetic energy of a molecule is proportional to the absolute temperature.
Answer:
(a) 1 : 1

Question 9.
A uniform rope having mass m hangs vertically from a rigid support. A transverse wave pulse is produced at the lower end. Which of the following plots shows the correct variation of speed v with height h from the lower end?
(a)
(b)
(c)
(d)
Answer:

(d)

Question 10.
In a simple hormonic oscillation, the acceleration against displacement for one complete oscillation will be ………………………
(a) An ellipse
(b) A circle
(c) A parabola
(d) A straight line
Answer:
(d) A straight line

Question 11.
A shell is fired from a canon with velocity v m/s at an angle 0 with the horizontal direction. At the highest point in the path it explodes into two pieces of equal mass. One of the pieces retraces it path of the cannon and the speed in m/s of the other piece immediately after the. explosion is ………………………..
(a) 3v cos θ
(b) 2v cos θ
(c) \(\frac{3}{2}\)v cos θ
(d) \(\frac { \sqrt { 3 } }{ 2 } \) cos θ
Hint:
Velocity at the highest point = horizontal component of velocity = V cos θ
Momentum of shell before explosion = mv cos θ
Momentum of two pieces after explosion = \(\frac{m}{2}\) (- V cos θ) + \(\frac{m}{2}\) v
Law of conservation of momentum mv cos θ = –\(\frac{mv}{2}\)cos θ + \(\frac{m}{2}\) v
∴ V = 3V cos θ
Answer:
(a) 3v cos θ

Question 12.
In which process, the p – v indicator diagram is a straight line parallel to volume axis?
(a) Isothermal
(b) Adiabatic
(c) Isobaric
(d) Irreversible
Answer:
(c) Isobaric

Question 13.
For a liquid to rise in capillary tube, the angle of contact should be ………………………….
(a) Acute
(b) Obtuse
(c) Right
(d) None of these
Answer:
(a) Acute

Question 14.
The increase in internal energy of a system is equal to the work done on the system which process does the system undergo?
(a) Isochoric
(b) Adiabatic
(c) Isobaric
(d) Isothermal
Answer:
(b) Adiabatic

Question 15.
The change in frequency due to Doppler effect does not depend on …………………………
(a) The speed of the source
(b) The speed of the observer
(c) The frequency of the source
(d) Separation between the source and the observer
Answer:
(d) Separation between the source and the observer

PART – II

Answer any six questions in which Q. No 23 is compulsory. [6 × 2 = 12]

Question 16.
What are the advantages of SI system?
Answer:

1. This system makes use of only one unit for one physical quantity, which means a rational system of units
2. In this system, all the derived units can be easily obtained from basic and supplementary units, which means it is a coherent system of units.
3. It is a metric system which means that multiples and submultiples can be expressed as powers of 10.

Question 17.
Using the principle of homogunity of dimensions, check dimensionally the given equations are correct,
(a) \(\mathbf{T}^{2}=\frac{4 \pi^{2} r^{3}}{\mathbf{G}}\)
(b) \(T^{2}=\frac{4 \pi^{2} r^{3}}{G M}\)?
Answer:
Here G-gravitational constant
r – radius of orbit M – mass
Dimensional formula for T = T
Dimensional formula for r = L
Dimensional formula for G = M^-1L³T^-2
Dimensional formula for M = M
(a) T² M° L° = [L³] [M L^-3T^-2]
T² M° L° = L° MT² – Not correct

(b) T² = [L³][ML^-3T²][M^-1]
T² = T² – Dimensionally correct

Question 18.
Find out the workdone required to extract water from the well of depth 20 m. Weight of water and backet is 2.8 kg wt?
Answer:
Workdone, W = mgh
W = (Weight) × depth
= 2.8 × 20
W = 56 J

Question 19.
Is a single isolated force possible in nature?
Answer:
No. According to Newton’s third law, for every action, there is an equal and opposite reaction. So, whatever case we consider, if there is an action there is always a reaction. So it is impossible.

Question 20.
State the factors on which the moment of inertia of a body depends?
Answer:

1. Mass of body
2. Size and shape of body
3. Mass distribution w.r.t. axis of rotation
4. Position and orientation of rotational axis

Question 21.
If a drop of water falls on a very hot iron, it takes long time to evaporate. Explain why?
Answer:
When a drop of water falls on a very hot iron it gets insulated from the hot iron due to a thin layer of water vapour which is a bad conductor of heat. It takes quite long to evaporate as heat is conducted from hot iron to the drop through the insulating layer of water vapour very slowly.

Question 22.
What is meant by gravitational field. Give its unit?
Answer:
The gravitational field intensity \(\vec { E } \)₁, at a point is defined as the gravitational force experienced by unit mass at that point. It’s unit N kg^-1.

Question 23.
Why dimensional methods are applicable only up to three quantities?
Answer:
Understanding dimensions is of utmost importance as it helps us in studying the nature of physical quantities mathematically. The basic concept of dimensions is that we can add or subtract only those quantities which have same dimensions. Also, two physical quantities are equal if they have same dimensions, these basic ideas help us in deriving the new relation between physical quantities, it is just like units.

Question 24.
Why does a porter bend forward while carrying a sack of rice on his back?
Answer:
When a porter carries a sack of rice, the line of action of his centre of gravity will go away from the body. It affects the balance, to avoid this he bends. By which centre of gravity will realign within the body again. So balance is maintained.

PART – III

Answer any six questions in which Q.No. 29 is compulsory. [6 × 3 = 18]

Question 25.
Explain variation of ‘g’ with latitude?
Answer:
When an object is on the surface for the Earth, it experiences a centrifugal force that depends on the latitude of the object on Earth. If the Earth were not spinning, the force on the object would have been mg. However, the object experiences an additional centrifugal force due to spinning of the Earth.
OP_z, cos λ = \(\frac{PZ}{OP}\) = \(\frac{R’}{R}\)
R’ = R cos λ

where λ is is the latitude. The component of centrifugal acceleration experienced by the object in the direction opposite to g is
a_PQ = ω²R cos λ = ω²R cos² λ
Since R’ = R cos λ
Therefore, g’ = g – ω’²R cos²λ
From the above expression, we can infer that at equator, λ = 0, g’ = g – ω²R. The acceleration due to gravity is minimum. At poles λ = 90; g1 = g. it is maximum. At the equator, g’ is minimum.

Question 26.
Cap you associate a vector with
(a) the length of a wire bent into a loop
(b) a plane area
(c) a sphere.
Answer:
(a) We cannot associate a vector with the length of a wire bent into a loop, this is cause the length of the loop does not have a definite direction.

(b) We can associate a vector with a plane area. Such a vector is called area vector and its direction is represented by a normal drawn outward to the area.

(c) The area of a sphere does not point in any difinite direction. However, we can associate a null vector with the area of the sphere. We cannot associate a vector with the volume of a sphere.

Question 27.
What is mean by inertia? Explain its types with example?
Answer:
The inability of objects to move on its own or change its state of motion is called inertia.
Inertia means resistance to change its state. There are three types of inertia:

1. Inertia of rest: The inability of an object to change its state of rest is called inertia of rest.
Example:

• When a stationary bus starts to move, the passengers experience a sudden backward push.
• A book lying on the table will remain at rest until it is moved by some external agencies.

2. Inertia of motion: The inability of an object to change its state of uniform speed (constant speed) on its own is called inertia of motion.
Example:

• When the bus is in motion, and if the brake is applied suddenly, passengers move forward and hit against the front seat.
• An athlete running in a race will continue to run even after reaching the finishing point.

3. Inertia of direction: The inability of an object to change its direction of motion on its own is called inertia of direction.
Example:

• When a stone attached to a string is in whirling motion, and if the string is cut suddenly, the stone will not continue to move in circular motion but moves tangential to the circle.
• When a bus moving along a straight line takes a turn to the right. The passengers are thrown towards left.

Question 28.
A light body and body with greater mass both are having equal kinetic energy. Among these two which one will have greater linear momentum?
Answer:
Given Data:
E₁ – E₂

then P₂ > P₁
i.e; a heavier body has greater linear momemtum.

Question 29.
Three particles of masses m₁ = 1 kg, m₂ = 2 kg and m₃ = 3 kg are placed at the corners of an equilateral triangle of side lm as shown in Figure. Find the position of center of mass?
Answer:
The center of mass of an equilateral triangle lies at its geometrical center G.
The positions of the mass m₁, m₂ and m₃ are at positions A, B and C as shown in the Figure. From the given position of the masses, the coordinates of the masses m₁ and m₂ are easily marked as (0,0) and (1,0) respectively.

To find the position of m3 the Pythagoras theorem is applied. As the ∆DBC is a right angle triangle,
BC² = CD² + DB²
CD² = BC² – DB²
CD² = 1² – (\(\frac{1}{2}\))² = 1 – (\(\frac{1}{4}\)) = \(\frac{3}{4}\)
CD = \(\frac { \sqrt { 3 } }{ 2 } \)

The position of mass m₃ is or (0.5, 0.5\(\sqrt{3}\))
X coordìnate of center of mass,
y_CM = \(\frac{m_{1} y_{1}+m_{2} y_{2}+m_{3} y_{3}}{m_{1}+m_{2}+m_{3}}\)
y_CM = \(\frac { \sqrt { 3 } }{ 4 } \) m
∴ The coordinates of center of mass G (x_CM, y_CM) is (\(\frac{7}{12}\), \(\frac { \sqrt { 3 } }{ 4 } \))

Question 30.
Define precision and accuracy. Explain with one example?
Answer:
The accuracy of a measurement is a measure of how close the measured value is to the true value of the quantity. Precision of a measurement is a closeness of two or more measured values to each other.

The true value of a certain length is near 5.678 cm. In one experiment, using a measuring instrument of resolution 0.1 cm, the measured value is found to be 5.5 cm. In another experiment using a measuring instrument of greater resolution, say 0.01 cm, the length is found to be 5.38 cm. We find that the first measurement is more accurate as it is closer to the true value, but it has lesser precision. On the contrary, the second measurement is less accurate, but it is more precise.

Question 31.
Derive an expression for total acceleration in the non uniform circular motion?
Answer:
If the speed of the object in circular motion is not constant, then we have non-uniform circular motion. For example, when the bob attached to a string moves in vertical circle, the speed of the bob is not the same at all time. Whenever the speed is not same in circular motion, the particle will have both centripetal and tangential acceleration as shown in the figure.

The resultant acceleration is obtained by vector sum of centripetal and tangential acceleration. Since centripetal acceleration is \(\frac { v^{ 2 } }{ r } \), the magnitude of this resultant acceleration is given by
a_R = \(\sqrt{a_{t}^{2}+\left(\frac{v^{2}}{r}\right)^{2}}\)

This resultant acceleration makes an angle θ with the radius vector as shown in figure.
This angle is given by tan θ = \(\frac{a_{t}}{\left(v^{2} / r\right)}\)

Question 32.
Calculate the value of adiabatic exponent for monoatomic molecule?
Answer:
Monoatomic molecule:
Average kinetic energy of a molecule = [\(\frac{3}{2}\)kT]
Total energy of a mole of gas = \(\frac{3}{2}\) kT × N_A = \(\frac{3}{2}\)RT
For one mole, the molar specific heat at constant volume

Question 33.
At what temperature will the rms speed of oxygen molecules become just sufficient for escaping from the Earth’s surface, (mass of oxygen molecule : 2.76 × 10^-26kg Boltzmann’s constant (k_B) = 1.38 × 10^-23 J mol^-1 k^-1
Answer:

PART – IV

Answer all the questions. [5 × 5 = 25]

Question 34 (a).
State kegler’s laws of planetary motion?
Answer:
1. Law of Orbits:
Each planet moves around the Sun in an elliptical orbit with the Sun at one of the foci.

2. Law of area:
The radial vector (line joining the Sun to a planet) sweeps equal areas in equal intervals of time.

3. Law of period:
The square of the time period of revolution of a planet around the Sun in its elliptical orbit is directly proportional to the cube of the semi-major axis of the ellipse.
T² ∝ a³
\(\frac { T^{ 2 } }{ a^{ 3 } } \) = Constant

(b) The distance of planet Jupiter from the sun is 5.2 times that of the earth. Find the period of resolution of Jupiter around the sun?
Answer:
Here r₁ = 5.2 r_e; T_J = ?; T_e = 1 year

= 11.86 years

[OR]

(c) Explain the propagation of errors in multiplication?
Answer:
Error in the product of two quantities:
Let ∆A and ∆B be the absolute errors in the two quantities A, and B, respectively. Consider the product Z = AB,
The error AZ in Z is given by Z ± AZ = (A ± ∆A) (B ± ∆B)
= (AB) ± (A ∆ B) ± (B ∆ A) ± (∆A • ∆B)
Dividing L.H.S by Z and R.H.S by AB, we get,
1 ± \(\frac{∆Z}{Z}\) = 1 ± \(\frac{∆B}{B}\) ± \(\frac{∆A}{A}\) ± \(\frac{∆A}{A}\). \(\frac{∆B}{B}\)
As ∆A/A, ∆B/B are both small quantities, their product term \(\frac{∆A}{A}\).\(\frac{∆B}{B}\) can be neglected.
The maximum fractional error in Z is
\(\frac{∆Z}{Z}\) = ± (\(\frac{∆A}{A}\) + \(\frac{∆B}{B}\))

(d) The period of oscillation of a simple pendulum in the experiment is recorded as 2.63 s, 2.56 s, 2.42s, 271s and 2.80s respectively. Calculate the average absolute error?
Answer:
Mean absolute error = \(\frac{\Sigma\left|\Delta \mathrm{T}_{i}\right|}{n}\)
∆T_m = \(\frac{0.01+0.06+0.20+0.09+0.18}{5}\)
∆T_in = \(\frac{0.54}{5}\) = 0.108s = 0.1 1s (Rounded of 2^nd decimal place).

Question 35 (a).
Explain in detail the triangle law of vector addition?
Answer:
Let us consider two vectors \(\vec { A } \) and \(\vec { B } \) as shown in figure.

To find the resultant of the two vectors we apply the triangular law of addition as follows:

Represent the vectors \(\vec { A } \) and \(\vec { B } \) by the two adjacent sides of a triangle taken in the same order. Then the resultant is given by the third side of the triangle as shown in figure.

To explain further, the head of the first vector \(\vec { A } \) is connected to the tail of the second vector \(\vec { B } \). Let θ be the angle between \(\vec { A } \) and \(\vec { B } \). Then \(\vec { R } \) is the resultant vector connecting the tail of the first vector A to the head of the second vector B.

The magnitude of R (resultant) is given geometrically by the length of \(\vec { R } \) (OQ) and the direction of the resultant vector is the angle between \(\vec { R } \) and \(\vec { A } \). Thus we write \(\vec { R } \) = \(\vec { A } \) + \(\vec { B } \).

1. Magnitude of resultant vector:
The magnitude and angle of the resultant vector are determined by using triangle law of vectors as follows. From figure, consider the triangle ABN, which is obtained by extending the side OA to ON. ABN is a right angled triangle.

From figure, let R is the magnitude of the resultant of \(\vec { A } \) and \(\vec { B } \).
cos θ = \(\frac{AN}{B}\) ∴AN = B cos θ ans sin θ = \(\frac{BN}{B}\) ∴ BN = B sin θ
For ∆OBN, we have OB² = ON² + BN²

2. Direction of resultant vectors: If θ is the angle between \(\vec { A } \) and \(\vec { B } \), then

(b) State and prove Bernoulli’s theorem for a flow of incompressible, non-viscous, and streamlined flow of fluid?
Answer:
Bernoulli’s theorem:
According to Bernoulli’s theorem, the sum of pressure energy, kinetic energy, and potential energy per unit mass of an incompressible, non-viscous fluid in a streamlined flow remains a constant. Mathematically,
\(\frac { P }{ \rho } \) + \(\frac{1}{2}\)v² + gh = Constant
This is known as Bernoulli’s equation.

Proof: Let us consider a flow of liquid through a pipe AB. Let V be the volume of the liquid when it enters A in a time t which is equal to the volume of the liquid leaving B in the same time. Let a_A, v_A and P_A be the area of cross section of the tube, velocity of the liquid and pressure exerted by the liquid at A respectively.

Let the force exerted by the liquid at A is
F_A = P_Aa_A

Distance travelled by the liquid in time t is d = v_at

Therefore, the work done is W = F_Ad = P_Aa_Av_At
But a_Av_At = a_Ad = V, volume of the liquid entering at A.

Thus, the work done is the pressure energy (at A), W = P_Ad = P_AV
Pressure energy per unit volume at
A = \($\frac{\text { Pressure energy }}{\text { Volume }}$\) = \(\frac{P_{A} V}{V}\) = P_A

Pressure energy per unit mass
A = \($\frac{\text { Pressure energy }}{\text { Mass }}$\) = \(\frac{P_{A} V}{m}\) = \(\frac{P_{A}}{\frac{m}{V}}=\frac{P_{A}}{\rho}\)

Since m is the mass of the liquid entering at A in a given time, therefore, pressure energy of the liquid at A is
EP_A = P_AV = P_AV × (\(\frac{m}{m}\)) = m\(\frac { P_{ A } }{ \rho } \)

Potential energy of the liquid at A,
PE_A = mg h_A

Due to the flow of liquid, the kinetic energy of the liquid at A,
KE_A = \(\frac{1}{2} m v_{\mathrm{A}^{2}}\)

Therefore, the total energy due to the flow of liquid at A,
E_A = EP_A + KE_A + PE_A
E_A = m \(m \frac{P_{A}}{\rho}+\frac{1}{2} m v_{A}^{2}+m g h_{A}\)

Similarly, let a_B, v_B and P_B be the area of cross section of the tube, velocity of the liquid and pressure exerted by the liquid at B. Calculating the total energy at F_B, we get
E_B = m \(m \frac{P_{B}}{\rho}+\frac{1}{2} m v_{B}^{2}+m g h_{B}\)
From the law of conservation of energy,
E_A = E_B

Thus, the above equation can be written as
\(\frac{P}{\rho g}+\frac{1}{2} \frac{v^{2}}{g}\) + h = Constant

The above equation is the consequence of the conservation of energy which is true until there is no loss of energy due to friction. But in practice, some energy is lost due to friction.

This arises due to the fact that in a fluid flow, the layers flowing with different velocities exert frictional forces on each other. This loss of energy is generally converted into heat energy. Therefore, Bernoulli’s relation is strictly valid for fluids with zero viscosity or non-viscous liquids. Notice that when the liquid flows through a horizontal pipe, then
h = 0 ⇒ \(\frac{P}{\rho g}+\frac{1}{2} \frac{v^{2}}{g}\) = Constant

Question 36 (a).
What are the limitations of dimensional analysis?
Answer:
Limitations of Dimensional analysis

1. This method gives no information about the dimensionless constants in the formula like 1, 2, …………….. π, e, etc.
2. This method cannot decide whether the given quantity is a vector or a scalar.
3. This method is not suitable to derive relations involving trigonometric, exponential and logarithmic functions.
4. It cannot be applied to an equation involving more than three physical quantities.
5. It can only check on whether a physical relation is dimensionally correct but not the correctness of the relation.

For example, using dimensional analysis, s = ut + \(\frac{1}{3}\)at² is dimensionally correct whereas the correct relation is s = ut + \(\frac{1}{2}\)at²

(b) The escape velocity v of a body depends on

1. The acceleration due to gravity ‘g’ of the planet
2. The radius R of the planet. Establish dimensionally the relation for the escape velocity?

Answer:
\(v \propto g^{a} \mathrm{R}^{b} \Rightarrow v=k g^{a} \mathrm{R}^{b}\), K → dimensionally proportionality constant.
[v] = [g]^a [R]^b
[M⁰L¹T^-1] = [M⁰L¹T^-2]^a [M⁰L¹T¹⁰]^b
equating powers
1 = a + b
-1 = -2a ⇒ a = \(\frac{1}{2}\)
b = 1 – a = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
∴ v = k\(\sqrt{gR}\)

[OR]

(c) Discuss the law of transverse vibrations In stretched string?
Answer:
Laws of transverse vibrations in stretched strings:
There are three laws of transverse vibrations of stretched strings which are given as follows:

(I) The law of length:
For a given wire with tension T (which is fixed) and mass per unit length p (fixed) the frequency varies inversely with the vibrating length. Therefore,
f ∝\(\frac{1}{l}\) ⇒ f = \(\frac{C}{2}\)
⇒1 × f = C, where C is constant

(II) The law of tension:
For a given vibrating length I (fixed) and mass per unit length p (fixed) the frequency varies directly with the square root of the tension T,
f ∝\(\sqrt{T}\)
⇒f = A\(\sqrt{T}\), where A is constant

(III) The law of mass:
For a given vibrating length l (fixed) and tension T (fixed) the frequency varies inverely with the square root of the mass per unit length µ,
f = \(\frac{1}{\sqrt{\mu}}\)
⇒f = \(\frac{B}{\sqrt{\mu}}\), where B is constant

(d) Explain how to determine the frequency of tuning for k using sonometer?
Answer:
Working: A transverse stationary or standing wave is produced and hence, at the knife edges P and Q, nodes are formed. In between the knife edges, anti-nodes are formed. If the length of the vibrating element is l then
l = \(\frac{\lambda}{2}\) ⇒ λ = 2l
Let f be the frequency of the vibrating element, T the tension of in the string and µ the mass per unit length of the string. Then using equation ,we get
f = \(\frac{v}{\lambda}=\frac{1}{2 l} \sqrt{\frac{T}{\mu}}\) in Hertz …………………. (1)

Let ρ be the density of the material of the string and d be the diameter of the string. Then the mass per unit length µ,

Question 37.
(a) To move an object, which one is easier, push or pull? Explain?
Answer:
When a body is pushed at an arbitrary angle θ (o to \(\frac{π}{2}\)), the applied force F can be resolved into two components as F sin e parallel to the surface and F cos θ perpendicular to the surface as shown in figure. The total downward force acting on the body is mg + F cos θ. It implies that the normal force acting on the body increases. Since there is
no acceleration along the vertical direction the normal force N is equal to
N_push = mg + F cos θ ………………………. (1)
As a result the maximal static friction also increases and is equal to
\(f_{s}^{\max }=\mu_{r} N_{p u s h}=\mu_{s}(m g+F \cos \theta)\) ………………… (2)
Equation (2) shows that a greater force needs to be applied to push the object into motion.
When an object is pulled at an angle θ, the applied force is resolved into two components as shown in figure. The total downward force acting on the object is
N_pull = mg – F cos θ ……………….. (3)

Equation (3) shows that the normal force needs is less than N_push. From equations (1) and (3), it is easier to pull an object than to push to make it move.

[OR]

(b) Derive an expression for the velocities of two objects colliding elastically in one dimension?
Answer:
Consider two elastic bodies of masses m₁ and m₂ moving in a straight line (along positive x direction) on a frictionless horizontal surface as shown in figure.

In order to have collision, we assume that the mass m₁ moves, faster than mass m₂ i.e., u₁ > u₂. For elastic collision, the total linear momentum and kinetic energies of the two bodies before and after collision must remain the same.

From the law of conservation of linear momentum,
Total momentum before collision (ρ_i) = Total momentum after collision (ρ_f)
m₁u₁ + m₂u₂ = m₁v₁ + m₂ v₁ …………………. (1)
or m₁ (u₁ – v₁) = m₂(v₂ – u₂) …………………… (2)
Furthur,

For elastic collision,
Total kinetic energy before collision KE_i = Total kinetic energy after collision KE_f
\(\frac{1}{2} m_{1} u_{1}^{2}+\frac{1}{2} m_{2} u_{2}^{2}=\frac{1}{2} m_{1} v_{1}^{2}+\frac{1}{2} m_{2} v_{2}^{2}\) ………………….. (3)
\(m_{1}\left(u_{1}^{2}-v_{1}^{2}\right)=m_{2}\left(v_{2}^{2}-u_{2}^{2}\right)\)
After simplifying and rearranging the terms,
Using the formula a² – b² = (a + b) (a – b), we can rewrite the above equation as
\(m_{1}\left(u_{1}+v_{1}\right)\left(u_{1}-v_{1}\right)=m_{2}\left(v_{2}+u_{2}\right)\left(v_{2}-u_{2}\right)\) ……………….. (4)
Dividing the equation (4) by (2) we get

Equation (5) can be written as
u₁ – u₂ = -(v₁ – v₂)
This means that for any elastic head on collision, the relative speed of the two elastic bodies after the collision has the same magnitude as before collision but in opposite direction. Further note that this result is independent of mass.
Rewriting the above equation for v₁ and v₂,
v₁ = v₂ + u₂ – u₁ …………………….. (6)
or v₂ = u₁ + v₁ – u₁ …………………….. (7)
To find the final velocities V₁ and v₂:
Substituting equation (5) in equation (2) gives the velocity of m₁ as
m₁ (u₁ – v₁) = m₂ (u₁ + v₁ – u₂ – u₂)
m (u₁ – v₁) = m₂ (u₁ + v₁ – 2u₂)
m₁u₁ – m₁v₁ = m₂u₁ + m₂v₁ + 2m₂u₂
m₁u₁ – m₂u₁ + 2m₂u₂ = m₁v₁ + m₂v₁
(m₁ – m₂)u₁ + 2m₂u₂ = (m₁ + m₂) v₁
or v₁ = \(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right)\) u₁  + \(\left(\frac{2 m_{2}}{m_{1}+m_{2}}\right)\) u₂
Similarly, by substituting (6) in equation (2) or substituting equation (8) in equation (7), we get the final m₂ as
v₂ = \(\left(\frac{2 m_{1}}{m_{1}+m_{2}}\right)\) u₁ + \(\left(\frac{m_{2}-m_{1}}{m_{1}+m_{2}}\right)\) u₂ …………………. (9)

Question 38 (a).
Prove that at points near the surface of the Earth the gravitational potential energy of the object is v = mgh?
Answer:
When an object of mass m is raised to a height h, the potential energy stored in the object is mgh. This can be derived using the general expression for gravitational potential energy. Consider the Earth and mass system, with r, the distance between the mass m and the Earth’s centre. Then the gravitational potential energy.
U = –\(\frac{\mathrm{GM}_{e} m}{r}\) …………………… (1)

Here r = R_e + h, where Re is the radius of the Earth, h is the height above the Earth’s surface

By using Binomial expansion and neglecting the higher order

Replace this value and we get,
U = \(-\frac{\mathrm{GM}_{e} m}{\mathrm{R}_{e}}\left(1-\frac{h}{\mathrm{R}_{e}}\right)\) ………………… (4)

We know that, for a mass m on the Earth’s surface,
\(\mathrm{G} \frac{\mathrm{M}_{e} m}{\mathrm{R}_{e}}=m g \mathrm{R}_{e}\) …………………… (5)

Substituting equation (4) in (5) we get,
U = -mgR_e + mgh ………………….. (6)

It is clear that the first term in the above expression is independent of the height h. For example, if the object is taken from height h₁ to h₂, then the potential energy at h₁ is
U(h₁) = -mgR_e + mgh₁ …………………… (7)
and the potential energy at h₂ is
U(h₂) = -mgR_e + mgh₂ …………………… (8)

The potential energy differenqe between h₁ and h₂ is
U(h₂) – U(h₁) = mg(h₁-h₂) …………………. (9)

The term mgR_e in equation (7) and (8) plays no role in the result. Hence in the equation (6) the first term can be omitted or taken to zero. Thus it can be stated that the gravitational potential energy stored in the particle of mass m at a height h from the surface of the Earth is U = mgh. On the surface of the Earth, U = 0, since h is zero.

[OR]

(b) Derive an expression for Radius of gyration?
Answer:
For bulk objects of regular shape with uniform mass distribution, the expression for moment of inertia about an axis involves their total mass and geometrical features like radius, length, breadth, which take care of the shape and the size of the objects.

But, we need an expression for the moment of inertia which could take care of not only the mass, shape and size of objects, but also its orientation to the axis of rotation. Such an expression should be general so that it is applicable even for objects of irregular shape and non-uniform distribution of mass. The general expression for moment of inertia is given as,
I = MK²

where, M is the total mass of the object and K is called the radius of gyration. The radius of gyration of an object is the perpendicular distance from the axis of rotation to an equivalent point mass, which would have the same mass as well as the same moment of inertia of the object.

As the radius of gyration is distance, its unit is m. Its dimension is L. A rotating rigid body with respect to any axis, is considered to be made up of point masses m₁, m₂, m₃, . . . mn at perpendicular distances (or positions) r₁, r₂, r₃ . . . r_n respectively as shown in figure. The moment of inertia of that object can be written as,

I = \(\sum m_{1} r_{1}^{2}=m_{1} r_{1}^{2}+m_{2} r_{2}^{2}+m_{3} r_{3}^{2}+\ldots .+m_{n} r_{n}^{2}\)
If we take all the n number of individual masses to be equal
m = m₁ = m, = m₂ = m₃ = ……………… = m_n
then

I = MK²

where, nm is the total mass M of the body and K is the radius of gyration.

The expression for radius of gyration indicates that it is the root mean square (rms) distance of the particles of the body from the axis of rotation. In fact, the moment of inertia of any object could be expressed in the form, I = MK²

For example, let us take the moment of inertia of a uniform rod of mass M and length l. Its moment of inertia with respect to a perpendicular axis passing through the center of mass is,
I = \(\frac{1}{12}\)Ml²
In terms of radius of gyration, I = MK²
Hence, MK² = \(\frac{1}{12}\)Ml²
K² = \(\frac{1}{12}\)l²
K = \(\frac{1}{12}\) or K = \(\frac{1}{2 \sqrt{3}} l\) or K = (0.289)l

Students can download Maths Chapter 7 Mensuration Ex 7.4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 7 Mensuration Ex 7.4

Question 1.
An aluminium sphere of radius 12 cm is melted to make a cylinder of radius 8 cm. Find the height of the cylinder.
Answer:
Sphere – Radius r₁ = 12 cm
Cylinder – Radius r₂ = 8 cm
h₂ = ?
Volume of cylinder = Volume of sphere melted

∴ Height of the cylinder made = 36 cm.

Question 2.
Water is flowing at the rate of 15 km per hour through a pipe of diameter 14 cm into a rectangular tank which is 50 m long and 44 m wide. Find the time in which the level of water in the tanks will rise by 21 cm.
Answer:
Length of the rectangular tank (l) = 50 m = 5000 cm
Width of the rectangular tank (b) = 44 m = 4400 cm
Level of water in the tank (h) = 21 cm
Volume of the tank = l × b × h cu. units = 5000 × 4400 × 21 cm³
Radius of the pipe (r) = 7 cm
Speed of the water = 15 km/hr.
(h) = 15000 × 100 cm / hr.
Volume of water flowing in one hour

Question 3.
A conical flask is full of water. The flask has base radius r units and height h units, the water poured into a cylindrical flask of base radius x r units. Find the height of water in the cylindrical flask.
Answer:
Radius of the conical flask = r units
Height of the conical flask = h units
Volume of the conical flask = \(\frac{1}{3} \pi r^{2} h\) cu.units
Radius of the cylindrical flask = x r units
Let the height of the cylindrical flask be “H” units
Volume of the cylindrical flask = Volume of the Conical flask

Height of the cylindrical flask = \(\frac{h}{3 x^{2}}\) units

Question 4.
A solid right circular cone of diameter 14 cm and height 8 cm is melted to form a hollow sphere. If the external diameter of the sphere is 10 cm, find the internal diameter.
Answer:
Radius of a cone (V) = 7 cm
Height of a cone (h) = 8 cm
External radius of the hollow sphere (R) = 5 cm
Let the internal radius be “x”
Volume of the hollow sphere = Volume of the Cone


Internal diameter of the Hollowsphere = 2 × 3 = 6 cm.

Question 5.
Seenu’s house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (underground tank) which is in the shape of a cuboid. The sump has dimensions 2 m × 1.5 m × 1 m. The overhead tank has its radius of 60 cm and height 105 cm. Find the volume of the water left in the sump after the overhead tank has been completely filled with water from the sump which has been full, initially.
Answer:
Length of the cuboid tank (l) = 2 cm = 200 cm
Breadth of the cuboid tank (b) = 1.5 cm = 150 cm
Height of the tank (h) = 1 m = 100 cm
Volume of the cuboid = l × b × h cu. units
= 200 × 150 × 100 cm³
= 30,00,000 cm³
Radius of the tank (r) = 60 cm
Height of the tank (h) = 105 cm
Volume of the cylindrical tank = πr²h cu. units
= \(\frac{22}{7}\) × 60 × 60 × 105 cm³
= 22 × 60 × 60 × 15 cm³
= 1188000 cm³
Volume of water left in the sump = Volume of the sump – Volume of the tank
= 3000000 – 1188000 cm³
= 1812000 cm³

Question 6.
The internal and external diameter of a hollow hemispherical shell is 6 cm and 10 cm respectively. If it is melted and recast into a solid cylinder of diameter 14 cm, then find the height of the cylinder.
Answer:
Internal radius of the shell (r) = 3 cm
External radius of the shell (R) = 5 cm
Radius of the cylinder (r) = 7 cm
Let the height of the cylinder be “h”
Volume of the cylinder = Volume of the hemispherical shell

Height of the cylinder = 1.33 cm

Question 7.
A solid sphere of radius 6 cm is melted into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 5 cm and its height is 32 cm, then find the thickness of the cylinder.
Answer:
Radius of a sphere (r) = 6 cm
External radius of the cylinder (R) = 5 cm
Height of the cylinder (h) = 32 cm
Let the internal radius of the cylinder be ‘x’
Volume of the hollow cylinder = Volume of a sphere
πh (R² – r²) = \(\frac{4}{3}\) πr³
π × 32 (5 + x) (5 – x) = \(\frac{4}{3}\) × π × 6 × 6 × 6
32 (25 – x²) = 4 × 2 × 6 × 6
25 – x² = 9
x² = 25 – 9 = 16
x = √16 = 4
Thickness of the cylinder = 5 – 4 = 1 cm.

Question 8.
A hemispherical bowl is filled to the brim with juice. The juice is poured into a cylindrical vessel whose radius is 50% more than its height. If the diameter is same for both the bowl and the cylinder then find the percentage of juice that can be transferred from the bowl into the cylindrical vessel.
Answer:
Let the height of the cylinder be “h”
radius is 50% more than the height


From (1) and (2) we get,
Volume of the cylinder = Volume of the hemisphere
It is possible to transfer the full quantity from the bowl into the cylindrical vessel.
100 % of the juice can be transferred.

Students can download 6th Social Science Term 2 Economics Chapter 1 Economics-An Introduction Questions and Answers, Notes, Samacheer Kalvi 6th Social Science Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Social Science Economics Solutions Term 2 Chapter 1 Economics-An Introduction

Samacheer Kalvi 6th Social Science Economics-An Introduction Text Book Back Questions and Answers

I. Fill in the blanks

1. The producers of food grains are ……………..
2. Collection of honey is a …………….. occupation.
3. The conversion of raw materials into finished goods is called ……………..
4. According to Gandhiji the villages are …………….. of the nation.
5. The percentage of population in the cities of Tamil Nadu is ……………..

Answer:

1. Farmers
2. Primary
3. Secondary activities
4. backbone
5. 47%

II. Match the following

Answer:
1. – c
2. – d
3. – a
4. – b
5. – d

III. Match and find the odd pair

Answer:
1. – d
2. – c
3. – b
4. – a

IV. Choose the correct answer

1. Agriculture is a (primary / Secondary) occupation.
2. Economic activities are divided on the basis of (ownership / use)
3. Sugar Industries are (Primary / Secondary) activity.
4. Agro based industry (Cotton / Furniture)
5. Dairy farming is a (Public sector/Co-operative sector)

Answer:

1. Primary
2. use
3. Secondary
4. Cotton
5. Co-operative sector

V. Answer the following questions

Question 1.
Sandhai – Define
Answer:
In villages once in a week or month, all things are sold in a particular place at a specific time to meet the needs of the people. That is called Sandai.

Question 2.
What is called the barter system?
Answer:
A system of exchanging goods for other goods is called a barter system. Example: Exchange a bag or rice for enough clothes.

Question 3.
What is trade?
Answer:
Trade involves the transfer of goods or services from one person to another often in exchange of money.

Question 4.
What is Savings?
Answer:
The amount from the income which is left for future needs after consumption is called sayings.

Question 5.
What was the necessity for the invention of money?
Answer:

1. When traders exchange commodities there arises a difference in the value of the commodity.
2. To solve this problem people invented money.

Question 6.
What was the reason for the development of settlements near water bodies?
Answer:

1. Rivers act as the main source for the cultivation of crops.
2. So early man settled permanently near the rivers.

Question 7.
What are called secondary occupation?
Answer:
The raw materials obtained from the primary activities are converted into finished products is called a secondary occupation.

Question 8.
Name the city-centered industries.
Answer:
Cement, iron, and Aluminium industries, seafood processing are some of the city centered industries.

VI. Answer the following in detail

Question 1.
List out the important primary occupations of your district.
Answer:

1. Agriculture
2. Cattle rearing
3. Collection of fruits, nuts, honey, and medicinal herbs.

Question 2.
Mention the manufacturing industries found in your district.
Answer:

1. Cotton textiles
2. Spinning and weaving
3. Food processing industries
4. Beedi production
5. Wind power generations

Question 3.
How are the industries classified on the basis of raw materials?
Answer:
On the basis of raw materials industries are classified as

1. Agro-Based Industries – Cotton textiles, Sugar mills, and Food processing.
2. Forest-Based Industries – Paper mills, Furniture making, Building materials.
3. Mineral Based Industries – Cement, Iron, Aluminium Industries.
4. Marine Based Industries – Seafood processing.

Question 4.
Write down the occupations in the service sector.
Answer:
The service sector serves the people to fulfill their daily needs like:

1. Transport – Roadways, Railways, Waterways, Airways.
2. Communication – Post, Telephone, Information Technology.
3. Trade – Procurement of goods, selling.
4. Banking – Money Transaction, Banking Services.

Question 5.
What do you know about the features of cities?
Answer:

1. A city is a large human settlement.
2. The high density of population.
3. Four-way roads, flyovers, skyscrapers, parks.
4. Educational institution, hospital, Government offices.
5. Private and public industries and technological institutions.
6. Employment opportunities permanent monthly income, basic requirements are

VII. Fill in the tabular column given below

Activity:
Write the lyrics of Bharathiyar’s Analyze the lyrics and write down the commodities which were exchanged in yesteryears with the help of the teacher.

(1) Wheat
(2) Betel
(3) Tusk

VIII. Stick picture

Samacheer Kalvi 6th Social Science Economics-An Introduction Additional Important Questions and Answers

I. Fill in the blanks Answer

1. The permanent settlements near the rivers were called ……………
2. More than …………… percentage of the world’s population live in cities.
3. The …………… sector serves the people to fulfill their daily needs.
4. One who uses the products is called ……………
5. …………… are the real shadow of cities.

Answer:

1. Villages
2. 50
3. Service
4. Consumer
5. Villages

II. Choose the correct answer

Question 1.
Tertiary activities are also called as sector ……………
(a) Private
(b) Service
(c) Public
Answer:
(b) Service

Question 2.
Secondary and tertiary activities are …………… centred activities.
(a) City
(b) Town
(c) Village
Answer:
(a) City

Question 3.
…………… is the main occupation in villages.
(a) Mining
(b) Fishing
(c) Farming
Answer:
(c) Farming

III. Answer the following questions

Question 1.
Sandhai – Define
Answer:
In villages, once in a week or month, things are sold in a particular place at a specific time to meet the needs of the people. That is called Sandhai.

Question 2.
What is called the barter system?
Answer:

1. A system of exchanging goods for other goods is called a barter system.
2. Example: Exchange a bag or rice for enough clothes.

Question 3.
What are consumer goods?
Answer:
The finished goods which are brought from the market to fulfill the daily needs of the consumers are called consumer goods.

Question 4.
Who are cultivators?
Answer:
Persons who are involved in farming and grazing are called cultivators or farmers.

Question 5.
How are industries classified?
Answer:
Industries are classified on the basis of the:

1. Availability of raw materials
2. Capital
3. Ownership

Question 6.
Name the sectors that are helpful in the economic development of our country.
Answer:
Agriculture and Industries are helpful in the economic development of our country.

IV. Mind map

Students can Download Tamil Nadu 11th Physics Model Question Paper 5 English Medium Pdf, Tamil Nadu 11th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

TN State Board 11th Physics Model Question Paper 5 English Medium

General Instructions:

1. The question paper comprises of four parts.
2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. All questions of Part I, II, III and IV are to be attempted separately.
4. Question numbers 1 to 15 in Part I are Multiple Choice Questions of one mark each.
   These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 16 to 24 in Part II are two-mark questions. These are to be answered in about one or two sentences.
6. Question numbers 25 to 33 in Part III are three-mark questions. These are to be answered in about three to five short sentences.
7. Question numbers 34 to 38 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.

Time: 3 Hours
Maximum Marks: 70

PART – I

Answer all the questions: [15 × 1 = 15]

Question 1.
Two protons are travelling. along the same straight path but in opposite directions. The relative velocity between the two is ……………………
(a) c
(b) \(\frac{c}{2}\)
(c) 2c
(d) 0
Hint:
One of the velocity V₁ = V; Other velocity V₂ = -V
Relative velocity (V_rel) = \(\frac{V_{1}-V_{2}}{\left[1+\frac{V^{2}}{C^{2}}\right]}\) = \(\frac{V-(-V)}{\left[1+\frac{V^{2}}{C^{2}}\right]}\) = \(\frac{2v}{2}\)
V = C
V_relative = C
Answer:
(a) c

Question 2.
If the Earth stops rotating about its own axis, g remains unchanged at …………………..
(a) Equator
(b) Poles
(c) Latitude of 45°
(d) No where
Answer:
(b) Poles

Question 3.
When train stops, the passenger moves forward. It is due to ……………………
(a) Inertia of passenger
(b) Inertia of train
(c) Gravitational pull by Earth
(d) None of the above
Answer:
(a) Inertia of passenger

Question 4.
A particle of mass m moves in the xy plane with a velocity v along the straight line AB. If the angular momention of the particle with respect to origin O is L_A when it is at A and L_B when it is at B, then …………………….
(a) L_A = L_B
(b) L_A < L_B
(c) L_A > L_B
(d) The relationship between L_A and L_B depends uopn the slope of the line AB

Hint:
Magnitude of L is, L = mvr sin ϕ = mvd
d = r sin ϕ is the distance of closest approach of the particle so the origin, as ‘d’ is same for both particles.
So, L _A = L_B
Answer:
(a) L_A = L_B

Question 5.
A couple produces ……………………….
(a) Pure rotation
(b) Pure translation
(c) Rotation and translation
(d) No motion
Answer:
(a) Pure rotation

Question 6.
A body starting from rest has an acceleration of 20 ms~2 the distance travelled by it in the sixth second is ……………………..
(a) 110 m
(b) 130m
(c) 90m
(d) 50 m
Hint:
Distance travelled in n^th second, u = 0
S_n = u + \(\frac{1}{2}\)a(2n – 1)
S₆ = 0 + \(\frac{1}{2}\) × 20 × (2 × 6 – 1); S₆ = 110 m
Answer:
(a) 110 m

Question 7.
A lift of mass 1000 kg, which is moving with an acceleration of 1m/s² in upward direction has tension has developed in its string is ………………………
(a) 9800 N
(b) 10800 N
(c) 11000 N
(d) 10000 N
Hint:
Tension, T = mg + ma = m(g + a) = 1000 (10 + 1)
T = 11000 N
Answer:
(c) 11000 N

Question 8.
The relation between acceleration and displacement of four particles are given below ………………………..
(a) a_x = 2x
(b) a_x = + 2x²
(c) a_x = -2x²
(d) a_x = -2x
Answer:
(d) a_x = -2x

Question 9.
A sonometer wire is vibrating in the second overtone. In the wire there are, ……………………..
(a) Two nodes and two antinodes
(b) One node and two antinodes
(c) Four nodes and three antinodes
(d) Three nodes and three antinodes
Answer:
(d) Three nodes and three antinodes

Question 10.
Which of the following is the graph between the light (h) of a projectile and time (t), when it is projected from the ground ………………………..
(a)
(b)
(c)
(d)
Answer:
(c)

Question 11.
According to kinetic theory of gases, the rms velocity of the gas molecules is directly proportional to ………………………
(a) \(\sqrt{T}\)
(b) T³
(c) T
(d) T⁴
Hint:
The rms velocity, V_rms = \(\sqrt{3KT/m}\) ⇒ V_rms ∝ \(\sqrt{T}\)
Answer:
(a) \(\sqrt{T}\)

Question 12.
A body of mass m moving with velocity v collides head on with another body of mass 2m which is initially at rest. The ratio of K.E of colliding body before and after collision will be ……………………..
(a) 1 : 1
(b) 2 : 1
(c) 4 : 1
(d) 9 : 1
Hint:
KE of colliding bodies before collision = \(\frac{1}{2}\) mv²
After collision the mass = m + 2m = 3m
velocity becomes V’ = \(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right)\)v = \(\frac{mv}{3m}\) = \(\frac{v}{3}\)
KE after collision = \(\frac{1}{2}\)m (\(\frac{V}{3}\)² = \(\frac{1}{9}\) (\(\frac{1}{2}\) mv²)
\(\frac{\mathrm{KE}_{\text {before }}}{\mathrm{KE}_{\text {after }}}=\frac{\frac{1}{2} \mathrm{mv}^{2}}{\frac{1}{9}\left(\frac{1}{2} \mathrm{mv}^{2}\right)}=9: 1\)
Answer:
(d) 9 : 1

Question 13.
Four particles have velocity 1, 0, 2 and 3ms^-1. The root mean square velocity of the particles is ……………………..
(a) 3.5 ms^-1
(b) \(\sqrt{3.5}\) ms^-1
(c) 1.5ms^-1
(d) Zero
Hint:

Answer:
(b) \(\sqrt{3.5}\) ms^-1

Question 14.
Two vibrating tuning forks produce progressive waves given by y₁ = 4 sin 500 πt and y₂ = 2 sin 506 πt where t is in seconds Number of beat produced per minute is ………………………
(a) 360
(b) 180
(c) 3
(d) 60
Hint:

f₂ – f₁ = 3 = beats per sec and 3 × 60 = 180 beats per min

Answer:
(b) 180

Question 15.
Workdone by a simple pendulum in one complete oscillation is …………………………..
(a) Zero
(b) Jmg
(c) mg cos θ
(d) mg sin θ
Answer:
(a) Zero

PART – II

Answer any six questions in which Q. No 23 is compulsory. [6 × 2 = 12]

Question 16.
A girl is swinging in the sitting position. How will the period of the swing be changed if she stands up?
Answer:
This can be explained using the concept of a simple pendulum. We know that the time period of a simple pendulum is given by
T = 2π\(\sqrt{l/g}\) i.e; T ∝\(\sqrt{l}\)
When the girl stands up, the distance between the point of suspension and the centre of mass of the swinging body decreases i.e., l decreases, so T will also decrease.

Question 17.
A car starts to move from rest with uniform acceleration 10 ms^-2 then after 2 sec, what is its velocity?
Answer:
a =10 ms^-2;
t = 2s;
w = 0;
v = ?
v = u + at
v = 0 + 10 × 2
= 20 ms^-1

Question 18.
State Lami’s theorem?
Answer:
If a system of three concurrent and coplanar forces is in equilibrium, then Lami’s theorem states that the magnitude of each force of the system is proportional to sine of the angle between the other two forces. The constant of proportionality is same for all three forces.

Question 19.
Due to the action of constant torque, a wheel from rest makes n rotations in t seconds? Show that the angular acceleration of a wheel as \(\frac{4 \pi n}{t^{2}}\) rad s^-2
Answer:
Initial angluar velocity ω₀ = 0
Number of rotations in t seconds = n
angular displacement θ = 2πn
but, θ = ω₀t + \(\frac{1}{2}\)αt²
2πn = \(\frac{1}{2}\)αt²
α = \(\frac{4 \pi n}{t^{2}}\)

Question 20.
Why a given sound is louder in a hall than in the open?
Answer:
In a hall, repeated reflections of sound take place from the walls and the ceiling. These reflected sounds mix with original sound which results in increase the intensity of sound. But in open, no such a repeated reflection is possible. .’. sound will not be louder as in hall.

Question 21.
What are the differences between connection and conduction?
Answer:
Conduction:
Conduction is the process of direct transfer of heat through matter due to temperature difference. When two objects are in direct contact with one another, heat will be transferred from the hotter object to the colder one. The objects which allow heat to travel easily through them are called conductors.

Convection:
Convection is the process in which heat transfer is by actual movement of molecules in fluids such as liquids and gases. In convection, molecules move freely from one place to another.

Question 22.
Why two holes are made to empty an oil tin?
Answer:
When oil comes out through a tin with one hole, the pressure inside the tin becomes less than the atmospheric pressure, soon the oil stops flowing out. When two holes are made in the tin, air keeps on entering the tin through the other hole and maintains pressure inside.

Question 23.
If the length of the simple pendulum is increased by 44% from its original length, calculate the percentage increase in time period of the pendulum?
Answer:
Since T ∝ \(\sqrt{l}\) = Constant \(\sqrt{l}\)

∴ T_f = 1.2 T_i = T_i + 20% T_i

Question 24.
When do the real gases obey more correctly the gas equation PV = nRT?
Answer:
An ideal gas is one whose molecules have zero volume and no mutual force between them. At low pressure, the volume of a gas is large and so the volume occupied by the molecules is negligible in comparison to the volume of the gas.

At high temperature, the molecules have large velocities and so the intermolecular force has no influence on their motion. Hence at low pressure and high temperature, the behaviour of real gases approach the ideal gas behaviour.

PART – III

Answer any six questions in which Q.No. 29 is compulsory. [6 × 3 = 18]

Question 25.
A stone is thrown upwards with a speed v from the top of a tower. It reaches the ground with a velocity 3v. What is the height of the tower?
Answer:
From equation of motion,
v’ = u + at ……………….. (1)
h = ut + \(\frac{1}{2}\) at²
here, v’ = av; u = v; a = +g
Using equ. (1)
3v = v + gt ⇒ 3v – v = gt
t = \(\frac{2v}{g}\)

Substitute ‘t’ value in equ. (2)
h = v(\(\frac{2v}{g}\)) + \(\frac{1}{2}\)g(\(\frac{2v}{g}\))² = \(\frac { 2v^{ 2 } }{ g } \) + \(\frac{1}{2}\)g (\(\frac{2v}{g}\))²
h = \(\frac { 2v^{ 2 } }{ g } \) + \(\frac { 2v^{ 2 } }{ g } \)
= \(\frac { 4v^{ 2 } }{ g } \) g = 10 ms^-2
= \(\frac { 4v^{ 2 } }{ 10 } \); h = \(\frac { 2v^{ 2 } }{ 5 } \)

Question 26.
An object is projected at an angle such that the horizontal range is 4 times of the maximum height. What is the angle of projection of the object?
Answer:
Given:
Horizontal range = 4 H_max
Horizontal range = \(\frac{u^{2} \sin 2 \theta}{g}\) = \(\frac{2 u^{2} \sin \theta \cos \theta}{g}\)
Maximum height = \(\frac{u^{2} \sin ^{2} \theta}{2 g}\)
as given, \(\frac{2 u^{2} \sin \theta \cos \theta}{g}\) = \(\frac{4 u^{2} \sin ^{2} \theta}{2 g}\)
2 cos θ = 2 sin θ
tan θ = 1
∴ θ = 45°

Question 27.
A room contains oxygen and hydrogen molecules in the ratio 3 : 1. The temperature of the room is 27°C. The molar mass of 0₂ is 32 g mol^-1 and for H₂, 2 g mol^-1. The value of gas constant R is 8.32 J mol^-11 k^-1. Calculate rms speed of oxygen and hydrogen molecule?
Answer:
(a) Absolute Temperature T = 27°C = 27 + 273 = 300 K.
Gas constant R = 8.32 J mol^-1 K^-1
For Oxygen molecule: Molar mass

M = 32 gm/mol = 32 × 10^-3 kg mol^-1
rms speed v_rms = \(\sqrt { \frac { 3RT }{ M } } \) = \(\sqrt{\frac{3 \times 8.32 \times 300}{32 \times 10^{-3}}}\) = 483.73 ms^-1 ~ 484ms^-1

For Hydrogen molecule: Molar mass M = 2 × 10^-3 kg mol^-1
rms speed v_rms = \(\sqrt { \frac { 3RT }{ M } } \) = \(\sqrt{\frac{3 \times 8.32 \times 300}{2 \times 10^{-3}}}\) = 1934 ms^-1 = 1.93 K ms^-1

Note that the rms speed is inversely proportional to \(\sqrt{M}\) and the molar mass of oxygen is 16 times higher than molar mass of hydrogen. It implies that the rms speed of hydrogen is 4 times greater than rms speed of oxygen at the same temperature. \(\frac{1934}{484}\) ~ 4.

Question 28.
Explain about an angle of friction?
Answer:
The angle of friction is defined as the angle between the normal force (N) and the resultant force (R) of normal force and maximum friction force (\(f_{s}^{\max }\))

In the figure the resultant force is R = \(\sqrt{\left(f_{s}^{\max }\right)^{2}+\mathrm{N}^{2}}\)
tan θ = \(\frac{f_{s}^{\max }}{\mathrm{N}}\) ………………….. (1)

But from the frictional relation, the object begins to slide when \(f_{s}^{\max }=\mu_{\mathrm{s}} \mathrm{N}\)
or when \(\frac{f_{s}^{\max }}{\mathrm{N}}\) = µ_s ………………….. (2)

From equations (1) and (2) the coefficient of static friction is
µ_s = tan θ ……………………. (3)
The coefficient of static friction is equal to tangent of the angle of friction.

Question 29.
How does resolve a vector into its component? Explain?
Answer:
component of a resolve:
In the Cartesian coordinate system any vector \(\vec { A } \) can be resolved into three components along x, y and z directions. This is shown in figure. Consider a 3-dimensional coordinate system. With respect to this a vector can be written in component form as
\(\vec { A } \) = A_x \(\hat { i } \) + A_y\(\hat { j } \) + A_z\(\hat { k } \)
Components of a vector in 2 dimensions and 3 dimensions

Here Ax is the x-component of \(\vec { A } \), Ay is the y-component of \(\vec { A } \) and A_z is the z component of \(\vec { A } \).
In a 2-dimensional Cartesian coordinate system (which is shown in the figure) the vector \(\vec { A } \) is given by
\(\vec { A } \) = A_x \(\hat { i } \) + A_y \(\hat { j } \)

If \(\vec { A } \) makes an angle θ with x axis, and A_x and A_y are the components of A along x-axis and y-axis respectively, then as shown in figure,
A_x θ = A cos θ, A = A sin θ
where ‘A’ is the magnitude (length) of the vector \(\vec { A } \), A = \(\sqrt{\mathrm{A}_{x}^{2}+\mathrm{A}_{y}^{2}}\)

Question 30.
Derive an expression for energy of an orbiting satellite?
Answer:
The total energy of the satellite is the sum of its kinetic energy and the gravitational potential energy. The potential energy of the satellite is,
U = \(-\frac{\mathrm{GM}_{s} \mathrm{M}_{\mathrm{E}}}{\left(\mathrm{R}_{\mathrm{E}}+h\right)}\) ………………….. (1)

Here M_s -mass of the satellite, M_E -mass of the Earth, R_E – radius of the Earth.
The Kinetic energy of the satellite is
K.E = \(\frac{1}{2}\) M_sv² ………………….. (2)

Here v is the orbital speed of the satellite and is equal to
v = \(\sqrt{\frac{\mathrm{GM}_{\mathrm{E}}}{\left(\mathrm{R}_{\mathrm{E}}+h\right)}}\)

Substituting the value of v in (2) the kinetic energy of the satellite becomes,
K.E = \(\frac{1}{2} \frac{\mathrm{GM}_{\mathrm{E}} \mathrm{M}_{s}}{\left(\mathrm{R}_{\mathrm{E}}+h\right)}\)

Therefore the total energy of the satellite is
E = \(\frac{1}{2}\) \(\frac{\mathrm{GM}_{\mathrm{E}} \mathrm{M}_{s}}{\left(\mathrm{R}_{\mathrm{E}}+h\right)}-\frac{\mathrm{GM}_{s} \mathrm{M}_{\mathrm{E}}}{\left(\mathrm{R}_{\mathrm{E}}+h\right)}\)
E = \(-\frac{\mathrm{GM}_{s} \mathrm{M}_{\mathrm{E}}}{\left(\mathrm{R}_{\mathrm{E}}+h\right)}\)
The total energy implies that the satellite is bound to the Earth by means of the attractive gravitational force.

Note:
As h approaches ∞, the total energy tends to zero. Its physical meaning is that the satellite is completely free from the influence of Earth’s gravity and is not bound to Earth at large distance.

Question 31.
Explain in detail Newton’s law of cooling?
Answer:
Newton’s law of cooling:
Newton’s law of cooling body is directly proportional to the difference in the temperature between that body and its surroundings.
\(\frac{dQ}{dT}\) ∝(T – T_s) …………………. (1)
The negative sign indicates that the quantity of heat lost by liquid goes on decreasing with time. Where,

T = Temperature of the object
T_s = Temperature of the surrounding

From the graph in figure it is clear that the rate of cooling is high initially and decreases with falling temperature.

Let us consider an object of mass m and specific heat capacity s at temperature T. Let T_s be the temperature of the surroundings. If the temperature falls by a small amount dT in time dt, then the amount of heat lost is,
dQ = msdT …………………….. (2)

Dividing both sides of equation (2) by dt
\(\frac{dQ}{dT}\) = \(\frac{msdT}{dt}\) ………………….. (3)

From Newton’s law of cooling
\(\frac{dQ}{dT}\) ∝(T – T_s)
\(\frac{dQ}{dT}\) = -a(T – T_s) ………………………… (4)

Where a is some positive constant.
From equation (3) and (4)
-a (T – T_s) = ms\(\frac{dT}{dt}\)
\(\frac{d \mathrm{T}}{\mathrm{T}-\mathrm{T}_{s}}\) = -a\(\frac{a}{ms}\) dt …………………… (5)

Integrating equation (5) on both sides,

Where b₁ is the constant of integration. Taking exponential both sides we get,
T = T_s + \(b_{2} e^{\frac{-a}{m s} t}\) …………………….. (6)
Here b₂ = e^b1 Constant

Question 32.
Explain Laplace’s correction?
Answer:
Laplace’s correction: In 1816, Laplace satisfactorily corrected this discrepancy by assuming that when the sound propagates through a medium, the particles oscillate very rapidly such that the compression and rarefaction occur very fast.

Hence the exchange of heat produced due to compression and cooling effect due to rarefaction do not take place, because, air (medium) is a bad conductor of heat. Since, temperature is no longer considered as a constant here, sound propagation is an adiabatic process. By adiabatic considerations, the gas obeys Poisson’s law (not Boyle’s law as Newton assumed), which is
PV^γ = Constant …………………. (1)
where, γ = \(\frac { C_{ p } }{ C_{ v } } \) which is the ratio between specific heat at constant pressure and specific heat at constant volume. Differentiating equation (1) on both the sides, we get
\(V^{ \gamma }dP+P(\gamma ^{ V\gamma -1 }dV)=0\)

or

\(\gamma \mathrm{P}=-\mathrm{V} \frac{d p}{d \mathrm{V}}=\mathrm{B}_{\mathrm{A}}\) ………………….. (2)
where, B_A is the adiabatic bulk modulus of air. Now, substituting equation (2) in equation
V = \(\sqrt{\frac{B}{\rho}}\), the speed of sound in air is
v_A = \(\sqrt{\frac{\mathrm{B}_{\mathrm{A}}}{\rho}}=\sqrt{\frac{\gamma \mathrm{P}}{\rho}}=\sqrt{\gamma v_{\mathrm{T}}}\)
Since air contains mainly, nitrogen, oxygen, hydrogen etc, (diatomic gas), we take γ = 1.47. Hence, speed of sound in air is v_A = (\(\sqrt{1.4}\)) (280 m s^-1) = 331.30 ms^-1, which is very much closer to experimental data.

Question 33.
Explain types of equilibrium?
Answer:

PART – IV

Answer all the questions. [5 × 5 = 25]

Question 34 (a).
What are the applications of dimensional analysis?
Verify s = ut + \(\frac{1}{2}\)at² by dimensional analysis?
Answer:

Given equation is dimensionally correct as the dimensions on the both side are same. Applications of dimensional analysis

1. Convert a physical quantity from one system of units to another.
2. Check the dimensional correctness of a given physical equation.
3. Establish relations among various physical quantities.

[OR]

(b) Explain the types of equilibrium with suitable examples?
Answer:
Translational motion – A book resting on a table.
Rotational equilibrium – A body moves in a circular path with constant velocity.
Static equilibrium – A wall-hanging, hanging on the wall.
Dynamic equilibrium – A ball decends down in a fluid with its terminal velocity.
Stable equilibrium – A table on the floor A pencil
Unstable equilibrium – standing on its tip.
Neutral equilibrium – A dice rolling on a game board.

Question 35 (a)
Explain the motion of block connected by a string in vertical motion?
Answer:
When objects are connected by strings and a force F is applied either vertically or horizontally or along an inclined plane, it produces a tension T in the string, which affects the acceleration to an extent. Let us discuss various cases for the same.

Vertical motion:
Consider two blocks of masses m₁ and m₂ (m₁ > m₂) connected by a light and inextensible string that passes over a pulley as shown in Figure 1.

Let the tension in the string be T and acceleration a.

When the system is released, both the blocks start, Two blocks connected by a string moving, m₂ vertically upward and m₁ downward with same acceleration a. The gravitational force m₁g on mass m₁ is used in lifting the mass m₂.

The upward direction is chosen as y direction. The free body diagrams of both masses are shown in Figure 2.

Applying Newton’s second law for mass m₂
T\(\hat { j } \) – m₂\(\hat { j } \)g = m₂ a\(\hat { j } \)

The left hand side of the above equation is the total force that acts on m₂ and the right hand side is the product of mass and acceleration of m₂ in direction.

By comparing the components on both sides, we get
T -m₂g = m₂a ……………………. (1)

Similarly, applying Newton’s law second law of for mass m₁
T\(\hat { j } \) – m₁g\(\hat { j } \) = -m₁a\(\hat { j } \)

As mass m₁ moves downward (-\(\hat { j } \)), its accleration is along (-\(\hat { j } \))
By comparing the components on both sides, we get
T – m₁g = -m₁a
m₁g – T = m₁a …………………….. (2)

Adding equations (1) and (2), we get
m₁g – m₂g = m₁a + m₂a
(m₁g – m₂)g = (m₁ + m₂)a …………………….. (3)

From equation (3), the acceleration of both the masses is
a = \(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right)\)g ……………………… (4)

If both the masses are equal (m₁ = m₂), from equation (4)
a = 0

This shows that if the masses are equal, there is no acceleration and the system as a whole will be at rest. To find the tension acting on the string, substitute the acceleration from the equation (4)
T – m₂g = m₂ \(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right)\)g
T = m₂g + m₂\(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right)\)g ……………………… (5)
By taking m₂g common in the RHS of equation (5)

Equation (4) gives only magnitude of accleration.

For mass m₁ g the accleration vector is given by \(\vec{a}=-\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right) g \hat{j}\)
For mass m₂ g the accleration vector is given by \(\vec{a}=-\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right) g \hat{j}\)

[OR]

(b) Derive the kinematic equation of motion for constant acceleration?
Answer:
Consider an object moving in a straight line with uniform or constant acceleration ‘a’. Let u be the velocity of the object at time t = 0, and v be velocity of the body at a later time t.

Velocity – time relation:

(I) The acceleration of the body at any instant is given by the first derivative of the velocity with respect to time,
a = \(\frac{dv}{dt}\) or dv = a dt
Integrating both sides with the condition that as time changes from 0 to t, the velocity changes from u to v. For the constant acceleration,

Displacement – time relation:

(II) The velocity of the body is given by the first derivative of the displacement with respect to time.
v = \(\frac{ds}{dt}\) or ds = vdt
and since v = u + at,
We get ds = (u + at)dt
Assume that initially at time t = 0, the particle started from the origin. At a later time t, the particle displacement is s. Further assuming that acceleration is time-independent, we have
\(\int_{0}^{s} d s=\int_{0}^{t} u d t+\int_{0}^{t} a t d t \text { or } s=u t+\frac{1}{2} a t^{2}\) ……………………. (2)
Velocity – displacement relation

(III) The acceleration is given by the first derivative of velocity with respect to time.
a = \(\frac{dv}{dt}\) = \(\frac{dv}{ds}\) \(\frac{ds}{dt}\) = \(\frac{dv}{ds}\) v [since ds/dt = v] where s is displacement traversed.
This is rewritten as a = \(\frac{1}{2}\) \(\frac { dv^{ 2 } }{ s } \) or ds = \(\frac{1}{2a}\) d(v²)
Integrating the above equation, using the fact when the velocity changes from u² to v², displacement changes from u² to v², we get

We can also derive the displacement s in terms of initial velocity u and final velocity v.
From equation we can write,
at = v – u
Substitute this in equation, we get
s = ut + \(\frac{1}{2}\) (v -u)t
s = \(\frac{(u+v)t}{2}\)

Question 36 (a).
State and prove perpendicular axis theorem?
Answer:
Perpendicular axis theorem: This perpendicular axis theorem holds good only for plane laminar objects.

The theorem states that the moment of inertia of a plane laminar body about an axis perpendicular to its plane is equal to the sum of moments of inertia about two perpendicular axes lying in the plane of the body such that all the three axes are mutually perpendicular and have a common point.

Let the X and Y-axes lie in the plane and Z-axis perpendicular to the plane of the laminar object. If the moments of inertia of the body about X and Y-axes are Ix and IY respectively and Iz is the moment of inertia about Z-axis, then the perpendicular axis theorem could be expressed as,
I_z = I_x + I_y

To prove this theorem, let us consider a plane laminar object of negligible thickness on which lies the origin (O). The X and Y-axes lie on the plane and Z-axis is perpendicular to it as shown in figure. The lamina is considered to be made up of a large number of particles of mass m. Let us choose one such particle at a point P which has coordinates (x, y) at a distance r from O.

The moment of inertia of the particle about Z-axis is, mr².
The summation of the above expression gives the moment of inertia of the entire lamina about Z-axis as,
I_z = Σ mr²
Here, r² = x² + y²
Then, I_z = Σm(x² + y²)
I_z = Σmx² + Σmy²
In the above expression, the term Σmx² is the moment of inertia of the body about the Y-axis and similarly the term Σmy² is the moment of inertia about X-axis. Thus,
I_X = Σmy² and I_Y = Σmx²
Substituting in the equation for I_Z gives, I_Z = I_X + I_Y
Thus, the perpendicular axis theorem is proved.

[OR]

(b) Explain in detail the triangle law of addition?
Answer:
Let us consider two vectors \(\vec { A } \) and \(\vec { B } \) as shown in figure.

To find the resultant of the two vectors we apply the triangular law of addition as follows:

Represent the vectors \(\vec { A } \) and \(\vec { B } \) by the two adjacent sides of a triangle taken in the same order. Then the resultant is given by the third side of the triangle as shown in figure.

To explain further, the head of the first vector \(\vec { A } \) is connected to the tail of the second vector \(\vec { B } \). Let θ be the angle between A and B. Then R is the resultant vector connecting the tail of the first vector \(\vec { A } \) to the head of the second vector \(\vec { B } \).

The magnitude of \(\vec { R } \) (resultant) is given geometrically by the length of \(\vec { R } \)(OQ) and the direction of the resultant vector is the angle between \(\vec { R } \) and \(\vec { A } \). Thus we write \(\vec { R } \) = \(\vec { A } \) + \(\vec { B } \).
\(\overline { OQ } \) = \(\overline { OP } \) + \(\overline { PQ } \)

1. Magnitude of resultant vector:
The magnitude and angle of the resultant vector are determined by using triangle law of vectors as follows.

From figure, consider the triangle ABN, which is obtained by extending the side OA to ON. ABN is a right angled triangle.

From figure, let R is the magnitude of the resultant of \(\vec { A } \) and \(\vec { B } \).

For ∆OBN, we have OB² = ON² + BN²
⇒ R² = (A + B cos θ)² + (B sin θ)²
⇒ R² = A² + B² cos² θ + 2AB cos θ + B²sin² θ
⇒ R² = A² + B²(cos² θ + sin² θ) + 2AB cos θ
⇒R² = \(\sqrt{A^{2}+B^{2}+2 A B \cos \theta}\)

2. Direction of resultant vectors:
If θ is the angle between \(\vec { A } \) and \(\vec { B } \), then
|\(\vec { A } \) + \(\vec { B } \)| = \(\sqrt{A^{2}+B^{2}+2 A B \cos \theta}\)
If \(\vec { R } \) makes an angle α with \(\vec { A } \), then in ∆OBN,
tan α = \(\frac{BN}{ON}\) = \(\frac{BN}{OA+AN}\)
tan α = \(\frac{B \sin \theta}{A+B \cos \theta}\) ⇒ α = tan^-1\(\left(\frac{B \sin \theta}{A+B \cos \theta}\right)\)

Question 37 (a).
Explain in detail the various types of errors?
Answer:
The uncertainty in a measurement is called an error. Random error, systematic error and gross error are the three possible errors.

(I) Systematic errors:
Systematic errors are reproducible inaccuracies that are consistently in the same direction. These occur often due to a problem that persists throughout the .experiment. Systematic errors can be classified as follows.

(1) Instrumental errors:
When an instrument is not calibrated properly at the time of manufacture, instrumental errors may arise. If a measurement is made with a meter scale whose end is worn out, the result obtained will have errors. These errors can be corrected by choosing the instrument carefully.

(2) Imperfections in experimental technique or procedure:
These errors arise due to the limitations in the experimental arrangement. As an example, while performing experiments with a calorimeter, if there is no proper insulation, there will be radiation losses. This results in errors and to overcome these, necessary correction has to be applied

(3) Personal errors:
These errors are due to individuals performing the experiment, may be due to incorrect initial setting up of the experiment or carelessness of the individual making the observation due to improper precautions.

(4) Errors due to external causes:
The change in the external conditions during an experiment can cause error in measurement. For example, changes in temperature, humidity, or pressure during measurements may affect the result of the measurement.

(5) Least count error:
Least count is the smallest value that can be measured by the measuring instrument, and the error due to this measurement is least count error. The instrument’s resolution hence is the cause of this error. Least count error can be reduced by using a high precision instrument for the measurement.

(II) Random errors:
Random errors may arise due to random and unpredictable variations in experimental conditions like pressure, temperature, voltage supply etc. Errors may also be due to personal errors by the observer who performs the experiment. Random errors are sometimes called “chance error”.

When different readings are obtained by a person every time he repeats the experiment, personal error occurs. For example, consider the case of the thickness of a wire measured using a screw gauge. The readings taken may be different for different trials. In this case, a large number of measurements are made and then the arithmetic mean is taken.
If n number of trial readings are taken in an experiment, and the readings are
a₁, a₂, a₃, ……………………….. a_n. The arithmetic mean is

[OR]

(b) To move an object, which one is easier, push or pull? Explain?
Answer:
When a body is pushed at an arbitrary angle θ (0 to \(\frac{π}{2}\)), the applied force F can be resolved into two components as F sin θ parallel to the surface and F cos θ perpendicular to the surface as shown in figure. The total downward force acting on the body is mg + F cos θ. It implies that the normal force acting on the body increases. Since there is no acceleration along the vertical direction the normal force N is equal to
N_push = mg + F cos θ …………………. (1)
As a result the maximal static friction also increases and is equal to
\(f_{s}^{\max }=\mu_{r} N_{\text {push }}=\mu_{s}(m g+F \cos \theta)\) …………………. (2)
Equation (2) shows that a greater force needs to be applied to push the object into motion.

When an object is pulled at an angle 0, the applied force is resolved into two components as shown in figure. The total downward force acting on the object is
N_pull = mg – F cos θ …………………….. (3)

Question 38 (a).
Describe the method of measuring angle of repose?
Answer:
Angle of Repose Consider an inclined plane on which an object is placed, as shown in figure. Let the angle which this plane makes with the horizontal be θ. For small angles of θ, the object may not slide down. As θ is increased, for a particular value of θ, the object begins to slide down. This value is called angle of repose. Hence, the angle of repose is the angle of inclined plane with the horizontal such that an object placed on it begins to slide.

Let us consider the various forces in action here. The gravitational force mg is resolved into components parallel (mg sin θ) and perpendicular (mg cos θ) to the inclined plane. The component of force parallel to the inclined plane (mg sin θ) tries to move the object down. The component of force perpendicular to the inclined plane (mg cos θ) is balanced by the Normal force (N).
N = mg cos θ ……………… (1)

When the object just begins to move, the static friction attains its maximum value
f_s = \(f_{s}^{\max }\)

This friction also satisfies the relation
\(f_{s}^{\max }\) = µ_s = mg sin θ …………………… (2)

Equating the right hand side of equations (1) and (2),
\(\left(f_{s}^{\max }\right) / \mathrm{N}=\sin \theta / \cos \theta\)

From the definition of angle of friction, we also know that
tan θ = µ_s ……………………… (3) in which θ is the angle of friction.

Thus the angle of repose is the same as angle of friction. But the difference is that the angle of repose refers to inclined surfaces and the angle of friction is applicable to any type of surface.

[OR]

(b) A block of mass m slides down the plane inclined at an angle 60° with an acceleration g/2. Find the co-efficient of kinetic friction?
Answer:
Kinetic friction comes to play as the block is moving on the surface.
The forces acting on the mass are the normal force perpendicular to surface, downward gravitational force and kinetic friction along the surface.
Along the x-direction

There is no motion along the y-direction as normal force is exactly balanced by the mg cos θ.
mg cos θ = N = mg/2

[OR]

(c) Write a note on triangulation method and radar method to measure larger distances?
Answer:
Triangulation method for the height of an accessible object:
Let AB = h be the height of the tree or tower to 6e measured. Let C be the point of observation at distance x from B. Place a range finder at C and measure the angle of elevation, ACB = θ as shown in figure.

From right angled triangle ABC,
tan θ = \(\frac{AB}{BC}\) = \(\frac{h}{x}\)
(or) height h = x tan θ
Knowing the distance x. the height h can be detennined.

RADAR method:
The word RADAR stands for radio detection and ranging. A radar can be used to measure accurately the distance of a nearby planet such as Mars. In this method, radio waves are sent from transmitters which, after reflection from the planet, are detected by the receiver.

By measuring, the time interval (t) between the instants the radio waves are sent and received, the distance of the planet can be determined as where v is the speed of the radio wave. As the time taken (t) is for the distance covered during the forward and backward path of the radio waves, it is divided by 2 to get the actual distance of the object. This method can also be used to determine the height, at which an aeroplane flies from the ground.

[OR]

(d) Jupiter is at a distance of 824.7 million km from the earth. Its angular diameter is measured to be 35.75”. Calculate the diameter of jupiter?
Answer:
Given,
Distance of Jupiter = 824.7 × 10⁶ km = 8.247 × 10¹¹ m
angular diameter = 35.72 × 4.85 × 10^-6 rad = 173.242 × 10^-6 rad
= 1.73 × 10^-4rad
∴ Diameter of Jupiter D = θ × d = 1.73 × 10^-4 rad × 8.247 × 10¹¹ m
14.267 × 10⁷ m = 1.427 × 10⁸ m (or) 1.427 × 10⁵ km

Students can download 6th Social Science Term 3 History Chapter 3 The Age of Empires: Guptas and Vardhanas Questions and Answers, Notes, Samacheer Kalvi 6th Social Science Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Social Science History Solutions Term 3 Chapter 3 The Age of Empires: Guptas and Vardhanas

Samacheer Kalvi 6th Social Science The Age of Empires: Guptas and Vardhanas Text Book Back Questions and Answers

I. Choose the correct Answer

Question 1.
………………. was the founder of Gupta dynasty.
(a) Chandragupta I
(b) Sri Gupta
(c) Vishnu Gopa
(d) Vishnugupta
Answer:
(b) Sri Gupta

Question 2.
Prayog Prashasti was composed by ________
(a) Kalidasa
(b) Amarasimha
(c) Harisena
(d) Dhanvantri
Answer:
(c) Harisena

Question 3.
The monolithic iron pillar of Chandragupta is at ………………
(a) Mehrauli
(b) Bhitari
(c) Gadhva
(d) Mathura
Answer:
(a) Mehrauli

Question 4.
________ was the first Indian to explain the process Of surgery.
(a) Charaka
(b) Sushruta
(c) Dhanvantri
(d) Agnivasa
Answer:
(b) Sushrutal

Question 5.
……………… was the Gauda ruler of Bengal.
(a) Sasanka
(b) Maitraka
(c) Rajavardhana
(d) Pulikesin II
Answer:
(a) Sasanka

II. Match the statement with the reason and tick the appropriate answer

Question 1.
Assertion (A) : Chandragupta I crowned himself as a monarch of a large kingdom after eliminating various small states in Northern India.
Reason (R) : Chandragupta I married Kumaradevi of Lichchavi family.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are correct but R is not correct explanation of A.
(c) A is correct but R is not correct.
(d) A is not correct but R is correct.
Answer:
(a) Both A and R are true and R is the correct explanation of A

Question 2.
Statement I : Chandragupta II did not have cordial relationship with the rules of South India.
Statement II : The divine theory of kingship was practised by the Gupta rulers.
(a) Statement I is wrong but statement II is correct.
(b) Statement II is wrong but statement I is correct.
(c) Both the statements are correct.
(d) Both the statements are wrong.
Answer:
(a) Statement I is wrong but statement II is correct.

Question 3.
Which of the following is arranged in chronological order?
(a) Srigupta – Chandragupta I – Samudragupta – Vikramaditya
(b) Chandragupta I – Vikramaditya – Srigupta – Samudragupta
(c) Srigupta – Samudragupta – Vikramaditya – Chandragupta I
(d) Vikramaditya – Srigupta – Samudragupta – Chandragupta I
Answer:
(a) Srigupta – Chandragupta I – Samudragupta -Vikramaditya

Question 4.
Consider the following statements and find out which of the following statements (s) is/are correct.
(1) Lending money at high rate of interest was practised.
(2) Pottery and mining were the most flourishing industries,
(a) 1. is correct
(b) 2. is correct
(c) Both 1 and 2 are correct
(d) Both 1 and 2 are wrong
Answer:
(a) 1. is correct

Question 5.
Circle the odd one

Answer:
Samudragupta.

Answer:
Harshacharita.

III. Fill in the blanks Answer

1. ……………., the king of Ceylon, was a contemporary of Samudragupta.
2. A Buddhist monk from China ……………., visited India during the reign of Chandragupta II.
3. ……………. invasion led to the downfall of the Gupta Empire.
4. ……………. was the main revenue to the Government.
5. The official language of the Guptas was …………….
6. ……………., the Pallava king was defeated by Samudragupta.
7. ……………. was the popular king of the Vardhana dynasty.
8. Harsha shifted his capital from ……………. to Kanauj.

Answer:

1. Reign of
2. Fahien
3. Huns
4. Land tax
5. Sanskrit
6. Vishnugopa
7. Harsha Vardhana
8. Thaneswar

IV. State whether True or False

1. Dhanvantri was a famous scholar in the field of medicine.
2. The structural temples built during the Gupta period resemble the Indo – Aryan style.
3. Sati was not in practice in the Gupta Empire.
4. Harsha belonged to the Hinayana school of thought.
5. Harsha was noted for his religious intolerance.

Answer:

1. True
2. False
3. False
4. False
5. False

V. Match the following

Question 1.

Answer:
b) 2, 4, 1, 3, 5

Question 2.

Answer:
c) 3, 5, 1, 2, 4

VI. Answer in one or two sentences

Question 1.
Who was given the title Kaviraja? Why?
Answer:

1. The title Kaviraja was given to Samudragupta.
2. He was a great lover of poetry and music.
3. In one of the gold coins, he is portrayed playing the harp (Veenai)

Question 2.
What were the subjects taught at Nalanda University?
Answer:

1. At Nalanda University Buddhism was the main subject of study.
2. Other subjects like Yoga, Vedic literature, and medicine were also taught.

Question 3.
Explain the Divine Theory of Kingship.
Answer:

1. The divine theory of Kingship meant that the king is the representative of God on earth.
2. He is answerable only to God and not to anyone else.

Question 4.
Highlight the achievements of Guptas in metallurgy.
Answer:

1. Mining and metallurgy were the most flourishing industries during the Gupta period.
2. The most important evidence of development in metallurgy was the Mehrauli Iron Pillar installed by King Chandragupta in Delhi.
3. This monolithic iron pillar has lasted through the centuries without rusting.

Question 5.
Who were the Huns?
Answer:

1. Huns were the nomadic tribe, who under their great Attila were terrorizing Rome and Constantinople.
2. They came to India through Central Asia, defeated Skandagupta, and spread across central India.
3. Their chief Toromana crowned himself asking.
4. After him, his son Mihirakula ruled and got finally defeated by Yasodharman, ruler of Malwa.

Question 6.
Name the three kinds of tax collected during Harsha’s reign.
Answer:
A Bhaga, Hiranya, and Bali were three kinds of tax collected during Harsha’s reign.

Question 7.
Name the books authored by Harsha.
Answer:
The books authored by Harsha were Ratnavali, Nagananda, and Priyadharshika.

VII. Answer the following briefly

Question 1.
Write a note on Prashasti.
Answer:

1. Prashasti is a Sanskrit word, meaning communication or in praise of.
2. Court poets flattered their kings listing out their achievements.
3. These accounts were later engraved on pillars so that the people could read them.

Question 2.
Give an account of Samudragupta’s military conquests.
Answer:

1. Samudragupta was a great general and he carried on a vigorous campaign all over the country.
2. He defeated the Pallava king Vishnugopa.
3. He conquered nine kingdoms in northern India.
4. He reduced 12 rulers of southern India to the status of feudatories and to pay tribute.
5. He received homage from the rulers of East Bengal, Assam, Nepal, the eastern part of Punjab, and various tribes of Rajasthan.

Question 3.
Describe the land classification during the Gupta period.
Answer:
Classification of land during the Gupta period.

1. Kshetra – Cultivable land
2. Khila – Wasteland
3. Aprahata – Jungle (or) Forest land
4. Vasti – Habitable land
5. Gapata saraha – Pastoral and

Question 4.
Write about Sresti and Sarthavaha traders.
Answer:

1. Sresti: Sresti traders were usually settled at a standard place.
2. Sarthavaha: Sarthavaha traders caravan traders who carried their goods to different places.

Question 5.
Highlight the contribution of Guptas to architecture.
Answer:

1. From the earlier tradition of rock – out shrines, the Guptas were the first to construct temples.
2. These temples, adorned with towers and elaborate carvings, were dedicated to all Hindu deities.
3. The most notable rock-cut caves are found at Ajanta and Ellora, Bagh, and Udaygiri.
4. The structural temples built during this period resemble the Dravidian style.

Question 6.
Name the works of Kalidasa.
Answer:

1. Kalidasa’s famous dramas were Sakunthala, Malavikagnimitra and Vikramaoorvashiyam.
2. Other significant works were Meghaduta, Raghuvamsa, Kumarasambava and Ritusamhara

Question 7.
Estimate Harshvardhana as a poet and a dramatist.
Answer:

1. Harsha himself was a poet and dramatist.
2. Around him gathered the best of poets and artists.
3. His popular works are Ratnavali, Nagananda and Priyadharshika
4. is royal court was adorned by Banabhatta, Mayura, Hardatta, and Jayasena.

VIII. HOTs

Question 1.
The gold coins issued by Gupta kings indicate ………………
Answer:
(a) the availability of gold mines in the kingdom
(b) the ability of the people to work with gold
(c) the prosperity of the kingdom
(d) the extravagant nature of kings.
Answer:
(c) the prosperity of the kingdom

Question 2.
The famous ancient paintings at Ajanta were painted on __________
a. walls of caves
b. ceilings of temples
c. Rocks
d. papyrus
Answer:
a. walls of caves

Question 3.
Gupta period is remembered for ……………….
(a) renaissance in literature and art
(b) expeditions to southern India
(c) invasion of Huns
(d) religious tolerance
Answer:
(a) renaissance in literature and art

Question 4.
What did Indian scientists achieve in astronomy and mathematics during the Gupta period?
Answer:

1. The invention of zero and the consequent evolution of the decimal system was the legacy of Guptas to the modem world.
2. Aryabhatta, Varahamihira, and Brahmagupta were the foremost astronomers and mathematicians of the time.
3. Aryabhatta, in his book ‘ Surya Siddhanta’, explained the true causes of solar and lunar eclipses.
4. He was the first Indian astronomer to declare that the earth revolves around its own axis.
5. Dhanvantri was a famous scholar in the field of medicine.
6. He was a specialist in Ayurveda.
7. Charaka was a medical scientist.
8. Susruta was the first Indian to explain the process of surgery.

IX. Student activity (For Students)

1. Stage any one of the dramas of Kalidasa in the classroom.
2. Compare and contrast the society of Guptas with that of Mauryas.

X. Life Skills (For Students)

1. Collect information about the contribution of Aryabhatta, Varahamihira and Brahmagupta to astronomy.
2. Visit a nearby ISRO centre to know more about satellite launching.

XI. Answer Grid

Question 1.
Who was Toromana?
Answer:
Toromana was the chief of White Huns.

Question 2.
Name the high-ranking officials of the Gupta Empire.
Answer:
Dandanayakas and Maha dandanayakas.

Question 3.
Name the Gupta kings who performed AsVamedha yagna.
Answer:
Samudragupta and Kumaragupta I

Question 4.
Name the book which explained the causes for the lunar and solar eclipses,
Answer:
Surya Siddhanta

Question 5.
Name the first Gupta king to find a place on coins.
Answer:
Samudragupta

Question 6.
Which was the main source of information to know about the Samudragupta’s reign?
Answer:
Allahabad Pillar

Question 7.
Harsha was the worshipper in the beginning.
Answer:
Shiva

Question 8.
University reached its fame during the Harsha period.
Answer:
The Nalanda

Samacheer Kalvi 6th Social Science The Post-Mauryan India Additional Important Questions and Answers

I. Choose the Correct Answer:

Question 1.
The successor of Sri Gupta ……………
(a) Kumaragupta I
(b) Skandagupta
(c) Vishnugupta
(d) Ghatotkacha
Answer:
(d) Ghatotkacha

Question 2.
Sri Gupta was succeeded by _______
(a) Chandra Gupta
(b) Samundra Gupta
(c) Ghatotkacha
(d) Skanda Gupta
Answer:
(c) Ghatotkacha

Question 3.
The Huhs chief crowned himself as king.
(a) Yasodharman
(b) Attila
(c) Mihirakula
(d) Toromana
Answer:
(d) Toromana

Question 4.
Srimeghavarman was the ruler of _______
(a) Singapore
(b) Ceylon
(c) Malaysia
(b) Hansena
Answer:
(b) Ceylon

Question 5.
The place Harsha went to participate in the great Kumbhamela held.
(a) Allahabad
(b) Kasi
(c) Ayodhya
(d) Prayag
Answer:
(d) Prayag

II. Match the statement with the reason and tick the appropriate answer

Question 1.
Assertion (A) : The last of the great Guptas Narasimha Gupta I was paying tribute to Mihirakula.
Reason (R) : He stopped paying tribute to Mihirakula’s hostility towards Buddhism.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are correct but R is not the correct explanation of A.
(c) A is correct but R is not correct
(d) A is not correct but R is correct
Answer:
(b) Both A and R are correct but R is not the correct explanation of A

Question 2.
Statement I : Criminal law was not more severe than that of the Gupta age.
Statement II : Death punishment was the punishment for violation of the laws and for plotting against the king.
(a) Statement I is wrong but statement II is correct
(b) Statement II is wrong but statement I is correct.
(c) Both the statements are correct.
(d) Both the statements are wrong.
Answer:
d) Both the statements are wrong

III. Fill in the blanks

1. In the assembly at ……………. Harsha distributed his wealth.
2. The capital of China ……………. was a great center of art and learning.
3. ……………. was the wife of Chandragupta I.
4. The military campaigns of kings were financed through revenue ……………..
5. The peasants were required to pay various taxes and were reduced to the position of ……………..

Answer:

1. Prayag
2. Xian
3. Kumaradevi
4. Surpluses
5. serfs

IV. Match the following

Answer:
b) 4, 5, 2, 1, 3

V. Answer in one or two sentences

Question 1.
Write a note on ‘Lichchhavi’.
Answer:

1. Lichchhavi was an old gana – Sanga and its territory lay between the Ganges and the Nepal Terai.
2. Chandragupta, I married Kumaradevi of the famous and powerful lichchhavi family.

Question 2.
How did Chandragupta I crown himself the monarch of a larger kingdom?
Answer:

1. Chandragupta, I married Kumaradevi of the famous and powerful Lichchhavi family.
2. With the support of this family, Chandragupta eliminated various small states and| crowned himself the monarch of a larger kingdom.

Question 3.
What did the travel accounts of Fahien provide information about the condi¬tions of the people of Magadha?
Answer:

1. According to Fahien the people of Magadha were happy and prosperous.
2. Gaya was desolated. Kapilvasthu had become a jungle, but at Pataliputra people were rich and prosperous.

VII. Answer the following briefly

Question 1.
Name the officials employed by the Gupta rulers.
Answer:

1. High – ranking officials were called dandanayakas and mahadandnayakas.
2. The provinces known as deshas or bhuktis were administered by the governors designated as Uparikas. The districts such as vaishyas, were controlled by vishyapatis. At the village level, gramika and gramadhyaksha were the functionaries.
3. The military designations.
4. Baladhikrita (Commander of infantry)
5. Mahabaladhikrita (Commander of the cavalry)
6. Dutakas (spies)

Question 2.
Mention the importance of Fahien’s travel accounts.
Answer:

1. During the reign of Chandragupta II, the Buddhist monk Fahien visited India.
2. His travel accounts provided us information about the socio-economic, religious and moral conditions of the people of the Gupta age.
3. According to Fahien, the people of Magadha were happy and prosperous.
4. Justice was mildly administered and there was no death penalty.
5. Gaya was desolated, Kapilavasthu had become a jungle, but at Pataliputra, people were rich and prosperous.

VIII. Mind map

Students can Download Tamil Nadu 11th Maths Model Question Paper 4 English Medium Pdf, Tamil Nadu 11th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

TN State Board 11th Maths Model Question Paper 4 English Medium

General Instructions:

1. The question paper comprises of four parts.
2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. All questions of Part I, II, III and IV are to be attempted separately.
4. Question numbers 1 to 20 in Part I are Multiple Choice Questions of one mark each.
   These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 21 to 30 in Part II are two-mark questions. These are to be answered in about one or two sentences.
6. Question numbers 31 to 40 in Part III are three-mark questions. These are to be answered in above three to five short sentences.
7. Question numbers 41 to 47 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.

Time: 2:30 Hours
Maximum Marks: 90

PART – I

I. Choose the correct answer. Answer all the questions: [20 × 1 = 20]

Question 1.
If n(A) = 2 and n(B∪C) = 3 then n[(A × B) ∪ (A × C)] is ………………..
(a) 2³
(b) 3²
(c) 6
(d) 5
Answer:
(c) 6

Question 2.
For any two sets A and B, A∩(A∪B) = …………………….
(a) B
(b) ∅
(c) A
(d) none of these
Answer:
(c) A

Question 3.
cos 1° + cos 2° + cos 3° + cos 4° + cos 179° = …………………
(a) 0
(b) 1
(c) -1
(d) 89
Answer:
(a) 0

Question 4.
The value of log₉ 27 is ……………………
(a) \(\frac{2}{3}\)
(b) \(\frac{3}{2}\)
(c) \(\frac{3}{4}\)
(d) \(\frac{4}{3}\)
Answer:
(b) \(\frac{3}{2}\)

Question 5.
The value of \(\frac{\sin 3 \theta+\sin 5 \theta+\sin 7 \theta+\sin 9 \theta}{\cos 3 \theta+\cos 5 \theta+\cos 7 \theta+\cos 9 \theta}\) = ………………..
(a) tan3θ
(b) tan6θ
(c) cot3θ
(d) cot6θ
Answer:
(b) tan6θ

Question 6.
In 3 fingers the number of ways 4 rings can be worn in ……………………. ways.
(a) 43 – 1
(b) 34
(c) 68
(d) 64
Answer:
(d) 64

Question 7.
Everybody in a room shakes hands with everybody else. The total number of shake hands is 66. The number of persons in the room is ……………….
(a) 11
(b) 12
(c) 10
(d) 6
Answer:
(b) 12

Question 8.
The H.M of two positive number whose AM and G.M. are 16, 8 respectively is ………………..
(a) 10
(b) 6
(c) 5
(d) 4
Answer:
(d) 4

Question 9.
The co-efficient of the term independent of x in the expansion of (2x+\(\frac{1}{3x}\))⁶ is …………………
(a) \(\frac{160}{27}\)
(b) \(\frac{160}{27}\)
(c) \(\frac{80}{3}\)
(d) \(\frac{80}{9}\)
Answer:
(a) \(\frac{160}{27}\)

Question 10.
The value of \(\left|\begin{array}{lll}
a & 0 & 0 \\
0 & b & 0 \\
0 & 0 & c
\end{array}\right|^{2}\) is ………………..
(a) abc
(b) -abc
(c) 0
(d) a²b²c²
Answer:
(d) a²b²c²

Question 11.
The value of x for which the matrix A = \(\left[\begin{array}{cc}
e^{x-2} & e^{7+x} \\
e^{2+x} & e^{2 x+3}
\end{array}\right]\) is singular is …………………..
(a) 9
(b) 8
(c) 7
(d) 6
Answer:
(b) 8

Question 12.
If |\(\vec { a } \) + \(\vec { b } \)| = 60, |\(\vec { a } \) – \(\vec { b } \)| = 40 and |\(\vec { b } \)| = 46 then |\(\vec { a } \)| is …………………
(a) 42
(b) 12
(c) 22
(d) 32
Answer:
(c) 22

Question 13.
Given \(\vec { a } \) = 2\(\vec { i } \) + \(\vec { j } \) – 8\(\vec { k } \) and \(\vec { b } \) = \(\vec { i } \) + 3\(\vec { j } \) – 4\(\vec { k } \) then |\(\vec { a } \) + \(\vec { b } \)| = ………………….
(a) 13
(b) \(\frac{13}{3}\)
(c) \(\frac{4}{13}\)
(d) \(\frac{3}{13}\)
Answer:
(a) 13

Question 14.
If f(x) = \(\left\{\begin{array}{ccc}
k x & \text { for } & x \leq 2 \\
3 & \text { for } & 2
\end{array}\right.\) is continous at x = 2 then the value of k is ……………………
(a) \(\frac{3}{4}\)
(b) 0
(c) 1
(d) \(\frac{4}{3}\)
Answer:
(c) 1

Question 15.
If f: R→R is defined by f(x) = |x – 3| + |x – 4| for x∈R then \(\lim _{x \rightarrow 3^{-}}\) f(x) is equal to ………………..
(a) -2
(b) -1
(c) 0
(d) 1
Answer:
(c) 0

Question 16.
\(\lim _{x \rightarrow \infty}\left(\frac{x^{2}+5 x+3}{x^{2}+x+3}\right)^{x}\) is ………………..
(a) e⁴
(b) e²
(c) e³
(d) 1
Answer:
(a) e⁴

Question 17.
\(\int \frac{e^{x}\left(x^{2} \tan ^{-1} x+\tan ^{-1} x+1\right)}{x^{2}+1}\) dx is ………………..
(a) e tan^-1(x + 1)
(b) tan^-1(e^x) + c
(c) e^x \(\frac{\left(\tan ^{-1} x\right)^{2}}{2}\) + c
(d) e^xtan^-1x + c
Answer:
(d) e^xtan^-1x + c

Question 18.
∫ \(\frac { secx }{ \sqrt { cos2x } } \) dx = …………………..
(a) tan^-1(sin x) + c
(b) 2 sin^-1(tan x) + c
(c) tan^-1(cos x) + c
(d) sin^-1 (tan x) + c
Answer:
(d) sin^-1 (tan x) + c

Question 19.
\(\int \frac{e^{6 \log x}-e^{5 \log x}}{e^{4 \log x}-e^{3 \log x}}\) dx = ………………..
(a) x + c
(b) \(\frac { x^{ 3 } }{ 3 } \) + c
(c) \(\frac { 3 }{ x^{ 3 } } \) + c
(d) \(\frac { 1 }{ x^{ 2 } } \) + c
Answer:
(b) \(\frac { x^{ 3 } }{ 3 } \) + c

Question 20.
It is given that the events A and B are such that P(A) = \(\frac{1}{4}\), P(A/B) = \(\frac{1}{2}\), P(B/A) = \(\frac{2}{3}\) then P(B) = …………………
(a) \(\frac{1}{6}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{2}{3}\)
(d) \(\frac{1}{2}\)
Answer:
(b) \(\frac{1}{3}\)

PART – II

II. Answer any seven questions. Question No. 30 is compulsory. [7 × 2 = 14]

Question 21.
In the set Z of integers, define mRn if m – n is a multiple of 12. Prove that R is an equivalence relation?
Answer:
As m – m = 0 and 0 = 0 × 12, we have 0 is a multiple of 12; hence mRm proving that R is reflexive.
Let mRn. Then m – n = 12k for some integer k; thus n – m = 12(-k) and hence nRm.
This shows that R is symmetric.
Let mRn and nRp: then m – n = 12k and n – p = 12l for some integers k and l.
So m – p = 12(k + l) and hence mRp. This shows that R is transitive.
Thus R is an equivalence relation.

Question 22.
Simplify:
\(\frac { 1 }{ 2+\sqrt { 3 } } \) + \(\frac { 3 }{ 4-\sqrt { 5 } } \) + \(\frac { 6 }{ 7-\sqrt { 8 } } \)
Answer:

Question 23.
Find the value of sin 22 \(\frac{1}{2}\)°?
Answer:
We know that cos θ = 1 – 2 sin² \(\frac{θ}{2}\) ⇒ sin \(\frac{θ}{2}\) = ±\(\sqrt { \frac { 1-cos2\theta }{ 2 } } \)
Take θ = 45°, we get sin \(\frac{45°}{2}\) = ±\(\sqrt { \frac { 1-cos45°}{ 2 } } \), (taking positive sign only, since 22\(\frac{1}{2}\)° lies in the first quadrant)
Thus, sin 22\(\frac{1}{2}\)° = \(\sqrt{\frac{1-\frac{1}{\sqrt{2}}}{2}}=\frac{\sqrt{2-\sqrt{2}}}{2}\).

Question 24.
The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th
hour and wth hour?
Answer:
No. of bacteria at the beginning = 30
No. of bacteria after 1 hour = 30 × 2 = 60
No. of bactena after 2 hours = 30 × 2² = 30 × 4 = 120
No. of bacteria after 4 hours = 30 × 2⁴ = 30 × 16 = 480
No. of bacteria after n^th hour = 30 × 2ⁿ

Question 25.
If the sum of the distance of a moving point in a plane from the axis is 1, then find the locus of the point?
Answer:
Let coordinates of a moving point P be (x, y).
Given that the sum of the distances from the axis to the point is always 1.
∴|x| + |y| = 1 ⇒ x + y = 1
⇒- x- y = 1 ⇒ x + y = 1
⇒ x – y = 1
Hence, these equations give us the locus of the point P which is a square.

Question 26.
If (a, a + b, a + b + c) is one set of direction ratios of the line joining (1, 0, 0) and (0, 1, 0) then find a set of values of a, b, c?
Answer:
Let A be the point (1, 0, 0) and B be the point (0, 1, 0) (i.e.,) \(\overline { OA } \) = \(\hat { i } \) and \(\overline { OB } \) = \(\hat { j } \).
Then \(\overline { AB } \) = \(\overline { OB } \) – \(\overline { OA } \) = \(\hat { j } \) – \(\hat { i } \) = –\(\hat { i } \) + \(\hat { j } \)
= (-1, 1, 0)
= (a, a + b, a + b + c)
⇒ a = -1, a + b = 1 and a + b + c = 0
⇒ a = -1, ⇒ -1 + b = 1; a + b + c = 0
⇒ b = 2; -1 + 2 + c = 0 ⇒ c + 1 = 0
⇒ c = -1
∴ a = -1, b = 2, c = -1.
Note: if we taken \(\overline { BA } \) then we get a = 1, b = -2 and c = 1.

Question 27.
Find \(\frac{dy}{dx}\) for y = (x² + 4x + 6)⁵
Answer:
Let u = x² + 4x + 6
⇒ \(\frac{du}{dx}\) = 2x + 4
Now y = u⁵ = \(\frac{dy}{du}\) = 5u⁴
∴ \(\frac{dy}{dx}\) = \(\frac{dy}{du}\) × \(\frac{du}{dx}\) = 5u⁴ (2x + 4)
= 5(x² + 4x + 6)⁴ (2x + 4)
= 5(2x + 4) (x² + 4x + 6)⁴

Question 28.
Evaluate ∫\(\sqrt { 25x^{ 2 }-9 } \) dx?
Answer:

Question 29.
A bag contains 5 white and 7 black balls. 3 balls are drawn at random. Find the probability that

1. all are white
2. one white and 2 black.

Answer:
Number of white balls = 5
Number of black balls = 7
Total number of balls = 12
Selecting 3 from 12 balls can be done in
¹²C₃ = \(\frac{12 \times 11 \times 10}{3 \times 2 \times 1}\) = 220 ways
∴n(S) = 220

1. Let A be the selecting 3 white balls.
∴n(A) = ⁵C₃ = ⁵C₂ = \(\frac{5×3}{2×1}\) = 10
∴P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{10}{220}\) = \(\frac{1}{22}\)

2. Let B be the event of selecting one white and 2 black balls.
∴n(B) = ⁵C₁ × ⁷C₂ = (5) (\(\frac{7×6}{2×1}\)) = 5(21) = 105
∴P(B) = \(\frac{n(B)}{n(S)}\) = \(\frac{105}{220}\) = \(\frac{21}{44}\).

Question 30.
If (k, 2), (2, 4) and (3, 2) are vertices of the triangle of area 4 square units then determine the value of k?
Answer:
Area of ∆ with vertices (k, 2) (2, 4) and (3, 2) = \(\frac{1}{2}\) \(\left|\begin{array}{lll}
k & 2 & 1 \\
2 & 4 & 1 \\
3 & 2 & 1
\end{array}\right|\) = 4 given
⇒ \(\left|\begin{array}{lll}
k & 2 & 1 \\
2 & 4 & 1 \\
3 & 2 & 1
\end{array}\right|\) = 2(4) = 8
(i.e.,) k(4 – 2) – 2(2 – 3) + 1(4 – 12) ± 8
(i.e.,) 2k – 2(-1) + 1(-8) = ± 8
(i.e.,) 2k + 2 – 8 = 8
(i.e.,) 2k = 8 + 8 – 2 = 14
k = 14/2 = 7
∴k = 7
So k = 7 (or) k = -1.

2k + 2 – 8 = -8
⇒2k = – 8 + 8 – 2
2k = – 2
k = -1

PART – III

III. Answer any seven questions. Question No. 40 is compulsory. [7 × 3 = 21]

Question 31.
In the set Z of integers define mRn if m – n is a multiple of 12. Prove that R is an equivalence relation?

Question 32.
Prove that \(\frac{sin4x+sin2x}{cos4x+cos2x}\) = tan 3x?

Question 33.
A polygon has 90 diagonals. Find the number of its sides?

Question 34.
If n is an odd positive integer, prove that the coefficients of the middle terms in the expansion of (x + y)ⁿ are equal?

Question 35.
Find the equation of the line passing through the point (1, 5) and also divides the co-ordinate axes in the ratio 3 : 10?

Question 36.
Prove that \(\left|\begin{array}{ccc}
1 & x & x \\
x & 1 & x \\
x & x & 1
\end{array}\right|^{2}=\left|\begin{array}{ccc}
1-2 x^{2} & -x^{2} & -x^{2} \\
-x^{2} & -1 & x^{2}-2 x \\
-x^{2} & x^{2}-2 x & -1
\end{array}\right|\)

Question 37.
If G is the centroid of a traiangle ABC prove that \(\overline { GA } \) + \(\overline { GB } \) + \(\overline { GC } \) = 0

Question 38.
Find \(\frac{dy}{dx}\) for y = \(\sqrt { 1+tan2x } \)?

Question 39.
Evaluate \(\frac { \sqrt { x } }{ 1+\sqrt { x } } \) dx?

Question 40.
Find the relation between a and b if \(\underset { x\rightarrow 3 }{ lim } \) f(x) exists where f(x) = \(\left\{\begin{array}{cc}
a x+b & \text { if } x>3 \\
3 a x-4 b+1 \text { if } x<3
\end{array}\right.\)

PART – IV

IV. Answer all the questions. [7 × 5 = 35]

Question 41 (a).
From the curve y = |x|, draw(i) y = |x-1| + 1

1. y = |x + 1| + 1
2. y = |x + 2| – 3

[OR]

(b) Resolve into partial fraction \(\frac { x+4 }{ (x^{ 2 }-4)(x+1) } \)

Question 42 (a).
Find the number of positive integers greater than 6000 and less than 7000 which arc divisible by 5, provided that no digit is to be repeated?

[OR]

(b) If ⁿP_r = ⁿP_r+1 and ⁿC_r = ⁿC_r-1, find the values of n and r?

Question 43 (a).
In a ∆ABC, prove that b² sin 2C + c² sin 2B = 2bc sin A?

[OR]

(b) Differentiate the following s(t) = \(\sqrt[4]{\frac{t^{3}+1}{t^{3}-1}}\)?

Question 44 (a).
Find the equation of the lines make an angle 60° with the positive x axis and at a distance 5\(\sqrt{2}\) units measured from the point (4, 7) along the line x – y + 3 = 0

[OR]

(b) If y = A cos4x + B sin 4x, A and B are constants then Show that y₂ + 16y = 0

Question 45 (a).
Find the sum up to the 17^th term of the series \(\frac{1^{3}}{1}+\frac{1^{3}+2^{3}}{1+3}+\frac{1^{3}+2^{3}+3^{3}}{1+3+5}\) + …………..

[OR]

(b) A shopkeeper in a Nuts and Spices shop makes gifi packs of cashew nuts, raisins and almonds?

1. Pack I contains 100 gm of cashew nuts, 100 gm of raisins and 50 gm of almonds.
2. Pack-II contains 200 gm of cashew nuts, 100 gm of raisins and 100 gm of almonds.
3. Pack-III contains 250 gm of cashew nuts, 250 gm of raisins and 150 gm of almonds.
4. The cost of 50 gm of cashew nuts is ₹50, 50 gm of raisins is ₹10. and 50gm of almonds is ₹60. What is the cost of each gift pack?

Question 46 (a).
Find matrix C if A = \(\begin{bmatrix} 3 & 7 \\ 2 & 5 \end{bmatrix}\), B = \(\begin{bmatrix} -3 & 2 \\ 4 & -1 \end{bmatrix}\) and 5C + 28= A?

[OR]

(b) The probability that a new railway bridge will get an award for its design is 0.48, the probability that it will get an award for the efficient use of materials is 0.36, and that it will get both awards is 0.2. What is the probability, that

1. it will get at least one of the two awards
2. it will get only one of the awards.

Question 47 (a).
\(\underset { \alpha \rightarrow 0 }{ lim } \) \(\frac { sin(\alpha ^{ n }) }{ (sin\alpha )^{ m } } \)

[OR]

(b) Evaluate I = sin^-1 (\(\frac { 2x }{ (1+x)^{ 2 } } \)) dx?