Students can Download Tamil Nadu 11th Physics Model Question Paper 5 English Medium Pdf, Tamil Nadu 11th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
TN State Board 11th Physics Model Question Paper 5 English Medium
General Instructions:
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- All questions of Part I, II, III and IV are to be attempted separately.
- Question numbers 1 to 15 in Part I are Multiple Choice Questions of one mark each.
These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer - Question numbers 16 to 24 in Part II are two-mark questions. These are to be answered in about one or two sentences.
- Question numbers 25 to 33 in Part III are three-mark questions. These are to be answered in about three to five short sentences.
- Question numbers 34 to 38 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.
Time: 3 Hours
Maximum Marks: 70
PART – I
Answer all the questions: [15 × 1 = 15]
Question 1.
Two protons are travelling. along the same straight path but in opposite directions. The relative velocity between the two is ……………………
(a) c
(b) \(\frac{c}{2}\)
(c) 2c
(d) 0
Hint:
One of the velocity V1 = V; Other velocity V2 = -V
Relative velocity (Vrel) = \(\frac{V_{1}-V_{2}}{\left[1+\frac{V^{2}}{C^{2}}\right]}\) = \(\frac{V-(-V)}{\left[1+\frac{V^{2}}{C^{2}}\right]}\) = \(\frac{2v}{2}\)
V = C
Vrelative = C
Answer:
(a) c
![]()
Question 2.
If the Earth stops rotating about its own axis, g remains unchanged at …………………..
(a) Equator
(b) Poles
(c) Latitude of 45°
(d) No where
Answer:
(b) Poles
Question 3.
When train stops, the passenger moves forward. It is due to ……………………
(a) Inertia of passenger
(b) Inertia of train
(c) Gravitational pull by Earth
(d) None of the above
Answer:
(a) Inertia of passenger
![]()
Question 4.
A particle of mass m moves in the xy plane with a velocity v along the straight line AB. If the angular momention of the particle with respect to origin O is LA when it is at A and LB when it is at B, then …………………….
(a) LA = LB
(b) LA < LB
(c) LA > LB
(d) The relationship between LA and LB depends uopn the slope of the line AB
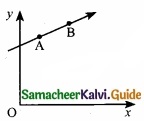
Hint:
Magnitude of L is, L = mvr sin ϕ = mvd
d = r sin ϕ is the distance of closest approach of the particle so the origin, as ‘d’ is same for both particles.
So, L A = LB
Answer:
(a) LA = LB
Question 5.
A couple produces ……………………….
(a) Pure rotation
(b) Pure translation
(c) Rotation and translation
(d) No motion
Answer:
(a) Pure rotation
![]()
Question 6.
A body starting from rest has an acceleration of 20 ms~2 the distance travelled by it in the sixth second is ……………………..
(a) 110 m
(b) 130m
(c) 90m
(d) 50 m
Hint:
Distance travelled in nth second, u = 0
Sn = u + \(\frac{1}{2}\)a(2n – 1)
S6 = 0 + \(\frac{1}{2}\) × 20 × (2 × 6 – 1); S6 = 110 m
Answer:
(a) 110 m
Question 7.
A lift of mass 1000 kg, which is moving with an acceleration of 1m/s2 in upward direction has tension has developed in its string is ………………………
(a) 9800 N
(b) 10800 N
(c) 11000 N
(d) 10000 N
Hint:
Tension, T = mg + ma = m(g + a) = 1000 (10 + 1)
T = 11000 N
Answer:
(c) 11000 N
![]()
Question 8.
The relation between acceleration and displacement of four particles are given below ………………………..
(a) ax = 2x
(b) ax = + 2x2
(c) ax = -2x2
(d) ax = -2x
Answer:
(d) ax = -2x
Question 9.
A sonometer wire is vibrating in the second overtone. In the wire there are, ……………………..
(a) Two nodes and two antinodes
(b) One node and two antinodes
(c) Four nodes and three antinodes
(d) Three nodes and three antinodes
Answer:
(d) Three nodes and three antinodes
![]()
Question 10.
Which of the following is the graph between the light (h) of a projectile and time (t), when it is projected from the ground ………………………..
(a) 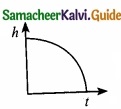
(b) 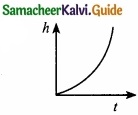
(c) 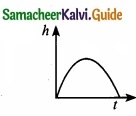
(d) 
Answer:
(c) 
Question 11.
According to kinetic theory of gases, the rms velocity of the gas molecules is directly proportional to ………………………
(a) \(\sqrt{T}\)
(b) T3
(c) T
(d) T4
Hint:
The rms velocity, Vrms = \(\sqrt{3KT/m}\) ⇒ Vrms ∝ \(\sqrt{T}\)
Answer:
(a) \(\sqrt{T}\)
Question 12.
A body of mass m moving with velocity v collides head on with another body of mass 2m which is initially at rest. The ratio of K.E of colliding body before and after collision will be ……………………..
(a) 1 : 1
(b) 2 : 1
(c) 4 : 1
(d) 9 : 1
Hint:
KE of colliding bodies before collision = \(\frac{1}{2}\) mv2
After collision the mass = m + 2m = 3m
velocity becomes V’ = \(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right)\)v = \(\frac{mv}{3m}\) = \(\frac{v}{3}\)
KE after collision = \(\frac{1}{2}\)m (\(\frac{V}{3}\)2 = \(\frac{1}{9}\) (\(\frac{1}{2}\) mv2)
\(\frac{\mathrm{KE}_{\text {before }}}{\mathrm{KE}_{\text {after }}}=\frac{\frac{1}{2} \mathrm{mv}^{2}}{\frac{1}{9}\left(\frac{1}{2} \mathrm{mv}^{2}\right)}=9: 1\)
Answer:
(d) 9 : 1
![]()
Question 13.
Four particles have velocity 1, 0, 2 and 3ms-1. The root mean square velocity of the particles is ……………………..
(a) 3.5 ms-1
(b) \(\sqrt{3.5}\) ms-1
(c) 1.5ms-1
(d) Zero
Hint:

Answer:
(b) \(\sqrt{3.5}\) ms-1
![]()
Question 14.
Two vibrating tuning forks produce progressive waves given by y1 = 4 sin 500 πt and y2 = 2 sin 506 πt where t is in seconds Number of beat produced per minute is ………………………
(a) 360
(b) 180
(c) 3
(d) 60
Hint:
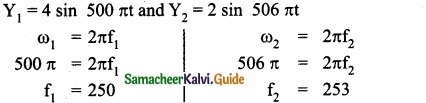
f2 – f1 = 3 = beats per sec and 3 × 60 = 180 beats per min
Answer:
(b) 180
Question 15.
Workdone by a simple pendulum in one complete oscillation is …………………………..
(a) Zero
(b) Jmg
(c) mg cos θ
(d) mg sin θ
Answer:
(a) Zero
PART – II
Answer any six questions in which Q. No 23 is compulsory. [6 × 2 = 12]
Question 16.
A girl is swinging in the sitting position. How will the period of the swing be changed if she stands up?
Answer:
This can be explained using the concept of a simple pendulum. We know that the time period of a simple pendulum is given by
T = 2π\(\sqrt{l/g}\) i.e; T ∝\(\sqrt{l}\)
When the girl stands up, the distance between the point of suspension and the centre of mass of the swinging body decreases i.e., l decreases, so T will also decrease.
Question 17.
A car starts to move from rest with uniform acceleration 10 ms-2 then after 2 sec, what is its velocity?
Answer:
a =10 ms-2;
t = 2s;
w = 0;
v = ?
v = u + at
v = 0 + 10 × 2
= 20 ms-1
![]()
Question 18.
State Lami’s theorem?
Answer:
If a system of three concurrent and coplanar forces is in equilibrium, then Lami’s theorem states that the magnitude of each force of the system is proportional to sine of the angle between the other two forces. The constant of proportionality is same for all three forces.
Question 19.
Due to the action of constant torque, a wheel from rest makes n rotations in t seconds? Show that the angular acceleration of a wheel as \(\frac{4 \pi n}{t^{2}}\) rad s-2
Answer:
Initial angluar velocity ω0 = 0
Number of rotations in t seconds = n
angular displacement θ = 2πn
but, θ = ω0t + \(\frac{1}{2}\)αt2
2πn = \(\frac{1}{2}\)αt2
α = \(\frac{4 \pi n}{t^{2}}\)
Question 20.
Why a given sound is louder in a hall than in the open?
Answer:
In a hall, repeated reflections of sound take place from the walls and the ceiling. These reflected sounds mix with original sound which results in increase the intensity of sound. But in open, no such a repeated reflection is possible. .’. sound will not be louder as in hall.
![]()
Question 21.
What are the differences between connection and conduction?
Answer:
Conduction:
Conduction is the process of direct transfer of heat through matter due to temperature difference. When two objects are in direct contact with one another, heat will be transferred from the hotter object to the colder one. The objects which allow heat to travel easily through them are called conductors.
Convection:
Convection is the process in which heat transfer is by actual movement of molecules in fluids such as liquids and gases. In convection, molecules move freely from one place to another.
Question 22.
Why two holes are made to empty an oil tin?
Answer:
When oil comes out through a tin with one hole, the pressure inside the tin becomes less than the atmospheric pressure, soon the oil stops flowing out. When two holes are made in the tin, air keeps on entering the tin through the other hole and maintains pressure inside.
![]()
Question 23.
If the length of the simple pendulum is increased by 44% from its original length, calculate the percentage increase in time period of the pendulum?
Answer:
Since T ∝ \(\sqrt{l}\) = Constant \(\sqrt{l}\)
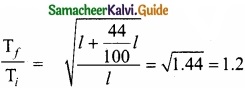
∴ Tf = 1.2 Ti = Ti + 20% Ti
Question 24.
When do the real gases obey more correctly the gas equation PV = nRT?
Answer:
An ideal gas is one whose molecules have zero volume and no mutual force between them. At low pressure, the volume of a gas is large and so the volume occupied by the molecules is negligible in comparison to the volume of the gas.
At high temperature, the molecules have large velocities and so the intermolecular force has no influence on their motion. Hence at low pressure and high temperature, the behaviour of real gases approach the ideal gas behaviour.
PART – III
Answer any six questions in which Q.No. 29 is compulsory. [6 × 3 = 18]
Question 25.
A stone is thrown upwards with a speed v from the top of a tower. It reaches the ground with a velocity 3v. What is the height of the tower?
Answer:
From equation of motion,
v’ = u + at ……………….. (1)
h = ut + \(\frac{1}{2}\) at2
here, v’ = av; u = v; a = +g
Using equ. (1)
3v = v + gt ⇒ 3v – v = gt
t = \(\frac{2v}{g}\)
Substitute ‘t’ value in equ. (2)
h = v(\(\frac{2v}{g}\)) + \(\frac{1}{2}\)g(\(\frac{2v}{g}\))2 = \(\frac { 2v^{ 2 } }{ g } \) + \(\frac{1}{2}\)g (\(\frac{2v}{g}\))2
h = \(\frac { 2v^{ 2 } }{ g } \) + \(\frac { 2v^{ 2 } }{ g } \)
= \(\frac { 4v^{ 2 } }{ g } \) g = 10 ms-2
= \(\frac { 4v^{ 2 } }{ 10 } \); h = \(\frac { 2v^{ 2 } }{ 5 } \)
![]()
Question 26.
An object is projected at an angle such that the horizontal range is 4 times of the maximum height. What is the angle of projection of the object?
Answer:
Given:
Horizontal range = 4 Hmax
Horizontal range = \(\frac{u^{2} \sin 2 \theta}{g}\) = \(\frac{2 u^{2} \sin \theta \cos \theta}{g}\)
Maximum height = \(\frac{u^{2} \sin ^{2} \theta}{2 g}\)
as given, \(\frac{2 u^{2} \sin \theta \cos \theta}{g}\) = \(\frac{4 u^{2} \sin ^{2} \theta}{2 g}\)
2 cos θ = 2 sin θ
tan θ = 1
∴ θ = 45°
Question 27.
A room contains oxygen and hydrogen molecules in the ratio 3 : 1. The temperature of the room is 27°C. The molar mass of 02 is 32 g mol-1 and for H2, 2 g mol-1. The value of gas constant R is 8.32 J mol-11 k-1. Calculate rms speed of oxygen and hydrogen molecule?
Answer:
(a) Absolute Temperature T = 27°C = 27 + 273 = 300 K.
Gas constant R = 8.32 J mol-1 K-1
For Oxygen molecule: Molar mass
M = 32 gm/mol = 32 × 10-3 kg mol-1
rms speed vrms = \(\sqrt { \frac { 3RT }{ M } } \) = \(\sqrt{\frac{3 \times 8.32 \times 300}{32 \times 10^{-3}}}\) = 483.73 ms-1 ~ 484ms-1
For Hydrogen molecule: Molar mass M = 2 × 10-3 kg mol-1
rms speed vrms = \(\sqrt { \frac { 3RT }{ M } } \) = \(\sqrt{\frac{3 \times 8.32 \times 300}{2 \times 10^{-3}}}\) = 1934 ms-1 = 1.93 K ms-1
Note that the rms speed is inversely proportional to \(\sqrt{M}\) and the molar mass of oxygen is 16 times higher than molar mass of hydrogen. It implies that the rms speed of hydrogen is 4 times greater than rms speed of oxygen at the same temperature. \(\frac{1934}{484}\) ~ 4.
![]()
Question 28.
Explain about an angle of friction?
Answer:
The angle of friction is defined as the angle between the normal force (N) and the resultant force (R) of normal force and maximum friction force (\(f_{s}^{\max }\))
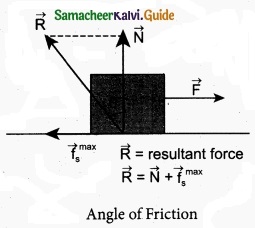
In the figure the resultant force is R = \(\sqrt{\left(f_{s}^{\max }\right)^{2}+\mathrm{N}^{2}}\)
tan θ = \(\frac{f_{s}^{\max }}{\mathrm{N}}\) ………………….. (1)
But from the frictional relation, the object begins to slide when \(f_{s}^{\max }=\mu_{\mathrm{s}} \mathrm{N}\)
or when \(\frac{f_{s}^{\max }}{\mathrm{N}}\) = µs ………………….. (2)
From equations (1) and (2) the coefficient of static friction is
µs = tan θ ……………………. (3)
The coefficient of static friction is equal to tangent of the angle of friction.
![]()
Question 29.
How does resolve a vector into its component? Explain?
Answer:
component of a resolve:
In the Cartesian coordinate system any vector \(\vec { A } \) can be resolved into three components along x, y and z directions. This is shown in figure. Consider a 3-dimensional coordinate system. With respect to this a vector can be written in component form as
\(\vec { A } \) = Ax \(\hat { i } \) + Ay\(\hat { j } \) + Az\(\hat { k } \)
Components of a vector in 2 dimensions and 3 dimensions
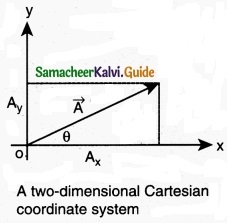
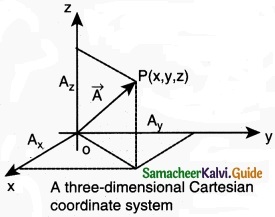
Here Ax is the x-component of \(\vec { A } \), Ay is the y-component of \(\vec { A } \) and Az is the z component of \(\vec { A } \).
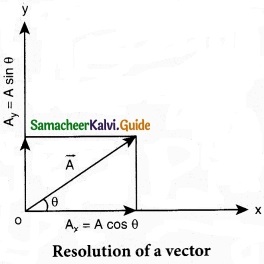
In a 2-dimensional Cartesian coordinate system (which is shown in the figure) the vector \(\vec { A } \) is given by
\(\vec { A } \) = Ax \(\hat { i } \) + Ay \(\hat { j } \)
If \(\vec { A } \) makes an angle θ with x axis, and Ax and Ay are the components of A along x-axis and y-axis respectively, then as shown in figure,
Ax θ = A cos θ, A = A sin θ
where ‘A’ is the magnitude (length) of the vector \(\vec { A } \), A = \(\sqrt{\mathrm{A}_{x}^{2}+\mathrm{A}_{y}^{2}}\)
Question 30.
Derive an expression for energy of an orbiting satellite?
Answer:
The total energy of the satellite is the sum of its kinetic energy and the gravitational potential energy. The potential energy of the satellite is,
U = \(-\frac{\mathrm{GM}_{s} \mathrm{M}_{\mathrm{E}}}{\left(\mathrm{R}_{\mathrm{E}}+h\right)}\) ………………….. (1)
Here Ms -mass of the satellite, ME -mass of the Earth, RE – radius of the Earth.
The Kinetic energy of the satellite is
K.E = \(\frac{1}{2}\) Msv2 ………………….. (2)
Here v is the orbital speed of the satellite and is equal to
v = \(\sqrt{\frac{\mathrm{GM}_{\mathrm{E}}}{\left(\mathrm{R}_{\mathrm{E}}+h\right)}}\)
Substituting the value of v in (2) the kinetic energy of the satellite becomes,
K.E = \(\frac{1}{2} \frac{\mathrm{GM}_{\mathrm{E}} \mathrm{M}_{s}}{\left(\mathrm{R}_{\mathrm{E}}+h\right)}\)
Therefore the total energy of the satellite is
E = \(\frac{1}{2}\) \(\frac{\mathrm{GM}_{\mathrm{E}} \mathrm{M}_{s}}{\left(\mathrm{R}_{\mathrm{E}}+h\right)}-\frac{\mathrm{GM}_{s} \mathrm{M}_{\mathrm{E}}}{\left(\mathrm{R}_{\mathrm{E}}+h\right)}\)
E = \(-\frac{\mathrm{GM}_{s} \mathrm{M}_{\mathrm{E}}}{\left(\mathrm{R}_{\mathrm{E}}+h\right)}\)
The total energy implies that the satellite is bound to the Earth by means of the attractive gravitational force.
Note:
As h approaches ∞, the total energy tends to zero. Its physical meaning is that the satellite is completely free from the influence of Earth’s gravity and is not bound to Earth at large distance.
![]()
Question 31.
Explain in detail Newton’s law of cooling?
Answer:
Newton’s law of cooling:
Newton’s law of cooling body is directly proportional to the difference in the temperature between that body and its surroundings.
\(\frac{dQ}{dT}\) ∝(T – Ts) …………………. (1)
The negative sign indicates that the quantity of heat lost by liquid goes on decreasing with time. Where,
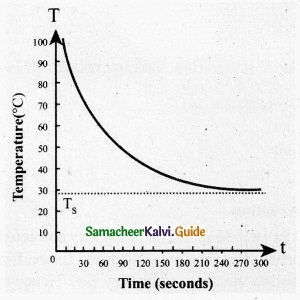
T = Temperature of the object
Ts = Temperature of the surrounding
From the graph in figure it is clear that the rate of cooling is high initially and decreases with falling temperature.
Let us consider an object of mass m and specific heat capacity s at temperature T. Let Ts be the temperature of the surroundings. If the temperature falls by a small amount dT in time dt, then the amount of heat lost is,
dQ = msdT …………………….. (2)
Dividing both sides of equation (2) by dt
\(\frac{dQ}{dT}\) = \(\frac{msdT}{dt}\) ………………….. (3)
From Newton’s law of cooling
\(\frac{dQ}{dT}\) ∝(T – Ts)
\(\frac{dQ}{dT}\) = -a(T – Ts) ………………………… (4)
Where a is some positive constant.
From equation (3) and (4)
-a (T – Ts) = ms\(\frac{dT}{dt}\)
\(\frac{d \mathrm{T}}{\mathrm{T}-\mathrm{T}_{s}}\) = -a\(\frac{a}{ms}\) dt …………………… (5)
Integrating equation (5) on both sides,

Where b1 is the constant of integration. Taking exponential both sides we get,
T = Ts + \(b_{2} e^{\frac{-a}{m s} t}\) …………………….. (6)
Here b2 = eb1 Constant
![]()
Question 32.
Explain Laplace’s correction?
Answer:
Laplace’s correction: In 1816, Laplace satisfactorily corrected this discrepancy by assuming that when the sound propagates through a medium, the particles oscillate very rapidly such that the compression and rarefaction occur very fast.
Hence the exchange of heat produced due to compression and cooling effect due to rarefaction do not take place, because, air (medium) is a bad conductor of heat. Since, temperature is no longer considered as a constant here, sound propagation is an adiabatic process. By adiabatic considerations, the gas obeys Poisson’s law (not Boyle’s law as Newton assumed), which is
PVγ = Constant …………………. (1)
where, γ = \(\frac { C_{ p } }{ C_{ v } } \) which is the ratio between specific heat at constant pressure and specific heat at constant volume. Differentiating equation (1) on both the sides, we get
\(V^{ \gamma }dP+P(\gamma ^{ V\gamma -1 }dV)=0\)
or
\(\gamma \mathrm{P}=-\mathrm{V} \frac{d p}{d \mathrm{V}}=\mathrm{B}_{\mathrm{A}}\) ………………….. (2)
where, BA is the adiabatic bulk modulus of air. Now, substituting equation (2) in equation
V = \(\sqrt{\frac{B}{\rho}}\), the speed of sound in air is
vA = \(\sqrt{\frac{\mathrm{B}_{\mathrm{A}}}{\rho}}=\sqrt{\frac{\gamma \mathrm{P}}{\rho}}=\sqrt{\gamma v_{\mathrm{T}}}\)
Since air contains mainly, nitrogen, oxygen, hydrogen etc, (diatomic gas), we take γ = 1.47. Hence, speed of sound in air is vA = (\(\sqrt{1.4}\)) (280 m s-1) = 331.30 ms-1, which is very much closer to experimental data.
![]()
Question 33.
Explain types of equilibrium?
Answer:

PART – IV
Answer all the questions. [5 × 5 = 25]
Question 34 (a).
What are the applications of dimensional analysis?
Verify s = ut + \(\frac{1}{2}\)at2 by dimensional analysis?
Answer:

Given equation is dimensionally correct as the dimensions on the both side are same. Applications of dimensional analysis
- Convert a physical quantity from one system of units to another.
- Check the dimensional correctness of a given physical equation.
- Establish relations among various physical quantities.
[OR]
(b) Explain the types of equilibrium with suitable examples?
Answer:
Translational motion – A book resting on a table.
Rotational equilibrium – A body moves in a circular path with constant velocity.
Static equilibrium – A wall-hanging, hanging on the wall.
Dynamic equilibrium – A ball decends down in a fluid with its terminal velocity.
Stable equilibrium – A table on the floor A pencil
Unstable equilibrium – standing on its tip.
Neutral equilibrium – A dice rolling on a game board.
![]()
Question 35 (a)
Explain the motion of block connected by a string in vertical motion?
Answer:
When objects are connected by strings and a force F is applied either vertically or horizontally or along an inclined plane, it produces a tension T in the string, which affects the acceleration to an extent. Let us discuss various cases for the same.
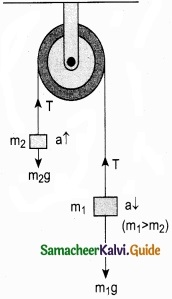
Vertical motion:
Consider two blocks of masses m1 and m2 (m1 > m2) connected by a light and inextensible string that passes over a pulley as shown in Figure 1.
Let the tension in the string be T and acceleration a.
When the system is released, both the blocks start, Two blocks connected by a string moving, m2 vertically upward and m1 downward with same acceleration a. The gravitational force m1g on mass m1 is used in lifting the mass m2.
The upward direction is chosen as y direction. The free body diagrams of both masses are shown in Figure 2.
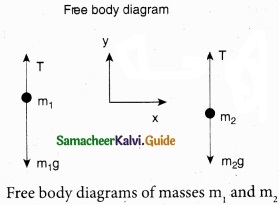
Applying Newton’s second law for mass m2
T\(\hat { j } \) – m2\(\hat { j } \)g = m2 a\(\hat { j } \)
The left hand side of the above equation is the total force that acts on m2 and the right hand side is the product of mass and acceleration of m2 in direction.
By comparing the components on both sides, we get
T -m2g = m2a ……………………. (1)
Similarly, applying Newton’s law second law of for mass m1
T\(\hat { j } \) – m1g\(\hat { j } \) = -m1a\(\hat { j } \)
As mass m1 moves downward (-\(\hat { j } \)), its accleration is along (-\(\hat { j } \))
By comparing the components on both sides, we get
T – m1g = -m1a
m1g – T = m1a …………………….. (2)
Adding equations (1) and (2), we get
m1g – m2g = m1a + m2a
(m1g – m2)g = (m1 + m2)a …………………….. (3)
From equation (3), the acceleration of both the masses is
a = \(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right)\)g ……………………… (4)
If both the masses are equal (m1 = m2), from equation (4)
a = 0
This shows that if the masses are equal, there is no acceleration and the system as a whole will be at rest. To find the tension acting on the string, substitute the acceleration from the equation (4)
T – m2g = m2 \(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right)\)g
T = m2g + m2\(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right)\)g ……………………… (5)
By taking m2g common in the RHS of equation (5)

Equation (4) gives only magnitude of accleration.
For mass m1 g the accleration vector is given by \(\vec{a}=-\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right) g \hat{j}\)
For mass m2 g the accleration vector is given by \(\vec{a}=-\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right) g \hat{j}\)
[OR]
(b) Derive the kinematic equation of motion for constant acceleration?
Answer:
Consider an object moving in a straight line with uniform or constant acceleration ‘a’. Let u be the velocity of the object at time t = 0, and v be velocity of the body at a later time t.
Velocity – time relation:
(I) The acceleration of the body at any instant is given by the first derivative of the velocity with respect to time,
a = \(\frac{dv}{dt}\) or dv = a dt
Integrating both sides with the condition that as time changes from 0 to t, the velocity changes from u to v. For the constant acceleration,
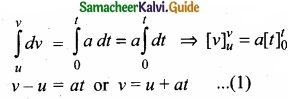
Displacement – time relation:
(II) The velocity of the body is given by the first derivative of the displacement with respect to time.
v = \(\frac{ds}{dt}\) or ds = vdt
and since v = u + at,
We get ds = (u + at)dt
Assume that initially at time t = 0, the particle started from the origin. At a later time t, the particle displacement is s. Further assuming that acceleration is time-independent, we have
\(\int_{0}^{s} d s=\int_{0}^{t} u d t+\int_{0}^{t} a t d t \text { or } s=u t+\frac{1}{2} a t^{2}\) ……………………. (2)
Velocity – displacement relation
(III) The acceleration is given by the first derivative of velocity with respect to time.
a = \(\frac{dv}{dt}\) = \(\frac{dv}{ds}\) \(\frac{ds}{dt}\) = \(\frac{dv}{ds}\) v [since ds/dt = v] where s is displacement traversed.
This is rewritten as a = \(\frac{1}{2}\) \(\frac { dv^{ 2 } }{ s } \) or ds = \(\frac{1}{2a}\) d(v2)
Integrating the above equation, using the fact when the velocity changes from u2 to v2, displacement changes from u2 to v2, we get
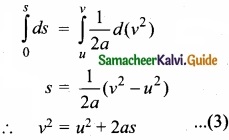
We can also derive the displacement s in terms of initial velocity u and final velocity v.
From equation we can write,
at = v – u
Substitute this in equation, we get
s = ut + \(\frac{1}{2}\) (v -u)t
s = \(\frac{(u+v)t}{2}\)
![]()
Question 36 (a).
State and prove perpendicular axis theorem?
Answer:
Perpendicular axis theorem: This perpendicular axis theorem holds good only for plane laminar objects.
The theorem states that the moment of inertia of a plane laminar body about an axis perpendicular to its plane is equal to the sum of moments of inertia about two perpendicular axes lying in the plane of the body such that all the three axes are mutually perpendicular and have a common point.
Let the X and Y-axes lie in the plane and Z-axis perpendicular to the plane of the laminar object. If the moments of inertia of the body about X and Y-axes are Ix and IY respectively and Iz is the moment of inertia about Z-axis, then the perpendicular axis theorem could be expressed as,
Iz = Ix + Iy
To prove this theorem, let us consider a plane laminar object of negligible thickness on which lies the origin (O). The X and Y-axes lie on the plane and Z-axis is perpendicular to it as shown in figure. The lamina is considered to be made up of a large number of particles of mass m. Let us choose one such particle at a point P which has coordinates (x, y) at a distance r from O.
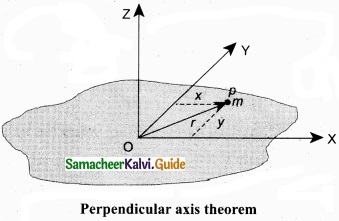
The moment of inertia of the particle about Z-axis is, mr2.
The summation of the above expression gives the moment of inertia of the entire lamina about Z-axis as,
Iz = Σ mr2
Here, r2 = x2 + y2
Then, Iz = Σm(x2 + y2)
Iz = Σmx2 + Σmy2
In the above expression, the term Σmx2 is the moment of inertia of the body about the Y-axis and similarly the term Σmy2 is the moment of inertia about X-axis. Thus,
IX = Σmy2 and IY = Σmx2
Substituting in the equation for IZ gives, IZ = IX + IY
Thus, the perpendicular axis theorem is proved.
[OR]
(b) Explain in detail the triangle law of addition?
Answer:
Let us consider two vectors \(\vec { A } \) and \(\vec { B } \) as shown in figure.
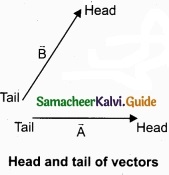
To find the resultant of the two vectors we apply the triangular law of addition as follows:
Represent the vectors \(\vec { A } \) and \(\vec { B } \) by the two adjacent sides of a triangle taken in the same order. Then the resultant is given by the third side of the triangle as shown in figure.
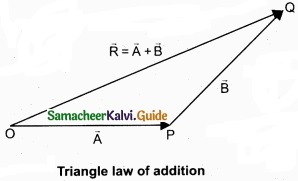
To explain further, the head of the first vector \(\vec { A } \) is connected to the tail of the second vector \(\vec { B } \). Let θ be the angle between A and B. Then R is the resultant vector connecting the tail of the first vector \(\vec { A } \) to the head of the second vector \(\vec { B } \).
The magnitude of \(\vec { R } \) (resultant) is given geometrically by the length of \(\vec { R } \)(OQ) and the direction of the resultant vector is the angle between \(\vec { R } \) and \(\vec { A } \). Thus we write \(\vec { R } \) = \(\vec { A } \) + \(\vec { B } \).
\(\overline { OQ } \) = \(\overline { OP } \) + \(\overline { PQ } \)
1. Magnitude of resultant vector:
The magnitude and angle of the resultant vector are determined by using triangle law of vectors as follows.
From figure, consider the triangle ABN, which is obtained by extending the side OA to ON. ABN is a right angled triangle.
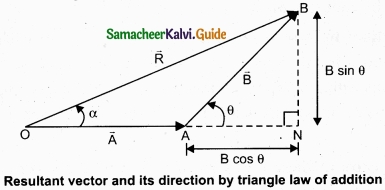
From figure, let R is the magnitude of the resultant of \(\vec { A } \) and \(\vec { B } \).
For ∆OBN, we have OB2 = ON2 + BN2
⇒ R2 = (A + B cos θ)2 + (B sin θ)2
⇒ R2 = A2 + B2 cos2 θ + 2AB cos θ + B2sin2 θ
⇒ R2 = A2 + B2(cos2 θ + sin2 θ) + 2AB cos θ
⇒R2 = \(\sqrt{A^{2}+B^{2}+2 A B \cos \theta}\)
2. Direction of resultant vectors:
If θ is the angle between \(\vec { A } \) and \(\vec { B } \), then
|\(\vec { A } \) + \(\vec { B } \)| = \(\sqrt{A^{2}+B^{2}+2 A B \cos \theta}\)
If \(\vec { R } \) makes an angle α with \(\vec { A } \), then in ∆OBN,
tan α = \(\frac{BN}{ON}\) = \(\frac{BN}{OA+AN}\)
tan α = \(\frac{B \sin \theta}{A+B \cos \theta}\) ⇒ α = tan-1\(\left(\frac{B \sin \theta}{A+B \cos \theta}\right)\)
![]()
Question 37 (a).
Explain in detail the various types of errors?
Answer:
The uncertainty in a measurement is called an error. Random error, systematic error and gross error are the three possible errors.
(I) Systematic errors:
Systematic errors are reproducible inaccuracies that are consistently in the same direction. These occur often due to a problem that persists throughout the .experiment. Systematic errors can be classified as follows.
(1) Instrumental errors:
When an instrument is not calibrated properly at the time of manufacture, instrumental errors may arise. If a measurement is made with a meter scale whose end is worn out, the result obtained will have errors. These errors can be corrected by choosing the instrument carefully.
(2) Imperfections in experimental technique or procedure:
These errors arise due to the limitations in the experimental arrangement. As an example, while performing experiments with a calorimeter, if there is no proper insulation, there will be radiation losses. This results in errors and to overcome these, necessary correction has to be applied
(3) Personal errors:
These errors are due to individuals performing the experiment, may be due to incorrect initial setting up of the experiment or carelessness of the individual making the observation due to improper precautions.
(4) Errors due to external causes:
The change in the external conditions during an experiment can cause error in measurement. For example, changes in temperature, humidity, or pressure during measurements may affect the result of the measurement.
(5) Least count error:
Least count is the smallest value that can be measured by the measuring instrument, and the error due to this measurement is least count error. The instrument’s resolution hence is the cause of this error. Least count error can be reduced by using a high precision instrument for the measurement.
(II) Random errors:
Random errors may arise due to random and unpredictable variations in experimental conditions like pressure, temperature, voltage supply etc. Errors may also be due to personal errors by the observer who performs the experiment. Random errors are sometimes called “chance error”.
When different readings are obtained by a person every time he repeats the experiment, personal error occurs. For example, consider the case of the thickness of a wire measured using a screw gauge. The readings taken may be different for different trials. In this case, a large number of measurements are made and then the arithmetic mean is taken.
If n number of trial readings are taken in an experiment, and the readings are
a1, a2, a3, ……………………….. an. The arithmetic mean is

[OR]
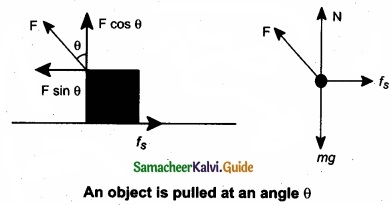
(b) To move an object, which one is easier, push or pull? Explain?
Answer:
When a body is pushed at an arbitrary angle θ (0 to \(\frac{π}{2}\)), the applied force F can be resolved into two components as F sin θ parallel to the surface and F cos θ perpendicular to the surface as shown in figure. The total downward force acting on the body is mg + F cos θ. It implies that the normal force acting on the body increases. Since there is no acceleration along the vertical direction the normal force N is equal to
Npush = mg + F cos θ …………………. (1)
As a result the maximal static friction also increases and is equal to
\(f_{s}^{\max }=\mu_{r} N_{\text {push }}=\mu_{s}(m g+F \cos \theta)\) …………………. (2)
Equation (2) shows that a greater force needs to be applied to push the object into motion.
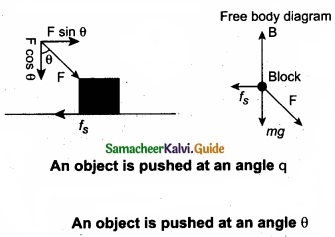
When an object is pulled at an angle 0, the applied force is resolved into two components as shown in figure. The total downward force acting on the object is
Npull = mg – F cos θ …………………….. (3)
![]()
Question 38 (a).
Describe the method of measuring angle of repose?
Answer:
Angle of Repose Consider an inclined plane on which an object is placed, as shown in figure. Let the angle which this plane makes with the horizontal be θ. For small angles of θ, the object may not slide down. As θ is increased, for a particular value of θ, the object begins to slide down. This value is called angle of repose. Hence, the angle of repose is the angle of inclined plane with the horizontal such that an object placed on it begins to slide.
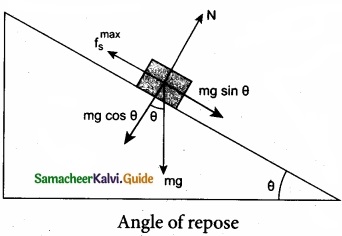
Let us consider the various forces in action here. The gravitational force mg is resolved into components parallel (mg sin θ) and perpendicular (mg cos θ) to the inclined plane. The component of force parallel to the inclined plane (mg sin θ) tries to move the object down. The component of force perpendicular to the inclined plane (mg cos θ) is balanced by the Normal force (N).
N = mg cos θ ……………… (1)
When the object just begins to move, the static friction attains its maximum value
fs = \(f_{s}^{\max }\)
This friction also satisfies the relation
\(f_{s}^{\max }\) = µs = mg sin θ …………………… (2)
Equating the right hand side of equations (1) and (2),
\(\left(f_{s}^{\max }\right) / \mathrm{N}=\sin \theta / \cos \theta\)
From the definition of angle of friction, we also know that
tan θ = µs ……………………… (3) in which θ is the angle of friction.
Thus the angle of repose is the same as angle of friction. But the difference is that the angle of repose refers to inclined surfaces and the angle of friction is applicable to any type of surface.
[OR]
(b) A block of mass m slides down the plane inclined at an angle 60° with an acceleration g/2. Find the co-efficient of kinetic friction?
Answer:
Kinetic friction comes to play as the block is moving on the surface.
The forces acting on the mass are the normal force perpendicular to surface, downward gravitational force and kinetic friction along the surface.
Along the x-direction
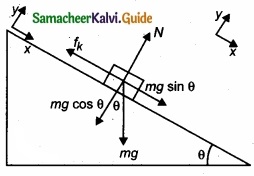
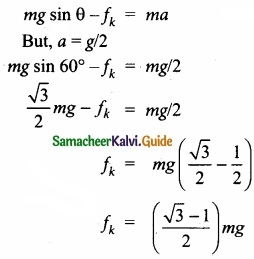
There is no motion along the y-direction as normal force is exactly balanced by the mg cos θ.
mg cos θ = N = mg/2

[OR]
(c) Write a note on triangulation method and radar method to measure larger distances?
Answer:
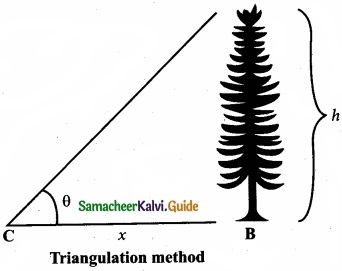
Triangulation method for the height of an accessible object:
Let AB = h be the height of the tree or tower to 6e measured. Let C be the point of observation at distance x from B. Place a range finder at C and measure the angle of elevation, ACB = θ as shown in figure.
From right angled triangle ABC,
tan θ = \(\frac{AB}{BC}\) = \(\frac{h}{x}\)
(or) height h = x tan θ
Knowing the distance x. the height h can be detennined.
RADAR method:
The word RADAR stands for radio detection and ranging. A radar can be used to measure accurately the distance of a nearby planet such as Mars. In this method, radio waves are sent from transmitters which, after reflection from the planet, are detected by the receiver.
By measuring, the time interval (t) between the instants the radio waves are sent and received, the distance of the planet can be determined as where v is the speed of the radio wave. As the time taken (t) is for the distance covered during the forward and backward path of the radio waves, it is divided by 2 to get the actual distance of the object. This method can also be used to determine the height, at which an aeroplane flies from the ground.

[OR]
(d) Jupiter is at a distance of 824.7 million km from the earth. Its angular diameter is measured to be 35.75”. Calculate the diameter of jupiter?
Answer:
Given,
Distance of Jupiter = 824.7 × 106 km = 8.247 × 1011 m
angular diameter = 35.72 × 4.85 × 10-6 rad = 173.242 × 10-6 rad
= 1.73 × 10-4rad
∴ Diameter of Jupiter D = θ × d = 1.73 × 10-4 rad × 8.247 × 1011 m
14.267 × 107 m = 1.427 × 108 m (or) 1.427 × 105 km