Bhagya

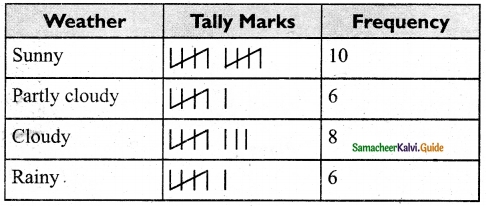
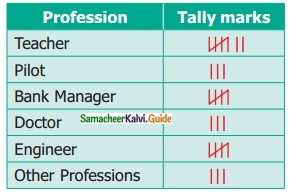
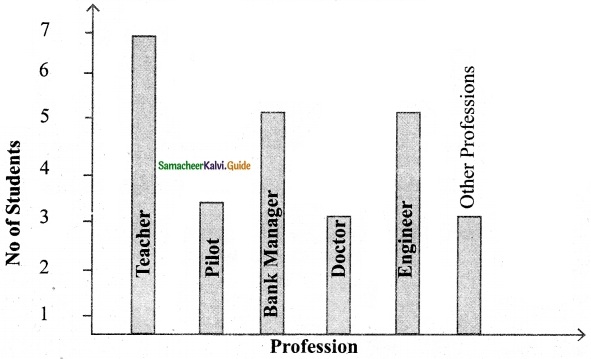
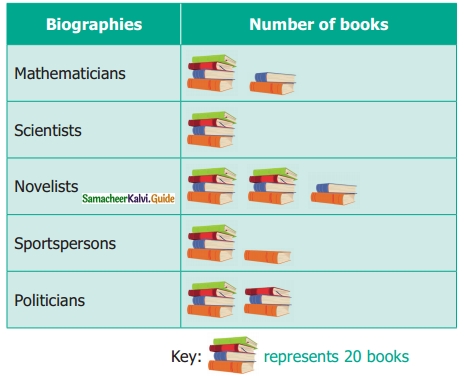
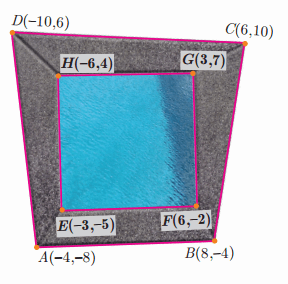
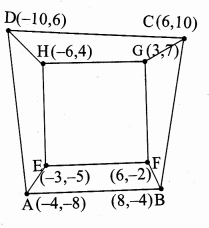
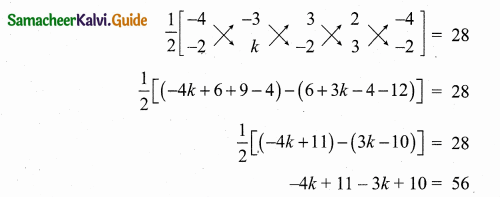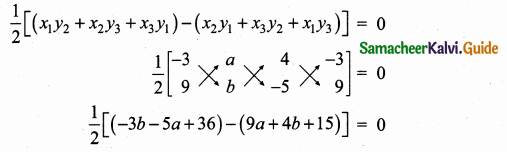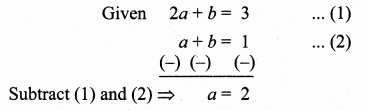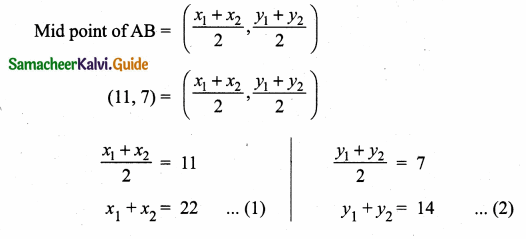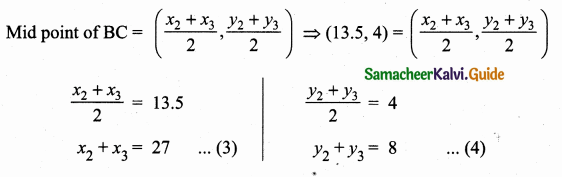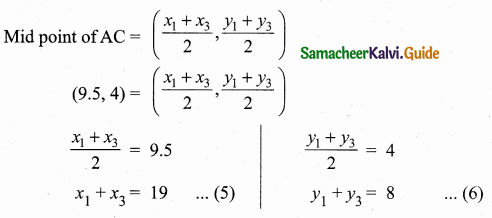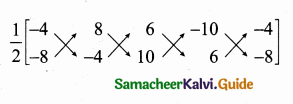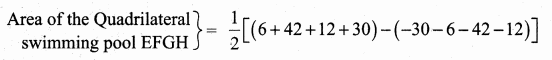Students can download Maths Chapter 6 Trigonometry Ex 6.3 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 6 Trigonometry Ex 6.3

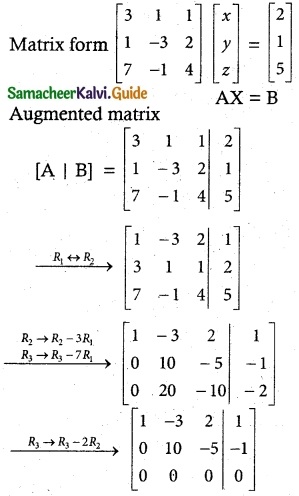
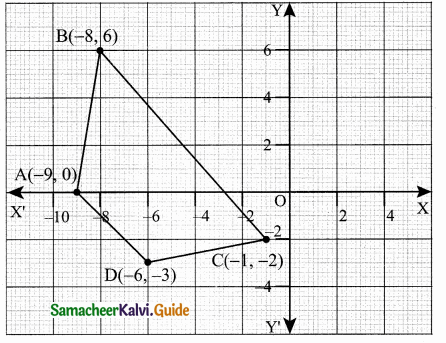
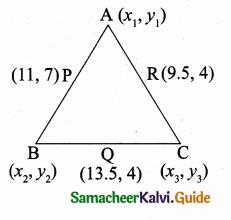
Question 1.
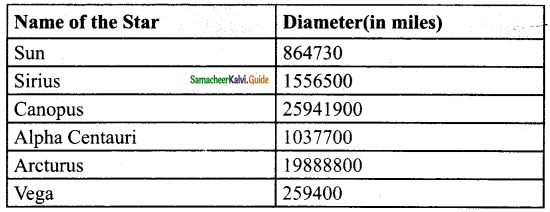
From the top of a rock 50 \(\sqrt { 3 }\) m high, the angle of depression of a car on the ground is observed to be 30°. Find the distance of the car from the rock.
Answer:
Let the distance of the car from the rock is “x” m

In the right ∆ ABC, tan 30° = \(\frac { AB }{ BC } \)
\(\frac{1}{\sqrt{3}}=\frac{50 \sqrt{3}}{x}\)
x = 50 \(\sqrt { 3 }\) × \(\sqrt { 3 }\) = 50 × 3
= 150 m
∴ Distance of the car from the rock = 150 m

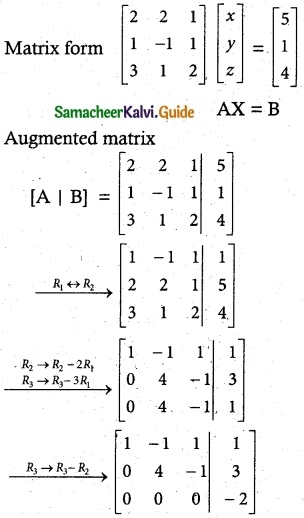
Question 2.
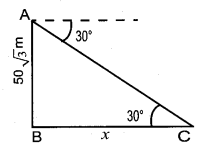
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building.
Answer:
Let the height of the first building AD be “x” m
∴ EC = 120 – x
In the right ∆ CDE,
tan 45° = \(\frac { CE }{ CD } \)

1 = \(\frac { 120-x }{ 70 } \) ⇒ 70 = 120 – x
x = 50 cm
∴ The height of the first building is 50 m

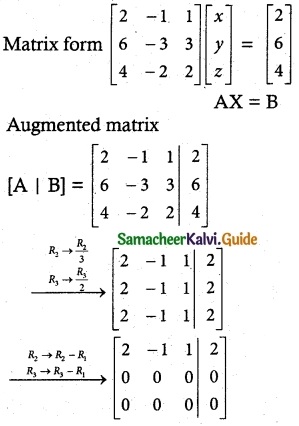
Question 3.
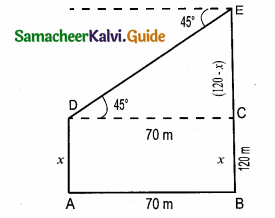
From the top of the tower 60 m high the anles of depression the top and bottom of a vertical lamp post are observed be 38° and 60° respectively
Find the height of the lamp post. (tan 38° = 0.7813,\(\sqrt { 3 }\) = 1.732)
Answer:
Let the height of the lamp post be “h”
The height of the tower (BC) = 60 m
∴ EC = 60 – h
Let AB be x
In the right ∆ ABC,

tan 60° = \(\frac { BC }{ AB } \)
\(\sqrt { 3 }\) = \(\frac { 60 }{ x } \)
x = \(\frac{60}{\sqrt{3}}\) ……..(1)
In the right ∆ DEC, tan 38° = \(\frac { EC }{ DE } \)
0.7813 = \(\frac { 60-h }{ x } \)
x = \(\frac { 60-h }{ 0.7813 } \) …….(2)
From (1) and (2) we get
\(\frac{60}{\sqrt{3}}\) = \(\frac { 60-h }{ 0.7813 } \)
60 × 0.7813 = 60 \(\sqrt { 3 }\) – \(\sqrt { 3 }\) h
\(\sqrt { 3 }\) h = 60 \(\sqrt { 3 }\) – 46.88
= 60 × 1.732 – 46.88
= 103.92 – 46.88
1.732 h = 57.04 ⇒ h = \(\frac { 57.04 }{ 1.732 } \)
h = \(\frac { 570440 }{ 1732 } \) = 32.93 m
∴ Height of the lamp post = 32.93 m

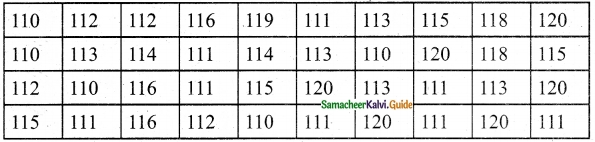
Question 4.
An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are
60° and 30° respectively. Find the distance between the two boats. (\(\sqrt { 3 }\) = 1.732)
Answer:
C and D are the position of the two boats.
Let the distance between the two boats be “x”
Let BC = y
∴ BD = (x + y)

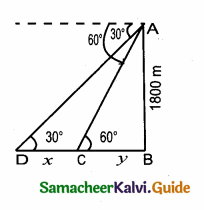
In the right ∆ ABC, tan 30° = \(\frac { AB }{ BD } \)
\(\frac{1}{\sqrt{3}}\) = \(\frac { 1800 }{ x+y } \)
x + y = 1800 \(\sqrt { 3 }\)
y = 1800 \(\sqrt { 3 }\) – x ……(1)
In the right ∆ ABC, tan 60° = \(\frac { AB }{ BC } \)
\(\sqrt { 3 }\) = \(\frac { 1800 }{ y } \)
y = \(\frac{1800}{\sqrt{3}}\) ……….(2)
From (1) and (2) we get
\(\frac{1800}{\sqrt{3}}\) = 1800 \(\sqrt { 3 }\) – x
1800 = 1800 × 3 – \(\sqrt { 3 }\)x
\(\sqrt { 3 }\)x = 5400 – 1800
x = \(\frac{3600}{\sqrt{3}}=\frac{3600 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}=\frac{3600 \times \sqrt{3}}{3}\)
= 1200 × 1.732 = 2078.4 m
Distance between the two boats = 2078.4 m

Question 5.
From the top of a lighthouse, the angle of depression of two ships on the opposite sides of it are observed to be 30° and 60°. If the height of the lighthouse is h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance between the ships is \(\frac{4 h}{\sqrt{3}}\) m.
Answer:
A and C be the position of two ships.
Let AB be x and BC be y. Distance between the two ships is x + y

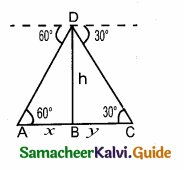
In the right ∆ ABD, tan 60° = \(\frac { BD }{ AB } \)
\(\sqrt { 3 }\) = \(\frac { h }{ x } \)
x = \(\frac{h}{\sqrt{3}}\) ……(1)
In the right ∆ BCD,
tan 30° = \(\frac { BD }{ BC } \)
\(\frac{1}{\sqrt{3}}\) = \(\frac { h }{ y } \)
y = \(\sqrt { 3 }\) h
Distance between the two ships (x + y) = \(\frac{h}{\sqrt{3}}+\sqrt{3} h\)
= \(\frac{h+3 h}{\sqrt{3}}=\frac{4 h}{\sqrt{3}}\)
Hence it is verified

Question 6.
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is 30 \(\sqrt { 3 }\) feet from the entrance of the lift, find the speed of the lift which is descending.
Answer:
Let the speed of the lift is “x” feet / minute
Distance AB = 2 x feet (speed × time)
BC = (90 – 2x)
In the right ∆ BCD,

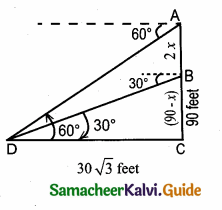
tan 30° = \(\frac { BC }{ DC } \)
\(\frac{1}{\sqrt{3}}=\frac{90-2 x}{30 \sqrt{3}}\)
\(\sqrt { 3 }\) (90 – 2x) = 30\(\sqrt { 3 }\)
(90 – 2x) = \(\frac{30 \sqrt{3}}{\sqrt{3}}\) ⇒ (90 – 2x) = 30
2x = 60
x = \(\frac { 60 }{ 2 } \) = 30
x = 30 feet/minute
Speed of the lift = 30 feet / minute (or) [ \(\frac { 30 }{ 60 } \) second) 0.5 feet / second

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.6 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.6

Question 1.
Test for consistency and if possible, solve the following systems of equations by rank method.
(i) x – y + 2z = 2, 2x + y + 4z = 7, 4x – y + z = 4
Solution:
Matrix form

The system is consistent.
ρ(A) ρ[A|B] = 3 = n
it has unique solution.
Writing the equivalent equations from echelon form
x – y + 2z = 2 ………… (1)
3y = 3 ⇒ y = 1
-7z = -7
z = 1
(1)⇒ x – y + 2z = 2
x – 1 + 2 = 2
x = 1
∴ Solution is x = 1, y = 1, z = 1

(ii) 3x + y + z = 2, x – 3y + 2z = 1, 7x – y + 4z = 5
Solution:

ρ(A) = 2 ρ[A | B] = 2
ρ(A) = ρ[A | B] = 2 < n
The system is consistent. It has infinitely many solution.
Writing the equivalent equations from echelon form.
x – 3y + 2z = 1 ………. (1)
10y – 5z = -1 ………. (2)
Put z = t.
(2) ⇒ 10y – 5z = -1
10y = -1 + 5z = 5t – 1

(iii) 2x + 2y + z = 5, x – y + z = 1, 3x + y + 2z = 4
Solution:

ρ(A) = 2 ρ[A | B] = 3
ρ(A) ≠ ρ[A | B] = 2 < n
∴ The system is inconsistent. It has no solution.

(iv) 2x – y + z = 2, 6x – 3y + 3z = 6, 4x – 2y + 2z = 4
Solution:

ρ(A) = 1 ρ[A | B] = 1
ρ(A) = ρ[A | B] = 1 < n.
∴ The system reduces into a single equation.
∴ It is consistent and has infinitely many solutions.
Writing the equivalent equations from echelon form
2x – y + z = 2
Put y = s, z = t
2x – s + t = 2
2x = 2 + s – t
x = \(\frac {2+s-t}{2}\)
(x, y, z) = (\(\frac {2+s-t}{2}\), s, t) ∀ s, t ∈ R

Question 2.
Find the value of k for which the equations kx – 2y + z = 1, x – 2ky + z = -2, x – 2y + kz = 1 have
(i) no solution
(ii) unique solution
(iii) infinitely many solution.
Solution:

[∵ 2 – k – k² = -(k² + k – 2)
= -(k + 2)(k – 1)
= (k + 2)(1 – k)]
case (i)
If k = 1
ρ(A) = 2, ρ(A | B) = 3.
ρ(A) ≠ ρ(A | B)
The system is inconsistent and it has no solution.

Case (ii)
If k ≠ 1, k ≠ -2
ρ(A) = 3, ρ(A | B) = 3 = n
The system is consistent and it has unique solution.

Case (iii)
If k = -2
ρ(A) = 2, ρ(A | B) = 2
The system is consistent and it has infinitely many solution.

Question 3.
Investigate the values of λ and µ the system of linear equations 2x + 3y + 5z = 9, 7x + 3y – 5z = 8, 2x + 3y + λz = µ, have
(i) no solution
(ii) a unique solution
(iii) an infinite number of solutions.
Solution:

Case (i)
If λ = 5, µ ≠ 9
ρ(A) = 2, ρ(A | B) = 3
ρ(A) ≠ ρ(A | B)
The system is inconsistent. It has no solution.

Case (ii)
If λ = 5, µ ≠ 9
ρ(A) = 3, ρ(A | B) = 3
ρ(A) = ρ(A | B) = 3 = n
The system is consistent. It has unique solution.

Case (iii)
If λ = 5, µ = 9
ρ(A) = 2, ρ(A | B) =2
ρ(A) = ρ(A | B) = 2 < n
The system is consistent. It has infinitely many solution.

Students can download Maths Chapter 5 Statistics Ex 5.4 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 5 Statistics Ex 5.4

Miscellaneous Practice Problems

Question 1.
The heights (in centimeters) of 40 children are.

Prepare a tally marks table.
Solution:

Question 2.
There are 1000 students in a school. Data regarding the mode of transport of the students is given below. Draw a pictograph to represent the data.

Solution:
Mode of transport of the students
Scale: 1 Unit=100 Students

Question 3.
The following pictograph shows the total savings of a group of friends in a year. Each .picture represents a saving of Rs.100. Answer the following questions.

(i) What is the Ratio of Ruby’s saving to that of Thasnim’s?
(ii) What is the ratio of Kuzhali’s savings to that of others?
(iii) How much is Iniya’s savings?
(iv) Find the total amount of savings of all the friends?
(v) Ruby and Kuzhali save the same amount. Say True or False.
Solution:
(i) Ratio of Ruby’s saving to that of Thasnim’s
\(=\frac{\text { Ruby’s saving }}{\text { Thasnim’s saving }}=\frac{5 \times 100}{4 \times 100}=\frac{5}{4}=5: 4\)
Ratio of Ruby’s saving to that of Thasnims = 5 : 4
(ii) Ratio of Kuzhali’s savings to that of others
\(=\frac{\text { kuzhali’s saving }}{\text { others saving }}=\frac{5 \times 100}{19 \times 100}=\frac{5}{19}=5: 19\)
Ratio of Kuzhali’s saving to that of others = 5 : 19
(iii) Iniya’s saving = 3 × 100 = ₹ 300
(iv) Saving of all the friends = (5 + 7 + 4 + 5 + 3) × 100 = 24 × 100 = ₹ 2400.
Total savings = ₹ 2400
(v) True.

Challenging Problems

Question 4.
The table shows the numbers of moons that orbit each of the planets in oar solar system.

Make a Bar graph for the above data.
Solution:
Number of moons that orbit each of the planets in our solar system
Scale: 1 Unit = 2 moons

Question 5.
The prediction of the weather in the month of September is given below.

(i) Make a frequency table of the types of weather by reading the calendar.
(ii) How many days are either cloudy or partly cloudy?
(iii) How many days do not have rain? Give two ways to find the answer?
(iv) Find the ratio of the number of Sunny days to Rainy days.
Solution:
(i)
(ii) 14 days
(iii) 24 days (30 – 6 = 24 days)
(iv) 10 : 6

Question 6.
26 students were interviewed to find out what they want they to become in future. Their responses are given in the following table.

Represent this data using pictograph.
Solution:
Students responses in an interview about their future profession
Scale: 1 Unit = 1 student

Question 7.
Yasmin of class VI was given a task to count the number of books which are biographies, in her school library. The information collected by her is represented as follows.

Observe the pictograph and answer the following questions.
(i) Which title has the maximum number of biographies?
(ii) Which title has the minimum number of biographies?
(iii) Which title has exactly half the number of biographies as Novelists?
(iv) How many biographies are there on the title of sportspersons?
(v) What is the total number of biographies in the library?
Solution:
(i) ‘The title Novelists’ have the maximum number of biographies
(ii) ‘The title Scientists’ have a minimum number of biographies.
(iii) ‘Sportspersons’ title has exactly half the number of biographies as Novelist.
(iv) \((1 \times 20)+\frac{20}{4}=20+5=25\) biographies are there in the title sportsperson.
(v) 8 × 20 = 160 biographies are there in the library.

Question 8.
The bar graph illustrates the results of a survey conducted on vehicles crossing over a Toll Plaza in one hour.

Observe the bar graph carefully and fill up the following table.

Solution:
Vans = 50; Buses = 40; Cars = 65; Others = 15
Total Vehicles = 245

Question 9.
The lengths (in the nearest centimeter) of 30 drumsticks are given as follows.

Draw the bar graph showing the same information.
Solution:
The lengths (in nearest cm) of drumsticks
Scale : 1 Unit = 1 drumstick

Students can download Maths Chapter 5 Coordinate Geometry Ex 5.1 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.1

Question 1.
Find the area of the triangle formed by the points
(i) (1,-1), (-4, 6) and (-3, -5)
(ii) (-10, -4), (-8, -1) and (-3, -5)
Solution:
(i) Let the vertices A (1, -1), B (-4, 6) and C (-3, -5)


= \(\frac { 1 }{ 2 } \) [(6 + 20 + 3) – (4 – 18 – 5)] = \(\frac { 1 }{ 2 } \) [29 – (-19)] = \(\frac { 1 }{ 2 } \) [29 + 19]
= \(\frac { 1 }{ 2 } \) × 48 = 24 sq. units.
Area of ∆ABC = 24 sq. units

(ii) Let the vertices be A(-10, -4), B(-8 -1) and C(-3, -5)

Area of ∆ABC = \(\frac { 1 }{ 2 } \)[(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)]
= \(\frac { 1 }{ 2 } \) [(50 + 3 + 32) – (12 + 40 + 10)]

= \(\frac { 1 }{ 2 } \) [85 – (62)] = \(\frac { 1 }{ 2 } \) [23] = 11.5
Area of ∆ACB = 11.5 sq.units

Question 2.
Determine whether the sets of points are collinear?
(i) (-\(\frac { 1 }{ 2 } \),3)
(ii) (a,b + c), (b,c + a) and (c,a + b)
Solution:
(i) Let the points be A (-\(\frac { 1 }{ 2 } \),3), B (-5, 6) and C(-8, 8)
Area of ∆ABC = \(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₃ + x₁y₃)]
= \(\frac { 1 }{ 2 } \) [(- 3 – 40 – 24) – (-15 – 48 – 4)]

= \(\frac { 1 }{ 2 } \) [-67 + 67] = \(\frac { 1 }{ 2 } \) × 0 = 0
Area of a ∆ is 0.
∴ The three points are collinear.

(ii) Let the points be A (a, b + c), B (b, c + a) and C (c, a + b)
Area of the triangle = \(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)]

Since the area of a triangle is 0.
∴ The given points are collinear.

Question 3.
Vertices of given triangles are taken in order and their areas are provided aside. In each case, find the value of ‘p’

Solution:
(i) Let the vertices be A (0,0) B (p, 8), c (6, 2)
Area of a triangle = 20 sq. units
\(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)] = 20

\(\frac { 1 }{ 2 } \) [(0 + 2p + 0) – (0 + 48 + 0)] = 20
\(\frac { 1 }{ 2 } \) [2p – 48] = 20
2p – 48 = 40 ⇒ 2p = 40 + 48
p = \(\frac { 88 }{ 2 } \) = 44
The value of p = 44

(ii) Let the vertices be A (p, p), B (5, 6) and C (5, -2)
Area of a triangle = 32 sq. units
\(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)] = 32

\(\frac { 1 }{ 2 } \) [6p – 10 + 5p) – (5p + 30 – 2p)] = 32
\(\frac { 1 }{ 2 } \) [11 p – 10 – 3p – 30] = 32
11p – 10 – 3p – 30 = 64
8p – 40 = 64
8p = 64 + 40 ⇒ 8p = 104
p = \(\frac { 104 }{ 8 } \) = 13
The value of p = 13

Question 4.
In each of the following, find the value of ‘a’ for which the given points are collinear.
(i) (2,3), (4, a) and (6, -3)
(ii) (a, 2 – 2a), (-a + 1, 2a) and (-4 -a, 6 – 2a).
Solution:
(i) Let the points be A (2, 3), B(4, a) and C(6, -3).
Since the given points are collinear.
Area of a triangle = 0
\(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)] = 0)

\(\frac { 1 }{ 2 } \) [(2a – 12 + 18) – (12 + 6a – 6)] = 0
2a + 6 – (6 + 6a) = 0
2a + 6 – 6 – 6a = 0
-4a = 0 ⇒ a = \(\frac { 0 }{ 4 } \) = 0
The value of a = 0

(ii) Let the points be A (a, 2 – 2a), B (-a + 1, 2a) C (-4 -a, 6 – 2a).
Since the given points are collinear.
Area of a ∆ = 0

6a² – 2a – 2 – (-2a² – 6a + 2) = 0
6a² – 2a – 2 + 2a² + 6a – 2 = 0
8a² + 4a – 4 = 0 (Divided by 4)
2a² + a – 1 = 0
2a² + 2a – a – 1 = 0
2a (a + 1) – 1 (a + 1) = 0

(a + 1) (2a – 1) = 0
a + 1 = 0 (or) 2a – 1 = 0
a = -1 (or) 2a = 1 ⇒ a = \(\frac { 1 }{ 2 } \)
The value of a = -1 (or) \(\frac { 1 }{ 2 } \)

Question 5.
Find the area of the quadrilateral whose vertices are at
(i) (-9, -2), (-8, -4), (2, 2) and (1, -3)
(ii) (-9, 0), (-8,6), (-1, -2) and (-6, -3)
Solution:
(i) Let the vertices A (-9, -2), B(-8, -4), C(2, 2) and D(1, -3).
Plot the vertices in a graph.

[Note: Consider the points in counter clock wise order]

Area of the Quadrilateral ABDC = \(\frac { 1 }{ 2 } \) [36 + 24 + 2 – 4 – (16 – 4 – 6 – 18)]
= \(\frac { 1 }{ 2 } \) [58 – (-12)] – \(\frac { 1 }{ 2 } \)[58 + 12]
= \(\frac { 1 }{ 2 } \) × 70 = 35 sq. units 2
Area of the Quadrilateral = 35 sq. units

(ii) Let the vertices A(-9, 0), B(-8, 6), C(-1, -2) and D(-6, -3)
Plot the vertices in a graph and take them in counter – clock wise order.
Area of the Quadrilateral DCB

= \(\frac { 1 }{ 2 } \) [33 + 35] = \(\frac { 1 }{ 2 } \) × 68 = 34 sq. units
Area of the Quadrilateral = 34 sq. units

Question 6.
Find the value of k, if the area of a quadrilateral is 28 sq. units, whose vertices are (-4, -2), (-3, k), (3, -2) and (2, 3)
Solution:
Let the vertices A (-A, -2), B (-3, k), C (3, -2) and D (2, 3)
Area of the Quadrilateral = 28 sq. units
\(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) – (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)] = 28

-7k + 21 = 56
-7k = 56 – 21
-7k = 35 ⇒ 7k = – 35
k = – \(\frac { 35 }{ 7 } \) = -5
The value of k = -5

Question 7.
If the points A(-3, 9), B(a, b) and C(4, -5) are collinear and if a + b = 1, then find a and b.
Solution:
Since the three points are collinear
Area of a ∆ = 0

-3b – 5a + 36 – 9a – 4b – 15 = 0
-7b – 14a + 21 = 0
(÷ by 7) – b – 2a + 3 = 0
2a + b – 3 = 0

Substitute the value of a = 2 in (2) ⇒ 2 + b = 1
b = 1 – 2 = -1
The value of a = 2 and b = -1

Question 8.
Let P(11, 7), Q(13.5, 4) and R(9.5, 4) be the midpoints of the sides AB, BC and AC respectively of ∆ABC . Find the coordinates of the vertices A, B and C. Hence find the area of ∆ABC and compare this with area of ∆PQR.
Solution:
Let the vertices of the ∆ABC be A(x₁,y₁), B(x₂,y₂), C(x₃,y₃)

Question 9.
In the figure, the quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio.

Solution:

= \(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) – (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)]
= \(\frac { 1 }{ 2 } \) [(16 + 80 + 36 + 80) – (-64 – 24 – 100 – 24)]
= \(\frac { 1 }{ 2 } \) [212 – (-212)]

= \(\frac { 1 }{ 2 } \) [212 + 212] = \(\frac { 1 }{ 2 } \) [424] = 212 sq. units

= \(\frac { 1 }{ 2 } \) [90 – (-90)]

= \(\frac { 1 }{ 2 } \) [90 + 90]
= \(\frac { 1 }{ 2 } \) × 180 = 90 sq. units
Area of the patio = Area of the Quadrilateral ABCD – Area of the Quadrilateral EFGH
= (212 – 90) sq. units
Area of the patio = 122 sq. units

Question 10.
A triangular shaped glass with vertices at A(-5, -4), B(l, 6) and C(7, -4) has to be painted. If one bucket of paint covers 6 square feet, how many buckets of paint will be required to paint the whole glass, if only one coat of paint is applied.
Solution:
Given the vertices of the triangular glass is A (-5, -4), B (1, 6), and C (7, -4)


= \(\frac { 1 }{ 2 } \) [(20 + 42 – 4) – (-28 – 4 – 30)]
= \(\frac { 1 }{ 2 } \) [58 – (-62)]
= \(\frac { 1 }{ 2 } \) [58 + 62]
= \(\frac { 1 }{ 2 } \) × 120 = 60 sq. feet
Number of cans to paint 6 square feet = 1
∴ Number of cans = \(\frac { 60 }{ 6 } \) = 10 ⇒ Number of cans = 10

Question 11.
In the figure, find the area of
(i) triangle AGF
(ii) triangle FED
(iii) quadrilateral BCEG.

Solution:
Area of a triangle = \(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)]
(i) Area of ∆AGF = \(\frac { 1 }{ 2 } \) [(-2.5 – 13.5 – 6) – (-13.5 – 1 – 15)]
= \(\frac { 1 }{ 2 } \) [-22 – (-29.5)]

= \(\frac { 1 }{ 2 } \) [-22 + 29.5]
= \(\frac { 1 }{ 2 } \) × 7.5 = 3.75 sq.units

(ii) Area of ∆FED = \(\frac { 1 }{ 2 } \) [(-2 + 4.5 + 3) – (4.5 + 1 – 6)]
= \(\frac { 1 }{ 2 } \) [5.5 – (-0.5)]

= \(\frac { 1 }{ 2 } \) [5.5 + 0.5] = \(\frac { 1 }{ 2 } \) × 6 = 3 sq.units

(iii)

= \(\frac { 1 }{ 2 } \) [(4 + 2 + 0.75 + 9) – (-4 -1.5 – 4.5 -2)]
= \(\frac { 1 }{ 2 } \) [15.75 + 12]
= \(\frac { 1 }{ 2 } \) [27.75] = 13.875
= 13.88 sq. units

Students can download Maths Chapter 6 Information Processing Ex 6.3 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 6 Information Processing Ex 6.3

Question 1.
How many Triangles are there in each of the following figures?

Solution:
(i) 12 triangles
(ii) 16 triangles
(iii) 32 triangles
(iv) 35 triangles

Question 2.
Find the number of dots in the tenth figure of the following patterns.

Solution:
(i) 55
(ii) 100

Question 3.

(i) Draw the next pattern.
(ii) Prepare a table for the number of dots used for each pattern.
(iii) Explain the pattern.
(iv) Find the number of dots in the 25th pattern.
Solution:

(iv) 350

Question 4.

Solution:
(i) 20 squares
(ii) 10 squares

Question 5.
How many circles are there in the following figure?

Solution:
7 circles

Question 6.
Find the minimum number of straight lines used in forming the following figures.

Solution:
(i) 10
(ii) 12

Students can download Maths Chapter 6 Information Processing Ex 6.2 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 6 Information Processing Ex 6.2

Question 1.
In the following magic triangle, arrange the numbers from 1 to 6, so that you get the same sum on all its sides.

Solution:
One of the answers is.

Question 2.
Using the numbers from 1 to 9
(i) Can you form a magic triangle?
(ii) How many magic triangles can be formed?
(iii) What are the sums of the sides of the magic triangle?

Solution:
(i) Yes
(ii) 5
(iii) 17, 19, 20, 21, 23

Question 3.
Arrange the odd numbers from 1 to 17 without repetition to get a sum of 30 on each side of the magic triangle.

Solution:

Question 4.
Put the numbers 1, 2, 3, 4, 5, 6 & 7 in the circles so that each straight line of three numbers add up to the same total.

Solution:

Question 5.
Place the number 1 to 12 in the 12 circles so that the sum of the numbers in each of the six lines of the star is 26. Use each number from 1 to 12 exactly once. Find more possible ways?

Solution:

Students can download Maths Chapter 2 Introduction to Algebra Ex 2.2 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 2 Introduction to Algebra Ex 2.2

Question 1.
Find in the blanks.
(i) The algebraic statement of ‘f’ decreased by 5 is _______
(ii) The algebraic statement of ‘s’ divided by 5 is _______
(iii) The verbal statement of ‘2m – 10’ is _______
(iv) If A’s age is ‘n’ years now, 7 years ago A’s age was ______
(v) If ‘p – 5’ gives 12 then ‘p’ is ______
Solution:
(i) f – 5
(ii) \(\frac { s }{ 5 }\)
(iii) 10 less than 2 times m (or) Take away 10 from the product of 2 and m
(iv) n – 7
(v) 17
Hint: p – 5 = 12 ⇒ n = 12 + 5 = 17

Question 2.
Say True or False.
(i) 10 more to three times ‘c’ is ‘3c + 13’.
(ii) If the cost of 10 rice bags is ‘t’, then the cost of 1 rice bag is \(\frac { t }{ 10 }\)
(iii) The statements ‘x’ divided by 3 and 3 divided by ‘x’ are the same.
(iv) The product of ‘q’ and 20 is ’20q’
(v) 7 less to 7 times ‘y’ is ‘7 – 7y’
Solution:
(i) False
Hint: 3c + 10
(ii) True
(iii) False
(iv) True
(v) False
Hint: 7y – 7

Question 3.
Express the following verbal statement to an algebraic statement.
(i) ‘t’ is added to 100
(ii) 4 times ‘q’
(iii) 8 is reduced by ‘y’
(iv) 56 added to 2 times ‘x’
(v) 4 less to 9 times of ‘y’
Solution:
(i) t + 100
(ii) 4q
(iii) 8 – y
(iv) 2x + 56
(v) 9y – 4

Question 4.
Express the following algebraic statement to a verbal statement.
(i) x ÷ 3
(ii) 5n – 12
(iii) 11 + 10x
(iv) 70s
Solution:
(i) x divided by 3.
(ii) 12 less to 5 times n.
(iii) 11 added to 10 times x
(iv) 7 times s.

Question 5.
The teacher asked two students to write the algebraic statement for the verbal statement “8 more than a number”. Vetri wrote ‘8 + x’ but Maran wrote ‘8x’. Who gave the correct answer?
Solution:
Let the number be x; 8 more than the number = 8 + x.
Vetri gave the correct answer as 8 + x.

Question 6.
Answer the following questions.
(i) If ‘n’ takes the value 3 then find the value of ‘n + 10’?
(ii) If ‘g’ is equal to 300 what is the value of ‘g – 1’ and ‘g + 1’?
(iii) What is the value of ‘s’, if ‘2s – 6’ gives 30?
Solution:
(i) n = 3
n + 10 = 3 + 10 = 13

(ii) g = 300
g – 1 = 300 – 1
= 299
g + 1 = 300 + 1
=301

(iii) 2s – 6 = 30
2s = 30 + 6
2s = 36
s = 36/2
s = 18

Question 7.
Complete the table and find the value of ‘k’ for which ‘k/3’ gives 5.

Solution:

\(\frac{k}{3}\) = 5
k = 15

Question 8.
The value of ‘y’ in y + 7 = 13 is
(a) y = 5
(b) y = 6
(c) y = 7
(d) y = 8
Solution:
(b) y = 6
Hint: y = 13 – 7 = 6

Question 9.
6 less to ‘n’ gives 8 is represented as
(a) n – 6 = 8
(b) 6 – n = 8
(c) 8 – n = 6
(d) n – 8 = 6
Solution:
(a) n – 6 = 8

Question 10.
The value of ‘c’ for which \(\frac{3c}{4}\) gives 18 is
(a) c = 15
(b) c = 21
(c) c = 24
(d) c = 27
Solution:
(c) c = 24

Students can download Maths Chapter 6 Information Processing Ex 6.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 6 Information Processing Ex 6.1

Question 1.
Suppose, you have two pairs of shorts, one is black and the other one is blue; three shirts which are white, blue and red. You again wish to make different combinations, but you always want to make sure that the shorts and shirt that you wear are of different colours. List and check how many combinations are possible now.
Solution:
6 combinations are possible
Black-White
Black-Blue
Black-Red
Blue-White
Blue-Blue
Blue-Red

Question 2.
You have two red and two blue blocks. How many different towers can you build that are four blocks high using these blocks? List all the possibilities.
Solution:
6 Possibilities,
R – B – R – B
R – R – B – B
B – R – R – B
B – R – B – R
B – B – R – R
R – B – B – R

Students can download Maths Chapter 2 Introduction to Algebra Ex 2.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 2 Introduction to Algebra Ex 2.1

Question 1.
Fill in the blanks:
(i) The letters a, b, c, .., x, y, z are used to represent _____
(ii) A quantity that takes _____ values is called a variable.
(iii) If there are 5 students on a bench, then the number of students in ‘n’ benches is ‘5 × n’. Here _____ is a variable.
Solution:
(i) Variables
(ii) Different
(iii) n

Question 2.
Say True or False.

(iii) If there are 11 players in a team, then there will be ’11 + q’ players in ‘q’ teams.
Solution:
(i) False
(ii) True
(iii) False

Question 3.
Draw the next two patterns and complete the table

Solution:

Question 4.
Use a variable to write the rule, which gives the number of ice candy sticks required to make the following patterns.

Solution:
(a) No of ice candy sticks used = 3 × n = 3n
(b) No of ice candy sticks used = 4 × n = 4n

Question 5.
The teacher forms groups of five students in a class. How many students will be there in ‘p’ groups?
Solution:
No of students in a group = 5
No of students in ‘p’ groups = 5 × p = 5p

Question 6.
Arivazhagan is 30 years younger than his father. Write Arivazhagan’s age in terms of his father’s age.
Solution:
Let Arivazhagan’s father’s age be x years
According to the problem,
Arivazhagan’s age = (x – 30) years

Question 7.
If ‘u’ is an even number, how would you represent
(i) the next even number?
(ii) the previous even number?
Solution:
(i) Difference between two even numbers = 2
Given that ‘u’ is an even number.
Next, the even number is u + 2.
(ii) Previous even number is u – 2.

Objective Type Questions

Question 8.
Variable means that it
(a) can take only a few values
(b) has a fixed value
(c) can take different values
(d) can take only 8 values
Solution:
(c) can take different values

Question 9.
‘6y’ means
(a) 6 + y
(b) 6 – y
(c) 6 × y
(d) \(\frac{6}{7}\)
Solution:
(c) 6 × y

Question 10.
Radha is ‘x’ years of age now. 4 years ago, her age was
(a) x – 4
(b) 4 – x
(c) 4 + x
(d) 4x
Solution:
(a) x – 4

Question 11.
The number of days in ‘w’ weeks is
(a) 30 + w
(b) 30w
(c) 7 + w
(d) 7w
Solution:
(d) 7w

Question 12.
The value of ‘x’ in the circle is

(a) 6
(b) 8
(c) 21
(d) 22
Solution:
(d) 22

Students can download Maths Chapter 1 Numbers Ex 1.6 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 1 Numbers Ex 1.6

Miscellaneous Practice Problems

Question 1.
Try to open my locked suitcase which has the biggest 5 digit odd number as the password comprising the digits 7, 5, 4, 3 and 8. Find the password.
Solution:
87543

Question 2.
As per the census of 2001, the population of four states are given below. Arrange the states in ascending and descending order of their population.

Solution:
Ascending Order: 6,85,48,437 < 7,21,47,030 < 7,26,26,809 < 9,12,76,115
Descending Order 9,12,76,115 > 7,26,26,809 > 7,21,47,030 > 6,85,48,437

Question 3.
Study the following table and answer the questions.

(i) How many tigers were there in 2011?
(ii) How many tigers were less in 2008 than in 1990?
(iii) Did the number of tigers increase or decrease between 2011 and 2014? If yes, by how much?
Solution:
(i) 1706
(ii) 2100
(iii) Yes, 2226 – 1706 = 520 tigers increased from 2011 to 2014

Question 4.
Mullaikodi has 25 bags of apples. In each bag, there are 9 apples. She shares them equally amongst her 6 friends. How many apples does each get? Are there any apples left over?
Solution:
No of apple bags = 25
Apples in each bag = 9
Total no of apples = 25 × 9 = 225
Apples shared among her 6 friends = 225 ÷ 6
So, among her 6 friends, each of them gets 37 apples and 3 apples are leftover.

Question 5.
Poultry has produced 15472 eggs and fits 30 eggs in a tray. How many trays do they need?
Solution:
No of eggs produced = 15472
No of eggs fits in a tray = 30
No of trays required = 15472 ÷ 30
Trays required = 515 + 1 (to fit the remaining 22 eggs) = 516
Quotient = 515
Remainder = 22

Challenging Problems

Question 6.
Read the table and answer the following questions.

(i) Write the Canopus star’s diameter in words, in the Indian and the International System.
(ii) Write the sum of the place values of 5 in Sirius star’s diameter in the Indian System.
(iii) Eight hundred sixty four million seven hundred thirty. Write in Indian System.
(iv) Write the diameter in words of Arcturus star in the International System
(v) Write the difference of the diameters of Canopus and Arcturus stars in the Indian and the International Systems.
Solution:
(i) 2,59,41,900
25,941,900
Indian System: Two crores fifty-nine lakh forty-one thousand nine hundred.
International System: Twenty-five million nine hundred forty-one thousand nine hundred.
(ii) 5,50,500
(iii) 864,000,730 (86,40,00,730)
(iii) Eighty-six crore forty lakh seven hundred thirty.
(iv) Nineteen million eight hundred eighty-eight thousand eight hundred. (19,888,800)
(v) Indian System: 60,53,100 – Sixty lakh fifty-three thousand one hundred International System: 6,053,100 – Six million fifty-three thousand one hundred.

Question 7.
Anbu asks Arivu Selvi to guess a five-digit odd number. He gives the following hints.
The digit in the 1000s place is less than 5
The digit in the 100s place is greater than 6
The digit in the 10s place is 8.
What is Arivu Selvi’s answer? Does she give more than one answer?
Solution:
There are more than one answers.
One of them is 54781
Some of the other numbers maybe 64783, 74785, 84787 and so on.

Question 8.
A Music concert is taking place in a stadium. A total of 7,689 chairs are to be put in rows of 90.
(i) How many rows will there be?
(ii) Will there be any chairs left over?
Solution:
Total no of chairs to be put = 7,689
Chairs in each row = 90
No of rows = 7689 ÷ 90
Hence, 84 + 1 = 85 rows are required to fill 7650 chairs
Chairs left over = 79 (If the no of rows = 84)

Question 9.
Round off the seven-digit number 29,75,842 to the nearest lakhs and ten lakhs. Are they the same?
Solution:
Yes. Both are same (30,00,000)

Question 10.
Find the 5 or 6 or 7 digit numbers from a newspaper or a magazine to get a rounded number to the nearest ten thousand.
Solution:
(i) 14276 \(\simeq\) 10000
(ii) 1,86945 \(\simeq\) 1,90000