Category: Class 10

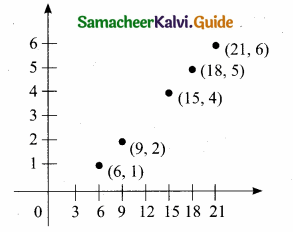
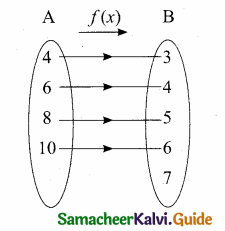
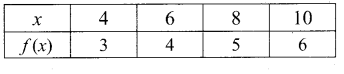
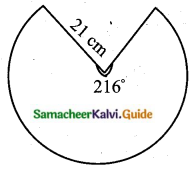
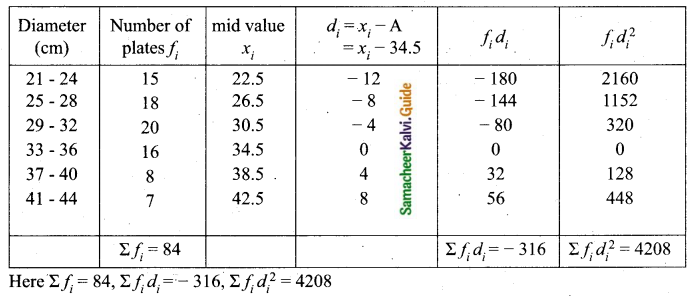
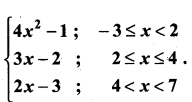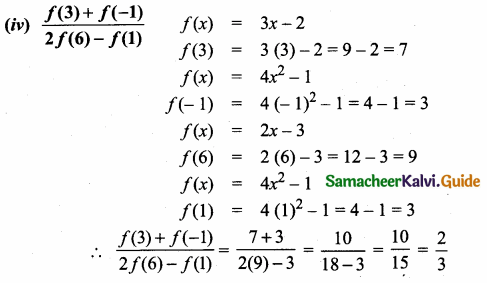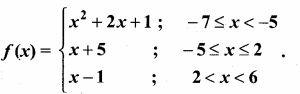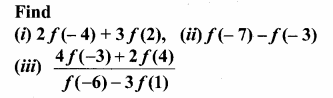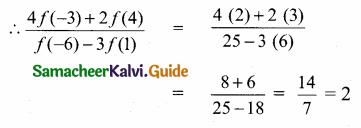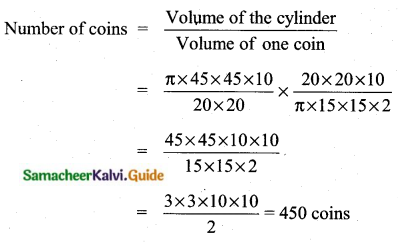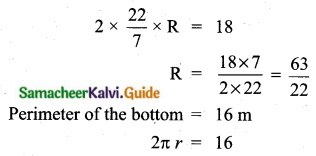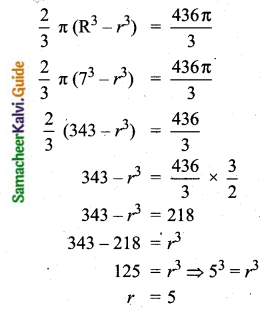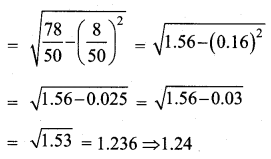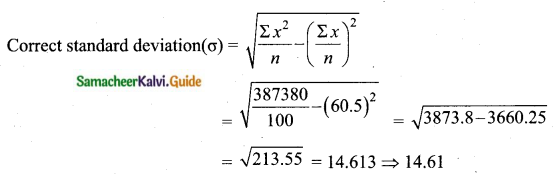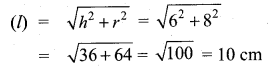Students can download Maths Chapter 2 Numbers and Sequences Ex 2.1 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.1

Question 1.
Find all positive integers which when divided by 3 leaves remainder 2.
Answer:
All the positive integers when divided by 3 leaves remainder 2
By Euclid’s division lemma
a = bq + r, 0 < r < b
a = 3q + r where 0 < q < 3
a leaves remainder 2 when divided by 3
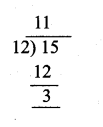
∴ The positive integers are 2, 5, 8, 11,…

Question 2.
A man has 532 flower pots. He wants to arrange them in rows such that each row contains 21 flower pots. Find the number of completed rows and how many flower pots are left over.
Solution:
Using Euclid’s division algorithm,
a = 21q + r, we get 532 = 21 × 25 + 7.
The remainder is 7.
No. of completed rows = 25, left over flower pots = 7 pots.

Question 3.
Prove that the product of two consecutive positive integers is divisible by 2.
Answer:
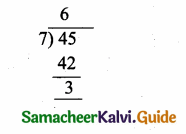
Let n – 1 and n be two consecutive positive integers, then the product is n (n – 1)
n(n – 1) = n² – n
We know that any positive integer is of the form 2q or 2q + 1 for same integer q

Case 1:
when n = 2 q
n² – n = (2q)² – 2q
= 4q² – 2q
= 2q (2q – 1)
= 2 [q (2q – 1)]
n² – n = 2 r
r = q(2q – 1)
Hence n² – n. divisible by 2 for every positive integer.

Case 2:
when n = 2q + 1
n² – n = (2q + 1 )² – (2q + 1 )
= (2q + 1) [2q + 1 – 1]
= 2q (2q + 1)
n² – n = 2r
r = q (2q + 1)
n² – n divisible by 2 for every positive integer.

Question 4.
When the positive integers be a, b and c are divided by 13, the respective remainders are 9, 7 and 10. Show that a + b + c is divisible by 13.
Solution:
Let the positive integers be a, b, and c.
a = 13 q + 9
b = 13q + 1
c = 13 q + 10
a + b + c = 13q + 9 + 13q + 7 + 13q + 10
= 39q + 26
= 13 (3q + 2)
which is divisible by 13.

Question 5.
Prove that square of any integer leaves the remainder either 0 or 1 when divided by 4.
Answer:
Let the integer be ” x ”
The square of its integer is “x² ”
Let x be an even integer
x = 2q + 0
x2 = 4q²
When x is an odd integer
x = 2k + 1
x² = (2k + 1)²
= 4k² + 4k + 1
= 4k (k + 1) + 1
= 4q + 1 [q = k(k + 1)]
It is divisible by 4
Hence it is proved

Question 6.
Use Euclid’s Division Algorithm to find the Highest Common Factor (H.C.F) of
(i) 340 and 412
(ii) 867 and 255
(iii) 10224 and 9648
(iv) 84, 90 and 120
Solution:
To find the H.C.F. of 340 and 412. Using Euclid’s division algorithm.
We get 412 = 340 × 1 + 72
The remainder 72 ≠ 0
Again applying Euclid’s division algorithm
340 = 72 × 4 + 52
The remainder 52 ≠ 0.
Again applying Euclid’s division algorithm
72 = 52 × 1 + 20
The remainder 20 ≠ 0.
Again applying Euclid’s division algorithm,
52 = 20 × 2 + 12
The remainder 12 ≠ 0.
Again applying Euclid’s division algorithm.
20 = 12 × 1 + 8
The remainder 8 ≠ 0.
Again applying Euclid’s division algorithm
12 = 8 × 1 + 4
The remainder 4 ≠ 0.
Again applying Euclid’s division algorithm
8 = 4 × 2 + 0
The remainder is zero.
Therefore H.C.F. of 340 and 412 is 4.

(ii) To find the H.C.F. of 867 and 255, using Euclid’s division algorithm.
867 = 255 × 3 + 102
The remainder 102 ≠ 0.
Again using Euclid’s division algorithm
255 = 102 × 2 + 51
The remainder 51 ≠ 0.
Again using Euclid’s division algorithm
102 = 51 × 2 + 0
The remainder is zero.
Therefore the H.C.F. of 867 and 255 is 51.

(iii) To find H.C.F. 10224 and 9648. Using Euclid’s division algorithm.
10224 = 9648 × 1 + 576
The remainder 576 ≠ 0.
Again using Euclid’s division algorithm
9648 = 576 × 16 + 432
Remainder 432 ≠ 0.
Again applying Euclid’s division algorithm
576 = 432 × 1 + 144
Remainder 144 ≠ 0.
Again using Euclid’s division algorithm
432 = 144 × 3 + 0
The remainder is zero.
There H.C.F. of 10224 and 9648 is 144.

(iv) To find H.C.F. of 84, 90 and 120.
Using Euclid’s division algorithm
90 = 84 × 1 + 6
The remainder 6 ≠ 0.
Again using Euclid’s division algorithm
84 = 6 × 14 + 0
The remainder is zero.
∴ The H.C.F. of 84 and 90 is 6. To find the H.C.F. of 6 and 120 using Euclid’s division algorithm.
120 = 6 × 20 + 0
The remainder is zero.
Therefore H.C.F. of 120 and 6 is 6
∴ H.C.F. of 84, 90 and 120 is 6.

Question 7.
Find the largest number which divides 1230 and 1926 leaving remainder 12 in each case.
Answer:
Find the HCF of ( 1230 – 12) and (1926- 12)
i.e HCF of 1218 and 1914
By Euclid’s division algorithm
1914 = 1218 × 1 + 696
The remainder 696 ≠ 0
By Euclid’s division algorithm
1218 = 696 × 1 + 522
The remainder 522 ≠ 0
Again by Euclid’s division algorithm
696 = 522 × 1 + 174
The remainder 174 ≠ 0 Again by Euclid’s division algorithm
522 = 174 × 3 + 0
The remainder is zero
∴ HCF of 1218 and 1914 is 174
The largest value is 174

Question 8.
If d is the Highest Common Factor of 32 and 60, find x and y satisfying d = 32x + 60y.
Solution:
Applying Euclid’s divison lemma to 32 and 60, we get
60 = 32 × 1 + 28 ……………. (i)
The remainder is 28 ≠ 0.
Again applying division lemma
32 = 28 × 1 + 4 ……………. (ii)
The remainder 4 ≠ 0.
Again applying division lemma
28 = 4 × 7 + 0 ………….. (iii)
The remainder zero.
∴ H.C.F. of 32 and 60 is 4.
From (ii), we get
32 = 28 × 1 + 4
⇒ 4 = 32 – 28 × 1
⇒ 4 = 32 – (60 – 32 × 1) × 1
⇒ 4 = 32 – 60 + 32
⇒ 4 = 32 × 2+(-1) × 60
∴ x = 2 and y = -1

Question 9.
A positive integer, when divided by 88, gives the remainder 61. What will be the remainder when the same number is divided by 11?
Answer:
Let the positive integer be “x”
x = 88 × y + 61 (a = pq + r)
since 88 is a multiple of 11
61 = 11 × 5 + 6
∴ The remainder is 6

Question 10.
Prove that two consecutive positive integers are always coprime.
Solution:
Let the numbers be I, I + 1:
They are co-prime if only +ve integer that divides both is 1.
I is given to be +ve integer.
So I = 1, 2, 3, ….
∴ One is odd and the other one is even. Hence H.C.F. of the two consecutive numbers is 1. Hence the result.

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.4

Question 1.
Find the next three terms of the following sequence.
(i) 8, 24, 72,…
(ii) 5, 1, -3, …
(iii) \(\frac { 1 }{ 4 } \), \(\frac { 2 }{ 9 } \), \(\frac { 3 }{ 16 } \)
(i) 216, 648, 1944 (This sequence is multiple of 3)
Next three terms are 216, 648, 1944
(ii) Next three terms are -7, -11, -15
(adding -4 with each term)
(iii) Next three terms are \(\frac { 4 }{ 25 } \),\(\frac { 5 }{ 36 } \) and \(\frac { 6 }{ 49 } \)
[using \(\frac{n}{(n+1)^{2}}\)]

Question 2.
Find the first four terms of the sequences whose nth terms are given by
(i) a_n = n³ – 2
(ii) a_n = (-1)ⁿ⁺¹ n(n+1)
(iii) a_n = 2n² – 6
Solution:
t_n = a_n = n³ -2
(i) a₁ = 1³ – 2 = 1 – 2 – 1
a₂ = 2³ – 2 = 8 – 2 = 6
a₃ = 3³ – 2 = 27 – 2 = 25
a₄ = 4³ – 2 = 64 – 2 = 62
∴ The first four terms are -1, 6, 25, 62, ……….

(ii) a_n = (-1)ⁿ⁺¹ n(n + 1)
a₁ = (-1)¹⁺¹ (1) (1 +1)
= (-1)² (1) (2) = 2
a₂ = (-1)²⁺¹ (2) (2 + 1)
= (-1)³ (2) (3)= -6
a₃ = (-1)³⁺¹ (3) (3 + 1)
= (-1)⁴ (3) (4) = 12
a₄ = (-1)⁴⁺¹ (4) (4 + 1)
= (-1)⁵ (4) (5) = -20
∴ The first four terms are 2, -6, 12, -20,…

(iii) a_n = 2n² – 6
a₁ = 2(1)² – 6 = 2 – 6 = -4
a₂ = 2(2)² – 6 = 8 – 6 = 2
a₃ = 2(3)² – 6 = 18 – 6 = 12
a₄ = 2(4)² – 6 = 32 – 6 = 26
∴ The first four terms are -4, 2, 12, 26, …

Question 3.
Find the n^th term of the following sequences
(i) 2, 5, 10, 17, ……
Answer:
(1² + 1);(2² + 1),(3² + 1),(4² + 1)….
n^th term is n² + 1
a_n = n² + 1

(ii) 0,\(\frac { 1 }{ 2 } \),\(\frac { 2 }{ 3 } \) ……
Answer:
(\(\frac { 1-1 }{ 1 } \)), (\(\frac { 2-1 }{ 2 } \)), (\(\frac { 3-1 }{ 3 } \)) …..
n^th term is \(\frac { n-1 }{ n } \)
a_n = \(\frac { n-1 }{ n } \)

(iii) 3,8,13,18,…….
Answer:
[5(1) -2], [5(2) – 2], [5(3) – 2], [5(4) – 2] ….
The n^th term is 5n – 2
a_n = 5n – 2

Question 4.
Find the indicated terms of the sequences whose n^th terms are given by

(i) a_n = \(\frac { 5n }{ n+2 } \) ; a₆ and a₁₃
Answer:
a_n = \(\frac { 5n }{ n+2 } \)
a₆ = \(\frac { 5(6) }{ 6+2 } \) = \(\frac { 30 }{ 8 } \) = \(\frac { 15 }{ 4 } \)
a₁₃ = \(\frac { 5(13) }{ 13+2 } \) = \(\frac{5 \times 13}{15}\) = \(\frac { 13 }{ 3 } \)
a₆ = \(\frac { 15 }{ 4 } \), a₁₃ = \(\frac { 13 }{ 3 } \)

(ii) a_n = – (n² – 4); a₄ and a₁₁
Answer:
a_n = -(n² – 4)
a₄ = -(4² – 4)
= – (16 – 4)
= -12
a₁₁ = -(11² – 4)
= – (121 – 4)
= – 117
a₄ = -12 and a₁₁ = -117

Question 5.
Find a₈ and a₁₅ whose n^th term is a_n

Answer:

Question 6.
If a₁ = 1, a₂ = 1 and a_n = 2a_n-1 + a_n-2, n > 3, n ∈ N, then find the first six terms of the sequence.
Solution:
a₁ = 1, a₂ = 1, a_n = 2a_n-1 + a_n-2
a₃ = 2a_(3-1) + a_(3-2)
= 2a₂ + a₁
= 2 × 1 + 1 = 3
a₄ = 2a_(4-1) + a_(4-2)
= 2a₃ + a₂
= 2 × 3 + 1 = 7
a₅ = 2a_(5-1) + a_(5-2)
= 2a₄ + a₃
= 2 × 7 + 3 = 17
a₆ = 2a_(6-1) + a_(6-2)
= 2a₅ + a₄
= 2 × 17 + 7
= 34 + 7
= 41
∴ The first six terms of the sequence are 1, 1, 3, 7, 17, 41 ………..

Students can download Maths Chapter 1 Relations and Functions Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Additional Questions

I. Multiple Choice Questions.

Question 1.
If n(A × B) = 15 and B = {1, 3, 7} then n(A) is ……………
(1) 3
(2) 5
(3) 1
(4) 15
Answer:
(2) 5
Hint: B(A × B) = 15
n(A) × n(B) = 15
n(A) × 3 = 15
n(A) = \(\frac { 15 }{ 3 } \) = 5

Question 2.
If A = {a, b,c) B = {b, d, e}
C = {a, e, i, o, u} then n [A ∩ C] × B] is
(1) 18
(2) 36
(3) 9
(4) 3
Answer:
(4) 3
Hint:
A ∩ C = {a,b,c} ∩ {a, e, i, o, u}
= {a}
n(A ∩ C) = 1
n[(A ∩ C) × B] = n(A ∩ C) × n(B)
= 1 × 3
= 3

Question 3.
If there are 28 relation from a set A = {2,4, 6, 8} to a set B, then the number of elements in B is ………………
(1) 7
(2) 14
(3) 5
(4) 4
Answer:
(1) 7
Hint: n(A) = 4
n(A × B) = 28
n(A) × n(B) = 28
4 × n(B) = 28
n(B) = \(\frac { 28 }{ 4 } \) = 7

Question 4.
The ordered pairs (a + 1, 4) (3, 4a + b) are equal then (a, b) is ………………..
(1) (4, 20)
(2) (20, 4)
(3) (-4, 20)
(4) (20, -4)
Answer:
(3) (-4, 20)
Hint: (a + 7, 4) = (3, 4a + b)
a + 7 = 3
a = 3 – 7
= – 4
4a + b = 4
4(-4) + b = 4
-16 + b = 4
b = 4 + 16 = 20
The pair (a, 6) is (-4, 20)

Question 5.
The range of the relation R = {(x, x³) / x} is a prime number less than 13} is …………………
(1) (2,3,5,7,11)
(2) (4,9,25,49,121)
(3) (8,27, 125,343, 1331)
(4) (1,8,27, 125,343, 1331)
Answer:
(3) (8, 27, 125,343, 1331)
Hint: x = {2, 3, 5, 7, 11}
Range (x³) = {8, 27, 125, 343, 1331}

Question 6.
If {( x, 2), (4, y) } represents an identity function, then (x, y) is
(1) (2, 4)
(2) (4, 2)
(3) (2, 2)
(4) (4, 4)
Answer:
(1) (2, 4)
Hint: In an identity function each element is associated with itself.

Question 7.
If {(7, 11), (5, a)} represents a constant
function, then the value of ‘a’ is
(1) 7
(2) 11
(3) 5
(4) 9
Answer:
(2) 11
Hint: All the images are same in a constant function.

Question 8.
Given f(x) = (- 1)^x is a function from N to Z. Then the range of f is
(1) {1}
(2) N
(3) { 1,- 1 }
(4) Z
Answer:
(3) {1, – 1}
Hint: f(x) = (- 1)^x = ± 1

Question 9.
If f = { (6, 3), (8, 9), (5, 3), (-1, 6) }, then the pre-images of 3 are
(1) 5 and-1
(2) 6 and 8
(3) 8 and-1
(4) 6 and 5
Answer:
(4) 6 and 5.
Hint: The Pre images of 3 are 6 and 5

Question 10.
Let A= { 1, 3, 4, 7, 11 }, B = {-1, 1, 2, 5, 7, 9 } and f : A → B be given by
f = {(1, -1), (3,2), (4, 1), (7, 5), (11, 9)}.
Then f is ………………….
(1) one-one
(2) onto
(3) bijective
(4) not a function
Answer:
(1) one – one
Hint:

Question 11.
The given diagram represents
(1) an onto function
(2) a constant function
(3) an one-one function
(4) not a function

Answer:
(4) not a function
Hint: 2 has two images 4 and 2.
It is not a function.

Question 12.
If A = { 5, 6, 7 }, B = { 1, 2, 3, 4, 5 }and f: A → B is defined by f(x) = x – 2, then the range of f is …………….
(1) {1,4, 5}
(2) {1,2, 3, 4, 5}
(3) { 2, 3, 4 }
(4) { 3, 4, 5 }
Answer:
(4) {3, 4, 5}
Hint: f(x) = x – 2
f(5) = 5 – 2 = 3
f(6) = 6 – 2 = 4
f(7) = 7 – 2 = 5
Range of f = {3, 4, 5}

Question 13.
If f(x) = x² + 5, then f(-4) = ………
(1) 26
(2) 21
(3) 20
(4) – 20
Answer:
(2) 21
Hint: f(x) = x² + 5
f(- 4) = (-4)² + 5 = 16 + 5 = 21

Question 14.
If the range of a function is a singleton set, then it is ……………..
(1) a constant function
(2) an identity function
(3) a bijective function
(4) an one-one function
Answer:
(1) a constant function
Hint: Every element of the first set has same image in the second set.

Question 15.
If f : A → B is a bijective function and if n(A) = 5 , then n(B) is equal to ………………
(1) 10
(2) 4
(3) 5
(4) 25
Answer:
(3) 5
Hint: If A and B are Bijective (one-one and onto) function then n (A) = n (B)

Question 16.
If f: R → R defined by f(x) = 3x – 6 and g : R → R defined by g(x) = 3x + k if fog – gof then the value of k is …………………..
(1) – 5
(2) 5
(3) 6
(4) -6
Answer:
(4) – 6
Hint: f(x) = 3x – 6 ;g(x) = 3x + k
fog = f[g(x)]
= f(3x + k)
= 3 (3x + k) – 6
= 9x + 3k – 6
g o f = g[f(x)]
= g(3x – 6)
= 3(3x – 6 ) + k
= 9x – 18 + k
But fog = gof
9x + 3k – 6 = 9x – 18 + k
3k – k = -18 + 6
2k = -12
k = \(\frac { -12 }{ 2 } \) = -6

Question 17.
If f(x) = x² – x then f (x – 1) – f(x + 1) is ……………….
(1) 4x
(2) 4x + 2
(3) 2 – 4x
(4) 4x – 2
Answer:
(3) 2 – 4x
Hint: f(x – 1) = (x – 1)² – (x – 1)
= x² – 2x + 1 – x + 1
= x² – 3x + 2
f(x + 1) = (x + 1)² – (x + 1)
= x² + 2x + 1 – x – 1
= x² + x
f(x – 1) – f(x + 1) = x² – 3x + 2 – (x2 + x)
= x² – 3x + 2 – x² – x
= -4x + 2 = 2 – 4x

Question 18.
If K(x) = 3x – 9 then L (x) = 7x – 10 then LOK is ……………..
(1) 21x + 73
(2) – 21x + 73
(3) 21x – 73
(4) 22x – 73
Answer:
(3) 21x – 73
Hint: K (x) = 3x – 9 ; L(x) = 7x – 10
LOK = L[K(x)]
= L (3x – 9)
= 7(3x – 9) – 10
= 21x – 63 – 10
= 21x – 73

Question 19.
Composition of function is ……………..
(1) commutative
(2) associative
(3) commutative and associative
(4) not associative
Answer:
(2) associative

Question 20.
A comet is heading for Jupiter with acceleration a = 50 kms^-2. The velocity of the comet at time ”t” is given by f(t) = at² – at + 1. Then the velocity at time t = 5 seconds is …………..
(1) 900kms^-1
(2) 1001 kms^-1
(3) 2001 kms^-1
(4) 50 kms^-1
Answer:
(2) 1001 kms^-1
Hint: f(t) = at² – at + 1
m = 50(5)² – 50(5) + 1
= 1250 – 250 + 1
= 1001 kms^-1

II. Answer the following questions.

Question 1.
f(x) = (1 + x)
f(x) = (2x – 1)
Show that fo(g(x)) = gof(x)
Solution:
f(x) = 1 + x
g(x) = (2x – 1)
fog(x) = f(g(x)) = f(2x – 1)
= 1 + 2x – 1 = 2x ………….. (1)
gof(x) = g(f(x)) = g(1 + x) = 2(1 + x) = 1
= 2 + 2x – 1
= 2x + 1 ……………. (2)
(1) ≠ (2)
∴ fog(x) + gof(x) It is verified.

Question 2.
If A × B = {(a, x) (a, y) (b, x) (b, y) (c, x) (c, y)} then find A and B
Answer:
A × B = {(a, x) (a, y) (b, x) (b, y) (c, x) (c, y)}
A = {a, b, c}
B = {x,y}

Question 3.
Let A = {x ∈ w/3 < x < 7},
B = {x ∈ N/0 < x < 3}, C = {x ∈ w/x < 2}
verify A × (B ∩ C) = (A × B) ∩ (A × C)
Answer:
A = {4,5,6} ; B = {1,2} C = {0, 1}
B ∩ C = {1,2} ∩ {0, 1}
= {1}
A × (B ∩ C) = {4,5,6} × {1}
= {(4, 1) (5, 1) (6, 1)} …. (1)
A × B = {4,5,6} × {1,2}
= {(4, 1) (4, 2) (5, 1) (5, 2) (6, 1) (6, 2)}
A × C = {4,5,6} x {0, 1}
= {(4,0) (4,1) (5,0)
(5, 1) (6, 0) (6, 1)}
(A × B) ∩ (A × C) = {(4, 1) (5, 1) (6, 1)}…. (2)
From (1) and (2) we get
A × (B ∩ C) = (A × B) ∩ (A × C)

Question 4.
Let A = {10, 11, 12, 13, 14}; B = {0, 1, 2, 3, 5} and f_i: A → B, i = 1, 2, 3. State the type of function for the following (give reason):
(i) f₁ = {(10,1), (11,2), (12,3), (13,5), (14,3)}
Answer:
The element 12 and 14 in A have same image 3 in B.

∴ It is not one-one function.
The element ‘0’ in B has no preimage in A
∴ It is not onto function
So the given function is neither one – one nor onto function.

(ii) f₂ = {(10,1), (11,1), (12,1), (13,1), (14,1)}
Answer:
f₂ is a constant function

(iii) f₃ = {(10,0), (11,1), (12,2), (13,3), (14,5)}
Answer:
f₃ is one-one and onto function (or) bijective function.

Question 5.
If X = {1, 2, 3, 4, 5}, Y = {1, 3, 5, 7, 9} determine which of the following relations from X to Y are functions? Give reason for your answer. If it is a function, state its type.
(i) R1 = {(x,y)| y = x + 2,x ∈ X,y ∈ Y}
Answer:
Given y = x + 2
When x = 1 ; y = 1 + 2 = 3
When x = 2 ; y = 2 + 2 = 4
When x = 3 ; y = 3 + 2 = 5
When x = 4 ; y = 4 + 2 = 6
When x = 5 ; y = 5 + 2 = 7

R₁ = {1,3), (2,4), (3, 5), (4, 6), (5,7)}
R₁ is not a function ; 2 and 4 has no image in Y.

(ii) R₂ = {(1,1), (2,1), (3,3), (4,3), (5,5)}
Answer:
R₂ is a function.
Every element of X has unique image in Y.
1 and 2 have same image 1
3 and 4 have same image 3
It is not one – one function …. (1)
7 and 9 has no pre image in X
It is not an onto function …. (2)

From (1) and (2) we know that, it is
neither one – one nor onto function.

(iii) R₃ = {(1,1), (1,3), (3,5), (3,7), (5,7)}
Answer:
R₃ is not a function.
1 has two images 1 and 3
3 has two images 5 and 7

(iv) R₄ = {(1,3), (2,5), (4,7), (5,9), (3,1)}
Answer:
Every element of X has unique image in
Y. Range = Co-domain
R₄ is a function.

It is an one-one and onto function (or) bijective function

Question 6.
A= {-2,-1, 1, 2} and f = {(x,\(\frac { 1 }{ x } \)) ; x ∈ A}
Write down the range of f. Is f a function from A to A?
Answer:
Given, f = (x,\(\frac { 1 }{ x } \)) ; So f(x) = \(\frac { 1 }{ x } \)
f (-2) = \(\frac { 1 }{ -2 } \) = – \(\frac { 1 }{ 2 } \) ; f(-1) = \(\frac { 1 }{ -1 } \) = -1
f(1) = \(\frac { 1 }{ 1 } \) = 1 ; f(2) = \(\frac { 1 }{ 2 } \) = \(\frac { 1 }{ 2 } \)
Range of f = {\(\frac { -1 }{ 2 } \), -1, 1, \(\frac { 1 }{ 2 } \)}
It is not a function from A to A since – \(\frac { 1 }{ 2 } \) ,\(\frac { 1 }{ 2 } \) ∈ A

Question 7.
Let A = {1, 2, 3, 4, 5}, B = N and f: A → B be defined by f(x) = x². Find the range of f. Identify the type of function.
Solution:
A = {1, 2, 3, 4, 5}
B = {1, 2, 3, 4 ….}
f: A → B, f(x) = x²
∴ f(1) = 1² = 1
f(2) = 2² = 4
f(3) = 3² = 9
f(4) = 4² = 16
f(5) = 5² = 25
∴ Range of f = {1, 4, 9, 16, 25)
Elements in A have been different elements in B. Therefore it is one-one function. But not all the elements in B have preimages in A. Therefore it is not on-to function.

Question 8.
Let A = { 1, 2, 3, 4, 5 }, B = N and f: A → B be defined by f(x) = x².
Find the range of f. Identify the type of function.
Answer:
Now, A = { 1, 2, 3, 4, 5 };
B = { 1, 2, 3, 4, … }
Given f: A → B and f(x) = x²
f(1) = 1² = 1;
f(2) = 4;
f(3) = 9;
f(4) = 16;
f(5) = 25.
Range of f = {1, 4, 9, 16, 25}
Since distinct elements are mapped into distinct images, it is a one-one function.
However, the function is not onto, since 3 ∈ B but there is no x ∈ A
such that
f(x) = x² = 3.

Question 9.
Identify the type of function.


Answer:
(i) Many – one into
(ii) One – one onto
(iii) Constant function
(iv) One – one into

Question 10.
Find the domain and range of the following
(i) f = {(1, 2), (2, 3), (3, 4), (4, 5) (5, 6)}
(ii) R = {(-2, 4), (-1,1), (2,4), (1,1) (-3, 9)}
Answer:
(i) f = {( 1,2), (2, 3), (3, 4), (4, 5) (5, 6)}
Domain = {1,2, 3,4, 5}
Range = {2, 3, 4, 5, 6}

(ii) R = {(-2,4), (-1, 1),(2,4), (1,1) (-3,9)}
Domain = {-2, -1,2, 1,-3} (or)
= {-3,-2,-1, 1,2}
Range = {4, 1, 9} (or) {1, 4, 9}

Question 11.
Given P ={-2,-1, 0,1}
Q = {1,-2, 6,-3}
R = {x,y/y = x² – 3 x ∈ P,y ∈ Q}
(i) List the elements of R
(ii) Is the relation a function? If so identity the function
Answer:
P = {-2, -1, 0, 1}; Q = {1, -2,6, -3}
y = x2- 3 x ∈ P, y ∈ Q
When x = -2 ⇒ y = (-2)² – 3 = 4 – 3 = 1
When x = -1 ⇒ y = (-1 )² – 3 = 1 – 3 = -2
When x = 0 ⇒ y = (0)² – 3 = 0 -3 = -3
When x = 1 ⇒ y = 1² – 3 = 1 – 3 = -2
(i) R = {(-2,1), (-1,-2), (0,-3), (1,-2)}
(ii) Yes the relation is a function many – one into function.

Question 12.
Given f(x) = 3x – 2; g(x) = 2x² find
(i) fog and
(ii) gof what do you find
Answer:
f(x) = 3x – 2 ; g(x) = 2x²
(i) f o g = f[g(x)]
= f(2x²)
= 3(2x²) – 2
= 6x² – 2

(ii) g o f = g [f(x)]
= g (3x – 2)
= 2(3x – 2)²
= 2(9x² + 4 – 12x)
= 18x² – 24x + 8
we find that fog ≠ gof
Composition of function is not commutative.

Question 13.
If f: R → R is defined by f(x) = ax + 3 and g: R → R is defined by g (x) = 4x – 3 find a so that fog = gof
Answer:
f(x) = ax + 3 ; g(x) = 4x -3
fog = f[g(x)]
= f(4x – 3)
= a (4x – 3) + 3
= 4ax – 3a + 3
gof = g [f(x)]
= g (ax + 3)
= 4 (ax + 3) – 3
= 4 ax + 12 – 3
= 4ax + 9
But fog = gof
4ax – 3a + 3 = 4ax + 9
-3a + 3 = 9
– 3a = 6
a = – 2
The value of a = – 2

Question 14.
Given f(x) = 3 + x ; g(x) = x² ;
h(x) = \(\frac { 1 }{ x } \) find fo (goh)
Answer:
f(x) = 3 + x ; g (x) = x², h(x) = \(\frac { 1 }{ x } \)
goh = g[h(x)]
= g (\(\frac { 1 }{ x } \))
= (\(\frac { 1 }{ x } \))²
goh = \(\frac{1}{x^{2}}\)
fo(goh) = f (\(\frac{1}{x^{2}}\))
= 3 + \(\frac{1}{x^{2}}\)

Question 15.
If f(x) = x + 3 where A = {4, 6, 8,10} B = {7, 9,11,13} and f: A → B
(i) Draw the arrow diagram
(ii) Why type of function is f.
Answer:
A= {4, 6, 8, 10}
f(x) = x + 3
f(4) = 4 + 3 = 7
f(6) = 6 + 3 = 9
f(8) = 8 + 3 = 11
f(10) = 10 + 3 = 13

(ii) one – one onto function

III. Answer the following Questions

Question 1.
Given A = {2,3, 5}, B = {1,2,3}
C = {2, 5}, D = {2,3, 5} check if
(A ∩ C) × (B ∩ D) = (A × B) ∩ (C × D)
Answer:
A ∩ C = {2, 3, 5} ∩ (2, 5}
= (2,5}
B ∩ D = {1,2,3} ∩ {2,3,5}
= {2,3}
(A ∩ C) × (B ∩ D) = {2, 5} × {2, 3}
= {(2, 2) (2, 3) (5, 2) (5, 3)} …. (1)
A × B = {2,3,5} × {1,2,3}
= {(2,1) (2, 2) (2, 3)
(3, 1) (3, 2) (3, 3)
(5, 1) (5, 2) (5, 3)}
C × D = {2, 5} × {2, 3, 5}
= {(2, 2) (2, 3) (2, 5) (5, 2) (5, 3) (5, 5)}
(A × B) ∩ (C × D) = {(2,2) (2, 3) (5, 2) (5, 3)} …. (2)
From (1) and (2) we get
(A ∩ C) × (B ∩ D) = (A × B) ∩ (C × D)

Question 2.
Study the relation given below an set- builder form. Represent each of them by
(a) an arrow diagram
(b) a graph
(c) a set in roster.
If {{x,y}/y = 2x + 1; x < 10 and y < 12 x ∈ N, y ∈ N}
Answer:
y = 2x + 1
when x = 1 ⇒ y = 2(1) + 1 = 2 + 1 = 3
when x = 2 ⇒ y = 2(2) + 1 = 4 + 1 = 5
when x = 3 ⇒ y = 2(3) + 1 = 6 + 1 = 7
when x = 4 ⇒ y = 2(4) + 1 = 8 + 1 = 9
when x = 5 ⇒ y = 2(5) + 1 = 10 + 1 = 11
f = {(1,3) (2, 5) (3, 7) (4, 9) (5, 11)}

(a) Arrow diagram

(b) A graph

(c) Roster form: R = {(1,3) (2,5) (3,7) (4,9) (5,11)}

Question 3.
State whether the following graphs represents a function. Give reason for your answer.





Answer:
(i) The given graph represents a function. The vertical line cuts the graph at most one point R

(ii) The vertical line cuts the graph at most one point Q. The given graph represents a function.

(iii) The vertical line cuts the graph at A and B. The given graph does not represents a function.

(iv) The vertical line cuts the graph at A and B. The given graph does not represents a function.

(v) The vertical line cuts the graph at most one point R. The given graph represents a function.

Question 4.
Let A = {6, 9,15,18, 21}; B = {1, 2, 4, 5, 6} and f: A → B be defined by f(x) = \(\frac { x-3 }{ 3 } \) Represent f by, (i) an arrow diagram, (ii) a set of ordered pairs, (iii) a table, (iv) a graph.
Given, A = {6, 9, 15, 18, 21}, B = {1, 2, 4, 5, 6}
f(x) = \(\frac { x-3 }{ 3 } \)
f(6) = \(\frac { 6-3 }{ 3 } \) = \(\frac { 3 }{ 3 } \) = 1
f(9) = \(\frac { 9-3 }{ 3 } \) = \(\frac { 6 }{ 3 } \) = 2
f(15) = \(\frac { 15-3 }{ 3 } \) = \(\frac { 12 }{ 3 } \) = 4
f(18) = \(\frac { 18-3 }{ 3 } \) = \(\frac { 12 }{ 3 } \) = 4
f(18) = \(\frac { 18-3 }{ 3 } \) = \(\frac { 15 }{ 3 } \) = 5
f(21) = \(\frac { 21-3 }{ 3 } \) = \(\frac { 18 }{ 3 } \) = 6

(i) an arrow diagram

(ii) a set of ordered pairs
f = {(6,1), (9, 2), (15, 4), (18, 5), (21,6)}

(iii) a table

(iv) a graph

Question 5.
Let A = {4,6,8,10} and B = {3,4,5,6,7}. If f: A → B is defined by f(x) = \(\frac { 1 }{ 2 } \) x + 1 then represent f by (i) an arrow diagram, (ii) a set of ordered pairs and, (iii) a table.
Answer:
Given, A = {4, 6, 8, 10}
B = {3, 4, 5, 6, 7}
f(x) = \(\frac { x }{ 2 } \) + 1
f(4) = \(\frac { 4 }{ 2 } \) + 1 = 2 + 1 = 3
f(6) = \(\frac { 6 }{ 2 } \) + 1 = 3 + 1 = 4
f(8) = \(\frac { 8 }{ 2 } \) + 1 = 4 + 1 = 5
f(10) = \(\frac { 10 }{ 2 } \) + 1 = 5 + 1 = 6

(i) an arrow diagram

(ii) a set of ordered pairs
f = {(4, 3), (6, 4), (8, 5), (10, 6)}

(iii) a table

Question 6.
A function f[- 3, 7 ) → R is defined as follows f(x) =

Find (i) f(5) + f(6)
(ii) f(1) – f(-3)
(iii) f(-2) – f(4)
(iv) \(\frac{f(3)+f(-1)}{2 f(6)-f(1)}\)
Answer:
Given, f(x) = 4x² – 1; x = {-3, -2, -1, 0, 1}
f(x) = 3x – 2; x = {2,3,4}
f(x) = 2x – 3; x = {5,6}
(i) f(5) + f(6)
f(x) = 2x – 3
f(5) = 2(5) – 3 = 10 – 3 = 7
f(6) = 2(6) – 3 = 12 – 3 = 9
∴ f(5) + f(6) = 7 + 9 = 16

(ii) f(1) – f(-3)
f(x) = 4x² – 1
f(1) = 4(1)² – 1 = 4 – 1 = 3
f(-3) = [4(-3)² – 1]
= 4 (9) – 1
= 36 – 1 = 35
∴ f(1) – f(-3) = 3 – (35) = -32

(iii) f(-2) – f(4)
f(x) = 4x² – 1
f(-2) = 4(-2)² – 1 = 4(4) – 1 = 16 – 1 = 15
f(x) = 3x – 2
f(4) = [3(4) – 2] = 12 – 2 = 10
∴ f(-2) – f(4) = 15 – 10 = 5

Question 7.
A function f : [- 7, 6) → R is defined as follows


Answer:
Given, f(x) = x² + 2x + 1 ; x = {-7, -6}
f(x) = x + 5 ; x = {-5, -4, -3, -2, -1, 0, 1, 2}
f(x) = x – 1; x{3, 4, 5}

(i) 2f(- 4) + 3f(2)
f(x) = x + 5
f(-4) = -4 + 5 = 1
f(2) = 2 + 5 = 7
∴ 2f(-4) + 3 f(2) = 2(1) + 3(7) = 2 + 21 = 23

(ii) f(-7) – f(-3)
f(x) = x² + 2x + 1
f(-7) = (-7)² + 2(-7) + 1 = 49 – 14 + 1 = 36
f(x) = x + 5
f(-3) = -3 + 5 = 2
∴ f(-7) – f(-3) = 36 – 2 = 34

(iii) \(\frac{4 f(-3)+2 f(4)}{f(-6)-3 f(1)}\)
f(x) = x + 5
f(-3) = -3 + 5 = 2
f(x) = x – 1
f(4) = 4 – 1 = 3
f(x) = x² + 2x + 1
f(-6) = (-6)² + 2(-6) + 1 = 36 – 12 + 1 = 25
f(x) = x + 5
f(1) = 1 + 5 = 6

Question 8.
Let A= { 0,1, 2, 3 } and B = {1, 3, 5, 7, 9 } be two sets. Let f: A → B be a function given by f (x) = 2x + 1. Represent this function as
(i) a set of ordered pairs
(ii) a table
(iii) an arrow diagram and
(iv) a graph.
Answer:
A = {0, 1, 2, 3}, B = { 1, 3, 5, 7, 9 },f(x) = 2x + 1
f(0) = 2(0) + 1 = 1, f(1) = 2(1) + 1 = 3 ,f(2) = 2(2) + 1 = 5, f(3) = 2(3) + 1 = 7

(i) Set of ordered pairs
The given function/can be represented as a set of ordered pairs as
f = {(0, 1), (1, 3), (2, 5), (3,7)}

(ii) Table form
Let us represent f using a table as shown below.

(iii) Arrow Diagram
Let us represent f by an arrow diagram.
We draw two closed curves to represent the sets A and B. Here each element of A and its unique image element in B are related with an arrow.

(iv) Graph
We are given that
f = {(x,f(x)) | x ∈ A} = {(0,1), (1, 3), (2, 5), (3, 7)}. Now, the points (0, 1), (1, 3), (2, 5) and (3, 7) are plotted on the plane as shown below.
The totality of all points represent the graph of the function.

Question 9.
A. function f: [1, 6) → R is defined as follows

(Here, [1, 6) = {x ∈ R : 1 ≤ x < 6})
Find the value of
(i) f(5)
(ii) f(3)
(iii) f(1)
(iv) f(2) – f(4)
(v) 2f(5) – 3f(1).
Answer:
(i) Let us find f(5). Since 5 lies between 4 and 6, we have to use f(x) = 3x² – 10.
Thus, f(5) = 3(5²) – 10 = 65.

(ii) To find f(3), note that 3 lies between 2 and 4.
So, we use f(x) = 2x – 1 to calculate f(3).
Thus, f(3) = 2(3) – 1 = 5.

(iii) Let us find f(1).
Now, 1 is in the interval 1 < x < 2
Thus, we have to use f(x) = 1 + x to obtain f(1) = 1 + 1 = 2.

(iv) f (2) – f(4)
Now, 2 is in the interval 2 < x < 4 and so, we use f(x) = 2x – 1.
Thus, f(2) = 2(2) -1 = 3.
Also, 4 is in the interval 4 < x < 6. Thus, we use f(x) = 3x² – 10
Therefore, f(4) = 3(4²) – 10 = 3(16) – 10 = 48 – 10 = 38.
Hence, f(2) – f(4) = 3 – 38 = -35.

(v) To calculate 2 f (5) – 3f (1), we shall make use of the values that we have already calculated in (i) and (iii). Thus, 2f(5) – 3f(1) = 2(65) – 3(2) = 130 – 6 – 124.

Question 10.
Given f(x) = 5x + 2; g(x) = 2x – 3;
h(x) = 3x + 1. Verify fo (goh) = (fog) oh
Answer:
f(x) = 5x + 2 ; g(x) = 2x – 3; h(x) = 3x + 1
L.H.S. = fo (goh)
goh = g[h(x)]
= g(3x + 1)
= 2(3x + 1) – 3
= 6x – 1
fo (goh) = f[goh (x)]
= f(6x – 1)
= 5 (6x – 1) + 2
= 30 x – 5 + 2
fo (goh) = 30x – 3 ….(1)
R.H.S. = (fog) oh
fog = f[g(x)]
= f(2x – 3)
= 5(2x – 3) + 2
= 30x – 5 + 2
fo (goh) = 30x – 3 …..(1)
R.H.S. = (fog) oh
fog = f[g(x)]
= f(2x – 3)
= 5 (2x – 3)
= 5 (2x – 3) + 2
= 10x – 15 + 2
= 10x – 13
(fog) oh = fog [h(x)]
= fog (3x + 1)
= 10 (3x + 1) – 13
= 30x + 10 – 13
= 30x – 3 ….(2)
From (1) and (2) we get L.H.S. = R.H.S.
fo(goh) = (fog) oh

Question 11.
Given f(x) = x² + 4; g(x) = 3x – 2;
h(x) = x – 5. Show that the composition of functions is associative.
Answer:
f(x) = x² + 4 ; g(x) – 3x – 2; h(x) = x – 5
To prove fo (goh) = (fog) oh
L.H.S. fo (goh)
goh = g[h(x)]
= g(x – 5)
= 3(x – 5) – 2
= 3x – 15 – 2
goh = 3x – 17
fo (goh) = f [goh (x)]
= f(3x – 17)
= (3x – 17)² + 4
= 9x² + 289 – 102 x + 4
= 9x² – 102x + 293 ….(1)
R.H.S. = (fog) oh
fog – f[g(x)]
= f(3x-2)
= (3x – 2)² + 4
= 9×2 + 4 – 12x + 4
= 9×2 – 12x + 8
(fog) oh = fog [h(x)]
= fog (x – 5)
= 9(x – 5)² – 12 (x – 5) + 8
= 9(x² + 25 – 10x) – 12x + 60 + 8
= 9x² + 225 – 90x – 12x + 60 + 8
= 9x² – 102x + 293 ….(2)
From (1) and (2) we get fo (goh) = (fog) oh.
Composition of function is associative

Question 12.
Given f(x) = x – 2; g(x) = 3x + 5; h(x) = 2x – 3. Verify that (goh) of = go (hof)
Answer:
f(x) = x – 2 ; g(x) = 3x + 5; h(x) = 2x – 3
L.H.S. (goh) of
goh = g[h(x)]
= g(2x – 3)
= 3(2x – 3) + 5
= 6x – 9 + 5
= 6x – 4
(goh) of = goh [f(x)]
= goh (x – 2)
= 6(x – 2) – 4
= 6x – 12 – 4
= 6x – 16 ….(1)

R.H.S. go(hof)
hof = h[f(x)]
= h(x- 2)
= 2(x – 2) – 3
= 2x – 4 – 3
= 2x – 7
go(hof) = g [hof (x)]
= g (2x – 7)
= 3(2x – 7) + 5
= 6x – 21 + 5
= 6x – 16 ….(2)
From (1) and (2) we get (goh) of = go(hof)

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.3 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.3

Question 1.
Find the least positive value of x such that

(i) 71 = x (mod 8)
Answer:
71 = 7 (mod 8)
∴ The value of x = 7

(ii) 78 + x = 3 (mod 5)
78 + x – 3 = 5n (n is any integer)
75 + x = 5n
(Let us take x = 5)
75 + 5 = 80 (80 is a multiple of 5)
∴ The least value of x is 5

(iii) 89 = (x + 3) (mod 4)
89 – (x + 3) = 4n
(n may be any integer)
89 – x – 3 = 4n
89 – x = 4n
86 – x is a multiple of 4
(84 is a multiple of 4)
86 – 2 = 4n
84 = 4n
The value of x is 2

(iv) 96 = \(\frac { x }{ 7 } \) (mod 5)
96 – \(\frac { x }{ 7 } \) = 5n (n may be any integer)
672 – x = 35n (multiple of 35 is 665)
672 – 7 = 665
∴ The value of x = 7

(v) 5x = 4 (mod 6)
5x – 4 = 6n (n may be any integer)
5x = 6n + 4
x = \(\frac { 6n+4 }{ 5 } \)
Substitute the value of n as 1, 6, 11, 16 …. as n values in x = \(\frac { 6n+4 }{ 5 } \) which is divisible by 5.
2, 8, 14, 20,…………
The least positive value is 2.

Question 2.
If x is congruent to 13 modulo 17 then 7x -3 is congruent to which number modulo 17?
Solution:
x ≡ 13 (mod 17)
Let p be the required number …………. (1)
7x – 3 ≡ p (mod 17) ………….. (2)
From (1),
x – 13 = 17n for some integer M.
x – 13 is a multiple of 17.
x must be 30.
∴ 30 – 13 = 17
which is a multiple of 17.
From (2),
7 × 30 – 3 ≡ p (mod 17)
210 – 3 ≡ p (mod 17)
207 ≡ p (mod 17)
207 ≡ 3 (mod 17)
∴ P ≡ 3

Question 3.
Solve 5x ≡ 4 (mod 6)
5x – 4 = 6n (n may be any integer)
5x = 6n + 4
x = \(\frac{6 n+4}{5}\)
The value of n 1, 6, 11, 16 ……..
∴ The value of x is 2, 8, 14, 20 …………..

Question 4.
Solve 3x – 2 = 0 (mod 11)
Answer:
Given 3x – 2 = 0(mod 11)
3x – 2 = 11n (n may be any integer)
3x = 2 + 11n
x = \(\frac { 11n+2 }{ 3 } \)
Substitute the value of n = 2, 5, 8, 11 ….
When n ≡ 2 ⇒ x = \(\frac { 22+2 }{ 3 } \) = \(\frac { 24 }{ 3 } \) = 8
When n = 5 ⇒ x = \(\frac { 55+2 }{ 3 } \) = \(\frac { 57 }{ 3 } \) = 19
When n = 8 ⇒ x = \(\frac { 88+2 }{ 3 } \) = \(\frac { 90 }{ 3 } \) = 30
When n = 11 ⇒ x = \(\frac { 121+2 }{ 3 } \) = \(\frac { 123 }{ 3 } \) = 41
∴ The value of x is 8, 19, 30,41

Question 5.
What is the time 100 hours after 7 a.m.?
Answer:
100 ≡ x (mod 12) Note: In a clock every 12 hours
100 ≡ 4 (mod 12) the numbers repeats.

The time repeat after 7 am is 7 + 4 = 11 o’ clock (or) 11 am.

Question 6.
What is time 15 hours before 11 p.m.?
Solution:
15 ≡ x (mod 12)
15 – x = 12n
15 – x is a multiple of 12 x must be 3.

∴ The time 15 hrs before 11 O’clock is 11 – 3 = 8 O’ clock i.e. 8 p.m

Question 7.
Today is Tuesday. My uncle will come after 45 days. In which day my uncle will be coming?
Answer:
Number of days in a week = 7
45 ≡ x (mod 7)
45 ≡ 3 (mod 7)

The value of x must be 3.
Three days after tuesday is friday uncle will come on friday.

Question 8.
Prove that 2ⁿ + 6 × 9ⁿ is always divisible by 7 for any positive integer n.
Solution:
2¹ + 6 × 9¹ = 2 + 54 = 56 is divisible by 7
When n = k,
2^k + 6 × 9^k = 7 m [where m is a scalar]
⇒ 6 × 9^k = 7 m – 2^k …………. (1)
Let us prove for n = k + 1
Consider 2^k+1 + 6 × 9^k+1 = 2^k+1 + 6 × 9^k × 9
= 2^k+1 + (7m – 2^k)9 (using (1))
= 2^k+1 + 63m – 9.2^k = 63m + 2^k.2¹ – 9.2^k
= 63m – 2^k (9 – 2) = 63m – 7.2^k
= 7 (9m – 2^k) which is divisible by 7
∴ 2ⁿ + 6 × 9ⁿ is divisible by 7 for any positive integer n

Question 9.
Find the remainder when 2⁸¹ is divided by 17?
Answer:
2⁸¹ ≡ x(mod 17)
2⁴⁰ × 2⁴⁰ × 2¹ ≡ x(mod 17)
(2⁴)¹⁰ × (2⁴)¹⁰ × 2¹ ≡ x(mod 17)
(16)¹⁰ × (16)¹⁰ × 2¹ ≡ x(mod 17)
(16²)⁵ × (16²)⁵ × 2¹ ≡ x(mod 17)
= 1 × 1 × 2 (mod 17)
[(16)² = 256 = 1 (mod 17)]
= 2 (mod 17)
2⁸¹ = 2(mod 17)
∴ x = 2
The remainder is 2

Question 10.
The duration of flight travel from Chennai to London through British Airlines is approximately 11 hours. The airplane begins its journey on Sunday at 23:30 hours. If the time at Chennai is four and half hours ahead to that of London’s time, then find the time at London, when will the flight lands at London Airport?
Answer:
Duration of the flight time = 11 hours
(Chennai to London)
Starting time on Sunday = 23 : 30 hour

Time difference is 4 \(\frac { 1 }{ 2 } \) horns ahead to london
The time to reach London airport = (10.30 – 4.30)
= 6 am
The first reach the london airport next day (monday) at 6 am

Students can download Maths Chapter 8 Statistics and Probability Ex 8.4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 8 Statistics and Probability Ex 8.4

Question 1.
If P (A) = \(\frac{2}{3}\), P(B) = \(\frac{2}{5}\), P(A ∪ B) = \(\frac{1}{3}\), then find P(A ∩ B).
Answer:
P(A ∪ B) = P (A) + P (B) – P (A ∩ B)
\(\frac{1}{3}=\frac{2}{3}+\frac{2}{5}\) – P (A ∩ B)

Question 2.
A and B are two events such that, P(A) = 0.42, P(B) = 0.48, and P(A∩B)=016. Find (i) P(not A)
(ii) P(not B)
(iii) P(A or B)
Solution:
(a) P(A) = 0.42 ;
P(B) = 0.48
P(A∩B) = 0.16
(i) P(not A) = P(\(\overline{\mathbf{A}}\)) = 1 – P(A) = 1 – 0.42 = 0.58
(ii) P(not B) = P(\(\overline{\mathbf{B}}\)) = 1 – P(B) = 1 – 0.48 = 0.52
(iii) P(A or B) = P(A∪B) = P(A) + P(B) – P(A∩B)
= 0.42 + 0.48 – 0.16
= 0.74

Question 3.
If A and B are two mutually exclusive events of a random experiment and P (not A) = 0.45, P (A ∪ B) = 0.65, then find P(B).
Answer:
P(not A) = 0.45
1 – P (A) = 0.45
P (A) = 1 – 0.45 = 0.55
P(A ∪ B) = P (A) + P (B)
0. 65 = 0.55 + P(B)
0. 65 – 0.55 = P(B)
0.10 = P (B)
P(B) = 0.1

Question 4.
The probability that atleast one of A and B occur is 0.6. If A and B occur simultaneously with probability 0.2, then find P(\(\overline{\mathbf{A}}\)) + P(\(\overline{\mathbf{B}}\)).
Solution:
P(A∪B) = 0.6
P(A∩B) = 0.2
P(A) + P(B) = [1 – P(A∪B)] + [1 – P(A∩B)] = [1 – 0.6] + [1 – 0.2]
= 0.4 + 0.8 = 1.2

Question 5.
The probability of happening of an event A is 0.5 and that of B is 0.3. If A and B are mutually exclusive events, then find the probability of neither A nor B happen.
Answer:
Here P(A) = 0.5, P (B) = 0.3
P(A ∪ B) = P (A) + P(B) [A and B are mutually exclusive]
= 0.5 + 0.3
= 0.8
Probability of neither A nor [P(A ∪ B)’] = 1 – P(A ∪ B) = 1 – 0.8 = 0.2

Question 6.
Two dice are rolled once. Find the probability of getting an even number on the first die or a total of face sum 8.
Answer:
Sample space = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n (S) = 36
Let A be the event of getting an even number on the first time
A = {(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n (A) = 18
\(P(A)=\frac{n(A)}{n(S)}=\frac{18}{36}\)
(ii) Let B be the event of getting a total of face sum 8.
B = {(2, 6) (3, 5) (4, 4) (5, 3) (6, 2)}
n(B) = 5
\(P(B)=\frac{n(B)}{n(S)}=\frac{5}{36}\)
A ∩ B = {(2, 6) (4, 4) (6, 2)}
n(A ∩ B) = 3
P(A ∩ B) = \(\frac{3}{36}\)
P(A ∪ B) = P (A) + P (B) – P (A ∩ B)

The required probability = \(\frac{5}{9}\)

Question 7.
From a well-shuffled pack of 52 cards, a card is drawn at random. Find the probability of its being either a red king or a black queen.
Answer:
n(S) = 52
Let A be the event of getting a red king
n(A) = 2
\(P(A)=\frac{n(A)}{n(S)}=\frac{2}{52}\)
Let B be the event of getting a black Queen king
n(B) = 2
\(P^{\prime}(B)=\frac{n(B)}{n(S)}=\frac{2}{52}\)
It A and B are mutually exclusive
P(A ∪ B) = P(A) + P(B)
\(=\frac{2}{52}+\frac{2}{52}=\frac{4}{52}=\frac{1}{13}\)
The required probability is \(\frac{1}{13}\)

Question 8.
A box contains cards numbered 3, 5, 7, 9,… 35, 37. A card is drawn at random from the box. Find the probability that the drawn card have either multiples of 7 or a prime number.
Answer:
Sample space = {3, 5, 7, 9,…….,35, 37}
n(S) = 18
Let A be the event of getting a multiple of 7
A = {7, 21, 35}
n(A) = 3
\(P(A)=\frac{n(A)}{n(S)}=\frac{3}{18}\)
Let B be the event of getting a prime number
B = {3, 5, 7,11, 13, 17, 19, 23, 29, 31, 37}
n(B) = 11

Probability of getting a multiple of 7 or a prime number = \(\frac{13}{18}\)

Question 9.
Three unbiased coins are tossed once. Find the probability of getting atmost 2 tails or atleast 2 heads.
Answer:
Sample space = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n(S) = 8
Let A be the event of getting atmost 2 tails.
A = {HTT, THT, TTH, HHT, HTH, THH, HHH}
n(A) = 7

Probability of getting atmost two tails or atleast 2 heads = \(\frac{7}{8}\)

Question 10.
The probability that a person will get an electrification contract is \(\frac{3}{5}\) and the probability that he will not get plumbing contract is \(\frac{5}{8}\). The probability of getting atleast one contract is \(\frac{5}{7}\). What is the probability that he will get both?
Answer:
Let A and B represent the event of getting electrification control and plumbing contract.


Probability of getting both the job is \(\frac{73}{280}\)

Question 11.
In a town of 8000 people, 1300 are over 50 years and 3000 are females. It is known that 30% of the females are over 50 years. What is the probability that a chosen individual from the town is either a female or over 50 years?
Answer:
Total number of people in a town is 8000.
n(S) = 8000
Total number of females = 3000
Let A be the event of getting number of females
n(A) = 3000
\(P(A)=\frac{n(A)}{n(S)}=\frac{3000}{8000}\)
Number of people over 50 years = 1300
Let B be the event of getting number of people over 50 years.
n(B) = 1300
\(P(B)=\frac{n(B)}{n(S)}=\frac{1300}{8000}\)
Given 30% of the females are over 50 years.


Proability of getting either a female or over 50 years = \(\frac{17}{40}\)

Question 12.
A coin is tossed thrice. Find the probability of getting exactly two heads or atleast one tail or two consecutive heads.
Answer:
Sample space = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n(S) = 8
Let A be the event of getting exactly two heads.
A = {HHT, HTH, THH}
n(A) = 3
\(P(A)=\frac{n(A)}{n(S)}=\frac{3}{8}\)
Let B be the event of getting atleast one tail
B = {HHT, HTH, HTT, THH, THT, TTH, TTT}
n(B) = 7
\(P(B)=\frac{n(B)}{n(S)}=\frac{7}{8}\)
Let C be the event of getting consecutively
C = {HHH, HHT, THH}
n(C) = 3



The probability is 1.

Question 13.
If A, B, C are any three events such that probability of B is twice as that of probability of A and probability of C is thrice as that of probability of A and if P (A ∩ B) = \(\frac{1}{6}\), P(B ∩ C) = \(\frac{1}{4}\), P(A ∩ C) = \(\frac{1}{8}\), P(A ∪ B ∪ C) = \(\frac{9}{10}\) and P (A ∩ B ∩ C) = \(\frac{1}{15}\), then find P(A), P(B) and P(C)?
Answer:
By the given condition,
P(B) = 2 P(A), P(C) = 3 P(A)
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(A ∩ C) + P(A ∩ B ∩ C)

Question 14.
In a class of 35, students are numbered from 1 to 35. The ratio of boys and girls is 4 : 3. The roll numbers of students begin with boys and end with girls. Find the probability that a student selected is either a boy with prime roll number or a girl with composite roll number or an even roll number.
Answer:
Sample space (S) = {1, 2, 3,… ,35}
n(S) = 35
Total number of students = 35
Number of boys = \(\frac{4}{7}\) × 35 = 20 [Boys Numbers = {1, 2, 3,…, 20}]
Number of girls = \(\frac{3}{7}\) × 35 = 15 [Girls Numbers = { 21, 22,…, 35}]
Let A be the event of getting a boy role number with prime number
A = {2, 3, 5, 7, 11, 13, 17, 19}
n(A) = 8
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}\) = \(\frac{8}{35}\)
Let B be the event of getting girls roll number with composite number.
B = {21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35}
n(B) = 12
P(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}\) = \(\frac{12}{35}\)
Let C be the event of getting an even roll number.
C = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34}
n(C) = 17


Probability of getting roll number is \(\frac{29}{35}\)

Students can download Maths Chapter 7 Mensuration Unit Exercise 7 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 7 Mensuration Unit Exercise 7

Question 1.
The barrel of a fountain-pen cylindrical in shape is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen will be used for writing 330 words on an average. How many words can be written using a bottle of ink containing one-fifth of a litre?
Answer:

Question 2.
A hemispherical tank of radius 1.75 m is full of water. It is connected with a pipe which empties the tank at the rate of 7 litres per second. How much time will it take to empty the tank completely?
Answer:
Radius of the hemispherical tank = 1.75 m
Volume of the tank = \(\frac{2}{3} \pi r^{3}\) cu.units

Time taken = \(\frac{11229.17}{7}\) = 1604.17 seconds = 26.74 minutes = 27 minutes (approximately)

Question 3.
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r units.
Answer:
Radius of a cone = Radius of a hemisphere = r unit

Height of a cone = r units
(height of the cone = radius of a hemisphere)
Maximum volume of the cone

Question 4.
An oil funnel of the tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion by 8 cm and the diameter of the top of the funnel be 18 cm, then find the area of the tin sheet required to make the funnel.
Answer:

Total height of oil funnel = 22 cm
Height of the cylindrical portion = 10 cm
Height of the frustum (h) = 22 – 10 = 12 cm
Radius of the cylindrical portion = 4 cm
Radius of the bottom of the frustum = 4 cm
Top radius of the funnel (frustum) = \(\frac{18}{2}\) = 9 cm
Area of the tin sheet required = C.S.A of the frustum + C.S.A of the cylinder
= π (R + r) l + 2πrh sq. units.
= [π(9 + 4) \(\sqrt{12^{2}+(9-4)^{2}}\) + 2π × 4 × 10] cm²
= π [13 × \(\sqrt{144+25}\) + 25 + 80] cm²
= \(\frac{22}{7}\) [13 × 13 + 80] cm²
= \(\frac{22}{7}\) [169 + 80] cm²
= \(\frac{22}{7}\) × 249 cm²
= 782.57 cm²
Area of sheet required to make the funnel = 782.57 cm²

Question 5.
Find the number of coins, 1.5 cm in diameter and 2 mm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Answer:
Radius of the cylinder = \(\frac{4.5}{2}\) cm
Height of the cylinder = 10 cm
Volume of the cylinder = πr²h cu. units


Number of coins = 450

Question 6.
A hollow metallic cylinder whose external radius is 4.3 cm and internal radius is 1.1 cm and the whole length is 4 cm is melted and recast into a solid cylinder of 12 cm long. Find the diameter of a solid cylinder.
Answer:
External radius of the hollow cylinder R = 4.3 cm
Internal radius of the hollow cylinder r = 1.1 cm
Length of the cylinder (h) = 4 cm
Length of the solid cylinder (H) = 12 cm
Let the radius of the solid cylinder be “x”
Volume of the solid cylinder = Volume of the hollow cylinder

Diameter of the solid cylinder = 2 × 2.4 = 4.8 cm

Question 7.
The slant height of a frustum of a cone is 4 m and the perimeter of circular ends are 18 m and 16 m. Find the cost of painting its curved surface area at ₹ 100 per sq. m.
Answer:
Slant height of a frustum (l) = 4 m
Perimeter of the top part = 18 m
2πR = 18


Cost of painting = ₹ 100 × 68 = ₹ 6800

Question 8.
A hemispherical hollow bowl has material of volume cubic \(\frac{436 \pi}{3}\) cubic cm. Its external diameter is 14 cm. Find its thickness.
Answer:
External radius of a hemisphere (R) = 7 cm
Volume of a hemi-spherical bowl = \(\frac{436 \pi}{3}\) cm³

Internal radius = 5 cm
Thickness of the hemisphere = (7 – 5) cm = 2 cm

Question 9.
The volume of a cone is 1005\(\frac{5}{7}\) cu. cm. The area of its base is 201\(\frac{1}{7}\) sq. cm. Find the slant height of the cone.
Answer:
Area of the base of a cone = 201\(\frac{1}{7}\) sq. cm

Question 10.
A metallic sheet in the form of a sector of a circle of radius 21 cm has a central angle of 216°. The sector is made into a cone by bringing the bounding radii together. Find the volume of the cone formed.
Answer:

Radius of a cone (r) = 21 cm
Central angle (θ) = 216°
Let “R” be the radius of a cone
Circumference of the base of a cone = arc length of the sector
2πR = \(\frac{\theta}{360} \times 2 \pi r\)

Students can download Maths Chapter 8 Statistics and Probability Ex 8.3 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 8 Statistics and Probability Ex 8.3

Question 1.
Write the sample space for tossing three coins using tree diagram.
Answer:
Sample space = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

Question 2.
Write the sample space for selecting two balls from a bag containing 6 balls numbered 1 to 6 (using tree diagram).
Answer:
Sample space = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

Question 3.
If A is an event of a random experiment such that P(A) : P(\(\bar{A}\)) = 17 : 15 and n(s) = 640 then find (i) P(\(\bar{A}\))
(ii) n(A)
Answer:

Question 4.
A coin is tossed thrice. What is the probability of getting two consecutive tails?
Answer:
Sample space = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n(S) = 8
Let A be the event of getting consecutive tails
A = {HTT, TTH, TTT}
n(A) = 3
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{3}{8}\)

Question 5.
At a fete, cards bearing numbers 1 to 1000, one number on one card are put in a box. Each player selects one card at random and that card is not replaced. If the selected card has a perfect square number greater than 500, the player wins a prize. What is the probability that
(i) the first player wins a prize
(ii) the second player wins a prize if the first has won?
Solution:
22² = 484
31² = 961
23² = 529
32² = 1024
23, 24, 25, 26, 27, 28, 29, 30, 31 has squares below 500 × 1000.
(i) P(first player wins a prize) = \(\frac{9}{1000}\)
(ii) P(second player ins if first has won) = \(\frac{8}{999}\)

Question 6.
A bag contains 12 blue balls and x red balls. If one ball is drawn at random (i) what is the probability that it will be a red ball? (ii) If 8 more red balls are put in the bag, and if the probability of drawing a red ball will be twice that of the probability in (i), then find x.
Answer:
Sample space = 12 + x
n(S) = x + 12
(i) Let A be the event of getting a red ball
n(A) = x
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}\) = \(\left(\frac{x}{x+12}\right)\)
(ii) 8 more red balls are added
Sample space = x + 12 + 8 = x + 20
Number of red balls = x + 8
Probability of drawing red ball = \(\frac{x+8}{x+20}\)
By the given condition
\(\frac{x+8}{x+20}=2\left(\frac{x}{x+12}\right)\)
(x + 8)(x + 12) = 2x(x + 20)
x² + 20x + 96 = 2x² + 40x
x² + 20x – 96 = 0
(x + 24)(x – 4) = 0
x = -24 (or) x = 4
The value of x = 4 (Number of balls will not be negative)
The probability of getting red balls = \(\left(\frac{x}{x+12}\right)=\frac{4}{16}=\frac{1}{4}\)

Question 7.
Two unbiased dice are rolled once. Find the probability of getting
(i) a doublet (equal numbers on both dice)
(ii) the product as a prime number
(iii) the sum as a prime number
(iv) the sum as 1
Answer:
(i) Sample space = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36
Let A be the event of getting doublet
A = {(1, 1) (2, 2) (3, 3) (4, 4) (5, 5) (6, 6)}
n(A) = 6
\(P(A)=\frac{n(A)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)
(ii) Let B be the event of getting a product is a prime number.
B = {(1, 2) (1, 3) (1, 5) (2, 1) (3, 1) (5, 1)}
n(B) = 6
\(P(B)=\frac{n(B)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)
(iii) Let C be the event of getting a sum is a prime number
C = {(1, 1) (1, 2) (1, 4) (1, 6) (2, 1) (2, 3) (2, 5) (3, 2), (3, 4) (4, 1) (4, 3) (5, 2) (5, 6) (6, 1) (6, 5)}
n(C) = 15
\(P(C)=\frac{n(C)}{n(S)}=\frac{15}{36}=\frac{5}{12}\)
(iv) Let D be the event of getting a sum is 1
n(D) = 0
\(P(D)=\frac{n(D)}{n(S)}=\frac{0}{36}=0\)
Probability of getting a sum is 1 is 0

Question 8.
Three fair coins are tossed together. Find the probability of getting
(i) all heads
(ii) atleast one tail
(iii) atmost one head
(iv) atmost two tails
Solution:
Possible outcomes = {(HHH), (THH), (HTH), (HHT), (TTH), (THT), (HTT), (TTT)}
No. of possible outcomes = 2 × 2 × 2 = 8
(i) Prob(all heads) = \(\frac{1}{8}\)
(ii) Atleast one tail = {(THH), (HTH), (HHT), (TTH), (THT), (HTT), (TTT)}
Prob(atleast one tail) = \(\frac{7}{8}\)
(iii) Atmost one head = {(HTT), (THT), (TTH), (TTT)}
∴ Prob(atmost one head) = \(\frac{4}{8}=\frac{1}{2}\)
(iv) Atmost two tail = {(HHH), (THH), (HTH), (HHT), (TTH), (THT), (HTT)}
∴ Prob(atmost two tail) = \(\frac{7}{8}\)

Question 9.
Two dice are numbered 1, 2, 3, 4, 5, 6 and 1, 1, 2, 2, 3, 3 respectively. They are rolled and the sum of the numbers on them is noted. Find the probability of getting each sum from 2 to 9 separately.
Answer:
1st dice A = {1, 2, 3, 4, 5, 6}
2nd dice B = {1, 1, 2, 2, 3, 3}
Sample Space (S) = {(1, 1), (1, 1), (1, 2), (1, 2), (1, 3), (1, 3), (2, 1), (2, 1), (2, 2), (2, 2), (2, 3), (2, 3), (3, 1), (3, 1), (3, 2), (3, 2), (3, 3), (3, 3), (4, 1), (4, 1), (4, 2), (4, 2), (4, 3), (4, 3), (5, 1), (5, 1), (5, 2), (5, 2), (5, 3), (5, 3),(6, 1), (6, 1), (6, 2), (6, 2), (6, 3), (6, 3)}
n(S) = 36
(i) Let A₁ be the event of getting sum is 2
A1 = {(1, 1) (1, 1)}
n(A₁) = 2
\(P\left(A_{1}\right)=\frac{n\left(A_{1}\right)}{n(S)}=\frac{2}{36}=\frac{1}{18}\)
(ii) Let A₂ be the event of getting a sum is 3.
A₂ = {(1, 2) (1, 2) (2, 1) (2, 1)}
n(A₂) = 4
\(P\left(A_{2}\right)=\frac{4}{36}=\frac{1}{9}\)
(iii) Let A₃ be the event of getting a sum is 4.
A₃ = {(1, 3) (1, 3) (2, 2) (2, 2) (3, 1) (3, 1)}
n(A₃) = 6
\(P\left(A_{3}\right)=\frac{6}{36}=\frac{1}{6}\)
(iv) Let A₄ be the event of getting a sum is 5.
A₄ = {(2, 3) (2, 3) (3, 2) (3, 2) (4, 1) (4, 1)}
n(A₄) = 6
\(P\left(A_{4}\right)=\frac{6}{36}=\frac{1}{6}\)
(v) Let A₅ be the event of getting a sum is 6.
A₅ = {(3, 3) (3, 3) (4, 2) (4, 2) (5, 1) (5, 1)}
n(A₅) = 6
\(P\left(A_{5}\right)=\frac{6}{36}=\frac{1}{6}\)
(vi) Let A₆ be the event of getting a sum is 7.
A₆ = {(4, 3) (4, 3) (5, 2) (5, 2) (6, 1) (6, 1)}
n(A₆) = 6
\(P\left(A_{6}\right)=\frac{6}{36}=\frac{1}{6}\)
(vii) Let A₇ be the event of getting a sum is 8.
A₇ = {(5, 3) (5, 3) (6, 2) (6, 2)}
n(A₇) = 4
\(P\left(A_{7}\right)=\frac{4}{36}=\frac{1}{9}\)
(viii) Let A₈ be the event of getting a sum is 9.
A₈ = {(6, 3) (6, 3)}
n(A₈) = 2
\(P\left(A_{8}\right)=\frac{2}{36}=\frac{1}{18}\)

Question 10.
A bag contains 5 red balls, 6 white balls, 7 green balls, 8 black balls. One ball is drawn at random from the bag. Find the probability that the ball drawn is
(i) white
(ii) black or red
(iii) not white
(iv) neither white nor black
Answer:
Sample space (S) = 5 + 6 + 7 + 8
n(S) = 26
(i) Let A be the event of getting a white ball
n(A) = 6
\(P(A)=\frac{n(A)}{n(S)}\)
\(P(A)=\frac{6}{26}=\frac{3}{13}\)
(ii) Let A be the event of getting a black ball
n(A) = 8
\(P(A)=\frac{n(A)}{n(S)}=\frac{8}{26}\)
Let B be the event of getting a red ball
n(B) = 5
\(P(B)=\frac{n(B)}{n(S)}=\frac{5}{26}\)
Probability of getting black or red ball
P(A ∪ B) = P (A) + P (B)
= \(\frac{8}{26}+\frac{5}{26}=\frac{13}{26}=\frac{1}{2}\)
(iii) Not white probability of getting white ball
P(A) = \(\frac{3}{13}\) from (i)
Probability of not getting white ball P(\(\bar{A}\)) = 1 – P(A)
\(1-\frac{3}{13}=\frac{13-3}{13}=\frac{10}{13}\)
(iv) Probability of getting a white ball.
P(A) = \(\frac{6}{26}\) (from 1)
Let B be the event of getting a black ball
n(B) = 8
\(P(B)=\frac{n(B)}{n(S)}=\frac{8}{26}\)
P(A ∪ B) = P(A) + P(B) = \(\frac{6}{26}+\frac{8}{26}=\frac{14}{26}\)
Probability of neither white nor black P(A ∪ B)’ = 1 – P(A ∪ B)
= \(1-\frac{14}{26}\)
= \(\frac{26-14}{26}=\frac{12}{26}=\frac{6}{13}\)

Question 11.
In a box there are 20 non-defective and some defective bulbs. If the probability that a bulb selected at random from the box found to be defective is \(\frac{3}{8}\) then, find the number of defective bulbs.
Answer:
Let the number of defective bulbs be “x”
Sample space (S) = 20 + x
n(S) = 20 + x
Let A be the event of getting to be defective
n(A) = x
\(P(A)=\frac{n(A)}{n(S)}\)
⇒ \(\frac{3}{8}=\frac{x}{20+x}\)
⇒ 8x = 3(20 + x) = (60 + 3x)
⇒ 8x – 3x = 60
⇒ 5x = 60
⇒ x = \(\frac{60}{5}\)
⇒ x = 12
Number of defective bulbs = 12

Question 12.
The king and queen of diamonds, queen and jack of hearts, jack and king of spades are removed from a deck of 52 playing cards and then well shuffled. Now one card is drawn at random from the remaining cards. Determine the probability that the card is
(i) a clavor
(ii) a queen of red card
(iii) a king of black card
Answer:
King diamond + Queen diamonds = 1 + 1 = 2 …….(1)
Queen hearts + Jack of hearts = 1 + 1 = 2 …….(2)
Jack spade + King of spades =1 + 1 = 2 …….(3)
Remaining number of cards = 52 – (6)
n(S) = 46
(i) Let A be the event of getting a clavor
n (A) = 13
\(P(A)=\frac{n(A)}{n(S)}=\frac{13}{46}\)
(ii) Let B be the event of getting a queen of red card
n(B) = 2
But the above two cards are removed from (1) and (2)
n(B) = 0
\(P(B)=\frac{n(B)}{n(S)}=\frac{0}{46}=0\)
(iii) Let B be the event of getting a king of black card
n(B) = (2 – 1) [from (3) one black card is removed]
n (B) = 1
\(P(B)=\frac{n(B)}{n(S)}=\frac{1}{46}\)

Question 13.
Some boys are playing a game, in which the stone thrown by them landing in a circular region given in the figure is considered as win and landing other than the circular region is considered as a loss. What is the probability to win the game?
Answer:

Area of a rectangle = l × b sq. feet = 3 × 4 sq. feet = 12 sq. feet
sample space (S) = 12
n(S) = 12
Let A be the event of getting the stone landing in a circular region
n(A) = Area of a circle
= πr²
= π × 1 × 1 (radius of a circle = 1 feet)
= π

Probability to win the game = \(\frac{11}{42}\) (or) \(\frac{157}{600}\)

Question 14.
Two customers Priya and Amuthan are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any one day as on another day. What is the probability that both will visit the shop on
(i) the same day
(ii) different days
(iii) consecutive days?
Answer:
Sample space (S) = 6 × 6 = 36
n(S) = 36
[priya and Amuthan are visiting a particular shop in any one of 6 days is 6 × 6 = 36]
(i) Let A be the event of getting both are shopping on the same day
A = {(Mon, Mon) (Tue, Tue) (Wed, Wed) (Thu, Thu) (Fri, Fri) (Sat, Sat)}
n(A) = 6
\(P(A)=\frac{n(A)}{n(S)}\)
\(=\frac{6}{36}=\frac{1}{6}\)
(ii) Let B be the event of shopping in different days.
n(B) = 36 – 6 = 30
\(P(B)=\frac{n(B)}{n(S)}\)
\(=\frac{30}{36}=\frac{5}{6}\)
(iii) Let C be the event of shopping consecutive days
C = {(Mon, Tue) (Tue, Wed) (Wed, Thu) (Thu, Fri) (Fri, Sat)}
n(C) = 5
P(C) = \(\frac{n(\mathrm{C})}{n(\mathrm{S})}\) = \(\frac{5}{36}\)

Question 15.
In a game, the entry fee is ₹ 150. The game consists of tossing a coin 3 times. Dhana bought a ticket for entry. If one or two heads show, she gets her entry fee back. If she throws 3 heads, she receives double the entry fees. Otherwise, she will lose. Find the probability that she
(i) gets double entry fee
(ii) just gets her entry fee
(iii) loses the entry fee.
Answer:
Sample space (S) = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n(S) = 8
(i) Let A be the event of getting double entry fee (only getting 3 heads)
n(A) = 1
\(P(A)=\frac{n(A)}{n(S)}=\frac{1}{8}\)
(ii) Let B be the event of getting her entry fee (one or two heads to show)
n(B) = Probability of one head + Probability of 2 head
= \(\frac{3}{8}+\frac{3}{8}=\frac{6}{8}=\frac{3}{4}\)
(iii) To loss the entry means not getting the head (only tail)
n(C) = 1
\(P(C)=\frac{n(C)}{n(S)}=\frac{1}{8}\)

Students can download Maths Chapter 8 Statistics and Probability Ex 8.2 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 8 Statistics and Probability Ex 8.2

Question 1.
The standard deviation and mean of a data are 6.5 and 12.5 respectively. Find the coefficient of variation.
Answer:
Standard deviation of a data (σ) = 6.5
Mean of the data (\(\bar{x}\)) = 12.5
Coefficient of variation = \(\frac{\sigma}{\bar{x}} \times 100 \%\)
= \(\frac{6.5}{12.5} \times 100 \%=52 \%\)
Coefficient of variation = 52%

Question 2.
The standard deviation and coefficient of variation of a data are 1.2 and 25.6 respectively. Find the value of mean.
Answer:
Standard deviation (σ) = 1.2
Coefficient of variation = 25.6

Question 3.
If the mean and coefficient of variation of a data are 15 and 48 respectively, then find the value of standard deviation.
Answer:
Mean (\(\bar{x}\)) = 15
Co efficient of variation = 48

Question 4.
If n = 5, \(\bar{x}\) = 6, Σx² = 765, then calculate the coefficient of variation.
Answer:

Question 5.
Find the coefficient of variation of 24, 26, 33, 37, 29, 31.
Answer:
Arrange in ascending order we get 24, 26, 29, 31, 33, 37
Assumed mean = 29

Question 6.
The time taken (in minutes) to complete homework by 8 students in a day are given by 38, 40, 47, 44, 46, 43, 49, 53. Find the coefficient of variation.
Answer:
Arrange in ascending order we get, 38, 40, 43, 44, 46, 47, 49, 53.
Assumed mean = 46


= \(\frac{453}{45}\)%
= 10.066
Coefficient of variation = 10.07%

Question 7.
The total marks scored by two students Sathya and Vidhya in 5 subjects are 460 and 480 with standard deviation of 4.6 and 2.4 respectively. Who is more consistent in performance?
Answer:
Total marks scored by sathya = 460
Total marks scored by vidhya = 480
Number of subjects = 5
Mean marks of sathya = \(\frac{460}{5}\)
\(\bar{x}\) = 92%
Given standard deviation, (σ) = 4.6

Vidhya coefficient of variation is less than Sathya.
Vidhya is more consistent.

Question 8.
The mean and standard deviation of marks obtained by 40 students of a class in three subjects Mathematics, Science and Social Science are given below.

Which of the three subjects shows the highest variation and which shows the lowest variation in marks?
Answer:
(i) Mathematics:
Mean (\(\bar{x}\)) = 56
Standard deviation (σ) = 12
Coefficient variation (CV₁) = \(\frac{\sigma}{\bar{x}} \times 100=\frac{12}{56} \times 100\)

Science shows the highest variation
Social science shows the lowest variation

Question 9.
The temperature of two cities A and B in the winter season are given below.

Find which city is more consistent in temperature changes?
Answer:
(i) city A:
Assumed mean = 22




C.V of city A < C.V of city B
City A is more consistent in temperature change.

Students can download Maths Chapter 8 Statistics and Probability Ex 8.1 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 8 Statistics and Probability Ex 8.1

Question 1.
Find the range and coefficient of range of the following data.
(i) 63, 89, 98, 125, 79, 108, 117, 68
(ii) 43.5, 13.6, 18.9, 38.4, 61.4, 29.8
Answer:
(i) Here the largest value (L) = 125
The smallest value (S) = 63
Range = L – S = 125 – 63 = 62

Question 2.
If the range and the smallest value of a set of data are 36.8 and 13.4 respectively, then find the largest value.
Solution:
If the range = 36.8 and
the smallest value = 13.4 then
the largest value = L = R + S
= 36.8 + 13.4 = 50.2

Question 3.
Calculate the range of the following data.

Answer:
Smallest value (S) = 400
Largest value (L) = 650
Range = L – S = 650 – 400 = 250

Question 4.
A teacher asked the students to complete 60 pages of a record notebook. Eight students have completed only 32, 35, 37, 30, 33, 36, 35 and 37 pages. Find the standard deviation of the pages yet to be completed by them.
Answer:
The remaining number of pages to be completed is 60 – 32; 60 – 35; 60 – 37; 60 – 30; 60 – 33; 60 – 36; 60 – 35 and 60 – 37
The pages to be completed are, 28, 25, 23, 30, 27, 24, 25, and 23
Arrange in ascending order we get, 23, 23, 24, 25, 25, 27, 28 and 30

Question 5.
Find the variance and standard deviation of the wages of 9 workers given below:
₹ 310, ₹ 290, ₹ 320, ₹ 280, ₹ 300, ₹ 290, ₹ 320, ₹ 310, ₹ 280.
Answer:
Arrange in ascending order we get,
280, 280, 290, 290, 300, 310, 310, 320 and 320
Assumed mean = 300


Variance = 222.222
Standard deviation = √Variance = √222.222 = 14.907 = 14.91
Variance = 222.22
Standard deviation = 14.91

Question 6.
A wall clock strikes the bell once at 1 o’clock, 2 times at 2 o’clock, 3 times at 3 o’clock and so on. How many times will it strike in a particular day? Find the standard deviation of the number of strikes the bell make a day.
Answer:
Wall clock strikes the bell in 12 hours
1, 2, 3, 4, 5,… ,12
Wall clock strikes in a day (24 hours)
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24.
Assumed mean = 14



The standard deviation of bell strike in a day is 6.9

Question 7.
Find the standard deviation of the first 21 natural numbers.
Answer:
Here n = 21
The standard deviation of the first ‘n’ natural numbers,

The standard deviation of the first 21 natural numbers = 6.06

Question 8.
If the standard deviation of a data is 4.5 and if each value of the data is decreased by 5, then find the new standard deviation.
Solution:
If the standard deviation of a data is 4.5 and each value of the data decreased by 5, the new standard deviation does not change and it is also 4.5.

Question 9.
If the standard deviation of a data is 3.6 and each value of the data is divided by 3, then find the new variance and new standard deviation.
Answer:
The standard deviation of the data = 3.6
Each value of the data is divided by 3
New standard deviation = \(\frac{3.6}{3}\) = 1.2
New Variance = (1.2)² = 1.44 [∴ Variance = (S.D)²]
New standard Deviation = 1.2
New variance = 1.44

Question 10.
The rainfall recorded in various places of five districts in a week are given below.

Find its standard deviation.
Answer:
Assumed mean = 60

Question 11.
In a study about viral fever, the number of people affected in a town were noted as

Find its standard deviation.
Answer:
Assumed mean = 35

Question 12.
The measurements of the diameters (in cms) of the plates prepared in a factory are given below. Find the standard deviation.

Answer:
Assumed mean = 34.5

Question 13.
The time taken by 50 students to complete a 100 meter race are given below. Find its standard deviation.

Answer:
Assumed mean = 11


Standard deviation (σ) = 1.24

Question 14.
For a group of 100 candidates, the mean and standard deviation of their marks were found to be 60 and 15 respectively. Later on, it was found that the scores 45 and 72 were wrongly entered as 40 and 27. Find the correct mean and standard deviation.
Answer:
Number of candidates = 100
n = 100
Mean (\(\bar{x}\)) = 60
standard deviation (σ) = 15
Mean (\(\bar{x}\)) = \(\frac{\Sigma x}{n} \Rightarrow 60=\frac{\Sigma x}{100}\)
Σx = 6000
Correct total = 6000 + (45 – 40) + ( 72 – 27) = 6000 + 5 + 45 = 6050
Correct mean (\(\bar{x}\)) = \(\frac{6050}{100}\) = 60.5
Given standard deviation = 15


Correct mean = 60.5
Correct standard deviation (σ) = 14. 61

Question 15.
The mean and variance of seven observations are 8 and 16 respectively. If five of these are 2, 4, 10, 12 and 14, then find the remaining two observations.
Answer:
Let the missing two observations be ‘a’ and ‘b’
Arithmetic mean = 8

Students can download Maths Chapter 7 Mensuration Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 7 Mensuration Additional Questions

I. Multiple Choice Questions:

Question 1.
The curved surface area of a right circular cylinder of radius 1 cm and height 1 cm is equal to ______
(1) π cm²
(2) 2π cm²
(3) 3π cm²
(4) 2 cm²
Answer:
(2) 2π cm²
Hint:
C.S.A of a cylinder = 2πrh sq. units = 2 × π × 1 × 1 cm² = 2π cm²

Question 2.
The total surface area of a solid right circular cylinder whose radius is half of its height h is equal to ______ sq. units.
(1) \(\frac{3}{2} \pi h\)
(2) \(\frac{2}{3} \pi h^{2}\)
(3) \(\frac{3}{2} \pi h^{2}\)
(4) \(\frac{2}{3} \pi h\)
Answer:
(3) \(\frac{3}{2} \pi h^{2}\)
Hint:
T.S.A = 2πr(h + r)
[radius is half of the height]
= \(2 \pi \times \frac{h}{2}\left(\frac{h}{2}+h\right)\)
= \(=\pi h\left(\frac{3 h}{2}\right)=\frac{3}{2} \pi h^{2}\) sq. units

Question 3.
Base area of a right circular cylinder is 80 cm². If its height is 5 cm, then the volume is equal to _______
(1) 400 cm³
(2) 16 cm³
(3) 200 cm³
(4) \(\frac{400}{3}\) cm³
Answer:
(1) 400 cm³
Hint:
Volume of a cylinder = πr²h cu. units
[Base area (πr²) = 80 cm² = 80 × 5 cm³ = 400 cm³

Question 4.
If the total surface area of a solid right circular cylinder is 200π cm² and its radius is 5 cm, then the sum of its height and radius is ______
(1) 20 cm
(2) 25 cm
(3) 30 cm
(4) 15 cm
Answer:
(1) 20 cm
Hint:
T.S.A of a cylinder = 200π cm²
2πr (h + r) = 200π
2 × 5 (h + r) = 200
(h + r) = 20 cm

Question 5.
The curved surface area of a right circular cylinder whose radius is a units and height is b units, is equal to ______
(1) πa²b sq.cm
(2) 2πab sq.cm
(3) 2π sq.cm
(4) 2 sq.cm
Answer:
(2) 2πab sq.cm .
Hint:
C.S.A. of a cylinder = 2πrh sq. units = 2 × π × a × b sq. cm = 2πab sq. cm

Question 6.
Radius and height of a right circular cone and that of a right circular cylinder are respectively, equal. If the volume of the cylinder is 120 cm³, then the volume of the cone is equal to _______
(1) 1200 cm³
(2) 360 cm³
(3) 40 cm³
(4) 90 cm³
Answer:
(3) 40 cm³
Hint:
Volume of the cone = \(\frac{1}{3}\) × volume of the cylinder
= \(\frac{1}{3}\) × 120 cm³
= 40 cm³

Question 7.
If the diameter and height of a right circular cone are 12 cm and 8 cm respectively, then the slant height is
(1) 10 cm
(2) 20 cm
(3) 30 cm
(4) 96 cm
Answer:
(1) 10 cm
Hint:
Slant height of a cone

Question 8.
If the circumference at the base of a right circular cone and the slant height are 120π cm and 10 cm respectively, then the curved surface area of the cone is equal to ______
(1) 1200π cm²
(2) 600π cm²
(3) 300π cm²
(4) 600 cm²
Answer:
(2) 600π cm²
Hint:
Circumference (2πr) = 120π cm
Slant height (l) = 10 cm;
Curved surface area of a cone = πrl sq. units
= \(\frac{120 \pi}{2}\) × 10 cm² = 600π cm²

Question 9.
If the volume and the base area of a right circular cone are 48π cm and 12π cm respectively, then the height of the cone is equal to ______
(1) 6 cm
(2) 8 cm
(3) 10 cm
(4) 12 cm
Answer:
(4) 12 cm
Hint:
Volume of a cone = 48π cm³
[Base area (πr²) = 12π]
\(\frac{1}{3}\) πr²h = 48π
\(\frac{1}{3}\) × 12π × h = 48π
[Substitute πr² = 12π]
h = \(\frac{48}{4}\) = 12 cm

Question 10.
If the height and the base area of a right circular cone are 5 cm and 48 sq.cm respectively, then the volume of the cone is equal to _______
(1) 240 cm³
(2) 120 cm³
(3) 80 cm³
(4) 480 cm³
Answer:
(3) 80 cm³
Hint:
Volume of a cone (V) = \(\frac{1}{3}\) πr²h sq. units
Base area (πr²) = 48 sq. cm
V = \(\frac{1}{3}\) × 48 × 5 = 80 cm³

Question 11.
The ratios of the respective heights and the respective radii of two cylinders are 1 : 2 and 2 : 1 respectively. Then their respective volumes are in the ratio _______
(1) 4 : 1
(2) 1 : 4
(3) 2 : 1
(4) 1 : 2
Answer:
(3) 2 : 1
Hint:
h₁ : h₂ = 1 : 2
r₁ : r₂ = 2 : 1
Ratio of their volumes
= \(\frac{1}{3} \pi r_{1}^{2} h_{1}: \frac{1}{3} \pi r_{2}^{2} h_{2}\)
= 22 × 1 : 12 × 2 = 4 : 2 = 2 : 1

Question 12.
If the radius of a sphere is 2 cm, then the curved surface area of the sphere is equal to ________
(1) 8π cm²
(2) 16 cm²
(3) 12π cm²
(4) 16π cm²
Answer:
(4) 16π cm²
Hint:
C.S.A of a sphere = 4πr² sq. units
[radius = 2 cm]
= 4 × π × 22 cm²
= 16π cm²

Question 13.
The total surface area of a solid hemisphere of diameter 2 cm is equal to _______
(1) 12 cm²
(2) 12π cm²
(3) 4π cm²
(4) 3π cm²
Answer:
(4) 3π cm²
Hint:
Radius of a hemisphere = \(\frac{2}{2}\) = 1 cm
Total surface area of a hemisphere = 3πr² sq. units = 3 × π × 12 cm² = 3π cm²

Question 14.
If the volume of a sphere is \(\frac{9}{16} \pi\) cu.cm, then its radius is ________
(1) \(\frac{4}{3}\) cm
(2) \(\frac{3}{4}\) cm
(3) \(\frac{3}{2}\) cm
(4) \(\frac{2}{3}\) cm
Answer:
(2) \(\frac{3}{4}\) cm
Hint:
Volume of the sphere = \(\frac{9}{16} \pi\)

Question 15.
The surface areas of two spheres are in the ratio of 9 : 25. Then their volumes are in the ratio _______
(1) 81 : 625
(2) 729 : 15625
(3) 27 : 75
(4) 27 : 125
Answer:
(4) 27 : 125
Hint:
Ratio of their surface area = 9 : 25

Question 16.
The total surface area of a solid hemisphere whose radius is a units, is equal to ________
(1) 2πa² sq. units
(2) 3πa² sq. units
(3) 3πa sq. units
(4) 3a² sq. units
Answer:
(2) 3πa² sq. units
Hint:
T.S.A. of a solid hemisphere = 3πr² sq. units
= 3 × π × a × a sq.units
= 3πa² sq. units

Question 17.
If the surface area of a sphere is 100π cm², then its radius is equal to ______
(1) 25 cm
(2) 100 cm
(3) 5 cm
(4) 10 cm
Answer:
(3) 5 cm
Hint:
Surface area of a sphere = 100π cm²
4πr² = 100π
r² = 25
r = √25 = 5 cm

Question 18.
If the surface area of a sphere is 36π cm², then the volume of the sphere is equal to _______
(1) 12π cm³
(2) 36π cm³
(3) 72π cm³
(4) 108π cm³
Answer:
(2) 36π cm³
Hint:
Surface area of a sphere = 36π cm²
4πr² = 36π
r² = 9
r = 3 cm
Volume of a sphere = \(\frac{4}{3} \pi r^{3}\) cu. units
= \(\frac{4}{3} \pi\) × 3 × 3 × 3 cm³ = 36π cm³

Question 19.
If the total surface area of a solid hemisphere is 12π cm² then its curved surface area is equal to ______
(1) 6π cm²
(2) 24π cm²
(3) 36π cm²
(4) 8π cm²
Answer:
(4) 8π cm²
Hint:
T.S.A of a hemisphere = 12π cm²
3πr² = 12π
r² = 4
r = 2
Curved surface area of a hemisphere = 2πr² = 2 × π × 4 = 8π cm²

Question 20.
If the radius of a sphere is half of the radius of another sphere, then their respective volumes are in the ratio _____
(1) 1 : 8
(2) 2 : 1
(3) 1 : 2
(4) 8 : 1
Answer:
(1) 1 : 8
Hint:
\(r_{1}=\frac{r_{2}}{2} \Rightarrow \frac{r_{1}}{r_{2}}=\frac{1}{2} \Rightarrow r_{1}: r_{2}=1: 2\)

II. Answer the following questions:

Question 1.
Curved surface area and circumference at the base of a solid right circular cylinder are 4400 sq.cm and 110 cm respectively. Find its height and diameter.
Answer:
Given, Circumference of the base of a cylinder = 110 cm
2πr = 110 ……. (1)
Curved surface area = 4400 cm²
2πrh = 4400 cm² ……. (2)
From (1) & (2), \(\frac{(2)}{(1)} \Rightarrow \frac{2 \pi r h}{2 \pi r}=\frac{4400}{110}=40 \mathrm{cm}\)
Height of the cylinder (h) = 40 cm
From (1), 2πr = 110
2 × \(\frac{22}{7}\) × r = 110
r = \(\frac{35}{2}\)
We know that, diameter (d) = 2 × radius
d = 2 × \(\frac{35}{2}\) = 35 cm
Diameter of the Circular cylinder = 35 cm

Question 2.
A mansion has 12 right cylindrical pillars each having radius 50 cm and height 3.5 m. Find the cost of painting the lateral surface of the pillars at ₹ 20 per square metre.
Answer:
Given, Radius of a cylinder (r) = 50 cm = 0.5 m
Height of a cylinder (h) = 3.5 m
Curved surface area of a pillar = 2πrh sq. units
Curved surface area of 12 pillars = 12 × 2πrh
= 12 × 2 × \(\frac{22}{7}\) × 0.5 × 3.5 m²
= 132 sq. m.
Cost for painting the lateral surface of pillars per metre = ₹ 20
Cost of painting = 132 × ₹ 20 = ₹ 2640

Question 3.
The total surface area of a solid right circular cylinder is 231 cm². Its curved surface area is two thirds of the total surface area. Find the radius and height of the cylinder.
Answer:
Given, Total surface area of a cylinder (T.S. A) = 231 sq.cm
Curved surface area = \(\frac{2}{3}\) × T.S.A = \(\frac{2}{3}\) × 231 = 154 cm²
2πrh = 154 cm² …… (1)
Total surface area = 231 cm²
2πr (h + r) = 231
2πrh + 2πr²= 231
154 + 2πr² = 231 [from (1)]
2πr² = 231 – 154 = 77

Radius of the cylinder = 3.5 cm
Height of the cylinder = 7 cm

Question 4.
The total surface area of a solid right circular cylinder is 1540 cm². If the height is four times the radius of the base, then find the height of the cylinder.
Answer:
Given, Let the radius of the cylinder be ‘r’
Height of a cylinder (h) = 4r (by given condition)
Total surface area = 1540 cm²
2πr(h + r) = 1540 cm²

Height of the cylinder = 4r = 4 × 7 = 28 cm

Question 5.
If the vertical angle and the radius of a right circular cone are 60° and 15 cm respectively, then find its height and slant height.
Answer:
Given, In the figure, OAB is a cone and OC ⊥ AB
∠AOC = \(\frac{60^{\circ}}{2}\) = 30°
In the right ∆OAC, tan 30° = \(\frac{\mathrm{AC}}{\mathrm{OC}}\)

Slant Height of the cone (l) = 15 × 2 = 30 cm

Question 6.
The central angle and radius of a sector of a circular disc are 180° and 21 cm respectively. If the edges of the sector are joined together to make a hollow cone, then find the radius of the cone.
Answer:

Given, Radius of a sector (r) = 21 cm
The angle of the sector (θ) = 180°
Let “R” be the radius of the cone.
Circumference of the base of a cone = Arc length of the sector

Radius of the cone (R) = 10.5 cm

Question 7.
If the curved surface area of a solid hemisphere is 2772 sq.cm, then find its total surface area.
Answer:
Given, the Curved surface area of a solid hemisphere = 2772 cm²
2πr² = 2772

Total surface area = 3πr² sq. units
= 3 × \(\frac{22}{7}\) × 21 × 21
= 4158 sq.cm
Aliter:
C.S.A of a hemisphere = 2772 cm²
2πr² = 2772 cm²
πr² = \(\frac{2772}{2}\) = 1386 cm
T.S.A of a hemisphere = 3πr² sq.units = 3 × 1386 cm² = 4158 cm²

Question 8.
An inner curved surface area of a hemispherical dome of a building needs to be painted. If the circumference of the base is 17.6 m, find the cost of painting it at the rate of ₹ 5 per sq. m.
Answer:
Given, Circumference of the dome = 17.6 m
2πr = 17.6
\(r=\frac{17.6 \times 7}{2 \times 22}=\frac{8.8 \times 7}{22}=2.8 \mathrm{m}\)
Curved surface area of the dome = 2πr² sq. units
= 2 × \(\frac{22}{7}\) × 2.8 × 2.8 m²
= 49.28 m²
Cost of painting for one sq.metre = ₹ 5
Cost of painting the curved surface = 49.28 × ₹ 5 = ₹ 246.40

Question 9.
Volume of a solid cylinder is 62.37 cu.cm. Find the radius if its height is 4.5 cm.
Answer:
Given, Height of a cylinder (h) = 4.5 cm
Volume of a solid cylinder = 62.37 cu. cm

Radius of a cylinder (r) = 2.1 cm

Question 10.
A rectangular sheet of metal foil with dimension 66 cm × 12 cm is rolled to form a cylinder of height 12 cm. Find the volume of the cylinder.
Answer:
After rolling the rectangular sheet into a cylinder

Volume of the cylinder = 4158 cm³

Question 11.
The circumference of the base of a 12 m high wooden solid cone is 44 m. Find the volume.
Answer:
Given, Height of the wooden solid cone (h) = 12 m
Circumference of the base = 44 m
2πr = 44
r = \(\frac{44 \times 7}{2 \times 22}\) = 7 m
Volume of the wooden solid = \(\frac{1}{3} \pi r^{2} h\) cu. units
= \(\frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times 12 \mathrm{m}^{3}\)
= 88 × 7
= 616 m³
Volume of the solid = 616 m³

Question 12.
Find the volume of the largest right circular cone that can be cut out of a cube whose edge is 14 cm.
Answer:
Given, Edge of the cube = 14 cm
The largest circular cone is cut out from the cube.
Radius of the cone (r) = \(\frac{14}{2}\) = 7 cm
Height of the cone (h) = 14 cm
Volume of a cone

Volume of a cone = 718.67 cm³

Question 13.
The thickness of a hemispherical bowl is 0.25 cm. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl. (Take π = \(\frac{22}{7}\))
Answer:
Let r, R and w be the inner and outer radii and thickness of the hemispherical bowl respectively.

Given that r = 5 cm, w = 0.25 cm
R = r + w = 5 + 0.25 = 5.25 cm
Now, outer surface area of the bowl = 2πR²
= 2 × \(\frac{22}{7}\) × 5.25 × 5.25
= 173.25 sq. cm
Thus, the outer surface area of the bowl = 173.25 sq. cm

Question 14.
Volume of a hollow sphere is \(\frac{11352}{7}\) cm3. If the outer radius is 8 cm, find the inner radius of the sphere. (Take π = \(\frac{22}{7}\))
Answer:
Let R and r be the outer and inner radii of the hollow sphere respectively.
Let V be the volume of the hollow sphere.

Hence, the inner radius r = 5 cm

Question 15.
How many litres of water will a hemispherical tank whose diameter is 4.2 m?
Answer:
Radius of the tank = \(\frac{4.2}{2}\) = 2.1 m
Volume of the hemisphere
= \(\frac{2}{3} \pi r^{3}\) cu.units
= \(\frac{2}{3} \times \frac{22}{7} \times 2.1 \times 2.1 \times 2.1 \mathrm{m}^{3}\)
= 19.404 m³
= 19.404 x 1000 lit
= 19,404 litres

III. Answer the following questions.

Question 1.
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
Answer:

For cylindrical part:
Radius (r) = 7 cm
Height (h) = 6 cm
Curved surface area = 2πrh = 2 × \(\frac{22}{7}\) × 7 × 6 cm² = 264 cm²
For hemispherical part:
Radius (r) = 7 cm
Surface area (h) = 2πr²
= 2 × \(\frac{22}{7}\) × 7 × 7 cm²
= 308 cm²
Total surface area = (264 + 308) = 572 cm²

Question 2.
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.
Answer:

Question 3.
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2.
Answer:

For cylinderical part:
Height (h) = 2.4 cm
Diameter (d) = 1.4 cm
Radius (r) = 0.7 cm
Total surface area of the cylindrical part

For conical part:
Base area (r) = 0.7 cm
Height (h) = 2.4 cm

Question 4.
A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Answer:
Diameter of the cylindrical well = 7 m
Radius of the cylinder (r) = \(\frac{7}{2}\) m
Depth of the well (h) = 20 m
Volume = πr²h
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 20 \mathrm{m}^{3}\)
= 22 × 7 × 5 m³
Volume of the earth taken out = 22 × 7 × 5 m³
Now this earth is spread out to form a cuboidal platform having
Length (l) = 22 m
Breadth (b) = 14 m
Let ‘h’ be the height of the platform.
Volume of the platform = 22 × 14 × h m³
Volume of the platform = Volume of the earth taken out
22 × 14 × h = 22 × 7 × 5
\(h=\frac{22 \times 7 \times 5}{22 \times 14}=\frac{5}{2} \mathrm{m}=2.5 \mathrm{m}\)
Thus, the required height of the platform is 2.5 m.

Question 5.
The perimeters of the ends of the frustum of a cone are 207.24 cm and 169.56 cm. If the height of the frustum is 8 cm, find the whole surface area of the frustum. [Use π = 3.14]
Answer:

Let the radii of circular ends are R and r [R > r]
Perimeter of circular ends are 207.24 cm and 169.56 cm
2πR = 207.24 cm

The whole surface area of the frustum = π [(R² + r²) + (R + r) l]
Required whole surface area of the frustum
= 3.14 [33² + 27² + (33 + 27) × 10] cm²
= 3.14 [1089 + 729 + 600] cm²
= 3.14 [2418] cm²
= 7592.52 cm²

Question 6.
A cuboid-shaped slab of iron whose dimensions are 55 cm × 40 cm × 15 cm is melted and recast into a pipe. The outer diameter and thickness of the pipe are 8 cm and 1 cm respectively. Find the length of the pipe. (Take π = \(\frac {22}{7}\))
Answer:

Let h₁ be the length of the pipe
Let R and r be the outer and inner radii of the pipe respectively.
Iron slab:
Volume = lbh = 55 × 40 × 15 cm³
Iron pipe:
Outer diameter, 2R = 8 cm
Outer radius, R = 4 cm
Thickness, w = 1 cm
Inner radius, r = R – w = 4 – 1 = 3 cm
Now, the volume of the iron pipe = Volume of the iron slab

Time is taken by the pipe to empty half of the tank = 3 hours 12 minutes.

Question 7.
The perimeter of the ends of a frustum of a cone are 44 cm and 8.4π cm. If the depth is 14 cm., then find its volume.
Answer:
Given let the radius of the top of the frustum be “R” and the radius of the bottom of the frustum be “r”

Question 8.
A tent is in the shape of a right circular cylinder surmounted by a cone. The total height and the diameter of the base are 13.5 m and 28 m. If the height of the cylindrical portion is 3 m, find the total surface area of the tent.
Answer:

Given, Total height of solid = 13.5 cm
Diameter of the cylinder (d) = 28 m
Height of a cylinder (h) = 3 m
Height of a conical portion = 13.5 – 3 = 10.5 m
From the diagram, Radius of a cone = Radius of a cylinder
Radius (r) = 14 m