Samacheer Kalvi 10th Maths Guide Chapter 8 Statistics and Probability Ex 8.3

Students can download Maths Chapter 8 Statistics and Probability Ex 8.3 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 8 Statistics and Probability Ex 8.3

Question 1.
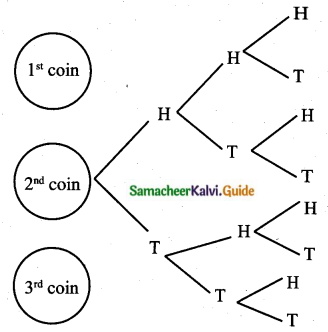
Write the sample space for tossing three coins using tree diagram.
Answer:
Sample space = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

Question 2.
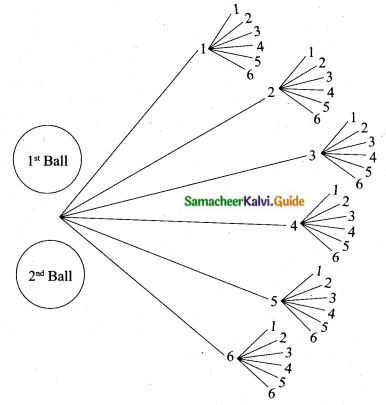
Write the sample space for selecting two balls from a bag containing 6 balls numbered 1 to 6 (using tree diagram).
Answer:
Sample space = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

Question 3.
If A is an event of a random experiment such that P(A) : P(\(\bar{A}\)) = 17 : 15 and n(s) = 640 then find (i) P(\(\bar{A}\))
(ii) n(A)
Answer:

Question 4.
A coin is tossed thrice. What is the probability of getting two consecutive tails?
Answer:
Sample space = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n(S) = 8
Let A be the event of getting consecutive tails
A = {HTT, TTH, TTT}
n(A) = 3
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{3}{8}\)

Question 5.
At a fete, cards bearing numbers 1 to 1000, one number on one card are put in a box. Each player selects one card at random and that card is not replaced. If the selected card has a perfect square number greater than 500, the player wins a prize. What is the probability that
(i) the first player wins a prize
(ii) the second player wins a prize if the first has won?
Solution:
22² = 484
31² = 961
23² = 529
32² = 1024
23, 24, 25, 26, 27, 28, 29, 30, 31 has squares below 500 × 1000.
(i) P(first player wins a prize) = \(\frac{9}{1000}\)
(ii) P(second player ins if first has won) = \(\frac{8}{999}\)

Question 6.
A bag contains 12 blue balls and x red balls. If one ball is drawn at random (i) what is the probability that it will be a red ball? (ii) If 8 more red balls are put in the bag, and if the probability of drawing a red ball will be twice that of the probability in (i), then find x.
Answer:
Sample space = 12 + x
n(S) = x + 12
(i) Let A be the event of getting a red ball
n(A) = x
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}\) = \(\left(\frac{x}{x+12}\right)\)
(ii) 8 more red balls are added
Sample space = x + 12 + 8 = x + 20
Number of red balls = x + 8
Probability of drawing red ball = \(\frac{x+8}{x+20}\)
By the given condition
\(\frac{x+8}{x+20}=2\left(\frac{x}{x+12}\right)\)
(x + 8)(x + 12) = 2x(x + 20)
x² + 20x + 96 = 2x² + 40x
x² + 20x – 96 = 0
(x + 24)(x – 4) = 0
x = -24 (or) x = 4
The value of x = 4 (Number of balls will not be negative)
The probability of getting red balls = \(\left(\frac{x}{x+12}\right)=\frac{4}{16}=\frac{1}{4}\)

Question 7.
Two unbiased dice are rolled once. Find the probability of getting
(i) a doublet (equal numbers on both dice)
(ii) the product as a prime number
(iii) the sum as a prime number
(iv) the sum as 1
Answer:
(i) Sample space = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36
Let A be the event of getting doublet
A = {(1, 1) (2, 2) (3, 3) (4, 4) (5, 5) (6, 6)}
n(A) = 6
\(P(A)=\frac{n(A)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)
(ii) Let B be the event of getting a product is a prime number.
B = {(1, 2) (1, 3) (1, 5) (2, 1) (3, 1) (5, 1)}
n(B) = 6
\(P(B)=\frac{n(B)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)
(iii) Let C be the event of getting a sum is a prime number
C = {(1, 1) (1, 2) (1, 4) (1, 6) (2, 1) (2, 3) (2, 5) (3, 2), (3, 4) (4, 1) (4, 3) (5, 2) (5, 6) (6, 1) (6, 5)}
n(C) = 15
\(P(C)=\frac{n(C)}{n(S)}=\frac{15}{36}=\frac{5}{12}\)
(iv) Let D be the event of getting a sum is 1
n(D) = 0
\(P(D)=\frac{n(D)}{n(S)}=\frac{0}{36}=0\)
Probability of getting a sum is 1 is 0

Question 8.
Three fair coins are tossed together. Find the probability of getting
(i) all heads
(ii) atleast one tail
(iii) atmost one head
(iv) atmost two tails
Solution:
Possible outcomes = {(HHH), (THH), (HTH), (HHT), (TTH), (THT), (HTT), (TTT)}
No. of possible outcomes = 2 × 2 × 2 = 8
(i) Prob(all heads) = \(\frac{1}{8}\)
(ii) Atleast one tail = {(THH), (HTH), (HHT), (TTH), (THT), (HTT), (TTT)}
Prob(atleast one tail) = \(\frac{7}{8}\)
(iii) Atmost one head = {(HTT), (THT), (TTH), (TTT)}
∴ Prob(atmost one head) = \(\frac{4}{8}=\frac{1}{2}\)
(iv) Atmost two tail = {(HHH), (THH), (HTH), (HHT), (TTH), (THT), (HTT)}
∴ Prob(atmost two tail) = \(\frac{7}{8}\)

Question 9.
Two dice are numbered 1, 2, 3, 4, 5, 6 and 1, 1, 2, 2, 3, 3 respectively. They are rolled and the sum of the numbers on them is noted. Find the probability of getting each sum from 2 to 9 separately.
Answer:
1st dice A = {1, 2, 3, 4, 5, 6}
2nd dice B = {1, 1, 2, 2, 3, 3}
Sample Space (S) = {(1, 1), (1, 1), (1, 2), (1, 2), (1, 3), (1, 3), (2, 1), (2, 1), (2, 2), (2, 2), (2, 3), (2, 3), (3, 1), (3, 1), (3, 2), (3, 2), (3, 3), (3, 3), (4, 1), (4, 1), (4, 2), (4, 2), (4, 3), (4, 3), (5, 1), (5, 1), (5, 2), (5, 2), (5, 3), (5, 3),(6, 1), (6, 1), (6, 2), (6, 2), (6, 3), (6, 3)}
n(S) = 36
(i) Let A₁ be the event of getting sum is 2
A1 = {(1, 1) (1, 1)}
n(A₁) = 2
\(P\left(A_{1}\right)=\frac{n\left(A_{1}\right)}{n(S)}=\frac{2}{36}=\frac{1}{18}\)
(ii) Let A₂ be the event of getting a sum is 3.
A₂ = {(1, 2) (1, 2) (2, 1) (2, 1)}
n(A₂) = 4
\(P\left(A_{2}\right)=\frac{4}{36}=\frac{1}{9}\)
(iii) Let A₃ be the event of getting a sum is 4.
A₃ = {(1, 3) (1, 3) (2, 2) (2, 2) (3, 1) (3, 1)}
n(A₃) = 6
\(P\left(A_{3}\right)=\frac{6}{36}=\frac{1}{6}\)
(iv) Let A₄ be the event of getting a sum is 5.
A₄ = {(2, 3) (2, 3) (3, 2) (3, 2) (4, 1) (4, 1)}
n(A₄) = 6
\(P\left(A_{4}\right)=\frac{6}{36}=\frac{1}{6}\)
(v) Let A₅ be the event of getting a sum is 6.
A₅ = {(3, 3) (3, 3) (4, 2) (4, 2) (5, 1) (5, 1)}
n(A₅) = 6
\(P\left(A_{5}\right)=\frac{6}{36}=\frac{1}{6}\)
(vi) Let A₆ be the event of getting a sum is 7.
A₆ = {(4, 3) (4, 3) (5, 2) (5, 2) (6, 1) (6, 1)}
n(A₆) = 6
\(P\left(A_{6}\right)=\frac{6}{36}=\frac{1}{6}\)
(vii) Let A₇ be the event of getting a sum is 8.
A₇ = {(5, 3) (5, 3) (6, 2) (6, 2)}
n(A₇) = 4
\(P\left(A_{7}\right)=\frac{4}{36}=\frac{1}{9}\)
(viii) Let A₈ be the event of getting a sum is 9.
A₈ = {(6, 3) (6, 3)}
n(A₈) = 2
\(P\left(A_{8}\right)=\frac{2}{36}=\frac{1}{18}\)

Question 10.
A bag contains 5 red balls, 6 white balls, 7 green balls, 8 black balls. One ball is drawn at random from the bag. Find the probability that the ball drawn is
(i) white
(ii) black or red
(iii) not white
(iv) neither white nor black
Answer:
Sample space (S) = 5 + 6 + 7 + 8
n(S) = 26
(i) Let A be the event of getting a white ball
n(A) = 6
\(P(A)=\frac{n(A)}{n(S)}\)
\(P(A)=\frac{6}{26}=\frac{3}{13}\)
(ii) Let A be the event of getting a black ball
n(A) = 8
\(P(A)=\frac{n(A)}{n(S)}=\frac{8}{26}\)
Let B be the event of getting a red ball
n(B) = 5
\(P(B)=\frac{n(B)}{n(S)}=\frac{5}{26}\)
Probability of getting black or red ball
P(A ∪ B) = P (A) + P (B)
= \(\frac{8}{26}+\frac{5}{26}=\frac{13}{26}=\frac{1}{2}\)
(iii) Not white probability of getting white ball
P(A) = \(\frac{3}{13}\) from (i)
Probability of not getting white ball P(\(\bar{A}\)) = 1 – P(A)
\(1-\frac{3}{13}=\frac{13-3}{13}=\frac{10}{13}\)
(iv) Probability of getting a white ball.
P(A) = \(\frac{6}{26}\) (from 1)
Let B be the event of getting a black ball
n(B) = 8
\(P(B)=\frac{n(B)}{n(S)}=\frac{8}{26}\)
P(A ∪ B) = P(A) + P(B) = \(\frac{6}{26}+\frac{8}{26}=\frac{14}{26}\)
Probability of neither white nor black P(A ∪ B)’ = 1 – P(A ∪ B)
= \(1-\frac{14}{26}\)
= \(\frac{26-14}{26}=\frac{12}{26}=\frac{6}{13}\)

Question 11.
In a box there are 20 non-defective and some defective bulbs. If the probability that a bulb selected at random from the box found to be defective is \(\frac{3}{8}\) then, find the number of defective bulbs.
Answer:
Let the number of defective bulbs be “x”
Sample space (S) = 20 + x
n(S) = 20 + x
Let A be the event of getting to be defective
n(A) = x
\(P(A)=\frac{n(A)}{n(S)}\)
⇒ \(\frac{3}{8}=\frac{x}{20+x}\)
⇒ 8x = 3(20 + x) = (60 + 3x)
⇒ 8x – 3x = 60
⇒ 5x = 60
⇒ x = \(\frac{60}{5}\)
⇒ x = 12
Number of defective bulbs = 12

Question 12.
The king and queen of diamonds, queen and jack of hearts, jack and king of spades are removed from a deck of 52 playing cards and then well shuffled. Now one card is drawn at random from the remaining cards. Determine the probability that the card is
(i) a clavor
(ii) a queen of red card
(iii) a king of black card
Answer:
King diamond + Queen diamonds = 1 + 1 = 2 …….(1)
Queen hearts + Jack of hearts = 1 + 1 = 2 …….(2)
Jack spade + King of spades =1 + 1 = 2 …….(3)
Remaining number of cards = 52 – (6)
n(S) = 46
(i) Let A be the event of getting a clavor
n (A) = 13
\(P(A)=\frac{n(A)}{n(S)}=\frac{13}{46}\)
(ii) Let B be the event of getting a queen of red card
n(B) = 2
But the above two cards are removed from (1) and (2)
n(B) = 0
\(P(B)=\frac{n(B)}{n(S)}=\frac{0}{46}=0\)
(iii) Let B be the event of getting a king of black card
n(B) = (2 – 1) [from (3) one black card is removed]
n (B) = 1
\(P(B)=\frac{n(B)}{n(S)}=\frac{1}{46}\)

Question 13.
Some boys are playing a game, in which the stone thrown by them landing in a circular region given in the figure is considered as win and landing other than the circular region is considered as a loss. What is the probability to win the game?
Answer:

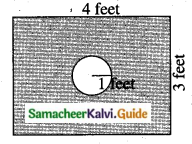
Area of a rectangle = l × b sq. feet = 3 × 4 sq. feet = 12 sq. feet
sample space (S) = 12
n(S) = 12
Let A be the event of getting the stone landing in a circular region
n(A) = Area of a circle
= πr²
= π × 1 × 1 (radius of a circle = 1 feet)
= π

Probability to win the game = \(\frac{11}{42}\) (or) \(\frac{157}{600}\)

Question 14.
Two customers Priya and Amuthan are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any one day as on another day. What is the probability that both will visit the shop on
(i) the same day
(ii) different days
(iii) consecutive days?
Answer:
Sample space (S) = 6 × 6 = 36
n(S) = 36
[priya and Amuthan are visiting a particular shop in any one of 6 days is 6 × 6 = 36]
(i) Let A be the event of getting both are shopping on the same day
A = {(Mon, Mon) (Tue, Tue) (Wed, Wed) (Thu, Thu) (Fri, Fri) (Sat, Sat)}
n(A) = 6
\(P(A)=\frac{n(A)}{n(S)}\)
\(=\frac{6}{36}=\frac{1}{6}\)
(ii) Let B be the event of shopping in different days.
n(B) = 36 – 6 = 30
\(P(B)=\frac{n(B)}{n(S)}\)
\(=\frac{30}{36}=\frac{5}{6}\)
(iii) Let C be the event of shopping consecutive days
C = {(Mon, Tue) (Tue, Wed) (Wed, Thu) (Thu, Fri) (Fri, Sat)}
n(C) = 5
P(C) = \(\frac{n(\mathrm{C})}{n(\mathrm{S})}\) = \(\frac{5}{36}\)

Question 15.
In a game, the entry fee is ₹ 150. The game consists of tossing a coin 3 times. Dhana bought a ticket for entry. If one or two heads show, she gets her entry fee back. If she throws 3 heads, she receives double the entry fees. Otherwise, she will lose. Find the probability that she
(i) gets double entry fee
(ii) just gets her entry fee
(iii) loses the entry fee.
Answer:
Sample space (S) = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n(S) = 8
(i) Let A be the event of getting double entry fee (only getting 3 heads)
n(A) = 1
\(P(A)=\frac{n(A)}{n(S)}=\frac{1}{8}\)
(ii) Let B be the event of getting her entry fee (one or two heads to show)
n(B) = Probability of one head + Probability of 2 head
= \(\frac{3}{8}+\frac{3}{8}=\frac{6}{8}=\frac{3}{4}\)
(iii) To loss the entry means not getting the head (only tail)
n(C) = 1
\(P(C)=\frac{n(C)}{n(S)}=\frac{1}{8}\)