Samacheer Kalvi 10th Maths Guide Chapter 1 Relations and Functions Additional Questions

Students can download Maths Chapter 1 Relations and Functions Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Additional Questions

I. Multiple Choice Questions.

Question 1.
If n(A × B) = 15 and B = {1, 3, 7} then n(A) is ……………
(1) 3
(2) 5
(3) 1
(4) 15
Answer:
(2) 5
Hint: B(A × B) = 15
n(A) × n(B) = 15
n(A) × 3 = 15
n(A) = \(\frac { 15 }{ 3 } \) = 5

Question 2.
If A = {a, b,c) B = {b, d, e}
C = {a, e, i, o, u} then n [A ∩ C] × B] is
(1) 18
(2) 36
(3) 9
(4) 3
Answer:
(4) 3
Hint:
A ∩ C = {a,b,c} ∩ {a, e, i, o, u}
= {a}
n(A ∩ C) = 1
n[(A ∩ C) × B] = n(A ∩ C) × n(B)
= 1 × 3
= 3

Question 3.
If there are 28 relation from a set A = {2,4, 6, 8} to a set B, then the number of elements in B is ………………
(1) 7
(2) 14
(3) 5
(4) 4
Answer:
(1) 7
Hint: n(A) = 4
n(A × B) = 28
n(A) × n(B) = 28
4 × n(B) = 28
n(B) = \(\frac { 28 }{ 4 } \) = 7

Question 4.
The ordered pairs (a + 1, 4) (3, 4a + b) are equal then (a, b) is ………………..
(1) (4, 20)
(2) (20, 4)
(3) (-4, 20)
(4) (20, -4)
Answer:
(3) (-4, 20)
Hint: (a + 7, 4) = (3, 4a + b)
a + 7 = 3
a = 3 – 7
= – 4
4a + b = 4
4(-4) + b = 4
-16 + b = 4
b = 4 + 16 = 20
The pair (a, 6) is (-4, 20)

Question 5.
The range of the relation R = {(x, x³) / x} is a prime number less than 13} is …………………
(1) (2,3,5,7,11)
(2) (4,9,25,49,121)
(3) (8,27, 125,343, 1331)
(4) (1,8,27, 125,343, 1331)
Answer:
(3) (8, 27, 125,343, 1331)
Hint: x = {2, 3, 5, 7, 11}
Range (x³) = {8, 27, 125, 343, 1331}

Question 6.
If {( x, 2), (4, y) } represents an identity function, then (x, y) is
(1) (2, 4)
(2) (4, 2)
(3) (2, 2)
(4) (4, 4)
Answer:
(1) (2, 4)
Hint: In an identity function each element is associated with itself.

Question 7.
If {(7, 11), (5, a)} represents a constant
function, then the value of ‘a’ is
(1) 7
(2) 11
(3) 5
(4) 9
Answer:
(2) 11
Hint: All the images are same in a constant function.

Question 8.
Given f(x) = (- 1)^x is a function from N to Z. Then the range of f is
(1) {1}
(2) N
(3) { 1,- 1 }
(4) Z
Answer:
(3) {1, – 1}
Hint: f(x) = (- 1)^x = ± 1

Question 9.
If f = { (6, 3), (8, 9), (5, 3), (-1, 6) }, then the pre-images of 3 are
(1) 5 and-1
(2) 6 and 8
(3) 8 and-1
(4) 6 and 5
Answer:
(4) 6 and 5.
Hint: The Pre images of 3 are 6 and 5

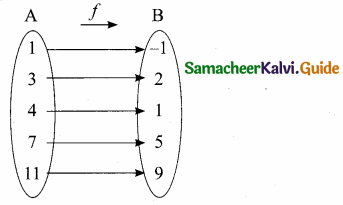
Question 10.
Let A= { 1, 3, 4, 7, 11 }, B = {-1, 1, 2, 5, 7, 9 } and f : A → B be given by
f = {(1, -1), (3,2), (4, 1), (7, 5), (11, 9)}.
Then f is ………………….
(1) one-one
(2) onto
(3) bijective
(4) not a function
Answer:
(1) one – one
Hint:

Question 11.
The given diagram represents
(1) an onto function
(2) a constant function
(3) an one-one function
(4) not a function

Answer:
(4) not a function
Hint: 2 has two images 4 and 2.
It is not a function.

Question 12.
If A = { 5, 6, 7 }, B = { 1, 2, 3, 4, 5 }and f: A → B is defined by f(x) = x – 2, then the range of f is …………….
(1) {1,4, 5}
(2) {1,2, 3, 4, 5}
(3) { 2, 3, 4 }
(4) { 3, 4, 5 }
Answer:
(4) {3, 4, 5}
Hint: f(x) = x – 2
f(5) = 5 – 2 = 3
f(6) = 6 – 2 = 4
f(7) = 7 – 2 = 5
Range of f = {3, 4, 5}

Question 13.
If f(x) = x² + 5, then f(-4) = ………
(1) 26
(2) 21
(3) 20
(4) – 20
Answer:
(2) 21
Hint: f(x) = x² + 5
f(- 4) = (-4)² + 5 = 16 + 5 = 21

Question 14.
If the range of a function is a singleton set, then it is ……………..
(1) a constant function
(2) an identity function
(3) a bijective function
(4) an one-one function
Answer:
(1) a constant function
Hint: Every element of the first set has same image in the second set.

Question 15.
If f : A → B is a bijective function and if n(A) = 5 , then n(B) is equal to ………………
(1) 10
(2) 4
(3) 5
(4) 25
Answer:
(3) 5
Hint: If A and B are Bijective (one-one and onto) function then n (A) = n (B)

Question 16.
If f: R → R defined by f(x) = 3x – 6 and g : R → R defined by g(x) = 3x + k if fog – gof then the value of k is …………………..
(1) – 5
(2) 5
(3) 6
(4) -6
Answer:
(4) – 6
Hint: f(x) = 3x – 6 ;g(x) = 3x + k
fog = f[g(x)]
= f(3x + k)
= 3 (3x + k) – 6
= 9x + 3k – 6
g o f = g[f(x)]
= g(3x – 6)
= 3(3x – 6 ) + k
= 9x – 18 + k
But fog = gof
9x + 3k – 6 = 9x – 18 + k
3k – k = -18 + 6
2k = -12
k = \(\frac { -12 }{ 2 } \) = -6

Question 17.
If f(x) = x² – x then f (x – 1) – f(x + 1) is ……………….
(1) 4x
(2) 4x + 2
(3) 2 – 4x
(4) 4x – 2
Answer:
(3) 2 – 4x
Hint: f(x – 1) = (x – 1)² – (x – 1)
= x² – 2x + 1 – x + 1
= x² – 3x + 2
f(x + 1) = (x + 1)² – (x + 1)
= x² + 2x + 1 – x – 1
= x² + x
f(x – 1) – f(x + 1) = x² – 3x + 2 – (x2 + x)
= x² – 3x + 2 – x² – x
= -4x + 2 = 2 – 4x

Question 18.
If K(x) = 3x – 9 then L (x) = 7x – 10 then LOK is ……………..
(1) 21x + 73
(2) – 21x + 73
(3) 21x – 73
(4) 22x – 73
Answer:
(3) 21x – 73
Hint: K (x) = 3x – 9 ; L(x) = 7x – 10
LOK = L[K(x)]
= L (3x – 9)
= 7(3x – 9) – 10
= 21x – 63 – 10
= 21x – 73

Question 19.
Composition of function is ……………..
(1) commutative
(2) associative
(3) commutative and associative
(4) not associative
Answer:
(2) associative

Question 20.
A comet is heading for Jupiter with acceleration a = 50 kms^-2. The velocity of the comet at time ”t” is given by f(t) = at² – at + 1. Then the velocity at time t = 5 seconds is …………..
(1) 900kms^-1
(2) 1001 kms^-1
(3) 2001 kms^-1
(4) 50 kms^-1
Answer:
(2) 1001 kms^-1
Hint: f(t) = at² – at + 1
m = 50(5)² – 50(5) + 1
= 1250 – 250 + 1
= 1001 kms^-1

II. Answer the following questions.

Question 1.
f(x) = (1 + x)
f(x) = (2x – 1)
Show that fo(g(x)) = gof(x)
Solution:
f(x) = 1 + x
g(x) = (2x – 1)
fog(x) = f(g(x)) = f(2x – 1)
= 1 + 2x – 1 = 2x ………….. (1)
gof(x) = g(f(x)) = g(1 + x) = 2(1 + x) = 1
= 2 + 2x – 1
= 2x + 1 ……………. (2)
(1) ≠ (2)
∴ fog(x) + gof(x) It is verified.

Question 2.
If A × B = {(a, x) (a, y) (b, x) (b, y) (c, x) (c, y)} then find A and B
Answer:
A × B = {(a, x) (a, y) (b, x) (b, y) (c, x) (c, y)}
A = {a, b, c}
B = {x,y}

Question 3.
Let A = {x ∈ w/3 < x < 7},
B = {x ∈ N/0 < x < 3}, C = {x ∈ w/x < 2}
verify A × (B ∩ C) = (A × B) ∩ (A × C)
Answer:
A = {4,5,6} ; B = {1,2} C = {0, 1}
B ∩ C = {1,2} ∩ {0, 1}
= {1}
A × (B ∩ C) = {4,5,6} × {1}
= {(4, 1) (5, 1) (6, 1)} …. (1)
A × B = {4,5,6} × {1,2}
= {(4, 1) (4, 2) (5, 1) (5, 2) (6, 1) (6, 2)}
A × C = {4,5,6} x {0, 1}
= {(4,0) (4,1) (5,0)
(5, 1) (6, 0) (6, 1)}
(A × B) ∩ (A × C) = {(4, 1) (5, 1) (6, 1)}…. (2)
From (1) and (2) we get
A × (B ∩ C) = (A × B) ∩ (A × C)

Question 4.
Let A = {10, 11, 12, 13, 14}; B = {0, 1, 2, 3, 5} and f_i: A → B, i = 1, 2, 3. State the type of function for the following (give reason):
(i) f₁ = {(10,1), (11,2), (12,3), (13,5), (14,3)}
Answer:
The element 12 and 14 in A have same image 3 in B.

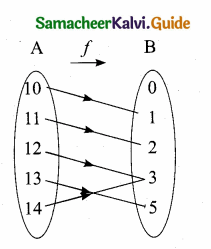
∴ It is not one-one function.
The element ‘0’ in B has no preimage in A
∴ It is not onto function
So the given function is neither one – one nor onto function.

(ii) f₂ = {(10,1), (11,1), (12,1), (13,1), (14,1)}
Answer:
f₂ is a constant function

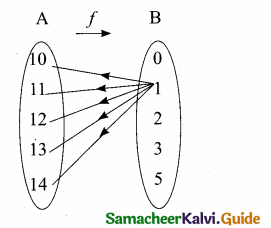
(iii) f₃ = {(10,0), (11,1), (12,2), (13,3), (14,5)}
Answer:
f₃ is one-one and onto function (or) bijective function.

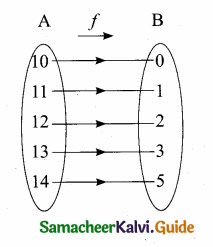
Question 5.
If X = {1, 2, 3, 4, 5}, Y = {1, 3, 5, 7, 9} determine which of the following relations from X to Y are functions? Give reason for your answer. If it is a function, state its type.
(i) R1 = {(x,y)| y = x + 2,x ∈ X,y ∈ Y}
Answer:
Given y = x + 2
When x = 1 ; y = 1 + 2 = 3
When x = 2 ; y = 2 + 2 = 4
When x = 3 ; y = 3 + 2 = 5
When x = 4 ; y = 4 + 2 = 6
When x = 5 ; y = 5 + 2 = 7

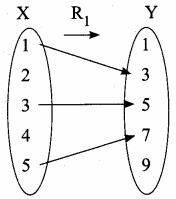
R₁ = {1,3), (2,4), (3, 5), (4, 6), (5,7)}
R₁ is not a function ; 2 and 4 has no image in Y.

(ii) R₂ = {(1,1), (2,1), (3,3), (4,3), (5,5)}
Answer:
R₂ is a function.
Every element of X has unique image in Y.
1 and 2 have same image 1
3 and 4 have same image 3
It is not one – one function …. (1)
7 and 9 has no pre image in X
It is not an onto function …. (2)

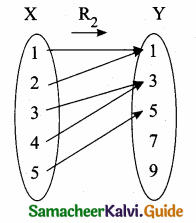
From (1) and (2) we know that, it is
neither one – one nor onto function.

(iii) R₃ = {(1,1), (1,3), (3,5), (3,7), (5,7)}
Answer:
R₃ is not a function.
1 has two images 1 and 3
3 has two images 5 and 7

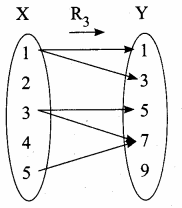
(iv) R₄ = {(1,3), (2,5), (4,7), (5,9), (3,1)}
Answer:
Every element of X has unique image in
Y. Range = Co-domain
R₄ is a function.

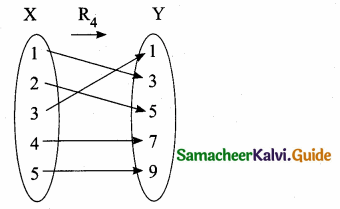
It is an one-one and onto function (or) bijective function

Question 6.
A= {-2,-1, 1, 2} and f = {(x,\(\frac { 1 }{ x } \)) ; x ∈ A}
Write down the range of f. Is f a function from A to A?
Answer:
Given, f = (x,\(\frac { 1 }{ x } \)) ; So f(x) = \(\frac { 1 }{ x } \)
f (-2) = \(\frac { 1 }{ -2 } \) = – \(\frac { 1 }{ 2 } \) ; f(-1) = \(\frac { 1 }{ -1 } \) = -1
f(1) = \(\frac { 1 }{ 1 } \) = 1 ; f(2) = \(\frac { 1 }{ 2 } \) = \(\frac { 1 }{ 2 } \)
Range of f = {\(\frac { -1 }{ 2 } \), -1, 1, \(\frac { 1 }{ 2 } \)}
It is not a function from A to A since – \(\frac { 1 }{ 2 } \) ,\(\frac { 1 }{ 2 } \) ∈ A

Question 7.
Let A = {1, 2, 3, 4, 5}, B = N and f: A → B be defined by f(x) = x². Find the range of f. Identify the type of function.
Solution:
A = {1, 2, 3, 4, 5}
B = {1, 2, 3, 4 ….}
f: A → B, f(x) = x²
∴ f(1) = 1² = 1
f(2) = 2² = 4
f(3) = 3² = 9
f(4) = 4² = 16
f(5) = 5² = 25
∴ Range of f = {1, 4, 9, 16, 25)
Elements in A have been different elements in B. Therefore it is one-one function. But not all the elements in B have preimages in A. Therefore it is not on-to function.

Question 8.
Let A = { 1, 2, 3, 4, 5 }, B = N and f: A → B be defined by f(x) = x².
Find the range of f. Identify the type of function.
Answer:
Now, A = { 1, 2, 3, 4, 5 };
B = { 1, 2, 3, 4, … }
Given f: A → B and f(x) = x²
f(1) = 1² = 1;
f(2) = 4;
f(3) = 9;
f(4) = 16;
f(5) = 25.
Range of f = {1, 4, 9, 16, 25}
Since distinct elements are mapped into distinct images, it is a one-one function.
However, the function is not onto, since 3 ∈ B but there is no x ∈ A
such that
f(x) = x² = 3.

Question 9.
Identify the type of function.


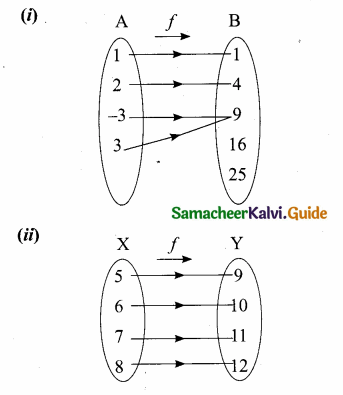
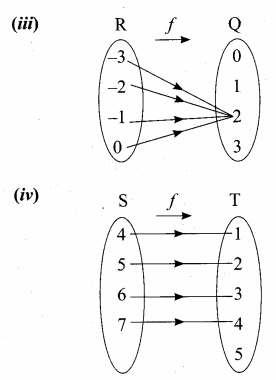
Answer:
(i) Many – one into
(ii) One – one onto
(iii) Constant function
(iv) One – one into

Question 10.
Find the domain and range of the following
(i) f = {(1, 2), (2, 3), (3, 4), (4, 5) (5, 6)}
(ii) R = {(-2, 4), (-1,1), (2,4), (1,1) (-3, 9)}
Answer:
(i) f = {( 1,2), (2, 3), (3, 4), (4, 5) (5, 6)}
Domain = {1,2, 3,4, 5}
Range = {2, 3, 4, 5, 6}

(ii) R = {(-2,4), (-1, 1),(2,4), (1,1) (-3,9)}
Domain = {-2, -1,2, 1,-3} (or)
= {-3,-2,-1, 1,2}
Range = {4, 1, 9} (or) {1, 4, 9}

Question 11.
Given P ={-2,-1, 0,1}
Q = {1,-2, 6,-3}
R = {x,y/y = x² – 3 x ∈ P,y ∈ Q}
(i) List the elements of R
(ii) Is the relation a function? If so identity the function
Answer:
P = {-2, -1, 0, 1}; Q = {1, -2,6, -3}
y = x2- 3 x ∈ P, y ∈ Q
When x = -2 ⇒ y = (-2)² – 3 = 4 – 3 = 1
When x = -1 ⇒ y = (-1 )² – 3 = 1 – 3 = -2
When x = 0 ⇒ y = (0)² – 3 = 0 -3 = -3
When x = 1 ⇒ y = 1² – 3 = 1 – 3 = -2
(i) R = {(-2,1), (-1,-2), (0,-3), (1,-2)}
(ii) Yes the relation is a function many – one into function.

Question 12.
Given f(x) = 3x – 2; g(x) = 2x² find
(i) fog and
(ii) gof what do you find
Answer:
f(x) = 3x – 2 ; g(x) = 2x²
(i) f o g = f[g(x)]
= f(2x²)
= 3(2x²) – 2
= 6x² – 2

(ii) g o f = g [f(x)]
= g (3x – 2)
= 2(3x – 2)²
= 2(9x² + 4 – 12x)
= 18x² – 24x + 8
we find that fog ≠ gof
Composition of function is not commutative.

Question 13.
If f: R → R is defined by f(x) = ax + 3 and g: R → R is defined by g (x) = 4x – 3 find a so that fog = gof
Answer:
f(x) = ax + 3 ; g(x) = 4x -3
fog = f[g(x)]
= f(4x – 3)
= a (4x – 3) + 3
= 4ax – 3a + 3
gof = g [f(x)]
= g (ax + 3)
= 4 (ax + 3) – 3
= 4 ax + 12 – 3
= 4ax + 9
But fog = gof
4ax – 3a + 3 = 4ax + 9
-3a + 3 = 9
– 3a = 6
a = – 2
The value of a = – 2

Question 14.
Given f(x) = 3 + x ; g(x) = x² ;
h(x) = \(\frac { 1 }{ x } \) find fo (goh)
Answer:
f(x) = 3 + x ; g (x) = x², h(x) = \(\frac { 1 }{ x } \)
goh = g[h(x)]
= g (\(\frac { 1 }{ x } \))
= (\(\frac { 1 }{ x } \))²
goh = \(\frac{1}{x^{2}}\)
fo(goh) = f (\(\frac{1}{x^{2}}\))
= 3 + \(\frac{1}{x^{2}}\)

Question 15.
If f(x) = x + 3 where A = {4, 6, 8,10} B = {7, 9,11,13} and f: A → B
(i) Draw the arrow diagram
(ii) Why type of function is f.
Answer:
A= {4, 6, 8, 10}
f(x) = x + 3
f(4) = 4 + 3 = 7
f(6) = 6 + 3 = 9
f(8) = 8 + 3 = 11
f(10) = 10 + 3 = 13

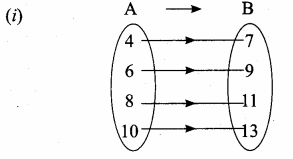
(ii) one – one onto function

III. Answer the following Questions

Question 1.
Given A = {2,3, 5}, B = {1,2,3}
C = {2, 5}, D = {2,3, 5} check if
(A ∩ C) × (B ∩ D) = (A × B) ∩ (C × D)
Answer:
A ∩ C = {2, 3, 5} ∩ (2, 5}
= (2,5}
B ∩ D = {1,2,3} ∩ {2,3,5}
= {2,3}
(A ∩ C) × (B ∩ D) = {2, 5} × {2, 3}
= {(2, 2) (2, 3) (5, 2) (5, 3)} …. (1)
A × B = {2,3,5} × {1,2,3}
= {(2,1) (2, 2) (2, 3)
(3, 1) (3, 2) (3, 3)
(5, 1) (5, 2) (5, 3)}
C × D = {2, 5} × {2, 3, 5}
= {(2, 2) (2, 3) (2, 5) (5, 2) (5, 3) (5, 5)}
(A × B) ∩ (C × D) = {(2,2) (2, 3) (5, 2) (5, 3)} …. (2)
From (1) and (2) we get
(A ∩ C) × (B ∩ D) = (A × B) ∩ (C × D)

Question 2.
Study the relation given below an set- builder form. Represent each of them by
(a) an arrow diagram
(b) a graph
(c) a set in roster.
If {{x,y}/y = 2x + 1; x < 10 and y < 12 x ∈ N, y ∈ N}
Answer:
y = 2x + 1
when x = 1 ⇒ y = 2(1) + 1 = 2 + 1 = 3
when x = 2 ⇒ y = 2(2) + 1 = 4 + 1 = 5
when x = 3 ⇒ y = 2(3) + 1 = 6 + 1 = 7
when x = 4 ⇒ y = 2(4) + 1 = 8 + 1 = 9
when x = 5 ⇒ y = 2(5) + 1 = 10 + 1 = 11
f = {(1,3) (2, 5) (3, 7) (4, 9) (5, 11)}

(a) Arrow diagram

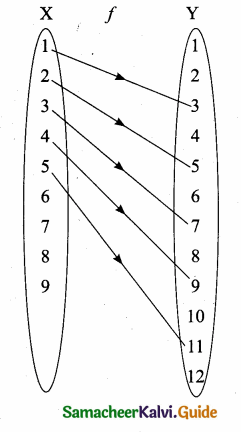
(b) A graph

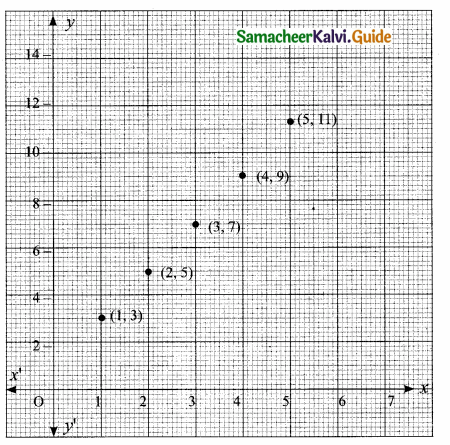
(c) Roster form: R = {(1,3) (2,5) (3,7) (4,9) (5,11)}

Question 3.
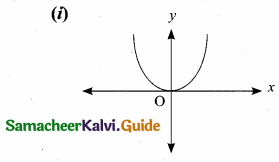
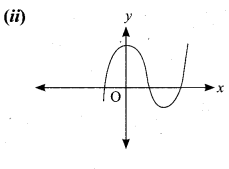
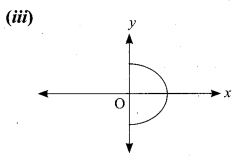
State whether the following graphs represents a function. Give reason for your answer.





Answer:
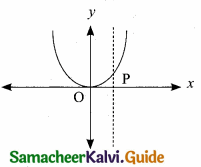
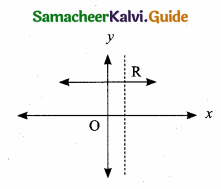
(i) The given graph represents a function. The vertical line cuts the graph at most one point R

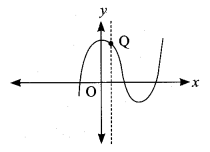
(ii) The vertical line cuts the graph at most one point Q. The given graph represents a function.

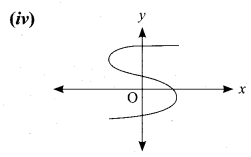
(iii) The vertical line cuts the graph at A and B. The given graph does not represents a function.

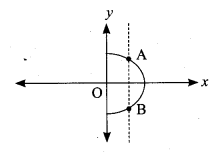
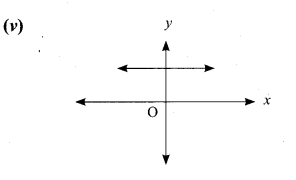
(iv) The vertical line cuts the graph at A and B. The given graph does not represents a function.

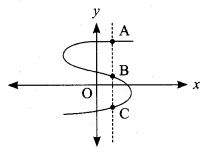
(v) The vertical line cuts the graph at most one point R. The given graph represents a function.

Question 4.
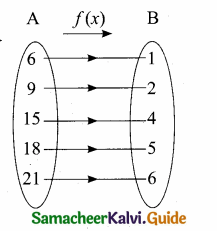
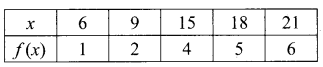
Let A = {6, 9,15,18, 21}; B = {1, 2, 4, 5, 6} and f: A → B be defined by f(x) = \(\frac { x-3 }{ 3 } \) Represent f by, (i) an arrow diagram, (ii) a set of ordered pairs, (iii) a table, (iv) a graph.
Given, A = {6, 9, 15, 18, 21}, B = {1, 2, 4, 5, 6}
f(x) = \(\frac { x-3 }{ 3 } \)
f(6) = \(\frac { 6-3 }{ 3 } \) = \(\frac { 3 }{ 3 } \) = 1
f(9) = \(\frac { 9-3 }{ 3 } \) = \(\frac { 6 }{ 3 } \) = 2
f(15) = \(\frac { 15-3 }{ 3 } \) = \(\frac { 12 }{ 3 } \) = 4
f(18) = \(\frac { 18-3 }{ 3 } \) = \(\frac { 12 }{ 3 } \) = 4
f(18) = \(\frac { 18-3 }{ 3 } \) = \(\frac { 15 }{ 3 } \) = 5
f(21) = \(\frac { 21-3 }{ 3 } \) = \(\frac { 18 }{ 3 } \) = 6

(i) an arrow diagram

(ii) a set of ordered pairs
f = {(6,1), (9, 2), (15, 4), (18, 5), (21,6)}

(iii) a table

(iv) a graph

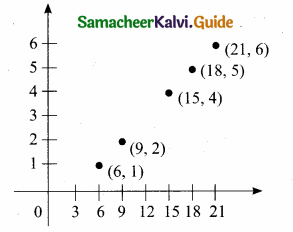
Question 5.
Let A = {4,6,8,10} and B = {3,4,5,6,7}. If f: A → B is defined by f(x) = \(\frac { 1 }{ 2 } \) x + 1 then represent f by (i) an arrow diagram, (ii) a set of ordered pairs and, (iii) a table.
Answer:
Given, A = {4, 6, 8, 10}
B = {3, 4, 5, 6, 7}
f(x) = \(\frac { x }{ 2 } \) + 1
f(4) = \(\frac { 4 }{ 2 } \) + 1 = 2 + 1 = 3
f(6) = \(\frac { 6 }{ 2 } \) + 1 = 3 + 1 = 4
f(8) = \(\frac { 8 }{ 2 } \) + 1 = 4 + 1 = 5
f(10) = \(\frac { 10 }{ 2 } \) + 1 = 5 + 1 = 6

(i) an arrow diagram

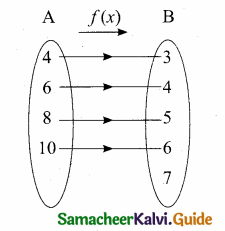
(ii) a set of ordered pairs
f = {(4, 3), (6, 4), (8, 5), (10, 6)}

(iii) a table

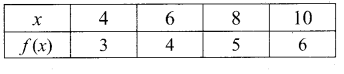
Question 6.
A function f[- 3, 7 ) → R is defined as follows f(x) =

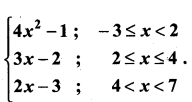
Find (i) f(5) + f(6)
(ii) f(1) – f(-3)
(iii) f(-2) – f(4)
(iv) \(\frac{f(3)+f(-1)}{2 f(6)-f(1)}\)
Answer:
Given, f(x) = 4x² – 1; x = {-3, -2, -1, 0, 1}
f(x) = 3x – 2; x = {2,3,4}
f(x) = 2x – 3; x = {5,6}
(i) f(5) + f(6)
f(x) = 2x – 3
f(5) = 2(5) – 3 = 10 – 3 = 7
f(6) = 2(6) – 3 = 12 – 3 = 9
∴ f(5) + f(6) = 7 + 9 = 16

(ii) f(1) – f(-3)
f(x) = 4x² – 1
f(1) = 4(1)² – 1 = 4 – 1 = 3
f(-3) = [4(-3)² – 1]
= 4 (9) – 1
= 36 – 1 = 35
∴ f(1) – f(-3) = 3 – (35) = -32

(iii) f(-2) – f(4)
f(x) = 4x² – 1
f(-2) = 4(-2)² – 1 = 4(4) – 1 = 16 – 1 = 15
f(x) = 3x – 2
f(4) = [3(4) – 2] = 12 – 2 = 10
∴ f(-2) – f(4) = 15 – 10 = 5

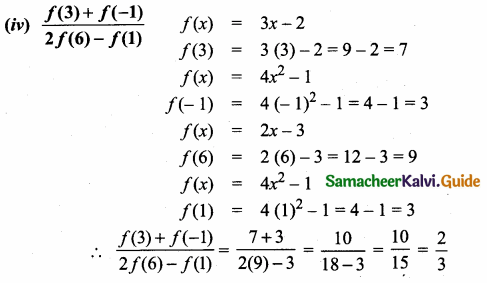
Question 7.
A function f : [- 7, 6) → R is defined as follows


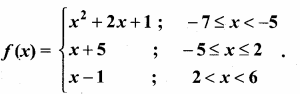
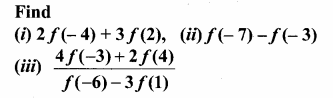
Answer:
Given, f(x) = x² + 2x + 1 ; x = {-7, -6}
f(x) = x + 5 ; x = {-5, -4, -3, -2, -1, 0, 1, 2}
f(x) = x – 1; x{3, 4, 5}

(i) 2f(- 4) + 3f(2)
f(x) = x + 5
f(-4) = -4 + 5 = 1
f(2) = 2 + 5 = 7
∴ 2f(-4) + 3 f(2) = 2(1) + 3(7) = 2 + 21 = 23

(ii) f(-7) – f(-3)
f(x) = x² + 2x + 1
f(-7) = (-7)² + 2(-7) + 1 = 49 – 14 + 1 = 36
f(x) = x + 5
f(-3) = -3 + 5 = 2
∴ f(-7) – f(-3) = 36 – 2 = 34

(iii) \(\frac{4 f(-3)+2 f(4)}{f(-6)-3 f(1)}\)
f(x) = x + 5
f(-3) = -3 + 5 = 2
f(x) = x – 1
f(4) = 4 – 1 = 3
f(x) = x² + 2x + 1
f(-6) = (-6)² + 2(-6) + 1 = 36 – 12 + 1 = 25
f(x) = x + 5
f(1) = 1 + 5 = 6

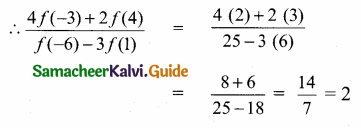
Question 8.
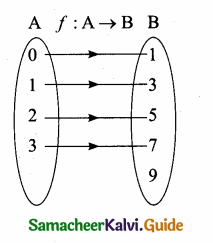
Let A= { 0,1, 2, 3 } and B = {1, 3, 5, 7, 9 } be two sets. Let f: A → B be a function given by f (x) = 2x + 1. Represent this function as
(i) a set of ordered pairs
(ii) a table
(iii) an arrow diagram and
(iv) a graph.
Answer:
A = {0, 1, 2, 3}, B = { 1, 3, 5, 7, 9 },f(x) = 2x + 1
f(0) = 2(0) + 1 = 1, f(1) = 2(1) + 1 = 3 ,f(2) = 2(2) + 1 = 5, f(3) = 2(3) + 1 = 7

(i) Set of ordered pairs
The given function/can be represented as a set of ordered pairs as
f = {(0, 1), (1, 3), (2, 5), (3,7)}

(ii) Table form
Let us represent f using a table as shown below.

(iii) Arrow Diagram
Let us represent f by an arrow diagram.
We draw two closed curves to represent the sets A and B. Here each element of A and its unique image element in B are related with an arrow.

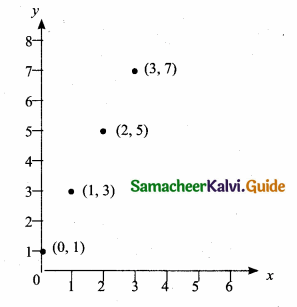
(iv) Graph
We are given that
f = {(x,f(x)) | x ∈ A} = {(0,1), (1, 3), (2, 5), (3, 7)}. Now, the points (0, 1), (1, 3), (2, 5) and (3, 7) are plotted on the plane as shown below.
The totality of all points represent the graph of the function.

Question 9.
A. function f: [1, 6) → R is defined as follows

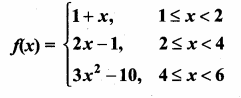
(Here, [1, 6) = {x ∈ R : 1 ≤ x < 6})
Find the value of
(i) f(5)
(ii) f(3)
(iii) f(1)
(iv) f(2) – f(4)
(v) 2f(5) – 3f(1).
Answer:
(i) Let us find f(5). Since 5 lies between 4 and 6, we have to use f(x) = 3x² – 10.
Thus, f(5) = 3(5²) – 10 = 65.

(ii) To find f(3), note that 3 lies between 2 and 4.
So, we use f(x) = 2x – 1 to calculate f(3).
Thus, f(3) = 2(3) – 1 = 5.

(iii) Let us find f(1).
Now, 1 is in the interval 1 < x < 2
Thus, we have to use f(x) = 1 + x to obtain f(1) = 1 + 1 = 2.

(iv) f (2) – f(4)
Now, 2 is in the interval 2 < x < 4 and so, we use f(x) = 2x – 1.
Thus, f(2) = 2(2) -1 = 3.
Also, 4 is in the interval 4 < x < 6. Thus, we use f(x) = 3x² – 10
Therefore, f(4) = 3(4²) – 10 = 3(16) – 10 = 48 – 10 = 38.
Hence, f(2) – f(4) = 3 – 38 = -35.

(v) To calculate 2 f (5) – 3f (1), we shall make use of the values that we have already calculated in (i) and (iii). Thus, 2f(5) – 3f(1) = 2(65) – 3(2) = 130 – 6 – 124.

Question 10.
Given f(x) = 5x + 2; g(x) = 2x – 3;
h(x) = 3x + 1. Verify fo (goh) = (fog) oh
Answer:
f(x) = 5x + 2 ; g(x) = 2x – 3; h(x) = 3x + 1
L.H.S. = fo (goh)
goh = g[h(x)]
= g(3x + 1)
= 2(3x + 1) – 3
= 6x – 1
fo (goh) = f[goh (x)]
= f(6x – 1)
= 5 (6x – 1) + 2
= 30 x – 5 + 2
fo (goh) = 30x – 3 ….(1)
R.H.S. = (fog) oh
fog = f[g(x)]
= f(2x – 3)
= 5(2x – 3) + 2
= 30x – 5 + 2
fo (goh) = 30x – 3 …..(1)
R.H.S. = (fog) oh
fog = f[g(x)]
= f(2x – 3)
= 5 (2x – 3)
= 5 (2x – 3) + 2
= 10x – 15 + 2
= 10x – 13
(fog) oh = fog [h(x)]
= fog (3x + 1)
= 10 (3x + 1) – 13
= 30x + 10 – 13
= 30x – 3 ….(2)
From (1) and (2) we get L.H.S. = R.H.S.
fo(goh) = (fog) oh

Question 11.
Given f(x) = x² + 4; g(x) = 3x – 2;
h(x) = x – 5. Show that the composition of functions is associative.
Answer:
f(x) = x² + 4 ; g(x) – 3x – 2; h(x) = x – 5
To prove fo (goh) = (fog) oh
L.H.S. fo (goh)
goh = g[h(x)]
= g(x – 5)
= 3(x – 5) – 2
= 3x – 15 – 2
goh = 3x – 17
fo (goh) = f [goh (x)]
= f(3x – 17)
= (3x – 17)² + 4
= 9x² + 289 – 102 x + 4
= 9x² – 102x + 293 ….(1)
R.H.S. = (fog) oh
fog – f[g(x)]
= f(3x-2)
= (3x – 2)² + 4
= 9×2 + 4 – 12x + 4
= 9×2 – 12x + 8
(fog) oh = fog [h(x)]
= fog (x – 5)
= 9(x – 5)² – 12 (x – 5) + 8
= 9(x² + 25 – 10x) – 12x + 60 + 8
= 9x² + 225 – 90x – 12x + 60 + 8
= 9x² – 102x + 293 ….(2)
From (1) and (2) we get fo (goh) = (fog) oh.
Composition of function is associative

Question 12.
Given f(x) = x – 2; g(x) = 3x + 5; h(x) = 2x – 3. Verify that (goh) of = go (hof)
Answer:
f(x) = x – 2 ; g(x) = 3x + 5; h(x) = 2x – 3
L.H.S. (goh) of
goh = g[h(x)]
= g(2x – 3)
= 3(2x – 3) + 5
= 6x – 9 + 5
= 6x – 4
(goh) of = goh [f(x)]
= goh (x – 2)
= 6(x – 2) – 4
= 6x – 12 – 4
= 6x – 16 ….(1)

R.H.S. go(hof)
hof = h[f(x)]
= h(x- 2)
= 2(x – 2) – 3
= 2x – 4 – 3
= 2x – 7
go(hof) = g [hof (x)]
= g (2x – 7)
= 3(2x – 7) + 5
= 6x – 21 + 5
= 6x – 16 ….(2)
From (1) and (2) we get (goh) of = go(hof)