Students can download Maths Chapter 7 Mensuration Unit Exercise 7 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 7 Mensuration Unit Exercise 7
Question 1.
The barrel of a fountain-pen cylindrical in shape is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen will be used for writing 330 words on an average. How many words can be written using a bottle of ink containing one-fifth of a litre?
Answer:


Question 2.
A hemispherical tank of radius 1.75 m is full of water. It is connected with a pipe which empties the tank at the rate of 7 litres per second. How much time will it take to empty the tank completely?
Answer:
Radius of the hemispherical tank = 1.75 m
Volume of the tank = \(\frac{2}{3} \pi r^{3}\) cu.units

Time taken = \(\frac{11229.17}{7}\) = 1604.17 seconds = 26.74 minutes = 27 minutes (approximately)
Question 3.
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r units.
Answer:
Radius of a cone = Radius of a hemisphere = r unit
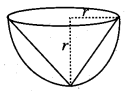
Height of a cone = r units
(height of the cone = radius of a hemisphere)
Maximum volume of the cone

Question 4.
An oil funnel of the tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion by 8 cm and the diameter of the top of the funnel be 18 cm, then find the area of the tin sheet required to make the funnel.
Answer:
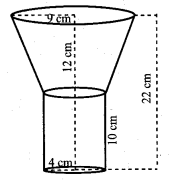
Total height of oil funnel = 22 cm
Height of the cylindrical portion = 10 cm
Height of the frustum (h) = 22 – 10 = 12 cm
Radius of the cylindrical portion = 4 cm
Radius of the bottom of the frustum = 4 cm
Top radius of the funnel (frustum) = \(\frac{18}{2}\) = 9 cm
Area of the tin sheet required = C.S.A of the frustum + C.S.A of the cylinder
= π (R + r) l + 2πrh sq. units.
= [π(9 + 4) \(\sqrt{12^{2}+(9-4)^{2}}\) + 2π × 4 × 10] cm2
= π [13 × \(\sqrt{144+25}\) + 25 + 80] cm2
= \(\frac{22}{7}\) [13 × 13 + 80] cm2
= \(\frac{22}{7}\) [169 + 80] cm2
= \(\frac{22}{7}\) × 249 cm2
= 782.57 cm2
Area of sheet required to make the funnel = 782.57 cm2
Question 5.
Find the number of coins, 1.5 cm in diameter and 2 mm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Answer:
Radius of the cylinder = \(\frac{4.5}{2}\) cm
Height of the cylinder = 10 cm
Volume of the cylinder = πr2h cu. units

Number of coins = 450
Question 6.
A hollow metallic cylinder whose external radius is 4.3 cm and internal radius is 1.1 cm and the whole length is 4 cm is melted and recast into a solid cylinder of 12 cm long. Find the diameter of a solid cylinder.
Answer:
External radius of the hollow cylinder R = 4.3 cm
Internal radius of the hollow cylinder r = 1.1 cm
Length of the cylinder (h) = 4 cm
Length of the solid cylinder (H) = 12 cm
Let the radius of the solid cylinder be “x”
Volume of the solid cylinder = Volume of the hollow cylinder

Diameter of the solid cylinder = 2 × 2.4 = 4.8 cm
Question 7.
The slant height of a frustum of a cone is 4 m and the perimeter of circular ends are 18 m and 16 m. Find the cost of painting its curved surface area at ₹ 100 per sq. m.
Answer:
Slant height of a frustum (l) = 4 m
Perimeter of the top part = 18 m
2πR = 18
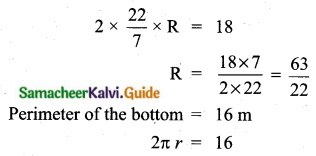

Cost of painting = ₹ 100 × 68 = ₹ 6800
Question 8.
A hemispherical hollow bowl has material of volume cubic \(\frac{436 \pi}{3}\) cubic cm. Its external diameter is 14 cm. Find its thickness.
Answer:
External radius of a hemisphere (R) = 7 cm
Volume of a hemi-spherical bowl = \(\frac{436 \pi}{3}\) cm3
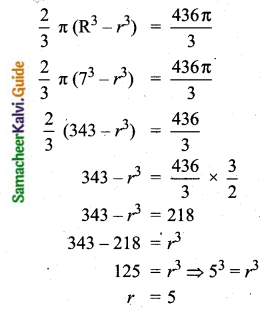
Internal radius = 5 cm
Thickness of the hemisphere = (7 – 5) cm = 2 cm
Question 9.
The volume of a cone is 1005\(\frac{5}{7}\) cu. cm. The area of its base is 201\(\frac{1}{7}\) sq. cm. Find the slant height of the cone.
Answer:
Area of the base of a cone = 201\(\frac{1}{7}\) sq. cm


Question 10.
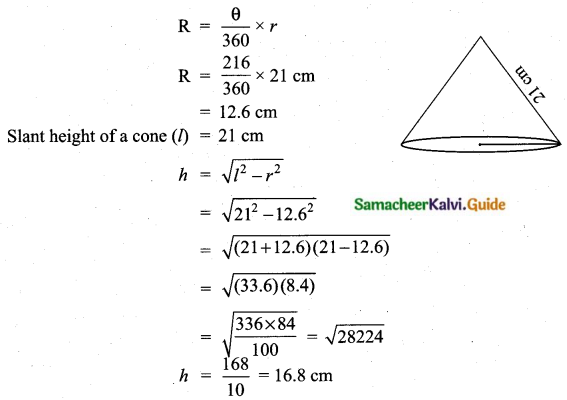
A metallic sheet in the form of a sector of a circle of radius 21 cm has a central angle of 216°. The sector is made into a cone by bringing the bounding radii together. Find the volume of the cone formed.
Answer:
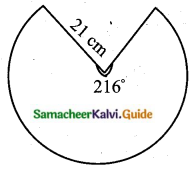
Radius of a cone (r) = 21 cm
Central angle (θ) = 216°
Let “R” be the radius of a cone
Circumference of the base of a cone = arc length of the sector
2πR = \(\frac{\theta}{360} \times 2 \pi r\)