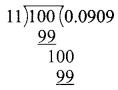Category: Class 9

Students can download Maths Chapter 4 Geometry Ex 4.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.2

Question 1.
The angles of a quadrilateral are in the ratio 2 : 4 : 5 : 7. Find all the angles.
Solution:
Let the angles of a quadrilateral be 2x, 4x, 5x, and 7x.
Total angle of a quadrilateral = 360°
2x + 4x + 5x + 7x = 360°
18° = 360°
x = \(\frac{360°}{18}\)
= 20°
2x = 2 × 20° = 40°; 4x = 4 × 20° = 80°;
5x = 5 × 20° = 100°; 7x = 7 × 20° = 140°
The angles of a quadrilateral are 40°, 80°, 100° and 140°.

Question 2.
In a quadrilateral ABCD, ∠A = 72° and ∠C is the supplementary of ∠A. The other two angles are 2x – 10 and x + 4. Find the value of x and the measure of all the angles.
Solution:

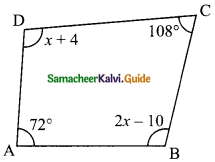
∠A = 72°
∠C = 180° – 12° (∠A and ∠C are supplementary)
= 108°
∠A + ∠B + ∠C + ∠D = 360° (Total angles of quadrilateral)
72° + 2x – 10 + 108° + x + 4 = 360°
3x + 174° = 360°
x = \(\frac{186°}{3}\)
= 62°
The value of x is 62°
∠B = 2x – 10
= 2(62°) – 10
= 124° – 10°
= 114°
∠D = x + 4
= 62° + 4
= 66°
The other angles are 114°, 62° and 66°.

Question 3.
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC.
Solution:
Since the diagonals of a rectangle AC and BD are equal and bisect each other

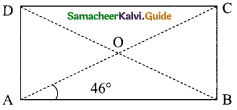
∴ OA = OB
∠OAB = ∠OBA = 46°
Each angle of a rectangle measures 90°
∠ABC = 90°
∠ABO + ∠OBC = 90°
46° + ∠OBC = 90°
∠OBC = 90°-46°
∴ ∠OBC = 44°

Question 4.
The lengths of the diagonals of a Rhombus are 12 cm and 16 cm. Find the side of the rhombus.
Solution:
Since the diagonals of a rhombus bisect each other at right angles

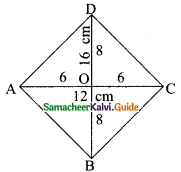
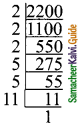
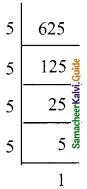
AO = \(\frac{1}{2}\)AC = \(\frac{1}{2}\) × 12 = 6 cm
BO = \(\frac{1}{2}\)BD = \(\frac{1}{2}\) × 16 = 8 cm
In the right triangle AOD
AD² = AO² + DO²
= 6² + 8²
= 36 + 64
= 100
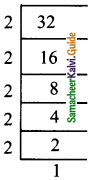
∴ AD = \(\sqrt{100}\)
= 10
∴ AB = BC = CD = AD = 10 cm.

Question 5.
Show that the bisectors of angles of a parallelogram form a rectangle.
Solution:
Given: A parallelogram in which bisector of angle A, B, C, D intersect at P, Q, R, S to form a quadrilateral PQRS.
To prove: Quadrilateral PQRS is a rectangle.
Proof: Since ABCD is a parallelogram. Therefore, AB || DC.

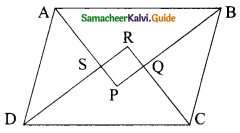
Now, AB || DC, and transversal AD cuts them, so we have
∠A + ∠D = 180°
\(\frac{1}{2}\)∠A + \(\frac{1}{2}\)∠D = \(\frac{180°}{2}\)
∠DAS + ∠ADS = 90°
But in ΔASD, we have
∠ADS + ∠DAS + ∠ASD = 180°
90° + ∠ASD = 180°
∠ASD = 90°
∠RSP = ∠ASD (vertically opposite angle)
∠RSP = 90°
Similarly, we can prove that
∠SRQ = 90°, ∠RQP = 90° and ∠QPS = 90°
Thus, PQRS is a quadrilateral each of whose angle is 90°.
Hence, PQRS is a rectangle.

Question 6.
If a triangle and a parallelogram lie on the same base and between the same parallels then prove that the area of the triangle is equal to half of the area of parallelogram.
Solution:
Let ΔAPB and parallelogram ABCD lie on base AB and between parallels AB and PC.
To show area ΔAPB = \(\frac{1}{2}\) Area (ABCD)
Now, draw BQ || AP. Then ABQP is a parallelogram.
Now area ABQP = Area ABCD
(They are on same base AB and between same parallels AB and PC)

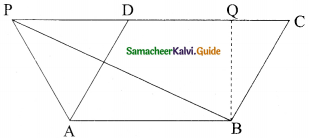
⇒ ΔPAB ≅ ΔBQP
Area PAB = Area BQP
= \(\frac{1}{2}\) Area ABQP
= \(\frac{1}{2}\) Area ABCD

Question 7.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure.

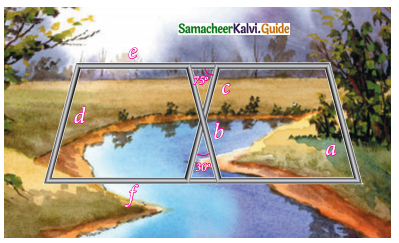
If a || b, c || d, e || f, find the marked angles between
(i) b and c
(ii) d and e
(iii) d and f
(iv) c and f
Solution:
(i) Angle between b and c = 30°
(vertically opposite angles)

(ii) Angle between d and e = 180° – 75° = 105°
(sum of the adjacent angles of a parallelogram is 180°)

(iii) Angle between d and f = 75°
(opposite angles of a parallelogram)

(iv) Angle between c and f = 180° – 75° = 105°
(Adjacent angles of a parallelogram)

Question 8.
In the given figure, ∠A = 64°, ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ΔABC, find x° and y°.

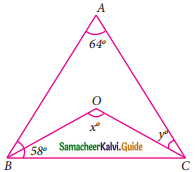
Solution:
In the given ΔABC
∠A = 64° and ∠B = 58°
∠C = 180°- (64° + 58°)
= 180° – 122°
= 58°
Since OC is the bisector of ∠C
y = \(\frac{58°}{2}\)
= 29°
Given ΔOBC
∠OCB = \(\frac{58°}{2}\) = 29°
∠OCB = 29°
∴ ∠BOC = 180°- (29° + 29°)
x = 180° – 58°
x = 122°
∠x = 122° and ∠y = 29°.

Question 9.
In the given figure, if AB = 2, BC = 6, AE = 6, BF = 8, CE = 7 and CF = 7, compute the ratio of the area of quadrilateral ABDE to the area of ΔCDF.

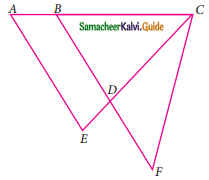
Solution:
Given: AB = 2 cm, BC = 6 cm, AE = 6 cm, BF = 8 cm, CE = 7 cm and CF = 7 cm
Consider ΔAEC and ΔBCF.
In ΔAEC, AE = 6 cm, EC = 7 cm and AC = 8 cm (2 + 6 = 8)
In ΔBCF, BC = 6 cm, CF = 7 cm and BF = 8 cm
∴ ΔAEC s ΔBCF
∴ Area of ΔAEC = Area of ΔBCF (Two triangles are similar areas are equal)
Subtract area of ΔBDC on both sides we get,
Area of ΔAEC – Area of ΔBDC = Area of ΔBCF – Area of ΔBDC
Area of quadrilateral ABDE = Area of ΔCDF

Question 10.
In the given figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length ”d” of the segment that is perpendicular to \(\overline { HE }\) and \(\overline { FG }\)?

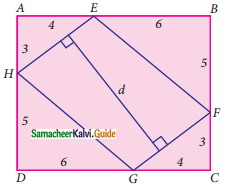
Solution:
In the given figure ABCD is a rectangle and EFGH is a parallelogram.
In the right triangle AEH
HE = \(\sqrt{AH^{2} + AE^{2}}\)
= \(\sqrt{3^{2} + 4^{2}}\)
= \(\sqrt{9 + 16}\)
= \(\sqrt{25}\)
HE = 5
∴ GF = 5 (HE and Gf are opposite sides of a parallelogram)
In the right triangle
GC = \(\sqrt{GF^{2} – FC^{2}}\)
= \(\sqrt{5^{2} – 3^{2}}\)
= \(\sqrt{25 – 9}\)
= \(\sqrt{16}\)
∴ DG = 10 – 6 = 4
Area of ΔAEH + Area of ΔBEF + Area of ΔFCG + Area of ΔHDG
= \(\frac{1}{2}\) × 3 × 4 + \(\frac{1}{2}\) × 6 × 5 + \(\frac{1}{2}\) × 3 × 4 + \(\frac{1}{2}\) × 5 × 6
= (6 + 15 + 6 + 15)
= 42
∴ Area of 4 triangles = 42
Area of the parallelogram = Area of the rectangle ABCD – Area of 4 triangles.
= 10 × 8 – 42
= 80 – 42
= 38
b × h = 38
5 × d = 38
d = \(\frac{38}{5}\)
= 7\(\frac{3}{5}\)
Length of d = 7\(\frac{3}{5}\) or 7.6

Question 11.
In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is \(\frac{9}{8}\) of the area of the parallelogram ABCD.

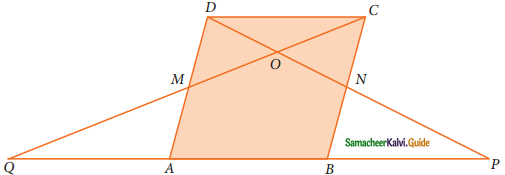
Solution:
Draw OX perpendicular to QP.
In ΔADP, MN = \(\frac{1}{2}\) AP,
In ΔBCQ, MN = \(\frac{1}{2}\) QB
So, AP = BQ (or) AB + BP = AB + QA
∴ PB = QA
∴ QA = AB = BP (or) QP = QA + AB + BP = 3 AB
Area of ΔOQP = \(\frac{1}{2}\) × QP × OX
= \(\frac{1}{2}\) × 3 AB × OX
= \(\frac{3}{2}\) × AB × OX
= \(\frac{3}{2}\) AB (OY + YX)
= \(\frac{3}{2}\) × AB × OY + \(\frac{3}{2}\) × AB × YX (AB = MN)
= \(\frac{3}{2}\) × MN × OY + \(\frac{3}{2}\) × AB × YX
= 3 Area ΔOMN + \(\frac{3}{2}\) + Area ΔBNM
= 3[\(\frac{1}{4}\) area of MNCD] + \(\frac{3}{2}\)[\(\frac{1}{2}\) area of ABCD]
= \(\frac{3}{4}\)[\(\frac{1}{2}\) area of ABCD] + \(\frac{3}{4}\)[area of ABCD]
= \(\frac{3}{8}\) area of ABCD + \(\frac{3}{4}\) area of ABCD
= area of ABCD [\(\frac{3}{8}\) + \(\frac{3}{4}\)]
= area of ABCD (\(\frac{3+6}{8}\))
= \(\frac{9}{8}\) area of ABCD.
Hence it is proved.

Students can download Maths Chapter 4 Geometry Ex 4.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.1

Question 1.
In the figure, AB is parallel to CD, find x.

Solution:
(i) Through T draw TE || AB.

∴ ∠BAT + ∠ATE = 180° (AB || TE)
140° + ∠ATE = 180°
∠ATE = 180°- 140° = 40°
Similarly ∠ETC + ∠TCD = 180° (TE || CD)
∠ETC+150° = 180°
∠ETC = 180°- 150° = 30°
x = ∠ATE + ∠ETC
= 40°+ 30° = 70°
x = 70°

(ii) Draw TE || AB.

∠ABT + ∠ETB = 180° (AB || TE)
48° + ∠ETB = 180°
∠ETB = 180° – 48° = 132°
Similarly ∠CDT + ∠DTE = 180°
24° + ∠DTE = 180°
∴ ∠DTE = 180° – 24°
= 156°
∴ ∠BTE + ∠ETD = 132° + 156°
= 288°
x = 288°

(iii) In the given figure AB || CD, AD is the transversal.
∠CDA = ∠BAD
= 53° (alternate angles are equal)
In ΔECD, ∠D = ∠A = 53° (Alternate angles are equal)
∠E + ∠C + ∠D = 180° (sum of the angles of a triangle)
x° + 38° + 53° = 180°
x° = 180°- 91°
= 89°
x = 89°

Question 2.
The angles of a triangle are in the ratio 1 : 2 : 3, find the measure of each angle of the triangle.
Solution:
The ratio of the angles of a triangle = 1 : 2 : 3.
Let the angles of a triangle be x, 2x and 3x.
x + 2x + 3x = 180° (Total angle of a triangle is 180°)
6x = 180°
x = \(\frac{180°}{6}\)
= 30°
x = 30°; 2x = 2 × 30° = 60°; 3x = 3 × 30° = 90°
Measures of the angles of a triangle = 30°, 60° and 90°.

Question 3.
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent:

(i) In ΔPQR and ΔABC
PQ = AB (Given)
RQ = BC (Given)
ΔABC is not congruent to ΔPQR.
If PR = AC then ΔABC ≅ ΔPQR

(ii) In ΔABD and ΔCDB
AB = CD (Given)
AD = BC (Given)
BD is common
By SSS congruency
ΔABD ≅ ΔCDB

(iii) In ΔPXY and ΔPXZ
PX is common.
XY = XZ (Given)
PY = PZ (Given)
By SSS congruency
ΔPXY ≅ ΔPXZ

(iv) In the given figure BD bisect AC
In ΔAOB and ΔOCD
OA = OC (Given)
∠AOB = ∠DOC (vertically opposite angles)
∠B = ∠D (Given)
By ASA congruency ΔAOB ≅ ΔOCD

(v) In the given figure AC and BD bisect each other at O.
∴ OA = OC (Given); OB = OD (Given)
∠AOB = ∠COD (vertically opposite angles)
By SAS congruency
ΔAOB ≅ ΔOCD

(vi) In the given figure
AB = AC (Given)
BM = MC (AM is the median of the ΔABC)
AM is common (By SSS congruency)
∴ ΔABM ≅ ΔACM

Question 4.
ΔABC and ΔDEF are two triangles in which AB = DF, ∠ACB = 70°, ∠ABC = 60°; ∠DEF = 70° and ∠EDF = 60°. Prove that the triangles are congruent.
Solution:

In ΔABC ∠B = 60° and ∠C = 70°
∴ ∠A = 180° – (60° + 70°)
= 180° – 130°
= 50°
In ΔDEF ∠E = 70° and ∠D = 60°
∠F = 180° – (70° + 60°)
= 180° – 130°
= 50°
∠A = ∠F = 50°
∠B = ∠D = 60°
∠C = ∠E = 70°
By AAA congruency
ΔABC ≅ ΔFDE
(or)
∠B = ∠D = 60°
∠C = ∠E = 70°
AB = FE
By ASA congruency
ΔABC ≅ ΔFDE

Question 5.
Find all the three angles of the ΔABC.

Solution:
∠A + ∠B = ∠ACD (An exterior angle of a triangle is sum of its interior opposite angles)
x + 35 + 2x – 5 = 4x – 15
3x + 30 = 4x – 15
30 + 15 = 4x – 3x
45° = x
∠A = x + 35°
= 45° + 35°
= 80°
∠B = 2x – 5
= 2(45°) – 5°
= 90° – 5°
= 85°
∠ACD = 4x – 15
= 4 (45°) – 15°
= 180° – 15°
= 165°
∠ACB = 180° – ∠ACD
= 180° – 165°
= 15°
∠A = 80°, ∠B = 85° and ∠C = 15°.

Students can download Maths Chapter 3 Algebra Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Additional Questions

I. Multiple choice questions

Question 1.
Which of the following is a monomial?
(a) 4x²
(b) a + b
(c) a + b + c
(d) a + b + c + d
Solution:
(a) 4x²

Question 2.
Which of the following is trinomial?
(a) -7z
(b) z² – 4y²
(c) x²y – xy² + y
(d) 12a – 9ab + 5b – 3
Solution:
(c) x²y – xy² + y

Question 3.
The sum of 5x²; -7x²; 8x²; 11x² and -9x² is ………
(a) 2x²
(b) 4x²
(c) 6x²
(d) 8x²
Solution:
(d) 8x²

Question 4.
The area of a rectangle with length 2l²m and breadth 3lm² is ………
(a) 6l³m³
(b) l³m³
(c) 2l³m³
(d) 4l³m³
Solution:
(a) 6l³m³

Question 5.
The coefficient of x² and x in 2x³ – 5x² + 6x – 3 are respectively ………
(a) 2, -5
(b) 2, 6
(c) – 5, 6
(d) -5, -3
Solution:
(c) – 5, 6

Question 6.
In the system 6x -2y = 3; kx – y = 2 has a unique solution then ………
(a) k = 3
(b) k ≠ 3
(c) k = 4
(d) k ≠ 4
Solution:
(b) k ≠ 3

Question 7.
A system of two linear equation in two variables is inconsistent. If their graphs ………
(a) coincide
(b) intersect only at a point
(c) do not intersect at any point
(d) cut the x-axis
Solution:
(c) do not intersect at any point

Question 8.
The system of equation x – 4y = 8; 3x – 12y = 24 ……….
(a) has infinitely many solution
(b) has no solution
(c) has a unique solution
(d) may or may not have a solution
Solution:
(a) has infinitely many solution

Question 9.
The solution set of x – ay = 4 and x + y = 0 is (1, -1) the value of a is ………
(a) -1
(b) 1
(c) -3
(d) 3
Solution:
(d) 3

Question 10.
The solution set of x + y = 7; x – y = 3 is ………
(a) (-5, -2)
(b) (-5, 2)
(c) (5, 2)
(d) (2, 5)
Solution:
(c) (5, 2)

II. Answer following Questions

Question 1.
What must be added to x⁴ – 3x² + 2x + 6 to get x⁴ – 2x³ – x + 8?
Solution:
Let A be the required number to be added.
(x⁴ – 3x² + 2x + 6) + A = x⁴ – 2x³ – x + 8
A = x⁴ – 2x³ – x + 8 – (x⁴ – 3x² + 2x + 6)
= x⁴ – 2x³ – x + 8 – x⁴ + 3x² – 2x – 6
= -2x³ + 3x² – 3x + 2
Hence -2x³ + 3x² – 3x + 2 must be added.

Question 2.
What must be subtracted to y⁴ + 2y³ – 3y + 8 to get y⁴ – 2y³ + 6?
Solution:
Let A be the required number to be subtracted.
(y⁴ + 2y³ – 3y² + 8) – A = y⁴ – 2y³ + 6
y⁴ + 2y³ – 3y² + 8 – (y⁴ – 2y³ + 6) = A
y⁴ + 2y³ – 3y² + 8 – y⁴ + 2y³ – 6 = A
4y³ – 3y² + 2 = A
Hence 4y³ – 3y² + 2 must be subtracted.

Question 3.
The area of a rectangle is x⁴ + 9x² + 20 sq.units and its length is x² + 4 units. Find its breadth in term of x.
Solution:
Let the breadth of a rectangle be “b”
Length of the rectangle = x² + 4
Area of the rectangle = x⁴ + 9x² + 20
Length × Breadth = x⁴ + 9x² + 20
(x² + 4) × b = x⁴ + 9x² + 20
b = \(\frac{x^{4}+9x^{2}+20}{x^{2}+4}\)
= x² + 5
breadth of a rectangle = x² + 5

Question 4.
Solve 3x + 4y = 24; 20x – 11y = 47 using cross multiplication method.
Solution:
3x + 4y – 24 = 0 → (1)
20x – 11y – 47 = 0 → (2)

\(\frac{x}{-452}\) = \(\frac{1}{-113}\)
-113 = -452
x = \(\frac{452}{113}\)
= 4
But \(\frac{y}{-339}\) = \(\frac{1}{-113}\)
-113y = -339
y = \(\frac{339}{113}\)
= 3
∴ The solution set is (4, 3)

Question 5.
A fraction such that if the numerator is multiplied by 3 and the denominator is reduced by 3, we get \(\frac{18}{11}\), but if the numerator is increased by 8 and the denominator is doubled, we get \(\frac{2}{5}\). Find the fraction.
Solution:
Let the numerator be x and the denominator be y
∴ The fraction is \(\frac{x}{y}\)
According to the given condition
\(\frac{3x}{y-3}\) = \(\frac{18}{11}\)
33x = 18(y – 3)
33x = 18y – 54
33x – 18y – 54 = 0
11x – 6y – 18 = 0 ……. (1)
According to the second condition
\(\frac{x+8}{2y}\) = \(\frac{2}{5}\)
5x + 40 = 4y
5x – 4y + 40 = 0 ……..(2)

∴ The fraction is = \(\frac{12}{25}\)

Question 6.
One number is greater than the thrice the other number by 2. If 4 times the smaller number exceeds the greater by 5, find the number.
Solution:
Let the greater number be x and the smaller number be “y” By the given first condition
x = 3y + 2
x – 3y = 2 ……(1)
Again by the given second condition
4y = x + 5
-x + 4y = 5 …….(2)
Add (1), (2) ⇒ y = 7
Substitute the value of y = 7 in (1)
x – 3(7) = 2
x = 2 + 21
= 23
The greater number is 23 and the smaller number is 7.

Question 7.
The cost of 11 pencils and 3 erasers is Rs 50 and the cost of 8 pencils and 3 erasers is Rs 38. Find the cost of 5 pencils and 5 erasers.
Solution:
Let the cost of a pencil be Rs x and the cost of an eraser be Rs y. According to the first condition.
11x + 3y = 50 …….(1)
According to the second condition
8x + 3y = 38 ……..(2)
(1) – (2) ⇒ 3x = 12
x = \(\frac{12}{3}\)
= 4
Substitute the value of x = 4 in (1)
11 (4) + 3y = 50
3y = 50 – 44
3y = 6
y = \(\frac{6}{3}\)
= 2
Cost of 5 pencils + 5 erasers = 5(4) + 5(2)
= 20 + 10
= 30
The required cost is Rs 30

Students can download Maths Chapter 3 Algebra Ex 3.15 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.15

Multiple Choice Questions.

Question 1.
If x³ + 6x² + kx + 6 is exactly divisible by x + 2, then k = 2
(a) 6
(b) -7
(c) -8
(d) 11
Solution:
(d) 11
Hint:
p(x) = x³ + 6x² + kx + 6
Given p(-2) = 0
(-2)³ + 6(-2)² + k(-2) + 6 = 0
-8 + 24 – 2k + 6 = 0
22 – 2k = 0
k = \(\frac{22}{2}\)
= 11

Question 2.
The root of the polynomial equation 2x + 3 = 0 is…….
(a) \(\frac{1}{3}\)
(b) –\(\frac{1}{3}\)
(c) –\(\frac{3}{2}\)
(d) –\(\frac{2}{3}\)
Solution:
(c) –\(\frac{3}{2}\)
Hint:
2x + 3 = 0
2x = – 3 ⇒ x = –\(\frac{3}{2}\)

Question 3.
The type of the polynomial 4 – 3x³ is ……..
(a) constant polynomial
(b) linear polynomial
(c) quadratic polynomial
(d) cubic polynomial
Solution:
(d) cubic polynomial

Question 4.
If x⁵¹ + 51 is divided by x + 1, then the remainder is …….
(a) 0
(b) 1
(c) 49
(d) 50
Solution:
(d) 50
Hint:
p(x) = x⁵¹ + 51
p(-1)= (-1)⁵¹ + 51
= -1 + 51
= 50

Question 5.
The zero of the polynomial 2x + 5 is ……..
(a) \(\frac{5}{2}\)
(b) –\(\frac{5}{2}\)
(c) \(\frac{2}{5}\)
(d) –\(\frac{2}{5}\)
Solution:
(b) –\(\frac{5}{2}\)
Hint:
2x + 5 = 0 ⇒ 2x = -5 ⇒ x = –\(\frac{5}{2}\)

Question 6.
The sum of the polynomials p(x) = x³ – x² – 2, q(x) = x² – 3x + 1
(a) x³ – 3x – 1
(b) x³ + 2x² – 1
(c) x³ – 2x² – 3x
(d) x³ – 2x² + 3x – 1
Solution:
(a) x³ – 3x – 1
Hint:
p(x) + q(x) = (x³ – x² – 2) + (x² – 3x + 1) = x³ – x² – 2 + x² – 3x + 1
= x³ – 3x – 1

Question 7.
Degree of the polynomial (y³ – 2) (y³ + 1) is
(a) 9
(b) 2
(c) 3
(d) 6
Solution:
(d) 6
(y³ – 2) (y³ + 1) = y⁶ + y³ – 2y³ – 2
= y⁶ – y³ – 2

Question 8.
Let the polynomials be
(A) -13q⁵ + 4q² + 12q
(B) (x² + 4)(x² + 9)
(C) 4q⁸ – q⁶ + q²
(D) –\(\frac{5}{7}\) y¹² + y³ + y⁵.
Then ascending order of their degree is
(a) A, B, D, C
(b) A, B, C, D
(c) B, C, D, A
(d) B, A, C, D
Solution:
(d) B, A, C, D

Question 9.
If p(a) = 0 then (x – a) is a …….. of p(x)
(a) divisor
(b) quotient
(c) remainder
(d) factor
Solution:
(d) factor

Question 10.
Zeros of (2 – 3x) is ……..
(a) 3
(b) 2
(c) \(\frac{2}{3}\)
(d) \(\frac{3}{2}\)
Solution:
(c) \(\frac{2}{3}\)

Question 11.
Which of the following has x -1 as a factor?
(a) 2x – 1
(b) 3x – 3
(c) 4x – 3
(d) 3x – 4
Solution:
(b) 3x – 3

Question 12.
If x – 3 is a factor of p(x), then the remainder is ……..
(a) 3
(b) -3
(c) p(3)
(d) p(-3)
Solution:
(c) p(3)

Question 13.
(x +y)(x² – xy + y²) is equal to ……..
(a) (x + y)³
(b) (x – y)³
(c) x³ + y³
(d) x³ – y³
Solution:
(c) x³ + y³

Question 14.
(a + b – c)² is equal to ……..
(a) (a – b + c)²
(b) (-a – b + c)²
(c) (a + b + c)²
(d) (a – b – c)²
Solution:
(b) (-a – b + c)²
Hint:
(a + b – c)² = a² + b² + c² + 2ab – 2bc – 2ac
(- a – b + c)² = a² + b² + c² + 2ab – 2bc – 2ac
(OR)
(- a – b + c)² = (-1)² (a + b + c)² (taking – 1 as common)
= (a + b – c)²

Question 15.
In an expression ax² + bx + c the sum and product of the factors respectively ……..
(a) a, bc
(b) b, ac
(c) ac, b
(d) bc, a
Solution:
(b) b, ac

Question 16.
If (x + 5) and (x – 3) are the factors of ax² + bx + c, then values of a, b and c are ………
(a) 1, 2, 3
(b) 1, 2, 15
(c) 1, 2, -15
(d) 1, -2, 15
Solution:
(c) 1, 2, -15
Hint:
(x + 5) (x – 3) = x² + (5 – 3) x + (5) (-3)
= x² + 2x – 15
compare with ax² + bx + c
a = 1, b = 2 and c = -15

Question 17.
Cubic polynomial may have maximum of ……… linear factors.
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(c) 3

Question 18.
Degree of the constant polynomial is ……..
(a) 3
(b) 2
(c) 1
(d) 0
Solution:
(d) 0

Question 19.
Find the value of m from the equation 2x + 3y = m. If its one solution is x = 2 and y = -2.
(a) 2
(b) -2
(c) 10
(d) 0
Solution:
(b) – 2
Hint:
The equation is 2x + 3y = m
Substitute x – 2 and y = -2 we get
2(2) + 3(-2) = m ⇒ 4 – 6 = m ⇒ -2 = m

Question 20.
Which of the following is a linear equation?
(a) x + \(\frac{1}{2}\) = 2
(b) x (x – 1) = 2
(c) 3x + 5 = \(\frac{2}{3}\)
(d) x³ – x = 5
Solution:
(c) 3x + 5 = \(\frac{2}{3}\)

Question 21.
Which of the following is a solution of the equation 2x – y = 6?
(a) (2, 4)
(b) (4, 2)
(c) (3, -1)
(d) (0, 6)
Solution:
(b) (4, 2)
Hint:
2x – y = 6
Substitute x – 4 and y = 2 we get
2(4) – 2 = 6 ⇒ 8 – 2 = 6 ⇒ 6 = 6
∴ (4, 2) is the solution

Question 22.
If (2, 3) is a solution of linear equation 2x + 3y = k then, the value of k is ……..
(a) 12
(b) 6
(c) 0
(d) 13
Solution:
(d) 13
Hint:
The equation is 2x + 3y = k
Substitute x = 2 and y = 3 we get,
2(2) + 3(3) = k ⇒ 4 + 9 = k ⇒ 13 = k

Question 23.
Which condition does not satisfy the linear equation ax + by + c = 0 ……..
(a) a ≠ 0, b = 0
(b) a = 0, b ≠ 0
(c) a = 0, b = 0, c ≠ 0
(d) a ≠ 0, b ≠ 0
Solution:
(c) a = 0, b = 0, c ≠ 0

Question 24.
Which of the following is not a linear equation in two variable?
(a) ax + by + c = 0
(b) 0x + 0y + c = 0
(c) 0x + by + c = 0
(d) ax + 0y + c = 0
Solution:
(b) 0x + 0y + c = 0
Hint:
0x + 0y + c = 0
0 + 0 + c = 0 ⇒ c = 0
There is no variable.
∴ It is not a linear equation

Question 25.
The value of k for which the pair of linear equations 4x + 6y – 1 = 0 and 2x + ky – 1 = 0 represents parallel lines is ……..
(a) k = 3
(b) k = 2
(c) k = 4
(d) k = -3
Solution:
(a) k = 3
Hint:
Slope of 4x + 6y – 1 = 0 is
6y = -4x + 1 ⇒ y = \(\frac{-4}{6}\) x + \(\frac{1}{6}\)
Slope = \(\frac{-4}{6}\) = \(\frac{-2}{3}\)
Slope of 2x + ky – 7 = 0
ky = -2x + 7
y = \(\frac{-2}{k}\)x + \(\frac{7}{k}\)
Slope of a line = \(\frac{-2}{k}\)
Since the lines are parallel
\(\frac{-2}{3}\) = \(\frac{-2}{k}\)
-2k = – 6
k = \(\frac{6}{2}\)
= 3

Question 26.
A pair of linear equations has no solution then the graphical representation is ……..

Solution:

Hint:
Since there is no solution the two lines are parallel. (l11m)

Question 27.
If \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\) where a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 then the given pair of linear equation has …….. solution(s).
(a) no solution
(b) two solutions
(c) unique
(d) infinite
Solution:
(c) unique
Hint:
Since it has unique solution
\(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\)

Question 28.
\(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\) where a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 then the given pair of linear equation has …….. solution(s).
(a) no solution
(b) two solutions
(c) infinite
(d) unique
Solution:
(a) no solution
Hint:
\(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\) the linear equation has no solution.

Question 29.
GCD of any two prime numbers is …….
(a) -1
(b) 0
(c) 1
(d) 2
Solution:
(c) 1

Question 30.
The GCD of x⁴ – y⁴ and x² – y² is ……..
(a) x⁴ – y⁴
(b) x² – y²
(c) (x + y)²
(d) (x + y)⁴
Solution:
(b) x² – y²
Hint:
x⁴ – y⁴ = (x²)² – (y²)²
= (x² + y²)(x² – y²)
x² – y² = (x² – y²)
G.C.D. = x² – y²

Students can download Maths Chapter 3 Algebra Ex 3.14 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.14

Question 1.
The sum of a two digit number and the number formed by interchanging the digits is 110. If 10 is subtracted from the first number, the new number is 4 more than 5 times the sums of the digits of the first number. Find the first number.
Solution:
Let the ten’s digit be x and the unit digit be y.
The number is 10x + y
If the digits are interchanged
The new number is 10y + x
By the given first condition
10x + y + 10y + x = 110
11x + 11y = 110
x + y = 10 → (1) (Divided by 11)
Again by the given second condition
10x + y – 10 = 5(x + y ) + 4
10x + y – 10 = 5x + 5y + 4
5x – 4y = 14 → (2)
(1) × 5 ⇒ 5x + 5y = 50 → (3)
(2) × 1 ⇒ 5x – 4y = 14 → (2)
(3) – (2) ⇒ 9y = 36
y = 36/9
= 4
Substitute the value of y = 4 in (1)
x + y = 10
x + 4 = 10
x = 10 – 4
= 6
∴ The number is (10 × 6 + 4) = 64

Question 2.
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes \(\frac{1}{2}\). Find the fraction.
Solution:
Let the numerator be “x” and the denominator be “y”
∴ The fraction is \(\frac{x}{y}\)
By the given first condition
x + y = 12 → (1)
Again by the second condition
\(\frac{x}{y+3}\) = \(\frac{1}{2}\)
2x = y + 3
2x – y = 3 → (2)
(1) + (2) ⇒ 3x = 15
x = \(\frac{15}{3}\) = 5
Substitute the value of x = 5 in (1)
5 + y = 12
y = 12 – 5
= 7
∴ The fraction is \(\frac{5}{7}\)

Question 3.
ABCD is a cyclic quadrilateral such that ∠A = (4y + 20)°, ∠B = (3y -5)°, ∠C = (4x)° and ∠D = (7x + 5)°. Find the four angles.
Solution:

ABCD is a cyclic quadrilateral ∠A + ∠C = 180°
(Sum of the opposite angles of a cyclic quadrilateral is 180°)
(4y + 20)° + (4x)° = 180°
4y + 20 + 4x = 180
4x + 4y = 180 – 20
4x + 4y = 160
x + y = 40 → (1) (divided by 4)
∠B + ∠D = 180° (Sum of the opposite angles of a cyclic quadrilateral)
(3y – 5)° + (7x + 5)° = 180°
3y – 5 + 7x + 5 = 180
7x + 3y = 180 → (2)
(1) × 3 ⇒ 3x + 3y = 120 → (3)
(3) – (2) ⇒ -4x = – 60
4x = 60
x = \(\frac{60}{4}\)
Substitute the value of x = 15 in (1)
15 + y = 40
y = 40 – 15 = 25
∠A = 4y + 20 = 4(25) + 20 = 100 + 20 = 120°
∴ ∠A = 120°
∠B = 3y – 5 = 3(25) – 5 = 75 – 5 = 70
∴ ∠B = 70°
∠C = 4x = 4(15) = 60
∴ ∠C = 60°
∠D = 7x + 5 = 7(15) + 5
∠D = 105 + 5 = 110°
∴ ∠A= 120°, ∠B = 70°, ∠C = 60° and ∠D = 110°

Question 4.
On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gains Rs 2000. But if he sells the T.V. at 10% gain and the fridge at 5% loss, he gains Rs.1500 on the transaction. Find the actual price of the T.V. and the fridge.
Solution:
Let the cost price of the TV be Rs “x” and the cost price of the fridge be Rs “y”.
By the given condition

Multiply by 20
x + 2y = 40000 → (1)
Again by the given second condition

Multiply by 20
2x – y = 30000 → (2)
(2) × 2 ⇒ 4x – 2y = 60000 → (3)
(1) + (3) ⇒ 5x + 0 = 100000
x = \(\frac{100000}{5}\)
= 20000
Substitute the value of x = 20000 in (1)
20000 + 2y = 40000
2y = 40000 – 20000
= 20000
y = \(\frac{20000}{2}\)
= 10000
Cost price of a TV = Rs 20,000
Cost price of a fridge = Rs 10,000

Question 5.
Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5. Find the numbers.
Solution:
Let the two numbers be x and y.
By the given first condition
x : y = 5 : 6
6x = 5y (Product of the extreme is equal to the product of the means)
6x – 5y = 0 → (1)
Again by the given second condition
x – 8 : y – 8 = 4 : 5
5(x – 8) = 4(y – 8)
5x – 40 = 4y – 32
5x – 4y = – 32 + 40
5x – 4y = 8 → (2)
(1) × 4 ⇒ 24x – 20y = 0 → (3)
(2) × 5 ⇒ 25x – 20y = 40 → (4)
(3) – (4) ⇒ – x + 0 = -40
∴ x = 40
Substitute the value of x = 40 in (1)
6(40) – 5y = 0
240 – 5y = 0 ⇒ – 5y = -240
5y = 240
y = \(\frac{240}{5}\)
= 48
The two numbers are 40 and 48 [∴ The ratio of the number = 40 : 48 are 5 : 6]

Question 6.
4 Indians and 4 Chinese can do a piece of work in 3 days. While 2 Indian and 5 Chinese can finish it in 4 days. How long would it take for 1 Indian to do it? How long would it ‘ take for 1 Chinese to do it?
Solution:
Let the time taken by a Indian be “x”
Time taken by a Chinese be “y”
Work done by a Indian in one day = \(\frac{1}{x}\)
Work done by a Chinese in one day = \(\frac{1}{y}\)
By the given first condition
(4 Indian + 4 Chinese) finish the work in 3 days
\(\frac{4}{x}\) + \(\frac{4}{y}\) = \(\frac{1}{3}\) → (1)
Again by the given second condition
(2 Indian + 5 Chinese) finish the work in 4 days
\(\frac{2}{x}\) + \(\frac{5}{y}\) = \(\frac{1}{4}\) → (2)
Solve the equation (1) and (2)
Let \(\frac{1}{x}\) = a; \(\frac{1}{y}\) = b
4a + 4b = \(\frac{1}{3}\)
12a + 12b = 1 → (3) (Multiply by 3)
2a + 5b = \(\frac{1}{4}\)
8a + 20b = 1 → (4) (Multiply by 4)
(3) × (2) ⇒ 24a + 24b = 2 → (5)
(4) × (3) ⇒ 24a + 60b = 3 → (6)
(5) – (6) ⇒ -36b = -1
b = \(\frac{1}{36}\)
Substitute the value of b = \(\frac{1}{36}\) in (3)
12a + 12(\(\frac{1}{36}\)) = 1
12a + \(\frac{1}{3}\) = 1
36a + 1 = 3
36a = 2
a = \(\frac{2}{36}\) = \(\frac{1}{18}\)
But \(\frac{1}{x}\) = a ⇒ \(\frac{1}{x}\) = \(\frac{1}{18}\)
x = 18
\(\frac{1}{y}\) = b ⇒ \(\frac{1}{y}\) = \(\frac{1}{36}\)
y = 36
∴ Time taken by a 1 Indian is 18 days
Time taken by a 1 Chinese is 36 days

Students can download Maths Chapter 2 Real Numbers Ex 2.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.3

Question 1.
Represent the following irrational numbers on the number line.
(i) \(\sqrt{3}\)
Solution:

Steps of construction:
1. Draw a line and mark a point A and B such that AB = 3 cm.
2. Mark a point C on this line such that BC = 1 cm.
3. Find the mid point of AC by drawing perpendicular bisector of AC and let it be “O”.
4. With O as centre and OC = OA as radius draw a semicircle.
5. Draw a line BD, which is perpendicular to AB at B.
6. Now BD = \(\sqrt{3}\) which can be marked in the number line as the value of BE = BD = \(\sqrt{3}\)

(ii) Represent \(\sqrt{4.7}\) on a number line.
Solution:

Steps of construction:
1. Draw a line and mark a point A and B such that AB = 4.7 cm.
2. Mark a point C on this line such that A BC = 1 cm.
3. Find the mid point of AC by drawing perpendicular bisector of AC and let it be “O”.
4. With O as centre and OC = OA as radius draw a semicircle.
5. Draw a line BD, which is perpendicular to AB at B.
6. Now BD = \(\sqrt{4.7}\), which can be marked in the number line as the value of BE = BD = \(\sqrt{4.7}\).

(iii) Represent \(\sqrt{6.5}\) on a number line.
Solution:

Steps of construction:
1. Draw a line and mark a point A and B such that AB = 6.5 cm.
2. Mark a point C on this line such that BC = 1 cm.
3. Find the mid point of AC by drawing perpendicular bisector of AC and let it be “O”.
4. With O as centre and OC = OA as radius draw a semicircle.
5. Draw a line BD, which is perpendicular to AB at B.
6. Now BD = \(\sqrt{6.5}\), which can be marked in the number line as the value of BE = BD = \(\sqrt{6.5}\)

Question 2.
Find any two irrational numbers between
(i) 0.3010011000111…. and 0.3020020002….
Solution:
Two irrational numbers between the given two rational numbers are 0.301202200222……. and 0.301303300333……..

(ii) \(\frac{6}{7}\) and \(\frac{12}{13}\)
Solution:
\(\frac{6}{7}\) = 0.\(\overline {857142}\)
\(\frac{12}{13}\) = 0.\(\overline {923076}\)
The two irrational numbers are 0.8616611666111…….. and 0.8717711777111………

(iii) \(\sqrt{2}\) and \(\sqrt{3}\)
Solution:

\(\sqrt{2}\) = 1.414
\(\sqrt{3}\) = 1.732
The two irrational numbers between \(\sqrt{2}\) and \(\sqrt{3}\) are 1.515511555……. and 1.616611666………..

Question 3.
Find any two rational numbers between 2.2360679……… and 2.236505500……….
Solution:
The two rational numbers are 2.2362 and 2.2363 (It has many answers)

Students can download Maths Chapter 2 Real Numbers Ex 2.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.2

Question 1.
Express the following rational numbers into decimal and state the kind of decimal expression.
(i) \(\frac{2}{7}\)
(ii) -5\(\frac{3}{11}\)
(iii) \(\frac{22}{3}\)
(iv) \(\frac{327}{200}\)
Solution:

(i) \(\frac{2}{7}\) = 0.2857142….
= 0.\(\overline {285714}\)
Non-terminating and recurring decimal expansion.

(ii) -5\(\frac{3}{11}\) = -5 + 0.272 = -5.272……..

= -5.\(\overline {27}\)
Non-terminating and recurring decimal expansion.

(iii) \(\frac{22}{3}\) = 7.333……..

= 7.\(\overline {3}\)
Non-terminating and recurring decimal expansion.

(iv) \(\frac{327}{200}\) = \(\frac{327}{2×100}\)

= \(\frac{3.27}{2}\)
= 1.635
Terminating decimal expansion.

Question 2.
Express \(\frac{1}{13}\) in decimal form. Find the length of the period of decimals.
Solution:

\(\frac{1}{13}\) = 0.07692307
= 0.\(\overline {076923}\)
Length of the period of decimal is 6.

Question 3.
Express the rational number \(\frac{1}{33}\) in recurring decimal form by using the recurring decimal expansion of \(\frac{1}{11}\). Hence write \(\frac{71}{33}\) in recurring decimal form.
Solution:

\(\frac{1}{11}\) = 0.0909……… = 0.\(\overline {09}\)
∴ \(\frac{1}{33}\) = \(\frac{1}{3}\) × \(\frac{1}{11}\)
= \(\frac{1}{3}\) × 0.0909 ……..
= 0.0303 …… = 0.\(\overline {03}\)
\(\frac{71}{33}\) = 2\(\frac{5}{33}\) = 2 + \(\frac{5}{33}\) = 2 + 5 × \(\frac{1}{33}\)
= 2 + 5 × 0.\(\overline {03}\)
2 + (5 × 0.030303 ……..)
2 + 0.151515 ………
2+ 0.\(\overline {15}\)
2.\(\overline {15}\)

Question 4.
Express the following decimal expression into rational numbers.
(i) 0.24
Solution:
Let x = 0.242424 ………. →(1)
100 x = 24.2424 ……… →(2)
(2) – (1) ⇒ 100 x – x = 24.2424 ……….. (-)
 0.2424 ……..
99 x = 24.0000
x = \(\frac{24}{99}\)
(or)
\(\frac{8}{33}\)

(ii) 2.327
Solution:
Let x = 2.327327327 ………. →(1)
1000 x = 2327.327327 ……… →(2)
(2) – (1) ⇒ 1000 x – x = 2327.327327 ……….. (-)
  2.327327 ……..
999 x = 2325.000
x = \(\frac{2325}{999}\)
(or)
\(\frac{775}{333}\)

(iii) – 5.132
Solution:
– 5.132 = -5 + \(\frac{1}{10}\) + \(\frac{3}{100}\) + \(\frac{2}{1000}\)
= \(\frac{-5000 + 100 +30 + 2}{1000}\) = \(\frac{-4868}{1000}\)
(or)
\(\frac{-1217}{250}\)

(iv) 3.17
Solution:
Let x = 3.1777 ………. →(1)
10 x = 31.777 ……… →(2)
100 x = 317.77 …….. →(3)
(3) – (2) ⇒ 100 x – 10 x = 317.77 ……….. (-)
 31.777 ……..
90 x = 286.000
x = \(\frac{286}{90}\)
(or)
\(\frac{143}{45}\)

(v) 17.215
Solution:
Let x = 17.2151515 ………. →(1)
10 x = 172.151515 ……… →(2)
100 x = 17215.1515 …….. →(3)
(3) – (2) ⇒ 1000 x – 10 x = 17215.1515 ……….. (-)
 17215.1515 ……..
990 x = 17043
x = \(\frac{17043}{990}\)
(or)
\(\frac{5681}{330}\)

(vi) -21.2137
Solution:
Let x = -21.213777 ………. →(1)
1000 x = -21213.777 ……… →(2)
100 x = -212137.77 …….. →(3)
(3) – (2) ⇒ 10000 x – 1000 x = -21213.777 ……….. (-)
-21213.777 ……..
9000 x = -190924
x = \(\frac{-190924}{9000}\)
(or)
\(\frac{-47731}{2250}\)

Question 5.
Without actual division, find which of the following rational numbers have terminating decimal expression.
(i) \(\frac{7}{128}\)
Solution:

\(\frac{7}{128}\) = \(\frac{7}{2^{7}}\)
∴ \(\frac{7}{128}\) has terminating decimal expression.

(ii) \(\frac{21}{15}\)
Solution:
\(\frac{21}{15}\) = \(\frac{7}{5}\) = \(\frac{7}{5^1}\)
\(\frac{21}{15}\) has terminating decimal expression.

(iii) 4\(\frac{9}{35}\)
Solution:
4\(\frac{9}{35}\) = \(\frac{149}{35}\)
4\(\frac{149}{5×7}\) (It is not in the form of \(\frac{P}{2^{m} × 5^{n}}\)
∴ 4\(\frac{9}{35}\) has non-terminating recurring decimal expression.

(iv) \(\frac{219}{2200}\)
Solution:

\(\frac{219}{2200}\) = \(\frac{219}{2^{3} × 5^{2} × 11}\) (It is not in the form of \(\frac{P}{2^{m} × 5^{n}}\)
∴ \(\frac{219}{2200}\) has non-terminating recurring decimal expression.

Students can download Maths Chapter 2 Real Numbers Ex 2.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.1

Question 1.
Which arrow best shows the position of \(\frac{11}{3}\) on the number line?

Solution:
D represent \(\frac{11}{3}\) on the number line.

Question 2.
Find any three rational numbers between \(\frac{-7}{11}\) and \(\frac{2}{11}\)
Solution:
Three rational numbers between \(\frac{-7}{11}\) and \(\frac{2}{11}\)
\(\frac{-6}{11}\), \(\frac{-5}{11}\), \(\frac{-4}{11}\), ……… \(\frac{1}{11}\)

Question 3.
Find any five rational numbers between
(i) \(\frac{1}{4}\) and \(\frac{1}{5}\)
Solution:
Converting the given rational numbers with the same denominators.
\(\frac{1}{4}\) = \(\frac{1×30}{4×30}\) = \(\frac{30}{120}\)
\(\frac{1}{5}\) = \(\frac{1×24}{5×24}\) = \(\frac{24}{120}\)
Five rational numbers between \(\frac{30}{120}\) and \(\frac{24}{120}\) are \(\frac{25}{120}\), \(\frac{26}{120}\), \(\frac{27}{120}\), \(\frac{28}{120}\) and \(\frac{29}{120}\)
Five rational numbers between \(\frac{1}{4}\) and \(\frac{1}{5}\) are \(\frac{25}{120}\), \(\frac{26}{120}\), \(\frac{27}{120}\), \(\frac{28}{120}\) and \(\frac{29}{120}\)
Other Method:
A rational numbers between \(\frac{1}{4}\) and \(\frac{1}{5}\) = \(\frac{1}{2}\)(\(\frac{1}{4}\)+\(\frac{1}{5}\)) = \(\frac{1}{2}\)(\(\frac{5+4}{20}\)) = \(\frac{1}{2}\) × \(\frac{9}{20}\) = \(\frac{9}{40}\)
A rational numbers between \(\frac{1}{4}\) and \(\frac{9}{40}\) = \(\frac{1}{2}\)(\(\frac{1}{4}\)+\(\frac{9}{40}\)) = \(\frac{1}{2}\)(\(\frac{10+9}{40}\)) = \(\frac{19}{80}\)
A rational numbers between \(\frac{1}{4}\) and \(\frac{19}{80}\) = \(\frac{1}{2}\)(\(\frac{1}{4}\)+\(\frac{19}{20}\)) = \(\frac{1}{2}\)(\(\frac{20+19}{80}\)) = \(\frac{39}{160}\)
A rational numbers between \(\frac{1}{4}\) and \(\frac{39}{160}\) = \(\frac{1}{2}\)(\(\frac{1}{4}\)+\(\frac{39}{160}\)) = \(\frac{1}{2}\)(\(\frac{40+39}{160}\)) = \(\frac{79}{320}\)
A rational numbers between \(\frac{1}{4}\) and \(\frac{79}{320}\) = \(\frac{1}{2}\)(\(\frac{1}{4}\)+\(\frac{79}{320}\)) = \(\frac{1}{2}\)(\(\frac{80+79}{320}\)) = \(\frac{159}{640}\)
∴ Five rational numbers are between \(\frac{9}{40}\), \(\frac{19}{80}\), \(\frac{39}{160}\), \(\frac{79}{320}\) and \(\frac{159}{640}\)

(ii) 0.1 and 0.11
Solution:
\(\frac{1×100}{10×100}\) = \(\frac{100}{1000}\)
\(\frac{11×10}{100×10}\) = \(\frac{110}{1000}\)
The five rational numbers are \(\frac{101}{1000}\), \(\frac{102}{1000}\), \(\frac{103}{1000}\), \(\frac{104}{1000}\), \(\frac{105}{1000}\), …….. (or)
The five rational numbers are 0.101, 0.102, 0.103, 0.104 and 0.105.

(iii) -1 and -2
Solution:
Converting to rational numbers, – 1 = \(-\frac{10}{11}\) and – 2 = \(-\frac{20}{10}\)
So five rational numbers between -2 and -1 are \(-\frac{11}{10}\), \(-\frac{12}{10}\), \(-\frac{13}{10}\), \(-\frac{14}{10}\), \(-\frac{15}{10}\).
Other Method:
A rational number between -1 and -2 = \(\frac{1}{2}\)[-1-2] = \(\frac{1}{2}\)[-3] = \(-\frac{3}{2}\)
A rational number between -1 and \(-\frac{3}{2}\) = \(\frac{1}{2}\)[-1 – \(\frac{3}{2}\)] = \(\frac{1}{2}\)(\(\frac{-2-3}{2}\)) = \(-\frac{5}{4}\)
A rational number between -1 and \(-\frac{5}{4}\) = \(\frac{1}{2}\)[-1 – \(\frac{5}{4}\)] = \(\frac{1}{2}\)(\(\frac{-4-5}{4}\)) = \(-\frac{9}{8}\)
A rational number between -1 and \(-\frac{9}{8}\) = \(\frac{1}{2}\)[-1 – \(\frac{9}{8}\)] = \(\frac{1}{2}\)(\(\frac{-8-9}{8}\)) = \(-\frac{17}{16}\)
A rational number between -1 and \(-\frac{17}{16}\) = \(\frac{1}{2}\)[1 – \(\frac{17}{16}\)] = \(\frac{1}{2}\)(\(\frac{-16-17}{16}\)) = \(\frac{1}{2}\) (\(\frac{-33}{16}\)) = \(\frac{-33}{32}\)
The five rational numbers are \(-\frac{3}{2}\), \(-\frac{5}{4}\), \(-\frac{9}{8}\), \(-\frac{17}{16}\), and \(\frac{-33}{32}\)

Students can download Maths Chapter 2 Real Numbers Ex 2.5 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.5

Question 1.
Write the following in the form of \(5^n\):
(i) 625
(ii) \(\frac{1}{5}\)
(iii) \(\sqrt{5}\)
(iv) \(\sqrt{125}\)
Solution:
(i) 625 = 5⁴

(ii) \(\frac{1}{5}\) = 5^-1
(iii) \(\sqrt{5}\) = \(5^\frac{1}{2}\)
(iv) \(\sqrt{125}\) = \(\sqrt{5^3}\) = \((5^3)^\frac{1}{2} = 5^\frac{3}{2}\)

Question 2.
Write the following in the form of \(4^n\):
(i) 16
(ii) 8
(iii) 32
Solution:
(i) 16
= 4 × 4
= 4²

(ii) 8
= 4 × 2
= 4 × \(\left(2^{2}\right)^{\frac{1}{2}} \)
= 4 \(\times 4^{\frac{1}{2}} \)
= 4\(^{1+\frac{1}{2}} \)
= 4\(^{\frac{2+1}{2}} \)
= 4\(^{3 / 2}\)

(iii) 32
= 4 × 4 × 2
= 4² × \(\left(2^{2}\right)^{\frac{1}{2}} \)
= 4\(^{2} \times 4^{\frac{1}{2}} \)
= 4\(^{2+\frac{1}{2}} \)
= 4\(^{\frac{4+1}{2}} \)
= 4\(^{\frac{5}{2}} \)

Question 3.
Find the value of
(i) (49)\(^\frac{1}{2}\)
(ii) (243)\(^\frac{2}{5}\)
(iii) (9)\(^\frac{-3}{2}\)
(iv) \((\frac{64}{125})^\frac{-2}{3}\)
Solution:
(i) 49\(^\frac{1}{2}\) = \((7^2)^\frac{1}{2}\) = 7\(^{2 × \frac{1}{2}}\) = 7
(ii) (243)\(^\frac{2}{5}\) = \((3^5)^\frac{2}{5}\) = 3\(^{5 × \frac{2}{5}}\) = 3² = 9

(iii) \(9^{\frac{-3}{2}}=\left(3^{2}\right)^{\frac{-3}{2}}=3^{2 \times \frac{-3}{2}}=3^{-3}=\frac{1}{3^{3}}=\frac{1}{27}\)
(iv) \(\left(\frac{64}{125}\right)^{\frac{-2}{3}}=\left(\frac{4^{3}}{5^{3}}\right)^{\frac{-2}{3}}=\left[\left(\frac{4}{5}\right)^{3}\right]^{\frac{-2}{3}}=\left(\frac{4}{5}\right)^{3 \times \frac{-2}{3}}=\left(\frac{4}{5}\right)^{-2}=\frac{4^{-2}}{5^{-2}}=\frac{5^{2}}{4^{2}}=\frac{25}{16} \)

Question 4.
Use a fractional index to write:
(i) \(\sqrt{5}\)
(ii) \(\sqrt[2]{7}\)
(iii) (\(\sqrt[3]{49})^{5}\)
(iv) \((\frac{1}{\sqrt[3]{100}})^{7}\)
Solution:
(i) \(\sqrt{5}\) = (5)\(^\frac{1}{2}\)
(ii) \(\sqrt[2]{7}\) = 7\(^\frac{1}{2}\)
(iii) \((\sqrt[3]{49})^{5}=\left[(49)^{\frac{1}{3}}\right]^{5}=\left[\left(7^{2}\right)^{\frac{1}{3}}\right]^{5}=\left(7^{\frac{2}{3}}\right)^{5}=7^{\frac{2}{3} \times 5}=7^{\frac{10}{3}}\)
(iv) \(\left(\frac{1}{\sqrt[3]{100}}\right)^{7}=\left[\frac{1}{\sqrt[3]{10^{2}}}\right]^{7}=\left[\frac{1}{\left(10^{2}\right)^{1 / 3}}\right]^{7}=\left[\frac{1}{10^{2 / 3}}\right]^{7}=\left(10^{\frac{-2}{3}}\right)^{7}=10^{\frac{-2}{3} \times 7}=10^{\frac{-14}{3}}\)

Question 5.
Find the 5th root of:
(i) 32
(ii) 243
(iii) 100000
(iv) \(\frac{1024}{3125}\)
Solution:
(i) \(\sqrt[5]{32}=(32)^{\frac{1}{5}}=\left(2^{5}\right)^{\frac{1}{5}}=2^{5 \times \frac{1}{5}} \) = 2

(ii) \(\sqrt[5]{243}=(243)^{\frac{1}{5}}=\left(3^{5}\right)^{\frac{1}{5}}=3^{5 \times \frac{1}{5}}\) = 3

(iii) \(\sqrt[5]{100000}=(100000)^{\frac{1}{5}}=\left(10^{5}\right)^{\frac{1}{5}}\)
= \(10^{5}\times{\frac{1}{5}}\)

Students can download Maths Chapter 2 Real Numbers Ex 2.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.4

Question 1.
Represent the following numbers on the number line.
(i) 5.348
Solution:
5.348 lies between 5 and 6.

Steps of construction:
1. Divide the distance between 5 and 6 into 10 equal intervals.
2. Mark the point 5.3 which is the sixth from the left of 6 and 3 from the right of 5.
3. 5.34 lies between 5.3 and 5.4. Divide the distance into 10 equal intervals.
4. Mark the point 5.34 which is sixth from the left of 5.40
5. 5.348 lies between 5.34 and 5.35. Divide the distance into 10 equal intervals.
6. Mark a point 5.348 which is second from the left of 5.350 and seventh form the right of 5.340

(ii) 6.\(\overline {4}\) upto 3 decimal places.
Solution:
6.\(\overline {4}\) = 6.4444
6.\(\overline {4}\) = 6.444 (correct to 3 decimal places)
The number lies between 6 and 7.

Steps of construction:
1. Divide the distance between 6 and 7 into 10 equal intervals.
2. Mark the point 6.4 which is the sixth from the left of 7 and fourth from the right of 6.
3. 6.44 lies between 6.44 and 6.45. Divide the distance into 10 equal intervals.
4. Mark the point 6.44 which is sixth from the left of 6.5 and fourth from the right of 6.40.
5. Mark the point 6.444 which is sixth from the left of 6.450 and fourth from the right of 6.440.

(ii) 4.\(\overline {73}\) upto 4 decimal places.
Solution:
4.\(\overline {73}\) = 4.737373……..
= 4.737374 (correct to 4 decimal places 4.7374 lies between 4 and 5)

Steps of construction:
1. Divide the distance between 4 and 5 into 10 equal parts.
2. Mark the point 4.7 which is third from the left of 5 and seventh from the right of 4.
3. 4.73 lies between 4.7 and 4.8. Divide the distance into 10 equal intervals.
4. Mark the point 4.73 which is seventh from the left of 4.80 and third from the left of 4.70.
5. 4.737 lies between 4.73 and 4.74. Divide the distance into 10 equal intervals.
6. Mark the point 4.737 which is third from the left of 4.740 and seventh from the right of 4.730.
7. 4.7374 lies between 4.737 and 4.738. Divide the distance into 10 equal intervals.
8. Mark the point 4.7374 which is sixth from the left of 4.7380 and fourth from the right of 4.7370.