Students can download Maths Chapter 3 Algebra Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Additional Questions
I. Multiple choice questions
Question 1.
Which of the following is a monomial?
(a) 4x²
(b) a + b
(c) a + b + c
(d) a + b + c + d
Solution:
(a) 4x²
Question 2.
Which of the following is trinomial?
(a) -7z
(b) z² – 4y²
(c) x²y – xy² + y
(d) 12a – 9ab + 5b – 3
Solution:
(c) x²y – xy² + y
![]()
Question 3.
The sum of 5x²; -7x²; 8x²; 11x² and -9x² is ………
(a) 2x²
(b) 4x²
(c) 6x²
(d) 8x²
Solution:
(d) 8x²
Question 4.
The area of a rectangle with length 2l²m and breadth 3lm² is ………
(a) 6l³m³
(b) l³m³
(c) 2l³m³
(d) 4l³m³
Solution:
(a) 6l³m³
Question 5.
The coefficient of x² and x in 2x³ – 5x² + 6x – 3 are respectively ………
(a) 2, -5
(b) 2, 6
(c) – 5, 6
(d) -5, -3
Solution:
(c) – 5, 6
![]()
Question 6.
In the system 6x -2y = 3; kx – y = 2 has a unique solution then ………
(a) k = 3
(b) k ≠ 3
(c) k = 4
(d) k ≠ 4
Solution:
(b) k ≠ 3
Question 7.
A system of two linear equation in two variables is inconsistent. If their graphs ………
(a) coincide
(b) intersect only at a point
(c) do not intersect at any point
(d) cut the x-axis
Solution:
(c) do not intersect at any point
Question 8.
The system of equation x – 4y = 8; 3x – 12y = 24 ……….
(a) has infinitely many solution
(b) has no solution
(c) has a unique solution
(d) may or may not have a solution
Solution:
(a) has infinitely many solution
![]()
Question 9.
The solution set of x – ay = 4 and x + y = 0 is (1, -1) the value of a is ………
(a) -1
(b) 1
(c) -3
(d) 3
Solution:
(d) 3
Question 10.
The solution set of x + y = 7; x – y = 3 is ………
(a) (-5, -2)
(b) (-5, 2)
(c) (5, 2)
(d) (2, 5)
Solution:
(c) (5, 2)
![]()
II. Answer following Questions
Question 1.
What must be added to x4 – 3x2 + 2x + 6 to get x4 – 2x3 – x + 8?
Solution:
Let A be the required number to be added.
(x4 – 3x2 + 2x + 6) + A = x4 – 2x3 – x + 8
A = x4 – 2x3 – x + 8 – (x4 – 3x2 + 2x + 6)
= x4 – 2x3 – x + 8 – x4 + 3x2 – 2x – 6
= -2x3 + 3x2 – 3x + 2
Hence -2x3 + 3x2 – 3x + 2 must be added.
Question 2.
What must be subtracted to y4 + 2y3 – 3y + 8 to get y4 – 2y3 + 6?
Solution:
Let A be the required number to be subtracted.
(y4 + 2y3 – 3y2 + 8) – A = y4 – 2y3 + 6
y4 + 2y3 – 3y2 + 8 – (y4 – 2y3 + 6) = A
y4 + 2y3 – 3y2 + 8 – y4 + 2y3 – 6 = A
4y3 – 3y2 + 2 = A
Hence 4y3 – 3y2 + 2 must be subtracted.
![]()
Question 3.
The area of a rectangle is x4 + 9x2 + 20 sq.units and its length is x2 + 4 units. Find its breadth in term of x.
Solution:
Let the breadth of a rectangle be “b”
Length of the rectangle = x2 + 4
Area of the rectangle = x4 + 9x2 + 20
Length × Breadth = x4 + 9x2 + 20
(x2 + 4) × b = x4 + 9x2 + 20
b = \(\frac{x^{4}+9x^{2}+20}{x^{2}+4}\)
= x2 + 5
breadth of a rectangle = x2 + 5
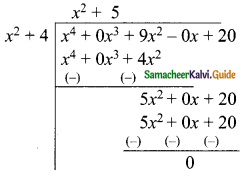
Question 4.
Solve 3x + 4y = 24; 20x – 11y = 47 using cross multiplication method.
Solution:
3x + 4y – 24 = 0 → (1)
20x – 11y – 47 = 0 → (2)
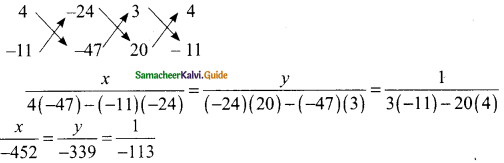
\(\frac{x}{-452}\) = \(\frac{1}{-113}\)
-113 = -452
x = \(\frac{452}{113}\)
= 4
But \(\frac{y}{-339}\) = \(\frac{1}{-113}\)
-113y = -339
y = \(\frac{339}{113}\)
= 3
∴ The solution set is (4, 3)
![]()
Question 5.
A fraction such that if the numerator is multiplied by 3 and the denominator is reduced by 3, we get \(\frac{18}{11}\), but if the numerator is increased by 8 and the denominator is doubled, we get \(\frac{2}{5}\). Find the fraction.
Solution:
Let the numerator be x and the denominator be y
∴ The fraction is \(\frac{x}{y}\)
According to the given condition
\(\frac{3x}{y-3}\) = \(\frac{18}{11}\)
33x = 18(y – 3)
33x = 18y – 54
33x – 18y – 54 = 0
11x – 6y – 18 = 0 ……. (1)
According to the second condition
\(\frac{x+8}{2y}\) = \(\frac{2}{5}\)
5x + 40 = 4y
5x – 4y + 40 = 0 ……..(2)
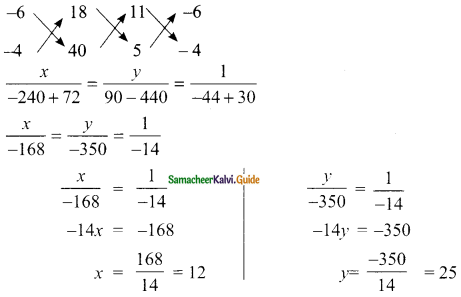
∴ The fraction is = \(\frac{12}{25}\)
![]()
Question 6.
One number is greater than the thrice the other number by 2. If 4 times the smaller number exceeds the greater by 5, find the number.
Solution:
Let the greater number be x and the smaller number be “y” By the given first condition
x = 3y + 2
x – 3y = 2 ……(1)
Again by the given second condition
4y = x + 5
-x + 4y = 5 …….(2)
Add (1), (2) ⇒ y = 7
Substitute the value of y = 7 in (1)
x – 3(7) = 2
x = 2 + 21
= 23
The greater number is 23 and the smaller number is 7.
![]()
Question 7.
The cost of 11 pencils and 3 erasers is Rs 50 and the cost of 8 pencils and 3 erasers is Rs 38. Find the cost of 5 pencils and 5 erasers.
Solution:
Let the cost of a pencil be Rs x and the cost of an eraser be Rs y. According to the first condition.
11x + 3y = 50 …….(1)
According to the second condition
8x + 3y = 38 ……..(2)
(1) – (2) ⇒ 3x = 12
x = \(\frac{12}{3}\)
= 4
Substitute the value of x = 4 in (1)
11 (4) + 3y = 50
3y = 50 – 44
3y = 6
y = \(\frac{6}{3}\)
= 2
Cost of 5 pencils + 5 erasers = 5(4) + 5(2)
= 20 + 10
= 30
The required cost is Rs 30