Students can download Maths Chapter 3 Algebra Ex 3.14 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.14
Question 1.
The sum of a two digit number and the number formed by interchanging the digits is 110. If 10 is subtracted from the first number, the new number is 4 more than 5 times the sums of the digits of the first number. Find the first number.
Solution:
Let the ten’s digit be x and the unit digit be y.
The number is 10x + y
If the digits are interchanged
The new number is 10y + x
By the given first condition
10x + y + 10y + x = 110
11x + 11y = 110
x + y = 10 → (1) (Divided by 11)
Again by the given second condition
10x + y – 10 = 5(x + y ) + 4
10x + y – 10 = 5x + 5y + 4
5x – 4y = 14 → (2)
(1) × 5 ⇒ 5x + 5y = 50 → (3)
(2) × 1 ⇒ 5x – 4y = 14 → (2)
(3) – (2) ⇒ 9y = 36
y = 36/9
= 4
Substitute the value of y = 4 in (1)
x + y = 10
x + 4 = 10
x = 10 – 4
= 6
∴ The number is (10 × 6 + 4) = 64
![]()
Question 2.
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes \(\frac{1}{2}\). Find the fraction.
Solution:
Let the numerator be “x” and the denominator be “y”
∴ The fraction is \(\frac{x}{y}\)
By the given first condition
x + y = 12 → (1)
Again by the second condition
\(\frac{x}{y+3}\) = \(\frac{1}{2}\)
2x = y + 3
2x – y = 3 → (2)
(1) + (2) ⇒ 3x = 15
x = \(\frac{15}{3}\) = 5
Substitute the value of x = 5 in (1)
5 + y = 12
y = 12 – 5
= 7
∴ The fraction is \(\frac{5}{7}\)
![]()
Question 3.
ABCD is a cyclic quadrilateral such that ∠A = (4y + 20)°, ∠B = (3y -5)°, ∠C = (4x)° and ∠D = (7x + 5)°. Find the four angles.
Solution:
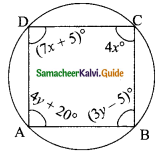
ABCD is a cyclic quadrilateral ∠A + ∠C = 180°
(Sum of the opposite angles of a cyclic quadrilateral is 180°)
(4y + 20)° + (4x)° = 180°
4y + 20 + 4x = 180
4x + 4y = 180 – 20
4x + 4y = 160
x + y = 40 → (1) (divided by 4)
∠B + ∠D = 180° (Sum of the opposite angles of a cyclic quadrilateral)
(3y – 5)° + (7x + 5)° = 180°
3y – 5 + 7x + 5 = 180
7x + 3y = 180 → (2)
(1) × 3 ⇒ 3x + 3y = 120 → (3)
(3) – (2) ⇒ -4x = – 60
4x = 60
x = \(\frac{60}{4}\)
Substitute the value of x = 15 in (1)
15 + y = 40
y = 40 – 15 = 25
∠A = 4y + 20 = 4(25) + 20 = 100 + 20 = 120°
∴ ∠A = 120°
∠B = 3y – 5 = 3(25) – 5 = 75 – 5 = 70
∴ ∠B = 70°
∠C = 4x = 4(15) = 60
∴ ∠C = 60°
∠D = 7x + 5 = 7(15) + 5
∠D = 105 + 5 = 110°
∴ ∠A= 120°, ∠B = 70°, ∠C = 60° and ∠D = 110°
![]()
Question 4.
On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gains Rs 2000. But if he sells the T.V. at 10% gain and the fridge at 5% loss, he gains Rs.1500 on the transaction. Find the actual price of the T.V. and the fridge.
Solution:
Let the cost price of the TV be Rs “x” and the cost price of the fridge be Rs “y”.
By the given condition

Multiply by 20
x + 2y = 40000 → (1)
Again by the given second condition
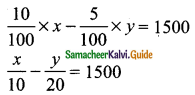
Multiply by 20
2x – y = 30000 → (2)
(2) × 2 ⇒ 4x – 2y = 60000 → (3)
(1) + (3) ⇒ 5x + 0 = 100000
x = \(\frac{100000}{5}\)
= 20000
Substitute the value of x = 20000 in (1)
20000 + 2y = 40000
2y = 40000 – 20000
= 20000
y = \(\frac{20000}{2}\)
= 10000
Cost price of a TV = Rs 20,000
Cost price of a fridge = Rs 10,000
![]()
Question 5.
Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5. Find the numbers.
Solution:
Let the two numbers be x and y.
By the given first condition
x : y = 5 : 6
6x = 5y (Product of the extreme is equal to the product of the means)
6x – 5y = 0 → (1)
Again by the given second condition
x – 8 : y – 8 = 4 : 5
5(x – 8) = 4(y – 8)
5x – 40 = 4y – 32
5x – 4y = – 32 + 40
5x – 4y = 8 → (2)
(1) × 4 ⇒ 24x – 20y = 0 → (3)
(2) × 5 ⇒ 25x – 20y = 40 → (4)
(3) – (4) ⇒ – x + 0 = -40
∴ x = 40
Substitute the value of x = 40 in (1)
6(40) – 5y = 0
240 – 5y = 0 ⇒ – 5y = -240
5y = 240
y = \(\frac{240}{5}\)
= 48
The two numbers are 40 and 48 [∴ The ratio of the number = 40 : 48 are 5 : 6]
![]()
Question 6.
4 Indians and 4 Chinese can do a piece of work in 3 days. While 2 Indian and 5 Chinese can finish it in 4 days. How long would it take for 1 Indian to do it? How long would it ‘ take for 1 Chinese to do it?
Solution:
Let the time taken by a Indian be “x”
Time taken by a Chinese be “y”
Work done by a Indian in one day = \(\frac{1}{x}\)
Work done by a Chinese in one day = \(\frac{1}{y}\)
By the given first condition
(4 Indian + 4 Chinese) finish the work in 3 days
\(\frac{4}{x}\) + \(\frac{4}{y}\) = \(\frac{1}{3}\) → (1)
Again by the given second condition
(2 Indian + 5 Chinese) finish the work in 4 days
\(\frac{2}{x}\) + \(\frac{5}{y}\) = \(\frac{1}{4}\) → (2)
Solve the equation (1) and (2)
Let \(\frac{1}{x}\) = a; \(\frac{1}{y}\) = b
4a + 4b = \(\frac{1}{3}\)
12a + 12b = 1 → (3) (Multiply by 3)
2a + 5b = \(\frac{1}{4}\)
8a + 20b = 1 → (4) (Multiply by 4)
(3) × (2) ⇒ 24a + 24b = 2 → (5)
(4) × (3) ⇒ 24a + 60b = 3 → (6)
(5) – (6) ⇒ -36b = -1
b = \(\frac{1}{36}\)
Substitute the value of b = \(\frac{1}{36}\) in (3)
12a + 12(\(\frac{1}{36}\)) = 1
12a + \(\frac{1}{3}\) = 1
36a + 1 = 3
36a = 2
a = \(\frac{2}{36}\) = \(\frac{1}{18}\)
But \(\frac{1}{x}\) = a ⇒ \(\frac{1}{x}\) = \(\frac{1}{18}\)
x = 18
\(\frac{1}{y}\) = b ⇒ \(\frac{1}{y}\) = \(\frac{1}{36}\)
y = 36
∴ Time taken by a 1 Indian is 18 days
Time taken by a 1 Chinese is 36 days
![]()