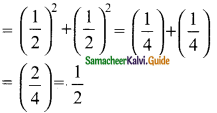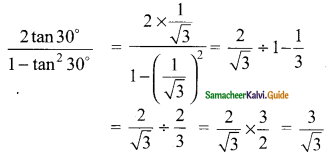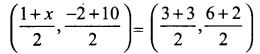Category: Class 9

Students can download Maths Chapter 8 Statistics Ex 8.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 8 Statistics Ex 8.2

Question 1.
Find the median of the given values: 47, 53, 62, 71, 83, 21, 43, 47, 41
Solution:
Arrange the values in ascending order we get
21, 41, 43, 47, 47, 53, 62, 71, 83
The number of values = 9 which is odd
Median = (\(\frac{9+1}{2})^{th}\) variable
= 5^th variable
∴ Median = 47

Question 2.
Find the median of the given data: 36, 44, 86, 31, 37, 44, 86, 35, 60, 51
Solution:
Arrange the values in ascending order we get
31, 35, 36, 37, 44, 44, 51, 60, 86, 86
The number of values = 10 which is even
Median = Average of (\(\frac{10}{2})^{th}\) and (\(\frac{10}{2}+1)^{th}\) value
= Average of 5^th and 6^th value
= \(\frac{44+44}{2}\)
= \(\frac{88}{2}\)
= 44
∴ Median = 44

Question 3.
The median of observation 11, 12, 14, 18, x + 2, x + 4, 30, 32, 35, 41 arranged in ascending order is 24. Find the values of x.
Solution:
The given observation is 11, 12, 14, 18, x + 2, x + 4, 30, 32, 35, 41 (is ascending order)
The number of values =10
Median = Average of (\(\frac{10}{2})^{th}\) and (\(\frac{10}{2}+1)^{th}\) value
= Average of 5^th and 6^th value
24 = \(\frac{x+2.+x+4}{2}\)
24 = \(\frac{2x+6}{2}\)
2x + 6 = 48
2x = 48 – 6
2x = 42
x = \(\frac{42}{2}\)
= 21
The value of x = 21

Question 4.
A researcher studying the behavior of mice has recorded the time (in seconds) taken by each mouse to locate its food by considering 13 different mice as 31, 33, 63, 33, 28, 29, 33, 27, 27, 34, 35, 28, 32. Find the median time that mice spent in searching its food.
Solution:
Arrange the value in ascending order we get
27, 27, 28, 28, 29, 31, 32, 33, 33, 33, 34, 35, 63
The number of values = 13 which is odd
Median = (\(\frac{13+1}{2})^{th}\) value
= (\(\frac{14}{2})^{th}\)
= 7th value
7th value is = 32
∴ Median = 32

Question 5.
The following are the marks scored by the students in the Summative Assessment exam.

Calculate the median.
Solution:

\(\frac{N}{2}\) = \(\frac{50}{2}\)
= 25
Here l = 30, f = 10; m = 24 and c = 10
Median = l + \(\frac{(\frac{N}{2}-m)×c}{f}\)
= 30 + \(\frac{(25-24)10}{10}\)
= 30 + 1
= 31
∴ Median = 31

Question 6.
The mean of five positive integers is twice their median. If four of the integers are 3, 4, 6, 9 and median is 6, then find the fifth integer.
Solution:
Let the 5th positive integer be x
\(\bar { x }\) = \(\frac{3+4+6+9+x}{5}\)
= \(\frac{22+x}{5}\)
Median = 6
Mean = 2 × median
\(\frac{22+x}{5}\) = 2 × 6
22 + x = 60
x = 60 – 22
= 38
The fifth integer is 38.

Students can download Maths Chapter 5 Coordinate Geometry Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Additional Questions

I. Multiple Choice Questions.

Question 1.
On which quadrant does the point (- 4, 3) lie?
(a) I
(b) II
(c) III
(d) IV
Solution:
(b) II

Question 2.
The point whose abscissa is 5 and lies on the x-axis is …….
(a) (-5, 0)
(b) (5, 5)
(c) (0, 5)
(d) (5, 0)
Solution:
(d) (5, 0)

Question 3.
A point which lies in the III quadrant is ……..
(a) (5, 4)
(b) (5, -4)
(c) (-5, -4)
(d) (-5, 4)
Solution:
(c) (-5, -4)

Question 4.
A point on the y-axis is ……..
(a) (1, 1)
(b) (6, 0)
(c) (0, 6)
(d) (-1, -1)
Solution:
(c) (0, 6)

Question 5.
The distance between the points (4, -1) and the origin is ……..
(a) \(\sqrt{24}\)
(b) \(\sqrt{37}\)
(c) \(\sqrt{26}\)
(d) \(\sqrt{17}\)
Solution:
(d) \(\sqrt{17}\)

Question 6.
The distance between the points (-1, 2) and (3, 2) is ……..
(a) \(\sqrt{14}\)
(b) \(\sqrt{15}\)
(c) 4
(d) 0
Solution:
(c) 4

Question 7.
The centre of a circle is (0, 0). One end point of a diameter is (5, -1), then the radius is …….
(a) \(\sqrt{24}\)
(b) \(\sqrt{37}\)
(c) \(\sqrt{26}\)
(d) \(\sqrt{17}\)
Solution:
(c) \(\sqrt{26}\)

Question 8.
The point (0, -3) lies on
(a) + ve x-axis
(b) + ve y-axis
(c) – ve x-axis
(d) – ve y-axis
Solution:
(d) – ve y-axis

Question 9.
The point which is on y-axis with ordinate -5 is ……..
(a) (0, -5)
(b) (-5, 0)
(c) (5, 0)
(d) (0, 5)
Solution:
(a) (0, -5)

Question 10.
The diagonal of a square formed by the points (1, 0), (0, 1), (-1, 0) and (0, -1) is …….
(a) 2
(b) 4
(c) √2
(d) 8
Solution:
(a) 2

Question 11.
The distance between the points (-2, 2) and (3, 2) is ……..
(a) 10 units
(b) 5 units
(c) 5√3 units
(d) 20 units
Solution:
(b) 5 units

Question 12.
The midpoint of the line joining the points (1, -1) and (-5, 3) is ……..
(a) (2, 1)
(b) (2, -1)
(c) (-2, -1)
(d) (-2, 1)
Solution:
(d) (-2, 1)

Question 13.
If the centroid of a triangle is at (1, 3) and two of its vertices are (-7, 6) and (8, 5) then the third vertex is ……..
(a) (-2, 2)
(b) (2, -2)
(c) (-2, -2)
(d) (2, 2)
Solution:
(b) (2, -2)

Question 14.
The ratio in which the X-axis divides the line segment joining the points (6, 4) and (1, -7) is ……..
(a) 1 : 2
(b) 2 : 3
(c) 4 : 7
(d) 7 : 4
Solution:
(c) 4 : 7

Question 15.
The centroid of a triangle (3, -5), (-7, 4) and (10, -2) is …….
(a) (2, -1)
(b) (2, 1)
(c) (-2, 1)
(d) (1, -2)
Solution:
(a) (2, -1)

II. Answer the Following Questions.

Question 1.
Show that the given points (1, 1), (5, 4), (-2, 5) are the vertices of an isosceles right angled triangle.
Solution:
Let A (1, 1), B (5, 4) and G (-2, 5)

AB = 5, AC = 5
∴ ABC is an isosceles triangle …….. (1)
BC² = AB² + AC²
50 = 25 + 25 ⇒ 50 = 50
∴ ∠A = 90° ……… (2)
From (1) and (2) we get ABC is an isosceles right angle triangle.

Question 2.
Show that the point (3, -2), (3, 2), (-1, 2) and (-1, -2) taken in order are the vertices of a square.
Solution:

= \(\sqrt{16}\)
= 4
AB = BC = CD = DA = 4. All the four sides are equal.
∴ ABCD is a Rhombus ……..(1)

Diagonal AC = Diagonal BD = \(\sqrt{32}\) ……..(2)
From (1) and (2) we get ABCD is a square.

Question 3.
Show that the point A (3, 7) B (6, 5) and C (15, -1) are collinear.
Solution:

AB + BC = AC ⇒ \(\sqrt{13}\) + 3\(\sqrt{13}\) = 4\(\sqrt{13}\)
∴ The points A, B, C are collinear.

Question 4.
Find the type of triangle formed by (-1, -1), (1, 1) and (-√, √3)
Solution:
Let the point A (-1, -1), B (1, 1) and C (-√3, √3)

AB = BC = AC = √8
∴ ABC is an equilateral triangle.

Question 5.
Find x such that PQ = QR where P(6, -1) Q(1, 3) and R(x, 8) respectively.
Solution:

But PQ = QR
\(\sqrt{(x-1)^{2}+25}\) = \(\sqrt{41}\)
Squaring on both sides
(x – 1)² + 25 = 41
(x – 1)² = 41 – 25 = 16
x – 1 = \(\sqrt{16}\) = ± 4
x – 1 = 4 (or) x – 1 = – 4
x = 5 (or) x = -4 + 1 = -3
The value of x = 5 or – 3

Question 6.
Find the coordinate of the point of trisection of the line segment joining (4, -1) and
Solution:
Let A (4, -1) and B (-2, -3) are the given points
Let P (a, b) and Q (c, d) be the points of trisection of AB.
∴ AP = PQ = QB

The required coordinate P is (2, –\(\frac{5}{3}\)) and Q is (0, –\(\frac{7}{3}\))

Question 7.
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
Solution:
Given points are A(-3, 10), B(6, -8) and P(-1, 6)
divides AB internally in the ratio m : n
By section formula.
A line divides internally in the ratio m : n the point P =

∴ \(\frac{6m-3n}{m+n}\) = -1
6m – 3n = -m – n
6m + m = 3n – n
7m = 2n ⇒ \(\frac{m}{n}\) = \(\frac{2}{7}\)
∴ m : n = 2 : 7
and
\(\frac{-8m+10n}{m+n}\) = 6
-8m + 10n = 6m + 6n
-8m – 6m = 6n – 10n
14m = 4n
∴ \(\frac{m}{n}\) = \(\frac{14}{4}\) = \(\frac{2}{7}\)
Hence P divides AB internally in the ratio 2 : 7

Question 8.
If (1, 2) (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find “x” and “y”.
Solution:
Let A(1, 2), B(4, y), C(x, 6) and D(3, 5)

Since ABCD is a parallelogram the diagonal bisect each other
Mid point of AC = Mid point of BD
(\(\frac{1+x}{2}\), 4) = (\(\frac{7}{2}\), \(\frac{y+5}{2}\))
\(\frac{1+x}{2}\) = \(\frac{7}{2}\)
1 + x = 7
x = 7 – 1
= 6
and
\(\frac{y+5}{2}\) = 4
y + 5 = 8
y = 8 – 5
= 3
∴ The value of x = 6 and y = 3

Students can download Maths Chapter 6 Trigonometry Ex 6.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.3

Question 1.
Find the value of the following:

(iii) tan 15° tan 30° tan 45° tan 60° tan 75°

Solution:
(i) cos 45° = \(\frac{1}{√2}\)

= 1² + 1² – 2(\(\frac{1}{√2}\))²
= 1 + 1 – 2(\(\frac{1}{2}\))
= 2 – 1
= 1

(ii) cos 60° = \(\frac{1}{2}\)

= 1 + 1 + 1 – 8(\(\frac{1}{2}\))²
= 3 – 8 × \(\frac{1}{4}\)
= 3 – 2
= 1

(iii) tan 30° = \(\frac{1}{√3}\), tan 45° = 1, tan 60° = √3
tan 15° . tan 30°. tan 45° . tan 60°. tan 75° = tan 15° . \(\frac{1}{√3}\) . 1 . √3 tan 75°
= tan 15° × tan 75° × \(\frac{1}{√3}\) × 1 × √3
= tan(90° – 75°) × \(\frac{1}{cot 75°}\) × 1 [tan 90° – θ = cot θ]
= cot 75° × \(\frac{1}{cot 75°}\) × 1
= 1

= 1 + 1
= 2

Students can download Maths Chapter 6 Trigonometry Ex 6.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.2

Question 1.
Verify the following equalities:
(i) sin² 60° + cos² 60° = 1
Solution:
sin 60° = \(\frac{√3}{2}\); cos 60° = \(\frac{1}{2}\)
L.H.S = sin² 60° + cos² 60°

L.H.S = R.H.S
Hence it is proved.

(ii) 1 + tan² 30° = sec² 30°
Solution:
tan 30° = \(\frac{1}{√3}\); sec 30° = \(\frac{2}{√3}\)
L.H.S = 1 + tan² 30°

∴ L.H.S = R.H.S
Hence it is proved.

(iii) cos 90° = 1 – 2sin² 45° = 2cos² 45° – 1
Solution:
cos 90° = 0, sin 45° = \(\frac{1}{√2}\), cos 45° = \(\frac{1}{√2}\)
cos 90° = 0 ……. (1)
1 – 2 sin² 45° = 1 – 2 (\(\frac{1}{√2}\))²
= 1 – 2 × \(\frac{1}{2}\)
= 1 – 1 = 0 → (2)
2 cos² 45° – 1 = 2(\(\frac{1}{√2}\))² – 1
= \(\frac{2}{2}\) – 1
= \(\frac{2 – 2}{2}\) = 0 → (3)
From (1), (2) and (3) we get
cos 90° = 1 – 2 sin² 45° = 2 cos² 45° – 1
Hence it is proved.

(iv) sin 30° cos 60° + cos 30° sin 60° = sin 90°
Solution:
sin 30° = \(\frac{1}{2}\); cos 60° = \(\frac{1}{2}\); cos 30° = \(\frac{√3}{2}\); sin 60° = \(\frac{√3}{2}\); sin 90° = 1
L.H.S = sin 30° cos 60° + cos 30° sin 60°

= 1
R.H.S = sin 90° = 1
L.H.S = R.H.S
Hence it is proved.

Question 2.
Find the value of the following:
(i) \(\frac{tan 45°}{cosec 30°}\) + \(\frac{sec 60°}{cot 45°}\) – \(\frac{5 sin 90°}{2 cos 0°}\)
(ii) (sin 90° + cos 60° + cos 45°) × (sin 30° + cos 0° – cos 45°)
(iii) sin²30° – 2 cos³ 60° + 3 tan⁴ 45°
Solution:
(i) tan 45° = 1, cosec 30° = 2; sec 60° = 2; cot 45° = 1; tan 45°, sin 90° = 1; cos 0° = 1

= 0

(ii) sin 90° = 1; cos 60° = \(\frac{1}{2}\); cos 45° = \(\frac{1}{√2}\); sin 30° = \(\frac{1}{2}\); cos 0° = 1
(sin 90° + cos 60° + cos 45°) × (sin 30° + cos 0° – cos 45°)

= \(\frac{7}{4}\)

(iii) sin 30° = \(\frac{1}{2}\); cos 60° = \(\frac{1}{2}\); tan 45° = 1
sin² 30° – 2 cos³ 60° + 3 tan⁴ 45°

= 3

Question 3.
Verify cos 3 A = 4 cos³ A – 3 cos A, when A = 30°
Solution:
L.H.S = cos 3 A
= cos 3 (30°)
= cos 90°
= 0
R.H.S = 4 cos³ A – 3 cos A
= 4 cos³ 30° – 3 cos 30°

= 0
∴ L.H.S = R.H.S
Hence it is proved.

Question 4.
Find the value of 8 sin2x, cos 4x, sin 6x, when x = 15°.
Solution:
8 sin 2x cos 4x sin 6x = 8 sin 2 (15°) × cos 4 (15°) × sin (6 × 15°)
= 8 sin 30° × cos 60° × sin 90°
= 8 × \(\frac{1}{2}\) × \(\frac{1}{2}\) × 1
= 2

Students can download Maths Chapter 6 Trigonometry Ex 6.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.1

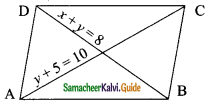
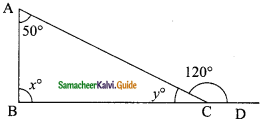
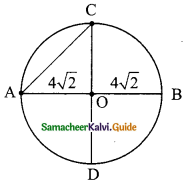
Question 1.
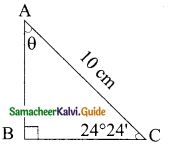
From the given figure, find all the trigonometric ratios of angle B.

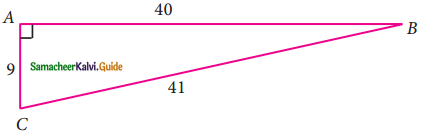
Solution:

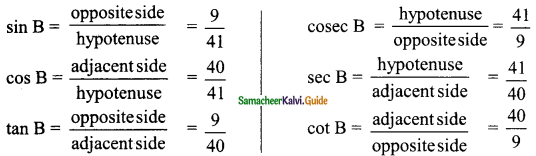
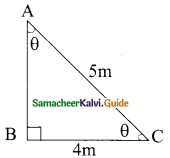
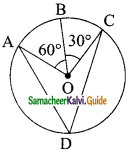
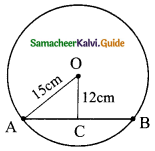
Question 2.
From the given figure, find the values of

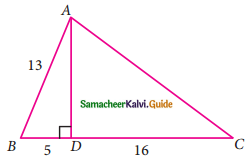
(i) sin B
(ii) sec B
(iii) cot B
(v) tan C
(vi) cosec C
Solution:
In the right ΔABD,
AD² = AB² – BD²
= 13² – 5²
= 169 – 25
= 144
AD = \(\sqrt{144}\)
= 12
In the right ΔADC,
AC² = AD² + DC²
= 12² + 16²
= 144 + 256
= 400
AC = \(\sqrt{400}\)
= 20

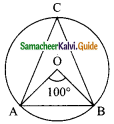
Question 3.
If 2 cos θ = √3, then find all the trigonometric ratios of angle θ.
Solution:

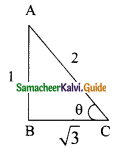
2 cos θ = √3 ⇒ cos θ = \(\frac{√3}{2}\)
AB² = AC² – BC²
= 2² – (√3)² ⇒ = 4 – 3 = 1
AB = √1 = 1

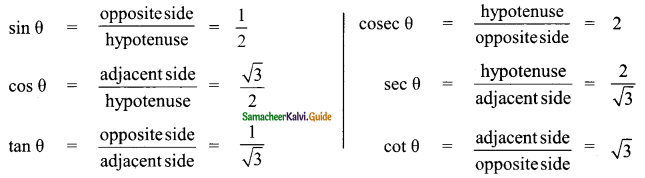
Question 4.
If cos A =\(\frac{3}{5}\), then find the value of \(\frac{sin A-cos A}{2 tan A}\)
Solution:

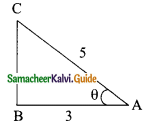
cos A = \(\frac{3}{5}\)
ΔABC
BC² = AC² – AB²
= 5² – 3²
= 25 – 9
= 16
BC = \(\sqrt{16}\) = 4
sin A = \(\frac{4}{5}\); tan A = \(\frac{4}{3}\)

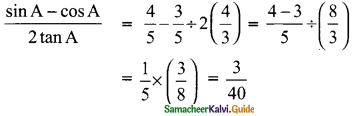
∴ The value of \(\frac{sin A-cos A}{2 tan A}\) = \(\frac{3}{40}\)

Question 5.
If cos A = \(\frac{2x}{1+x_{2}}\) then find the values of sin A and tan A in terms of x.
Solution:
cos A = \(\frac{2x}{1+x_{2}}\)
In the triangle ABC

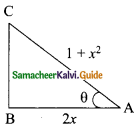
BC² = AC² – AB²
= (1 + x²)² – (2x)²
= 1 + x⁴ + 2x² – 4x²
= x⁴ – 2x² + 1
= (x² – 1)² (or) (1 – x²)² (using (a – b)²)
BC = \(\sqrt{(x^{2}-1)^{2}}\) (or) \(\sqrt{(1-x^{2})^{2}}\)
BC = x² – 1
The value of sin A = \(\frac{BC}{AC}\) = \(\frac{x²-1}{x²+1}\)
tan A = \(\frac{BC}{AB}\) = \(\frac{x²-1}{2x}\)
and
BC = 1 – x²
The value of sin A = \(\frac{1-x²}{1+x²}\)
tan A = \(\frac{1-x²}{2x}\)

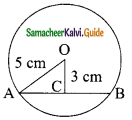
Question 6.
If sin θ = \(\frac{a}{\sqrt{a²+b²}}\) then show that b sin θ = a cos θ.
Solution:

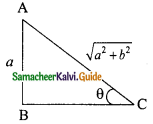
sin θ = \(\frac{a}{\sqrt{a²+b²}}\)
In the triangle ΔABC
BC² = AC² – AB²

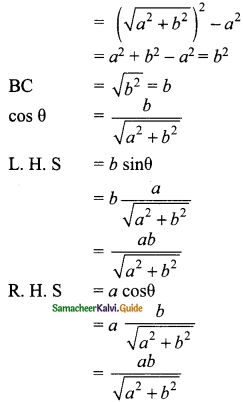
L. H. S = R. H. S

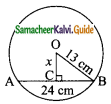
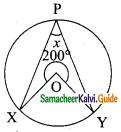
Question 7.
If 3 cot A = 2, then find the value of \(\frac{4sin A-3cos A}{2 sin A+3 Cos A}\)
Solution:

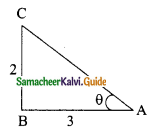
3 cot A = 2 ⇒ cot A = \(\frac{2}{3}\)
AC² = AB² + BC²
= 3² + 2²
= 9 + 4
AC = \(\sqrt{13}\)
cos A = \(\frac{AB}{AC}\) = \(\frac{3}{\sqrt{13}}\)
sin A = \(\frac{BC}{AC}\) = \(\frac{2}{\sqrt{13}}\)
The value of \(\frac{4sin A-3cos A}{2 sin A+3 Cos A}\)

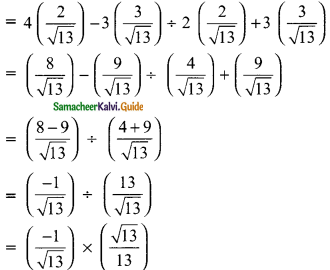
The value is (\(\frac{-1}{13}\))

Question 8.
If cos θ : sin θ = 1 : 2, then find the value of \(\frac{8cos θ-2cos θ}{4 cos θ+2 sin θ}\)
Solution:
cos θ : sin θ = 1 : 2

Aliter:
cos θ : sin θ = 1 : 2
2 cos θ = sin θ ⇒ 2 = \(\frac{sin θ}{cos θ}\) ⇒ 2 = tan θ

∴ The value is \(\frac{1}{2}\)

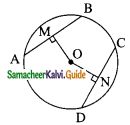
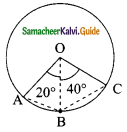
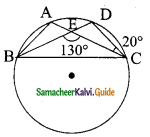
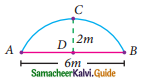
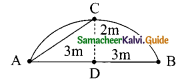
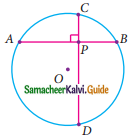
Question 9.
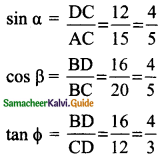
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅.

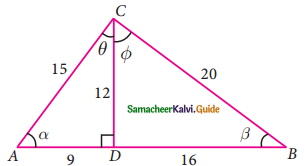
Solution:
In the ΔABC,
AB = 9 + 16 = 25
AC = 15; BC = 20
AB² = 25²
= 625 ……. (1)
AC² + BC² = 15² + 20²
= 225 + 400
= 625 …….. (2)
From (1) and (2) we get
AB² = AC² + BC²
ABC is a right angle triangle at C (Pythagoras theorem)
∴ ∠C = 90°
θ + ∅ = 90°
Also ADC is a right angle triangle ∠ADC = 90° (Given)
BDC is also a right angle triangle ∠BDC = 90° (since ADB is a straight line sum of the two angle is 180°)
From the given diagram

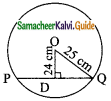
Question 10.
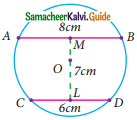
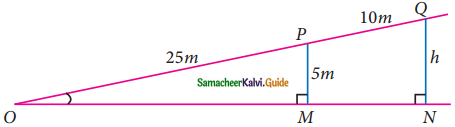
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios).

Solution:
Let the angle O be “θ”
In ΔONQ

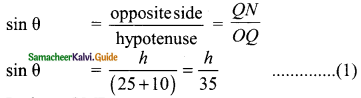
In ΔOMP
sin θ = \(\frac{PM}{OP}\) ⇒ sin θ = \(\frac{5}{25}\)
sin θ = \(\frac{1}{5}\) ……… (2)
From (1) and (2) we get
\(\frac{h}{35}\) = \(\frac{1}{5}\)
5 h = 35 ⇒ h = \(\frac{35}{5}\) = 7
The height of the kite from the ground is 7m.

Students can download Maths Chapter 6 Trigonometry Ex 6.5 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.5

Question 1.
If sin 30° = x and cos 60° = y, then x² + y² is …….
(a) \(\frac{1}{2}\)
(b) 0
(c) sin 90°
(d) cos 90°
Solution:
(a) \(\frac{1}{2}\)
Hint:
sin 30° = x = \(\frac{1}{2}\)
cos 60° = y = \(\frac{1}{2}\)
x² + y²

Question 2.
If tan θ = cot 37°, then the value of θ is ………
(a) 37°
(b) 53°
(c) 90°
(d) 1°
Solution:
(b) 53°
Hint:
tan θ = cot 37°
= cot (90° – 53°)
= tan 53°
The value of θ is 53°

Question 3.
The value of tan 72°. tan 18° is ………
(a) 0
(b) 1
(c) 18°
(d) 72°
Solution:
(b) 1
Hint:
tan 72° . tan 18° = tan 72° . tan (90° – 72°)
= tan 72° . cot 72°
= tan 72° × \(\frac{1}{tan 72°}\)
= 1

Question 4.
The value of \(\frac{2 tan 30°}{1 – tan^{2} 30°}\) is equal to ………
(a) cos 60°
(b) sin 60°
(c) tan 60°
(d) sin 30°
Solution:
(c) tan 60°
Hint:

= √3 = tan 60°

Question 5.
If 2 sin 2θ = √3 then the value of θ is ………
(a) 90°
(b) 30°
(c) 45°
(d) 60°
Solution:
(b) 30°
Hint:
2 sin 2θ = √3 ⇒ sin 2θ = \(\frac{√3}{2}\)
sin 2θ = sin 60° ⇒ 2θ = 60°
θ = 30°

Question 6.
The value of 3 sin 70° sec 20° + 2 sin 39° sec 51° is ………
(a) 2
(b) 3
(c) 5
(d) 6
Solution:
(c) 5
Hint:
3 sin 70° sec 20° + 2 sin 39° sec 51°
= 3. sin 70° . sec (90° – 70°) + 2 sin 39° . sec (90° – 39°)
= 3. sin 70° . cosec 70° + 2 sin 39° . cosec 39°
= 3. sin70° × \(\frac{1}{sin 70°}\) + 2 sin 39° × \(\frac{1}{sin 39°}\)
= 3 + 2
= 5

Question 7.
The value of \(\frac{1-tan^{2}45°}{1+tan^{2}45°}\) is ……..
(a) 2
(b) 1
(c) 0
(d) \(\frac{1}{2}\)
Solution:
(c) 0
Hint:
\(\frac{1-tan^{2}45°}{1+tan^{2}45°}\) = \(\frac{1-1}{1+1}\)
= \(\frac{0}{2}\) = 0

Question 8.
The value of cosec (70° + θ) – sec (20° + θ) + tan (65° + θ) – cot (25° + θ) is ……..
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(a) 0
Hint:
cosec (70° + θ) – sec (20° – θ) + tan (65° + θ) – cot (25° – θ)
= sec [90° – (70° + θ)] – sec (20° – θ) + tan (65° + θ) – tan [90° – (25° – θ)]
= sec (20° – θ) – sec (20° – θ) + tan (65° + θ) – tan (65° + θ)
= 0

Question 9.
The value of tan 1° . tan 2° . tan 3°…. tan 89° is ………
(a) 0
(b) 1
(c) 2
(d) \(\frac{√3}{2}\)
Solution:
(b) 1
Hint:
tan 1° . tan 2° . tan 3° …….. tan 89°
= tan (90° – 89°). tan (90° – 88°) .tan (90° – 87°) …….. tan 45° . tan (89°)
= cot 89° . cot 88°. cot 87°. ……. tan 45° …….. tan 87°. tan 88°. tan 89°
= 1

Question 10.
Given that sin α = \(\frac{1}{2}\) and cos β = \(\frac{1}{2}\), then the value of α + β is ………
(a) 0°
(b) 90°
(c) 30°
(d) 60°
Solution:
Hint:
sin α = \(\frac{1}{2}\)
sin 30° = \(\frac{1}{2}\) ∴ α = 30°
cos β = \(\frac{1}{2}\) ∴ β = 60°
∴ α + β = 30° + 60°
= 90°

Students can download Maths Chapter 5 Coordinate Geometry Ex 5.6 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.6

Question 1.
If the y-coordinate of a point is zero, then the point always lies ……..
(a) in the I quadrant
(b) in the II quadrant
(c) on x-axis
(d) on y-axis
Solution:
(c) on x-axis

Question 2.
The points (-5, 2) and (2, -5) lie in the ……….
(a) same quadrant
(b) II and III quadrant respectively
(c) II and IV quadrant respectively
(d) IV and II quadrant respectively
Solution:
(c) II and IV quadrant respectively

Question 3.
On plotting the points O (0, 0), A (3, -4), B (3, 4) and C (0, 4) and joining OA, AB, BC and CO, which of the following figure is obtained?
(a) Square
(b) Rectangle
(c) Trapezium
(d) Rhombus
Solution:
(c) Trapezium

Question 4.
If P (-1, 1), Q ( 3, -4), R (1, -1), S (-2, -3) and T (- 4, 4) are plotted on a graph paper, then the points in the fourth quadrant are ………
(a) P and T
(b) Q and R
(c) only S
(d) P and Q
Solution:
(b) Q and R

Question 5.
The point whose ordinate is 4 and which lies on the v-axis is ……….
(a) (4, 0)
(b) (0, 4)
(c) (1, 4)
(d) (4, 2)
Solution:
(b) (0, 4)

Question 6.
The distance between the two points (2, 3) and (1, 4) is ……..
(a) 2
(b) \(\sqrt{56}\)
(c) \(\sqrt{10}\)
(d) √2
Solution:
(d) √2
Hint:
\(\sqrt{(1-2)^{2}+(4+3)^{2}}\)
= \(\sqrt{(-1)^{2}+1^{2}}\)
= \(\sqrt{1+1}\)
= √2

Question 7.
If the points A (2, 0), B (-6, 0), C (3, a – 3) lie on the x-axis then the value of a is ……..
(a) 0
(b) 2
(c) 3
(d) -6
Solution:
(c) 3
Hint:
a – 3 = 0 ⇒ a = 3

Question 8.
If (x + 2, 4) = (5, y – 2), then the coordinates (x, y) are ………
(a) (7, 12)
(b) (6, 3)
(c) (3, 6)
(d) (2, 1)
Solution:
(c) (3, 6)
Hint:
x + 2 = 5
∴ x = 5 – 2 = 3
and
4 = y – 2
4 + 2 = y
∴ y = 6

Question 9.
If Q₁, Q₂, Q₃, Q₄ are the quadrants in a Cartesian plane then Q₂ ∩ Q₃ is ……..
(a) Q₁ U Q₂
(b) Q₂ U Q₃
(C) Null set
(d) Negative x-axis
Solution:
(c) Null set

Question 10.
The distance between the point (5, -1 ) and the origin is ………
(a) \(\sqrt{24}\)
(b) \(\sqrt{37}\)
(c) \(\sqrt{26}\)
(d) \(\sqrt{17}\)
Solution:
(c) \(\sqrt{26}\)
Hint:

Question 11.
The coordinates of the point C dividing the line segment joining the points P (2, 4) and Q (5, 7) internally in the ratio 2 : 1 is ……..
(a) (\(\frac{7}{2}, \frac{11}{2}\))
(b) (3, 5)
(c) (4, 4)
(d) (4, 6)
Solution:
(d) (4, 6)
Hint:
A line divides internally in the ratio m : n
m = 2, n = 1
x₁ = 2, x₂ = 5
y₁ = 4, y₂ = 7

= (4, 6)

Question 12.
If p (\(\frac{a}{3}, \frac{b}{2}\)) is the mid-point of the line segment joining A (-4, 3) and B (-2, 4) then (a, b) is ………
(a) (-9, 7)
(b) (-3, \(\frac{7}{2}\))
(c) (9, -7)
(d) (3, –\(\frac{7}{2}\))
Solution:
(a) (-9, 7)
Hint:
Mid point of a line

\(\frac{a}{3}\) = -3 ⇒ a = -9
\(\frac{b}{2}\) = \(\frac{7}{2}\) ⇒ b = 7
(a, b) is (-9, 7)

Question 13.
In what ratio does the point Q (1, 6) divide the line segment joining the points P (2, 7) and R(-2, 3) ………
(a) 1 : 2
(6) 2 : 1
(c) 1 : 3
(d) 3 : 1
Solution:
(c) 1 : 3
Hint:
A line divides internally in the ratio m : n the point P =
(\(\frac{mx_{2}+nx_{1}}{m+n}\), \(\frac{my_{2}+ny_{1}}{m+n}\))

(1, 6) = (\(\frac{-2m+2n}{m+n}\), \(\frac{3m+7n}{m+n}\))
\(\frac{-2m+2n}{m+n}\) = 1
-2m + 2n = m + nx
-3m = n – 2n
3m = n
\(\frac{m}{n}\) = \(\frac{1}{3}\)
∴ m : n = 1 : 3
and
\(\frac{3m+7n}{m+n}\) = 6
3m + 7n = 6m + 6n
6m – 3n = 7n – 6n
3m = n
\(\frac{m}{n}\) = \(\frac{1}{3}\)

Question 14.
If the coordinates of one end of a diameter of a circle is (3, 4) and the coordinates of its centre is (-3, 2), then the coordinate of the other end of the diameter is ……..
(a) (0, -3)
(b) (0, 9)
(c) (3, 0)
(d) (-9, 0)
Solution:
(d) (-9, 0)
Hint:
Let the other end of the diameter be (a, b)

Mid point of a line =
(\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\))
(-3, 2) = \(\frac{3+a}{2}, \frac{4+b}{2}\)
\(\frac{3+a}{2}\) = -3
3 + a = -6
a = -6 – 3 = -9
and
\(\frac{4+b}{2}\) = 2
4 + b = 4
b = 4 – 4 = 0
The other end is (-9, 0)

Question 15.
The ratio in which the x-axis divides the line segment joining the points A (a₁, b₁) and B (a₂, b₂) is ……..
(a) b₁ : b₂
(b) -b₁ : b₂
(c) a₁ : a₂
(d) -a₁ : a₂
Solution:
(b) -b₁ : b₂
Hint:
A line divides internally in the ratio m : n the point P is,
(\(\frac{mx_{2}+nx_{1}}{m+n}, \frac{my_{2}+ny_{1}}{m+n}\))

The point P is (a, 0) = (\(\frac{ma_{2}+na_{1}}{m+n}, \frac{mb_{2}+nb_{1}}{m+n}\))
∴ \(\frac{mb_{2}+nb_{1}}{m+n}\) = 0
mb₂ + nb₁ = 0 ⇒ mb₂ = -nb₁
\(\frac{m}{n}\) = \(\frac{b_{1}}{b_{2}}\)
∴ m : n = -b₁ : b₂

Question 16.
The ratio in which the x-axis divides the line segment joining the points (6, 4) and (1, -7) is ………
(a) 2 : 3
(b) 3 : 4
(c) 4 : 7
(d) 4 : 3
Solution:
(c) 4 : 7
Hint:
A line divides internally in the ratio m : n the point P

-7m + 4n = 0
4n = 7m
\(\frac{m}{n}\) = \(\frac{4}{7}\)
The ratio is 4 : 7

Question 17.
If the coordinates of the mid-points of the sides AB, BC and CA of a triangle are (3, 4), (1, 1) and (2, -3) respectively, then the vertices A and B of the triangle are ……….
(a) (3, 2), (2, 4)
(b) (4, 0), (2, 8)
(c) (3, 4), (2, 0)
(d) (4, 3), (2, 4)
Solution:
(b) (4, 0), (2, 8)
Hint:

x₁ + x₂ = 6 → (1)
y₁ + y₂ = 8 → (2)
x₂ + x₃ = 2 → (3)
y₂ + y₃ = 2 → (4)
x₁ + x₃ = 4 → (5)
y₁ + y₃ = -6 → (6)
Adding (1) + (3) + (5) we get,
2(x₁ + x₂ + x₃) = 3
x₁ + x₂ + x₃ = 6
x₁ + x₃ = 4
∴ x₂ = 6 – 4 = 2
x₂ + x₃ = 2
x₁ = 6 – 2 = 4
Adding (2) + (4) + (6) we get,
2 (y₁ + y₂ + y₃) = 4
y₁ + y₂ + y₃ = 2
y₂ + y₃ = 2
∴ y₁ = 2 – 2 = 0
y₁ + y₃ = -6
y₂ = 2 + 6 = 8
∴ The vertices A is (4, 0) and B is (2, 8).

Question 18.
The mid-point of the line joining (-a, 2b) and (-3a, -4b) is ……..
(a) (2a, 3b)
(b) (-2a, -b)
(c) (2a, b)
(d) (-2a, -3b)
Solution:
(b) (-2a, -b)
Mid points of line

= (-2a, -b)

Question 19.
In what ratio does the y-axis divides the line joining the points (-5, 1) and (2, 3) internally ………
(a) 1 : 3
(b) 2 : 5
(c) 3 : 1
(d) 5 : 2
Solution:
(d) 5 : 2
Hint:
When it cut the y-axis the point P is (0, a)
A line divides internally in the ratio m : n the point

2m – 5n = 0 ⇒ 2m = 5n
\(\frac{m}{n}\) = \(\frac{5}{2}\) ⇒ m : n = 5 : 2

Question 20.
If (1, -2), (3, 6), (x, 10) and (3, 2) are the vertices of the parallelogram taken in order, then the value of x is ………
(a) 6
(b) 5
(c) 4
(d) 3
Solution:
(b) 5
Hint:
Since ABCD is a parallelogram

Mid-point of AC = Mid-point of BD

\(\frac{1+x}{2}\) = \(\frac{6}{2}\) ⇒ 1 + x = 6 ⇒ x = 6 – 1 = 5
The value of x = 5

Students can download Maths Chapter 6 Trigonometry Ex 6.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.4

Question 1.
Find the value of the following:
(i) sin 49°
(ii) cos 74° 39′
(iii) tan 54° 26′
(iv) sin 21° 21′
(v) cos 33° 53′
(vi) tan 70° 17′
Solution:
(i) sin 49° = 0.7547

(ii) cos 74° 39′ = cos 74° 39′ + 3′
From the table we get,
cos 74° 36′ = 0.2656
Mean difference of 3 = 8
cos 74° 39′ = 0.2656 – 8
= 0.2648

(iii) tan 54° 26′ = tan 54° 24′
tan 54° 24′ = 1.3968
Mean difference of 2 = 17
tan 54° 26’ = 1.3968 + 17
= 1.3985

(iv) sin 21° 21′ = sin 21° 18’+ 3’
sin 21° 18’ = 0.3633
Mean difference of 3 = 8(+)
sin 21° 21′ = 0.3633 + 8
= 0.3641

(v) cos 33° 53′ = cos 33° 48’ + 5′
cos 33° 48′ = 0.8310
Mean difference of 5 = 8
cos 33° 53′ = 0.8310 – 8
= 0.8302

(vi) tan 70° 17′ = tan 70° 12’+ 5’
tan 70° 12′ = 2. 7776
Mean difference of 5 = 131
tan 70° 17′ = 2. 7776 + 131
= 2.7907

Question 2.
Find the value of θ if
(i) sin θ = 0.9975
(ii) cos θ = 0.6763
(iii) tan θ = 0.0720
(iv) cos θ = 0.0410
(v) tan θ = 7.5958
Solution:
(i) sin θ = 0.9975
From the table we get,
= 0.9974 + 0.0001
= 85° 54′ + 1′
= 85° 55′ (or) 85° 56′ (or) 85° 57

(ii) cos θ = 0.6763
= 0. 6769 – 0.0006′
= 47° 24′ + 3′
= 47° 27

(iii) tan θ = 0. 0720
= 0. 0717 + 0.0003
= 4° 6′ + 1′
= 4° 7′

(iv) cos θ = 0.0410
= 0.0419 – 0.0009
= 87° 36′ + 3′
= 87° 39′

(v) tan θ = 7. 5958
= 7. 5958 + 0 (from the natural table)
= 82° 30′ (tangent table)

Question 3.
Find the value of the following:
(i) sin 65° 39′ + cos 24° 57’ + tan 10° 10′
(ii) tan 70° 58′ + cos 15° 26′ – sin 84° 59′
Solution:
(i) sin 65° 39′ = 0.9111
cos 24° 57′ = 0.9066
tan 10° 10′ = 0.1793
sin 65° 39′ + cos 24° 57′ + tan 10° 10′
= 0.9111 + 0.9066 + 0.1793
= 1.9970
sin 65° 39′ + cos 24° 57′ + tan 10° 10′ = 1.9970

(ii) tan 70° 58′ = 2. 8982
cos 15° 26′ = 0. 9639
sin 84° 59′ = 0.9962
tan 70° 58′ + cos 15° 26′ – sin 84° 59′
= 2. 8982 + 0. 9639 – 0.9962
= 3.8621 – 0.9962
= 2.8659

Question 4.
Find the area of a right triangle whose hypotenuse is 10 cm and one of the acute angle is 24°24′.
Solution:
In the ΔABC,

sin 24° 24′ = \(\frac{AB}{AC}\)
0. 4131 = \(\frac{AB}{10}\)
∴ AB = 4.131 cm
In the ΔABC,
cos 24° 24′ = \(\frac{BC}{AC}\)
0.9107 = \(\frac{BC}{10}\)
∴ BC = 9.107 cm
Area of the right angle = \(\frac{1}{2}\) × BC × AB
= \(\frac{1}{2}\) × 9.107 × 4.131
= \(\frac{37.62}{2}\)
Area of the triangle = 18.81 cm²

Question 5.
Find the angle made by a ladder of length 5m with the ground, if one of its end is 4m away from the wall and the other end is on the wall.
Solution:
AC is the length of the ladder.

In the right ΔABC,
cos θ = \(\frac{BC}{AC}\)
cos θ = \(\frac{4}{5}\)
= 0.8
cos θ = 0.8000
θ = 36° 52′
Angle made by a ladder with the ground is 36° 52′

Question 6.
In the given figure, HT shows the height of a tree standing vertically. From a point P, the angle of elevation of the top of the tree (that is ∠P) measures 42° and the distance to the tree is 60 metres. Find the height of the tree.
Solution:
Let the height of the tree HT be “x”

In the ΔHTP,
tan 42° = \(\frac{HT}{PT}\)
0.9004 = \(\frac{x}{60}\)
x = 0.9004 × 60
= 54.024
The height of the tree = 54.02 m

Students can download Maths Chapter 4 Geometry Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Additional Questions

I. Multiple Choice Questions.

Question 1.
The angle sum of a convex polygon with number of sides 7 is ………
(a) 900°
(b) 1080°
(c) 1444°
(d) 720°
Solution:
(a) 900°

Question 2.
What is the name of a regular polygon of six sides?
(a) Square
(b) Equilateral triangle
(c) Regular hexagon
(d) Regular octagon
Solution:
(c) Regular hexagon

Question 3.
One angle of a parallelogram is a right angle. The name of the quadrilateral is ………
(a) square
(b) rectangle
(c) rhombus
(d) kite
Solution:
(b) rectangle

Question 4.
If all the four sides of a parallelogram are equal and the adjacent angles are of 120° and 60°, then the name of the quadrilateral is ………
(a) rectangle
(b) square
(c) rhombus
(d) kite
Solution:
(c) rhombus

Question 5.
In a parallelogram ∠A : ∠B = 1 : 2. Then ∠A ………
(a) 30°
(b) 60°
(c) 45°
(d) 90°
Solution:
(b) 60°

Question 6.
Which of the following is a formula to find the sum of interior angles of a quadrilateral of w-sides?
(a) \(\frac{n}{2}\) × 180°
(b) (\(\frac{n+1}{2}\)) 180°
(c) (\(\frac{n-1}{2}\)) 180°
(d) (n – 2) 180°
Solution:
(d) (n – 2) 180°

Question 7.
Diagonal of which of the following quadrilaterals do not bisect it into two congruent triangles?
(a) rhombus
(b) trapezium
(c) square
(d) rectangle
Solution:
(b) trapezium

Question 8.
The point of concurrency of the medians of a triangle is known as ………
(a) circumcentre
(b) incentre
(c) orthocentre
(d) centroid
Solution:
(d) centroid

Question 9.
Orthocentre of a triangle is the point of concurrency of ………
(a) medians
(b) altitudes
(c) angle bisectors
(d) perpendicular bisectors of side
Solution:
(b) altitudes

Question 10.
ABCD is a parallelogram as shown. Find x and y.

(a) 1, 7
(b) 2, 6
(c) 3, 5
(d) 4, 4
Solution:
(c) 3, 5

Question 11.
A circle divides the plane into part ………
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(c) 3

Question 12.
The longest chord of a circle is a of the circle……….
(a) radius
(b) diameter
(c) chord
(d) secant
Solution:
(b) diameter

Question 13.
Opposite angles of a cyclic quadrilateral are ………
(a) supplementary
(b) complementary
(c) equal
(d) none of these
Solution:
(a) supplementary

Question 14.
The value of x from figure is if ‘O’ is the centre of the circle ………

(a) 20 cm
(b) 15 cm
(c) 12 cm
(d) 5 cm
Solution:
(d) 5 cm

Question 15.
If PQ = x and ‘O’ is the centre of the circle, then x= ………

(a) 7 cm
(b) 14 cm
(c) 8 cm
(d) 13 cm
Solution:
(b) 14 cm

Question 16.
In figure OM = ON = 8cm and AB = 30 cm, then CD = ………

(a) 15 cm
(b) 30 cm
(c) 40 cm
(d) 10 cm
Solution:
(b) 30 cm

Question 17.
O is the centre of a circle, ∠AOB = 100°. Then angle ∠ ACB = ………

(a) 80°
(b) 40°
(c) 50°
(d) 60°
Solution:
(c) 50°

Question 18.
In,a circle, with center O, ∠AOB = 20°, ∠BOC = 40°, arc BC = 4 Then length of arc AB will be ………

(a) 8 cm
(b) 6 cm
(c) 2 cm
(d) 1 cm
Solution:
(c) 2 cm

Question 19.
In the figure , OC = 3cm and radius of circle is 5 cm. Then AB = ………

(a) 4 cm
(b) 5 cm
(c) 6 cm
(d) 8 cm
Solution:
(d) 8 cm

Question 20.
O is the centre of the circle. The value of x in the given diagram is ………

(a) 100°
(b) 160°
(c) 200°
(d) 80°
Solution:
(d) 80°

II. Answer the following questions.

Question 1.
In the figure find x° and y°.
Solution:
∠ACD = ∠A + ∠B
(An exterior angle of a triangle is sum of its interior opposite angles)
120° = 50° + x°
x° = 120° – 50°
= 70°
In the triangle ABC

∠A + ∠B + ∠ACB = 180° (Sum of the angles of a Δ)
50° + x + ∠ACB = 180°
50° + 70° + ∠ACB = 180°
∠ACB = 180° – 120°
y = 60°
(OR)
∠ACD + ∠ACB = 180° (Angles of a linear pair)
∠ACB = 180° – 120°
= 60°
The value of x = 70° and y = 60°.

Question 2.
The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Solution:
Let the angles of the quadrilateral be 3x, 5x, 9x and 13x.
Sum of all the angles of quadrilateral = 360°.
3x + 5x + 9x + 13x = 360°
30x = 360°
x = \(\frac{360°}{30}\)
= 12°
3x = 3 × 12 = 36°
5x = 5 × 12 = 60°
9x = 9 × 12 = 108°
13x = 13 × 12 = 156°
The required angles of quadrilateral are 36°, 60°, 108° and 156°.

Question 3.
Diagonal AC of a parallelogram ABCD bisects ∠A. Show that

(i) it bisects ∠C also
(ii) ABCD is a rhombus.
Solution:
We have a parallelogram ABCD in which diagonals AC bisect ∠A.
∠DAC = ∠BAC
(i) To prove that AC bisects ∠C
∴ ABCD is a parallelogram

∴ AB || DC and AC is a transversal
∴ ∠1 = ∠3 (Alternate interior angle) …….(1)
Also BC || AD and AC is a transversal
∴ ∠2 = ∠4 (Alternate interior angle) …….(2)
But AC bisects ∠A
∴ ∠1 = ∠2 ……… (3)
From (1), (2) and (3) we get
∠3 = ∠4
∴ AC bisects ∠C.

(ii) To prove that ABCD is a rhombus.
In ΔABC, we have ∠1 = ∠4 [∴ ∠ 1 = ∠2 = ∠4]
∴ BC = AB (side opposite to equal angles are equal) ……..(4)
Similarly AD = DC …….. (5)
But ABCD is a parallelogram AB = DC (Opposite sides of a parallelogram) ………(6)
From (4), (5) and (6) we have AB = BC = CD = DA.
Thus ABCD is a rhombus.

Question 4.
ABCD is a parallelogram and AP and CQ are perpendiculars from vertex A and C on diagonal BD.
Show that

(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ.
Solution:
(i) In ΔAPB and ΔCQD we have
∠APB = ∠CQD (90° each)
AB = CD (opposite sides of parallelogram ABCD)
∠ABP = ∠CDQ (AB || CD and AD is a transversal)
Using ASA congruency we have,
ΔAPB ≅ ΔCQD

(ii) Since ΔAPB ≅ ΔCQD
∴ Their corresponding parts are equal.
∴ AP = CQ.

Question 5.
ABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.

Solution:
In rectangle ABCD, P is the mid-point of AB.
Q is the mid-point of BC. R is the mid-point of CD.
S is the mid-point of DA. AC is the diagonal.
Now in ΔABC,
PQ = \(\frac{1}{2}\) AC and PQ || AC ……. (1)
Similarly in ΔACD,
SR = \(\frac{1}{2}\) AC and SR || AC ……. (2)
From (1) and (2) we get,
PQ = SR and PQ || SR
Similarly by joining BD, we have
PS = QR and PS || QR
i.e. Both pairs of opposite sides of quadrilateral PQRS are equal and parallel.
∴ PQRS is a parallelogram.

Question 6.
In the figure A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
Solution:

O is the centre of the circle. ∠AOB = 60° and ∠BOC = 30°
Sum of all the angles of quadrilateral = 360°.
∠AOB + ∠BOC = ∠AOC
∴ ∠AOC = 30° + 60°
= 90°
∠ADC = \(\frac{1}{2}\) × 90°
= 45°

Question 7.
In the given figure A, B, C and D are four points on a circle, AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
Solution:
In ΔCDE,

Exterior ∠BEC = Sum of interior opposite angle
130° = ∠EDC + ∠ECD
130° = ∠EDC + 20°
130° – 20° = ∠EDC
110° = ∠EDC
∴ ∠BAC = ∠BDC = 110° (Both the triangles are standing on the same base)
∠BAC = 110°

Question 8.
In the given figure KLMN is a cyclic quadrilateral. KD is the tangent at K. If ∠N is a diameter ∠NLK = 40° and ∠LNM = 50°. Find ∠MLN and ∠DKL.

Solution:
LN is a diameter
∠LMN = ∠LKN = 90° (Angle in a semi-circle)
∴ ∠MLN = 90° – 50°
= 40°
∠LNK = 90° – 40°
= 50°
∠DKL = ∠LKN = 50° (angles in the alternate segment)
∴ ∠DKL = 50°
∠MLN = 40° and ∠DKL = 50°

Question 9.
In the given figure ∠PQR = 100°, where P, Q and R are points on a circle with centre ‘O’. Find ∠OPR.

Solution:
∠PQR is the angle subtended by the chord PR in the minor segment.
reflex ∠POR = 2∠PQR
= 2 × 100°
= 200°
Now ∠POR + reflex ∠POR = 360°
∠POR + 200° = 360°
∠POR = 360° – 200°
= 160°
From the given diagram, POR is an isosceles triangle (∴ PO = OR = radii)
∴ ∠OPR = ∠ORP (angles opposite to equal sides)
In ΔOPR,
∠OPR + ∠ORP + ∠POR = 180°
∠OPR + ∠OPR + 160° = 180°
2∠OPR = 180° – 160°
2∠OPR = 20°
∠OPR = \(\frac{20°}{2}\)
= 10°
∴ ∠OPR = 10°

Question 10.
AB and CD are two parallel chords of a circle which are on either sides of the centre such that AB = 10 cm and CD = 24 cm. Find the radius if the distance between AB and CD is 17 cm.
Solution:

Given AB = 10 cm, CD = 24 cm and PQ = 17 cm.
PC = PD = \(\frac{24}{2}\)
= 12 cm
AQ = QB = \(\frac{10}{2}\)
= 5 cm
Let OP be x; OQ = (17 – x)
In the ΔOPC,
OC² = OP² + PC²
= x² + 12²
In the ΔOAQ,
OA² = AQ² + QO²
= 5² + (17 – x)²
= 25 + 289 + x² – 34x
= 314 + x² – 34x
But OA² = OC²
314 + x² – 34x = x² + 144
-34x = 144 – 314
-34x = -170
34x = 170
x = \(\frac{170}{34}\)
= \(\frac{10}{2}\)
= 5
We know,
OC² = x²+ 144
= 5² + 144
= 25 + 144
OC² = 169
But OC = \(\sqrt{169}\)
= 13
Radius of the circle = 13 cm
= x² + 144

Students can download Maths Chapter 4 Geometry Ex 4.7 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.7

Multiple Choice Questions

Question 1.
The exterior angle of a triangle is equal to the sum of two ……….
(a) Exterior angles
(b) Interior opposite angles
(c) Alternate angles
(d) Interior angles
Solution:
(b) Interior opposite angles

Question 2.
In the quadrilateral ABCD, AB = BC and AD = DC Measure of ∠BCD is …………..

(a) 150°
(b) 30°
(c) 105°
(d) 72°
Solution:
(c) 105°
Hint:
Join BD
∠DBC = 54°; ∠BDC = 21°
∴ ∠BCD = 180° – (54° + 21°)
= 180° – 75°
= 105°

Question 3.
ABCD is a square, diagonals AC and BD meet at O. The number of pairs of congruent triangles with vertex O are ……….

(a) 6
(b) 8
(c) 4
(d) 12
Solution:
(a) 6

Question 4.
In the given figure CE || DB then the value of x° is ………

(a) 45°
(b) 30°
(c) 75°
(d) 85°
∠B = 360° – (∠A + ∠D + ∠BCD)
= 360° – (110° + 75° + 60°)
= 360° – 245°
= 115°
∠DBC = 115° – 30°
= 85°
∴ ∠x = 85° (BD || CE) Alternate angles are equal

Question 5.
The correct statement out of the following is ……..

(a) ΔABC ≅ ΔDEF
(b) ΔABC ≅ ΔEDF
(c) ΔABC ≅ ΔFDE
(d) ΔABC ≅ ΔFED
Solution:
(d) ΔABC ≅ ΔFED

Question 6.
If the diagonal of a rhombus are equal, then the rhombus is a ……..
(a) Parallelogram but not a rectangle
(b) Rectangle but not a square
(c) Square
(d) Parallelogram but not a square
Solution:
(c) Square

Question 7.
If bisectors of ∠A and ∠B of a quadrilateral ABCD meet at O, then ∠AOB is ……..
(a) ∠C + ∠D
(b) \(\frac{1}{2}\) (∠C + ∠D)
(c) \(\frac{1}{2}\) ∠C + \(\frac{1}{3}\) ∠D
(d) \(\frac{1}{3}\) ∠C + \(\frac{1}{2}\) ∠D
Solution:
(b) \(\frac{1}{2}\) (∠C + ∠D)

Question 8.
The interior angle made by the side in a parallelogram is 90° then the parallelogram is a …….
(a) rhombus
(b) rectangle
(c) trapezium
(d) kite
Solution:
(b) rectangle
Hint:
Opposite sides are equal and each angle is 90° then it is a rectangle.

Question 9.
Which of the following statement is correct?
(a) Opposite angles of a parallelogram are not equal
(b) Adjacent angles of a parallelogram are complementary.
(c) Diagonals of a parallelogram are always equal.
(d) Both pairs of opposite sides of a parallelogram are always equal.
Solution:
(d) Both pairs of opposite sides of a parallelogram are always equal.

Question 10.
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is ………
(a) 40°
(b) 35°
(c) 50°
(d) 45°
Solution:
(b) 35°
Hint:
3x – 40 + x + 20 + 2x – 10 = 180° (Sum of the angles of a triangle is 180°)
6x – 30 = 180°
6x = 180°+ 30°
x = \(\frac{210°}{6°}\)
= 35°

Question 11.
PQ and RS are two equal chords of a circle with centre O such that ∠POQ = 70°, then ∠ORS = ……….
(a) 60°
(b) 70°
(c) 55°
(d) 80°
Solution:
(c) 55°
Hint:

∠POQ = 70° (Vertically opposite Angle)
∠ORS and ∠OSR are equal. (OR = OS radius of the circle)
∠ORS + ∠OSR + ∠ROS = 180°
x° + x° + 70° = 180°
2x + 70° = 180°
2x = 180° – 70° = 110°
x = \(\frac{110°}{2}\) = 55°
∴ ∠ORS = 55°

Question 12.
A chord is at a distance of 15cm from the centre of the circle of radius 25cm. The length of the chord is ……….
(a) 25cm
(b) 20cm
(c) 40cm
(d) 18cm
Solution:
(c) 40cm
Hint:

In the right triangle OAC,
AC² = OA² – OC²
= 25² – 15²
= (25 + 15) (25 – 15)
= 40 × 10
AC² = 400
AC = \(\sqrt{400}\)
= 20
Length of the chord AB = 20 + 20 = 40 cm.

Question 13.
In the figure, O is the centre of the circle and ∠ACB = 40° then ∠AOB = ………

(a) 80°
(b) 85°
(c) 70°
(d) 65°
Solution:
(a) 80°
Hint:
∠AOB = 2∠ACB (The angle subtended by an arc of the circle at the centre is double the angle subtended at the remaining part of the circle.)
= 2 × 40° = 80°

Question 14.
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is ……..
(a) 30°
(b) 20°
(c) 15°
(d) 25
Solution:
(a) 30°
Hint:

∠A + ∠C = 180° (Sum of the opposite angle of cyclic quadrilateral is 180°)
4x + 2x = 180°
x = \(\frac{180°}{6}\)
= 30°

Question 15.
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4cm. The radius of the circle is ………

(a) 8cm
(b) 4cm
(c) 6cm
(d) 10cm
Solution:
(i) 10cm
Hint:

Let the radius OD be x.
OE = OB – BE
= x – 4 (OB radius of the circle)
In the ΔOED,
OD² = OE² + ED²
x² = (x – 4)² + 8²
x² = x² + 16 – 8x + 64
8x = 80
x = \(\frac{80}{8}\)
= 10 cm
Radius of the circle = 10 cm.

Question 16.
In the figure, PQRS and PTVS are two cyclic quadrilaterals, If ∠QRS = 80°, then ∠TVS = ………

(a) 80°
(b) 100°
(c) 70°
(d) 90°
Solution:
(a) 80°
Hint:
∠SPQ = 180° – 80° (Opposite angles of a cyclic quadrilateral PQRS)
= 100°
In the cyclic quadrilateral PVTS,
∠V = 180° – 100° = 80° (Opposite angles of a cyclic quadrilateral)

Question 17.
If one angle of a cyclic quadrilateral is 75°, then the opposite angle is ………
(a) 100°
(b) 105°
(c) 85°
(d) 90°
Solution:
(b) 105°
Hint:
Opposite angles = 180° – 75°
= 105° (Sum of the opposite angle is 180°)

Question 18.
In the figure, ABCD is a cyclic quadrilateral in which DC produced to E and CF is drawn parallel to AB such that ∠ADC = 80° and ∠ECF = 20°, then BAD = ?

(a) 100°
(b) 20°
(c) 120°
(d) 110°
Solution:
(c) 120°
Hint:
∠BAD = ∠ABC + ∠ECF (By exterior angle property)
= 100° + 20°
= 120°

Question 19.
AD is a diameter of a circle and AB is a chord If AD = 30cm and AB = 24cm then the distance of AB from the centre of the circle is ………
(a) 10cm
(b) 9cm
(c) 8cm
(d) 6cm
Solution:
(b) 9cm
Hint:

In ΔAOC,
AO = 15 cm
AC = \(\frac{1}{2}\) AB
= \(\frac{1}{2}\) × 24
= 12 cm
In ΔAOC,
OC² = AO² – AC²
= 15² – 12²
= 225 – 144
= 81
OC = \(\sqrt{81}\)
= 9 cm

Question 20.
In the given figure, If OP = 17cm, PQ = 30cm and OS is perpendicular to PQ, then RS is ……….

(a) 10cm
(b) 6cm
(c) 7cm
(d) 9cm
Solution:
(d) 9cm
Hint:
In ΔOPR, OP = 17cm, PR = 30/2 = 15 cm.
OR² = OP² – PR²
= 17² – 15²
= (17 + 15) (17 – 15)
= 32 × 2
OR² = \(\sqrt{64}\)
= 8 cm
RS = OS – OR
= 17 – 8
= 9 cm