Students can download Maths Chapter 6 Trigonometry Ex 6.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.4
Question 1.
Find the value of the following:
(i) sin 49°
(ii) cos 74° 39′
(iii) tan 54° 26′
(iv) sin 21° 21′
(v) cos 33° 53′
(vi) tan 70° 17′
Solution:
(i) sin 49° = 0.7547
(ii) cos 74° 39′ = cos 74° 39′ + 3′
From the table we get,
cos 74° 36′ = 0.2656
Mean difference of 3 = 8
cos 74° 39′ = 0.2656 – 8
= 0.2648
(iii) tan 54° 26′ = tan 54° 24′
tan 54° 24′ = 1.3968
Mean difference of 2 = 17
tan 54° 26’ = 1.3968 + 17
= 1.3985
![]()
(iv) sin 21° 21′ = sin 21° 18’+ 3’
sin 21° 18’ = 0.3633
Mean difference of 3 = 8(+)
sin 21° 21′ = 0.3633 + 8
= 0.3641
(v) cos 33° 53′ = cos 33° 48’ + 5′
cos 33° 48′ = 0.8310
Mean difference of 5 = 8
cos 33° 53′ = 0.8310 – 8
= 0.8302
(vi) tan 70° 17′ = tan 70° 12’+ 5’
tan 70° 12′ = 2. 7776
Mean difference of 5 = 131
tan 70° 17′ = 2. 7776 + 131
= 2.7907
![]()
Question 2.
Find the value of θ if
(i) sin θ = 0.9975
(ii) cos θ = 0.6763
(iii) tan θ = 0.0720
(iv) cos θ = 0.0410
(v) tan θ = 7.5958
Solution:
(i) sin θ = 0.9975
From the table we get,
= 0.9974 + 0.0001
= 85° 54′ + 1′
= 85° 55′ (or) 85° 56′ (or) 85° 57
(ii) cos θ = 0.6763
= 0. 6769 – 0.0006′
= 47° 24′ + 3′
= 47° 27
(iii) tan θ = 0. 0720
= 0. 0717 + 0.0003
= 4° 6′ + 1′
= 4° 7′
![]()
(iv) cos θ = 0.0410
= 0.0419 – 0.0009
= 87° 36′ + 3′
= 87° 39′
(v) tan θ = 7. 5958
= 7. 5958 + 0 (from the natural table)
= 82° 30′ (tangent table)
Question 3.
Find the value of the following:
(i) sin 65° 39′ + cos 24° 57’ + tan 10° 10′
(ii) tan 70° 58′ + cos 15° 26′ – sin 84° 59′
Solution:
(i) sin 65° 39′ = 0.9111
cos 24° 57′ = 0.9066
tan 10° 10′ = 0.1793
sin 65° 39′ + cos 24° 57′ + tan 10° 10′
= 0.9111 + 0.9066 + 0.1793
= 1.9970
sin 65° 39′ + cos 24° 57′ + tan 10° 10′ = 1.9970
![]()
(ii) tan 70° 58′ = 2. 8982
cos 15° 26′ = 0. 9639
sin 84° 59′ = 0.9962
tan 70° 58′ + cos 15° 26′ – sin 84° 59′
= 2. 8982 + 0. 9639 – 0.9962
= 3.8621 – 0.9962
= 2.8659
Question 4.
Find the area of a right triangle whose hypotenuse is 10 cm and one of the acute angle is 24°24′.
Solution:
In the ΔABC,
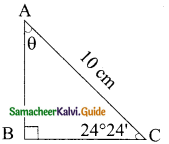
sin 24° 24′ = \(\frac{AB}{AC}\)
0. 4131 = \(\frac{AB}{10}\)
∴ AB = 4.131 cm
In the ΔABC,
cos 24° 24′ = \(\frac{BC}{AC}\)
0.9107 = \(\frac{BC}{10}\)
∴ BC = 9.107 cm
Area of the right angle = \(\frac{1}{2}\) × BC × AB
= \(\frac{1}{2}\) × 9.107 × 4.131
= \(\frac{37.62}{2}\)
Area of the triangle = 18.81 cm²
![]()
Question 5.
Find the angle made by a ladder of length 5m with the ground, if one of its end is 4m away from the wall and the other end is on the wall.
Solution:
AC is the length of the ladder.
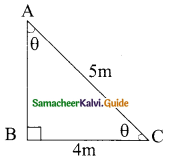
In the right ΔABC,
cos θ = \(\frac{BC}{AC}\)
cos θ = \(\frac{4}{5}\)
= 0.8
cos θ = 0.8000
θ = 36° 52′
Angle made by a ladder with the ground is 36° 52′
![]()
Question 6.
In the given figure, HT shows the height of a tree standing vertically. From a point P, the angle of elevation of the top of the tree (that is ∠P) measures 42° and the distance to the tree is 60 metres. Find the height of the tree.
Solution:
Let the height of the tree HT be “x”
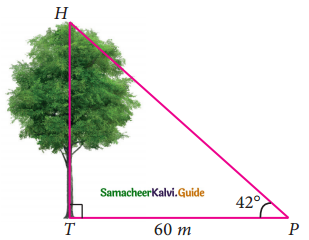
In the ΔHTP,
tan 42° = \(\frac{HT}{PT}\)
0.9004 = \(\frac{x}{60}\)
x = 0.9004 × 60
= 54.024
The height of the tree = 54.02 m
![]()