Category: Class 10

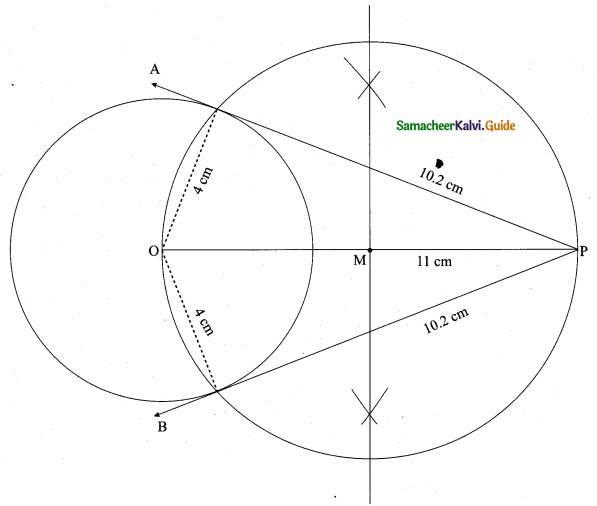
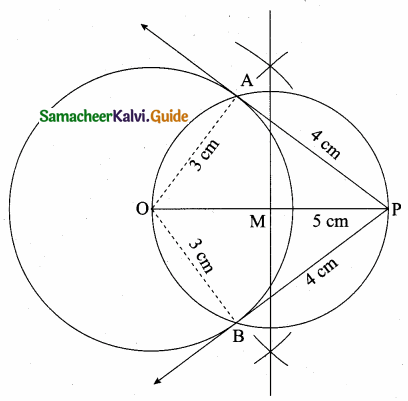
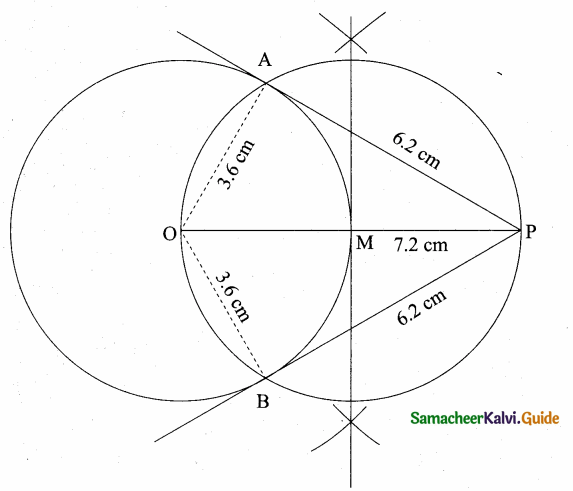
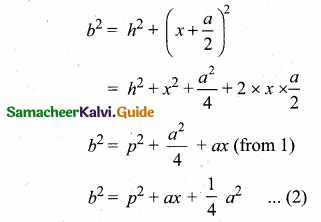Students can download Maths Chapter 6 Trigonometry Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 6 Trigonometry Additional Questions

I. Multiple Choice Questions

Question 1.
(1 – sin² θ) sec² θ = …………
(1) 0
(2) 1
(3) tan² θ
(4) cos² θ
Answer:
(2) 1
Hint: (1 – sin² θ) sec² θ = cos² θ sec² θ = cos² θ \(\frac{1}{\cos ^{2} \theta}\) = 1

Question 2.
(1 + tan² θ) sin² θ = ………….
(1) sin² θ
(2) cos² θ
(3) tan² θ
(4) cot² θ
Answer:
(3) tan² θ
Hint: (1 + tan² θ) sin² θ = sec² θ sin² θ = \(\frac{1}{\cos ^{2} \theta}\) sin² θ = \(\frac{\sin ^{2} \theta}{\cos ^{2} \theta}\) = tan² θ

Question 3.
(1 – cos² θ) (1 + cot² θ) = ………..
(1) sin² θ
(2) 0
(3) 1
(4) tan² θ
Answer:
(3) 1
Hint: (1 – cos² θ) (1 + cot² θ) = sin² θ cosec² θ = sin² θ. \(\frac{1}{\sin ^{2} \theta}\)= 1

Question 4.
sin (90° – θ) cos θ + cos (90° – θ) sin θ = …………..
(1) 1
(2) 0
(3) 2
(4) -1
Answer:
(1) 1
Hint: sin (90° – θ) cos θ + cos (90° – θ) sin θ = cos θ cos θ + sin θ sin θ = cos² θ + sin² θ = 1

Question 5.
1 – \(\frac{\sin ^{2} \theta}{1+\cos \theta}\) = ……………….
(1) cos θ
(2) tan θ
(3) cot θ
(4) cosec θ
Answer:
(1) cos θ
Hint:

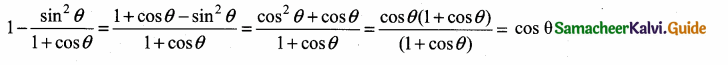
Question 6.
cos⁴ x – sin⁴ x = ……………
(1) 2 sin² x – 1
(2) 2 cos² x – 1
(3) 1 + 2 sin² x
(4) 1 – 2 cos² x
Answer:
(2) 2 cos² x – 1
Hint:
cos⁴ x – sin⁴ x (cos² x)² – (sin² x)²
= (cos² x + sin²x) (cos² x – sin²x)
= 1 (cos² x – sin² x)
= cos² x – (1 – cos² x)
cos² x – 1 + cos² x
= 2 cos² x – 1.

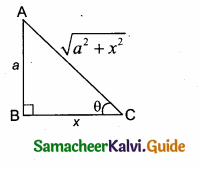
Question 7.
If tan θ = \(\frac { a }{ x } \) , then the value of \(\frac{x}{\sqrt{a^{2}+x^{2}}}\) = ………………
(1) cos θ
(2) sin θ
(3) cosec θ
(4) sec θ
Answer:
(1) cos θ
Hint:

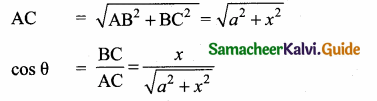
Question 8.
If x = a sec θ, y = b tan θ, then the value of \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = ………………..
(1) 1
(2) -1
(3) tan² θ
(4) cosec² θ
Answer:
(1) 1
Hint:

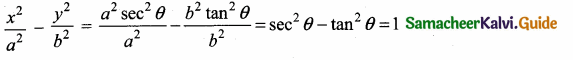
Question 9.
\(\frac{\sec \theta}{\cot \theta+\tan \theta}\) = ………..
(1) cot θ
(2) tan θ
(3) sin θ
(4) – cot θ
Answer:
(3) sin θ
Hint:

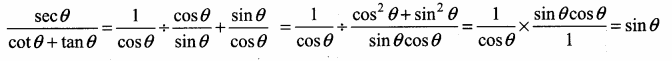
Question 10.

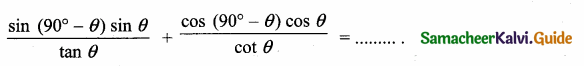
Answer:
(1) tan θ
(2) 1
(3) -1
(4) sin θ
Answer:
(2) 1
Hint:

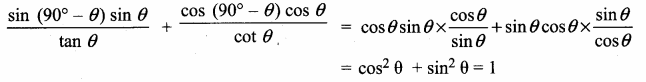
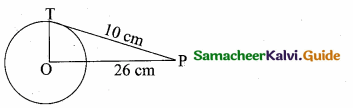
Question 11.
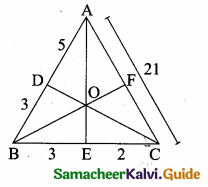
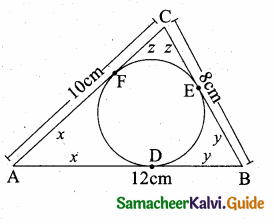
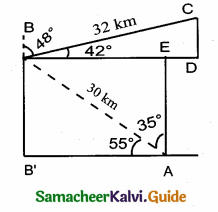
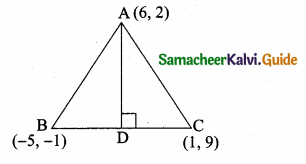
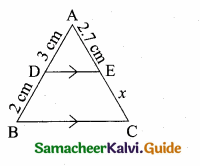
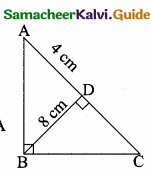
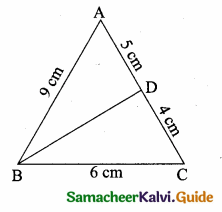
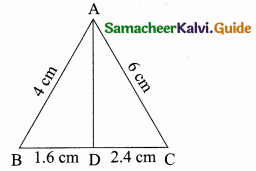
In the adjoining figure, AC = ………….

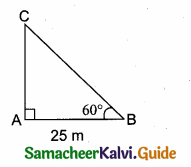
(1) 25m
(2) 25 \(\sqrt { 3 }\) m
(3) \(\frac{25}{\sqrt{3}}\)
(4) 25 \(\sqrt { 2 }\) m
Answer:
(2) 25 \(\sqrt { 3 }\) m
Hint:
tan θ = \(\frac { AC }{ AB } \) ⇒ tan 60° = \(\frac { AC }{ 25 } \) ⇒ AC = 25 \(\sqrt { 3 }\) m

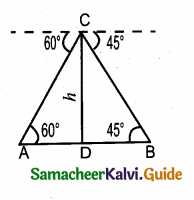
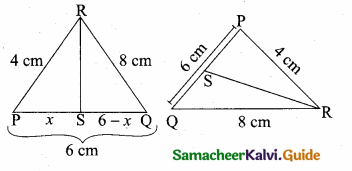
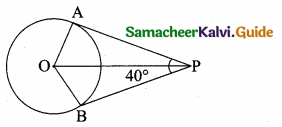
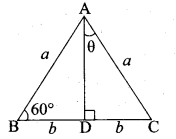
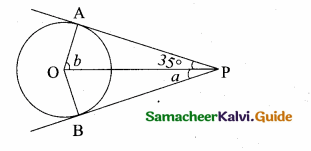
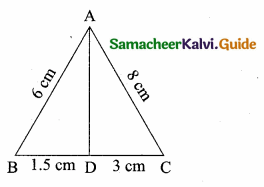
Question 12.
In the adjoining figure ∠ABC =

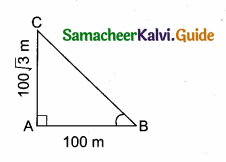
(1) 45°
(2) 30°
(3) 60°
(4) 50°
Answer:
(3) 60°
Hint:
tan B = \(\frac { AC }{ AC } \) = \(\frac{100 \sqrt{3}}{100}\) = \(\sqrt { 3 }\) ⇒ ∴ tan B = \(\sqrt { 3 }\) ⇒ ∠B = 60°

Question 13.
A man is 28.5 m away from a tower. His eye level above the ground is 1.5 m. The angle of elevation of the tower from his eyes is 45°. Then the height of the tower is …………..
(1) 30 m
(2) 27.5 m
(3) 28.5 m
(4) 27 m
Answer:
(1) 30 m
Hint:
tan 45° = \(\frac { AB }{ BC } \)

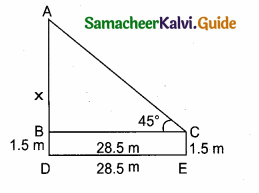
1 = \(\frac { x }{ 28.5 } \) ⇒ x = 28.5
Height of tower = 28.5 + 1.5 = 30 m

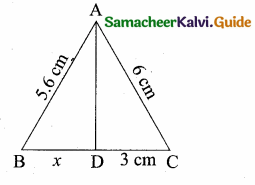
Question 14.
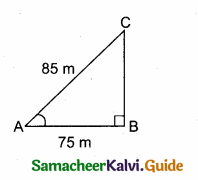
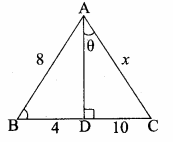
In the adjoining figure, sin θ = \(\frac { 15 }{ 17 } \) Then BC = ………….
(1) 85 m
(2) 65 m
(3) 95 m
(4) 75 m
Answer:
(4) 75 m
Hint:
sin θ = \(\frac { BC }{ AC } \) ⇒ \(\frac { 15 }{ 17 } \) = \(\frac { BC }{ 85 } \) ⇒ BC = \(\frac{85 \times 15}{17}\) = 75 m

Question 15.
(1 + tan² θ) (1 – sin θ) (1 + sin θ) = …………..
(1) cos² θ – sin² θ
(2) sin² θ – cos² θ
(3) sin² θ + cos² θ
(4) 0
Answer:
(3) sin² θ + cos² θ
Hint:
(1 + tan² θ) (1 – sin θ) (1 + sin θ) = (1 + tan² θ) (1 – sin² θ) = sec² θ × cos² θ = sec² θ × cos² θ = sec² θ × \(\frac{1}{\sec ^{2} \theta}\) = 1 = sin² θ + cos² θ

Question 16.
(1 + cot² θ) (1 – cos θ) (1 + cos θ) = ………………….
(1) tan² θ – sec² θ
(2) sin² θ – cos² θ
(3) sec² θ – tan² θ
(4) cos² θ – sin² θ
Answer:
(3) sec² θ – tan² θ
Hint:
(1 + cot² θ) (1 – cos θ) (1 + cos θ) = (1 + cot² θ) (1 – cos² θ) = cosec² θ. sin² θ
= \(\frac{1}{\sin ^{2} \theta}\) sin² θ = 1 = sec² θ – tan² θ.

Question 17.
(cos² θ – 1) (cot² θ + 1) + 1 = ……………….
(1) 1
(2) -1
(3) 2
(4) 0
Answer:
(4) 0
Hint:
(cos² θ – 1) (cot² θ + 1) + 1 = – sin² θ (cosec² θ) + 1 = – sin² θ \(\frac{1}{\sin ^{2} \theta}\) + 1 = -1 + 1 = 0

Question 18.
\(\frac{1+\tan ^{2} \theta}{1+\cot ^{2} \theta}\) = …………….
(1) cos² θ
(2) tan² θ
(3) sin² θ
(4) cot² θ
Answer:
(2) tan² θ
Hint:

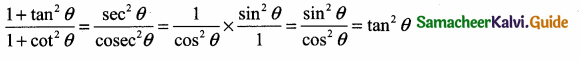
Question 19.
Sin² θ + \(\frac{1}{1+\tan ^{2} \theta}\) …………
(1) cosec² θ + cot² θ
(2) cosec² θ – cot² θ
(3) cot² θ – cosec² θ
(4) sin² θ – cos² θ
Answer:
(2) cosec² θ – cot² θ
Hint:
sin² θ + \(\frac{1}{1+\tan ^{2} \theta}\) = sin² θ + \(\frac{1}{\sec ^{2} \theta}\) = sin² θ + cos² θ = 1 cosec² θ – cot² θ

Question 20.
9 tan² θ – 9 sec² θ = ……..
(1) 1
(2) 0
(3) 9
(4) -9
Answer:
(4) -9
Hint:
9 tan² θ – 9 sec² θ = 9(tan² θ – sec² θ) = 9(-1) = -9

Question 21.
The length of shadow of a tower on the plane ground is \(\sqrt { 3 }\) times the height of the tower. The angle of elevation of sum is …………..
(1) 45°
(2) 30°
(3) 60°
(4) 90°
Ans.
(2) 30°
Hint: Let the height of the tower be “x”
Lenght of the shadow is \(\sqrt { 3 }\) x

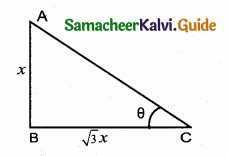
In the right ∆ ABC, tan θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{x}{\sqrt{3} x}=\frac{1}{\sqrt{3}}\)
= tan 30°
θ = 30°

Question 22.
A ladder makes an angle of 60° with the ground, when placed against a wall. If the foot of the ladder is 2m away from the wall, then the length of the ladder (in metres) is …………
(1) \(\frac{4}{\sqrt{2}}\) m
(2) 4 \(\sqrt { 3 }\) m
(3) 2 \(\sqrt { 2 }\) m
(4) 4 m
Answer:
(4) 4 m
Hint:
Let the length of the ladder be x.

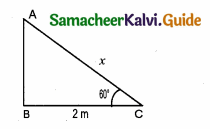
In ∆ ABC, cos 60° = \(\frac { BC }{ AC } \) = \(\frac { 2 }{ x } \)
\(\frac { 1 }{ 2 } \) = \(\frac { 2 }{ x } \) ⇒ x = 4m

Question 23.
The angle of depression of a car parked on the road from the top of a 150m high tower is 30°. The distance of the car from the tower (in metres) is ……….
(1) 150 \(\sqrt { 3 }\) m
(2) 150 \(\sqrt { 2 }\)
(3) 75 cm
(4) 50 \(\sqrt { 3 }\) m
Answer:
(4) 50 \(\sqrt { 3 }\) m
Hint:
Let the distance of the car from the tower is “x” m
In ∆ ABC, tan 30° = \(\frac { AB }{ BC } \)

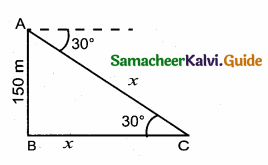
\(\frac{1}{\sqrt{3}}\) = \(\frac { 150 }{ x } \) ⇒ x = 150 \(\sqrt { 3 }\) m

Question 24.
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45°. Then the height of the tower (in meters) is ……….
(1) 50 \(\sqrt { 3 }\) m
(2) 50 m
(3) \(\frac{50}{\sqrt{2}}\) m
(4) \(\frac{50}{\sqrt{3}}\) m
Answer:
(4) \(\frac{50}{\sqrt{3}}\) m
Hint:
Let the height of the AB be “x”
On ∆ ABC
tan 45° = \(\frac { AB }{ BC } \)

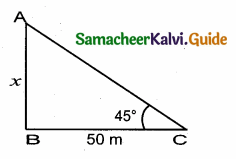
1 = \(\frac { x }{ 50 } \) ⇒ x = 50 m

Question 25.
If x = a cos θ and y = b sin θ, then b²x² + a²y² = ……………
(1) a²b²
(2) ab
(3) a4b4
(4) a² + b²
Answer:
(1) a²b²
Hint:
b²a² cos² θ + a² b² sin² θ = a²b² (cos² θ + sin² θ) = a²b² × 1 = a²b²

II. Answer The Following Questions.

Question 1.
Prove that sec² θ + cosec² θ = sec² θ cosec² θ
Answer:
L.H.S = sec² θ + cosec² θ

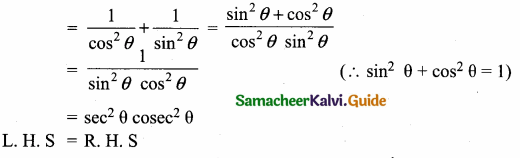
Question 2.
Prove that \(\frac{\sin \theta}{1-\cos \theta}\) = cosec θ + cot θ.
Answer:

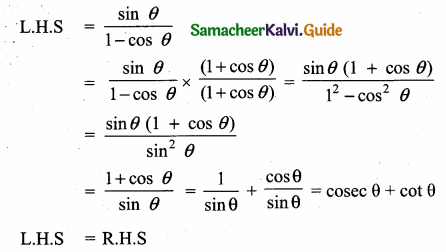
Question 3.
Prove that \(\frac{\cos \theta}{\sec \theta-\tan \theta}\) = 1 + sin θ
Answer:

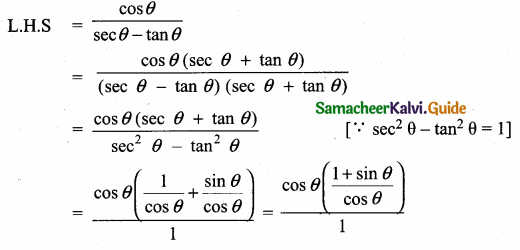
= 1 + sin θ = R.H.S
L.H.S = R.H.S

Question 4.
Prove that sec θ (1 – sin θ) (sec θ + tan θ) = 1
Answer:
L.H.S = sec θ (1 – sin θ) (sec θ + tan θ)

Question 5.
Prove that \(\frac{\sin \theta}{\csc \theta+\cot \theta}=1\) – cos θ
Answer:

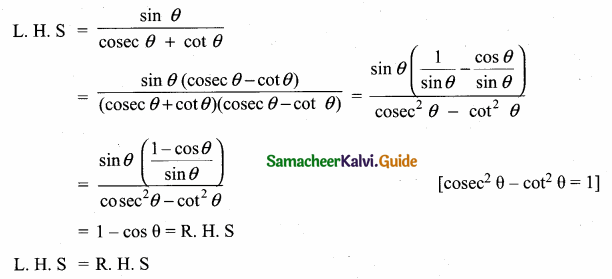
Question 6.
Prove the identify \(\frac{\sin \theta}{\csc \theta}+\frac{\cos \theta}{\sec \theta}=1\)
Answer:

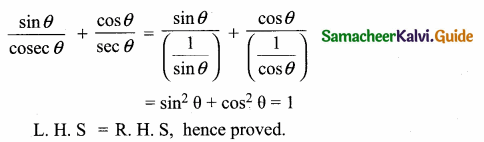
Question 7.
Prove the identify \(\sqrt{\frac{1-\cos \theta}{1+\cos \theta}}\) = cosec θ – cot θ
Answer:

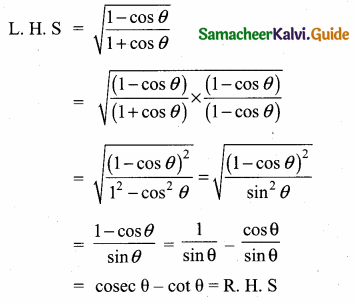
(∵ 1 – cos² θ = sin² θ)
L.H.S = R.H.S

Question 8.
Prove the identity [cosec (90° – θ) – sin (90° – θ)] [cosec θ – sin θ] [tan θ + cot θ] = 1
Answer:
Now, [cosec (90° – θ) – sin (90° – θ)] [cosec θ – sin θ] [tan θ + cot θ]

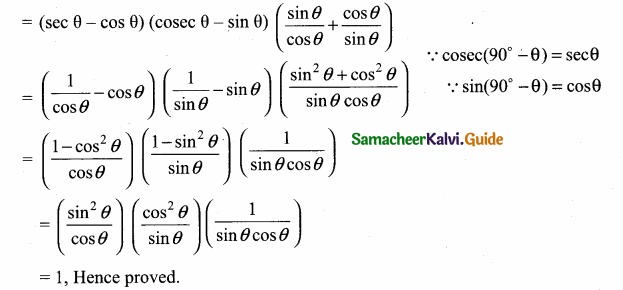
Question 9.
A kite is flying with a string of length 200 m. If the thread makes an angle 30° with the ground, find the distance of the kite from the ground level. (Here, assume that the string is along a straight line.)
Answer:
Let h denote the distance of the kite from the ground level.
In the figure, AC is the string
Given that ∠CAB = 30° and AC = 200 m.
In the right ∆ CAB,
sin 30 = \(\frac { BC }{ AC } \)

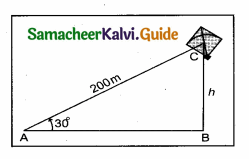
sin 30 = \(\frac { h }{ 200 } \)
⇒ h = 200 sin 30°
∴ h = 200 × \(\frac { 1 }{ 2 } \) = 100 m
Hence the distance of the kite from the ground level is 100 m.

Question 10.
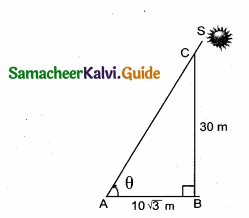
Find the angular elevation (angle of elevation from the ground level) of the Sun when the length of the shadow of a 30 m long pole is 10 \(\sqrt { 3 }\) m.
Answer:
Let S be the position of the Sun and BC be the pole.
Let AB denote the length of the shadow of the pole.
Let the angular elevation of the Sun be θ.
Given that AB = 10 \(\sqrt { 3 }\) m and BC = 30 m
In the right ∆ CAB,tan θ = \(\frac { BC }{ AB } \) = \(\frac{30}{10 \sqrt{3}}=\frac{3}{\sqrt{3}}\)
⇒ tan θ = \(\sqrt { 3 }\)
∴ θ = 60°
Thus, the angular elevation of the Sun from the ground level is 60°

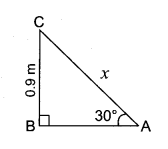
Question 11.
A ramp for unloading a moving truck, has an angle of elevation of 30°. If the top of the ramp is 0.9 m above the ground level, then find the length of the ramp.
Answer:
Let AC be the length of the ramp and AC = “x” metre
In the right angled ∆ ABC,
∠A = 30° and BC = 0.9 m
sin 30° = \(\frac { BC }{ AC } \)

\(\frac { 1 }{ 2 } \) = \(\frac { 0.9 }{ x } \)
x = 0.9 × 2 = 1.8 m
∴ Length of the ramp x = 1.8 m

Question 12.
A girl of height 150 cm stands in front of a lamp-post and casts a shadow of length 150 \(\sqrt { 3 }\) cm on the ground. Find the angle of elevation of the top of the lamp-post.
Answer:
The height of the girl (BC) = 150 cm
Length of the shadow = 150 \(\sqrt { 3 }\) cm
Let θ be the angle of elevation of the lamp post.

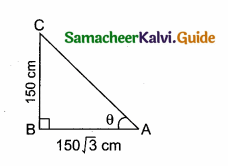
In θ = \(\frac{150}{150 \sqrt{3}}\) = \(\frac{1}{\sqrt{3}}\)

tan 30° = \(\frac{1}{\sqrt{3}}\) ⇒ ∴ θ = 30°
∴ Angle of elevation of the lamp post = 30°

Question 13.
Prove that \(\sqrt{\cot ^{2} \theta-\cos ^{2} \theta}\) = cot θ . cos θ
Answer:

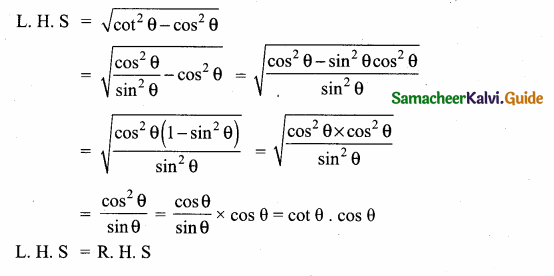
Question 14.
Prove that \(\frac{1+\sin \theta}{\cos \theta}+\frac{\cos \theta}{1+\sin \theta}\) = 2 sec θ
Answer:

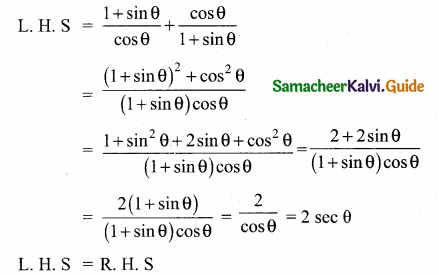
Question 15.
A tower is 100 \(\sqrt { 3 }\) metres high. Find the angle of elevation of its top from a point 100 metres away from its foot.
Answer:
Let MN be the tower of height 100 \(\sqrt { 3 }\) m
“O” be the point of observation such that OM = 100 m

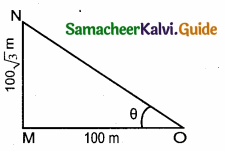
Let 0 be the angle of elevation
In the right ∆ OMN, we have
tan θ = \(\frac { MN }{ OM } \) = \(\frac{100 \sqrt{3}}{100}\)
tan θ = \(\sqrt { 3 }\) = tan 60°
∴ θ = 60°
Hence the angle of elevation is 60°

Question 16.
If sin θ = x and sec θ = y, then find the value of cot θ
Answer:
Given sin θ = x
y = sec θ = \(\frac{1}{\cos \theta}\)
∴ cos θ = \(\frac { 1 }{ y } \) ⇒ cot θ = \(\frac{\cos \theta}{\sin \theta}=\frac{1}{y} \div x\)
cot θ = \(\frac { 1 }{ xy } \)

Question 17.
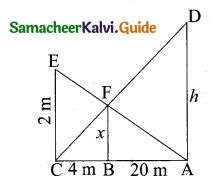
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° ( see figure).
Answer:
In the figure, let AC is the rope and AB is the pole. In right ∆ ABC, we have
\(\frac { AB }{ AC } \) = sin 30°
But, sin 30° = \(\frac { 1 }{ 2 } \)
\(\frac { AB }{ AC } \) = \(\frac { 1 }{ 2 } \) ⇒ \(\frac { AB }{ 20 } \) = \(\frac { 1 }{ 2 } \)
[∵ AC = 20 m]

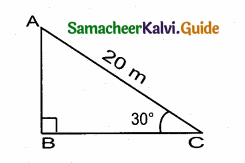
AB = 20 × \(\frac { 1 }{ 2 } \) = 10 m
Thus, the required height of the pole is 10 m.

Question 18.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Answer:
Let in the right ∆ AOB,
OB = Length of the string
AB = 60 m = Height of the kite.
In the right ∆ OAB

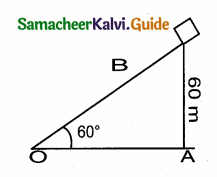
sin 60° = \(\frac { AB }{ OB } \)
\(\frac{\sqrt{3}}{2}\) = \(\frac { 60 }{ OB } \)
\(\sqrt { 3 }\) × OB = 120
OB = \(\frac{120}{\sqrt{3}}=\frac{120 \times \sqrt{3}}{3}\)
Lenght of the string = 40 \(\sqrt { 3 }\) = 40 \(\sqrt { 3 }\) m

Question 19.
Prove that sin⁶ θ + cos⁶ θ + 3 sin² θ cos² θ = 1
Answer:
L. H. S = sin⁶ θ + cos⁶ θ + 3 sin² θ cos² θ
= (sin² θ)³ + (cos² θ)³ + 3 sin² θ cos² θ
= (sin² θ + cos² θ)³ – 3 × sin² θ cos² θ (sin² θ + cos² θ) + 3 × sin² θ cos² θ
[Using a³ + h³ = (a + h)³ – 3 ab (a + h)]
= 1³ – 3 sin² θ cos² θ (1) + 3 sin² θ cos² θ
= 1 – 3 sin² θ cos² θ + 3 sin² θ cos² θ
= 1
L.H. S = R. H. S

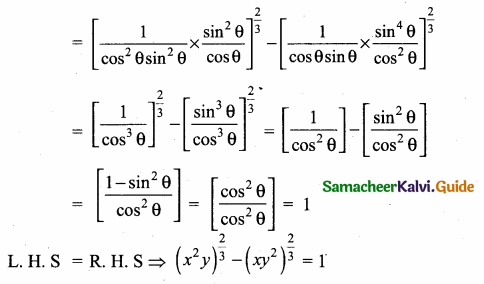
III. Answer The Following Questions.

Question 1.
Prove that \(\sqrt{\frac{\sec \theta-1}{\sec \theta+1}}+\sqrt{\frac{\sec \theta+1}{\sec \theta-1}}=2\) cosec θ
Answer:

Question 2.
Prove that \(\frac{1+\cos A}{\sin A}+\frac{\sin A}{1+\cos A}\) = 2 cosec A.
Answer:

Question 3.
Prove that 2 (sin⁶ θ + cos⁶ θ) – 3 (sin⁴ θ + cos⁴ θ) + 1 = θ
Answer:
consider, sin⁶ θ + cos⁶ θ
= (sin² θ)³ + (cos² θ)³
[Using a³ + b³ = (a + b)³ – 3 ab(a + b)]
= (sin² θ + cos² θ)³ – 3 sin² θ cos² θ (sin² θ + cos² θ)
= 1 – 3 sin² θ cos² θ
Now sin⁴ θ + cos⁴ θ = (sin² θ)² + (cos² θ)² (a² + b² = (a + b)² – 2 ab)
= (sin² θ + cos² θ)² – 2 (sin² θ cos² θ)
= 1 – 2 (sin² θ cos² θ)
L. H. S = 2 (sin⁶ θ + cos⁶ θ) – 3 (sin⁴ θ + cos⁴ θ) + 1
= 2(1 – 3 sin² θ cos² θ) – 3 (1 – 2 sin² θ cos² θ) + 1
= 2 – 6 sin² θ cos² θ – 3 + 6 sin² θ cos² θ + 1
= 3 – 3 = 0
L.H.S. = R.H.S

Question 4.
Prove that \(\frac{\sin \left(90^{\circ}-\theta\right)}{1+\sin \theta}+\frac{\cos \theta}{1-\cos \left(90^{\circ}-\theta\right)}\) = 2 sec θ
Answer:

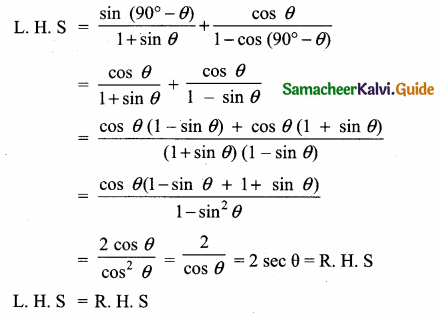
Question 5.
Prove that \(\frac{\tan \theta}{1-\cot \theta}+\frac{\cot \theta}{1-\tan \theta}\) = 1 + sec θ cosec θ
Answer:

Question 6.
Prove that \(\frac{\sin \left(90^{\circ}-\theta\right)}{1-\tan \theta}+\frac{\cos \left(90^{\circ}-\theta\right)}{1-\cot \theta}\) = cos θ + sin θ
Answer:

L.H.S = R.H.S
Hence Proved

Question 7.
Prove that \(\frac{\tan \left(90^{\circ}-\theta\right)}{\csc \theta+1}+\frac{\csc \theta+1}{\cot \theta}\) = 2 sec θ
Answer:

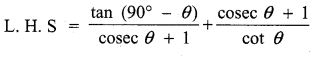
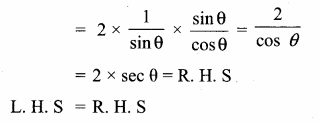
Question 8.
Prove that

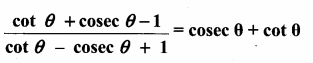
Answer:

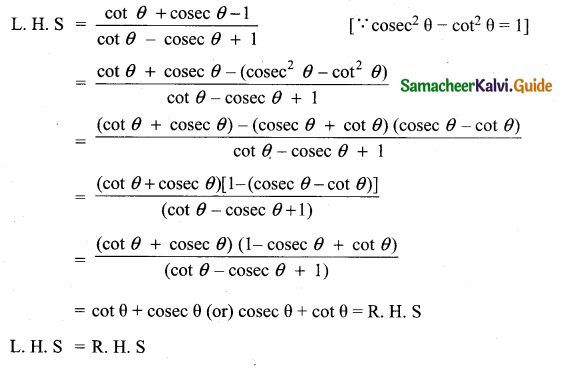
Question 9.
Prove that (1 + cot θ – cosec θ) (1 + tan θ + sec θ) = 2
Answer:
L.H.S = (1 + cot θ – cosec θ) (1 + tan θ + sec θ)

L. H. S = R. H. S
Hence proved

Question 10.
Prove that \(\frac{\sin \theta-\cos \theta+1}{\sin \theta+\cos \theta-1}=\frac{1}{\sec \theta-\tan \theta}\)
Answer:

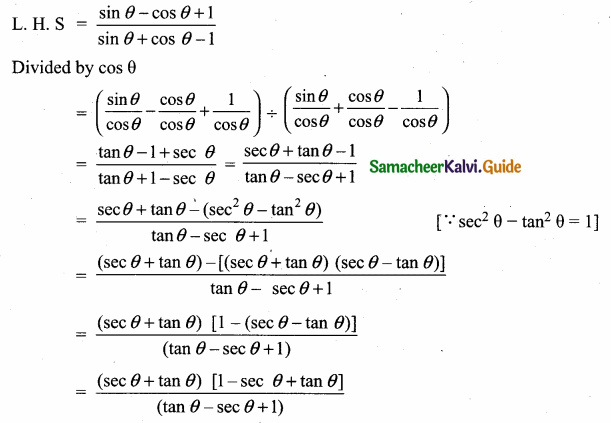
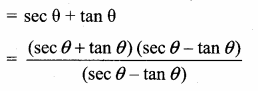
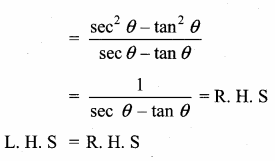
Question 11.
Prove that

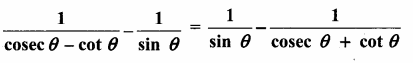
Answer:

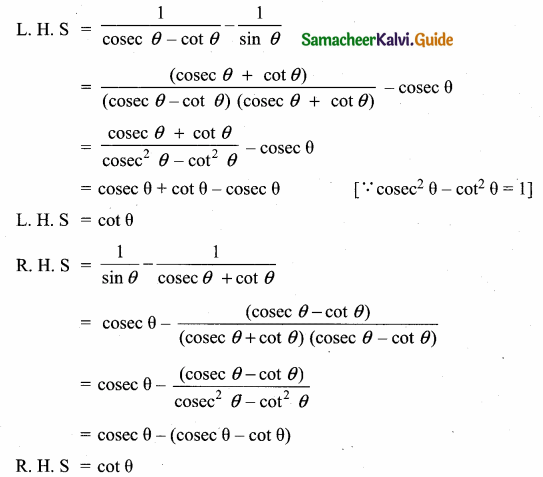
LHS = RHS
Hence proved

Question 12.
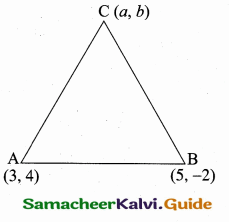
If tan θ = n tan α and sin θ = m sin α, then prove that cos² θ = \(\frac{m^{2}-1}{n^{2}-1}, n \neq \pm 1\)
Answer:
Given tan θ = n tan α and sin θ = m sin α
Let us eliminate using cosec² α – cot² α = 1

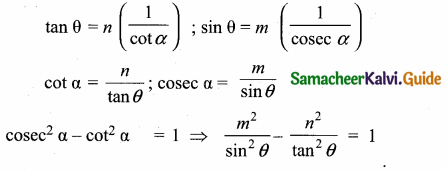
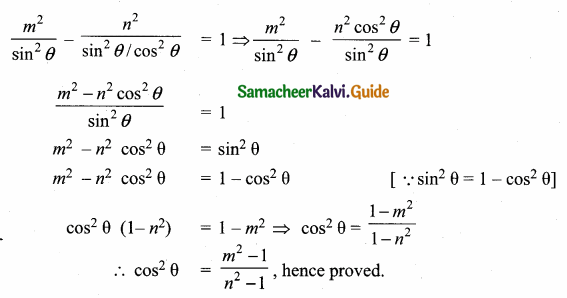
Question 13.
If sin θ, cos θ and tan θ are in G. P., then prove that cot⁶ θ – cot² θ = 1.
Answer:
Given, sin θ, cos θ, tan θ are in G. P., To prove cot⁶ θ – cot² θ = 1

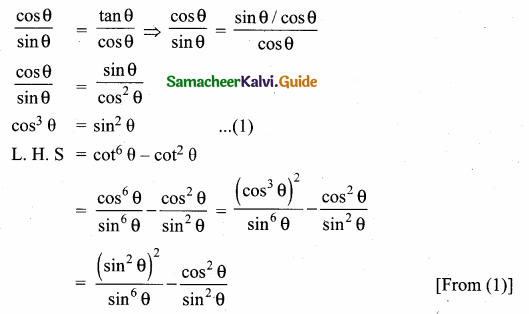
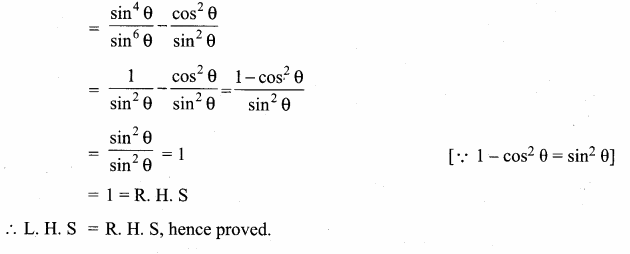
Question 14.
A person in an helicopter flying at a height of 700 m, observes two objects lying opposite to each other on either bank of a river. The angles of depression of the objects are 30° and 45°. Find the width of the river. (\(\sqrt { 3 }\) = 1. 732)
Answer:
Let C be the point of observation.
The objects A and B lying opposite to each other on either bank of a river.
Width of the river AB = AD + BD
In the right ∆ ACD,

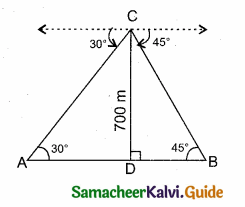
tan 30° = \(\frac { CD }{ AD } \) ⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac { 700 }{ AD } \)
∴ AD = 700 \(\sqrt { 3 }\)
In the right ∆ BCD tan 45° = \(\frac { CD }{ BD } \)
1 = \(\frac { 700 }{ BD } \) ⇒ BD = 700 m
∴ Width of the river = AD + BD
= 700 \(\sqrt { 3 }\) + 700 = 700 (\(\sqrt { 3 }\) + 1)
= 700 (1.732 + 1) = 700 × 2.732 m
= 1912.400 m
∴ Width of the river = 1912.4 m

Question 15.
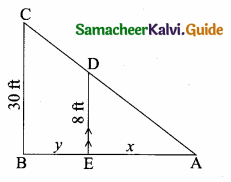
A person X standing on a horizontal plane, observes a bird flying at a distance of 100 m from him at an angle of elevation of 30°. Another person Y standing on the roof of a 20 m high building, observes the bird at the same time at an angle of elevation of 45°. If X and Y are on the opposite sides of the bird, then find the distance of the bird from Y.
Answer:
Let the position of the bird be “B”
Given, AY = 20 m, CD = 20 m, BX = 100 m, ∠BXD = 30° and ∠BYC = 45°
In the right ∆ BXD, sin 30° = \(\frac { BD }{ BX } \)
\(\frac { 1 }{ 2 } \) = \(\frac { BD }{ 100 } \) ⇒ BD = \(\frac{100 \times 1}{2}\) = 50 m

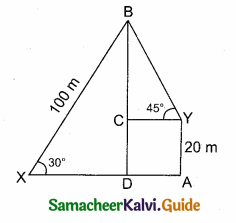
BC = BD – DC
BC = 50 m – 20 m = 30 m
In the right ∆ YBC, sin 45° = \(\frac { BC }{ BY } \)
\(\frac{1}{\sqrt{2}}\) = \(\frac { 30 }{ BY } \) ⇒ BY = 30\(\sqrt { 2 }\)
∴ Distance of the bird from the person Y is 30\(\sqrt { 2 }\) m

Question 16.
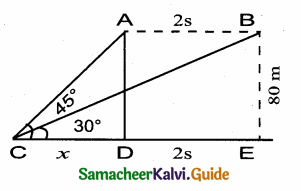
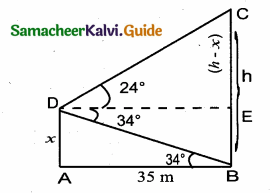
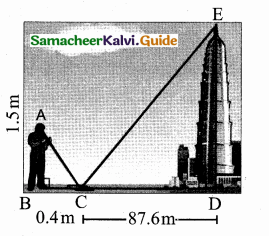
A boy is standing at some distance from a 30 m tall building and his eye level from the ground is 1.5 m. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Answer:
In the given figure A, B, C is a horizontal at the level of the boy
AD = A’D – AA’
AD = 30 – 1.5 = 28.5 m
Let the distance walked by the student CB is ‘x’ m.
Let AB be ‘y’ m
In the right ∆ ABD,tan 60° = \(\frac { AD }{ AB } \)
\(\sqrt { 3 }\) = \(\frac { 28.5}{ y } \)
y =\(\frac{28.5}{\sqrt{3}}\) …….(1)

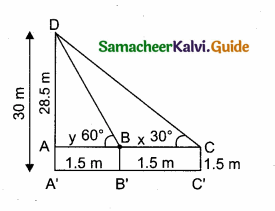
In the right ∆ ACD,tan 30° = \(\frac { AD }{ AC } \)
\(\frac{1}{\sqrt{3}}\) = \(\frac{28.5}{x+y}\) ⇒ x + y = 28.5 \(\sqrt { 3 }\)
y = 28.5 \(\sqrt { 3 }\) – x ………..(2)
From (1) and (2) we get,
\(\frac{28.5}{\sqrt{3}}\) = 28.5 \(\sqrt { 3 }\) – x
28.5 = 28.5 × 3 – \(\sqrt { 3 }\) x
\(\sqrt { 3 }\) x = 28.5 × 3 – 28.5
\(\sqrt { 3 }\) x = 28.5 × (3 – 1) = 28.5 × 2
\(\sqrt { 3 }\) x = 57.0 m
x = \(\frac{57}{\sqrt{3}}=\frac{57 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}\) ⇒ x = \(\frac{57 \times \sqrt{3}}{3}\) = 19 \(\sqrt { 3 }\) m.
∴ The distance walked by the boy = 19 \(\sqrt { 3 }\) m.

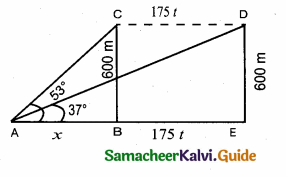
Question 17.
A straight highway leads to the foot of a tower. A man standing on the top of the tower spots a van at an angle of depression of 30°. The van is approaching the tower with a uniform speed. After 6 minutes, the angle of depression of the van is found to be 60°. How many more minutes will it take for the van to reach the tower?
Answer:
Let A be the point of observation. B and C be the positions of the van. Let the height of the tower AD be x. Let the speed of the van be “s”. C is the position of van after 6 minutes.
Time taken by the van from B to C be minutes.
Distance BC = 6 × s = 6 s (speed × time)
Let distance between CD be t s (time × speed)

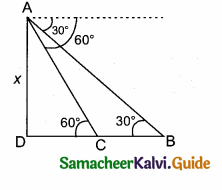
In the right ∆ ABD, tan 30° = \(\frac { AD }{ DB } \)


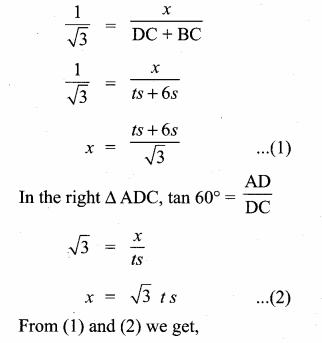
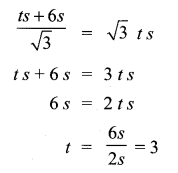
∴ 3 more minutes will be taken by the van to reach the tower.

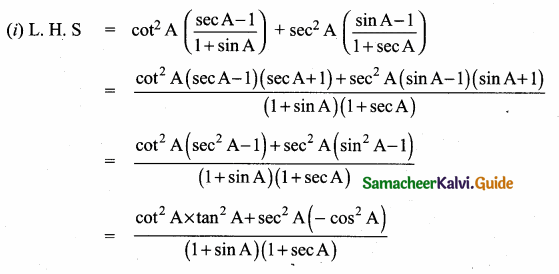
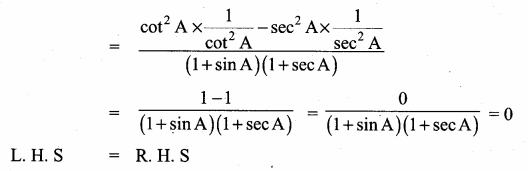
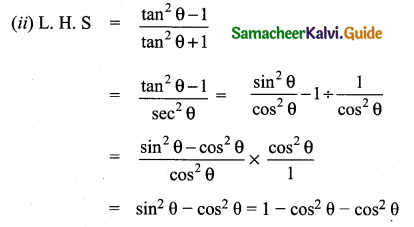
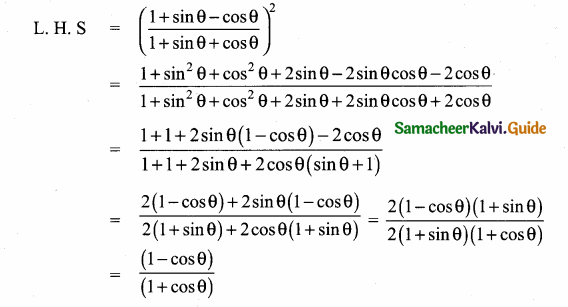
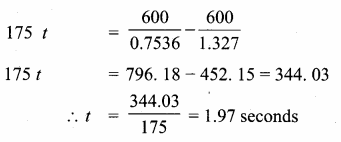
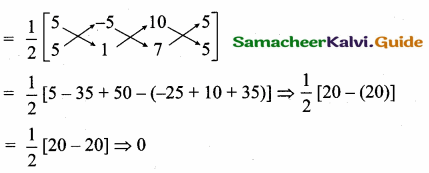
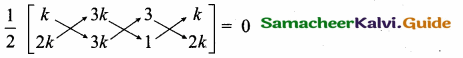
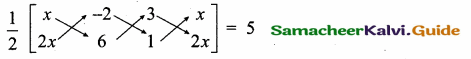
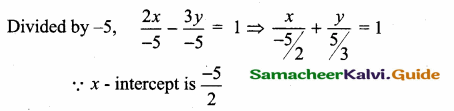
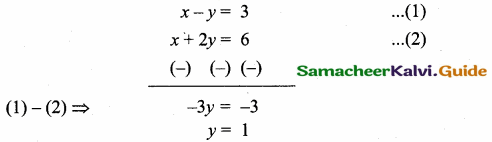
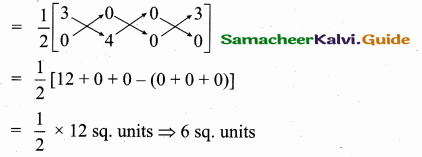
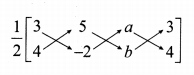
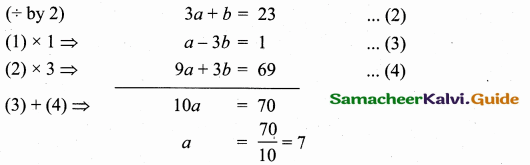
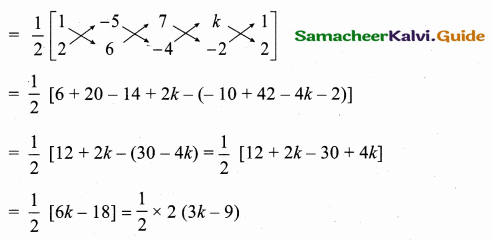
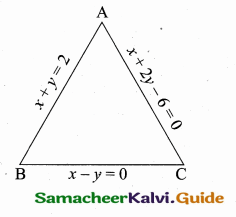
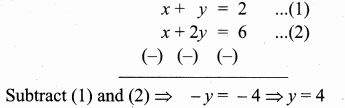
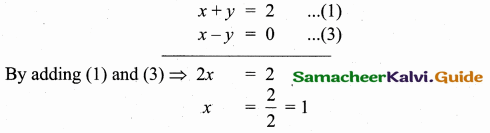
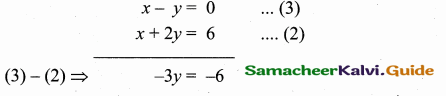
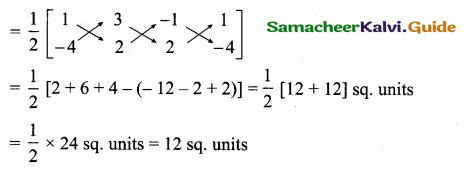
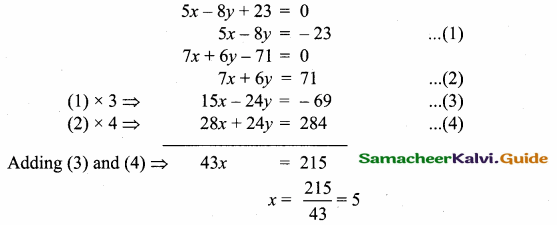
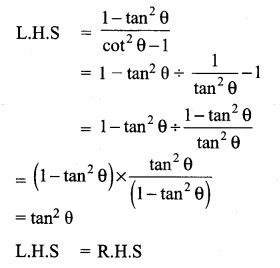
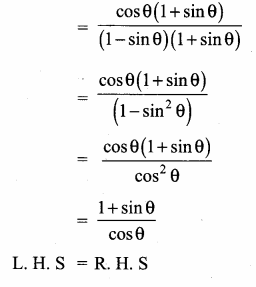
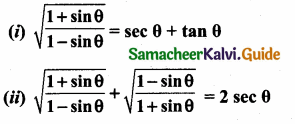
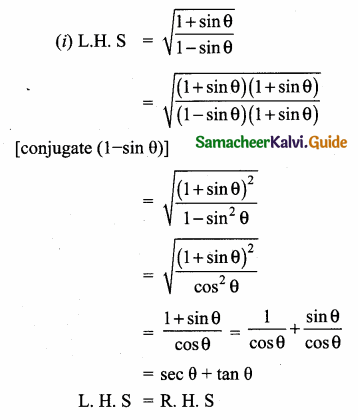
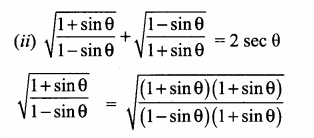
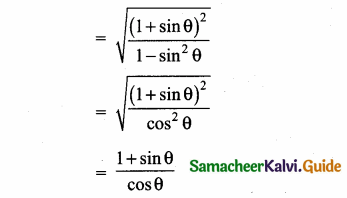
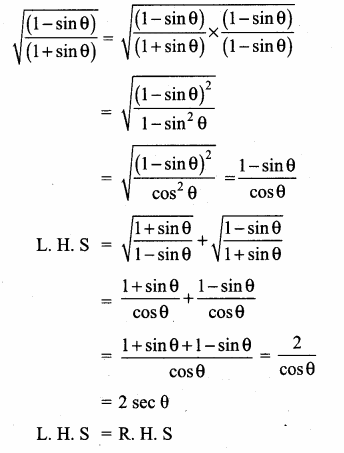
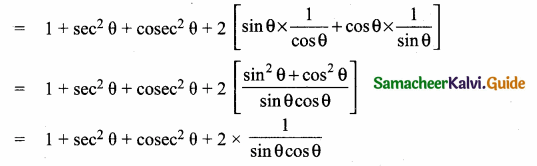
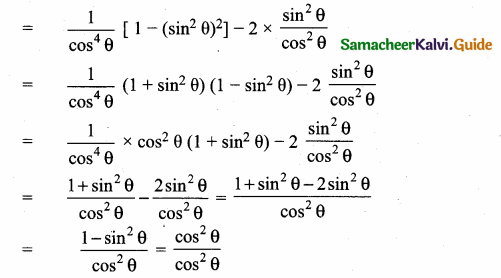
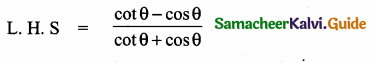
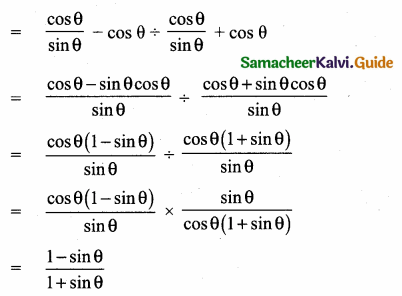
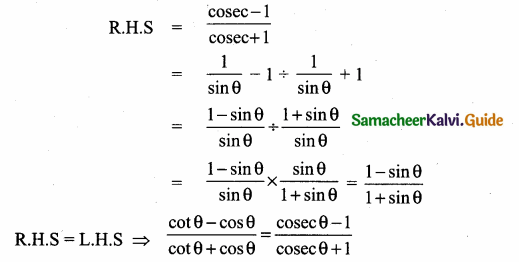
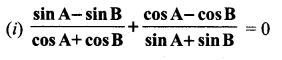
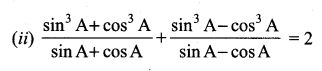
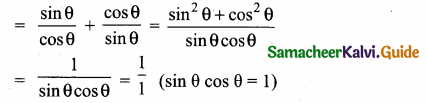
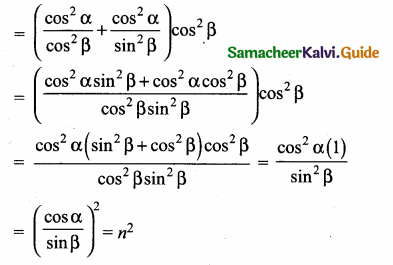
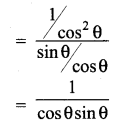
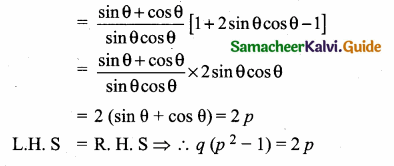
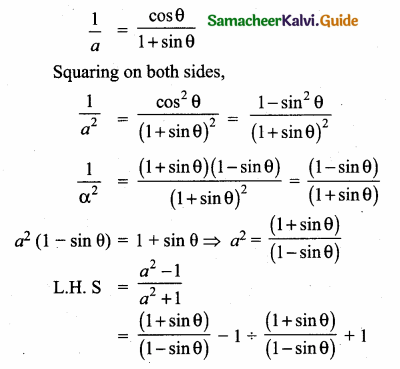
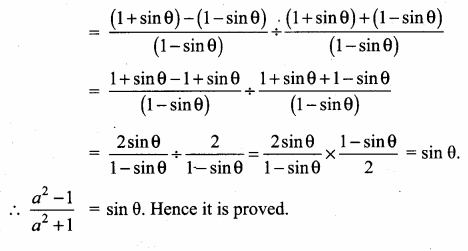
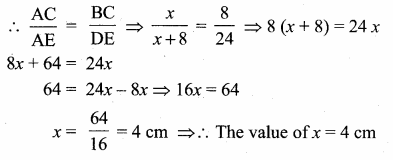
Students can download Maths Chapter 6 Trigonometry Unit Exercise 6 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 6 Trigonometry Unit Exercise 6

Question 1.
Prove that
(i) cot² A \(\left(\frac{\sec A-1}{1+\sin A}\right)\) + sec² A \(\left(\frac{\sin A-1}{1+\sec A}\right)\) = 0
(ii) \(\frac{\tan ^{2} \theta-1}{\tan ^{2} \theta+1}\) = 1 – 2 cos² θ
Answer:


Hence it is proved

= 1 – cos² θ
L.H.S = R.H.S
Hence it is proved.

Question 2.
Prove that
\(\left(\frac{1+\sin \theta-\cos \theta}{1+\sin \theta+\cos \theta}\right)^{2}=\left(\frac{1-\cos \theta}{1+\cos \theta}\right)\)
Answer:

LHS = RHS
Hence it is proved

Question 3.
If x sin² θ + y cos² θ = sin θ cos θ and x sin θ = y cos θ, then prove that x² + y² = 1.
Answer:
Given x sin² θ + y cos² θ = sin θ cos θ
x sin θ = y cos θ ……..(1)
x sin³ θ + y cos³ θ = sin θ cos θ
x sin θ (sin² θ) + y cos θ (cos² θ) = sin θ cos θ
x sin θ (sin² θ) + x sin θ (cos² θ) = sin θ cos θ
x sin θ (sin² θ + cos² θ) = sin θ cos θ
x sin θ = sin θ cos θ
x = cos θ
substitute x = cos θ in (1)
cos θ sin θ = y cos θ y = sin θ
L. H. S = x² + y² = cos² θ + sin² θ = 1
L.H. S = R.H.S
Hence it is proved.

Question 4.
If a cos θ – b sin θ = c, then prove that (a sin θ + b cos θ) = ± \(\sqrt{a^{2}+b^{2}-c^{2}}\).
Answer:
Given a cos θ – b sin θ = c
Squaring on both sides
(a cos θ – b sin θ)² = c²
a² cos² θ + b² sin² θ – 2 ab cos θ sin θ = c²
a² (1 – sin² θ) + b² (1 – cos² θ) – 2 ab cos θ sin θ = c²
a² – a² sin² θ + b² – b² cos² θ – 2 ab cos θ sin θ = c²
– a² sin² θ – B² – cos² θ – 2 ab cos θ sin θ = – a² – b² + c²
a² sin² θ + b² cos² θ + 2 ab cos θ sin θ = a² + b² – c²
(a sin θ + b cos θ)² – a² + b² – c²
a sin θ + b cos θ = ± \(\sqrt{a^{2}+b^{2}-c^{2}}\)
Hence it is proved.

Question 5.
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45° . The bird flies away horizontally in such away that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30° . Determine the speed at which the bird flies. (\(\sqrt { 3 }\) = 1.732)
Answer:

A is the initial position of the bird B is the final position of the bird Let the speed of the bird be “s”
Distance = speed × time
∴ AB = 2x
Let CD be x
∴ CE = x + 2s
In the ∆ CDA, tan 45° = \(\frac { AD }{ CD } \)
1 = \(\frac { 80 }{ x } \)
x = 80 ……..(1)
In the ∆ BCE
tan 30° = \(\frac { BE }{ CE } \)
\(\frac{1}{\sqrt{3}}\) = \(\frac { 80 }{ x+2s } \)
x + 2s = 80 \(\sqrt { 3 }\)
x = 80 \(\sqrt { 3 }\) – 2 s ………(2)
From (1) and (2) we get
80 \(\sqrt { 3 }\) – 2 s = 80
80 \(\sqrt { 3 }\) – 80 = 2 s ⇒ 80 (\(\sqrt { 3 }\) – 1) = 2 s
s = \(\frac{80(\sqrt{3}-1)}{2}\) = 40 (1.732 – 1) = 40 × 0.732 = 29.28
Speed of the flying bird = 29.28 m/sec

Question 6.
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37° at a given point. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
Answer:
Let C is the initial and D is the final position of the aeroplane.
Let the time taken by the aeroplane be “t”
∴ CD = 175 t (Distance = speed × time)

Let AB be x
∴ AE = x + 175 t
In the right ∆ ABC


∴ Time taken is 1. 97 seconds

Question 7.
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away.
(i) How far is B to the North of A?
(ii) How far is B to the West of A?
(iii) How far is C to the North of B?
(iv) How far is C to the East of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
Answer:

(i) To find the distance of B to the north of A
In ∆ ABB,

Distance of B to the North of A = 24. 58 km

(ii) Distance from B to the west of A is AB’
In ∆ ABB’
cos 55° = \(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}\)
0.5736 = \(\frac{A B^{\prime}}{30}\)
∴ AB’ = 0.5736 × 30 = 17. 21 km
Distance of B to the West of A is 17. 21 km

(iii) Distance from C to the North of B is CD
In the right ∆ BCD, sin 42° = \(\frac { CD }{ BC } \)
0.6691 = \(\frac { BD }{ 32 } \)
∴ CD = 0.6691 × 32 = 21.41 km
Distance of C to the North B is 21. 41 km

(iv) The distance of C to the East of B is BD
In the right ∆ BDC, cos 42° = \(\frac { BD }{ BC } \)
0.7431 = \(\frac { BD }{ 32 } \)
∴ BD = 0.7431 × 32
= 23.78 km
Distance of C to the East of B is 23.78 km.

Question 8.
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is 200 \(\left(\frac{\sqrt{3}+1}{\sqrt{3}}\right)\) meters, find the height of the lighthouse
Answer:
Let A and B the position of the first ship and the second ship
Distance = 200 \(\left(\frac{\sqrt{3}+1}{\sqrt{3}}\right)\) m
Let the height of the light house CD be “h”

In the right ∆ ACD, tan 60° = \(\frac { CD }{ AD } \)
\(\sqrt { 3 }\) = \(\frac { h }{ AD } \)
∴ AD = \(\frac{h}{\sqrt{3}}\) ……….(1)
In the right ∆ BCD
tan 45° = \(\frac { DC }{ BD } \)
1 = \(\frac { h }{ BD } \)
∴ BD = h
Distance between the two ships = AD + BD
200 (\(\frac{\sqrt{3}+1}{\sqrt{3}}\)) = \(\frac{h}{\sqrt{3}}\) + h ⇒ 200 (\(\sqrt { 3 }\) + 1) = h + \(\sqrt { 3 }\) h
200 (\(\sqrt { 3 }\) + 1) = h(1 + \(\sqrt { 3 }\)) ⇒ h = \(\frac{200(\sqrt{3}+1)}{(1+\sqrt{3})}\)
h = 200
Height of the light house = 200 m

Question 9.
A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34° . Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)
Answer:
Let the height of the statue be “h” m
Let AD be x
∴ EC = h – x
In the right ∆ ABD,

tan 34° = \(\frac { AD }{ AB } \)
0.6745 = \(\frac { x }{ 35 } \)
∴ x = 0.6745 × 35 ⇒ x = 23.61 m
In the right ∆ DEC ⇒ tan 24° = \(\frac { EC }{ DE } \)
0.4452 = \(\frac { h-x }{ 35 } \) ⇒ h – x = 0.4452 × 35
h – 23.61 = 15. 58 ⇒ h = 15.58 + 23.61 = 39.19 m
Height of the statue = 39.19 m

Students can download 10th Social Science History Chapter 3 World War II Questions and Answers, Notes, Samacheer Kalvi 10th Social Science Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Social Science Solutions History Chapter 3 World War II

Samacheer Kalvi 10th Social Science World War II Text Book Back Questions and Answers

I. Choose the correct answer

Question 1.
When did the Japanese formally sign of their surrender?
(a) 2 September, 1945
(b) 2 October, 1945
(c) 15 August, 1945
(d) 12 October, 1945
Answer:
(a) 2 September, 1945

Question 2.
Who initiated the formation of League of Nations?
(a) Roosevelt
(b) Chamberlain
(c) Woodrow Wilson
(d) Baldwin
Answer:
(a) Roosevelt

Question 3.
Where was the Japanese Navy defeated by the US Navy?
(a) Battle of Guadalcanal
(b) Battle of Midway
(c) Battle of Leningrad
(d) Battle of El Alamein
Answer:
(b) Battle of Midway

Question 4.
Where did the US drop its first atomic bomb?
(a) Kavashaki
(b) Innoshima
(c) Hiroshima
(d) Nagasaki
Answer:
(c) Hiroshima

Question 5.
Who were mainly persecuted by Hitler?
(a) Russians
(b) Arabs
(c) Turks
(d) Jews
Answer:
(d) Jews

Question 6.
Which Prime Minister of England who signed the Munich Pact with Germany?
(a) Chamberlain
(b) Winston Churchill
(c) Lloyd George
(d) Stanley Baldwin
Answer:
(a) Chamberlain

Question 7.
When was the Charter of the UN signed?
(a) June 26, 1942
(b) June 26, 1945
(c) January 1, 1942
(d) January 1, 1945
Answer:
(b) June 26, 1945

Question 8.
Where is the headquarters of the International Court of Justice located?
(a) New York
(b) Chicago
(c) London
(d) The Hague
Answer:
(d) The Hague

II. Fill in the blanks

1. Hitler attacked ……………… which was a demilitarized zone.
2. The alliance between Italy, Germany and Japan is known as ………………
3. ……………… started the Lend-Lease programme.
4. Britain Prime Minister ……………… resigned in 1940.
5. Saluting the bravery of the ……………… Churchill said that “Never was so much owed by so many to so few”.
6. ……………… is a device used to find out the enemy aircraft from a distance.
7. The Universal Declaration of Human Rights set forth fundamental human rights in ……………… articles.
8. After the World War II ……………… was voted into power in Great Britain.

Answers:

1. Rhineland
2. Rome – Berlin
3. Roosevelt
4. Chamberlain
5. Royal Air force
6. Radar
7. 30
8. Labour party

III. Choose the correct statement

Question 1.
(i) Banking was a major business activity among Jews.
(ii) Hitler persecuted the Jews.
(iii) In the concentration camps Jews were killed.
(iv) The United Nations has currently 129 member countries in it.
(a) (i) and (ii) are correct
(b) (i) and (Hi) are correct
(c) (iii) and (iv) are correct
(d) (i) is correct and (ii), (iii) and (iv) are wrong
Answer:
(a) (i) and (ii) are correct

Question 2.
Assertion (A): President Roosevelt realised that the United States had to change its policy of isolation.
Reason (R): He started a programme of Lend Lease in 1941.
(a) Both A and R are correct
(b) A is right but R is not the correct reason
(c) Both A and R are wrong
(d) R is right but it has no relevance to A
Answer:
(a) Both A and R are correct

IV. Match the Following

Answers:
A. (v)
B. (iv)
C. (i)
D. (ii)
E. (iii)

V. Answer the questions briefly

Question 1.
Mention the important clauses of the Treaty of Versailles relating to Germany.
Answer:

1. Germany was forced to give up territories to the west, north and east of the German border.
2. Germany had to be disarmed and was allowed to retain only a very restricted army, navy and air force.
3. Germany was expected to pay huge military and civilian cost of the war to the allied nations (approx. $ 25 billion).

Question 2.
Who were the three prominent dictators of the post World War I?
Answer:
The three prominent dictators of the post-World War I were Mussolini (Italy), Hitler (Germany) and Franco (Spain).

Question 3.
How did Hitler get the support from the people of Germany?
Answer:
Hitler was able to sway away the emotions of the German people by his great speeches. He promised them that he will return back the glorious Germany. His racial superiority of the Germans as a pure Aryan race and a deep-rooted hatred for jews made him get the support of his people.

Question 4.
Describe the Pearl Harbour incident.
Answer:
Pearl Harbour incident took place in December 1941 when japan attacked American naval installations in Pearl Harbour, Hawaii, without warning to cripple America’s Pacific fleet. Many battle ships and numerous fighter planes were destroyed. The US declared war on Japan, with Britain and China. This brought together both the Asia Pacific and the European war into one common cause. Most importantly, it brought the United States with its enormous resources into the war as a part of the Allies.

Question 5.
What do you know of Beveridge Report?
Answer:
The Report that was published in the United Kingdom in 1942 to improve the general welfare of the people is called as Beveridge Report. It proposed that the government should provide citizens with adequate income, healthcare, education housing and employment to overcome poverty and disease thereby improve general welfare.

Question 6.
Name the Bretton Woods Twins.
Answer:
The World Bank and the International Monetary Fund.

Question 7.
What are the objectives of the IMF?
Answer:

1. To foster global monetary co-operation
2. To secure Financial Stability
3. To facilitate International Trade
4. To promote high employment and sustainable economic growth.
5. To reduce poverty around the world.

VI. Answer the questions given under each caption

Question 1.
Battle of Stalingrad

(a) When did Germany attack Stalingrad?
Answer:
In August 1942, Germany attacked Stalingrad.

(b) What were the main manufactures of Stalingrad?
Answer:
The main manufactures of Stalingrad were armaments and tractors.

(c) What was the name of the plan formulated by Hitler to attack Stalingrad?
Answer:
Fall Blau or Operation Blue

(d) What is the significance of the Battle of Stalingrad?
Answer:
The people of Russia were grateful for Stalin’s conduct of the war. They regarded him as ‘a prodigy of patience, tenacity and vigilance, almost omnipresent, almost omniscient.

Question 2.
Japanese Aggression In South-east Asia

(a) Name the South-east Asian countries which fell to the Japanese.
Answer:
Guam, the Philippines, Hong Kong, Singapore, Malaya, the Dutch East Indies and the Burma all fell to the Japanese.

(b) Account for the setback of Allies in the Pacific region?
Answer:
The Allies had a setback in the Pacific region because of their inadequate preparation. The local people had to face the atrocities of the Japanese.

(c) What is the significance of Battle of Midway?
Answer:
The U.S. navy defeated the Japanese navy in the Battle of Midway. Thus, the battle is in favour of the Allies.

(d) What happened to the Indians living in Burma?
Answer:
The Indians living in Burma walked all the way to the Indian border facing many hardships. Many died of disease and exhaustion.

Question 3.
General Assembly and Security Council

(a) List the permanent member countries of the Security Council.
Answer:
The United States, Britain, France, Russia and China.

(b) What is the Holocaust?
Answer:
The word ‘holocaust’ is used to describe the genocide of nearly six million Jews by the Germans during the Second World War.

(c) Who was the Chairperson of the UN Commission on Human Rights?
Answer:
The widow of US President Franklin Roosevelt was the chairperson of the UN Commission on Human Rights.

(d) What is meant by veto?
Answer:
A veto is the power to unilaterally stop an official action, especially the enactment of legislation.

VII. Answer in detail

Question 1.
Attempt an essay on the rise and fall of Adolf Hitler.
Answer:

1. Adolf Hitler Was the founder of the National Socialist party, generally known as the Nazi party.
2. His great oratorical skill, his promise to bring back the glorious past of Germany, his support for the German race and hatred towards the Jews helped him to get people support.
3. He came to power in 1933 and ruled Germany till 1945.
4. He began to re-arm Germany and recruitment of new armed forces.
5. The manufacture of armaments and machinery for the army, navy and air force with large spending from government resulted in the revival of the economic condition and helped to solve the unemployment problem in the economy.
6. He followed aggressive policy and therefore in 1936, he invaded Rhine land, the demilitarized zone.
7. His alliance with Italy and Japan became Rome-Berlin-Tokyo axis.
8. He signed Munich pact stating Germany would not conquer any other territory, rather in 1939, he invaded Czechoslovakia.
9. His attack on Poland resulted in the declaration of war by Britain and France against Germany.
10. In 1941, German army invaded Russia. But the resistance of the German army and Russian winter defeated German army.
11. When the allied forces fought back, Germany also retaliated. Finally, Hitler committed suicide in 1945.
12. In 1945, allies occupied Berlin and Germany was divided as two sections after the war.

Question 2.
Analyse the effects of World War II.
Answer:
World War II was the most devastating war in history. It left a deep impact on the entire world. It changed the world in fundamental ways. Here are the effects of this War:

(i) The world got polarised into two main blocs led by superpowers, one led by the United States which followed anti-communist ideology, and the other by Soviet Russia which was essentially communist in nature. Europe was thus divided into two: Communist and non-communist.

(ii) The United States and the Soviet Union entered into a race to have more nuclear powered World War II 43 weapons. They built a large stockpile of such weapons. Meanwhile, Britain and France developed their own nuclear weapons.

(iii) Gradually there arose competition among countries. They began to devote large amount of resources in developing more and more powerful weapons with great destructive power, and defence spending skyrocketed in many countries.

(iv) It was realised that the League of Nations was ineffective and weak. So countries of the world decided not to repeat the mistake. Instead, many international agencies, in particular the United Nations, the World Bank and the International Monetary Fund came into existence providing a forum for countries large and small.

(v) Many other important social and economic changes also took place in the post-War world. Colonial powers were forced to give independence to former colonies in a process of decolonisation. India was the first country to get independence.

(vi) Women became the part of labour force in huge numbers. They became economically independent.

Question 3.
Assess the structure and activities of the UN.
Answer:
The charter of the United Nations was signed on June 26, 1945 by 51 nations. Now, the United Nations has 193 member states and each one has an equal vote in the UN.

Structure of UN:

The General Assembly: Meets once in a year. Issues of interest and points of conflict are discussed in the Assembly.

The Security Council: Consist of five permanent members (USA, Britain, France, Russia, China) and ten non-permanent members (elected in rotation). Each permanent member has the right to veto (A right to reject a decision).

UN Secretariat: Headed by the Secretary by law General. He is elected by the General Assembly on the recommendations of the Security Council. He, with his cabinet and officials run the UN.

International Court of Justice: Headquarters at the Hague in Holland.

The Economic and the Social Council: Co-ordinates all the social and economic work of the U.N. Headed by economists like Gunnar Myrdal.

Activities of the UN:

1. Human Rights, Refugees problem, climatic change, gender equality are the important issues taken over and deals with it. Earlier in 1960’s decolonisation was also a part of their activity.
2. UN peace keeping force acted in many areas of conflict all over the World. Indian army has been a part of it.
3. The preamble of the UN declares, its activities include human rights, equality of men and women.

VIII. Students Activity

Question 1.
A debate in the class on the success or failure of the UN in preserving World Peace.
Answer:
The students can take the following topics for debate and finally conclude, UN is successful as it has stopped the nations from bringing another war. Small to big clashes were/are handled by UN efficiently.

Argument for:
The topics of discussion for debate are:

1. Solving International conflicts: Since 1945, UN peacekeepers have undertaken over 60 field missions and negotiated 172 peaceful settlements that ended Regional conflicts.
2. Liberation from Colonial rule: Eighty nations and more than 750 million people have been freed from colonialism.
3. Human Rights: Custodian for the protection of human rights, discrimination against women, Children’s rights, torture, missing persons etc. in many countries.
4. Enhancing Human life: Specialised agencies of the UN engaged in enhancing all aspects of human life, including education, health, poverty reduction, climate change.
5. Treaties: More than 560 multilateral treaties on human rights, refugees, disarmament.

Argument against:

Non-proliferation Treaty (NPT): Signed by 190 nations, all live superpowers owned nuclear weapons. Later, several countries North Korea, Israel, Pakistan, India developed nuclear weapons.

Veto Power: Veto power has limited its effectiveness at critical times.

War Criminals: The International criminal court has prosecuted several war criminals. But it has been criticised for prosecuting only African leaders. But Western powers too have committed war crimes.

Israel Attack: Israel attacked homes schools, U.N. shelters in Gaza killing 2,200 Palestinians. The U.N. Security Council has failed any action against Israel.

Conclusion: U.N. is imperfect but it is also indispensable. It is successful as, it is avoiding any other war.

Question 3.
Marking the Allies and Axis countries, as well as important battlefields of World War II in a world map.
Answer:

IX. Map Work

Question 1.
Mark the following on the world map.
1. Axis Power Countries
2. Allied Power Countries
3. Hiroshima, Nagasaki, Hawai Island, Moscow, San Fransico
Answer:
(2)

(3)

Timeline:

Samacheer Kalvi 10th Social Science World War II Additional Important Questions and Answers

I. Choose the correct answer

Question 1.
The financial cost of the II World War was ……………….. times higher than that of the I World War.
(a) one
(b) three
(c) five
(d) seven
Answer:
(c) five

Question 2.
The coal mines given to France were ………
(a) Jharia
(b) Saar
(c) Bokaro
Answer:
(b) Saar

Question 3.
“Money in wheelbarrows to buy bread” in the 1920’s. Which country referred to here.
(a) Italy
(b) Austria
(c) Germany
(d) Spain
Answer:
(c) Germany

Question 4.
The principles of war and conquests was glorified by ………
(a) Moderates
(b) Dictators
(c) Extremists
Answer:
(b) Dictators

Question 5.
Hitler broke the Munich pact by invading ……………….. in 1939.
(a) Manchuria
(b) Sudetenland
(c) Poland
(d) Czechoslovakia
Answer:
(d) Czechoslovakia

Question 6.
Hitler demanded the surrender of ………
(a) Danzig
(b) Jutland
(c) Estonia
Answer:
(a) Danzig

Question 7.
The attack of ……………….. by Germany was the final act which result in the initiation of II World War.
(a) Britain
(b) France
(c) Russia
(d) Poland
Answer:
(d) Poland

Question 8.
The British Prime Minister during the Second World War was ………
(a) Sir Winston Churchill
(b) Clement Atlee
(c) Lloyd George
Answer:
(a) Sir Winston Churchill

Question 9.
The tactic followed by Germany to overrun other countries was called as:
(a) Sea-borne invasion
(b) Blitzkrieg
(c) Dunkirk
(d) None
Answer:
(b) Blitzkrieg

Question 10.
In ………, Hitler invaded Russia.
(a) 1940
(b) 1941
(c) 1943
Answer:
(b) 1941

Question 11.
“We shall fight in the fields and in the streets” ……………….. but, we shall never surrender.”- said by
(a) Winston Churchill
(b) Napoleon Bonaparte
(c) George Washington
(d) Roosevelt.
Answer:
(a) Winston Churchill

Question 12.
……………….. used the device radar for detecting aircraft at a distance in World War II.
(a) Germany
(b) Japan
(c) Britain
(d) USA
Answer:
(c) Britain

Question 13.
In September 1940, London was bombed mercilessly by German Air force. This action was called as:
(a) Spit fires
(b) Hurricanes
(c) Blitz
(d) Dunkirk
Answer:
(c) Blitz

Question 14.
Land lease programme of USA took place between the years:
(a) 1939 – 1945
(b) 1941 – 1945
(c) 1936 – 1940
(d) 1914 – 1918
Answer:
(b) 1941 – 1945

Question 15.
In the war between Germany and Russia in 1941, ……………….. was defeated.
(a) Germany
(b) Russia
(c) Britain
(d) None
Answer:
(a) Germany

Question 16.
Stalingrad I situated along the banks of the river:
(a) Miami
(b) Volga
(c) Hwang-Ho
(d) Marne
Answer:
(b) Volga

Question 17.
In the battle of Stalingrad, Germans used the code word ……………….. on Russia.
(a) Alamein
(b) Land lease
(c) Fall Blau
(d) Montegomary
Answer:
(c) Fall Blau

Question 18.
Mussolini was killed by a ……………….. partisan.
(a) Germany
(b) Italy
(c) Russia
(d) Britain
Answer:
(b) Italy

Question 19.
Mussolini was killed in:
(a) May 1945
(b) April 1944
(c) April 1945
(d) May 1946
Answer:
(c) April 1945

Question 20.
In 1945 ……………….. was divided into two sections.
(a) Germany
(b) Italy
(c) Bengal
(d) Russia
Answer:
(a) Germany

Question 21.
Japanese army indulged in the biggest slaughter in the place ……………….. in China.
(a) Manchuria
(b) Nanking
(c) Peking
(d) Shangai
Answer:
(b) Nanking

Question 22.
Japan announced surrendered to U.S on ……………….. 1945.
(a) 2nd September
(b) 15th August
(c) 3rd August
(d) 5th February
Answer:
(b) 15th August

Question 23.
The Security council has ……………….. members.
(a) 10
(b) 15
(c) 25
(d) 3
Answer:
(b) 15

Question 24.
At present, the United Nations has ……………….. member states.
(a) 196
(b) 195
(c) 194
(d) 193
Answer:
(d) 193

Question 25.
The World Bank is located at:
(a) Sweden
(b) New Zealand
(c) Washington
(d) New York
Answer:
(c) Washington

Question 26.
IMF has at present ……………….. member countries.
(a) 200
(b) 187
(c) 189
(d) 190
Answer:
(c) 189

Question 27.
IMF help the countries to solve their ……………….. position.
(a) debt
(b) Balance of payment
(c) Independency
(d) Trade
Answer:
(b) Balance of payment

Question 28.
The report published in 1942, in United Kingdom for the general welfare of the people was called as ……………….. report.
(a) Bretton Woods
(b) Beveridge
(c) Blitzkrieg
(d) Common wealth
Answer:
(b) Beveridge

Question 29.
……………….. party in Great Britain promised for a welfare state to the people.
(a) Communist party
(b) Democratic party
(c) Socialised party
(d) Labour party
Answer:
(d) Labour party

Question 30.
The benefits to the people can be achieved either through ……………….. transfers or free services.
(a) Cash
(b) Country
(c) State
(d) Regional
Answer:
(a) Cash

II. Fill in the blanks

1. World War II began in ……………… and ended in ………………
2. The Treaty of ……………… was signed at the end of World War I in 1919.
3. The Germans offered to pay ……………… billion gold marks to the allies.
4. The United States was faced with great depression after ………………
5. The National Socialist party in Germany was generally known as ………………
6. In 1938, Hitler signed the Munich pact with Prime Minister ………………
7. In 1939, Hitler invaded ……………… as against his promise in Munich pact.
8. Hitler showed hatred against ………………
9. Hitler came to power in ……………… and ruled till ………………
10. World War II was a ……………… war fought with tanks, submarines, bomber planes etc.
11. Britain and France declared war on Germany in ………………
12. In ………………, Italy and Japan joined the axis powers.
13. In September 1940, London war bombed by Germans mercilessly. This action was known as ………………
14. Blitzkrieg means ………………
15. The name of the Britain navy was ………………
16. The war between Britain and ……………… took place in Dunkirk in 1940.
17. The fighter planes of the British Royal force was called as ……………… and ………………
18. ……………… of America started the Land Lease programme.
19. Caucasus was famous for its ……………… in Russia.
20. Mussolini of Italy was killed by an ……………… partisan.
21. The battle of ……………… was considered to be the Great patriotic war by the Russians.
22. Italy surrendered to the allies in ………………
23. The Allied forces under the command of ……………… invaded Normanday in France.
24. Canton was called as ……………… in China.
25. On December 1941, ……………… attacked American naval installations in Pearl Harbour.
26. Guadalcanal is in the ……………… islands.
27. USA dropped an atomic bomb on ……………… and ……………… cities of Japan.
28. Japan announced their surrender on ………………
29. Japan formally signed their surrender marking the end of the World War II was ………………
30. ……………… and ……………… are the two super powers after the II World War.
31. US and Soviet Russia entered into a race to have more ………………
32. ………………, ………………, and ……………… came into existence after the II World War.
33. ……………… started entering into labour force in huge number after World War II.
34. In the process ofdecolonisation ……………… was the first country toget Independence.
35. The word ……………… refers the genocide of Jews by the Germans during Second World War.
36. A major outcome of the Holocaust was the creation of the State of ………………
37. ……………… became the Homeland for Jews after II World War.
38. The Un efforts to protect human rights at the global levei resulted in the UN commission on ………………
39. The Un adopted the Human Rights Charter on ………………
40. ……………… is observed globally as Human Rights Day.
41. Britain and United States gave a joint declaration called as ……………… in 1941 that helped in the formation of UNO.
42. ……………… were the axis powers of the II World War.
43. The initial member States of the UN were ……………… nations.
44. The Charter of the United Nations was signed on ………………
45. Each member State in U.N.has ……………… vote.
46. The UN functions almost like a ………………
47. There are ………………, ………………, ………………, ……………… wing for the UN.
48. Veto means ………………
49. ……………… has veto power.
50. ……………… permanent members are there in UN.
51. WHO means ………………
52. UNICEF means ………………
53. FAO means ………………
54. UNESCO expansion is ………………
55. UNDP expansion is ………………
56. The ……………… has been a port of peace keeping force of the UN in deployment to many parts of the World.
57. The World Bank and the IMP are referred to as ………………
58. The two main organs of the World Bank are ……………… and ………………
59. IBRD expansion is ………………
60. IDA expansion is ………………
61. The IDA lends money to the ……………… for development activities.
62. The loans sanctioned by IDA at low interest rates for development purposes are called as ………………
63. Soft loans are given for ……………… years.
64. The ……………… functions with private enterprises in developing countries.
65. IFC expansion is ………………
66. The World Bank is actively promoting the cause of improving the and eradicating the ………………
67. The IMF was the brainchild of ……………… and ………………
68. The initial member countries of IMF were ………………
69. Its primary objective is to ensure ……………… and development across the World.
70. The fund gives resources to countries facing ……………… problem.
71. The number of member countries of IMF at present are ……………… countries.
72. All the countries in the Western Europe are now ………………
73. The ……………… in Great Britain after World War I promised to look at the people from the cradle to the grave.
74. Legislations was enacted to provide comprehensive free health coverage to the citizens in Britain through ………………
75. The monetary benefits after World War II by Labour party was ………………, ……………… etc.

Answers:

1. 1939, 1945
2. Versailles
3. 100
4. 1929
5. Nazis
6. Chamberlin
7. Czechoslovakia
8. Jews
9. 1933, 1945
10. modem
11. 1939
12. 1940
13. Blitz
14. Lightning strike
15. Royal Navy
16. France
17. Spitfires, Hurricanes
18. President Roosevelt
19. Oil fields
20. Italian
21. Stalingrad
22. 1943
23. General Elsenhower
24. Guangzhou
25. Japan
26. Solomon
27. Hiroshima, Nagasaki
28. 15th August 1945
29. 2nd Sept 1945
30. United States, Soviet Russia
31. Nuclear weapons
32. United Nations, World Bank, International Monetary Fund
33. Women
34. India
35. Holocaust
36. Israel
37. Israel
38. Human Rights
39. 10th Dec 1948
40. 10th Dec 1948
41. Atlantic Charter
42. Germany, Italy, Japan
43. 51
44. June 26, 1945
45. One
46. Government
47. Executive, Judicial, Legislative, Co-ordinating
48. The right to block major decisions
49. Permanent members
50. Five
51. World Health Organisation
52. United Nations Children’s Fund
53. Food and Agricultural Organisation
54. UN educational, Scientific and Cultural Organisation
55. United Nations Development programme
56. Indian Army
57. Bretton Woods Twins
58. IBRD, IDA
59. International Bank for Reconstruction and Development
60. International Development Agency
61. Government
62. Soft loans
63. 50
64. IFC
65. International Finance Corporation
66. Environment, AIDS
67. Hary Dexter, John Maynard Keynes
68. 29
69. Financial Stability
70. Balance of payment
71. 189
72. Welfare states
73. Labour party
74. National Health Service
75. Old age pension, Child care services

III. Choose the correct statement

Question 1.
(i) The axis powers of World War II were Germany, Italy and Japan.
(ii) Russia attacked the American naval base at Pearl Harbour in 1941.
(iii) The UN adopted the historic human rights charter on 10th December 1947.
(iv) The executive wing of the UN is the UN Secretariat.
(a) (i) (ii) are correct
(b) (i) (ii) (iii) are correct
(c) (i) (iv) are correct
(d) (ii) (iv) are wrong.
Answer:
(c) (i) (iv) are correct

Question 2.
(i) Reparations refers to the compensation exacted from a defeated nation by the victorious nation.
(ii) Slaughter is compulsory military service.
(iii) Japanese navy was defeated by the US Navy at the battle of mid way.
(iv) Progression taxation by taxing the higher income groups at relatively high rates.
(a) (ii) (iii) (iv) are correct
(b) (ii) (iv) are wrong
(c) (iii) (iv) are correct
(d) (iii) (iv) are wrong.
Answer:
(a) (ii) (iii) (iv) are correct

Question 3.
(i) The Security Council of the UNO has fifteen members.
(ii) The mass killing of Jews in Nazi was called holocaust
(iii) Battle of Ex Alamein was considered one of the greatest battles by Russia.
(iv) The Japanese navy defeated the US navy in the battle of Midway.
(a) (i) (ii) are correct
(b) (ii) (iv) are correct
(c) (i) (ii) (iii) are correct
(d) (i) (iv) are wrong
Answer:
(a) (i) (ii) are correct

Question 4.
(i) The World Bank and the IMF are referred to as the Bretton Woods Twins.
(ii) The post World War I led to the rise of dictatorship in Italy, Germany, and Spain.
(iii) The post World War II changed the world into two blocks as communist and non communist.
(iv) The Shakespeare’s play the Merchant of Venice clearlv depicts the dislike and distrust of Jews among the Nazi people.
(a) (i) (ii) are correct
(b) (i) (ii) (iii) are wrong
(c) (i) (ii) (iii) (iv) are correct
(d) (iii) (iv) (ii) are wrong
Answer:
(c) (i) (ii) (iii) (iv) are correct

Question 5.
(i) IMF lends money from its resources to countries facing balance of payment problem.
(ii) The Munich pact was signed between Germany and the Soviet Union.
(iii) Huge worthless money for bread often refers to the Britain’s severe inflation after II World War.
(iv) Franco of Spain was the only dictatorship that emerged after II World War.
(a) (i) (ii) are correct
(b) (i) (iii) (iv) are correct
(c) (i) (ii) (iii) (iv) are wrong
(d) (i) (iv) are correct
Answer:
(a) (i) (ii) are correct

Question 6.
(i) Japanese extended their empire throughout South-east Asia.
(ii) Burma, Indonesia, Singapore, Malaya, Hong Kong, Philippines all fell to the Japanese.
(iii) Many Indians walked ail the way from Burma to the Indian border facing many sufferings.
(iv) Many Indians who stayed there suffered under the Japanese.
(a) (ii) (iv) are wrong
(b) (i) (ii) (iii) (iv) are correct
(c) (iii) (i) are correct
(d) (i) (ii) (iii) (iv) are wrong
Answer:
(b) (i) (ii) (iii) (iv) are correct

Question 7.
(i) Hitler was killed by his countrymen in 1945
(ii) Mussolini committed suicide in April 1945
(iii) The United States declared war on Japan on December 1944.
(iv) In 1938, Japan invaded China and seized Beijing.
(a) (ii) (iv) are wrong
(b) (i) (ii) (iii) (iv) are correct
(c) (i) (ii) are correct
(d) (i) (ii) (iii) (iv) are wrong
Answer:
(d) (i) (ii) (iii) (iv) are wrong

Question 8.
(i) In the year 1940, the British Prime Minister Chamberlain resigned.
(ii) The newly elected British Prime Minister next was Winston Churchill.
(iii) The end of World War II signalled a change in the world order and political configurations among the major powers.
(iv) The Treaty of Versailles ended the World War II.
(a) (i) (iv) are wrong
(b) (i) (ii) (iii) (iv) are correct
(c) (i) (ii) (iii) are correct
(d) (i) (ii) (iv) are correct
Answer:
(c) (i) (ii) (iii) are correct

IV. Assertion and Reason

Question 1.
Assertion (A): World War I (1914-18) and World War II (1939-45) are only referred as World wars.
Reason (R): The high death of the civilians and the soldiers and the extended area of the conflicts.
(a) Both A and R are correct
(b) A is correct but R is not the correct reason
(c) Both A and R are wrong
(d) R is correct but A is wrong.
Answer:
(a) Both A and R are correct

Question 2.
Assertion (A): The League remained an ineffectual international body. Reason (R): Along with the USA, as a non-member mainly Germany was determined to maintain a non-interventionist attitude.
(a) Both A and R are correct
(b) A is correct but R is not the correct reason
(c) Both A and R are wrong
(d) R is correct but A is wrong.
Answer:
(b) A is correct but R is not the correct reason

Question 3.
Assertion (A): Hitler invaded Austria and Czechoslovakia in 1938.
Reason (R): Hitler claimed all the German speaking people should be united into one nation.
(a) Both A and R are correct
(b) A is correct but R is not the correct reason
(c) Both A and R are wrong
(d) R is correct but A is not relevant to R.
Answer:
(a) Both A and R are correct

Question 4.
Assertion (A): The mood in Britain was not in favour of starting another war after World War I.
Reason (R): Just as the United States they wanted to be concerned with the revival of the economy after great depression.
(a) Both A and R are correct
(b) A is correct but R is not the correct reason
(c) Both A and R are wrong
(d) R is correct but A is not relevant to A.
Answer:
(b) A is correct but R is not the correct reason

Question 5.
Assertion (A): Germany developed a fleet of sub-marines which caused havoc in the Atlantic Ocean.
Reason (R): Germany ensured themselves for a sea-borne invasion on allies.
(a) Both A and R are correct
(b) A is right but R is not the correct explanation of A.
(c) Both A and R are wrong
(d) R is correct, which is not relevant to A.
Answer:
(b) A is right but R is not the correct explanation of A.

Question 6.
Assertion (A): The long term objective of Germany was to exploit Russia’s natural Resource oil.
Reason (R): German army invaded Russia.
(a) Both A and R are correct
(b) A is right but R is not the correct explanation of A
(c) Both A and R are wrong
(d) R is correct, which is not relevant to A.
Answer:
(a) Both A and R are correct

Question 7.
Assertion (A): Germans tried to capture the city of Stalingrad in Russia. Reason (R): Stalingrad was the militarised zone of Russia.
(a) Both A and R are correct
(b) A is right, but R is not the correct explanation of A
(c) Both A and R are wrong
(d) R is right, A is wrong.
Answer:
(b) A is right, but R is not the correct explanation of A

Question 8.
Assertion (A): Hitler committed suicide in April 1945.
Reason (R): The Allied forces in 1945, occupied parts of Berlin and began to attack Germany from the east.
(a) Both A and R are correct
(b) A is correct but R is not the correct explanation.
(c) Both A and R are wrong
(d) R is correct but A is not relevant to R.
Answer:
(a) Both A and R are correct

Question 9.
Assertion (A): The United States declared war on Japan.
Reason (R): In 1931, the Japanese army invaded Manchuria and in 1937, invaded China and seized Beijing.
(a) Both A and R are correct
(b) A is correct but R is not the correct explanation of A
(c) Both A and R are wrong
(d) R is correct but R is not relevant to A.
Answer:
(b) A is correct but R is not the correct explanation of A

Question 10.
Assertion (A): U.S. dropped an atomic bomb on Hiroshima and another bomb was dropped on Nagasaki.
Reason (R): U.S. developed hatred over the development of two cities Hiroshima and Nagasaki.
(a) Both A and R are correct
(b) A is correct, but R is not the correct explanation of A
(c) Both A and R are wrong
(d) R is correct but it is the correct reason for A.
Answer:
(b) A is correct, but R is not the correct explanation of A

Question 11.
Assertion (A): The U.S. and the Soviet Union followed communist and non¬communist ideas.
Reason (R): Countries began to devote large amount of resources in developing dangerous weapons.
(a) Both A and R are correct
(b) A is correct, but not relevant to R
(c) Both A and R are wrong
(d) R is correct, but not relevant to A.
Answer:
(c) Both A and R are wrong

V. Match the Following

Question 1.
Match the Column I with Column II.

Answer:
A. (iv)
B. (i)
C. (v)
D. (vi)
E. (iii)

Question 2.
Match the Column I with Column II.

Answer:
A. (v)
B. (i)
C. (vi)
D. (iii)
E. (ii)

VI. Answer the questions briefly

Question 1.
What are soft loans?
Answer:
The loans that are sanctioned by the International Development Agency to the Governments for developmental activities are called as soft loans. They are given at very low rate of interest of 50 years.

Question 2.
Did Munich Pact bring peace for some time? How?
Answer:

1. In September 1938, Hitler threatened Czechoslovakia.
2. The British Prime Minister Neville chamberlain initiated talks and signed Munich pact,
3. Hitler promised not to take any more Czech territory.
4. Chamberlain believed that he had achieved “Peace for some time”. But within six months Hitler seized the remainder of Czechoslovakia. So Munich pact has brought peace only for some time.

Question 3.
What do you know about the World Bank?
Answer:
The World bank consists of two main organs namely The International Bank for Reconstruction and Development (IBRD) and the International Development Agency (IDA). Together they are called as the World Bank.

Question 4.
Why did America declare war on Japan?
Answer:

1. The Japanese had attacked the American fleet stationed at Pearl Harbour on December 7, 1941.
2. This disastrous attack forced the Americans to enter into the war.
3. The very next day the USA declared war on Japan.

Question 5.
What are the axis powers and the ally powers of II World War?
Answer:
Germany, Italy, Japan – Axis powers.
Britain, France, Russia, USA – Ally powers.

Question 6.
Name the countries involved in World War II.
Answer:

1. The allies countries were under the leadership of Britain. [Britain, France, Russia and U.S.A]
2. The axis countries were under the leadership of Germany. [Germany, Italy and Japan]

Question 7.
What was the immediate cause of the II World War?
Answer:
The main and immediate cause of the II World War was the aggressive, military, dictatorship attitude of Germany, fast-developing Japan. Hitler’s attack on Poland in 1939, resulted in the declaration of the War by Britain and France.

Question 8.
Write a brief note on security council.
Answer:

1. The council has five permanent members and ten non-permanent members.
2. The five permanent members are the USA, UK, France, Russian Federation and China,
3. The non-permanent members are elected by the General Assembly for two years term,
4. The permanent members have the right to veto for any council decision.
5. Its main responsibility is to maintain International peace and security.

Question 9.
What is ECOSOC? What are its organs?
Answer:
The Economic and Social Council, is the UN organ which is responsible for co-ordinating all the economic and social work of the United Nations. The Regional Economic commissions functioning for regional development across the various regions of the World are its organs. (Asia pacific, West Asia, Europe, Africa, Latin America).

Question 10.
Name some of the specialized agencies of the UNO.
Answer:

1. The World Health Organisation [WHO]
2. The United Nations Educational Scientific and Cultural Organisation(UNESCO)
3. The United Nation’s Children’s Fund (UNICEF)
4. The International Labour Organisation (ILO)
5. Food and Agricultural Organisation (FAO)
6. International Monetary Fund (IMF)
7. International Bank for Reconstruction and Development (IBRD)

VII. Answer the questions given under each caption

Question 1.
Causes of the Second World War.

(a) Name the treaty signed by Japan, Italy and Germany.
Answer:
Italy – Germany – Japan signed the Rome – Berlin – Tokyo Axis treaty.

(b) Mention some of the ideologies that emerged after the First World War.
Answer:
Democracy, Communism, Fascism and Nazism.

(c) What was the policy followed by the statesmen of the major world powers?
Answer:
The statesmen of the major world powers followed the policy of appeasement.

(d) What did Hitler violate?
Answer:
He violated the Munich Pact.

Question 2.
Munich Pact

(a) Who concluded the Munich pact with Germany?
Answer:
In 1938, Prime Minister Chamberlain concluded the Munich pact with Germany.

(b) What did Hitler do in 1939?
Answer:
In 1939, Hitler invaded Czechoslovakia breaking the munich pact that Germany would not attack any other country.

(c) Which act of Hitler made Britain and France declare war on Germany?
Answer:
His act of attack on Poland made Britain and France declare war on Germany.

(d) What were the weapons used in World War II?
Answer:
Heavy military equipment such as tanks, sub-marines, battleships, aircraft carriers, fighter planes and bomber planes.

Question 3.
Organs of the UNO

(a) Name the major organs of the UNO.
Answer:

1. The General Assembly
2. The Security Council
3. The Economic and Social Council
4. The Trusteeship Council
5. The International Court of Justice
6. The Secretariat

(b) Who was elected as the President of the UN General Assembly in 1953?
Answer:
Mrs. Vijaya Lakshmi Pandit

(c) What is the function of the Trusteeship Council?
Answer:
The Trusteeship Council looks after certain territories placed under the trusteeship of the UNO.

(d) How is the Secretary-General of the UNO appointed?
Answer:
The Secretary-General is appointed by the General Assembly on the advice of the Security Council.

Question 4.
Birth of Israel.

(a) What is meant by Holocaust?
Answer:
Holocaust refers to the mass killing of jews by the Germans during World War II.

(b) What was the major outcome of the Holocaust?
Answer:
The major outcome of the Holocaust was the creation of the State of Israel as a homeland for the Jews.

(c) What did the Israel occupy?
Answer:
The Israel has occupied large parts of Palestinian homelands.

(d) From whom does Israel get the support from?
Answer:
Israel get the vast support from the United States.

Question 5.
The United Nations

(a) Who took the first initiative for the formation of the United Nations?
Answer:
The United states and the Britain in 1941.

(b) Name the joint declaration they issued?
Answer:
The Atlantic Charter was the name of the joint declaration they issued.

(c) How many countries accepted the declaration at first?
Answer:
The declaration of the United Nations was accepted by 26 countries, on New years Day 1942.

(d) How many nations signed the charter? When?
Answer:
On June 26, 1945, 51 nations signed the charter.

Question 6.
International Monetary Fund (IMF)

(a) On whose idea the International Monetary Fund was initiated?
Answer:
Harry Dexter white and John Maynard Keynes ideas brought the emergence of IMF.

(b) When was it formally organised?
Answer:
It was formally organised in 1945 with 29 member countries (at present 189).

(c) What were the three main agendas of the IMF?
Answer:

1. To promote International monetary co-operation.
2. To expand International trade.
3. To bring exchange stability.

(d) State the main reason of its funding?
Answer:
The IMF lends money from its resources to countries facing Balance of payment problems.

VIII. Answer in detail

Question 1.
What were the results of Second World War?
Answer:

1. The destruction to life and property was on a much larger scale than the First World War.
2. Over 50 millions lost their lives.
3. It sounded the death knell to dictatorship in Germany and Italy.
4. Germany was occupied by the Allied forces, and later it was divided into two parts.
5. The West Germany was controlled by Britain, France and America and the East Germany by Russia.
6. At the end of the war, Japan was occupied by American forces under General Mc. Arthur.
7. The war weakened Britain and France.
8. America and Russia emerged as super powers.
9. The war did not end totalitarianism in Russia. A cold war started between Russia and America.
10. The war quickened the phase of national movements in Asia and Africa.
11. India, Burma, Egypt, Ceylon and Malaya won their freedom from Britain.
12. Philippines got independence from America.
13. Indo-china got independence from France.
14. Indonesia got independence from the Dutch.
15. The European countries gave up the policy of colonialism and imperialism.
16. The United Nations Organisation was set up to maintain international peace and harmony. It works hard to maintain international co-operation and for the promotion of human welfare.

Question 2.
Write a note on international Monetary Fund (IMF).
Answer:

1. International Monetary Fund was established in 1945 after the Bretton Woods conference in 1944 along with the World Bank.
2. It is located in the Washington in United States.
3. The idea of starting of IMF was given by Harry Dexter, White and John Maynard Keynes, a famous economist.
4. The initial members of the IMF were 29. Now, there are 189 member countries with IMF,
5. The main objectives of IMF include to foster global monetary co-operation, to secure financial stability, to facilitate trade, promote employment, to sustain economic growth and reduce poverty all over the world.
6. The fund lends money to its member countries to correct their balance of payment position if they are unable to pay for their imports.
7. The funding from IMF is not very easy as it strictly imposes restrictions on lending.
8. It imposes the developing nations to tighten the budgets and reduce fiscal expenditure.

Question 3.
Write a note on the UN Commission of Human Rights.
Answer:

1. Human Rights means the fundamental freedom for all human beings without any differences in race, sex, language and religion.
2. The UN efforts to protect human rights on a global basis resulted in the formation of the UN commission on Human Rights.
3. A committee was set up for its formation. It was headed by the wife of FDR of USA, after his death.
4. The other members of the commission included Charles Malik from Lebanon, P.C.Chang from China, Rene Casin from France.
5. The Commission set forth with 30 articles.
6. The UN adopted this historic charter on 10th December 1948.
7. This day, the 10th December is observed as Human Rights Day all over the World.
8. According to the Franklin and Eleanor institute in New York, reports, from 1948 till now, nearly 90 National constitutions are part of this Human Rights Commission of UN.

Students can download 10th Science Chapter 1 Laws of Motion Questions and Answers, Notes, Samacheer Kalvi 10th Science Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Science Solutions Chapter 1 Laws of Motion

Samacheer Kalvi 10th Science Laws of Motion Text Book Back Questions and Answers

I. Choose the correct answer

Question 1.
Inertia of a body depends on:
(a) weight of the object
(b) acceleration due to gravity of the planet
(c) mass of the object
(d) both (a) & (b)
Answer:
(c) mass of the object

Question 2.
Impulse is equals to ______ .
(a) rate of change of momentum
(b) rate of force and time
(c) change of momentum
(d) rate of change of mass.
Answer:
(c) change of momentum

Question 3.
Newton’s III law is applicable:
(a) for a body is at rest
(b) for a body in motion
(c) both (a) & (b)
(d) only for bodies with equal masses
Answer:
(b) for a body in motion

Question 4.
Plotting a graph for momentum on the X-axis and time on Y-axis. Slope of momentum – time graph gives _____
(a) Impulsive force
(b) Acceleration
(c) Force
(d) Rate of force.
Answer:
(c) Force

Question 5.
In which of the following sport the turning effect of force is used?
(a) swimming
(b) tennis
(c) cycling
(d) hockey
Answer:
(c) cycling

Question 6.
The unit of ‘g’ is ms^-2. It can be also expressed as:
(a) cm s^-2
(b) N kg^-1
(c) N m²kg^-1
(d) cm²s^-2
Answer:
(a) cm s^-2

Question 7.
One kilogram force equals to _____ .
(a) 9.8 dyne
(b) 9.8 × 10⁴ N
(c) 98 × 10⁴ dyne
(d) 980 dyne.
Answer:
(c) 98 × 10⁴ dyne

Question 8.
The mass of a body is measured on planet Earth as M kg. When it is taken to a planet of radius half that of the Earth then its value will be ….. kg.
(a) 4 M
(b) 2 M
(c) M/4
(d) M
Answer:
(c) M/4

Question 9.
If the Earth shrinks to 50% of its real radius its mass remaining the same, the weight of a body on the Earth will:
(a) decrease by 50%
(b) increase by 50%
(c) decrease by 25%
(d) increase by 300%
Answer:
(c) decrease by 25%

Question 10.
To project the rockets which of the following principle(s) is / (are) required?
(a) Newton’s third law of motion
(b) Newton’s law of gravitation
(c) law of conservation of linear momentum
(d) both a and c.
Answer:
(d) both a and c.

II. Fill in the blanks

1. To produce a displacement …….. is required.
2. Passengers lean forward when the sudden brake is applied in a moving vehicle. This can be explained by ……….
3. By convention, the clockwise moments are taken as ……… and the anticlockwise moments are taken as ……….
4. …….. is used to change the speed of the car.
5.  A man of mass 100 kg has a weight of …….. at the surface of the Earth.

Answer:

1. force
2. inertia
3. negative, positive
4. Accelerator
5. Weight = m × g = 100 × 9.8 = 980 N

III. State whether the following statements are true or false. Correct the statement if it is false.

1. The linear momentum of a system of particles is always conserved.
2. Apparent weight of a person is always equal to his actual weight.
3. Weight of a body is greater at the equator and less at the polar region.
4. Turning a nut with a spanner having a short handle is so easy than one with a long handle.
5. There is no gravity in the orbiting space station around the Earth. So the astronauts feel weightlessness.

Answer:

1. True
2. False – Apparent weight of a person is not always equal to his actual weight.
3. False – Weight of a body is minimum at the equator. It is maximum at the poles.
4. False – Turning a nut with a spanner having a longer handle is so easy than one with a short handle.
5. False – Astronauts are falling freely around the earth due to their huge orbital velocity.

IV. Match the following.

Answer:
A. (ii)
B. (Hi)
C. (iv)
D. (i)

V. Assertion and Reasoning.

Mark the correct choice as:
(a) If both the assertion and the reason are true and the reason is the correct explanation of assertion.
(b) If both the assertion and the reason are true, but the reason is not the correct explanation of the assertion.
(c) Assertion is true, but the reason is false.
(d) Assertion is false, but the reason is true.
1. Assertion: The sum of the clockwise moments is equal to the sum of the anticlockwise moments.
Reason: The principle of conservation of momentum is valid if the external force on the system is zero.
2. Assertion: The value of ‘g’ decreases as height and depth increases from the surface of the Earth.
Reason: ‘g’ depends on the mass of the object and the Earth.
Answer:
1. (b)
2. (c)

VI. Answer Briefly.

Question 1.
Define inertia. Give its classification.
Answer:
The inherent property of a body to resist any change in its state of rest or the state of uniform motion, unless it is influenced upon by an external unbalanced force, is known as ‘inertia’.
Classifications:

1. Inertia of rest
2. Inertia of motion
3. Inertia of direction

Question 2.
Classify the types of force based on their application.
Answer:
Based on the direction in which the forces act, they can be classified into two types as:

1. Like parallel forces: Two or more forces of equal or unequal magnitude acting along the same direction, parallel to each other are called like parallel forces.
2. Unlike parallel forces: If two or more equal forces or unequal forces act along with opposite directions parallel to each other, then they are called, unlike parallel forces.

Question 3.
If a 5 N and a 15 N forces are acting opposite to one another. Find the resultant force and the direction of action of the resultant force.
Answer:
F₁ = 5 N
F₂ = 15 N
∴ Resultant force F_R = F₁ – F₂
= 5 – 15 = -10 N
It acts in the direction of the force of 15 N (F₂).

Question 4.
Differentiate mass and weight.
Answer:
Ratio of masses of planets is
m₁ = m₂ = 2 : 3
Ratio of radii
R₁ = R₂ = 4 : 7
We know

Question 5.
Define the moment of a couple.
Answer:
When two equal and unlike parallel forces applied simultaneously at two distinct points constitute a couple. A couple results in causes the rotation of the body. This rotating effect of a couple is known as the moment of a couple.

Question 6.
State the principle of moments.
Answer:
Principle of moments states that if a rigid body is in equilibrium on the action of a number of like (or) unlike parallel forces then the algebraic sum of the moments in the clockwise direction is equal to the algebraic sum of the moments in the anticlockwise direction.

Question 7.
State Newton’s second law.
Answer:
The force acting on a body is directly proportional to the rate of change of linear momentum of the body and the change in momentum takes place in the direction of the force.

Question 8.
Why a spanner with a long handle is preferred to tighten screws in heavy vehicles?
Answer:
When a spanner is having a long handle, the turning effect of the applied force is more when the distance between the fixed edge and the point of application of force is more. Hence a spanner with a long handle is preferred to tighten screws in heavy vehicles.

Question 9.
While catching a cricket ball the fielder lowers his hands backwards. Why?
Answer:
While catching a cricket ball the fielder lowers his hands backwards, so increase the time during which the velocity of the cricket ball decreases to zero. Therefore the impact of force on the palm of the fielder will be reduced.

Question 10.
How does an astronaut float in a space shuttle?
Answer:
Astronauts are not floating but falling freely around the earth due to their huge orbital velocity. Since spaceshuttle and astronauts have equal acceleration, they are under free fall condition. (R = 0) Hence, both the astronauts and the space station are in the state of weightlessness.

VII. Solve the given problems.

Question 1.
Two bodies have a mass ratio of 3 : 4 The force applied on the bigger mass produces an acceleration of 12 ms². What could be the acceleration of the other body, if the same force acts on it.
Answer:
Ratio of masses m₁ : m₂ = 3 : 4
Acceleration of m₂ is a₂ = 12 m/s²
Force acting of m₂ is F₂ = m₂a₂
F₂ = 4 × 12 = 48N
but F₂ = F₁
∴ Force acting on m₁ is F₁ = 48N
∴ Acceleration of m₁ = a₁ = \(\frac{F_1}{m_1}\)
a₁ = \(\frac{48}{3}\)
= 16 m/s²
Acceleration of the other body ax = 16 m/s²

Question 2.
A ball of mass 1 kg moving with a speed of 10 ms-1 rebounds after a perfect elastic collision with the floor. Calculate the change in linear momentum of the ball.
Answer:
Given mass = 1 kg, speed = 10 ms^-1
Initial momentum = mu = 1 × 10 = 10 kg ms^-1
Final momentum = -mu = -10 kg ms^-1
Change in momentum = final momentum – initial momentum = -mu – mu
Change in momentum = -20 kg ms^-1

Question 3.
A mechanic unscrew a nut by applying a force of 140 N with a spanner of length 40 cm. What should be the length of the spanner if a force of
40 N is applied to unscrew the same nut?
Answer:
Force acting on the screw F₁ = 140 N
Length of a spanner d₁ = 40 × 10^-2 m
Second force applied to the screw F₂ = 40 N
Let the length of spanner be d₂
According to the Principle of moments,
F₁ × d₁ = F₂ × d₂
= 140 × 40 = 40 × d₂
∴ d₂ = \(\frac{140×40}{40}\)
= 140 × 10^-2 m
Length of a spanner = 140 × 10^-2 m

Question 4.
The ratio of masses of two planets is 2 : 3 and the ratio of their radii is 4 : 7. Find the ratio of their accelerations due to gravity.
Answer:
Ratio of masses of two planets is
m₁ : m₂ = 2 : 3
Ratio of their radii,
R₁ : R₂ = 4 : 7
We know g
Img 2
∴ g₁ : g₂ = 49 : 24

VIII. Answer in Detail.

Question 1.
What are the types of inertia? Give an example for each type.
Answer:
Types of Inertia:
(i) Inertia of rest: The resistance of a body to change its state of rest is called inertia of rest.
E.g.: When you vigorously shake the branches of a tree, some of the leaves and fruits are detached and they fall down (Inertia of rest).

(ii) The inertia of motion: The resistance of a body to change its state of motion is called inertia of motion.
E.g.: An athlete runs some distance before jumping. Because this will help him jump longer and higher. (Inertia of motion)

(iii) Inertia of direction: The resistance of a body to change its direction of motion is called inertia of direction.
E.g.: When you make a sharp turn while driving a car, you tend to lean sideways, (Inertia of direction).

Question 2.
State Newton’s laws of motion.
Answer:
(i) Newton’s First Law : States that “every body continues to be in its state of rest or the state of uniform motion along a straight line unless it is acted upon by some external force”.

(ii) Newton’s Second Law : States that “the force acting on a body is directly proportional to the rate of change of linear momentum of the body and the change in momentum takes place in the direction of the force”.

(iii) Newton’s third law : States that “for every action, there is an equal and opposite reaction. They always act on two different bodies”.

Question 3.
Deduce the equation of a force using Newton’s second law of motion.
Answer:
Let, ‘m’ be the mass of a moving body, moving along a straight line with an initial speed V. After a time interval of ‘t’, the velocity of the body changes to v due to the impact of an unbalanced external force F.
Initial momentum of the body P_i = mu
Final momentum of the body P_f = mv
Change in momentum Δp = P_i – P_f – mv – mu
By Newton’s second law of motion,
Force, F ∝ rate of change of momentum
F ∝ change in momentum / time
F ∝ \(\frac{mv-mu}{t}\)
F = \(\frac {km(v-u)}{t}\)
Here, k is the proportionality constant.
k = 1 in all systems of units. Hence,
F = \(\frac {m(v-u)}{t}\)
Since,
acceleration = change in velocity/time,
a = (v – u)/t.
Hence, we have F = m × a
Force = mass × acceleration

Question 4.
State and prove the law of conservation of linear momentum.
Answer:

Proof:
Let two bodies A and B having masses m₁ and m₂ move with initial velocity u₁ and u₂ in a straight line. Let the velocity of the first body be higher than that of the second body, i.e,, u₁ > u₂. During an interval of time t second, they tend to have a collision. After the impact, both of them move along the same straight line with a velocity v₁ and v₂ respectively.
Force on body B due to A,
F_B = m₂(v₂ – u₂)/t
Force on body A due to B,
F_A = m₁(v₁ – u₁)/t
By Newton’s III law of motion,
Action force = Reaction force
F_A = -F_B
m₁(v₁ – u₁)/t = -m₂ (v₂ – u₂)/t
m₁ v₁ + m₂ v₂ = m₁ u₁ + m₂ u₂
The above equation confirms in the absence of an external force, the algebraic sum of the momentum after collision is numerically equal to the algebraic sum of the momentum before collision.
Hence the law of conservation of linear momentum is proved.

Question 5.
Describe rocket propulsion.
Answer:

1. Propulsion of rockets is based on the law of conservation of linear momentum as well as Newton’s III law of motion.
2. Rockets are filled with fuel (either liquid or solid) in the propellant tank. When the rocket is fired, this fuel is burnt and hot gas is ejected with high speed from the nozzle of the rocket, producing a huge momentum.
3. To balance this momentum, an equal and opposite reaction force is produced in the combustion chamber, which makes the rocket project forward.
4. While in motion, the mass of the rocket gradually decreases, until the fuel is completely burnt out.
5. Since there is no net external force acting on it, the linear momentum of the system is conserved.
6. The mass of the rocket decreases with altitude, which results in the gradual increase in the velocity of the rocket.
7. At one stage, it reaches a velocity, which is sufficient to just escape from the gravitational pull of the Earth. This velocity is called escape velocity.

Question 6.
State the universal law of gravitation and derive its mathematical expression.
Answer:
Newton’s universal law of gravitation states that every particle of matter in this universe attracts every other particle with a force. This force is directly proportional to the product of their masses and inversely proportional to the square of the distance between the centres of these masses. The direction of the force acts along the line joining the masses.

Force between the masses is always attractive and it does not depend on the medium where they are placed.

Let, m₁ and m₂ be the masses of two bodies A and B placed r metre apart in space
Force
F ∝ m₁ × m₂
F ∝ 1/r²
On combining the above two expressions
F ∝ \(\frac{m_1×m_2}{r^2}\)
F = \(\frac{Gm_1 m_2}{r^2}\)
Where G is the universal gravitational constant. Its value in SI unit is 6.674 × 10^-11 N m² kg^-2.

Question 7.
Give the applications of gravitation.
Answer:

1. Dimensions of the heavenly bodies can be measured using the gravitation law. Mass of the Earth, the radius of the Earth, acceleration due to gravity, etc. can be calculated with higher accuracy.
2. Helps in discovering new stars and planets.
3. One of the irregularities in the motion of stars is called ‘Wobble’ lead to the disturbance in the motion of a planet nearby. In this condition, the mass of the star can be calculated using the law of gravitation.
4. Helps to explain germination of roots is due to the property of geotropism, which is the property of a root responding to the gravity.
5. Helps to predict the path of the astronomical bodies.

IX. HOT questions.

Question 1.
Two blocks of masses 8 kg and 2 kg respectively lie on a smooth horizontal surface in contact with one other. They are pushed by a horizontally applied force of 15 N. Calculate the force exerted on the 2 kg mass.
Answer:
Mass of first block m₁ = 8 kg
Mass of second block m₂ = 2 kg
Total mass M = 8 + 2 = 10 kg
Force applied F = 15 N
∴ Acceleration a = \(\frac{F}{M}\)
\(\frac{15}{10}\) = 1.5 m/s²
Force exerted on the 2 kg mass,
F = ma
= 2 × 1.5 = 3 N

Question 2.
A heavy truck and bike are moving with the same kinetic energy. If the .mass of the truck is four times that of the bike, then calculate the ratio of their momenta. (Ratio of momenta = 1 : 2)
Answer:
Let the mass of truck be m₁
Let the mass of bike be m₂
m₁ = 4m₂
∴ \(\frac{m_1}{m_2}\) = 4
Kinetic energy K.E₁ = K.E₂
∴ m₂, \({ v }_{ 1 }^{ 2 }\) = m₂\({ v }_{ 1 }^{ 2 }\)

Ratio of momenta be P₁ : P₂

∴ Ratio of their momenta = 2 : 1

Question 3.
“Wearing helmet and fastening the seat belt is highly recommended for safe journey” Justify your answer using Newton’s laws of motion.
Answer:
(i) According to Newton’s Second Law, when you fall from a bike on the ground with a force equal to your mass and acceleration of the bike.
According to Newton’s Third Law, an equal and opposite reacting force on the ground is exerted on your body. When you do not wear a helmet, this reacting force can cause fatal head injuries. So it is important to wear helmet for a safe journey.

(ii) Inertia in the reason that people in cars need to wear seat belts. A moving car has inertia, and so do the riders inside it. When the driver applies the brakes, an unbalanced force in applied to the car. Normally the bottom of the seat applies imbalanced force friction which slows the riders down as the car slows. If the driver stops the car suddenly, however, this force is not exerted over enough time to stop the motion of the riders. Instead, the riders continue moving forward with most of their original speed because of their inertia.

Samacheer Kalvi 10th Science Laws of Motion Additional Important Questions and Answers

I. Choose the correct answer.

Question 1.
When a force is exerted on an object, it can change its:
(a) state
(b) shape
(c) position
(d) all the above
Answer:
(d) all the above

Question 2.
When the train stops, the passenger moves forward, It is due to ______ .
(a) Inertia of passenger
(b) Inertia of train
(c) gravitational pull by the earth
(d) None of the above.
Answer:
(a) Inertia of passenger

Question 3.
Force is a …….. quantity.
(a) vector
(b) fundamental
(c) scalar
(d) none
Answer:
(a) vector

Question 4.
The force of gravitation is ________ .
(a) repulsive
(b) conservative
(c) electrostatic
(d) non – conservative.
Answer:
(b) conservative

Question 5.
The laws of motion of a body is given by:
(a) Galileo
(b) Archimedis
(c) Einstein
(d) Newton
Answer:
(d) Newton

Question 6.
A bodyweight 700 N on earth. What will be its weight on a planet having 1 / 7 of earth’s mass and half of the earth’s radius?
(a) 400 N
(b) 300 N
(c) 200 N
(d) 100 N.
Answer:
(a) 400 N

Question 7.
From the following statements write down that which is not applicable to mass of an object:
(a) It is a fundamental quantity
(b) It is measured using physical balance
(c) It is measured using spring balance
(d) It is the amount of matter.
Answer:
(c) It is measured using spring balance

Question 8.
Newton’s first law of motion defines:
(a) inertia
(b) force
(c) acceleration
(d) both inertia and force
Answer:
(d) both inertia and force

Question 9.
Mechanics is divided into ____ types.
(a) one
(b) two
(c) three
(d) four.
Answer:
(b) two

Question 10.
When an object undergoes acceleration:
(a) its velocity increases
(b) its speed increases
(c) its motion is uniform
(d) a force always acts on it
Answer:
(d) a force always acts on it

Question 11.
On what factor does inertia of a body depend?
(a) volume
(b) area
(c) mass
(d) density
Answer:
(c) mass

Question 12.
_____ deals with the motion of bodies without considering the cause of motion.
(a) Inertia
(b) Force
(c) Kinematics
(d) kinetics.
Answer:
(c) Kinematics

Question 13.
If mass of an object is m, velocity v, acceleration a and applied force is F and momentum P is given by:
(a) P = m × v
(b) P = m × a
(c) P = \(\frac{m}{v}\)
(d) P = \(\frac{v}{m}\)
Answer:
(a) P = m × v

Question 14.
Which of the following is a vector quantity?
(a) speed
(b) distance
(c) momentum
(d) time
Answer:
(c) momentum

Question 15.
Unit of momentum in SI system is ______ .
(a) ms^-1
(b) Kg ms^-2
(c) Kg ms^-1
(d) ms^-2
Answer:
(c) Kg ms^-1

Question 16.
Force is measured based on:
(a) Newton’s first law
(b) Newton’s second law
(c) Newton’s third law
(d) All the above
Answer:
(b) Newton’s second law

Question 17.
Force measures rate of change of:
(a) acceleration
(b) velocity
(c) momentum
(d) distances
Answer:
(c) momentum

Question 18.

The rotating or turning effect of a force about a fixed point or fixed axis is called _____ .
(a) Force
(b) momentum
(c) torque
(d) couples.
Answer:
(c) torque

Question 19.
The physical quantity which is equal to the rate of change of momentum is:
(a) displacement
(b) acceleration
(c) force
(d) impulse
Answer:
(c) force

Question 20.
The momentum of a massive object at rest is:
(a) very large
(b) very small
(c) zero
(d) infinity
Answer:
(c) zero

Question 21.
The velocity which is sufficient to just escape from the gravitational pull of the earth is _____ .
(a) drift velocity
(b) escape velocity
(c) gradual velocity
(d) final velocity.
Answer:
(b) escape velocity

Question 22.
A force applied on an object is equal to:
(a) product of mass and velocity
(b) sum of mass and velocity of an object
(c) product of mass and acceleration
(d) sum of mass and acceleration
Answer:
(c) product of mass and acceleration

Question 23.
Action and reaction do not balance each other because they:
(a) act on the same body
(b) do not act on the same body
(c) are in opposite direction
(d) are unequal
Answer:
(b) do not act on the same body

Question 24.
The value of variation of accelaration due to gravity (g) is ______ at the centre of the earth.
(a) one
(b) zero
(c) ∞
(d) \(\frac{1}{\infty}\).
Answer:
(b) zero

Question 25.
Action and reaction forces are:
(a) equal in magnitude
(b) equal in direction
(c) opposite in direction
(d) both equal in magnitude and opposite in direction
Answer:
(d) both equal in magnitude and opposite in direction

Question 26.
If mass of a body is doubled then its acceleration becomes:
(a) halved
(b) doubled
(c) thrice
(d) zero
Answer:
(a) halved

Question 27.
The principle involved in the working of a jet plane is:
(a) Newton’s first law
(b) Conservation of momentum
(c) Law of inertia
(d) Newton’s second law
Answer:
(b) Conservation of momentum

Question 28.
_____ of a body is defined as the quantity of matter contained in the object.
(a) weight
(b) mass
(c) force
(d) momentum.
Answer:
(b) mass

Question 29.
A gun gets kicked back when a bullet is fired. It is a good example of Newton’s:
(a) gravitational law
(b) first law
(c) second law
(d) third law
Answer:
(d) third law

Question 30.
To change the state or position of an object force is essential.
(a) balanced
(b) unbalanced
(c) electric
(d) elastic
Answer:
(b) unbalanced

Question 31.
When a bus starts suddenly the passengers in the standing position are pushed backwards, this action is due to:
(a) first law of motion
(b) second law of motion
(c) third law of motion
(d) conservation of momentum
Answer:
(a) first law of motion

Question 32.
When a body at rest breaks into two pieces of equal masses, then the parts will move:
(a) in same direction
(b) along different directions
(c) in opposite directions with unequal speeds
(d) in opposite directions with equal speeds
Answer:
(d) in opposite directions with equal speeds

Question 33.
The principle of function of a jet aeroplane is based on:
(a) first law of motion
(b) second law of motion
(c) third law of motion
(d) all the above
Answer:
(c) third law of motion

Question 34.
Which of the following has the largest inertia?
(a) pin
(b) book
(c) pen
(d) table
Answer:
(d) table

Question 35.
An athlete runs a long path before taking a long jump to increase:
(a) energy
(b) inertia
(c) momentum
(d) force
Answer:
(c) momentum

Question 36.
The weight of a person is 50 kg. The weight of that person on the surface
(a) 50 N
(b) 35 N
(c) 380 N
(d) 490 N
Answer:
(d) 490 N

Question 37.
Which is incorrect statement about the action and reaction referred to Newton’s third law of motion?
(a) They are equal
(b) They are opposite
(c) They act on the same object
(d) They act on two different objects
Answer:
(c) They act on the same object

Question 38.
The tendency of a force to rotate a body about a given axis is called:
(a) turning effect of a force
(b) moment of force
(c) torque
(d) all the above
Answer:
(d) all the above

Question 39.
The magnitude of the moment of force is:
(a) product of force and the perpendicular distance
(b) product of force and velocity
(c) ratio of force to the acceleration
(d) ratio of force to the perpendicular distance
Answer:
(a) product of force and the perpendicular distance

Question 40.
If the force rotates the body in the anticlockwise direction, then the moment is called:
(a) clockwise moment
(b) anticlockwise moment
(c) couple
(d) torque
Answer:
(b) anticlockwise moment

Question 41.
Anticlockwise moment is:
(a) positive
(b) negative
(c) opposite
(d) zero
Answer:
(a) positive

Question 42.
Clockwise moment or torque is:
(a) zero
(b) always one
(c) negative
(d) positive
Answer:
(c) negative

Question 43.
SI unit of moment of force is:
(a) Nm^-2
(b) Nm^-1
(c) Ns
(d) Nm
Answer:
(d) Nm

Question 44.
Moment of force produces:
(a) acceleration
(b) linear motion
(c) velocity
(d) angular acceleration
Answer:
(d) angular acceleration

Question 45.
Two equal and opposite forces whose lines of action do not coincide are said to constitute a:
(a) couple
(b) torque
(c) unlike force
(d) parallel force
Answer:
(a) couple

Question 46.
Couple produces:
(a) translatory motion
(b) rotatory motion
(c) translatory as well as rotatory motion
(d) neither translatory nor rotatory
Answer:
(b) rotatory motion

Question 47
……. is an example of couple.
(a) opening or closing a tap
(b) turning of a key in a lock
(c) steering wheel of car
(d) all the above
Answer:
(d) all the above

Question 48.
Force of attraction between any two objects in the universe is called:
(a) gravitational force
(b) mechanical force
(c) magnetic force
(d) electrostatic force
Answer:
(a) gravitational force

Question 49.
Universal law of gravitation was given by:
(a) Archimedes
(b) Aryabhatta
(c) Kepler
(d) Newton
Answer:
(d) Newton

Question 50.
The force of gravitation between two bodies does not depend on:
(a) product of their masses
(b) their separation
(c) sum of their masses
(d) gravitational constant
Answer:
(c) sum of their masses

Question 51.
Law of gravitation is applicable to:
(a) heavy bodies only
(b) small sized objects
(c) light bodies
(d) objects of any size
Answer:
(d) objects of any size

Question 52.
The value of gravitational constant (G) is:
(a) different at different places
(b) same at all places in the universe
(c) different at all places of earth
(d) same only at all the places of earth
Answer:
(b) same at all places in the universe

Question 53.
The unit of gravitational constant is:
(a) Nm² kg
(b) kgms^-2
(c) Nm² kg^-2
(d) ms^-2
Answer:
(c) Nm² kg^-2

Question 54.
The weight of an object is:
(a) the quantity of matter it contains
(b) its inertia
(c) same as its mass
(d) the force with which it is attracted by the earth
Answer:
(d) the force with which it is attracted by the earth

Question 55.
In vacuum, all freely failing objects have the same:
(a) speed
(b) velocity
(c) force
(d) acceleration
Answer:
(d) acceleration

Question 56.
The acceleration due to gravity:
(a) has the same value everywhere in space
(b) has the same value everywhere on earth
(c) varies with the latitude on earth
(d) is greater on moon due to its smaller diameter
Answer:
(c) varies with the latitude on earth

Question 57.
When an object is thrown up, the force of gravity:
(a) is opposite to the direction of motion
(b) is in the same direction as direction of motion
(c) decreases as it rises up
(d) increases as it rises up
Answer:
(a) is opposite to the direction of motion

Question 58.
The SI unit of acceleration due to gravity ‘g’ is:
(a) ms^-1
(b) ms
(c) ms^-2
(d) ms²
Answer:
(c) ms^-2

Question 59.
What happens to the value of ‘g’ as we go higher from surface of earth?
(a) decreases
(b) increases
(c) no change
(d) zero
Answer:
(a) decreases

Question 60.
Mass of a body on moon is:
(a) the same as that on the earth
(b) \(\frac{1}{6}\)th of that at the surface of the earth
(c) 6 times as that on the earth
(d) none of these
Answer:
(a) the same as that on the earth

Question 61.
At which place is the value of ‘g’ is zero?
(a) at poles
(b) at centre of the earth
(c) at equator
(d) above the earth
Answer:
(b) at centre of the earth

Question 62.
The weight of the body is maximum:
(a) at the centre of the earth
(b) on the surface of earth
(c) above the surface of earth
(d) none of the above
Answer:
(b) on the surface of earth

Question 63.
A rock is brought from the surface of the moon to the earth, then its:
(a) weight will change
(b) mass will change
(c) both mass and weight will change.
(d) mass and weight will remain the same
Answer:
(a) weight will change

Question 64.
Why is the acceleration due to gravity on the surface of the moon is lesser than that on the surface of earth?
(a) because mass of moon is less
(b) radius of moon is less
(c) mass and radius of moon is large
(d) mass and radius of moon is less
Answer:
(d) mass and radius of moon is less

Question 65.
if the distance between two bodies is doubled, then the gravitational force between them is:
(a) halved
(b) doubled
(c) reduced to one-fourth
(d) increased by one fourth
Answer:
(c) reduced to one-fourth

Question 66.
The unit newton can also be written as:
(a) kgm
(b) kgms^-1
(c) kgms^-2
(d) kgm^-2s
Answer:
(c) kgms^-2

Question 67.
A bus starts for rest and moves after 4 seconds. Its velocity is 100 ms 1. Its uniform acceleration is:
(a) 10 ms^-2
(b) 25 ms^-2
(c) 400 ms^-2
(d) 2.5 ms^-2
Answer:
(b) 25 ms^-2

Question 68.
A body of mass 10 kg increases its velocity from 2 m/s to 8 m/s within 4 second by the application of a constant force. The magnitude of the applied force is:
(a) 1.5 N
(b) 30 N
(c) 15 N
(d) 150 N
Answer:
(c) 15 N

Question 69.
The moment of force in clockwise direction is the moment in the anticlockwise direction.
(a) equal to
(b) lesser than
(c) greater than
(d) none
Answer:
(a) equal to

Question 70.
Which one of the following is scalar quantity?
(a) momentum
(b) moment of force
(c) speed
(d) velocity
Answer:
(c) speed

Question 71.
Which of the following changes the direction of motion of a body?
(a) momentum
(b) force
(c) energy
(d) mass
Answer:
(b) force

Question 72.
When one makes a sharp turns while driving a car he tends to lean sideways due to:
(a) inertia
(b) inertia of rest
(c) inertia of motion
(d) inertia of direction
Answer:
(d) inertia of direction

Question 73.
The unit of momentum is:
(a) kg m
(b) m/s²
(c) kg m/s
(d) joule
Answer:
(c) kg m/s

Question 74.
Moment of a force is given by τ =
(a) \(\frac{F}{d}\)
(b) F × 2d
(c) \(\frac{F}{d}\)
(d) F × d
Answer:
(d) F × d

Question 75.
Which of the following work on the principle of torque?
(a) Gears
(b) Seasaw
(c) steering wheel
(d) all the above
Answer:
(d) all the above

Question 76.
The SI unit of gravitational constant
(a) Nm²/g
(b) Nm²kg²
(c) Nm²/g^-2
(d) Nmkg
Answer:
(c) Nm²/g^-2

Question 77.
What is the value of gravitational constant?
(a) 6.674 × 10^-11 Nm²/g^-2
(b) 9.8 × 10^-11 Nm²/g^-2
(c) 6.647 × 10^-11 Nm²/g^-2
(d) 13.28 × 10^-11 Nm²/g^-2
Answer:
(a) 6.674 × 10^-11 Nm²/g^-2

Question 78.
The value of mass of the Earth is:
(a) 6.972 × 10²⁴ kg
(b) 6.792 × 10²⁴ kg
(c) 5.972 × 10²⁴ kg
(d) 2.936 × 10²⁴ kg
Answer:
(c) 5.972 × 10²⁴ kg

Question 79.
At poles of the Earth, weight of the body is:
(a) minimum
(b) maximum
(c) zero
(d) infinity
Answer:
(b) maximum

Question 80.
Where will the value of acceleration due to gravity be minimum?
(a) poles of the earth
(b) centre of the earth
(c) equator of the earth
(d) space
Answer:
(d) space

Question 81.
When an elevator is at rest:
(a) Apparent weight is greater than the actual weight
(b) Apparent weight is less than the actual weight
(c) Apparent weight is equal to the actual weight
(d) None of the above
Answer:
(c) Apparent weight is equal to the actual weight

Question 82.
In a lift, apparent weight of a body is equal to zero when the lift is;
(a) at rest
(b) moving upwards
(c) moving downwards
(d) falling down freely
Answer:
(d) falling down freely

Question 83.
When the lift is moving upward with an acceleration ‘o’ the apparent weight of the body is:
(a) lesser than actual weight
(b) greater than actual weight
(c) equal to actual weight
(d) zero
Answer:
(b) greater than actual weight

Question 84.
When an elevator is moving downward, the apparent weight of a person who is in that elevator is:
(a) maximum
(b) zero
(c) minimum
(d) infinity
Answer:
(c) minimum

Question 85.
Which law helps to predict the path of the astronomical bodies?
(a) Newton’s law of motion
(b) Newton’s law of gravitation
(c) Newton’s law of cooling
(d) Pascal’s law
Answer:
(b) Newton’s law of gravitation

II. Fill in the blanks.

1. If force – mass × acceleration, then momentum = ………
2. If liquid hydrogen is for rocket, then …….. is for MRI.
3. Inertia: (f) Mass then momentum: ……… Recoil of the gun: (ii) Newton’s third law: then flight of Jet Planes and Rockets: ………
4. Newton’s first law of motion: definition of force and inertia then Newton’s third law of motion: ….(i)….. while Newton’s second law of motion: ……(ii)…….
5. Newton’s first law: qualitative definition of force Newton’s second law: …..(i)…… The value of g: 9.8 ms-2 then Gravitational constant: …..(ii)……
6. Force: vector then momentum: …….(i)……. Balanced force: resultant of the two forces is zero then……(ii)…….. : resultant forces are responsible for change in position or state.
7. Momentum is the product of …….. and …….
8. To produce an acceleration of 1 m/s² in an object of mass 1 kg. The force required is ……… and for 3 kg of mass to produce same acceleration, the force required is ……….
9. Two or more forces are acting in an object and does not change its position, the forces are ………. and it is essential to act some ………. force, to change the state or position of an object.
10. ……… deals with bodies that are at rest under the action of force.
11. A branch of mechanics that deals with the motion of the bodies considering the cause of motion is called ………
12. If m is the mass of a body moving with velocity v then its momentum is given by P = ……..
13. A system of forces can be brought to equilibrium by applying ………. in opposite direction.
14. Torque is a ……… quantity.
15. Steering wheel transfers a torque to the wheels with ………..
16. The mathematical form of the principle of moments is ………..
17. Change in momentum takes place in the ………. of ………
18. 1 Newton = ……..
19. If a force F acts on a body for a time t’s then the impulse is ………
20. 1 kg f = ………
21. The force of attraction between two objects is directly proportional to the product of their ……. and inversely proportional to the square of the ………. between them.
22. The value of g varies with ……… and ………
23. The value of gravitational constant is ……… at all places but the value of acceleration due to gravity ………..
24. The relation between g and G is ………
Answer:
1. mass × velocity
2. liquid helium
3. (i) Mass and velocity, (ii) Law of conservation of momentum
4. (i) Law of conservation of momentum, (ii) Measure of force
5. (i) Quantitative definition of force, (ii) 6.673 × 10^-11 Nm²kg^-2
6. (i) vector, (ii) imbalanced force
7. mass, velocity
8. 1 N, 3 N
9. balanced, unbalanced
10. Statics
11. kinetics
12. mv
13. equilibriant
14. vector
15. less effort
16. F₁ × d₁ = F₂ × d₂
17. direction, force
18. 10⁵ dyne
19. I = F × t
20. 9.8 N
21. masses, distance
22. altitude, depth
23. same, differs
24. g = \(\frac{GM}{R^2}\)

III. State whether the following statements are true or false. Correct the statement if it is false.

1. Newton’s first law explains inertia:
2. If a motion depends on force then it is called as natural motion.
3. The resistance of a body to change its state of motion is known as inertia of motion.
4. Linear momentum = mass × acceleration.
5. Two equal force acting in opposite directions are called unlike parallel forces.
6. If the resultant force of three force acting on body is zero then the forces are called balanced forces.
7. Torque is a scalar quantity.
8. Moment of couple = Force × ⊥r distance between line of action of forces
9. Principle of moments states that moment in clockwise direction = Moment in anti clockwise direction.
10. 1 Newton = 1 g cm s^-2
11. Impulse = Force
12. Propulsion of rockets is based Newton’s third law of motion and conservation of linear momentum.
13. The value of universal gravitational constant is 6.674 × 10^-11 Nm² kg^-2
14. The relation between g and G is g = \(\frac{Gm}{R^2}\)
15. The value of acceleration due to gravity decreases as the altitude of the body increases.
16. In a ‘free fall’ motion acceleration of the body is equal to the acceleration due to gravity.
Answer:
1. True
2. False – If a motion does not depend on force then it is called as natural motion.
3. True
4. False – Linear momentum = mass × velocity
5. True
6. True
7. False – Torque is a vector quantity
8. True
9. True
10. False – 1 Newton = 1 kg ms^-2
11. False – Impulse = Change in momentum
12. True
13. True
14. False – The relation between g and G is g = \(\frac{GM}{R^2}\)
15. True
16. True

IV. Match the following.

Question 1.
Match the column A with column B.

Answer:
A. (iv)
B. (i)
C. (iii)
D. (v)
E. (ii)

Question 2.
Match the column A with column B.

Answer:
A. (iv)
B. (v)
C. (ii)
D. (i)
E. (iii)

Question 3.
Match the column A with column B.

Answer:
A. (ii)
B. (iv)
C. (v)
D. (i)
E. (iii)

Question 4.
Match the column A with column B.

Answer:
A. (iv)
B. (v)
C. (i)
D. (ii)

V. Assertion and Reasoning.

Question 1.
Assertion: While travelling in a motor car we tend to remain at rest with respect to the seat.
Reason: While travelling in a motor car we tend to move along the car with respect to the ground.
(a) Both Assertion and Reason are false.
(b) Assertion is true but Reason is false.
(c) Assertion is false but Reason is true.
(d) Both Assertion and Reason are true.
Answer:
(d) Both Assertion and Reason are true.

Question 2.
Assertion: When we kick a football it will roll over; when we kick a stone of the size of the football, it remains unmoved.
Reason: Inertia of a body depends mainly on its mass.
(a) Both Assertion and Reason are true and Reason explains Assertion.
(b) Both Assertion and Reason are true but Reason doesn’t explain Assertion.
(c) Both Assertion and Reason are false.
(d) Assertion is true but Reason is false.
Answer:
(a) Both Assertion and Reason are true and Reason explains Assertion.

Question 3.
Assertion: In a gun-bullet experiment, the acceleration of the gun is much lesser than the acceleration of the bullet.
Reason: The gun has much smaller mass than the bullet.
(a) Both Assertion and Reason are false.
(b) Assertion is true but Reason is false.
(c) Assertion is false but Reason is true.
(d) Both Assertion and Reason are true.
Answer:
(b) Assertion is true but Reason is false.

Question 4.
Assertion: When a bullet is fired from a gun, the bullet moves forward, the gun moves backward.
Reason: Total momentum before collision is equal to the total momentum .after collision.
(a) Both Assertion and Reason are true and Reason explains Assertion.
(b) Both Assertion and Reason are true but Reason doesn’t explain Assertion.
(c) Assertion is true but Reason is false.
(d) Assertion is false but Reason is true.
Answer:
(b) Both Assertion and Reason are true but Reason doesn’t explain Assertion.

Question 5.
Assertion: A person whose mass on earth is 125 kg will have his mass on moon as 250 kg.
Reason: Mass varies from place to place.
(a) Both Assertion and Reason are true and Reason explains Assertion.
(b) Both Assertion and Reason are true but Reason doesn’t explain Assertion.
(c) Both Assertion and Reason are false.
(d) Assertion is true but Reason is false.
Answer:
(c) Both Assertion and Reason are false.

Question 6.
Assertion: During turning a cyclist negotiates of the curve, while a man sitting in the car leans outwards of the curve.
Reason: An acceleration is acting towards the centre of the curve.
(a) If both the assertion and the reason are true and the reason is the correct explanation of assertion.
(b) If both the assertion and the reason are true, but the reason is not the correct explanation of assertion.
(c) Assertion is true, but the reason is false.
(d) Assertion is false, but the reason is true.
Answer:
(c) Assertion is true, but the reason is false.

Question 7.
Assertion: On a rainy day, it is difficult to drive a car at high speed.
Reason: The valve of coefficient of friction is lowered due to polishing of the surface.
(a) If both the assertion and the reason are true and the reason is the correct explanation of assertion.
(b) If both the assertion and the reason are true, but the reason is not the correct explanation of assertion.
(c) Assertion is true, but the reason is false.
(d) Assertion is false, but the reason is true.
Answer:
(a) If both the assertion and the reason are true and the reason is the correct explanation of assertion.

Question 8.
Assertion: A rocket moves forward by pushing the air backwards.
Reason: It derives the necessary thrust to move forwarded according to Newton’s third law of motion.
(a) If both the assertion and the reason are true and the reason is the correct explanation of assertion.
(b) If both the assertion and the reason are true, but the reason is not the correct explanation of assertion.
(c) Assertion is true, but the reason is false.
(d) Assertion is false, but the reason is true.
Answer:
(a) If both the assertion and the reason are true and the reason is the correct explanation of assertion.

Question 9.
Assertion: A mass in the elevator which is falling freely, does not experience gravity.
Reason: Inertial and gravitational masses have equivalence.
(a) If both the assertion and the reason are true and the reason is the correct explanation of assertion.
(b) If both the assertion and the reason are true, but the reason is not the correct explanation of assertion.
(c) Assertion is true, but the reason is false.
(d) Assertion is false, but the reason is true.
Answer:
(c) Assertion is true, but the reason is false.

Question 10.
Assertion: The intensity of gravitational field varies with respect to height and depth of a body on the Earth.
Reason: The value of gravitational field intensity depends on height and depth of a body.
(a) If both the assertion and the reason are true and the reason is the correct explanation of assertion.
(b) If both the assertion and the reason are true, but the reason is not the correct explanation of assertion.
(c) Assertion is true, but the reason is false.
(d) Assertion is false, but the reason is true.
Answer:
(d) Assertion is false, but the reason is true.

VI. Answer briefly.

Question 1.
What is meant by mechanics? How can it be classified?
Answer:
Mechanics is the branch of physics that deals with the effect of force on bodies. It is divided into two branches namely statics and dynamics.

Question 2.
What is statics?
Answer:
Statics deals with the bodies, which are at rest under the action of forces.

Question 3.
What is dynamics?
Answer:
Dynamics is the study of moving bodies under the action of forces.

Question 4.
What is Kinematics?
Answer:
Kinematics deals with the motion of bodies without considering the cause of motion.

Question 5.
What is Kinetics?
Answer:
Kinetics deals with the motion of bodies considering the cause of motion.

Question 6.
Define momentum. State its unit.
Answer:
The product of mass and velocity of a moving body gives the magnitude of linear momentum. It acts in the direction of the velocity of the object.
Its S.I unit is kg ms^-1.

Question 7.
What is meant by a force?
Answer:
Force is one that changes or tends to change the state of rest or of uniform motion of a body.

Question 8.
State the effects of force.
Answer:

1. Produces or tries to produce the motion of a static body.
2. Stops or tries to stop a moving body.
3. Changes or tries to change the direction of motion of a moving body.

Question 9.
What is resultant force?
Answer:
When several forces act simultaneously on the same body, then the combined effect of the multiple forces can be represented by a single force, which is termed as ‘resultant force’.

Question 10.
What are balanced forces?
Answer:
If the resultant force of all the forces acting on a body is equal to zero, then the body will be in equilibrium. Such forces are called balanced forces.

Question 11.
What are unbalanced forces?
Answer:
Forces acting on an object which tend to change the state of rest or of uniform motion of it are called unbalanced forces.

Question 12.
What is meant by equilibriant?
Answer:
A system can be brought to equilibrium by applying another force, which is equal to the resultant force in magnitude, but opposite in direction. Such force is called as ‘Equilibriant’.

Question 13.
What is meant by couple? State few examples.
Answer:
Two equal and unlike parallel forces applied simultaneously at two distinct points constitute a couple. The line of action of the two forces does not coincide.
Eg: Turning a tap, winding or unwinding a screw, spinning of a top, etc.

Question 14.
A sudden application of brakes may cause injury to passengers in a car by collision with panels in front?
Answer:
With the application of brakes, the car slows down but our body tends to continue in the same state of motion because of inertia.

Question 15.
When we are standing in a bus which begins to move suddenly, we tend to fall backwards. Why?
Answer:
This is because a sudden start of the bus brings motion to the bus as well as to our feet in contact with the floor of the bus. But the rest of our body opposes this motion because of its inertia.

Question 16.
While travelling through a curved path, passengers in a bus tend to get thrown to one side. Justify.
Answer:
When an unbalanced force is applied by the engine to change the direction of motion of the bus, passengers move to one side of the seat due to inertia of their body.

Question 17.
Define momentum of an object.
Answer:
The momentum of an object is defined as the product of its mass and velocity.

Question 18.
Define One newton.
Answer:
The amount of force required for a body of mass 1 kg produces an acceleration of 1 ms^-2, 1 N = 1 kg ms^-2.

Question 19.
Define one dyne.
Answer:
The amount of force required for a body of mass 1 gram produces an acceleration of 1 cm s^-2, 1 dyne = 1 g cm s^-2; also
1 N = 10⁵ dyne.

Question 20.
What is unit force?
Answer:
The amount of force required to produce an acceleration of 1 ms^-2 in a body of mass 1 kg is called ‘unit force’.

Question 21.
What are the values of 1 kg f and 1 g f.
Answer:
1 kg f= 1 kg × 9.8 m s^-2 = 9.8 N;
1 g f = 1 g × 980 cm s^-2 = 980 dyne

Question 22.
What is meant by impulsive force?
Answer:
A large force acting for a very short interval of time is called as ‘Impulsive force’.

Question 23.
What is meant by impulse?
Answer:
When a force F acts on a body for a period of time t, then the product of force and time is known as ‘impulse’ represented by ‘J’
Impulse, J = F × t

Question 24.
Prove that impulse is equal to the magnitude of change in momentum.
Answer:
By Newton’s second law,
F = ΔP/t (Δ refers to change)
ΔP = F × t
J = ΔP
F × t = ΔP
Impulse is also equal to the magnitude of change in momentum. Its unit is kg ms^-1 or N s.

Question 25.
How can the change in momentum be achieved?
Answer:
Change in momentum can be achieved in two ways. They are:

1. A large force acting for a short period of time and
2. A smaller force acting for a longer period of time.

Question 26.
State an example for change in momentum.
Answer:
Automobiles are fitted with springs and shock absorbers to reduce jerks while moving on uneven roads.

Question 27.
A spring balance is fastened to a wall and another spring balance is attached to its hole and is pulled steadily. Do both the spring balances show different readings on their scales. Give reason.
Answer:
No, both the spring balances show same reading. Because both action and reaction are equal and opposite.

Question 28.
When a gun is fired it recoils, Give reason.
Answer:
When a gun is fired it exerts forward force on the bullet. The bullet exerts an equal and opposite reaction force on the gun. This results in the recoil of the gun.

Question 29.
Action and reaction are equal and opposite. But they do not cancel each other. Give reason.
Answer:
They do not cancel each other because they never act on the same body. Since they act on different bodies, they do not cancel each other.

Question 30.
Why does a cricket player, pulls his arms back with the ball while catching a ball?
Answer:
(i) The cricket player stops the speeding ball suddenly in a very short time. The high value of velocity of the ball will be decreased to zero, in a very short time and it will result in a high retardation.
(ii) When the player pulls his arms with the ball, he increases the value of time and so retardation is also decreased and retardation force is lesser than before and the palm of player is not hurt.

Question 31.
When a sailor jumps forward, the boat moves backward. State the action and reaction in the above case.
Answer:
Action – a sailor jumps forward.
Reaction – movement of the boat.

Question 32.
It is easier to stop a tennis ball than a cricket ball moving with the same velocity.
Answer:
This is because the mass of tennis ball is less than the cricket ball. So it has lesser momentum and hence smaller force is required to stop the tennis ball.

Question 33.
Define moment of force.
Answer:
The magnitude of the moment of force about a point is defined as the product of the magnitude of force and perpendicular distance of the point from the line of action of the force.

Question 34.
Draw the diagram of a couple.
Answer:

Question 35.
What do you know about moment of a couple?
Answer:
Moment of a couple is the product of force and perpendicular distance between the line of action of forces.
M = F × S

Question 36.
It is easier to open a door by applying the force at the free end. Justify.
Answer:
(i) If the force is applied at the handle of the door to open it, only small force is required. That means larger the perpendicular distance, lesser is the force needed to turn the body.

(ii) From this it is easy to conclude that the turning effect of a body about an axis depends not only on the magnitude of the force but also on the perpendicular distance of the line of action of the applied force from the axis of rotation.

Question 37.
A force can rotate a nut when applied by a wrench.
Answer:
(a) What is meant by moment of force?
Answer:
The turning effect of force acting on a body about an axis is called the moment of force.

(b) Name the factors on which the turning effect of a force depend on.
Answer:
Turning effect of force depends on-

1. The magnitude of the force applied and
2. The distance of line of action of the force from the axis of rotation.

Question 38.
What is meant by weightlessness?
Answer:
Whenever a body or a person falls freely under the action of Earth’s gravitational force alone, it appears to have zero weight. This state is referred to as ‘weightlessness’.

Question 39.
What is meant by moment of a force?
Answer:
The turning effect of force acting on a body about an axis is called moment of force.

Question 40.
What is meant by gravitational force?
Answer:
The gravitational force is the force of attraction between objects in the universe.

Question 41.
In which direction does gravitational force act?
Answer:
The gravitational force acts along the line joining the centres of two objects.

Question 42.
(a) When a horse suddenly starts running, the rider falls backward. Give reason.
Answer:
This is because the lower part of the rider which is in contact with the horse, comes into motion. While his upper part tends to remain at rest due to inertia.

(b) Coin falls into the tumbler when the card is given a sudden jerk. State the fact that is utilized in this illustration.
Answer:
inertia.

Question 43.
(a) Why it is difficult to walk on a slippery floor or sand?
Answer:
Because we are unable to push (action) such a ground sufficiently hard. As a result, the force of reaction is not sufficient to help us to move forward.

(b) State the law related to this.
Answer:
Newton’s third law of motion.

Question 44.
State the numerical value and unit of gravitational constant.
Answer:
The numerical value of gravitational constant is 6.673 × 10^-11 Nm² kg^-2.
Its unit is Nm² kg^-2.

Question 45.
What is meant by acceleration due gravity?
Answer:
The acceleration produced in a body on account of the force of gravity is called acceleration due to gravity.

Question 46.
Write the expression of acceleration due to gravity.
Answer:
Acceleration due to gravity g = \(\frac{GM}{R^2}\)
where G is gravitational constant.
M is the mass of the earth.
R is radius of the earth.

Question 47.
Deduce the value of mass of earth.
Answer:
Mass of earth M = \(\frac{gR^2}{G}\)
g = 9.8 m/s²
R = 6.38 × 10⁶ m
G = 6.673 × 10^-11 Nm² kg^-2

= 5.98 × 10²⁴ kg

Question 48.
What happens to the gravitational force between two objects if the masses of both objects are doubled?
Answer:
If the masses of both objects are doubled, then gravitational force between them will be increased to four times.

Question 49.
The mass of a body is 60 kg. What will be its mass when it is placed on the moon?
Answer:
The mass of a body on the moon is 60 kg. There will be no change in mass because it is still made up of same amount of matter.

Question 50.
When an object is taken to the moon, is there any change in weight?
Answer:
Yes. The weight of a object will be decreased because the gravitational force is weak i.e., the value of acceleration due to gravity becomes less on the moon.

Question 51.
Gravitational force acts on all objects is proportional to their masses. But a heavy object falls slower than a light object. Give reason.
Answer:
It is true that gravitational force between all objects are in proportion to their masses. But in free fall of objects, acceleration produced in a body is due to gravitational force is independent of mass of object that’s why a heavy object does not fall faster.

Question 52.
A falling apple is attracted towards the earth.
(a) Does the apple attract the earth?
Answer:
Yes. According to Newton’s third Law. The apple attracts the earth.

(b) Why doesn’t earth move towards an apple?
Answer:
According to Newton’s second Law, for a given force, acceleration a ∝ \(\frac{1}{m}\). Here mass of an apple is negligibly small compared to earth. So we cannot see the earth moving towards an apple.

Question 53.
Observe the figure and write the answer:
Answer:

(a) The force which balance A exerts on balance B is called …….
Answer:
The force which balance A exerts on balance B is called action.

(b) The force of balance B on balance A is called ……..
Answer:
The force of balance B on balance A is called opposite reaction.

Question 54.
What is meant by apparent weight?
Answer:
Apparent weight is the weight of the body acquired due to the action of gravity and other external forces acting on the body.

Question 55.
What is meant by free fall?
Answer:
When the person in a lift moves down with an acceleration (a) equal to the , acceleration due to gravity (g), i.e., when a = g, this motion is called as ‘free fall’. Here, the apparent weight (R = m (g – g) = 0) of the person is zero.

VII. Solve the given problems.

Question 1.
The ratio of masses of two bodies is 1 : 3 and the ratio of applied forces on them is 4 : 9. Calculate the ratio of their accelerations.
Answer:
Ratio of masses m₁ : m₂ = 1 : 3
Ratio of applied forces F₁ : F₂ = 4 : 9
Accelerations a = \(\frac{F}{m}\)
Acceleration of first body,
a₁ = \(\frac{F_1}{m_1}\)
= \(\frac{4}{1}\) = 4
Acceleration of second body,
a₂ = \(\frac{F_2}{m_2}\)
Ratio of their accelerations is 4 : 3

Question 2.
What is acceleration produced by a force of 12 N exerted on an object of mass 3 kg?
Answer:
F = 12 N; m = 3 kg ; a = ?
F = ma; a = F/m = \(\frac{4}{1}\) = 4 m/s²
The acceleration produced a = 4 m/s².

Question 3.
A certain force exerted for 1.2 s raises the speed of an object from 1.8 m/s to 4.2 m/s. Later, the same force is applied for 2 s. How much does the speed change in 2 s.
Answer:
t = 1.2 s; u = 1.8 m/s; v = 4.2 m/s
acceleration a = \(\frac{v-u}{t}\)
= \(\frac{4.2-1.8}{1.2}\) = \(\frac{2.4}{1.2}\)
= 2 m/s²
Now, the force applied is the same, it will produce the same acceleration.
Change in speed = acceleration × time for which force is applied.
= 2 × 2 = 4 m/s
Change in speed = 4 m/s.

Question 4.
A constant force acts on an object of mass 10 kg for a duration of 4 s. It increases the objects velocity from 2 ms^-1 to 8 ms^-1. Find the magnitude of the applied force.
Answer:
Mass of an object m = 10 kg
Initial velocity u = 2 ms^-1
Final velocity v = 8 ms^-1
We know, force F = \(\frac{m(v-u)}{t}\)
F = \(\frac{10(8-2)}{4}\)
= \(\frac{10×6}{4}\)
= 15 N

Question 5.
Which would require a greater force for accelerating a 2 kg of mass at 4 ms^-2 or a 3 kg mass at 2 ms^-2?
Answer:
We know, force F = ma
Given m₁ = 2 kg a₁ = 4 ms^-2
m₂ = 3 kg a₂ = 2 ms^-2
F₁ = m₁ a₁ = 2 × 4 = 8 N
F₂ = m₂ a₂ = 3 × 2 = 6 N
∴ F₁ > F₂.
Thus, accelerating 2 kg mass at 4 ms^-2 would require a greater force.

Question 6.
A bullet of mass 15 g is horizontally fired with a velocity 100 ms^-1 from a pistol of mass 2 kg. What is the recoil velocity of the pistol?
Answer:
The mass of the bullet, m₁ = 15 g = 0.015 kg
Mass of the pistol, m₂ = 2 kg
Initial velocity of the bullet, u₁ = 0
Initial velocity of the pistol, u₂ = 0
Final velocity of the bullet, v₁ = + 100 ms^-1
(The direction of the bullet is taken from left to right-positive, by convention) Recoil velocity of the pistol = v₂
Total momentum of the pistol and bullet before firing.
= m₁ u₁ + m₂ u₁
= (0.015 × 0) + (2 × 0)
= 0
Total momentum of the pistol and bullet after firing.
= m₁ v₁ + m₂ v₂
= (0.015 × 100) + (2 × v₂)
= 1.5 + 2v₂
According to the law of conservation of momentum,
Total momentum after firing = Total momentum before firing.
1.5 + 2v₂ = 0
2v₂ = -1.5
v₂ = – 0.75 ms^-1
Negative sign indicates that the direction in which the pistol would recoil is opposite to that of the bullet, that is, right to left.

Question 7.
A 10 g bullet is shot from a 5 kg gun with a velocity of 400 m/s. what is the speed of recoil of the gun?
Answer:
Mass of bullet, m₁ = 10 g
= 10 × 10^-3 kg = 10^-2 kg
Mass of gun, m₂ = 5 kg
Velocity of bullet, v₁ = 400 m/s
speed of recoil of gun v₂ = ?
Total momentum of bullet and gun after firing = total momentum before firing.
m₁ v₁ + m₂ v₂ = 0
v₂ = –\(\frac{m_1 v_1}{m_2}\)
= \(\frac{-10_{-2}×400}{5}\) = -0.8 m/’s.
The speed of recoil of the gun v₂ = -0.8 m/’s.
Negative sign shows that the gun moves in a direction opposite to that of the bullet.

Question 8.
The figure represents two bodies of masses 10 kg and 20 kg, moving with an initial velocity of 10 ms^-1 and 5 ms^-1 respectively. They collide with each other. After collision, they move with velocities 12 ms^-1 and 4 ms^-1 respectively. The time of collision is 2 s. Now calculate F₂ and F₂.
Answer:

m₁ = 10 kg
m₂ = 20 kg
u₁ = 10 ms^-1
u₂ = 5 ms^-1
v₁ = 12 ms^-1
v₂ = 4 ms^-1
Time of collision, t = 2 s
∴ Force acting on 20 kg object
F₁ = m₂ (\(\frac{v_2-u_2}{t}\))
= 20(\(\frac{4-5}{2}\))
F₁ = -10 N
Force acting on 10 kg object
F₂ = m₁ (\(\frac{v_1-u_1}{t}\))
= 10(\(\frac{12-10}{2}\))
F₂ = 10 N

Question 9.
The mass of an object is 5 kg. What is its weight on the earth?
Answer:
Mass, m = 5 kg
Acceleration due to gravity,
g = 9.8 ms^-2
Weight, W = m × g
W = 5 × 9.8 = 49 N
Therefore, the weight of the object is 49 N.

Question 10.
Calculate the force of gravitation between two objects of masses 80 kg and 120 kg kept at a distance of 10 m from each other. Given, G = 6.67 × 10^-11 Nm² / kg².
Answer:
m₁ = 80 kg, m₂ = 120 kg, r = 10 m,
G = 6.67 × 10^-11 Nm² / kg², F = ?

= 64.032 × 10^-10 N
The force of gravitation between two objects = 64.032 × 10^-10 N.

Question 11.
Calculate the value of acceleration due to gravity on moon. Given mass of moon = 7.4 × 10²² kg. radius of moon = 1740 km.
Answer:

= 1.63 ms²
The acceleration due to gravity = 1.63 ms^-2.

Question 12.
State Newton’s law of gravitation. Write an expression for acceleration due to gravity on the surface of the earth. If the ratio of acceleration due to gravity of two heavenly bodies is 1 : 4 and the ratio of their radii is 1 : 3, what will be the ratio of their masses?
Answer:
Newton’s law of gravitation states that every object in the universe attracts every other object with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
F = \(\frac{Gm_{1}m_{2}}{d^{2}}\)
Acceleration due to gravity g = \(\frac{GM}{R^{2}}\)
Where G is gravitational constant
M is the mass of the earth
R is radius of the earth
Ratio of acceleration due to gravity = 1 : 4
Ratio of radii of two bodies = 1 : 3
Acceleration due to gravity is g

Dividing Equation (1) by equation (2) we get

∴ M₁ : M₂ = 1 : 36
∴ Ratio of their masses = 1 : 36

Question 13.
A bomb of mass 3 kg, initially at rest, explodes into two parts of 2 kg and 1 kg. The 2 kg mass travels with a velocity of 3 m/s. At what velocity will the 1 kg mass travel?
Answer:
Mass of a bomb m = 3 kg
Initial velocity of the bomb v = 0
Mass of the first part m₁ = 2 kg
Velocity of the first part v₁= 3 m/s
Mass of the second part m₂ = 1 kg
Let the velocity of the second part be v₂.
By the law of conservation of momentum
mv = m₁ v₁ + m₂ v₂
3 × 0 = 2 × 3 + 1 × v₂
0 = 6 + v₂
∴ v₂ = -6 m/s
Velocity of the 1 kg mass = -6 m/s

Question 14.
Two ice skaters of weight 60 kg and 50 kg are holding the two ends of a rope. The rope is taut. The 60 kg man pulls the rope with 20 N force. What will be the force exerted by the rope on the other person? What will be their respective acceleration?
Answer:
Mass of first ice skater = 50 kg
Mass of second ice skater = 60 kg
Force applied by second ice skater = 20 N
When the rope is taut, the force exerted by the rope on the other person is 20 N.

= 0.33 m/s²

VIII. Answer in detail.

Question 1.
Explain the types of forces.
Answer:
Based on the direction in which the forces act, they can be classified into two types as:
1. Like parallel forces : Two or more forces of equal or unequal magnitude acting along the same direction, parallel to each other are called like parallel forces.
2. Unlike parallel forces : If two or more equal forces or unequal forces act along opposite directions parallel to each other, then they are called unlike parallel forces.

Question 2.
Tabulate the action of forces with their resultant and diagram.
Answer:

Question 3.
Explain the applications of torque.
Answer:
1. Gears : A gear is a circular wheel with teeth around its rim. It helps to change the speed of rotation of a wheel by changing the torque and helps to transmit power.

2. Seasaw : Most of you have played on the seasaw. Since there is a difference in the weight of the persons sitting on it, the heavier person lifts the lighter person. When the heavier person comes closer to the pivot point (fulcrum) the distance of the line of action of the force decreases. It causes less amount of torque to act on it. This enables the lighter person to lift the heavier person.

3. Steering Wheel : A small steering wheel enables you to manoeuore a car easily by transferring a torque to the wheels with less effort.

Question 4.
State and explain principle of moments.
Answer:
When a number of like or unlike parallel forces act on a rigid body and the body is in equilibrium, then the algebraic sum of the moments in the clockwise direction is equal to the algebraic sum of the moments in the anticlockwise direction. In other words, at equilibrium, the algebraic sum of the moments of all the individual forces about any point is equal to zero.

In the illustration given in figure, the force F₁ produces an anticlockwise rotation at a distance d₁ from the point of pivot P (called fulcrum) and the force F₂ produces a clockwise rotation at a distance d₂ from the point of pivot P. The principle of moments can be written as follows:
Moment of clockwise direction = Moment of anticlockwise direction
F₁ × d₁ = F₂ × d₂

Question 5.
Explain the illustrations for Newton’s third law of motion briefly.
Answer:
Newton’s third law states that ‘for every action, there is an equal and opposite reaction.They always act on two different bodies.
If a body A applies a force F_A on a body B, then the body B reacts with force F_B on the body A, which is equal to F_A in magnitude, but opposite in direction. F_B = -F_A
Eg:
(i) When birds fly they push the air downwards with their wings (Action) and the air pushes the bird upwards(Reaction).
(ii) When a person swims he pushes the water using the hands backwards (Action), and the water pushes the swimmer in the forward direction (Reaction).
(iii) When you fire a bullet, the gun recoils backward and the bullet is moving forward (Action) and the gun equalises this forward action by moving backward (Reaction).

Question 6.
Derive the relation between acceleration due to gravity (g) and Gravitational constant G.
Answer:

When a body is at rests on the surface of the Earth, it is acted upon by the gravitational force of the Earth. Let us compute the magnitude of this force in two ways. Let, M be the mass of the Earth and m be the mass of the body. The entire mass of the Earth is assumed to be concentrated at its centre. The radius of the Earth is R = 6378 km = 6400 km approximately. By Newton’s law of gravitation, the force acting on the body is given by
F = \(\frac{GMm}{R^2}\)
Here, the radius of the body considered is negligible when compared with the Earth’s radius. Now, the same force can be obtained from Newton’s second law of motion.
According to this law, the force acting on the body is given by the product of its mass and acceleration (called as weight). Here, acceleration of the body is under the action of gravity hence a = g
F = ma = mg …….. (1)
F = weight = mg ……… (2)
Comparing equations (1) and (2), we get
mg = \(\frac{GMm}{R^2}\)
Acceleration due to gravity g = \(\frac{GM}{R^2}\)

Question 7.
Tabulate the apparent weight of person moving in a lift when lift is
(i) moving upwards
(ii) moving downwards
(iii) at rest
(iv) falling down freely.
Answer:

IX. HOT Questions

Question 1.
What gives the measure of inertia?
Answer:
Mass of a body gives the measure of inertia.

Question 2.
Is any external force required to keep a body in uniform motion?
Answer:
No, external force is not required to keep a body in uniform motion.

Question 3.
Which law of motion gives the measure of force?
Answer:
Newton’s second law of motion.

Question 4.
Write the second law of motion in vector form.
Answer:
\(\vec { F } =m\vec { a }\)
Where, \(\vec { F }\) – force, m – mass, \(\vec { a }\) – acceleration.

Question 5.
What is the net force acting on a cork that floats on water? Why?
Answer:
The net force is zero, because the weight of the cork is balanced by the upthrust of water on it.

Question 6.
What is the relation between newton and dyne?
Answer:
1 newton = 105 dyne

Question 7.
A person is standing on a weighing machine placed nearly a door. What will be the effect of the reading of the machine if a person presses the edge of the door upward?
Answer:
The reading of the machine will increase.

Question 8.
A bomb explode in mid-air into two equal fragments. What is the relation between the direction of motion of the two fragments?
Answer:
The two fragments will fly off in exactly opposite directions.

Question 9.
Which law explains the following situation, Athlete runs a certain distance before long jump.
Answer:
Law of inertia which is Newton’s first law of motion.

Question 10.
Is impulse a scalar?
Answer:
No, impulse is a vector quantity.

Question 11.
When a lift moves with uniform velocity, what is its
(i) acceleration and
(ii) the apparent weight of the person standing inside the lift.
Answer:
(i) Acceleration of the lift is zero.
(ii) The apparent weight of a person standing inside the lift is equal to his true weight since R = mg.

Question 12.
When a lift falls freely, what happens to the apparent weight of a body in the lift.
Answer:
The apparent weight of the body in the lift is equal to zero. Since
R = m(g – g) = 0

Question 13.
When a body falls freely it appears to have zero weight. Give reason.
Answer:
When a body falls freely, it acts under the action of gravitational force alone. Hence it appears to have zero weight.

Students can download Maths Chapter 5 Coordinate Geometry Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Additional Questions

I. Multiple Choice Questions

Question 1.
If the three points (-3, 7), (a, 1), (-3, 2) are collinear then the value of “a” is
(1) 0
(2) -1
(3) -3
(4) 1
Answer:
(3) -3
Hint:
Since the three points are collinear
Area of a ∆ = 0

-3 + 2a – 21 – (7a – 3 – 6) = 0 ⇒ 2a – 24 – 7a + 9 = 0
– 5a – 15 = 0 ⇒ – 5(a + 3) = 0
a + 3 = 0 ⇒ a = -3

Question 2.
If A (5, 5), B (-5, 1), C (10, 7) lie in a straight line, then the area of ∆ ABC is …………….
(1) \(\frac { 13 }{ 2 } \) sq.units
(2) 9 sq.units
(3) 25 sq.units
(4) 0
Answer:
(4) 0
Hint:
Area of the ∆^le

Question 3.
In a rectangle ABCD, area of ∆ ABC is \(\frac { 31 }{ 2 } \) sq. units. Then the area of rectangle is ……………
(1) 62 sq. units
(2) 31 sq. units
(3) 60 sq. units
(4) 30 sq. units
Answer:
(2) 31 sq. units
Hint:
In a rectangle area of ∆ ABC and area of ∆ ACD are equal.
Area of rectangle ABCD = 2 × \(\frac { 31 }{ 2 } \) = 31 sq.units

Question 4.
If the points (k, 2k), (3k, 3k) and (3,1) are collinear, then k is ……………..
(1) \(\frac { 1 }{ 3 } \)
(2) – \(\frac { 1 }{ 3 } \)
(3) \(\frac { 2 }{ 3 } \)
(4) – \(\frac { 2 }{ 3 } \)
Answer:
(2) – \(\frac { 1 }{ 3 } \)
Hint:
Since the three points are collinear. Area of a ∆ = 0

3k² + 3k + 6k – (6k² + 9k + k) = 0 ⇒ 3k² + 9k – 6k² – 10k = 0
-3 k² – k = 0 ⇒ -k(3k + 1) = 0
3k + 1 = 0 ⇒ 3 k = -1 ⇒ k = – \(\frac { 1 }{ 3 } \)

Question 5.
If the area of the triangle formed by the points (x, 2x), (-2, 6) and (3, 1) is 5 square units then x = ………….
(1) 2
(2) \(\frac { 3 }{ 5 } \)
(3) 3
(4) 5
Answer:
(1) 2
Hint:
Area of the triangle = 5 sq. units

6x – 2 + 6x – (-4x + 18 + x) = 10 ⇒ 12x – 2 – (-3x + 18) = 10
12x – 2 + 3x – 18 = 10
15x – 20 = 10 ⇒ 15x = 10 + 20 = 30
x = \(\frac { 30 }{ 15 } \) = 2

Question 6.
The slope of a line parallel to y-axis is equal to …………..
(1) 0
(2) -1
(3) 1
(4) not defined
Answer:
(4) not defined

Question 7.
In a rectangle PQRS, the slope of PQ = \(\frac { 5 }{ 6 } \) then the slope of RS is ………..
(1) \(\frac { -5 }{ 6 } \)
(2) \(\frac { 6 }{ 5 } \)
(3) \(\frac { -6 }{ 5 } \)
(4) \(\frac { 5 }{ 6 } \)
Answer:
\(\frac { 5 }{ 6 } \)
Hint:
In a rectangle opposite sides are parallel.
∴ Slope of the line RS is \(\frac { 5 }{ 6 } \).

Question 8.
The y – intercept of the line y = 2x is ………
(1) 1
(2) 2
(3) \(\frac { 1 }{ 2 } \)
(4) 0
Answer:
(4) 0

Question 9.
The straight line given by the equation y = 5 is …………..
(1) Parallel to x – axis
(2) Parallel to y – axis
(3) Passes through the origin
(4) None of these
Answer:
(1) Parallel to x – axis

Question 10.
The x – intercept of the line 2x – 3y + 5 = 0 is ………….
(1) \(\frac { 5 }{ 2 } \)
(2) \(\frac { -5 }{ 2 } \)
(3) \(\frac { 2 }{ 5 } \)
(4) \(\frac { -2 }{ 5 } \)
Answer:
(2) \(\frac { -5 }{ 2 } \)
Hint:
2x – 3y + 5 = 0 ⇒ 2x – 3y = – 5

Question 11.
The lines 3x – 5y + 1 = 0 and 5x + ky + 2 = 0 are perpendicular if the value of k is ………..
(1) -5
(2) 3
(3) -3
(4) 5
Answer:
(2) 3
Hint:
Slope of the first line (m₁) = \(\frac { -3 }{ -5 } \) = \(\frac { 3 }{ 5 } \)
Slope of the second line (m₂) = \(\frac { -5 }{ k } \)
Since the two lines are perpendicular.
m₁ × m₂ = -1
\(\frac { 3 }{ 5 } \) × \(\frac { -5 }{ k } \) = -1 ⇒ \(\frac { -3 }{ k } \) = -1
-k = -3 ⇒ The value of k = 3

Question 12.
If x – y = 3 and x + 2y = 6 are the diameters of a circle then the centre is at the point ………..
(1) (0, 0)
(2) (1, 2)
(3) (1, -1)
(4) (4, 1)
Answer:
(4) (4, 1)
Hint:
Centre of the circle is the intersection of the two diameters.

Centre of the circle is (4, 1)

Question 13.
The line 4x + 3y – 12 = 0 meets the x-axis at the point ……….
(1) (4, 0)
(2) (3, 0)
(3) (-3, 0)
Answer:
(2) (3,0)
Hint:
4x + 3y – 12 = 0 meet the x-axis the value of y = 0
4x- 12 = 0 ⇒ 4x = 12
x = \(\frac { 12 }{ 4 } \) = 3 ⇒ The point is (3, 0)

Question 14.
The equation of a straight line passing through the point (2, -7) and parallel to x-axis is ……………….
(1) x = 2
(2) x = -7
(3) y = -7
(4) y = 2
Answer:
(3) y = -7
Hint:
Equation of a line parallel to x-axis is y = -7

Question 15.
The equation of a straight line having slope 3 and y intercept – 4 is ………………
(1) 3x – y – 4 = 0
(2) 3x + y – 4 = 0
(3) 3x – y + 4 = 0
(4) 3x – y + 4 = 0
Answer:
(1) 3x – y – 4 = 0
Hint. The equation of a line is y = mx + c
y = 3 (x) + (-4) ⇒ y = 3x – 4
3x – y – 4 = 0

II. Answer the following questions:

Question 1.
If the points (3, – 4) (1, 6) and (- 2, 3) are the vertices of a triangle, find its area.
Answer:
Let the vertices A (3, – 4), B (1, 6) and C (- 2, 3)

Area of ∆ ABC = \(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁, – (x₂y₁ + x₃y₂ + x₁y₃)]

Area of a ∆ = 18 sq. units

Question 2.
If the area of the triangle formed by the points (1,2) (2,3) and (a, 4) is 8 sq. units, find a.
Answer:
Area of a triangle = 8 sq. units.

\(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)] = 8.
\(\frac { 1 }{ 2 } \) [3 + 8 + 2a – (4 + 3a + 4)] = 8
11 + 2a – 8 – 3a= 16 ⇒ – a + 3 = 16
– a = 16 – 3 ⇒ a = -13
The value of a = -13

Question 3.
If the points A (2, 5), B (4, 6) and C (8, a) are collinear find the value of “a” using slope concept.
Answer:
Since the three points are collineal
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of AB = Slope of BC
\(\frac { 6-5 }{ 4-2 } \) = \(\frac { a-6 }{ 8-4 } \) ⇒ \(\frac { 1 }{ 2 } \) = \(\frac { a-6 }{ 4 } \) ⇒ 2a – 12 = 4 ⇒ 2a = 16
a = \(\frac { 16 }{ 2 } \) = 8 ⇒ The value of a = 8

Question 4.
If the points (x,y) is collinear with the points (a, 0) and (0, b) then prove that \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
Answer:
Let A (x, y), B (a, 0), C(0, b)
Since the three points are collinear
Slope of AB = Slope of BC
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
\(\frac { 0-y }{ a-x } \) = \(\frac { b-0 }{ 0-a } \)
\(\frac { -y }{ a-x } \) = \(\frac { b }{ -a } \)
ay = b (a – x)
ay = ba – bx
ay + bx = ab
Divided by ab
\(\frac { ay }{ ab } \) + \(\frac { bx }{ ab } \) = \(\frac { ab }{ ab } \)
\(\frac { y }{ b } \) + \(\frac { x }{ a } \) = 1 ⇒ \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1

Question 5.
A straight line passes through (1, 2) and has the equation y – 2x – k = 0. Find k.
Answer:
The given line is y – 2x – k = 0
It passes through (1,2)
(2) -2 (1) -k = 0 ⇒ 2 – 2 – k = 0
0 – k = 0 ⇒ k = 0
The value of k = 0

Question 6.
If a line passes through the mid point of AB where A is (3, 0) and B is (5, 4) and makes an angle 60° with x – axis find its equation.
Answer:

Slope of a line = tan 60°
= \(\sqrt { 3 }\)
Equation of a line is y – y₁ = m (x – x₁)
y – 2 = \(\sqrt { 3 }\) (x – 4)
y – 2 = \(\sqrt { 3 }\) x – 4 \(\sqrt { 3 }\)
\(\sqrt { 3x }\) – y + 2 – 4\(\sqrt { 3 }\) = 0

Question 7.
Find the equation of the line through (3, 2) and perpendicular to the line joining (4, 5) and (1,2)
Answer:
Slope of a line = \(\frac { 2-5 }{ 1-4 } \) ⇒ \(\frac { -3 }{ -3 } \) = 1
Slope of the line perpendicular to it is – 1
Equation of the line joining -1 and (3, 2) is
y – y₁ = m (x – x₁) ⇒ y – 2 = -1(x – 3)
y – 2 = -x + 3 ⇒ x + y – 5 = 0

Question 8.
P and Q trisect the line segment joining the points (2, 1) and (5, – 8). If the point P lies on 2x – y + k = 0, then find the value of k.
Answer:

A line divides internally in the ratio 1 : 2
A line divide internally in the ratio l : m

The point P = (\(\frac { 5+4 }{ 3 } \),\(\frac { -8+2 }{ 3 } \))
= (\(\frac { 9 }{ 3 } \),\(\frac { -6 }{ 3 } \)) = (3, -2)
The given line 2x – y + k = 0 passes through the point (3,-2)
2 (3) – (- 2) + k = 0
6 + 2 + k = 0
8 + k = 0
k = – 8
The value of k = – 8

Question 9.
The line 4x + 3y – 12 = 0 intersect the X, Y – axis at A and B respectively. Fine the area of ∆AOB.
Answer:
The equation of the line AB is 4x + 3y – 12 = 0

4x + 3y = 12
\(\frac { 4x }{ 12 } \) + \(\frac { 3y }{ 12 } \) = 1 ⇒ \(\frac { x }{ 3 } \) + \(\frac { y }{ 4 } \) = 1
The point A is (3, 0) (it intersect the X – axis)
and B is (0, 4) (it intersect the Y – axis)
Area of ∆ AOB = \(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ (x₂y₁ + x₃y₂ + x₁y₃)]

Question 10.
Find the equation of the line passing through (4, 5) and making equal intercept in the axes.
Answer:
Let the equal intercept on the axes be a, a.
Equation of the line is \(\frac { x }{ a } \) + \(\frac { y }{ a } \) = 1 (Given equal intercepts)
The line passes through (4, 5)
\(\frac { 4 }{ a } \) + \(\frac { 5 }{ a } \) = 1 ⇒ \(\frac { 9 }{ a } \) = 1 ⇒ a = 9
The equation of the line is \(\frac { x }{ 9 } \) + \(\frac { y }{ 9 } \) = 1
Multiply by 9
x + y – 9 = 0

Question 11.
Find the equation of the line passing through (2, – 1) and whose intercepts on the axes are equal in magnitude but opposite in sign.
Answer:
Let the x – intercept be “a” and y intercept be = “-a”
The equation of the line is
\(\frac { x }{ a } \) + \(\frac { y }{ -a } \) = 1 (y – intercept is – a)
\(\frac { x }{ a } \) – \(\frac { y }{ a } \) = 1
It passes through (2, -1)
\(\frac { 2 }{ a } \) – \(\frac { (-1) }{ a } \) = 1
\(\frac { 2 }{ a } \) + \(\frac { 1 }{ a } \) = 1 ⇒ \(\frac { 3 }{ a } \) = 1
a = 3
The equation of the line is
\(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
\(\frac { x }{ 3 } \) + \(\frac { y }{ -3 } \) = 1 ⇒ \(\frac { x }{ 3 } \) – \(\frac { y }{ 3 } \) = 1
x – y = 3
The equation is x – y – 3 = 0

Question 12.
The straight line cuts the coordinate axes at A and B. If the mid point of AB is (3,2) then find the equation of AB.
Answer:
Let the point A be (a, 0) and B be (0, b)


The point A (6, 0) and B (0, 4)
Equation of the line AB is

III. Answer the following questions

Question 1.
If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the ‘ coordinates of any point “c”, if AC = BC and Area of triangle ABC = 10 sq. units.
Answer:
Let the coordinates C be (a, 6) then AC = BC
AC² = BC²
(a – 3)² + (b – 4)² = (a – 5)² + (b + 2)²
a² + 9 – 6a + b² + 16 – 8b = a² + 25 – 10a + b² + 4 – 4b
a² + b² + 25 – 6a – 86 = a² + b² + 29 – 10a + 4b

25 – 6a – 8b = 29 – 10a + 46
4a – 12b = 4 ⇒ a – 3b = 1 ………… (1)
Area of ∆ ABC = 10 sq. units
\(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)] = 10

-6 + 5b + 4a – (20 – 2a + 3b) = 20
-6 + 5b + 4a – 20 + 2a – 3b = 20
6a + 2b – 26 = 20 ⇒ 6a + 2b = 46

Substitute the value of a = 7 in (2)
3 (7) + b = 23 ⇒ b = 23 – 21 = 2
The coordinate C is (7, 2)

Question 2.
The four vertices of a Quadrilateral are (1,2) (- 5,6) (7, – 4) and (k, – 2) taken in order. If the area of the Quadrilateral is 9 sq. units, find the value of k.
Answer:
Let A (1, 2) B (- 5, 6) C (7, – 4) and D (k, – 2)
Area of the
Quadrilateral ABCD = \(\frac { 1 }{ 2 } \)[(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) – (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)]

Area of the Quadrilateral ABCD = 3k – 9
Given area of a Quadrilateral is 9 sq. units.
3k – 9 = 9 ⇒ 3k = 18 ⇒ k = \(\frac { 18 }{ 3 } \) = 6
The value of k = 6

Question 3.
Find the area of a triangles whose three sides are having the equations x + y = 2, x – y = 0 and x + 2y – 6 = 0.
Answer:
Find the three vertices of the triangles by solving their equation.
To find vertices A


Substitute the value of y = 4 in (1)
x + 4 = 2 ⇒ x = 2 – 4 = -2
The vertices A is (- 2, 4)
To find vertices B

Substitute the value of x = 1 in (1)
1 + y = 2 ⇒ y = 2 – 1 = 1
The vertices B is (1, 1)
To find vertices C

y = \(\frac { 6 }{ 3 } \) = 2
Substitute the value y = 2 in (3)
x – 2 = 0 ⇒ x = 2
The vertices C is (2, 2)

Area of the ∆ BC = 3 sq. units

Question 4.
Verify the Median of a triangle divides into two triangles of equal areas whose vertices are A (4, – 6), B (3, – 2) and C (5, 2)
Answer:

Let D be the mid point of AC .
Mid point of AC = (\(\frac { 5+4 }{ 2 } \),\(\frac { 2-6 }{ 2 } \)) = (\(\frac { 9 }{ 2 } \),-2)
Area of the triangle = \(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)]

Area of ∆ ADB = Area of ∆ BDC
A median divides the triangle of equal areas.

Question 5.
Find the area of the ∆ ABC with A (1, – 4) and the mid points of sides through A being (2,-1) and (0,-1)
Answer:
Let the coordinates of B and C are (a, b) and (c, d) respectively.
Sides through A are AB and AC

Mid point of AB = (\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\))
(2, -1) = (\(\frac { 1+a }{ 2 } \),\(\frac { -4+b }{ 2 } \))
\(\frac { 1+a }{ 2 } \) = 2
1 + a = 4
a = 4 – 1
= 3
The point B is (3,2)
\(\frac { -4+b }{ 2 } \) = -1
-4 + b = -2
b = -2 + 4
= 2
Mid point of AC = (\(\frac { 1+c }{ 2 } \),\(\frac { -4+d }{ 2 } \))
(0,-1) = (\(\frac { 1+c }{ 2 } \),\(\frac { -4+d }{ 2 } \))
\(\frac { 1+c }{ 2 } \) = 0
1 + c = 0
c = 0 – 1
= – 1
The point C is (-1,2)
\(\frac { -4+d }{ 2 } \) = -1
– 4 + d = -2
d = – 2 + 4
= 2
Thus the coordinates of the vertices of ∆ ABC are A (1, – 4) B (3, 2) and C (- 1, 2)
Area of ∆ ABC = \(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)]

Area of ∆ ABC = 12 sq. units

Question 6.
Find the equation of the straight lines passing through (- 3, 10) whose sum of the intercepts is 8.
Answer:
Let the “x” intercept be “a” and y intercept be “b”
Sum of the intercepts = 8
a + b = 8 ⇒ b = 8 – a
Equation of a line is \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1 ⇒ \(\frac { x }{ a } \) + \(\frac { y }{ 8-a } \) = 1
It passes through (-3,10)
\(\frac { -3 }{ a } \) + \(\frac { 10 }{ 8-a } \) = 1
\(\frac { -3(8-a)+10a }{ a(8-a) } \) = 1
-24 + 3a + 10a = 8a – a²
-24 + 13a = 8a – a²
a² + 5a – 24 = 0 ⇒ (a + 8) (a – 3) = 0
a + 8 = 0 (or) a – 3 = 0 ⇒ a = -8 (or) a = 3
The equation of a line is a
a = -8
\(\frac { x }{ -8 } \) + \(\frac { y }{ 8+8 } \) = 1
\(\frac { x }{ -8 } \) + \(\frac { y }{ 16 } \) = 1
-2x + y = 16
2x – y + 16 = 0
a = 3
\(\frac { x }{ 3 } \) + \(\frac { y }{ 5 } \) = 1
5x + 3y = 15
5x + 3y – 15 = 0
The equation of the lines are 2x – y + 16 = 0 (or) 5x + 3y – 15 = 0.

Question 7.
If (5, – 3), (- 5, 3), (6, 6) are the mid points of the sides of a triangle, find the equation of the sides.
Answer:
Since D, E, F are the mid points of ∆ ABC
EF || AB, FD || BC and DE || AC
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of EF = \(\frac { 6-3 }{ 6+5 } \) = \(\frac { 3 }{ 11 } \)
Since EF || AB; Slope of AB = \(\frac { 3 }{ 11 } \)
Equation of AB is
y – y₁ = m (x – x₁)
y + 3 = \(\frac { 3 }{ 11 } \) (x – 5)
3x – 15 = 11y + 33
3x – 11y – 15 – 33 = 0
3x – 11y – 48 = 0
Slope of DE = Slope of AC
Slope of DE = \(\frac { 3+3 }{ -5-5 } \) = \(\frac { 6 }{ -10 } \) = –\(\frac { 6 }{ 10 } \) = –\(\frac { 3 }{ 5 } \)
Slope of AC = – \(\frac { 3 }{ 5 } \)
Equation of AC is
y – y₁ = m (x – x₁)

y – 6 = – \(\frac { 3 }{ 5 } \) (x – 6) ⇒ 5y – 30 = -3x + 18
3x + 5y – 30 – 18 = 0 ⇒ 3x + 5y – 48 = 0
Slope of DF = Slope of BC
Slope of DF = \(\frac { 6+3 }{ 6-5 } \) = \(\frac { 9 }{ 1 } \) = 9
Slope of BC = 9
Equation of the line BC is
y – y₁ = m(x – x₁)
y – 3 = 9 (x + 5) ⇒ 9x + 45 = y – 3
9x – y + 45 + 3 = 0 ⇒ 9x – y + 48 = 0
Equation of the sides are
3x – 11y – 48 = 0 ; 9x – y + 48 = 0 and 3x + 5y – 48 = 0

Question 8.
Find the equation of the straight line passing through the point of intersection of the lines 5x – 8y + 23 = 0 and 7x + 6y – 71 = 0 and is perpendicular to the line joining the points (5,1) and (-2, 2)
Answer:

Substitute the value of x in (1)
5 (5) – 8y = – 23 ⇒ 25 – 8y = – 23
-8y = – 23 – 25 ⇒ -8y = – 48
y = \(\frac { 48 }{ 8 } \) = 6
The point of intersection is (5,6)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of the line joining the points (5,1) and (-2,2) = \(\frac { 2-1 }{ -2-5 } \)
= \(\frac { 1 }{ -7 } \) = – \(\frac { 1 }{ 7 } \)
Slope of the perpendicular line is = 7
Equation of a line is
y – y₁ = m(x – x₁) ⇒ y – 6 = 7 (x – 5)
y – 6 = 7x – 35 ⇒ -7x + y – 6 + 35 = 0
7x – y – 29 = 0

Question 9.
Find the equation of the line passing through the point of intersection of 4x – y – 3 = 0 and x + y – 2 = 0 and perpendicular to 2x – 5y + 3 = 0.
Answer:

x = \(\frac { 5 }{ 5 } \) = 1
Substitute the value of x = 1 in (2)
1 + y = 2
y = 2 – 1 = 1
The point of intersection is (1, 1)
Any line perpendicular to 2x – 5y + 3 = 0 is
5x + 2y + k = 0
It passes through (1,1)
5(1) + 2(1) + k = 0 ⇒ 5 + 2 + k = 0
7 + k = 0 ⇒ k = -7
The line is 5x + 2y – 7 = 0

Question 10.
Find the equation of the line through the point of intersection of the lines 2x + y – 5 = 0 and x + y – 3 = 0 and bisecting the line segment joining the points (3, – 2) and (- 5, 6).
Answer:

x = 2
Substitute the value of x = 2 in (2)
2 + y = 3
y = 3 – 2 = 1
The point of intersection is (2, 1)
Mid point of the line joining the points (3,-2) and (-5,6)

Mid point of the line
Equation of the line joining the points (2, 1) and (-1,2) is

x – 2 = -3 (y – 1)
x – 2 = -3y + 3
x + 3y – 5 = 0
The equation of the line is x + 3y – 5 = 0

Students can download Maths Chapter 6 Trigonometry Ex 6.1 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 6 Trigonometry Ex 6.1

Question 1.
Prove the following identities.
(i) cot θ + tan θ = sec θ cosec θ
(ii) tan⁴ θ + tan² θ = sec⁴ θ – sec² θ
Answer:
(i) L. H. S = cot θ + tan θ
= \(\frac{\cos \theta}{\sin \theta}+\frac{\sin \theta}{\cos \theta}\)
= \(\frac{\cos ^{2} \theta+\sin ^{2} \theta}{\sin \theta \cos \theta}\)
[cos² θ + sin² θ = 1]
= \(\frac{1}{\sin \theta \cos \theta}\)
= sec θ . cosec θ = R. H. S
∴ cot θ + tan θ = sec θ cosec θ

(ii) tan⁴ θ + tan² θ = sec⁴ θ – sec² θ
L.H.S = tan⁴ θ + tan² θ
= tan² θ (tan² θ + 1)
= tan² θ sec² θ
R.H.S = sec⁴ θ – sec² θ
= sec² θ (sec² θ – 1)
= sec² θ tan² θ
L.H.S = R.H.S
∴ tan⁴ θ + tan² θ = sec⁴ θ – sec² θ

Question 2.
Prove the following identities.
(i) \(\frac{1-\tan ^{2} \theta}{\cot ^{2} \theta-1}\) = tan² θ
(ii) \(\frac{\cos \theta}{1+\sin \theta}\) = sec θ – tan θ
Answer:
(i) \(\frac{1-\tan ^{2} \theta}{\cot ^{2} \theta-1}\) = tan² θ

(ii) \(\frac{\cos \theta}{1+\sin \theta}\) = sec θ – tan θ

Aliter:
L.H.S = \(\frac{\cos \theta}{1-\sin \theta}\)
[conjugate (1 – sin θ)]

Question 3.
Prove the following identities.

Solution:

Question 4.
Prove the following identities.
(i) sec⁶ θ = tan⁶ θ + 3 tan² θ sec² θ + 1
(ii) (sin θ + sec θ)² + (cos θ + cosec θ)² = 1 + (sec θ + cosec θ)²
Answer:
(i) sec⁶ θ = tan⁶ θ + 3 tan² θ sec² θ + 1
L.H.S = sec⁶ θ
= (sec² θ)³ = (1 + tan² θ)³
= 1 + (tan² θ)³ + 3 (1) (tan² θ) (1 + tan² θ) [(a + b)³ = a³ + b³ + 3 ab (a + b)]
= 1 + tan⁶ θ + 3 tan² θ(1 + tan² θ)
= 1 + tan⁶ θ + 3 tan² θ (sec² θ)
= 1 + tan⁶ θ + 3 tan² θ sec² θ
= tan⁶ θ + 3 tan² θ sec² θ + 1
L.H.S = R.H.S

(ii) (sin θ + sec θ)² + (cos θ + cosec θ)² = 1 + (sec θ + cosec θ)²
L.H.S = (sin θ + sec θ)² + (cos θ + cosec θ)²]
= [sin² θ + sec² θ + 2 sin θ sec θ + cos² θ + cosec² θ + 2 cos θ cosec θ]
= (sin² θ + cos² θ) + (sec² θ + cosec² θ) + 2 (sin θ sec θ + cos θ cosec θ)

= 1 + sec² θ + cosec² θ + 2 sec θ cosec θ
= 1 + (sec θ + cosec θ)²
L.H.S = R.H.S
∴ (sin θ + sec θ)² + (cos θ + cosec θ)² = 1 + (sec θ + cosec θ)²

Question 5.
Prove the following identities.
(i) sec⁴ θ (1 – sin⁴ θ) – 2 tan² θ = 1
(ii) \(\frac{\cot \theta-\cos \theta}{\cot \theta+\cos \theta}=\frac{\csc \theta-1}{\csc \theta+1}\)
Answer:
(i) L.H.S = sec⁴ θ (1 – sin⁴ θ) – 2 tan² θ

L.H.S = R.H.S
∴ sec⁴ θ (1 – sin⁴ θ) – 2 tan² θ = 1

(ii) \(\frac{\cot \theta-\cos \theta}{\cot \theta+\cos \theta}=\frac{\csc \theta-1}{\csc \theta+1}\)

Question 6.
Prove the following identities.


Answer:

Question 7.
(i) If sin θ + cos θ = \(\sqrt { 3 }\), then prove that tan θ + cot θ = 1.
(ii) If \(\sqrt { 3 }\) sin θ – cos θ = θ, then show that tan 3θ = \(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\)
Answer:
sin θ + cos θ = \(\sqrt { 3 }\) (squaring on both sides)
(sin θ + cos θ)² = (\(\sqrt { 3 }\))²
sin² θ + cos² θ + 2 sin θ cos θ = 3
1 + 2 sin θ cos θ = 3
2 sin θ cos θ = 3 – 1
2 sin θ cos θ = 2
∴ sin θ cos θ = 1
L.H.S = tan θ + cot θ

L.H.S = R.H.S ⇒ tan θ + cot θ = 1

(ii) If \(\sqrt { 3 }\) sin θ – cos θ = 0
To prove tan 3θ = \(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\)
\(\sqrt { 3 }\) sin θ – cos θ = 0
\(\sqrt { 3 }\) sin θ = cos θ
\(\frac{\sin \theta}{\cos \theta}=\frac{1}{\sqrt{3}}\)
tan θ = tan 30°
θ = 30°
L.H.S = tan 3θ°
= tan3 (30°)
= tan 90°
= undefined (∝)

∴ tan 3θ = \(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\)

Question 8.
(i) If \(\frac{\cos \alpha}{\cos \beta}=m\) and \(\frac{\cos \alpha}{\cos \beta}=n\) then prove that (m2 + n2) cos2 β = n2
(ii) If cot θ + tan θ = x and sec θ – sec θ – cos θ = y, then prove that (x2y)2/3 – (xy2)2/3 = 1
Answer:
(i) L.H.S = (m² + n²) cos² β

L.H.S = R.H.S ⇒ ∴ (m² + n²) cos² β = n²

(ii) Given cot θ + tan θ = x sec θ – cos θ = y
x = cot θ + tan θ
x = \(\frac{1}{\tan \theta}\) + tan θ
= \(\frac{1+\tan ^{2} \theta}{\tan \theta}\) = \(\frac{\sec ^{2} \theta}{\tan \theta}\)

y = sec θ – cos θ
= \(\frac{1}{\cos \theta}-\cos \theta=\frac{1-\cos ^{2} \theta}{\cos \theta}\)
y = \(\frac{\sin ^{2} \theta}{\cos \theta}\)

Question 9.
(i) If sin θ + cos θ = p and sec θ + cosec θ = q, then prove that q (p² – 1) = 2 p
(ii) If sin θ (1 + sin² θ) = cos² θ, then prove that cos⁶ θ – 4 cos⁴ θ + 8 cos² θ = 4
Answer:
(i) p = sin θ + cos θ
p² = (sin θ + cos θ)²
= sin² θ + cos² θ + 2 sin θ cos θ = 1 + 2 sin θ cos θ
q = sec θ + cosec θ
= \(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}=\frac{\sin \theta+\cos \theta}{\sin \theta \cos \theta}\)
L.H.S = q(p² – 1)

(ii) sin θ (1 + sin² θ) = cos² θ
sin θ (1 + 1 – cos² θ) = cos² θ
sin θ (2 – cos² θ) = cos² θ
Squaring on both sides,
sin² θ (2 – cos² θ)² = cos⁴ θ
(1 – cos² θ) (4 + cos⁴ θ – 4 cos² θ) = cos⁴ θ
4 cos⁴ θ – 4 cos² θ – cos⁶ θ + 4 cos⁴ θ = cos⁴ θ
4 + 5 cos⁴ θ – 8 cos² θ – cos⁶ θ = cos⁴ θ
– cos⁶ θ + 5 cos⁴ θ – cos⁴ θ – 8 cos² θ = -4
– cos⁶ θ + 4 cos⁴ θ – 8 cos² θ = -4
cos⁶ θ – 4 cos⁴ θ + 8 cos² θ = 4
Hence it is proved

Question 10.
If \(\frac{\cos \theta}{1+\sin \theta}\) = \(\frac { 1 }{ a } \), then prove that \(\frac{a^{2}-1}{a^{2}+1}\) = sin θ
Answer:

Students can download Maths Chapter 5 Coordinate Geometry Ex 5.3 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.3

Question 1.
Find the equation of a straight line passing through the mid-point of a line segment joining the points (1, -5), (4, 2) and parallel to (i) X axis (ii) Y axis
Solution:
Mid point of the line joining to points (1, -5), (4, 2)
Mid point of the line = (\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\))
= (\(\frac { 1+4 }{ 2 } \),\(\frac { -5+2 }{ 2 } \)) = (\(\frac { 5 }{ 2 } \),\(\frac { -3 }{ 2 } \))

(i) Any line parallel to X-axis. Slope of a line is 0.
Equation of a line is y – y₁ = m (x – x₁)
y + \(\frac { 3 }{ 2 } \) = 0 (x – \(\frac { 5 }{ 2 } \))
y + \(\frac { 3 }{ 2 } \) = 0 ⇒ \(\frac { 2y+3 }{ 2 } \) = 0
2y + 3 = 0

(ii) Equation of a line parallel to Y-axis is
x = \(\frac { 5 }{ 2 } \) ⇒ 2x = 5
2x – 5 = 0

Question 2.
The equation of a straight line is 2(x – y) + 5 = 0. Find its slope, inclination and intercept on the Y axis.
Solution:
Equation of a line is
2 (x – y) + 5 = 0
2 x – 2y + 5 = 0
-2y = -2x – 5
2y = 2x + 5
y = \(\frac { 2x }{ 2 } \) + \(\frac { 5 }{ 2 } \)
y = x + \(\frac { 5 }{ 2 } \)
Slope of line = 1
Y intercept = \(\frac { 5 }{ 2 } \)
tan θ = 1
tan θ = tan 45°
∴ angle of inclination = 45°

Question 3.
Find the equation of a line whose inclination is 30° and making an intercept -3 on the Y axis.
Solution:
Angle of inclination = 30°
Slope of a line = tan 30°
(m) = \(\frac{1}{\sqrt{3}}\)
y intercept (c) = -3
Equation of a line is y = mx + c
y = \(\frac{1}{\sqrt{3}}\) x – 3
\(\sqrt { 3 }\) y = x – 3 \(\sqrt { 3 }\)
∴ x – \(\sqrt { 3 }\) y – 3 \(\sqrt { 3 }\) = 0

Question 4.
Find the slope and y intercept of \(\sqrt { 3x }\) + (1 – \(\sqrt { 3 }\))y = 3.
Solution:
The equation of a line is \(\sqrt { 3 }\)x + (1 – \(\sqrt { 3 }\))y = 3
(1 – \(\sqrt { 3 }\))y = \(\sqrt { 3 }\) x + 3

Question 5.
Find the value of ‘a’, if the line through (-2,3) and (8,5) is perpendicular to y = ax + 2
Solution:
Given points are (-2, 3) and (8, 5)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac { 5-3 }{ 8+2 } \) = \(\frac { 2 }{ 10 } \) = \(\frac { 1 }{ 5 } \)
Slope of a line y = ax + 2 is “a”
Since two lines are ⊥^r
m₁ × m₂ = -1
\(\frac { 1 }{ 5 } \) × a = -1 ⇒ \(\frac { a }{ 5 } \) = -1 ⇒ a = -5
∴ The value of a = -5

Question 6.
The hill in the form of a right triangle has its foot at (19,3). The inclination of the hill to the ground is 45°. Find the equation of the hill joining the foot and top.
Solution:
Slope of AB (m) = tan 45°
= 1
Equation of the hill joining the foot and the top is
y – y₁ = m(x – x₁)
y – 3 = 1 (x – 19)

y – 3 = x – 19
– x + y – 3 + 19 = 0
– x + y + 16 = 0
x – y – 16 = 0
The required equation is x – y – 16 = 0

Question 7.
Find the equation of a line through the given pair of points.
(i) (2,\(\frac { 2 }{ 3 } \)) and (\(\frac { -1 }{ 2 } \),-2)
(ii) (2,3) and (-7,-1)
Solution:
(i) Equation of the line passing through the point (2,\(\frac { 2 }{ 3 } \)) and (\(\frac { -1 }{ 2 } \),-2)


-5(3y – 2) = -8 × 2 (x – 2)
-15y + 10= -16 (x – 2)
-15y + 10= -16x + 32
16x – 15y + 10 – 32 = 0
16x – 15y – 22 = 0
The required equation is 16x – 15y – 22 = 0

(ii) Equation of the line joining the point (2, 3) and (-7, -1) is

-9 (y – 3) = -4 (x – 2)
-9y + 27 = – 4x + 8
4x – 9y + 27 – 8 = 0
4x – 9y + 19 = 0
The required equation is 4x – 9y + 19 = 0

Question 8.
A cat is located at the point(-6, -4) in xy plane. A bottle of milk is kept at (5,11). The cat wish to consume the milk travelling through shortest possible distance. Find the equation of the path it needs to take its milk.
Solution:

Equation of the line joining the point is
\(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
\(\frac { y+4 }{ 11+4 } \) = \(\frac { x+6 }{ 5+6 } \)
\(\frac { y+4 }{ 15 } \) = \(\frac { x+6 }{ 11 } \)
15(x + 6) = 11(y + 4)
15x + 90 = 11y + 44
15x – 11y + 90 – 44 = 0
15x – 11y + 46 = 0
The equation of the path is 15x – 11y + 46 = 0

Question 9.
Find the equation of the median and altitude of AABC through A where the vertices are A(6,2), B(-5, -1) and C(1,9).
Solution:
(i) To find median


Equation of the median AD is

2(x – 6) = -8 (y – 2)
2x – 12= -8y + 16
2x + 8y – 28 = 0
(÷ by 2) x + 4y – 14 = 0
∴ Equation of the median is x + 4y – 14 = 0
Equation of the altitude is 3x + 5y – 28 = 0

(ii) To find the equation of the altitude

Slope of BC = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac { 9+1 }{ 1+5 } \)
= \(\frac { 10 }{ 6 } \) = \(\frac { 5 }{ 3 } \)
Slope of the altitude = – \(\frac { 3 }{ 5 } \)
Equation of the altitude AD is
y – y1 = m (x – x₁)
y – 2 = – \(\frac { 3 }{ 5 } \) (x – 6)
-3 (x – 6) = 5 (y – 2)
-3x + 18 = 5y – 10
-3x – 5y + 18 + 10 = 0
-3x – 5y + 28 = 0
3x + 5y – 28 = 0

Question 10.
Find the equation of a straight line which has slope \(\frac { -5 }{ 4 } \) and passing through the point (-1,2).
Solution:
Slope of a line (m) = \(\frac { -5 }{ 4 } \)
The given point (x₁, y₁) = (-1, 2)
Equation of a line is y – y₁ = m (x – x₁)
y – 2= \(\frac { -5 }{ 4 } \) (x + 1)
5(x + 1) = -4(y – 2)
5x +5 = -4y + 8
5x + 4y + 5 – 8 = 0
5x + 4y – 3 = 0
The equation of a line is 5x + 4y – 3 = 0

Question 11.
You are downloading a song. The percenty (in decimal form) of mega bytes remaining to get downloaded in x seconds is given by y = -0.1x + 1.
(i) graph the equation.
(ii) find the total MB of the song.
(iii) after how many seconds will 75% of the song gets downloaded?
(iv) after how many seconds the song will be downloaded completely?
Solution:
(i) y = – 0. 1x + 1

(ii) y = -0.1x + 1
x → seconds
y → Mega byte of the song.
The total mega byte of the song is at the beginning that is when x = 0
y = 1 mega byte

(iii) When 75% of song gets downloaded 25% remains.
In other words y = 25%
y = 0.25
By using the equation we get
0.25 = -0.1x + 1
0.1 x = 0.75
x = \(\frac { 0.75 }{ 0.1 } \) = 7.5 seconds

(iv) When song is downloaded completely the remaining percent is zero.
i.e y = 0
0 = -0.1 x + 1
0.1 x = 1 second
x = \(\frac { 1 }{ 0.1 } \) = \(\frac { 1 }{ 1 } \) × 10
x = 10 seconds

Question 12.
Find the equation of a line whose intercepts on the x and y axes are given below.
(i) 4, -6
(ii) -5, – 4
Solution:
(i) x intercept (a) = 4; y intercept (b) = – 6
Equation of a line is \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
\(\frac { x }{ 4 } \) + \(\frac { y }{ -6 } \) = 1 ⇒ \(\frac { x }{ 4 } \) – \(\frac { y }{ 6 } \) = 1
(LCM of 4 and 6 is 12)
3x – 2y = 12
3x – 2y – 12 = 0
The equation of a line is 3x – 2y – 12 = 0

(ii) x intercept (a) = -5; y intercept (b) = \(\frac { 3 }{ 4 } \)
Equation of a line is \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1 ⇒ \(\frac{x}{-5}+\frac{y}{\frac{3}{4}}=1\)
\(\frac { x }{ -5 } \) + \(\frac { 4y }{ 3 } \) = 1
(LCM of 5 and 3 is 15)
– 3x + 20y = 15
– 3x + 20y – 15 = 0
3x – 20y + 15 = 0
∴ Equation of a line is 3x – 20y + 15 = 0

Question 13.
Find the intercepts made by the following lines on the coordinate axes.
(i) 3x – 2y – 6 = 0
(ii) 4x + 3y + 12 = 0
Solution:
(i) 3x – 2y – 6 =0.
x intercept when y = 0
⇒ 3x – 6 = 0
⇒ x = 2
y intercept when x = 0
⇒ 0 – 2y – 6 = 0
⇒ y = -3
(ii) 4x + 3y + 12 = 0. x intercept when y = 0
⇒ 4x + 0 + 12 = 0
⇒ x = -3
y intercept when x = 0
⇒ 0 + 3y + 12 = 0
⇒ y = -4

Question 14.
Find the equation of a straight line.
(i) passing through (1,-4) and has intercepts which are in the ratio 2 : 5
(ii) passing through (-8, 4) and making equal intercepts on the coordinate axes.
Solution:
(i) Let the x-intercept be 2a and the y intercept 5 a
The equation of a line is
\(\frac { x }{ a } \) + \(\frac { y }{ a } \) = 1 ⇒ \(\frac { x }{ 2a } \) + \(\frac { y }{ 5a } \) = 1
The line passes through the point (1, -4)
\(\frac { 1 }{ 2a } \) + \(\frac { (-4) }{ 5a } \) = 1 ⇒ \(\frac { 1 }{ 2a } \) – \(\frac { 4 }{ 5a } \) = 1
Multiply by 10a
(L.C.M of 2a and 5a is 10a)
5 – 8 = 10a ⇒ -3 = 10a
a = \(\frac { -3 }{ 10 } \)
The equation of the line is

Multiply by 3
-5x – 2y = 3 ⇒ -5x – 2y – 3 = 0
5x + 2y + 3 = 0
The equation of a line is 5x + 2y + 3 = 0

(ii) Let the x-intercept andy intercept “a”
The equation of a line is
\(\frac { x }{ a } \) + \(\frac { y }{ a } \) = 1
The line passes through the point (-8, 4)
\(\frac { -8 }{ a } \) + \(\frac { 4 }{ a } \) = 1
\(\frac { -8+4 }{ a } \) = 1
-4 = a
The equation of a line is
\(\frac { x }{ -4 } \) + \(\frac { y }{ -4 } \) = 1
Multiply by -4
x + y = -4
x + y + 4 = 0
The equation of the line is x + y + 4 = 0

Students can download Maths Chapter 4 Geometry Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 4 Geometry Additional Questions

I. Multiple choice questions

Question 1.
If a straight line intersects the sides AB and AC of a ∆ABC at D and E respectively and is parallel to BC, then \(\frac { AE }{ AC } \) = …………
(1) \(\frac { AD }{ DB } \)
(2) \(\frac { AD }{ DB } \)
(3) \(\frac { DE }{ BC } \)
(4) \(\frac { AD }{ EC } \)
Answer:
(2) \(\frac { AD }{ DB } \)

Hint:
By BPT theorem,
\(\frac { AE }{ AC } \) = \(\frac { AD }{ AB } \)

Question 2.
In ∆ABC, DE is || to BC, meeting AB and AC at D and E. If AD = 3 cm, DB = 2 cm and AE = 2.7 cm, then AC is equal to ……..
(1) 6.5 cm
(2) 4.5 cm
(3) 3.5 cm
(4) 3.5 cm
Answer:
(2) 4.5 cm
Hint:
By BPT theorem,

\(\frac { AD }{ DB } \) = \(\frac { AE }{ EC } \)
\(\frac { 3 }{ 2 } \) = \(\frac { 2.7 }{ EC } \)
∴ EC = \(\frac{2.7 \times 2}{3}\) = 1.8 CM
AC = AE + EC
= 2.7 + 1.8 = 4.5 cm

Question 3.
In ∆PQR, RS is the bisector of ∠R. If PQ = 6 cm, QR = 8 cm, RP = 4 cm then PS is equal to …………..
(1) 2 cm
(2) 4 cm
(3) 3 cm
(4) 6 cm
Answer:
(2) 2 cm
Hint:

By ABT theorem,
\(\frac { PS }{ SQ } \) = \(\frac { PR }{ QR } \) ⇒ \(\frac { x }{ 6-x } \) = \(\frac { 4 }{ 8 } \)
24 – 4x = 8x ⇒ 24 = 12x
x = 2
PS = 2 cm

Question 4.
In figure, if \(\frac { AB }{ AC } \) = \(\frac { BD }{ DC } \), ∠B = 40° and ∠C = 60°, then ∠BAD = ……………
(1) 30°
(2) 50°
(3) 80°
(4) 40°
Answer:
(4) 40°
Hint:
\(\frac { AB }{ AC } \) = \(\frac { BD }{ DC } \)

AD is the internal bisector of ∠BAC
∠A + ∠B + ∠C = 180°
∠A + 40° + 60° = 180° ⇒ ∠A = 80°
∴ ∠BAC = \(\frac { 80 }{ 2 } \) = 40°

Question 5.
In the figure, the value x is equal to …………
(1) 4.2
(2) 3.2
(3) 0.8
(4) 0.4

Answer:
(2) 3.2
Hint:
By Thales theorem
(DE || BC)
\(\frac { AD }{ BD } \) = \(\frac { AE }{ EC } \)
\(\frac { x }{ 8 } \) = \(\frac { 4 }{ 10 } \) ⇒ x = \(\frac{8 \times 4}{10}\) = 3.2

Question 6.
In triangles ABC and DEF, ∠B = ∠E, ∠C = ∠F, then ………….
(1) \(\frac { AB }{ DE } \) = \(\frac { CA }{ EF } \)
(2) \(\frac { BC }{ EF } \) = \(\frac { AB }{ FD } \)
(3) \(\frac { AB }{ DE } \) = \(\frac { BC }{ EF } \)
(4) \(\frac { CA }{ FD } \) = \(\frac { AB }{ EF } \)
Answer:
(3) \(\frac { AB }{ DE } \) = \(\frac { BC }{ EF } \)
Hint:

Question 7.
From the given figure, identify the wrong statement.

(1) ∆ADB ~ ∆ABC
(2) ∆ABD ~ ∆ABC
(3) ∆BDC ~ ∆ABC
(4) ∆ADB ~ ∆BDC
Answer:
(2) ∆ ABD ~ ∆ ABC

Question 8.
If a vertical stick 12 m long casts a shadow 8 m long on the ground and at the same time a tower casts a shadow 40 m long on the ground, then the height of the tower is …………..
(1) 40 m
(2) 50 m
(3) 75 m
(4) 60 m
Answer:
(4) 60 m
Hint:

\(\frac { AB }{ DE } \) = \(\frac { BC }{ EF } \)
\(\frac { 12 }{ h } \) = \(\frac { 8 }{ 40 } \); h = \(\frac{40 \times 12}{8}\) = 60

Question 9.
The sides of two similar triangles are in the ratio 2:3, then their areas are in the ratio ………….
(1) 9 : 4
(2) 4 : 9
(3) 2 : 3
(4) 3 : 2
Answer:
(2) 4 : 9
Hint:
Ratio of the Area of two similar triangle
= 2² : 3² = 4 : 9
[squares of their corresponding sides]

Question 10.
Triangles ABC and DEF are similar. If their areas are 100 cm² and 49 cm² respectively and BC is 8.2 cm then EF = …………….
(1) 5.47 cm
(2) 5.74 cm
(3) 6.47 cm
(4) 6.74 cm
Answer:
(2) 5.74 cm
Hint:

Question 11.
The perimeters of two similar triangles are 24 cm and 18 cm respectively.
If one side of the first triangle is 8 cm, then the corresponding side of the other triangle is ………
(1) 4 cm
(2) 3 cm
(3) 9 cm
(4) 6 cm
Answer:
(4) 6 cm
Hint:

Question 12.
A point P is 26 cm away from the centre O of a circle and PT is the tangent drawn from P to the circle 10 cm, then OT is equal to …………
(1) 36 cm
(2) 20 cm
(3) 18 cm
(4) 24 cm
Answer:
(4) 24 cm
Hint:

OT² = OP² – PT²
= 26² – 10²
= (26 + 10) (26 – 10)
OT² = 36 × 16
OT = 6 × 4 = 24 cm

Question 13.
In the figure, if ∠PAB = 120° then ∠BPT = ……….

(1) 120°
(2) 30°
(3) 40°
(4) 60°
Answer:
(4) 60°
Hint:
∠BCP + ∠PAB = 180°
(sum of the opposite angles of a cyclic quadrilateral)
∠BCP = 180° – 120° = 60°
∠BPT = 60°
(By tangent chord theorem)

Question 14.
If the tangents PA and PB from an external point P to circle with centre O are inclined to each other at an angle of 40°, then ∠POA = ………………
(1) 70°
(2) 80°
(3) 50°
(4) 60°
Answer:
(1) 70°
Hint:
∠OPA = \(\frac { 40 }{ 2 } \) = 20°
In ∆OAP.
∠POA + ∠OAP + ∠APO = 180°
(sum of the angles of a triangle)

∠POA + 90° + 20° = 180°
∠POA = 180° – 110° = 70°

Question 15.
In the figure, PA and PB are tangents to the circle drawn from an external point P. Also CD is a tangent to the circle at Q. If PA = 8 cm and CQ = 3 cm, then PC is equal to ……….

(1) 11 cm
(2) 5 cm
(3) 24 cm
(4) 38 cm
Answer:
(2) 5 cm
Hint:
PA = PB (tangent of a circle)
PB = 8 cm
PC + BC = 8
PA + QC = (BC = QC tangent)
PC + 3 = 8
∴ PC = 8 cm – 3 cm = 5 cm

Question 16.
∆ABC is a right angled triangle where ∠B = 90° and BD ⊥ AC. If BD = 8 cm, AD = 4 cm, then CD is …………
(1) 24 cm
(2) 16 cm
(3) 32 cm
(4) 8 cm
Answer:
(2) 16 cm
Hint:
∆DCB ~ ∆DBA
\(\frac { DC }{ DB } \) = \(\frac { DB }{ DA } \)

DB² = DC × DA
8² = DC × 4
DC = \(\frac { 64 }{ 4 } \) = 16 cm

Question 17.
The areas of two similar triangles are 16 cm2 and 36 cm2 respectively. If the altitude of the first triangle is 3 cm, then the corresponding altitude of the other triangle is
(1) 6.5 cm
(2) 6 cm
(3) 4 cm
(4) 4.5 cm
Answer:
(4) 4.5 cm
Hint:

Question 18.
The perimeter of two similar triangles ∆ABC and ∆DEF are 36 cm and 24 cm respectively. If DE =10 cm, then AB is …………
(1) 12 cm
(2) 20 cm
(3) 15 cm
(4) 18 cm
Answer:
(3) 15 cm
Hint:
Perimeter of

Question 19.
In the given diagram θ is ………….
(1) 15°
(2) 30°
(3) 45°
(4) 60°

Answer:
(2) 30°
Hint:
∠BAD = 180° – 150° = 30°
= 180° – 150° = 30°
∠DAC = θ = 30°

Question 20.
If AD is the bisector of ∠A then AC is …………

(1) 12
(2) 16
(3) 18
(4) 20
Answer:
(4) 20
Hint. In ∆ABC, AD is the internal bisector of ∠A
\(\frac { BD }{ DC } \) = \(\frac { AB }{ AC } \)
\(\frac { 4 }{ 10 } \) = \(\frac { 8 }{ x } \)
4x = 10 × 8
x = \(\frac{10 \times 8}{4}\) = 20 cm

Question 21.
In ∆ABC and ∆DEF, ∠A = ∠E and ∠B = ∠F. Then AB : AC is ………….
(1) DE : DF
(2) DE : EF
(3) EF : ED
(4) DF : EF
Answer:
(3) EF : ED
Hint:

\(\frac { AB }{ EF } \) = \(\frac { BC }{ FD } \) = \(\frac { AC }{ ED } \)

Question 22.
Two circles of radius 8.2 cm and 3.6 cm touch each other externally, the distance between their centres is ………….
(1) 1.8 cm
(2) 4.1 cm
(3) 4.6 cm
(4) 11.8 cm
Answer:
(4) 11.8 cm
Hint:
Distance between the two centres

= r₁ + r₂
= 8.2 + 3.6
= 11.8 cm

Question 23.
In the given diagram PA and PB are tangents drawn from P to a circle with centre O. ∠OPA = 35° then a and b is …………

(1) a = 30°, b = 60°
(2) a = 35°, b = 55°
(3) a = 40°, b = 50°
(4) a = 45°, b = 45°
Answer:
(2) a = 35°, b = 55°
Hint:
∠OAP = 90° (tangent of the circle)
∠AOP + ∠OPA + ∠PAO = 180°
b + 35° + 90° = 180°
b = 180° – 125°
= 55°
OP is the angle bisector of ∠P
∴ a = 35°

II. Answer the following questions

Question 1.
The image of a man of height 1.8 m, is of length 1.5 cm on the film of a camera. If the film is 3 cm from the lens of the camera, how far is the man from the camera?
Solution:
Let AB be the height of the man, CD be the height of the image of the man of height 1.8 m (180 cm). LM be the distance between man and lens. LN be the distance between Lens and the film.

Given, AB = 1.8 m (180 cm)
CD = 1.5 cm and LN = 3 cm
Consider ∆ LAB and ∆ LCD
∠ALB = ∠DLC (vertically opposite angles)
∠LAB = ∠LDC (alternate angles) (AB || CD)
∴ ∆ LAB ~ ∆ LDC (AA similarity)
∴ \(\frac { AB }{ CD } \) = \(\frac { LM }{ LN } \) ⇒ \(\frac { 180 }{ 1.5 } \) = \(\frac { x }{ 3 } \) ⇒ 1.5x = 180 × 3
x = \(\frac{180 \times 3}{1.5}\) = \(\frac{180 \times 3 \times 10}{15}\)
x = 360 cm (or) 3.6 m
∴ The distance between the man and the camera = 3.6 cm

Question 2.
A girl of height 120 cm is walking away from the base of a lamp-post at a speed of 0. 6 m/sec. If the lamp is 3.6 m above the ground level, then find the length of her shadow after 4 seconds.
Solution:
Let AB be the height of the lamp-post above the ground level.
AB = 3.6 m = 360 cm
Let CD be the height of the girl.
CD = 1.2 m = 120 cm
The distance travelled by the girl in 4 seconds (AC)
= 4 × 0.6 = 2.4m = 240 cm
Consider ∆ECD and ∆EAB
Given (CD || AB)
∠EAB = ∠ECD = 90°
∠E is common

∴ ∆ EAB = ∆ ECD = 90°
\(\frac { AB }{ CD } \) = \(\frac { AE }{ CE } \)
= \(\frac { x+240 }{ x } \) ⇒ 3 = \(\frac { x+240 }{ x } \)
3x = x + 240
2x = 240 ⇒ x = \(\frac { 240 }{ 2 } \) = 120 cm
∴ Lenght of girls shadow after 4 seconds = 120 cm

Question 3.
In ∆ ABC, AB = AC and BC = 6 cm. D is a point on the side AC such that AD = 5 cm and CD = 4 cm. Show that ∆BCD ~ ∆ACB and hence find BD.
Solution:
Given, In ∆ ABC, AB = AC = 9 cm and BC = 6 cm, AD = 5 cm and CD = 4 cm
\(\frac { BC }{ AC } \) = \(\frac { 6 }{ 9 } \) = \(\frac { 2 }{ 3 } \) …..(1)
\(\frac { CD }{ CB } \) = \(\frac { 4 }{ 6 } \) = \(\frac { 2 }{ 3 } \) ……..(2)

From (1) and (2) we get,
\(\frac { BC }{ AC } \) = \(\frac { CD }{ CB } \)
In ∆ BCD and ∆ ACB
∠C = ∠C (common angle)
\(\frac { BC }{ AC } \) = \(\frac { CD }{ CB } \)
∴ ∆ BCD ~ ∆ ACB
\(\frac { BD }{ AB } \) = \(\frac { BC }{ AC } \) ⇒ \(\frac { BD }{ 9 } \) = \(\frac { 6 }{ 9 } \) ⇒ ∴ BD = 6 cm

Question 4.
The lengths of three sides of a triangle ABC are 6 cm, 4 cm and 9 cm. ∆PQR ~ ∆ABC. One of the lengths of sides of APQR is 35 cm. What is the greatest perimeter possible for ∆PQR?
Solution:
Given, ∆ PQR ~ ∆ ABC

Perimeter of ∆ ABC = 6 + 4 + 9 = 19 cm
When the perimeter of ∆ PQR is the greatest only the corresponding side QR must be equal to 35 cm

Question 5.
A man sees the top of a tower in a mirror which is at a distance of 87.6 m from the tower. The mirror is on the ground, facing upward. The man is 0.4 m away from the mirror, and the distance of his eye level from the ground is 1.5 m. How tall is the tower? (The foot of man, the mirror and the foot of the tower lie along a straight line).
Solution:
Let AB and ED be the heights of the man and the tower respectively. Let C be the point of incidence of the tower in the mirror.
In ∆ ABC and ∆ EDC, we have

∠ABC = ∠EDC = 90°
∠BCA = ∠DCE
(angular elevation is same at the same instant, i.e., the angle of incidence and the angle of reflection are same.)
∴ ∆ ABC ~ ∆ EDC (AA similarity criterion)
Thus,
\(\frac { ED }{ AB } \) = \(\frac { DC }{ BC } \) (corresponding sides are proportional)
ED = \(\frac { DC }{ BC } \) × AB = \(\frac { 87.6 }{ 0.4 } \) × 1.5 = 328.5
Hence, the height of the tower is 328.5 m.

Question 6.
In ∆ PQR, given that S is a point on PQ such that ST || QR and \(\frac { PS }{ SQ } \) = \(\frac { 3 }{ 5 } \). If PR = 5.6 cm, then find PT.
Solution:
In ∆ PQR, we have ST || QR and by Thales theorem,
\(\frac { PS }{ SQ } \) = \(\frac { PT }{ TR } \) …….(1)
Let PT = x
Thus, TR = PR – PT = 5.6 – x

From (1), we get PT = TR (\(\frac { PS }{ SQ } \))
x = (5.6 – x) (\(\frac { 3 }{ 5 } \))
5x = 16.8 – 3x
8x = 16.8
x = \(\frac { 16.8 }{ 8 } \) = 2.1
That is PT = 2.1 cm

Question 7.
In a ∆ ABC, D and E are points on the sides AB and AC respectively such that DE || BC. If AD = 4x – 3, BD = 3x – 1, AE = 8x – 7 and EC = 5x – 3, then find the value of x.
Solution:
In ∆ ABC, DE || BC. By BPT theorem. (Thales theorem)
We get \(\frac { AD }{ DB } \) = \(\frac { AE }{ EC } \) ⇒ \(\frac { 4x-3 }{ 3x-1 } \) = \(\frac { 8x-7 }{ 5x-3 } \)

(8x – 7) (3x – 1) = (4x – 3) (5x – 3)
24x² – 8x – 21x + 7 = 20x² – 12x – 15x + 9
24x² – 8x – 21x + 7 = 20x² – 27x + 9
24x² – 29x + 7 – 20x² + 27x – 9 = 0
∴ 4x² – 2x – 2 = 0
÷ 2 ⇒ 2x² – x – 1 = 0
(x – 1) (2x + 1) = 0

x – 1 = 0 (or) 2x + 1 = 0
x = 1 (or) 2x = – 1
x = – \(\frac { 1 }{ 2 } \) ⇒ since, x ≠ – \(\frac { 1 }{ 2 } \)
∴ The value of x = 1

Question 8.
In the figure AC || BD and CE || DF. if OA = 12 cm, AB = 9cm, OC = 8 cm and EF = 4.5 cm, then find FO.
Solution:

In OBD, AC || BD
∴ \(\frac { OA }{ AB } \) = \(\frac { OC }{ CD } \) (By Thales theorem)
\(\frac { 12 }{ 9 } \) = \(\frac { 8 }{ CD } \)
∴ CD = \(\frac{9 \times 8}{12}\) = 6 CM
In ODF, CE || DF
\(\frac { OC }{ CD } \) = \(\frac { OE }{ EF } \) (By Thales theorem)
\(\frac { 8 }{ 6 } \) = \(\frac { OE }{ 4.5 } \) ⇒ OE = \(=\frac{8 \times 4.5}{6}\) = 6 cm
FO = FE + EO = 4.5 + 6 = 10.5 cm
∴ The value of FO = 10.5 cm

Question 9.
Check whether AD is the bisector of ∠A of ∆ABC in each of the following.
(i) AB = 4 cm, AC = 6 cm, BD 1.6 cm, and CD = 2.4 cm.
Solution:
\(\frac { BD }{ DC } \) = \(\frac { 1.6 }{ 2.4 } \) = \(\frac { 16 }{ 24 } \) = \(\frac { 2 }{ 3 } \) …..(1)
\(\frac { AB }{ AC } \) = \(\frac { 4 }{ 6 } \) = \(\frac { 2 }{ 3 } \) ……..(2)
From (1) and (2) we get,

\(\frac { BD }{ DC } \) = \(\frac { AB }{ AC } \)
By the converse of angle bisector theorem we have,
∴ AD is the internal bisector of ∠A

(ii) AB = 6 cm, AC = 8 cm, BD = 1.5 cm and CD = 3 cm
Solution:
\(\frac { BD }{ DC } \) = \(\frac { 1.5 }{ 3 } \) = 0.5 …….(1)
\(\frac { AB }{ AC } \) = \(\frac { 6 }{ 8 } \) = \(\frac { 3 }{ 4 } \) …….(2)

From (1) and (2) we get,
\(\frac { BD }{ DC } \) ≠ \(\frac { AB }{ AC } \)
Hence AD is not the bisector of ∠A.

Question 10.
In a ∆ABC, AD is the internal bisector of ∠A, meeting BC at D. If AB 5.6 cm, AC = 6 cm and DC = 3 cm, find BC.
Solution:
Given, AB = 5.6 cm, AC = 6 cm, DC = 3 cm
Let BD be x
In ∆ ABC, AD is the internal bisector of ∠A.
By Angle bisector theorem, we have,

\(\frac { BD }{ DC } \) = \(\frac { AB }{ AC } \) ⇒ \(\frac { x }{ 3 } \) = \(\frac { 5.6 }{ 6 } \)
x = \(\frac{3 \times 5.6}{6}\) = 2.8 cm
∴ BC = BD + DC = 2.8 + 3 = 5.8 cm
Length of BC = 5.8 cm

Question 11.
In the figure, tangents PA and PB are drawn to a circle with centre O from an external point P. If CD is a tangent to the circle at E and AP = 15 cm, find the perimeter of ∆PCD.
Solution:
We know that the lengths of the two tangents from an exterior point to a circle are equal.
∴ CA = CE, DB = DE and PA = PB
Now, the perimeter of ∆PCD

= PC + CD + DP
= PC + CE + ED + DP
= PC + CA + DB + DP
= PA + PB = 2 PA (PB = PA)
Thus, the perimeter of APCD = 2 × 15 = 30 cm

Question 12.
ABCD is a quadrilateral such that all of its sides touch a circle. If AB = 6 cm, BC = 6.5 cm and CD = 7 cm, then find the length of AD.
Solution:
Let P, Q, R and S be the points where the circle touches the quadrilateral.
We know that the lengths of the two tangents drawn from an exterior point to a circle are equal. Thus, we have,

AP = AS, BP = BQ, CR = CQ and DR = DS
Hence, AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ AB + CD = AD + BC
⇒ AD = AB + CD – BC
= 6 + 7 – 6.5 = 6.5
Thus, AD = 6.5 cm

Question 13.
A man goes 10 m due east and then 24 m due north. Find the distance from the starting point.
Solution:
Let the initial position of the man be “O” and the final position be B.
In the ∆AOB,

OB² = OA² + AB²
OB² = 10² + 24²
= 100 + 576 = 676
OB = \(\sqrt { 676 }\) = 26 m
The man is at a distance of 26 m from the starting point.

Question 14.
Suppose AB, AC and BC have lengths 13, 16 and 20 respectively. If \(\frac { AF }{ FB } \) = \(\frac { 4 }{ 5 } \) and \(\frac { CE }{ EA } \) = \(\frac { 5 }{ 12 } \) Find BD and DC.
Solution:
Given that AB = 13, AC = 16 and BC = 20. Let BD = JC and DC = y.
Using Ceva’s theorem we have

\(\frac { BD }{ DC } \) × \(\frac { CE }{ EA } \) × \(\frac { AF }{ FB } \) = 1 ………(1)
Substitute the given values
\(\frac { x }{ y } \) × \(\frac { 5 }{ 12 } \) × \(\frac { 4 }{ 5 } \) = 1 ⇒ \(\frac { x }{ y } \) × \(\frac { 1 }{ 3 } \) = 1
\(\frac { x }{ y } \) = 3 ⇒ x = 3y
x – 3y = 0 ……(2)
Given BC = 20
x + y = 20 …..(3)
Subtract (2) and (3)

Question 15.
ABC is a right – angled triangle at B. Let D and E be any two points on AB and BC respectively. prove that AE² + CD² = AC² + DE².
Solution:
In the right ∆ ABE right- angled at B.
AE² = AB² + BE² …..(1)
In the right ∆ DBC,CD² = BD² + BC² ………(2)
Adding (1) and (2) we get
AE² + CD² = AB² + BE² + BD² + BC²
= (AB² + BC²) + (BC² + BD²)
AE² + CD² = AC² + DE²
Hence it is proved

[AC² = AB² + BC²]
[DE² = BE² + BD²]

III. Answer the following questions

Question 1.
A point O in the interior of a rectangle ABCD is joined to each of the vertices A, B, C and D. Prove that OA² + OC² = OB² + OD².
Solution:
Given: O is any point inside the rectangle ABCD.
To prove: OA² + OC² = OB² + OD²
Construction: Through “O” draw EF || AB.
Proof: Using Pythagoras theorem

In the right ∆OEA,
∴ OA²= OE² + AE² …(1)
(By Pythagoras theorem)
In the right ∆OFC,
OC² = OF² + FC² …(2)
(By Pythagoras theorem)
OB² = OF² + FB² … (3)
(By Pythagoras theorem)
In the right ∆OED,
OD² = OE² + ED² … (4)
(By Pythagoras theorem)
By adding (3) and (4) we get
OB² + OD² = OF² + FB² + OE² + ED²
= (OE² + FB²) + (OF² + ED²)
= (OE² + EA²) + (OF² + FC²)
[FB = EA and ED = FC]
OB² + OD² = OA² + OC² using (1) and (2)

Question 2.
A lotus is 20 cm above the water surface in a pond and its stem is partly below the water surface. As the wind blew, the stem is pushed aside so that the lotus touched the water 40 cm away from the original position of the stem. How much of the stem was below the water surface originally?
Solution:
Let O be the bottom of the stem immersed in water.
Let B be the lotus, AB be the length of the stem above the water surface
AB = 20 cm
Let OA be the length of the stem below the water surface
Let OA = x cm
Let C be the point where the lotus touches the water surface when the wind blow.
OC = OA + AB
OC = x + 20 cm
In ∆ AOC, OC² = OA² + AC²
(x + 20)² = x² + 40²
x² + 400 + 40x = x² + 1600

40x = 1600 – 400
40x = 1200
x = \(\frac { 1200 }{ 40 } \) = 30 cm
The stem is 30 cm below the water surface.

Question 3.
In the figure, DE || BC and \(\frac { AD }{ BD } \) = \(\frac { 3 }{ 5 } \), calculate the value of

Solution:
(i) Given, DE || BC and \(\frac { AD }{ BD } \) = \(\frac { 3 }{ 5 } \)
Let AD = 3k and BD = 5k; AB = 3k + 5k = 8k
In ∆^le ABC and ∆ADE
∠A = ∠A (common angle)
∠ABC = ∠ADE (corresponding angle)
Since DE || BC
∴ ∆ ABC ~ ∆ ADE

(ii) Let Area of ∆ ADE be 9k and Area of ∆ ABC be 64 k
Area of ∆ BCED = Area of ∆ ABC – Area of ∆ ADE
= 64 k – 9 k
= 55 k

Question 4.
A boy is designing a diamond shaped kite, as shown in the figure where AE = 16 cm, EC = 81 cm. He wants to use a straight cross bar BD. How long should it be?
Solution:
Let in AB be “x”, BE be “z” and BC be “y”
In the right ∆ AEB,
AB² = AE² + BE²
x² = 16² + Z² …….(1)
In the right ∆ BEC,
BC² = EC² + BE²
y² = 81² + z² ……(2)

In the right ∆ ACD,
AC² = AD² + DC²
97² = x² + y² ….(3)
Add (1) and (2) ⇒ x² + y² = 162 + z² + 81² + z²
x² + y² = 2z² + 16² + 81²
97² = 2z² + 16² + 81² (from 3)
9409 = 2z² + 256 + 6561
= 2z² + 6817
2z² = 9409 – 6817 = 2592
z² = \(\frac { 2592 }{ 2 } \) = 1296
z = \(\sqrt { 1296 }\) = 36
∴ Length of cross bar BD = 2 × BE = 2 × 36 = 72 cm

Question 5.
Find the unknown values in each of the following figures. All lengths are given in centimetres (All measures are not in scale)

Solution:
(i) In ∆ ABC and ∆ ADE,
∠A = ∠A (common angle)
∠ABC = ∠ADE (corresponding angle) [BC || DE]
∆ ABC ~ ∆ ADE (By AAA similarity)

In ∆ EAG and ∆ ECF,
∠E || ∠E (common angle)
∠ECF = ∠EAG (corresponding angle)
Given CF || AG
∆ EAG ~ ∆ ECF
\(\frac { EC }{ EA } \) = \(\frac { CF }{ AG } \) ⇒ \(\frac { 8 }{ x+8 } \) = \(\frac { 6 }{ y } \) ⇒ \(\frac { 8 }{ 12 } \) = \(\frac { 6 }{ y } \) (x = 4)
8y = 6 × 12
y = \(\frac{12 \times 6}{8}\) = 9 cm
∴ The value of x = 4 cm and y = 9 cm.

(ii) In ∆ HBC and ∆ HFG,
∠H = ∠H (common angle)
∠HFG = ∠HBC (corresponding angle)
Given FG || BC
\(\frac { HF }{ HB } \) = \(\frac { FG }{ BC } \) ⇒ \(\frac { 4 }{ 10 } \) = \(\frac { x }{ 9 } \) ⇒ 10x = 36
x = 3.6 cm
In ∆ FBD and ∆ FHD,
∠BFD = ∠HFG (vertically opposite angle)
∠FBD = ∠FHG (Alternate angles)
By AA similarity
∆ FBD ~ ∆ FHG
\(\frac { FG }{ FD } \) = \(\frac { FH }{ FB } \) ⇒ \(\frac { x }{ 3+y } \) = \(\frac { 4 }{ 6 } \)
4 (3 + y) = 3.6 × 6
3 + y = \(\frac{3.6 \times 6}{4}\) = 5.4 ⇒ y = 5.4 – 3 = 2.4 cm
In ∆ AEG and ∆ ABC,
∠A = ∠A (common angle)
∠AEG = ∠ABC (corresponding angles)
Given EG || BC
\(\frac { AE }{ AB } \) = \(\frac { EG }{ BC } \)
\(\frac { z }{ z+5 } \) = \(\frac { x+y }{ 9 } \) ⇒ \(\frac { z }{ z+5 } \) = \(\frac { 3.6+2.4 }{ 9 } \)
\(\frac { z }{ z+5 } \) = \(\frac { 6 }{ 9 } \) ⇒ \(\frac { z }{ z+5 } \) = \(\frac { 2 }{ 3 } \)
3z = 2z + 10 ⇒ 3z – 2z = 10 ⇒ z = 10
∴ The values of x = 3.6 cm, y = 2.4 cm and z = 10 cm.

Question 6.
The internal bisector of ∠A of AABC meets BC at D and the external bisector of ∠A meets BC produced at E. Prove that \(\frac { BD }{ BE } \) = \(\frac { CD}{ CE } \)
Solution:
Given: In ∆ ABC, AD is the internal bisector of ∠A meets BC at D. AE is the external bisector of ∠A meets BC produced to E.
To Proof: \(\frac { BD }{ BE } \) = \(\frac { CD }{ CE } \)

Proof: In ∆ ABC, AD is the internal bisector of ∠A.
By ABT theorem we have,
∴ \(\frac { BE }{ CD } \) = \(\frac { AB }{ AC } \) ……….(1)
In ∆ABC, AE is the external bisector of ∠A.
By ABT theorem we have,
∴ \(\frac { BE }{ CE } \) = \(\frac { AB }{ AC } \) ……….(2)
From (1) and (2) we get
\(\frac { BD }{ CD } \) = \(\frac { BE }{ CE } \) ⇒ ∴ \(\frac { BD }{ BE } \) = \(\frac { CD }{ CE } \)

Question 7.
In a quadrilateral ABCD, the bisectors of ∠B and ∠D intersect on AC at E. Prove that \(\frac { AB }{ BC } \) = \(\frac { AD }{ DC } \)
Solution:
Given: ABCD is a quadrilateral. BE is the bisector of ∠B intersecting AC at E, DE is the bisector of ∠D intersecting AC at E.
To proove: \(\frac { AB }{ BC } \) = \(\frac { AD }{ DC } \)
Proof: In ∆ABC, BE is the internal bisector of ∠D.
By Angle bisector theorem we have,
\(\frac { AE }{ EC } \) = \(\frac { AB }{ BC } \) ……..(1)

In ∆ ACD, DE is the internal bisector of ∠C.
By Angle bisector theorem we have,
∴ \(\frac { AE }{ EC } \) = \(\frac { AD }{ DC } \) ……….(2)
From (1) and (2) we get,
\(\frac { AB }{ BC } \) = \(\frac { AD }{ DC } \)

Question 8.
ABCD is a quadrilateral with AB parallel to DC. A line drawn parallel to AB meets AD at P and BC at Q. Prove that \(\frac { AP }{ PD } \) = \(\frac { BQ }{ QC } \)
Solution:
Given: ABCD is a quadrilateral. AB || DC.
The line PQ intersect AD at P and BC at Q

To prove: \(\frac { AP }{ PD } \) = \(\frac { BQ }{ QC } \)
Proof: In the ∆ABC, OQ || AB
By BPT, theorem we have, \(\frac { AO }{ OC } \) = \(\frac { BQ}{ QC } \) ……………(1)
In the ∆ACD, PO || DC
By BPT, theorem we have, \(\frac { AO }{ OC } \) = \(\frac { AP }{ PD } \) ……..(2)
From (1) and (2) we get, \(\frac { AP }{ PD } \) = \(\frac { BQ }{ QC } \)

Question 9.
D is the midpoint of the side BC of AABC. If P and Q are points on AB and on AC such that DP bisects ∠BDA and DQ bisects ∠ADC, then prove that PQ || BC.
Solution:
In ∆ABD,DP is the angle bisector of ∠BDA.
∴ \(\frac { AP }{ PB } \) = \(\frac { AD }{ BD } \) (angle bisector theorem) ……..(1)
In ∆ADC, DQ is the bisector of ∠ADC
∴ \(\frac { AQ }{ QC } \) = \(\frac { AD }{ DC } \) (angle bisector theorem) ……….(2)

But, BD = DC (D is the midpoint of BC)
Now (2) ⇒ ∴ \(\frac { AQ }{ QC } \) = \(\frac { AD }{ BD } \)
From (1) and (3) We get,
∴ \(\frac { AP }{ PB } \) = \(\frac { AQ }{ QC } \)
Thus PQ || BC (converse of thales theorem)

Question 10.
ABCD is a trapezium with AB || DC. The diagonal AC and BD intersect at E. If ∆AED ~ ∆BEC. Prove that AD = BC.
Solution:
By given data ABCD is a trapezium with AB || DC.
In ∆ ECD and ∆ ABE

∠EDC = ∠EBA
∠ECD = ∠EAB
∴ ∆ DEC ~ ∆ BEA by AA – similarity
\(\frac { DE }{ BE } \) = \(\frac { EC }{ EA } \) = \(\frac { DC }{ BA } \)
\(\frac { DE }{ BE } \) = \(\frac { EC }{ EA } \)
\(\frac { DE }{ EC } \) = \(\frac { BE }{ EA } \) ……….(1)

Also given ∆ DEA ~ ∆ CEB
\(\frac { DE }{ CE } \) = \(\frac { EA }{ EB } \) = \(\frac { DA }{ CB } \)
\(\frac { DE }{ CE } \) = \(\frac { EA }{ EB } \) …………(2)
From (1) and (2) we get
\(\frac { BE }{ EA } \) = \(\frac { EA }{ EB } \) ⇒ EB² = EA²
∴ EB = EA
Substitute in (2) we get
\(\frac { EA }{ EA } \) = \(\frac { DA }{ CB } \)
1 = \(\frac { DA }{ CB } \) ⇒ ∴ AD = DC Hence it is proved

Students can download Maths Chapter 4 Geometry Unit Exercise 4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 4 Geometry Unit Exercise 4

Question 1.
In the figure, if BD ⊥ AC and CE ⊥ AB , prove that
(i) ∆ AEC ~ ∆ADB
(ii) \(\frac { CA }{ AB } \) = \(\frac { CE }{ DB } \)

Solution:
(i) ∠AEC = ∠ADB = 90° ∠A is common By AA – Similarity.
∴ ∆AEC ~ ∆ADB
Since the two triangles are similar

(ii) \(\frac { AE }{ AD } \) = \(\frac { AC }{ AB } \) = \(\frac { EC }{ DB } \)
\(\frac { AC }{ AB } \) = \(\frac { CE }{ DB } \)

Question 2.
In the given figure AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.

Solution:
In the given diagram ∆AEF and ∆ACD
∠AEF = ∠ACD = 90°
∠A is common
By AA – Similarity.
∴ ∆AEF ~ ∆ACD
\(\frac { AE }{ AC } \) = \(\frac { AF }{ AD } \) = \(\frac { EF }{ CD } \)
\(\frac { AE }{ AC } \) = \(\frac { EF }{ CD } \)
\(\frac { AE }{ AC } \) = \(\frac { 4 }{ x } \)
AC = \(\frac{\mathrm{AE} \times x}{4}\) …..(1)
In ∆EAB and ∆ECD,
∠EAB = ∠ECD = 90°
∠E is common
∆ ECD ~ ∆EAB
\(\frac { EC }{ EA } \) = \(\frac { ED }{ EB } \) = \(\frac { CD }{ AB } \)
\(\frac { EC }{ EA } \) = \(\frac { x }{ 6 } \)
EC = \(\frac{\mathrm{EA} \times x}{6}\) …….(2)
In ∆AEB; CD || AB
By Basic Proportionality Theorem
\(\frac { AB }{ CD } \) = \(\frac { EB }{ ED } \)
\(\frac { 6 }{ x } \) = \(\frac { 5+y }{ y } \)
x = \(\frac { 6y }{ y+5 } \) (EC = x) …….(3)
Add (1) and (2) we get
AC + EC = \(\frac{A E \times x}{4}+\frac{x \times E A}{6}\)
>
Substitute the value of x = 2.4 in (3)
2.4 = \(\frac { 6y }{ y+5 } \)
6y = 2.4y + 12
6y – 2.4y = 12 ⇒ 3.6 y = 12
y = \(\frac { 12 }{ 3.6 } \) = \(\frac { 120 }{ 36 } \) = \(\frac { 10 }{ 3 } \) = 3.3 cm
The value of x = \(\frac { 12 }{ 5 } \) (or) 2.4 cm and y = \(\frac { 10 }{ 3 } \) (or) 3.3 cm

Question 3.
O is any point inside a triangle ABC. The bisector of ∠AOB, ∠BOC and ∠COA meet the sides AB, BC and CA in point D, E and F respectively. Show that AD × BE × CF = DB × EC × FA.
Solution:
In ∆ABC the bisector meets AB at D, BC at E and AC at F.

The angle bisector AO, BO and CO intersect at “O”.
By Cevas Theorem
\(\frac { AD }{ DB } \) × \(\frac { BE }{ EC } \) × \(\frac { CF }{ AF } \) = 1
AD × BE × CF = DB × EC × AF
Hence it is proved

Question 4.
In the figure, ABC is a triangle in which AB = AC. Points D and E are points on the side AB and AC respectively such that AD = AE. Show that the points B, C, E and D lie on a same circle.

Solution:
∠B = ∠C (Given AB = AC)
AD + DB = AE + EC
BD = EC (Given AD = AE)
DE parallel BC Since AEC is a straight line.
∠AED + ∠CED = 180°
∠CBD + ∠CED = 180°
Similarly of the opposite angles = 180°
∴ BCED is a cyclic quadrilateral

Question 5.
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of 20 km/hr and the second train travels at 30 km/hr. After 2 hours, what is the distance between them?
Solution:
A is the position of the 1^st train.
B is the position of the 2^nd train.

Distance Covered in 2 hours
OA = 2 × 20 = 40 km
OB = 2 × 30 = 60 km
Distance between the train after 2 hours

Distance between
the two train = 72.11 km (or) 20\(\sqrt { 13 }\) km

Question 6.
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that
(i) b² = p² + ax + \(\frac{a^{2}}{4}\)
(ii) c² = p² – ax + \(\frac{a^{2}}{4}\)
(iii) a² + c² = 2 p² + \(\frac{a^{2}}{2}\)
Solution:
(i) Given ∠AED = 90°

ED = x; DC = \(\frac { a }{ 2 } \)
(D is the mid point of BC)
∴ EC = x + \(\frac { a }{ 2 } \), BE = \(\frac { a }{ 2 } \) – x
∴ In the right ∆ AED
AD² = AE² + ED²
p² = h² + x²
In the right ∆ AEC,
AC² = AE² + EC²

(ii) In the right triangle ABE,
AB² = AE² + BE²
c² = h² + (\(\frac { a }{ 2 } \) – x)²
c² = h² + \(\frac{a^{2}}{4}\) + x² – ax
c² = h² + x² + \(\frac { 1 }{ 4 } \) a² – ax
c² = p² – ax + \(\frac{a^{2}}{4}\) (from 1)

(iii) By adding (2) and (3)
b² + c² = p² + ax + \(\frac{a^{2}}{4}\) + p² – ax + \(\frac{a^{2}}{4}\)
= 2p² + \(\frac{2a^{2}}{4}\)
= 2p² + \(\frac{a^{2}}{2}\)

Question 7.
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
Solution:
Let the height of the tree AD be “h”.

In ∆ ACD and ∆ BCF,
∠A = ∠B = 90°
∠C is common
∆ ACD ~ ∆ BCF by AA similarity
\(\frac { AD }{ BF } \) = \(\frac { AC }{ BC } \)
\(\frac { h }{ x } \) = \(\frac { 24 }{ 2 } \) = 6
h = 6x ………(1)
In ∆ ACE and ∆ ABF,
∠C = ∠B = 90°
∠A is common
∴ ∆ ACE ~ ∆ ABF
\(\frac { CE }{ BF } \) = \(\frac { AC }{ AB } \)
\(\frac { 2 }{ x } \) = \(\frac { 24 }{ 20 } \)
24x = 20 × 2
x = \(\frac{20 \times 2}{24}=\frac{5 \times 2}{6}=\frac{10}{6}\)
x = \(\frac { 5 }{ 3 } \)
Substitute the value of x in (1)
h = 6 × \(\frac { 5 }{ 3 } \) = 10 m
∴ Height of the tree is 10 m

Question 8.
An emu which is 8 ft tail is standing at the foot of a pillar which is 30 ft high. It walks away from the pillar. The shadow of the emu falls beyond emu. What is the relation between the length of the shadow and the distance from the emu to the pillar?
Solution:
Let the shadow of the emu AE be “x” and BE be “y” ED || BC

By basic proportionality theorem
\(\frac { AE }{ AB } \) = \(\frac { ED }{ BC } \)
\(\frac { x }{ x+y } \) = \(\frac { 8 }{ 30 } \)
30x = 8x + 8y
22x – 8y = 0
(÷ by 2) 11x – 4y = 0
11x = 4y
x = \(\frac { 4 }{ 11 } \) × y
x = \(\frac { 4 }{ 11 } \) × distance from the pillar to emu
Length of = \(\frac { 4 }{ 11 } \) × distance from the shadow the pillar to emu

Question 9.
Two circles intersect at A and B. From a point P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.
Solution:
Proof:

A and B are the points intersecting the circles. Join AB.
∠P’PB = ∠PAB (alternate segment theorem)
∠PAB + ∠BAC = 180° …(1)
(PAC is a straight line)
∠BAC + ∠BDC = 180° …(2)
ABDC is a cyclic quadrilateral.
From (1) and (2) we get
∠P’PB = ∠PAB = ∠BDC
P’P and DC are straight lines.
PD is a transversal alternate angles are equal.
∴ P’P || DC.

Question 10.
Let ABC be a triangle and D, E, F are points on the respective sides AB, BC, AC (or their extensions).
Let AD : DB = 5 : 3, BE : EC = 3 : 2 and AC = 21. Find the length of the line segment CF.
Solution:

\(\frac { AD }{ DB } \) = \(\frac { 5 }{ 3 } \); \(\frac { BE }{ EC } \) = \(\frac { 3 }{ 2 } \); AC = 21
By Ceva’s theorem

Length of the line segment CF = 6 units

Students can download Maths Chapter 4 Geometry Ex 4.4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 4 Geometry Ex 4.4

Question 1.
The length of the tangent to a circle from a point P, which is 25 cm away from the centre is 24 cm. What is the radius of the circle?
Solution:
Let the radius AB be r. In the right ∆ ABO,
OB² = OA² + AB²
25² = 24² + r²

25² – 24² = r²
(25 + 24) (25 – 24) = r²
r = \(\sqrt { 49 }\) =7
Radius of the circle = 7 cm

Question 2.
∆ LMN is a right angled triangle with ∠L = 90°. A circle is inscribed in it. The lengths of the sides containing the right angle are 6 cm and 8 cm. Find the radius of the circle.
Solution:
LN = 6; ML = 8. In the right ∆ LMN,
MN² = LN² + LM²
= 6² + 8² = 36 + 64 = 100
MN = \(\sqrt { 100 }\) = 10

OA= OB = OC = r
AN = CN (Tangent of the circle)
LN – AL= CN
LN – r = CN
8 – r = CN ……(1)
MC = MB (tangent of the circle)
MC = ML – LB
MC = 6 – r …….(2)

Add (1) and (2)
MC + CN = (6 – r) + (8 – r)
MN = 14 – 2r
10 = 14 – 2r
2r = 14 – 10 = 4
r = \(\frac { 4 }{ 2 } \) = 2 cm
radius of the circle = 2 cm

Question 3.
A circle is inscribed in ∆ ABC having sides 8 cm, 10 cm and 12 cm as shown in figure, Find AD, BE and CF.

Solution:
AD = AF = x (tangent of the circle)
BD = BE = y (tangent of the circle)
CE = CF = z (tangent of the circle)
AB = AD + DB
x + y = 12 ……(1)
BC = BE + EC
y + z= 8 …….(2)
AC = AF + FC
x + z = 10 ……(3)
Add (1) (2) and (3)
2x + 2y + 2z = 12 + 8 + 10
x + y + z = \(\frac { 30 }{ 2 } \) = 15 …….(4)
By x + y = 12 in (4)
z = 3
y + z = 8 in (4)
x = 7
x + z = 10 in (4)
y = 5
AD = 7 cm; BE = 5 cm and CF = 3 cm

Question 4.
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120° . Find ∠OPQ.
Solution:
∠POQ = 180° – 120° = 60°
In ∆OPQ, we know

∠POQ + ∠OQP + ∠OPQ = 180°
(Sum of the angles of a ∆ is 180°)
60° + 90° + ∠OPQ = 180°
∠OPQ = 180° – 150° = 30°
∠OPQ = 30°

Question 5.
A tangent ST to a circle touches it at B. AB is a chord such that ∠ABT = 65°. Find ∠AOB, where “O” is the centre of the circle.
Solution:
Given ∠ABT = 65°
∠OBT = 90°(TB is the tangent of the circle)
∠ABO = 90° – 65° = 25°
∠ABO + ∠BOA + ∠OAB = 180°
25° + x + 25° = 180° (Sum of the angles of a ∆)

(OA and OB are the radius of the circle.
∴ ∠ABO = ∠BAO = 25°
x + 50 = 180°
x = 180° – 50° = 130°
∴ ∠BOA = 130°

Question 6.
In figure, O is the centre of the circle with radius 5 cm. T is a point such that OT = 13 cm and OT intersects the circle E, if AB is the tangent to the circle at E, find the length of AB.

Solution:
In the right ∆ OTP,
PT² = OT² – OP²
= 13² – 5²
= 169 – 25
= 144
PT = \(\sqrt { 144 }\) = 12 cm
Since lengths of tangent drawn from a point to circle are equal.
∴ AP = AE = x
AT = PT – AP
= (12 – x) cm
Since AB is the tangent to the circle E.
∴ OE ⊥ AB
∠OEA = 90°
∠AET = 90°
In ∆AET, AT² = AE² + ET²
In the right triangle AET,
AT² = AE² + ET²
(12 – x)² = x² + (13 – 5)²
144 – 24x + x² = x² + 64
24x = 80 ⇒ x = \(\frac { 80 }{ 24 } \) = \(\frac { 20 }{ 6 } \) = \(\frac { 10 }{ 3 } \)
BE = \(\frac { 10 }{ 3 } \) cm
AB = AE + BE
= \(\frac { 10 }{ 3 } \) + \(\frac { 10 }{ 3 } \) = \(\frac { 20 }{ 3 } \)
Lenght of AB = \(\frac { 20 }{ 3 } \) cm

Question 7.
In two concentric circles, a chord of length 16 cm of larger circle becomes a tangent to the smaller circle whose radius is 6 cm. Find the radius of the larger circle.
Solution:
Here AP = PB = 8 cm
In ∆OPA,
OA² = OP² + AP²

= 6² + 8²
= 36 + 64
= 100
OA = \(\sqrt { 100 }\) = 10 cm
Radius of the larger circle = 10 cm

Question 8.
Two circles with centres O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q, such that OP and O’ P are tangents to the two circles. Find the length of the common chord PQ.
Solution:
In ∆ OO’P
(O’O)² = OP² + O’P²
= 3² + 4²

= 9 + 16
(OO’)² = 25
∴ OO’ = 5cm
Since the line joining the centres of two intersecting circles is perpendicular bisector of their common chord.
OR ⊥ PQ and PR = RQ
Let OR be x, then O’R = 5 – x again Let PR = RQ = y cm
In ∆ ORP, OP² = OR² + PR²
9 = x² + y² …(1)
In ∆ O’RP, O’P² = O’R² + PR²
16 = (5 – x)² + y²
16 = 25 + x² – 10x + y²
16 = x² + y² + 25 – 10x
16 = 9 + 25 – 10x (from 1)
16 = 34 – 10x
10x = 34 – 16 = 18
x = \(\frac { 18 }{ 10 } \) = 1.8 cm
Substitute the value of x = 1.8 in (1)
9 = (1.8)² + y²
y² = 9 – 3.24
y² = 5.76
y = \(\sqrt { 5.76 }\) = 2.4 cm
Hence PQ = 2 (2.4) = 4.8 cm
Length of the common chord PQ = 4.8 cm

Question 9.
Show that the angle bisectors of a triangle are concurrent.
Solution:
Given: ABC is a triangle. AD, BE and CF are the angle bisector of ∠A, ∠B, and ∠C.
To Prove: Bisector AD, BE and CF intersect
Proof: The angle bisectors AD and BE meet at O. Assume CF does not pass through O. By angle bisector theorem.
AD is the angle bisector of ∠A
\(\frac { BD }{ DC } \) = \(\frac { AB }{ AC } \) …..(1)
BE is the angle bisector of ∠B

\(\frac { CE }{ EA } \) = \(\frac { BC }{ AB } \) …….(2)
CF is the angle bisector ∠C
\(\frac { AF }{ FB } \) = \(\frac { AC }{ BC } \) …….(3)
Multiply (1) (2) and (3)
\(\frac { BD }{ DC } \) × \(\frac { CE }{ EA } \) × \(\frac { AF }{ FB } \) = \(\frac { AB }{ AC } \) × \(\frac { BC }{ AB } \) × \(\frac { AC }{ BC } \)
So by Ceva’s theorem.
The bisector AD, BE and CF are concurrent.

Question 10.
In ∆ABC , with ∠B = 90° , BC = 6 cm and AB = 8 cm, D is a point on AC such that AD = 2 cm and E is the midpoint of AB. Join D to E and extend it to meet at F. Find BF.
Solution:
Consider ∆ABC. Then D, E and F are respective points on the sides AC, AB and BC.
By construction D, E, F are collinear.
By Menelaus’ theorem \(\frac { AE }{ EB } \) × \(\frac { BF }{ FC } \) × \(\frac { CD }{ DA } \) = 1 ……(1)
AD = 2 cm; AE = EB = 4 cm; BC = 6 cm; FC = FB + BC = x + 6
In ∆ABC, By Pythagoras theorem.

AC²= AB² + BC²
AC² = 8² + 6² = 64 + 36 = 100
AC = \(\sqrt { 100 }\) = 10
CD = AC – AD
= 10 – 2 = 8 cm
Substituting the values in (1) we get
\(\frac { 4 }{ 4 } \) × \(\frac { x }{ x+6 } \) × \(\frac { 8 }{ 2 } \) = 1
\(\frac { x }{ x+6 } \) × 4 = 1
4x = x + 6
3x = 6 ⇒ x = \(\frac { 6 }{ 3 } \) = 2
The value of BF = 2 cm

Question 11.
An artist has created a triangular stained glass window and has one strip of small length left before completing the window. She needs to figure out the length of left out portion based on the lengths of the other sides as shown in the figure.

Solution:
Given that AE = 3 cm, EC = 4 cm, CD = 10 cm, DB = 3 cm, AF = 5 cm.
Let FB be x
Using Ceva’s theorem we have
\(\frac { AE }{ EC } \) × \(\frac { CD }{ DB } \) × \(\frac { BF }{ AF } \) = 1
\(\frac { 3 }{ 4 } \) × \(\frac { 10 }{ 3 } \) × \(\frac { x }{ 5 } \) = 1
\(\frac { 2x }{ 4 } \) = 1
2x = 4 ⇒ x = \(\frac { 4 }{ 2 } \) = 2
The value of BF = 2

Question 12.
Draw a tangent at any point R on the circle of radius 3.4 cm and centre at P ?
Answer:
Given Radius = 3.4 cm


Steps of construction:

1. Draw a circle with centre “O” of radius 3.4 cm.
2. Take a point P on the circle Join OP.
3. Draw a perpendicular line TT’ to OP which passes through P.
4. TT’ is the required tangent.

Question 13.
Draw a circle of radius 4.5 cm. Take a point on the circle. Draw the tangent at that point using the alternate segment theorem.
Answer:
Radius of the circle = 4.5 cm


Steps of construction:

1. With O as centre, draw a circle of radius 4.5 cm.
2. Take a point L on the circle. Through L draw any chord LM.
3. Take a point M distinct from L and N on the circle, so that L, M, N are in anti-clockwise direction. Join LN and NM.
4. Through “L” draw tangent TT’such that ∠TLM = ∠MNL
5. TT’ is the required tangent.

Question 14.
Draw the two tangents from a point which is 10 cm away from the centre of a circle of radius 5 cm. Also, measure the lengths of the tangents.
Answer:
Radius = 5 cm; Distance = 10 cm


Steps of construction:

1. With O as centre, draw a circle of radius 5 cm.
2. Draw a line OP =10 cm.
3. Draw a perpendicular bisector of OP, which cuts OP at M.
4. With M as centre and MO as radius draw a circle which cuts previous circle at A and B.
5. Join AP and BP. AP and BP are the required tangents.

Verification: In the right ∆ OAP
PA² = OP² – OA²
= 10² – 5² = \(\sqrt { 100-25 }\) = \(\sqrt { 75 }\) = 8.7 cm
Lenght of the tangent is = 8.7 cm

Question 15.
Take a point which is 11 cm away from the centre of a circle of radius 4 cm and draw the two tangents to the circle from that point.
Answer:
Radius = 4 cm; Distance = 11 cm


Steps of construction:

1. With O as centre, draw a circle of radius 4 cm.
2. Draw a line OP = 11 cm.
3. Draw a perpendicular bisector of OP, which cuts OP at M.
4. With M as centre and MO as radius, draw a circle which cuts previous circle A and B.
5. Join AP and BP. AP and BP are the required tangents.

This the length of the tangents PA = PB = 10.2 cm
Verification: In the right angle triangle OAP
PA² = OP² – OA²
= 11² – 4² = 121 – 16 = 105
PA = \(\sqrt { 105 }\) = 10.2 cm
Length of the tangents = 10.2 cm

Question 16.
Draw the two tangents from a point which is 5 cm away from the centre of a circle of diameter 6 cm. Also, measure the lengths of the tangents.
Answer:
Radius = 3cm; Distance = 5cm.


Steps of construction:

1. With O as centre, draw a circle of radius 3 cm.
2. Draw a line OP = 5 cm.
3. Draw a perpendicular bisector of OP, which cuts OP at M.
4. With M as centre and MO as radius draw a circle which cuts previous circles at A and B.
5. Join AP and BP, AP and BP are the required tangents.

The length of the tangent PA = PB = 4 cm
Verification: In the right angle triangle OAP
PA² = OP² – OA²
= 5² – 3²
= 25 – 9
= 16 PA
= \(\sqrt { 16 }\) = 4 cm
Length of the tangent = 4 cm

Question 17.
Draw a tangent to the circle from the point P having radius 3.6 cm, and centre at O. Point P is at a distance 7.2 cm from the centre.
Answer:
Radius = 3.6; Distance = 7.2 cm.


Steps of construction:

1. With O as centre, draw a circle of radius 3.6 cm.
2. Draw a line OP = 7.2 cm.
3. Draw a perpendicular bisector of OP which cuts OP at M.
4. With M as centre and MO as radius draw a circle which cuts the previous circle at A and B.
5. Join AP and BP, AP and BP are the required tangents.

Length of the tangents PA = PB = 6.26 cm
Verification: In the right triangle ∆OAP
PA² = OP² – OA²
= 7.22 – 3.62 =(7.2 + 3.6) (7.2 – 3.6)
PA² = 10.8 × 3.6 = \(\sqrt { 38.88 }\)
PA = 6.2 cm
Length of the tangent = 6.2 cm