Students can download Maths Chapter 5 Coordinate Geometry Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Additional Questions
I. Multiple Choice Questions
Question 1.
If the three points (-3, 7), (a, 1), (-3, 2) are collinear then the value of “a” is
(1) 0
(2) -1
(3) -3
(4) 1
Answer:
(3) -3
Hint:
Since the three points are collinear
Area of a ∆ = 0
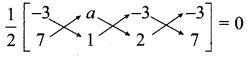
-3 + 2a – 21 – (7a – 3 – 6) = 0 ⇒ 2a – 24 – 7a + 9 = 0
– 5a – 15 = 0 ⇒ – 5(a + 3) = 0
a + 3 = 0 ⇒ a = -3
![]()
Question 2.
If A (5, 5), B (-5, 1), C (10, 7) lie in a straight line, then the area of ∆ ABC is …………….
(1) \(\frac { 13 }{ 2 } \) sq.units
(2) 9 sq.units
(3) 25 sq.units
(4) 0
Answer:
(4) 0
Hint:
Area of the ∆le
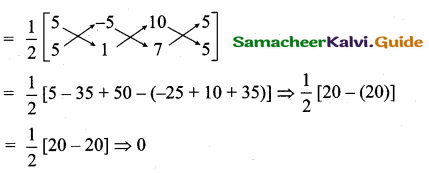
![]()
Question 3.
In a rectangle ABCD, area of ∆ ABC is \(\frac { 31 }{ 2 } \) sq. units. Then the area of rectangle is ……………
(1) 62 sq. units
(2) 31 sq. units
(3) 60 sq. units
(4) 30 sq. units
Answer:
(2) 31 sq. units
Hint:
In a rectangle area of ∆ ABC and area of ∆ ACD are equal.
Area of rectangle ABCD = 2 × \(\frac { 31 }{ 2 } \) = 31 sq.units
Question 4.
If the points (k, 2k), (3k, 3k) and (3,1) are collinear, then k is ……………..
(1) \(\frac { 1 }{ 3 } \)
(2) – \(\frac { 1 }{ 3 } \)
(3) \(\frac { 2 }{ 3 } \)
(4) – \(\frac { 2 }{ 3 } \)
Answer:
(2) – \(\frac { 1 }{ 3 } \)
Hint:
Since the three points are collinear. Area of a ∆ = 0
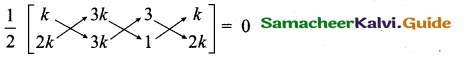
3k2 + 3k + 6k – (6k2 + 9k + k) = 0 ⇒ 3k2 + 9k – 6k2 – 10k = 0
-3 k2 – k = 0 ⇒ -k(3k + 1) = 0
3k + 1 = 0 ⇒ 3 k = -1 ⇒ k = – \(\frac { 1 }{ 3 } \)
![]()
Question 5.
If the area of the triangle formed by the points (x, 2x), (-2, 6) and (3, 1) is 5 square units then x = ………….
(1) 2
(2) \(\frac { 3 }{ 5 } \)
(3) 3
(4) 5
Answer:
(1) 2
Hint:
Area of the triangle = 5 sq. units
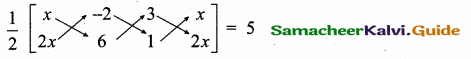
6x – 2 + 6x – (-4x + 18 + x) = 10 ⇒ 12x – 2 – (-3x + 18) = 10
12x – 2 + 3x – 18 = 10
15x – 20 = 10 ⇒ 15x = 10 + 20 = 30
x = \(\frac { 30 }{ 15 } \) = 2
![]()
Question 6.
The slope of a line parallel to y-axis is equal to …………..
(1) 0
(2) -1
(3) 1
(4) not defined
Answer:
(4) not defined
Question 7.
In a rectangle PQRS, the slope of PQ = \(\frac { 5 }{ 6 } \) then the slope of RS is ………..
(1) \(\frac { -5 }{ 6 } \)
(2) \(\frac { 6 }{ 5 } \)
(3) \(\frac { -6 }{ 5 } \)
(4) \(\frac { 5 }{ 6 } \)
Answer:
\(\frac { 5 }{ 6 } \)
Hint:
In a rectangle opposite sides are parallel.
∴ Slope of the line RS is \(\frac { 5 }{ 6 } \).
![]()
Question 8.
The y – intercept of the line y = 2x is ………
(1) 1
(2) 2
(3) \(\frac { 1 }{ 2 } \)
(4) 0
Answer:
(4) 0
Question 9.
The straight line given by the equation y = 5 is …………..
(1) Parallel to x – axis
(2) Parallel to y – axis
(3) Passes through the origin
(4) None of these
Answer:
(1) Parallel to x – axis
![]()
Question 10.
The x – intercept of the line 2x – 3y + 5 = 0 is ………….
(1) \(\frac { 5 }{ 2 } \)
(2) \(\frac { -5 }{ 2 } \)
(3) \(\frac { 2 }{ 5 } \)
(4) \(\frac { -2 }{ 5 } \)
Answer:
(2) \(\frac { -5 }{ 2 } \)
Hint:
2x – 3y + 5 = 0 ⇒ 2x – 3y = – 5
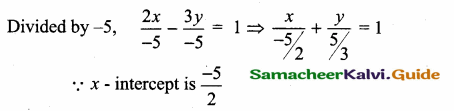
![]()
Question 11.
The lines 3x – 5y + 1 = 0 and 5x + ky + 2 = 0 are perpendicular if the value of k is ………..
(1) -5
(2) 3
(3) -3
(4) 5
Answer:
(2) 3
Hint:
Slope of the first line (m1) = \(\frac { -3 }{ -5 } \) = \(\frac { 3 }{ 5 } \)
Slope of the second line (m2) = \(\frac { -5 }{ k } \)
Since the two lines are perpendicular.
m1 × m2 = -1
\(\frac { 3 }{ 5 } \) × \(\frac { -5 }{ k } \) = -1 ⇒ \(\frac { -3 }{ k } \) = -1
-k = -3 ⇒ The value of k = 3
![]()
Question 12.
If x – y = 3 and x + 2y = 6 are the diameters of a circle then the centre is at the point ………..
(1) (0, 0)
(2) (1, 2)
(3) (1, -1)
(4) (4, 1)
Answer:
(4) (4, 1)
Hint:
Centre of the circle is the intersection of the two diameters.
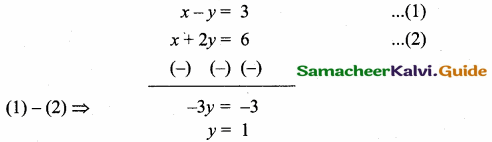
Centre of the circle is (4, 1)
![]()
Question 13.
The line 4x + 3y – 12 = 0 meets the x-axis at the point ……….
(1) (4, 0)
(2) (3, 0)
(3) (-3, 0)
Answer:
(2) (3,0)
Hint:
4x + 3y – 12 = 0 meet the x-axis the value of y = 0
4x- 12 = 0 ⇒ 4x = 12
x = \(\frac { 12 }{ 4 } \) = 3 ⇒ The point is (3, 0)
Question 14.
The equation of a straight line passing through the point (2, -7) and parallel to x-axis is ……………….
(1) x = 2
(2) x = -7
(3) y = -7
(4) y = 2
Answer:
(3) y = -7
Hint:
Equation of a line parallel to x-axis is y = -7
![]()
Question 15.
The equation of a straight line having slope 3 and y intercept – 4 is ………………
(1) 3x – y – 4 = 0
(2) 3x + y – 4 = 0
(3) 3x – y + 4 = 0
(4) 3x – y + 4 = 0
Answer:
(1) 3x – y – 4 = 0
Hint. The equation of a line is y = mx + c
y = 3 (x) + (-4) ⇒ y = 3x – 4
3x – y – 4 = 0
![]()
II. Answer the following questions:
Question 1.
If the points (3, – 4) (1, 6) and (- 2, 3) are the vertices of a triangle, find its area.
Answer:
Let the vertices A (3, – 4), B (1, 6) and C (- 2, 3)
Area of ∆ ABC = \(\frac { 1 }{ 2 } \) [x1y2 + x2y3 + x3y1, – (x2y1 + x3y2 + x1y3)]
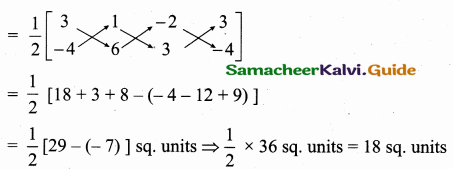
Area of a ∆ = 18 sq. units
![]()
Question 2.
If the area of the triangle formed by the points (1,2) (2,3) and (a, 4) is 8 sq. units, find a.
Answer:
Area of a triangle = 8 sq. units.
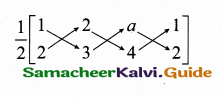
\(\frac { 1 }{ 2 } \) [x1y2 + x2y3 + x3y1 – (x2y1 + x3y2 + x1y3)] = 8.
\(\frac { 1 }{ 2 } \) [3 + 8 + 2a – (4 + 3a + 4)] = 8
11 + 2a – 8 – 3a= 16 ⇒ – a + 3 = 16
– a = 16 – 3 ⇒ a = -13
The value of a = -13
Question 3.
If the points A (2, 5), B (4, 6) and C (8, a) are collinear find the value of “a” using slope concept.
Answer:
Since the three points are collineal
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of AB = Slope of BC
\(\frac { 6-5 }{ 4-2 } \) = \(\frac { a-6 }{ 8-4 } \) ⇒ \(\frac { 1 }{ 2 } \) = \(\frac { a-6 }{ 4 } \) ⇒ 2a – 12 = 4 ⇒ 2a = 16
a = \(\frac { 16 }{ 2 } \) = 8 ⇒ The value of a = 8
![]()
Question 4.
If the points (x,y) is collinear with the points (a, 0) and (0, b) then prove that \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
Answer:
Let A (x, y), B (a, 0), C(0, b)
Since the three points are collinear
Slope of AB = Slope of BC
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
\(\frac { 0-y }{ a-x } \) = \(\frac { b-0 }{ 0-a } \)
\(\frac { -y }{ a-x } \) = \(\frac { b }{ -a } \)
ay = b (a – x)
ay = ba – bx
ay + bx = ab
Divided by ab
\(\frac { ay }{ ab } \) + \(\frac { bx }{ ab } \) = \(\frac { ab }{ ab } \)
\(\frac { y }{ b } \) + \(\frac { x }{ a } \) = 1 ⇒ \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
![]()
Question 5.
A straight line passes through (1, 2) and has the equation y – 2x – k = 0. Find k.
Answer:
The given line is y – 2x – k = 0
It passes through (1,2)
(2) -2 (1) -k = 0 ⇒ 2 – 2 – k = 0
0 – k = 0 ⇒ k = 0
The value of k = 0
Question 6.
If a line passes through the mid point of AB where A is (3, 0) and B is (5, 4) and makes an angle 60° with x – axis find its equation.
Answer:
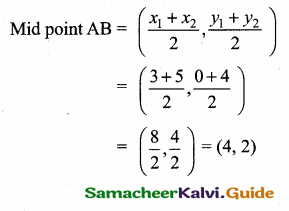
Slope of a line = tan 60°
= \(\sqrt { 3 }\)
Equation of a line is y – y1 = m (x – x1)
y – 2 = \(\sqrt { 3 }\) (x – 4)
y – 2 = \(\sqrt { 3 }\) x – 4 \(\sqrt { 3 }\)
\(\sqrt { 3x }\) – y + 2 – 4\(\sqrt { 3 }\) = 0
![]()
Question 7.
Find the equation of the line through (3, 2) and perpendicular to the line joining (4, 5) and (1,2)
Answer:
Slope of a line = \(\frac { 2-5 }{ 1-4 } \) ⇒ \(\frac { -3 }{ -3 } \) = 1
Slope of the line perpendicular to it is – 1
Equation of the line joining -1 and (3, 2) is
y – y1 = m (x – x1) ⇒ y – 2 = -1(x – 3)
y – 2 = -x + 3 ⇒ x + y – 5 = 0
Question 8.
P and Q trisect the line segment joining the points (2, 1) and (5, – 8). If the point P lies on 2x – y + k = 0, then find the value of k.
Answer:
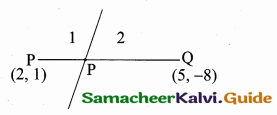
A line divides internally in the ratio 1 : 2
A line divide internally in the ratio l : m
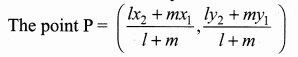
The point P = (\(\frac { 5+4 }{ 3 } \),\(\frac { -8+2 }{ 3 } \))
= (\(\frac { 9 }{ 3 } \),\(\frac { -6 }{ 3 } \)) = (3, -2)
The given line 2x – y + k = 0 passes through the point (3,-2)
2 (3) – (- 2) + k = 0
6 + 2 + k = 0
8 + k = 0
k = – 8
The value of k = – 8
![]()
Question 9.
The line 4x + 3y – 12 = 0 intersect the X, Y – axis at A and B respectively. Fine the area of ∆AOB.
Answer:
The equation of the line AB is 4x + 3y – 12 = 0
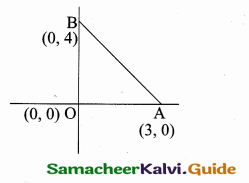
4x + 3y = 12
\(\frac { 4x }{ 12 } \) + \(\frac { 3y }{ 12 } \) = 1 ⇒ \(\frac { x }{ 3 } \) + \(\frac { y }{ 4 } \) = 1
The point A is (3, 0) (it intersect the X – axis)
and B is (0, 4) (it intersect the Y – axis)
Area of ∆ AOB = \(\frac { 1 }{ 2 } \) [x1y2 + x2y3 + x3y1 (x2y1 + x3y2 + x1y3)]
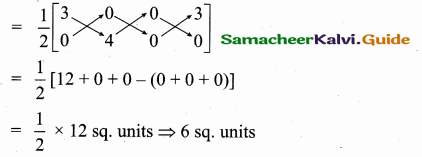
![]()
Question 10.
Find the equation of the line passing through (4, 5) and making equal intercept in the axes.
Answer:
Let the equal intercept on the axes be a, a.
Equation of the line is \(\frac { x }{ a } \) + \(\frac { y }{ a } \) = 1 (Given equal intercepts)
The line passes through (4, 5)
\(\frac { 4 }{ a } \) + \(\frac { 5 }{ a } \) = 1 ⇒ \(\frac { 9 }{ a } \) = 1 ⇒ a = 9
The equation of the line is \(\frac { x }{ 9 } \) + \(\frac { y }{ 9 } \) = 1
Multiply by 9
x + y – 9 = 0
![]()
Question 11.
Find the equation of the line passing through (2, – 1) and whose intercepts on the axes are equal in magnitude but opposite in sign.
Answer:
Let the x – intercept be “a” and y intercept be = “-a”
The equation of the line is
\(\frac { x }{ a } \) + \(\frac { y }{ -a } \) = 1 (y – intercept is – a)
\(\frac { x }{ a } \) – \(\frac { y }{ a } \) = 1
It passes through (2, -1)
\(\frac { 2 }{ a } \) – \(\frac { (-1) }{ a } \) = 1
\(\frac { 2 }{ a } \) + \(\frac { 1 }{ a } \) = 1 ⇒ \(\frac { 3 }{ a } \) = 1
a = 3
The equation of the line is
\(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
\(\frac { x }{ 3 } \) + \(\frac { y }{ -3 } \) = 1 ⇒ \(\frac { x }{ 3 } \) – \(\frac { y }{ 3 } \) = 1
x – y = 3
The equation is x – y – 3 = 0
Question 12.
The straight line cuts the coordinate axes at A and B. If the mid point of AB is (3,2) then find the equation of AB.
Answer:
Let the point A be (a, 0) and B be (0, b)
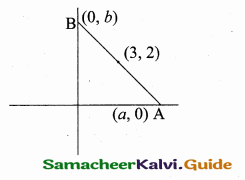
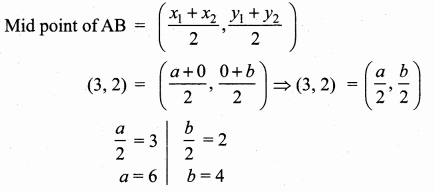
The point A (6, 0) and B (0, 4)
Equation of the line AB is
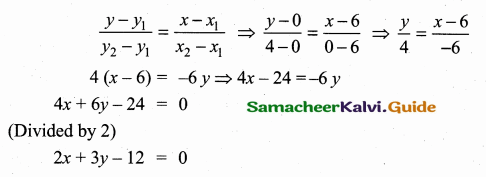
![]()
III. Answer the following questions
Question 1.
If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the ‘ coordinates of any point “c”, if AC = BC and Area of triangle ABC = 10 sq. units.
Answer:
Let the coordinates C be (a, 6) then AC = BC
AC2 = BC2
(a – 3)2 + (b – 4)2 = (a – 5)2 + (b + 2)2
a2 + 9 – 6a + b2 + 16 – 8b = a2 + 25 – 10a + b2 + 4 – 4b
a2 + b2 + 25 – 6a – 86 = a2 + b2 + 29 – 10a + 4b
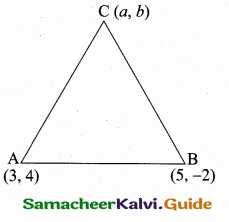
25 – 6a – 8b = 29 – 10a + 46
4a – 12b = 4 ⇒ a – 3b = 1 ………… (1)
Area of ∆ ABC = 10 sq. units
\(\frac { 1 }{ 2 } \) [x1y2 + x2y3 + x3y1 – (x2y1 + x3y2 + x1y3)] = 10
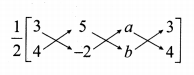
-6 + 5b + 4a – (20 – 2a + 3b) = 20
-6 + 5b + 4a – 20 + 2a – 3b = 20
6a + 2b – 26 = 20 ⇒ 6a + 2b = 46
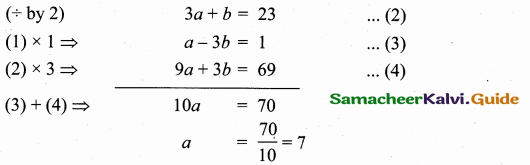
Substitute the value of a = 7 in (2)
3 (7) + b = 23 ⇒ b = 23 – 21 = 2
The coordinate C is (7, 2)
![]()
Question 2.
The four vertices of a Quadrilateral are (1,2) (- 5,6) (7, – 4) and (k, – 2) taken in order. If the area of the Quadrilateral is 9 sq. units, find the value of k.
Answer:
Let A (1, 2) B (- 5, 6) C (7, – 4) and D (k, – 2)
Area of the
Quadrilateral ABCD = \(\frac { 1 }{ 2 } \)[(x1y2 + x2y3 + x3y4 + x4y1) – (x2y1 + x3y2 + x4y3 + x1y4)]
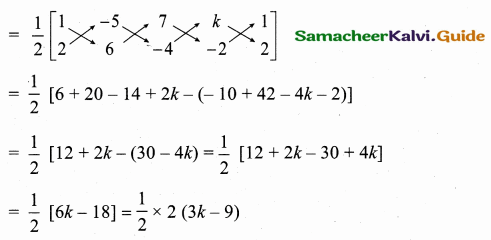
Area of the Quadrilateral ABCD = 3k – 9
Given area of a Quadrilateral is 9 sq. units.
3k – 9 = 9 ⇒ 3k = 18 ⇒ k = \(\frac { 18 }{ 3 } \) = 6
The value of k = 6
![]()
Question 3.
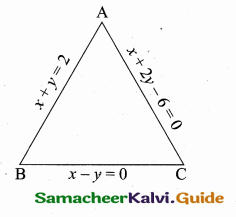
Find the area of a triangles whose three sides are having the equations x + y = 2, x – y = 0 and x + 2y – 6 = 0.
Answer:
Find the three vertices of the triangles by solving their equation.
To find vertices A
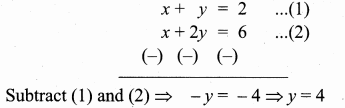
Substitute the value of y = 4 in (1)
x + 4 = 2 ⇒ x = 2 – 4 = -2
The vertices A is (- 2, 4)
To find vertices B
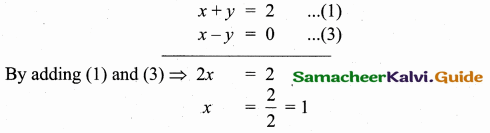
Substitute the value of x = 1 in (1)
1 + y = 2 ⇒ y = 2 – 1 = 1
The vertices B is (1, 1)
To find vertices C
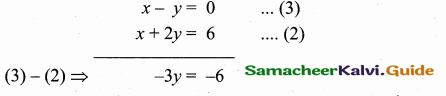
y = \(\frac { 6 }{ 3 } \) = 2
Substitute the value y = 2 in (3)
x – 2 = 0 ⇒ x = 2
The vertices C is (2, 2)
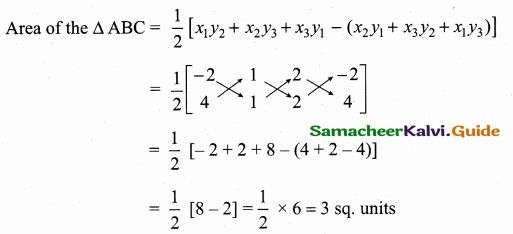
Area of the ∆ BC = 3 sq. units
![]()
Question 4.
Verify the Median of a triangle divides into two triangles of equal areas whose vertices are A (4, – 6), B (3, – 2) and C (5, 2)
Answer:
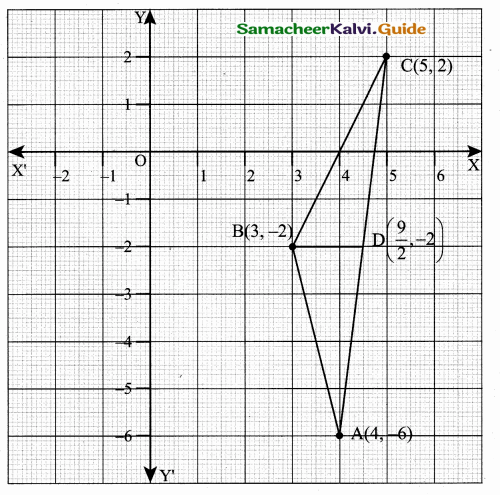
Let D be the mid point of AC .
Mid point of AC = (\(\frac { 5+4 }{ 2 } \),\(\frac { 2-6 }{ 2 } \)) = (\(\frac { 9 }{ 2 } \),-2)
Area of the triangle = \(\frac { 1 }{ 2 } \) [x1y2 + x2y3 + x3y1 – (x2y1 + x3y2 + x1y3)]
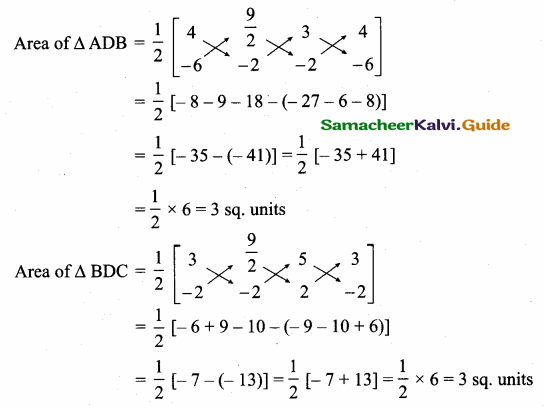
Area of ∆ ADB = Area of ∆ BDC
A median divides the triangle of equal areas.
![]()
Question 5.
Find the area of the ∆ ABC with A (1, – 4) and the mid points of sides through A being (2,-1) and (0,-1)
Answer:
Let the coordinates of B and C are (a, b) and (c, d) respectively.
Sides through A are AB and AC
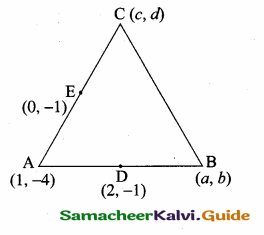
Mid point of AB = (\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\))
(2, -1) = (\(\frac { 1+a }{ 2 } \),\(\frac { -4+b }{ 2 } \))
\(\frac { 1+a }{ 2 } \) = 2
1 + a = 4
a = 4 – 1
= 3
The point B is (3,2)
\(\frac { -4+b }{ 2 } \) = -1
-4 + b = -2
b = -2 + 4
= 2
Mid point of AC = (\(\frac { 1+c }{ 2 } \),\(\frac { -4+d }{ 2 } \))
(0,-1) = (\(\frac { 1+c }{ 2 } \),\(\frac { -4+d }{ 2 } \))
\(\frac { 1+c }{ 2 } \) = 0
1 + c = 0
c = 0 – 1
= – 1
The point C is (-1,2)
\(\frac { -4+d }{ 2 } \) = -1
– 4 + d = -2
d = – 2 + 4
= 2
Thus the coordinates of the vertices of ∆ ABC are A (1, – 4) B (3, 2) and C (- 1, 2)
Area of ∆ ABC = \(\frac { 1 }{ 2 } \) [x1y2 + x2y3 + x3y1 – (x2y1 + x3y2 + x1y3)]
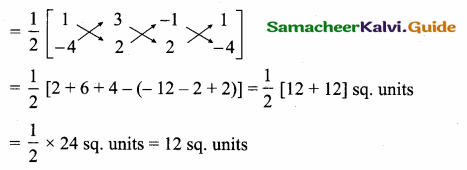
Area of ∆ ABC = 12 sq. units
![]()
Question 6.
Find the equation of the straight lines passing through (- 3, 10) whose sum of the intercepts is 8.
Answer:
Let the “x” intercept be “a” and y intercept be “b”
Sum of the intercepts = 8
a + b = 8 ⇒ b = 8 – a
Equation of a line is \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1 ⇒ \(\frac { x }{ a } \) + \(\frac { y }{ 8-a } \) = 1
It passes through (-3,10)
\(\frac { -3 }{ a } \) + \(\frac { 10 }{ 8-a } \) = 1
\(\frac { -3(8-a)+10a }{ a(8-a) } \) = 1
-24 + 3a + 10a = 8a – a2
-24 + 13a = 8a – a2
a2 + 5a – 24 = 0 ⇒ (a + 8) (a – 3) = 0
a + 8 = 0 (or) a – 3 = 0 ⇒ a = -8 (or) a = 3
The equation of a line is a
a = -8
\(\frac { x }{ -8 } \) + \(\frac { y }{ 8+8 } \) = 1
\(\frac { x }{ -8 } \) + \(\frac { y }{ 16 } \) = 1
-2x + y = 16
2x – y + 16 = 0
a = 3
\(\frac { x }{ 3 } \) + \(\frac { y }{ 5 } \) = 1
5x + 3y = 15
5x + 3y – 15 = 0
The equation of the lines are 2x – y + 16 = 0 (or) 5x + 3y – 15 = 0.
![]()
Question 7.
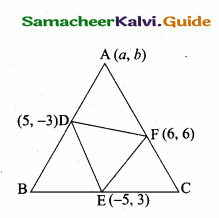
If (5, – 3), (- 5, 3), (6, 6) are the mid points of the sides of a triangle, find the equation of the sides.
Answer:
Since D, E, F are the mid points of ∆ ABC
EF || AB, FD || BC and DE || AC
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of EF = \(\frac { 6-3 }{ 6+5 } \) = \(\frac { 3 }{ 11 } \)
Since EF || AB; Slope of AB = \(\frac { 3 }{ 11 } \)
Equation of AB is
y – y1 = m (x – x1)
y + 3 = \(\frac { 3 }{ 11 } \) (x – 5)
3x – 15 = 11y + 33
3x – 11y – 15 – 33 = 0
3x – 11y – 48 = 0
Slope of DE = Slope of AC
Slope of DE = \(\frac { 3+3 }{ -5-5 } \) = \(\frac { 6 }{ -10 } \) = –\(\frac { 6 }{ 10 } \) = –\(\frac { 3 }{ 5 } \)
Slope of AC = – \(\frac { 3 }{ 5 } \)
Equation of AC is
y – y1 = m (x – x1)
y – 6 = – \(\frac { 3 }{ 5 } \) (x – 6) ⇒ 5y – 30 = -3x + 18
3x + 5y – 30 – 18 = 0 ⇒ 3x + 5y – 48 = 0
Slope of DF = Slope of BC
Slope of DF = \(\frac { 6+3 }{ 6-5 } \) = \(\frac { 9 }{ 1 } \) = 9
Slope of BC = 9
Equation of the line BC is
y – y1 = m(x – x1)
y – 3 = 9 (x + 5) ⇒ 9x + 45 = y – 3
9x – y + 45 + 3 = 0 ⇒ 9x – y + 48 = 0
Equation of the sides are
3x – 11y – 48 = 0 ; 9x – y + 48 = 0 and 3x + 5y – 48 = 0
![]()
Question 8.
Find the equation of the straight line passing through the point of intersection of the lines 5x – 8y + 23 = 0 and 7x + 6y – 71 = 0 and is perpendicular to the line joining the points (5,1) and (-2, 2)
Answer:
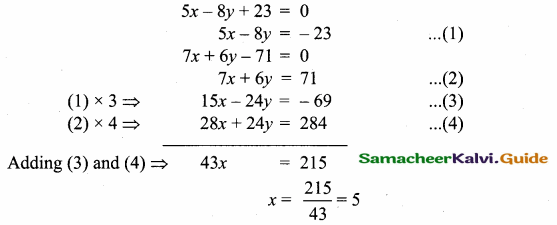
Substitute the value of x in (1)
5 (5) – 8y = – 23 ⇒ 25 – 8y = – 23
-8y = – 23 – 25 ⇒ -8y = – 48
y = \(\frac { 48 }{ 8 } \) = 6
The point of intersection is (5,6)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of the line joining the points (5,1) and (-2,2) = \(\frac { 2-1 }{ -2-5 } \)
= \(\frac { 1 }{ -7 } \) = – \(\frac { 1 }{ 7 } \)
Slope of the perpendicular line is = 7
Equation of a line is
y – y1 = m(x – x1) ⇒ y – 6 = 7 (x – 5)
y – 6 = 7x – 35 ⇒ -7x + y – 6 + 35 = 0
7x – y – 29 = 0
![]()
Question 9.
Find the equation of the line passing through the point of intersection of 4x – y – 3 = 0 and x + y – 2 = 0 and perpendicular to 2x – 5y + 3 = 0.
Answer:
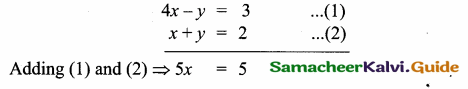
x = \(\frac { 5 }{ 5 } \) = 1
Substitute the value of x = 1 in (2)
1 + y = 2
y = 2 – 1 = 1
The point of intersection is (1, 1)
Any line perpendicular to 2x – 5y + 3 = 0 is
5x + 2y + k = 0
It passes through (1,1)
5(1) + 2(1) + k = 0 ⇒ 5 + 2 + k = 0
7 + k = 0 ⇒ k = -7
The line is 5x + 2y – 7 = 0
![]()
Question 10.
Find the equation of the line through the point of intersection of the lines 2x + y – 5 = 0 and x + y – 3 = 0 and bisecting the line segment joining the points (3, – 2) and (- 5, 6).
Answer:
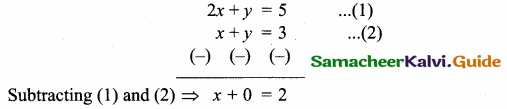
x = 2
Substitute the value of x = 2 in (2)
2 + y = 3
y = 3 – 2 = 1
The point of intersection is (2, 1)
Mid point of the line joining the points (3,-2) and (-5,6)
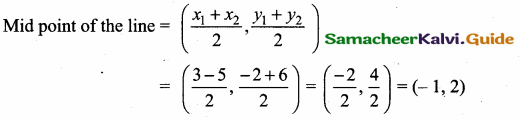
Mid point of the line
Equation of the line joining the points (2, 1) and (-1,2) is
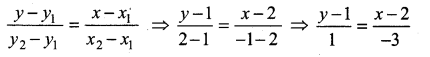
x – 2 = -3 (y – 1)
x – 2 = -3y + 3
x + 3y – 5 = 0
The equation of the line is x + 3y – 5 = 0