Bhagya

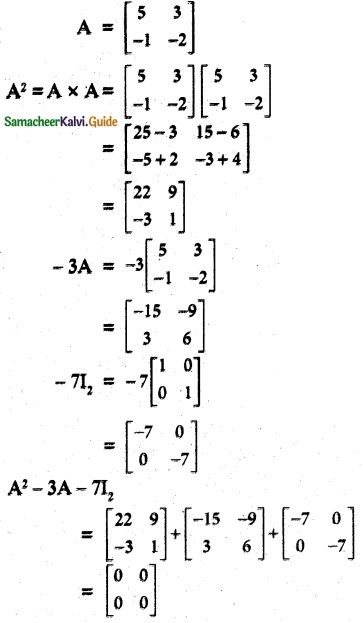
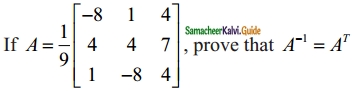
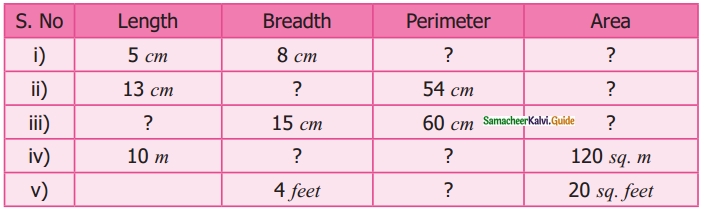
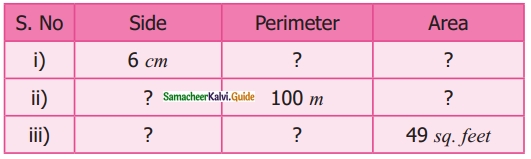
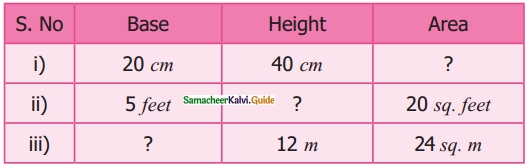
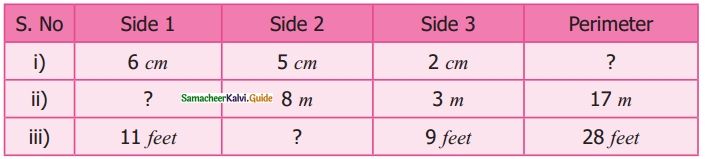
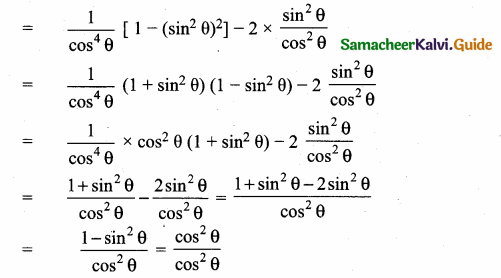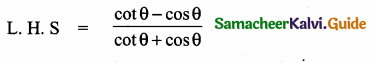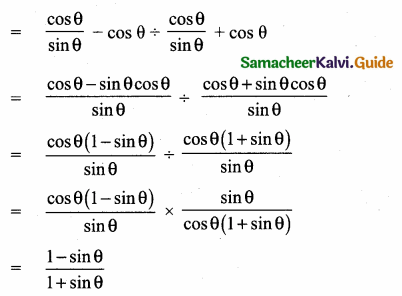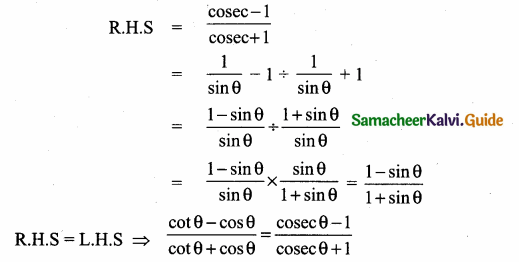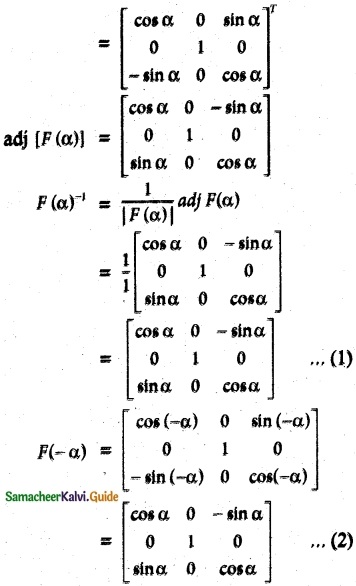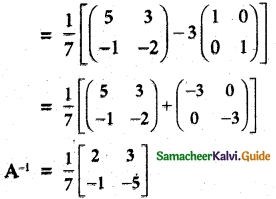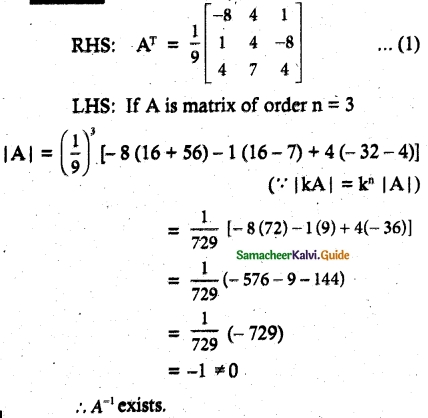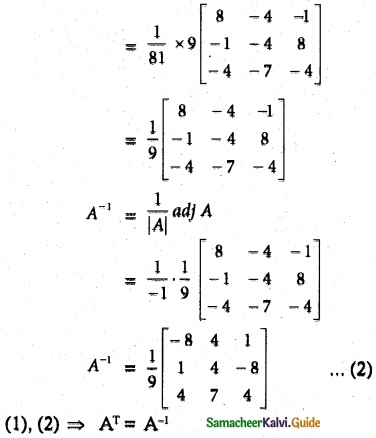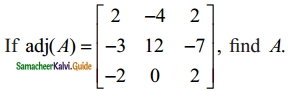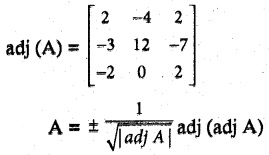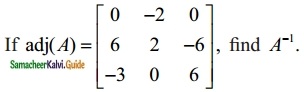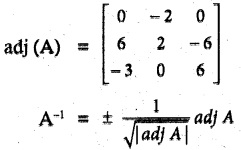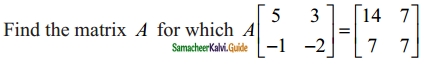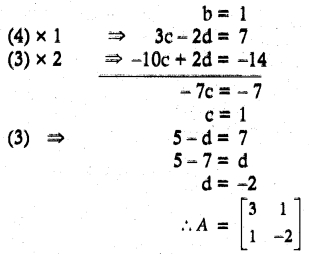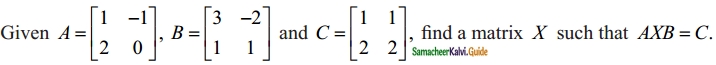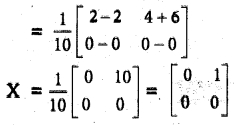Students can download Maths Chapter 5 Coordinate Geometry Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Additional Questions

I. Multiple Choice Questions

Question 1.
If the three points (-3, 7), (a, 1), (-3, 2) are collinear then the value of “a” is
(1) 0
(2) -1
(3) -3
(4) 1
Answer:
(3) -3
Hint:
Since the three points are collinear
Area of a ∆ = 0

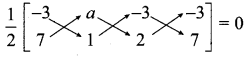
-3 + 2a – 21 – (7a – 3 – 6) = 0 ⇒ 2a – 24 – 7a + 9 = 0
– 5a – 15 = 0 ⇒ – 5(a + 3) = 0
a + 3 = 0 ⇒ a = -3

Question 2.
If A (5, 5), B (-5, 1), C (10, 7) lie in a straight line, then the area of ∆ ABC is …………….
(1) \(\frac { 13 }{ 2 } \) sq.units
(2) 9 sq.units
(3) 25 sq.units
(4) 0
Answer:
(4) 0
Hint:
Area of the ∆^le

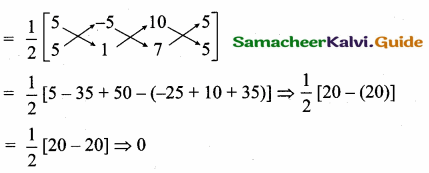
Question 3.
In a rectangle ABCD, area of ∆ ABC is \(\frac { 31 }{ 2 } \) sq. units. Then the area of rectangle is ……………
(1) 62 sq. units
(2) 31 sq. units
(3) 60 sq. units
(4) 30 sq. units
Answer:
(2) 31 sq. units
Hint:
In a rectangle area of ∆ ABC and area of ∆ ACD are equal.
Area of rectangle ABCD = 2 × \(\frac { 31 }{ 2 } \) = 31 sq.units

Question 4.
If the points (k, 2k), (3k, 3k) and (3,1) are collinear, then k is ……………..
(1) \(\frac { 1 }{ 3 } \)
(2) – \(\frac { 1 }{ 3 } \)
(3) \(\frac { 2 }{ 3 } \)
(4) – \(\frac { 2 }{ 3 } \)
Answer:
(2) – \(\frac { 1 }{ 3 } \)
Hint:
Since the three points are collinear. Area of a ∆ = 0

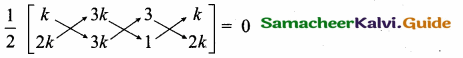
3k² + 3k + 6k – (6k² + 9k + k) = 0 ⇒ 3k² + 9k – 6k² – 10k = 0
-3 k² – k = 0 ⇒ -k(3k + 1) = 0
3k + 1 = 0 ⇒ 3 k = -1 ⇒ k = – \(\frac { 1 }{ 3 } \)

Question 5.
If the area of the triangle formed by the points (x, 2x), (-2, 6) and (3, 1) is 5 square units then x = ………….
(1) 2
(2) \(\frac { 3 }{ 5 } \)
(3) 3
(4) 5
Answer:
(1) 2
Hint:
Area of the triangle = 5 sq. units

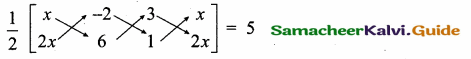
6x – 2 + 6x – (-4x + 18 + x) = 10 ⇒ 12x – 2 – (-3x + 18) = 10
12x – 2 + 3x – 18 = 10
15x – 20 = 10 ⇒ 15x = 10 + 20 = 30
x = \(\frac { 30 }{ 15 } \) = 2

Question 6.
The slope of a line parallel to y-axis is equal to …………..
(1) 0
(2) -1
(3) 1
(4) not defined
Answer:
(4) not defined

Question 7.
In a rectangle PQRS, the slope of PQ = \(\frac { 5 }{ 6 } \) then the slope of RS is ………..
(1) \(\frac { -5 }{ 6 } \)
(2) \(\frac { 6 }{ 5 } \)
(3) \(\frac { -6 }{ 5 } \)
(4) \(\frac { 5 }{ 6 } \)
Answer:
\(\frac { 5 }{ 6 } \)
Hint:
In a rectangle opposite sides are parallel.
∴ Slope of the line RS is \(\frac { 5 }{ 6 } \).

Question 8.
The y – intercept of the line y = 2x is ………
(1) 1
(2) 2
(3) \(\frac { 1 }{ 2 } \)
(4) 0
Answer:
(4) 0

Question 9.
The straight line given by the equation y = 5 is …………..
(1) Parallel to x – axis
(2) Parallel to y – axis
(3) Passes through the origin
(4) None of these
Answer:
(1) Parallel to x – axis

Question 10.
The x – intercept of the line 2x – 3y + 5 = 0 is ………….
(1) \(\frac { 5 }{ 2 } \)
(2) \(\frac { -5 }{ 2 } \)
(3) \(\frac { 2 }{ 5 } \)
(4) \(\frac { -2 }{ 5 } \)
Answer:
(2) \(\frac { -5 }{ 2 } \)
Hint:
2x – 3y + 5 = 0 ⇒ 2x – 3y = – 5

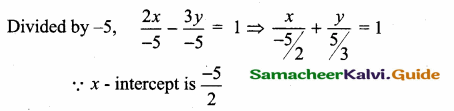
Question 11.
The lines 3x – 5y + 1 = 0 and 5x + ky + 2 = 0 are perpendicular if the value of k is ………..
(1) -5
(2) 3
(3) -3
(4) 5
Answer:
(2) 3
Hint:
Slope of the first line (m₁) = \(\frac { -3 }{ -5 } \) = \(\frac { 3 }{ 5 } \)
Slope of the second line (m₂) = \(\frac { -5 }{ k } \)
Since the two lines are perpendicular.
m₁ × m₂ = -1
\(\frac { 3 }{ 5 } \) × \(\frac { -5 }{ k } \) = -1 ⇒ \(\frac { -3 }{ k } \) = -1
-k = -3 ⇒ The value of k = 3

Question 12.
If x – y = 3 and x + 2y = 6 are the diameters of a circle then the centre is at the point ………..
(1) (0, 0)
(2) (1, 2)
(3) (1, -1)
(4) (4, 1)
Answer:
(4) (4, 1)
Hint:
Centre of the circle is the intersection of the two diameters.

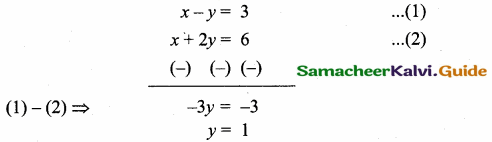
Centre of the circle is (4, 1)

Question 13.
The line 4x + 3y – 12 = 0 meets the x-axis at the point ……….
(1) (4, 0)
(2) (3, 0)
(3) (-3, 0)
Answer:
(2) (3,0)
Hint:
4x + 3y – 12 = 0 meet the x-axis the value of y = 0
4x- 12 = 0 ⇒ 4x = 12
x = \(\frac { 12 }{ 4 } \) = 3 ⇒ The point is (3, 0)

Question 14.
The equation of a straight line passing through the point (2, -7) and parallel to x-axis is ……………….
(1) x = 2
(2) x = -7
(3) y = -7
(4) y = 2
Answer:
(3) y = -7
Hint:
Equation of a line parallel to x-axis is y = -7

Question 15.
The equation of a straight line having slope 3 and y intercept – 4 is ………………
(1) 3x – y – 4 = 0
(2) 3x + y – 4 = 0
(3) 3x – y + 4 = 0
(4) 3x – y + 4 = 0
Answer:
(1) 3x – y – 4 = 0
Hint. The equation of a line is y = mx + c
y = 3 (x) + (-4) ⇒ y = 3x – 4
3x – y – 4 = 0

II. Answer the following questions:

Question 1.
If the points (3, – 4) (1, 6) and (- 2, 3) are the vertices of a triangle, find its area.
Answer:
Let the vertices A (3, – 4), B (1, 6) and C (- 2, 3)

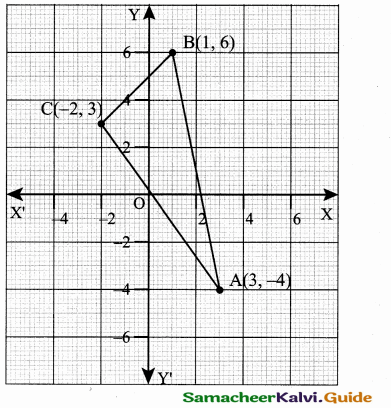
Area of ∆ ABC = \(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁, – (x₂y₁ + x₃y₂ + x₁y₃)]

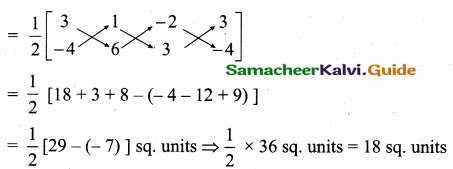
Area of a ∆ = 18 sq. units

Question 2.
If the area of the triangle formed by the points (1,2) (2,3) and (a, 4) is 8 sq. units, find a.
Answer:
Area of a triangle = 8 sq. units.

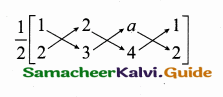
\(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)] = 8.
\(\frac { 1 }{ 2 } \) [3 + 8 + 2a – (4 + 3a + 4)] = 8
11 + 2a – 8 – 3a= 16 ⇒ – a + 3 = 16
– a = 16 – 3 ⇒ a = -13
The value of a = -13

Question 3.
If the points A (2, 5), B (4, 6) and C (8, a) are collinear find the value of “a” using slope concept.
Answer:
Since the three points are collineal
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of AB = Slope of BC
\(\frac { 6-5 }{ 4-2 } \) = \(\frac { a-6 }{ 8-4 } \) ⇒ \(\frac { 1 }{ 2 } \) = \(\frac { a-6 }{ 4 } \) ⇒ 2a – 12 = 4 ⇒ 2a = 16
a = \(\frac { 16 }{ 2 } \) = 8 ⇒ The value of a = 8

Question 4.
If the points (x,y) is collinear with the points (a, 0) and (0, b) then prove that \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
Answer:
Let A (x, y), B (a, 0), C(0, b)
Since the three points are collinear
Slope of AB = Slope of BC
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
\(\frac { 0-y }{ a-x } \) = \(\frac { b-0 }{ 0-a } \)
\(\frac { -y }{ a-x } \) = \(\frac { b }{ -a } \)
ay = b (a – x)
ay = ba – bx
ay + bx = ab
Divided by ab
\(\frac { ay }{ ab } \) + \(\frac { bx }{ ab } \) = \(\frac { ab }{ ab } \)
\(\frac { y }{ b } \) + \(\frac { x }{ a } \) = 1 ⇒ \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1

Question 5.
A straight line passes through (1, 2) and has the equation y – 2x – k = 0. Find k.
Answer:
The given line is y – 2x – k = 0
It passes through (1,2)
(2) -2 (1) -k = 0 ⇒ 2 – 2 – k = 0
0 – k = 0 ⇒ k = 0
The value of k = 0

Question 6.
If a line passes through the mid point of AB where A is (3, 0) and B is (5, 4) and makes an angle 60° with x – axis find its equation.
Answer:

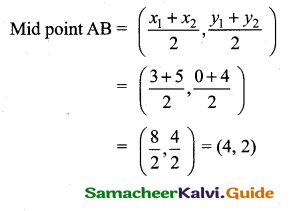
Slope of a line = tan 60°
= \(\sqrt { 3 }\)
Equation of a line is y – y₁ = m (x – x₁)
y – 2 = \(\sqrt { 3 }\) (x – 4)
y – 2 = \(\sqrt { 3 }\) x – 4 \(\sqrt { 3 }\)
\(\sqrt { 3x }\) – y + 2 – 4\(\sqrt { 3 }\) = 0

Question 7.
Find the equation of the line through (3, 2) and perpendicular to the line joining (4, 5) and (1,2)
Answer:
Slope of a line = \(\frac { 2-5 }{ 1-4 } \) ⇒ \(\frac { -3 }{ -3 } \) = 1
Slope of the line perpendicular to it is – 1
Equation of the line joining -1 and (3, 2) is
y – y₁ = m (x – x₁) ⇒ y – 2 = -1(x – 3)
y – 2 = -x + 3 ⇒ x + y – 5 = 0

Question 8.
P and Q trisect the line segment joining the points (2, 1) and (5, – 8). If the point P lies on 2x – y + k = 0, then find the value of k.
Answer:

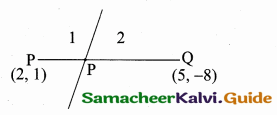
A line divides internally in the ratio 1 : 2
A line divide internally in the ratio l : m

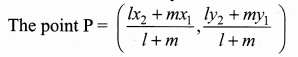
The point P = (\(\frac { 5+4 }{ 3 } \),\(\frac { -8+2 }{ 3 } \))
= (\(\frac { 9 }{ 3 } \),\(\frac { -6 }{ 3 } \)) = (3, -2)
The given line 2x – y + k = 0 passes through the point (3,-2)
2 (3) – (- 2) + k = 0
6 + 2 + k = 0
8 + k = 0
k = – 8
The value of k = – 8

Question 9.
The line 4x + 3y – 12 = 0 intersect the X, Y – axis at A and B respectively. Fine the area of ∆AOB.
Answer:
The equation of the line AB is 4x + 3y – 12 = 0

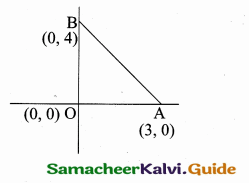
4x + 3y = 12
\(\frac { 4x }{ 12 } \) + \(\frac { 3y }{ 12 } \) = 1 ⇒ \(\frac { x }{ 3 } \) + \(\frac { y }{ 4 } \) = 1
The point A is (3, 0) (it intersect the X – axis)
and B is (0, 4) (it intersect the Y – axis)
Area of ∆ AOB = \(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ (x₂y₁ + x₃y₂ + x₁y₃)]

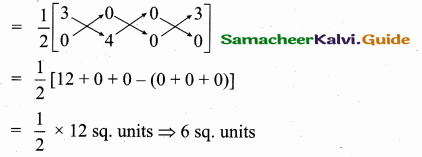
Question 10.
Find the equation of the line passing through (4, 5) and making equal intercept in the axes.
Answer:
Let the equal intercept on the axes be a, a.
Equation of the line is \(\frac { x }{ a } \) + \(\frac { y }{ a } \) = 1 (Given equal intercepts)
The line passes through (4, 5)
\(\frac { 4 }{ a } \) + \(\frac { 5 }{ a } \) = 1 ⇒ \(\frac { 9 }{ a } \) = 1 ⇒ a = 9
The equation of the line is \(\frac { x }{ 9 } \) + \(\frac { y }{ 9 } \) = 1
Multiply by 9
x + y – 9 = 0

Question 11.
Find the equation of the line passing through (2, – 1) and whose intercepts on the axes are equal in magnitude but opposite in sign.
Answer:
Let the x – intercept be “a” and y intercept be = “-a”
The equation of the line is
\(\frac { x }{ a } \) + \(\frac { y }{ -a } \) = 1 (y – intercept is – a)
\(\frac { x }{ a } \) – \(\frac { y }{ a } \) = 1
It passes through (2, -1)
\(\frac { 2 }{ a } \) – \(\frac { (-1) }{ a } \) = 1
\(\frac { 2 }{ a } \) + \(\frac { 1 }{ a } \) = 1 ⇒ \(\frac { 3 }{ a } \) = 1
a = 3
The equation of the line is
\(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
\(\frac { x }{ 3 } \) + \(\frac { y }{ -3 } \) = 1 ⇒ \(\frac { x }{ 3 } \) – \(\frac { y }{ 3 } \) = 1
x – y = 3
The equation is x – y – 3 = 0

Question 12.
The straight line cuts the coordinate axes at A and B. If the mid point of AB is (3,2) then find the equation of AB.
Answer:
Let the point A be (a, 0) and B be (0, b)


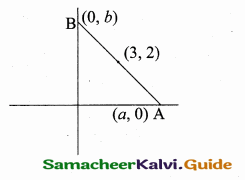
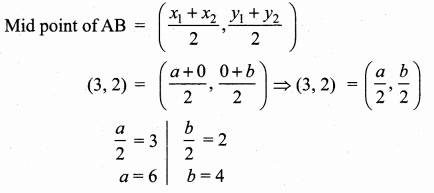
The point A (6, 0) and B (0, 4)
Equation of the line AB is

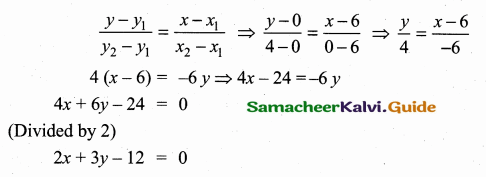
III. Answer the following questions

Question 1.
If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the ‘ coordinates of any point “c”, if AC = BC and Area of triangle ABC = 10 sq. units.
Answer:
Let the coordinates C be (a, 6) then AC = BC
AC² = BC²
(a – 3)² + (b – 4)² = (a – 5)² + (b + 2)²
a² + 9 – 6a + b² + 16 – 8b = a² + 25 – 10a + b² + 4 – 4b
a² + b² + 25 – 6a – 86 = a² + b² + 29 – 10a + 4b

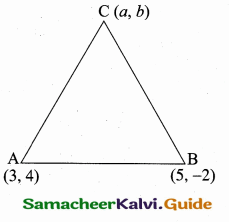
25 – 6a – 8b = 29 – 10a + 46
4a – 12b = 4 ⇒ a – 3b = 1 ………… (1)
Area of ∆ ABC = 10 sq. units
\(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)] = 10

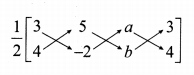
-6 + 5b + 4a – (20 – 2a + 3b) = 20
-6 + 5b + 4a – 20 + 2a – 3b = 20
6a + 2b – 26 = 20 ⇒ 6a + 2b = 46

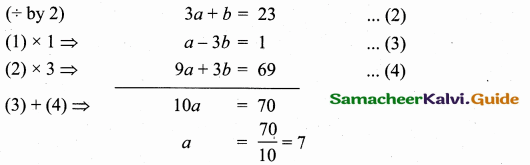
Substitute the value of a = 7 in (2)
3 (7) + b = 23 ⇒ b = 23 – 21 = 2
The coordinate C is (7, 2)

Question 2.
The four vertices of a Quadrilateral are (1,2) (- 5,6) (7, – 4) and (k, – 2) taken in order. If the area of the Quadrilateral is 9 sq. units, find the value of k.
Answer:
Let A (1, 2) B (- 5, 6) C (7, – 4) and D (k, – 2)
Area of the
Quadrilateral ABCD = \(\frac { 1 }{ 2 } \)[(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) – (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)]

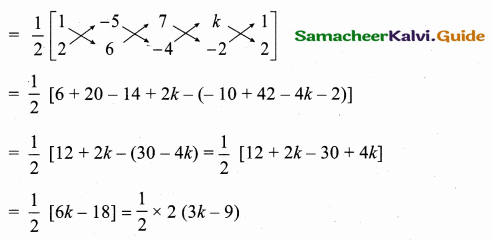
Area of the Quadrilateral ABCD = 3k – 9
Given area of a Quadrilateral is 9 sq. units.
3k – 9 = 9 ⇒ 3k = 18 ⇒ k = \(\frac { 18 }{ 3 } \) = 6
The value of k = 6

Question 3.
Find the area of a triangles whose three sides are having the equations x + y = 2, x – y = 0 and x + 2y – 6 = 0.
Answer:
Find the three vertices of the triangles by solving their equation.
To find vertices A


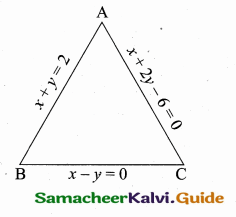
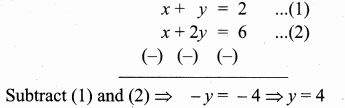
Substitute the value of y = 4 in (1)
x + 4 = 2 ⇒ x = 2 – 4 = -2
The vertices A is (- 2, 4)
To find vertices B

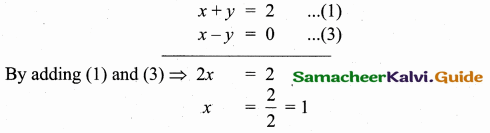
Substitute the value of x = 1 in (1)
1 + y = 2 ⇒ y = 2 – 1 = 1
The vertices B is (1, 1)
To find vertices C

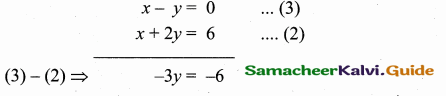
y = \(\frac { 6 }{ 3 } \) = 2
Substitute the value y = 2 in (3)
x – 2 = 0 ⇒ x = 2
The vertices C is (2, 2)

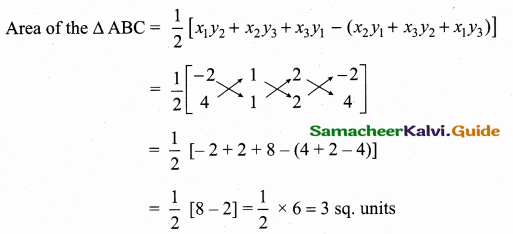
Area of the ∆ BC = 3 sq. units

Question 4.
Verify the Median of a triangle divides into two triangles of equal areas whose vertices are A (4, – 6), B (3, – 2) and C (5, 2)
Answer:

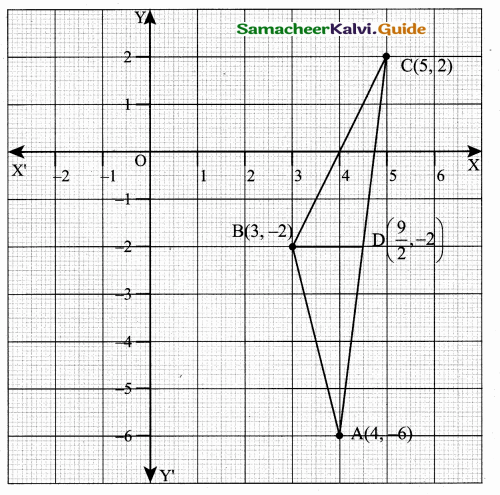
Let D be the mid point of AC .
Mid point of AC = (\(\frac { 5+4 }{ 2 } \),\(\frac { 2-6 }{ 2 } \)) = (\(\frac { 9 }{ 2 } \),-2)
Area of the triangle = \(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)]

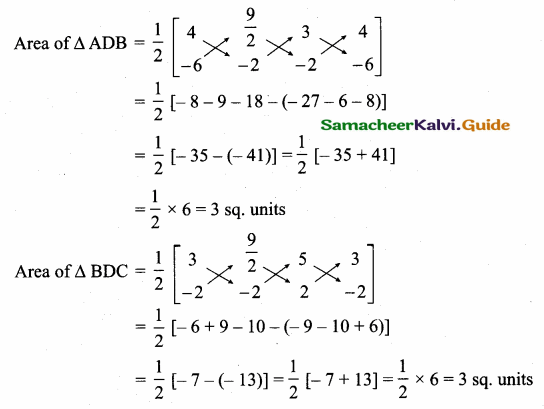
Area of ∆ ADB = Area of ∆ BDC
A median divides the triangle of equal areas.

Question 5.
Find the area of the ∆ ABC with A (1, – 4) and the mid points of sides through A being (2,-1) and (0,-1)
Answer:
Let the coordinates of B and C are (a, b) and (c, d) respectively.
Sides through A are AB and AC

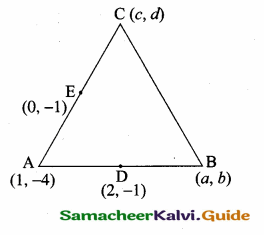
Mid point of AB = (\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\))
(2, -1) = (\(\frac { 1+a }{ 2 } \),\(\frac { -4+b }{ 2 } \))
\(\frac { 1+a }{ 2 } \) = 2
1 + a = 4
a = 4 – 1
= 3
The point B is (3,2)
\(\frac { -4+b }{ 2 } \) = -1
-4 + b = -2
b = -2 + 4
= 2
Mid point of AC = (\(\frac { 1+c }{ 2 } \),\(\frac { -4+d }{ 2 } \))
(0,-1) = (\(\frac { 1+c }{ 2 } \),\(\frac { -4+d }{ 2 } \))
\(\frac { 1+c }{ 2 } \) = 0
1 + c = 0
c = 0 – 1
= – 1
The point C is (-1,2)
\(\frac { -4+d }{ 2 } \) = -1
– 4 + d = -2
d = – 2 + 4
= 2
Thus the coordinates of the vertices of ∆ ABC are A (1, – 4) B (3, 2) and C (- 1, 2)
Area of ∆ ABC = \(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)]

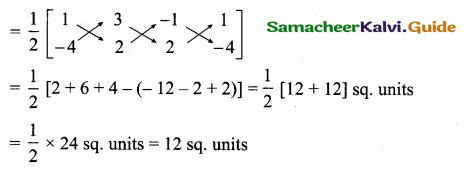
Area of ∆ ABC = 12 sq. units

Question 6.
Find the equation of the straight lines passing through (- 3, 10) whose sum of the intercepts is 8.
Answer:
Let the “x” intercept be “a” and y intercept be “b”
Sum of the intercepts = 8
a + b = 8 ⇒ b = 8 – a
Equation of a line is \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1 ⇒ \(\frac { x }{ a } \) + \(\frac { y }{ 8-a } \) = 1
It passes through (-3,10)
\(\frac { -3 }{ a } \) + \(\frac { 10 }{ 8-a } \) = 1
\(\frac { -3(8-a)+10a }{ a(8-a) } \) = 1
-24 + 3a + 10a = 8a – a²
-24 + 13a = 8a – a²
a² + 5a – 24 = 0 ⇒ (a + 8) (a – 3) = 0
a + 8 = 0 (or) a – 3 = 0 ⇒ a = -8 (or) a = 3
The equation of a line is a
a = -8
\(\frac { x }{ -8 } \) + \(\frac { y }{ 8+8 } \) = 1
\(\frac { x }{ -8 } \) + \(\frac { y }{ 16 } \) = 1
-2x + y = 16
2x – y + 16 = 0
a = 3
\(\frac { x }{ 3 } \) + \(\frac { y }{ 5 } \) = 1
5x + 3y = 15
5x + 3y – 15 = 0
The equation of the lines are 2x – y + 16 = 0 (or) 5x + 3y – 15 = 0.

Question 7.
If (5, – 3), (- 5, 3), (6, 6) are the mid points of the sides of a triangle, find the equation of the sides.
Answer:
Since D, E, F are the mid points of ∆ ABC
EF || AB, FD || BC and DE || AC
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of EF = \(\frac { 6-3 }{ 6+5 } \) = \(\frac { 3 }{ 11 } \)
Since EF || AB; Slope of AB = \(\frac { 3 }{ 11 } \)
Equation of AB is
y – y₁ = m (x – x₁)
y + 3 = \(\frac { 3 }{ 11 } \) (x – 5)
3x – 15 = 11y + 33
3x – 11y – 15 – 33 = 0
3x – 11y – 48 = 0
Slope of DE = Slope of AC
Slope of DE = \(\frac { 3+3 }{ -5-5 } \) = \(\frac { 6 }{ -10 } \) = –\(\frac { 6 }{ 10 } \) = –\(\frac { 3 }{ 5 } \)
Slope of AC = – \(\frac { 3 }{ 5 } \)
Equation of AC is
y – y₁ = m (x – x₁)

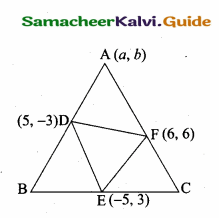
y – 6 = – \(\frac { 3 }{ 5 } \) (x – 6) ⇒ 5y – 30 = -3x + 18
3x + 5y – 30 – 18 = 0 ⇒ 3x + 5y – 48 = 0
Slope of DF = Slope of BC
Slope of DF = \(\frac { 6+3 }{ 6-5 } \) = \(\frac { 9 }{ 1 } \) = 9
Slope of BC = 9
Equation of the line BC is
y – y₁ = m(x – x₁)
y – 3 = 9 (x + 5) ⇒ 9x + 45 = y – 3
9x – y + 45 + 3 = 0 ⇒ 9x – y + 48 = 0
Equation of the sides are
3x – 11y – 48 = 0 ; 9x – y + 48 = 0 and 3x + 5y – 48 = 0

Question 8.
Find the equation of the straight line passing through the point of intersection of the lines 5x – 8y + 23 = 0 and 7x + 6y – 71 = 0 and is perpendicular to the line joining the points (5,1) and (-2, 2)
Answer:

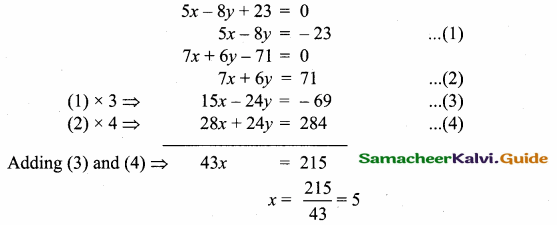
Substitute the value of x in (1)
5 (5) – 8y = – 23 ⇒ 25 – 8y = – 23
-8y = – 23 – 25 ⇒ -8y = – 48
y = \(\frac { 48 }{ 8 } \) = 6
The point of intersection is (5,6)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of the line joining the points (5,1) and (-2,2) = \(\frac { 2-1 }{ -2-5 } \)
= \(\frac { 1 }{ -7 } \) = – \(\frac { 1 }{ 7 } \)
Slope of the perpendicular line is = 7
Equation of a line is
y – y₁ = m(x – x₁) ⇒ y – 6 = 7 (x – 5)
y – 6 = 7x – 35 ⇒ -7x + y – 6 + 35 = 0
7x – y – 29 = 0

Question 9.
Find the equation of the line passing through the point of intersection of 4x – y – 3 = 0 and x + y – 2 = 0 and perpendicular to 2x – 5y + 3 = 0.
Answer:

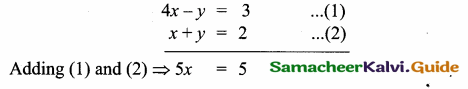
x = \(\frac { 5 }{ 5 } \) = 1
Substitute the value of x = 1 in (2)
1 + y = 2
y = 2 – 1 = 1
The point of intersection is (1, 1)
Any line perpendicular to 2x – 5y + 3 = 0 is
5x + 2y + k = 0
It passes through (1,1)
5(1) + 2(1) + k = 0 ⇒ 5 + 2 + k = 0
7 + k = 0 ⇒ k = -7
The line is 5x + 2y – 7 = 0

Question 10.
Find the equation of the line through the point of intersection of the lines 2x + y – 5 = 0 and x + y – 3 = 0 and bisecting the line segment joining the points (3, – 2) and (- 5, 6).
Answer:

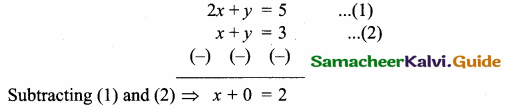
x = 2
Substitute the value of x = 2 in (2)
2 + y = 3
y = 3 – 2 = 1
The point of intersection is (2, 1)
Mid point of the line joining the points (3,-2) and (-5,6)

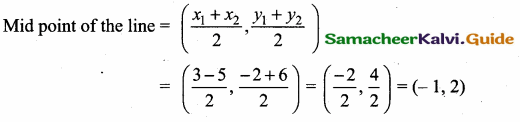
Mid point of the line
Equation of the line joining the points (2, 1) and (-1,2) is

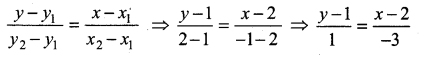
x – 2 = -3 (y – 1)
x – 2 = -3y + 3
x + 3y – 5 = 0
The equation of the line is x + 3y – 5 = 0

Students can download Maths Chapter 5 Information Processing Ex 5.2 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 5 Information Processing Ex 5.2

Miscellaneous Practice Questions 

Question 1.
Find HCF of 188 and 230 by Euclid’s game.
Solution:
By Euclid’s game HCF (a, b) = HCF (a, a – b) if a > b.
Here HCF (188, 230) = HCF (230, – 188) because 230 > 188
= HCF (188, 42) = HCF (146, 42)
= HCF (104, 42) = HCF (62, 42)
= HCF (42, 20) = HCF (22, 20)
= HCF (20,2) = HCF (18, 2) = 2
∴ HCF (230, 188) = 2

Question 2.
Write the numbers from 1 to 50. From that find the following.
i) The numbers which are neither divisible by 2 nor 7.
ii) The prime numbers between 25 and 40
iii) All square numbers upto 50.
Solution:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50.
i) The numbers neither divisible by 2 nor 7 are 9, 11, 13, 15, 17, 19, 23, 25, 27, 29, 31, 33, 37, 39, 41, 43, 45, 47.
ii) The prime numbers between 25 and 40 are 29, 31, 37.
iii) Square numbers upto 50 are 1, 4, 9, 16, 25, 36, 49

Question 3.
Complete the following pattern.
(i) 1 + 2 + 3 + 4 = 10
2 + 3 + 4 + 5 = 14
___ + 4 + 5 + 6 = ___
4 + 5 + 6 + ___ = ___

(ii) 1 + 3 + 5 + 7 = 16
___ + 5 + 7 + 9 = 24
5 + 7 + 9 + ___ = ___
7 + 9 + ___ + 13 = ___

(iii) AB, DEF, HIJK, ___ , STUVWX
(vi) 20, 19, 17, ___ , 10, 5
Solution:
(i) 3, 18; 7, 22
(ii) 3; 11, 32; 11, 40
(iii) MNOPQ
(iv) 14

Question 4.
Complete the table by using the following instructions.

A : It is the 6th term in the Fibonacci sequence.
B : The predecessor of 2.
C : LCM of 2 and 3.
D : HCF of 6 and 20.
E : The reciprocal of 1/5.
F : The opposite number of -7.
G : The first composite number.
H : Area of a square of side 3 cm.
I : The number of lines of symmetry of an equilateral triangle.
After completing the table, what do you observe? Discuss.
Solution:
A – 8, B – 1, C – 6, D – 2, E – 5, F – 7, G – 4, H – 9, I – 3

Question 5.
Assign the number for English alphabets as 1 for A, 2 for B upto 26 for Z. Find the meaning of

Solution:
GOOD MORNING

Question 6.
Replace the letter with symbols as + for A, – for B, × for C, and ÷ for D. Find the answer for the pattern 4B3C5A30D2 by doing the given operations.
Solution:
Given the symbols + for A; – for B; × for C; + for D .
∴ 4B3C5A30D2 becomes
4 – 3 × 5 + 30 ÷ 2 Using BIDMAS rule
4 – 3 × 5 + 30 ÷ 2 = 4 – 3 × 5 + 15[× done first]
= 4 – 15 + 15 [+ done second]
= 4 – 0 [+ done third]
= 4 [- done last]

Question 7.
Observe the pattern and find the word by hiding the Numbers 1 H 2 0 3 W, 4 A 5 R 6 E, 7 Y 8 0 9 U.
Solution:
HOW ARE YOU

Question 8.
Arrange the following from the eldest to the youngest. What do you get?

Solution:
Arranging from eldest to the youngest we get
F – refers to grandparents
A – refers to parents
M – refers to an uncle
I – refers to elder sister
L – refers to me
Y – refers to the younger brother
So we get FAMILY

Challenge Problems

Question 9.
Prepare a daily time schedule for evening study at home.
Solution:
5.00 pm to 6.00 pm – Mathematics
6.0 pm to 7.00 pm – Science
7.0 pm to 8.00 pm – Social Science
8. pm to 9.00 pm – Dinner & Recreation
9. pm to 10.00 pm – Tamil and English

Question 10.
Observe the geometrical pattern and answer the following questions.

(i) Write down the number of sticks used in each iterative pattern,
(ii) Draw the next figure in the pattern also find the total number of sticks used in it.
Solution:
(i) 3, 9, 18

Question 11.
Find the HCF of 28, 35, 42 by Euclid’s game.
Solution:
HCF of 28, 35, 42
HCF of (28, 35 – 28, 42 – 28)
28 = 2 × 2 × 7
7 = 1 × 7
14 = 2 × 7
HCF of (28, 7, 14) = 7

Question 12.
Follow the given instructions to fill your name in the OMR sheet.
1. The name should be written in capital letters from left to right.
2. One alphabet is to be entered in each box.
3. If any empty boxes are there at the end they should be left blank.
4. Ballpoint pen is to be used for shading the bubbles for the corresponding alphabets.

Solution:
Do your self.

Question 13.
Consider the Postal index number (PIN) written on the letters as follows: 604506; 604516; 604560; 604506; 604516; 604516; 604560; 604516; 604505; 604470; 604515; 604520; 604303; 604509; 604470. How the letters can be sorted as per Postal Index Numbers?
Solution:
604 is common for all postal index numbers. Compare the remaining 3 digits, 303, 470, 505, 506 (two) 509, 510. 515, 516 (Four), 520, 560 (two).

Students can download Maths Chapter 5 Information Processing Ex 5.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 5 Information Processing Ex 5.1

Question 1.
Study and complete the following pattern.
(i) 1 × 1 = 1
11 × 11 = 121
111 × 111 = 12321
1111 × 1111 = ?
11111 × 11111 = ?

Solution:
(i) 1234321, 123454321
(ii) 144, 60, 84, 36, 48, 15, 27

Question 2.
Find next three numbers in the following number patterns.
(i) 50, 51, 53, 56, 60……
(ii) 77, 69, 61, 53, ……
(iii) 10, 20, 40, 80,…
(iv) \(\frac{21}{33}\), \(\frac{321}{444}\), \(\frac{4321}{555}\)
Solution:

i) The pattern generating these numbers is
50, 50 + 1, 51 + 2, 53 + 3, 56 + 4, 60 + 5, 65 + 6, 71 + 7,
∴ 50, 51, 53, 56, 60, 65, 71, 78, ……
∴ The next three numbers will be 65, 71, 78

ii) The pattern generating these numbers is
77, 77 – 8, 69 – 8, 61 – 8, 53 – 8, 45 – 8, 37 – 8, 29
77, 69, 61, 53, 45, 37, 29, 21,
∴ The next three numbers will be 45, 37, 29.

iii) The pattern generating these numbers is
10, 10 + 10, 20 + 20, 40 + 40, 80 + 80, 160 + 160, 320 + 320,….
10, 20, 40, 80, 160, 320, 640,….
∴ The next three numbers will be 160, 320, 640.

(iv) \(\frac{54321}{66666}\), \(\frac{654321}{777777}\), \(\frac{7654321}{8888888}\)

Question 3.
Consider the Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…. Observe and complete the following table by understanding the number patterns? followed. After filling the table discuss the pattern followed in addition and subtraction, of the numbers of the sequence?

Solution:
(i) 12, 13 – 1 = 12
(ii) 33, 34 – 1 = 33
(iii) 1 + 3 + 8 + 21 + 55 = 88, 89 – 1 = 88

Question 4.
Complete the following patterns.

Solution:

Question 5.
Find the HCF of the following pair of numbers by Euclid’s game
(i) 25 and 35
(ii) 36 and 12
(iii) 15 and 29
Solution:
(i) HCF of (25, 35 – 25)
25 = 5 × 5
10 = 2 × 5
HCF of (25, 10) = 5

(ii) HCF of (36, 36 – 12)
36 = 2 × 2 × 3 × 3
24 = 2 × 2 × 2 × 3
HCF of (36, 24) = 2 × 2 × 3 = 12

(iii) HCF of (15, 29 -15)
15 = 3 × 5 × 1
14 = 2 × 7 × 1
HCF of (15, 14) = 1

Question 6.
Find HCF of 48 and 28. Also find the HCF of 48 and the number obtained by finding their difference.
Solution:
HCF of 48 and 28
48 = 2 × 2 × 2 × 2 × 3
28 = 2 × 2 × 7
HCF of (48, 28) = 2 × 2 = 4
HCF of (48, 48 – 28)
48 = 2 × 2 × 2 × 2 × 3
20 = 2 × 2 × 5
HCF of (48, 20) = 4

Question 7.
Give instructions to fill in a bank withdrawal form issued in a bank.
Solution:

• The name should be written in capital letters from left to right.
• Write the date of withdrawal on the right top comer of the form.
• Write the amount (in words) to be withdrawn in the space provided.
• Write the amount (in figures) to be withdrawn in the box provided.
• Put your signature at the right bottom above the ‘signature of the depositor’.

Question 8.
Arrange the name of your classmates alphabetically.
Solution:

Question 9.
Follow and execute the instructions given below.

(i) Write the number 10 in the place common to the three figures
(ii) Write the number 5 in the place common for square and circle only.
(iii) Write the number 7 in the place common for triangle and circle only.
(iv) Write the number 2 in the place common for triangle and square only.
(v) Write the numbers 12, 14, and 8 only in square, circle, and triangle respectively.
Solution:

Question 10.
Fill in the following information

Solution:

Objective Type Questions

Question 11.
The next term in the sequence 15, 17, 20, 22, 25, … is
(a) 28
(b) 29
(c) 27
Hint:
Add 2 and 3 alternatively
Solution:
(c) 27

Question 12.
What will be the 25th letter in the pattern? ABCAABBCCAAABBBCCC,…
(a) B
(b) C
(c) D
(d) A
Solution:
(a) B

Question 13.
The difference between 6th term add 5th term in the Fibonacci sequence is ___.
(a) 6
(b) 8
(c) 5
(d) 3
Solution:
(d) 3

Question 14.
The 11th term in the Lucas sequence 1, 3, 4, 7, is
(a) 199
(b) 76
(c) 123
(d) 47
Solution:
(a) 199

Question 15.
If the Highest Common Factor of 26 and 54 is 2, then HCF of 54 and 28 is .
(a) 26
(b) 2
(c) 54
(d) 1
Hint: HCF (54, 28) = HCF (28, 26) = 2
Solution:
(b) 2

Students can download Maths Chapter 4 Symmetry Ex 4.2 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 4 Symmetry Ex 4.2

Miscellaneous Practice Problems

Question 1.
Draw and answer the following.
(i) A triangle which has no line of symmetry.
(ii) A triangle which has only one line of symmetry
(iii) A triangle which has three lines of symmetry.
Solution:
(i) Scalene triangle
(ii) Isosceles triangle
(iii) Equilateral triangle

Question 2.
Find the alphabets in the box which have

(i) No line of symmetry
(ii) Rotational symmetry
(iii) Reflection symmetry
(iv) Reflection and rotational symmetry.
Solution:
i) The alphabets which have no line of symmetry are P, N, S, Z
ii) The alphabets which have Rotational symmetry are I, O, N, X, S, H, Z
iii) The alphabets which have reflection symmetry are A, M, E, D, I, K, O, X, H, U, V, W.
iv) The alphabets which has reflection and rotational symmetry are I, O, X, H.

Question 3.
For the following pictures, find the number of lines of symmetry and also find the order of rotation.

Solution:
(i) 0, 2
(ii) 1, 0
(iii) 2, 2
(iv) 8, 8
(v) 1, 0

Question 4.
The three-digit number 101 has rotational and reflection symmetry. Give five more examples of three-digit numbers that have both rotational and reflection symmetry
Solution:
The digits 0, 1, 8 have rotational and reflection symmetry.
∴ The three digits numbers 181, 111, 808, 818, 888 have both rotational and reflection symmetry.

Question 5.
Translate the given pattern and complete the design in a rectangular strips?

Solution:

Challenge Problems

Question 6.
Shade one square so that it possesses

(i) One line of symmetry
(ii) Rotational symmetry of order 2
Solution:

Question 7.
Join six identical squares so that atleast one side of a square fits exactly with any other side of the square and has reflection symmetry (any three ways).
Solution:

Question 8.
Draw the following
(i) A figure which has reflection symmetry but no rotational symmetry.
(ii) A figure which has rotational symmetry but no reflection symmetry.
(iii) A figure which has both reflection and rotational symmetry.
Solution:

Question 9.
Find the line of symmetry and the order of rotational symmetry’ of the given regular polygons and complete the following table and answer the questions given below.

i) A regular polygon of 10 sides will have ______ lines of symmetry.
ii) If a regular polygon has 10 lines of symmetry then its order of rotational symmetry is ______
iii) A regular polygon of ‘n’ sides has lines of symmetry and the order of rotational symmetry is ______
Solution:
(i) 10
(ii) 10
(iii) n, n

Question 10.
Colour the boxes in such a way that it possesses translation symmetry.

Solution:

Students can download Maths Chapter 4 Symmetry Ex 4.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 4 Symmetry Ex 4.1

Question 1.
Fill in the blanks
(i) The reflected image of the letter ‘q’ is …….
(ii) A rhombus has ………… lines of symmetry.
(iii) The order of rotational symmetry of the letter ‘Z’ is ……….
(iv) A figure is said to have rotational symmetry, if the order of rotation is atleast ……….
(v) ……… symmetry occurs when an object slides to new position.
Solution:
(i) P
(ii) two
(iii) 2
(iv) two
(v) Translation

Question 2.
Say True or False
(i) A rectangle has four lines of symmetry.
(ii) A shape has reflection symmetry if it has a line of symmetry.
(iii) The reflection of the name RANI is INAЯ.
(iv) Order of rotation of a circle is infinite.
(v) The number 191 has rotational symmetry.
Solution:
(i) False
(ii) True
(iii) False
(iv) True
(v) False

Question 3.
Match the following shapes with their number of lines of symmetry.

Solution:
(i) d
(ii) a
(iii) b
(iv) c

Question 4.
Draw the lines of symmetry of the following.

Solution:

Question 5.
Using the given horizontal line/ vertical line as a line of symmetry, complete each alphabet to discover the hidden word.

Solution:
(i) DECODE
(ii) KICK
(iii) BED
(iv) WAY
(v) MATY
(vi) TOMATO

Question 6.
Draw a line of symmetry of the given figures such that one hole coincides with the other hole(s) to make pairs.

Solution:

Question 7.
Complete the other half of the following figures such that the dotted line is the line of symmetry.

Solution:

Question 8.
Find the order of rotation for each of the following.

Solution:
(i) 2
(ii) 2
(iii) 4
(iv) 8
(v) 2

Question 9.
A standard die has six faces which are shown below. Find the order of rotational symmetry of each face of a die?

Solution:
(i) 4
(ii) 2
(iii) 2
(iv) 4
(v) 4
(vi) 2

Question 10.
What pattern is translated in the given border kolams?

Solution:

Objective Type Questions

Question 11.
Which of the following letter does not have a line of symmetry?
(a) A
(b) P
(c) T
(d) U
Hint: A, T, U have one line of symmetry
Solution:
(b) P

Question 12.
Which of the following is a symmetrical figure?

Solution:
(c)

Question 13.
Which word has a vertical line of symmetry?
(a) DAD
(b) NUN
(c) MAM
(d) EVE
Hint: D, N, E have no vertical line of symmetry
Solution:
D, N, E have no vertical line of symmetry

Question 14.
The order of rotational symmetry of 818 is ………
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b) 2

Question 15.
The order of rotational symmetry ★ is ___
(a) 5
(b) 6
(c) 7
(d) 8
Solution:
(a) 5

Students can download Maths Chapter 6 Trigonometry Ex 6.1 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 6 Trigonometry Ex 6.1

Question 1.
Prove the following identities.
(i) cot θ + tan θ = sec θ cosec θ
(ii) tan⁴ θ + tan² θ = sec⁴ θ – sec² θ
Answer:
(i) L. H. S = cot θ + tan θ
= \(\frac{\cos \theta}{\sin \theta}+\frac{\sin \theta}{\cos \theta}\)
= \(\frac{\cos ^{2} \theta+\sin ^{2} \theta}{\sin \theta \cos \theta}\)
[cos² θ + sin² θ = 1]
= \(\frac{1}{\sin \theta \cos \theta}\)
= sec θ . cosec θ = R. H. S
∴ cot θ + tan θ = sec θ cosec θ

(ii) tan⁴ θ + tan² θ = sec⁴ θ – sec² θ
L.H.S = tan⁴ θ + tan² θ
= tan² θ (tan² θ + 1)
= tan² θ sec² θ
R.H.S = sec⁴ θ – sec² θ
= sec² θ (sec² θ – 1)
= sec² θ tan² θ
L.H.S = R.H.S
∴ tan⁴ θ + tan² θ = sec⁴ θ – sec² θ

Question 2.
Prove the following identities.
(i) \(\frac{1-\tan ^{2} \theta}{\cot ^{2} \theta-1}\) = tan² θ
(ii) \(\frac{\cos \theta}{1+\sin \theta}\) = sec θ – tan θ
Answer:
(i) \(\frac{1-\tan ^{2} \theta}{\cot ^{2} \theta-1}\) = tan² θ

(ii) \(\frac{\cos \theta}{1+\sin \theta}\) = sec θ – tan θ

Aliter:
L.H.S = \(\frac{\cos \theta}{1-\sin \theta}\)
[conjugate (1 – sin θ)]

Question 3.
Prove the following identities.

Solution:

Question 4.
Prove the following identities.
(i) sec⁶ θ = tan⁶ θ + 3 tan² θ sec² θ + 1
(ii) (sin θ + sec θ)² + (cos θ + cosec θ)² = 1 + (sec θ + cosec θ)²
Answer:
(i) sec⁶ θ = tan⁶ θ + 3 tan² θ sec² θ + 1
L.H.S = sec⁶ θ
= (sec² θ)³ = (1 + tan² θ)³
= 1 + (tan² θ)³ + 3 (1) (tan² θ) (1 + tan² θ) [(a + b)³ = a³ + b³ + 3 ab (a + b)]
= 1 + tan⁶ θ + 3 tan² θ(1 + tan² θ)
= 1 + tan⁶ θ + 3 tan² θ (sec² θ)
= 1 + tan⁶ θ + 3 tan² θ sec² θ
= tan⁶ θ + 3 tan² θ sec² θ + 1
L.H.S = R.H.S

(ii) (sin θ + sec θ)² + (cos θ + cosec θ)² = 1 + (sec θ + cosec θ)²
L.H.S = (sin θ + sec θ)² + (cos θ + cosec θ)²]
= [sin² θ + sec² θ + 2 sin θ sec θ + cos² θ + cosec² θ + 2 cos θ cosec θ]
= (sin² θ + cos² θ) + (sec² θ + cosec² θ) + 2 (sin θ sec θ + cos θ cosec θ)

= 1 + sec² θ + cosec² θ + 2 sec θ cosec θ
= 1 + (sec θ + cosec θ)²
L.H.S = R.H.S
∴ (sin θ + sec θ)² + (cos θ + cosec θ)² = 1 + (sec θ + cosec θ)²

Question 5.
Prove the following identities.
(i) sec⁴ θ (1 – sin⁴ θ) – 2 tan² θ = 1
(ii) \(\frac{\cot \theta-\cos \theta}{\cot \theta+\cos \theta}=\frac{\csc \theta-1}{\csc \theta+1}\)
Answer:
(i) L.H.S = sec⁴ θ (1 – sin⁴ θ) – 2 tan² θ

L.H.S = R.H.S
∴ sec⁴ θ (1 – sin⁴ θ) – 2 tan² θ = 1

(ii) \(\frac{\cot \theta-\cos \theta}{\cot \theta+\cos \theta}=\frac{\csc \theta-1}{\csc \theta+1}\)

Question 6.
Prove the following identities.


Answer:

Question 7.
(i) If sin θ + cos θ = \(\sqrt { 3 }\), then prove that tan θ + cot θ = 1.
(ii) If \(\sqrt { 3 }\) sin θ – cos θ = θ, then show that tan 3θ = \(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\)
Answer:
sin θ + cos θ = \(\sqrt { 3 }\) (squaring on both sides)
(sin θ + cos θ)² = (\(\sqrt { 3 }\))²
sin² θ + cos² θ + 2 sin θ cos θ = 3
1 + 2 sin θ cos θ = 3
2 sin θ cos θ = 3 – 1
2 sin θ cos θ = 2
∴ sin θ cos θ = 1
L.H.S = tan θ + cot θ

L.H.S = R.H.S ⇒ tan θ + cot θ = 1

(ii) If \(\sqrt { 3 }\) sin θ – cos θ = 0
To prove tan 3θ = \(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\)
\(\sqrt { 3 }\) sin θ – cos θ = 0
\(\sqrt { 3 }\) sin θ = cos θ
\(\frac{\sin \theta}{\cos \theta}=\frac{1}{\sqrt{3}}\)
tan θ = tan 30°
θ = 30°
L.H.S = tan 3θ°
= tan3 (30°)
= tan 90°
= undefined (∝)

∴ tan 3θ = \(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\)

Question 8.
(i) If \(\frac{\cos \alpha}{\cos \beta}=m\) and \(\frac{\cos \alpha}{\cos \beta}=n\) then prove that (m2 + n2) cos2 β = n2
(ii) If cot θ + tan θ = x and sec θ – sec θ – cos θ = y, then prove that (x2y)2/3 – (xy2)2/3 = 1
Answer:
(i) L.H.S = (m² + n²) cos² β

L.H.S = R.H.S ⇒ ∴ (m² + n²) cos² β = n²

(ii) Given cot θ + tan θ = x sec θ – cos θ = y
x = cot θ + tan θ
x = \(\frac{1}{\tan \theta}\) + tan θ
= \(\frac{1+\tan ^{2} \theta}{\tan \theta}\) = \(\frac{\sec ^{2} \theta}{\tan \theta}\)

y = sec θ – cos θ
= \(\frac{1}{\cos \theta}-\cos \theta=\frac{1-\cos ^{2} \theta}{\cos \theta}\)
y = \(\frac{\sin ^{2} \theta}{\cos \theta}\)

Question 9.
(i) If sin θ + cos θ = p and sec θ + cosec θ = q, then prove that q (p² – 1) = 2 p
(ii) If sin θ (1 + sin² θ) = cos² θ, then prove that cos⁶ θ – 4 cos⁴ θ + 8 cos² θ = 4
Answer:
(i) p = sin θ + cos θ
p² = (sin θ + cos θ)²
= sin² θ + cos² θ + 2 sin θ cos θ = 1 + 2 sin θ cos θ
q = sec θ + cosec θ
= \(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}=\frac{\sin \theta+\cos \theta}{\sin \theta \cos \theta}\)
L.H.S = q(p² – 1)

(ii) sin θ (1 + sin² θ) = cos² θ
sin θ (1 + 1 – cos² θ) = cos² θ
sin θ (2 – cos² θ) = cos² θ
Squaring on both sides,
sin² θ (2 – cos² θ)² = cos⁴ θ
(1 – cos² θ) (4 + cos⁴ θ – 4 cos² θ) = cos⁴ θ
4 cos⁴ θ – 4 cos² θ – cos⁶ θ + 4 cos⁴ θ = cos⁴ θ
4 + 5 cos⁴ θ – 8 cos² θ – cos⁶ θ = cos⁴ θ
– cos⁶ θ + 5 cos⁴ θ – cos⁴ θ – 8 cos² θ = -4
– cos⁶ θ + 4 cos⁴ θ – 8 cos² θ = -4
cos⁶ θ – 4 cos⁴ θ + 8 cos² θ = 4
Hence it is proved

Question 10.
If \(\frac{\cos \theta}{1+\sin \theta}\) = \(\frac { 1 }{ a } \), then prove that \(\frac{a^{2}-1}{a^{2}+1}\) = sin θ
Answer:

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.1 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.1

Question 1.
Find the adjoint of the following:

Solution:

Question 2.
Find the inverse (if it exists) of the following.

Solution:
\(\begin{bmatrix} -2 & 4 \\ 1 & -3 \end{bmatrix}\)
|A| = 6 – 4 = 2 ≠ 0
∴ A^-1 exists. A is non singular.


|A| = 2(8-7)-3(6-3)+1(21-12)
= 2 – 9 + 9 = 2 ≠ 0. A^-1 exists.

Question 3.

Solution:
\(\left[\begin{array}{ccc}
\cos \alpha & 0 & \sin \alpha \\
0 & 1 & 0 \\
-\sin \alpha & 0 & \cos \alpha
\end{array}\right]\)
|F(α)| = cos α(cos α – 0) – 0 + sin α(0 + sin α)
= cos²α + sin²α = 1
|f(α)| = 1 ≠ 0. [F(α)]^-1 exists.


[∵ cos (-θ) = cos θ ; sin(-θ) = -sin θ]
from (1) and (2) we have
[F(α)]^-1 = F(-α)

Question 4.
If A = \(\begin{bmatrix} 5 & 3 \\ -1 & -2 \end{bmatrix}\), show that A² – 3A – 7I₂ = O₂. hence find A^-1
Solution:

∴ A² -3A – 7I₂ = O₂
Post multiply this equation by A^-1
A²A^-1 – 3A A^-1 – 7I₂ A^-1 = 0
A – 3I – 7A^-1 = 0
A – 3I = 7 A^-1
A^-1 = \(\frac {1}{7}\) (A – 3I)

Question 5.

Solution:

Question 6.
If A = \(\begin{bmatrix} 8 & -4 \\ -5 & 3 \end{bmatrix}\) verify that A(adj A) = (adj A) A = \(\left| A \right|\)I₂.
Solution:

(1), (2) and (3) ⇒ A (adj A) = (adj A)A = |A| I₂.

Question 7.

Solution:

Question 8.

Solution:

|adj (A)| = 2 (24 – 0) + 4 (- 6 – 14) + 2(0 + 24)
= 48 – 80 + 48 = 16

Question 9.

Solution:

|adj A| = 0 + 2(36 – 18) + 0 = 2(18) = 36

Question 10.

Solution:

Question 11.

Solution:


Hence proved

Question 12.

Solution:

Question 13.

Solution:
Given A × B × C
⇒ A^-1 A × B B^-1 = A^-1 C B^-1
I × I = A^-1 C B^-1
⇒ X = A^-1 CB^-1
let us find A^-1 and B^-1

Question 14.

Solution:


Hence proved.

Question 15.
Decrypt the received encoded message [2 -3] [20 4] with the encryption matrix \(\begin{bmatrix} -1 & -1 \\ 2 & 1 \end{bmatrix}\) and the decryption matrix as its inverse, where the system of codes are described by the numbers 1 – 26 to the letters A – Z respectively, and the number 0 to a blank space.
Solution:

So the sequence of decoded row matrics is [8 5] [12 16]
The receiver reads the message as “HELP”.

Students can download Maths Chapter 3 Perimeter and Area Ex 3.2 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 3 Perimeter and Area Ex 3.2

Miscellaneous Practice Problems

Question 1.
A piece of wire is 36 cm long. What will be the length of each side if we form
(i) a square
(ii) an equilateral triangle
Solution:

Given the length of the wire = 36 cm
i) When a square is formed out of it
The perimeter of the square = 36 cm
4 × side = 36
side = \(\frac{36}{4}\) = 9 cm
Side of the square

ii) When an equilateral triangle is formed out of it, its perimeter = 36 cm
i.e., side + side + side = 36 cm .
3 × side = 36 cm
side = \(\frac{36}{3}\) = 12 cm
One side of an equilateral triangle = 12 cm

Question 2.
From one vertex of an equilateral triangle with a side of 40 cm, an equilateral triangle with 6 cm side is removed. What is the perimeter of the remaining portion? The perimeter of the remaining portion
Solution:

= (40 + 34 + 6 + 34) cm
= 114 cm

Question 3.
Rahim and Peter go for a morning walk, Rahim walks around a. square path of side 50 m and Peter walks around a rectangular path with a length of 40 m and a breadth of 30 m. If both of them walk 2 rounds each, who covers more distance and by how much?
Solution:
Distance covered by Rahim
= 50 × 4 m
= 200 m
If he walks 2 rounds, distance covered = 2 × 200 m
= 400 m
Distance covered by peter
= 2 (40 + 30) m
= 2(70)m
= 140 m
If he walks 2 rounds, distance covered = 2 × 140 m
= 280 m
∴ Rahim covers more distance by (400 – 280) = 120 m

Question 4.
The length of a rectangular park is 14 m more than its breadth. If the perimeter of the park is 200 m, what is its length? Find the area of the park.
Solution:
Let the length be b + 14 m
breadth = b
perimeter = 200
2 (l + b) = 200
2 (b + 14 + b) = 200
2 (2b + 14) = 200
28 + 4b = 200
4b = 200 – 28
4b = 172 m
b = \(\frac{172}{4}\)
b = 43 m
Length = b + 14
= 43 + 14
Length l = 57 m
Area = l × b units
= 57 × 43 m²
= 2451 m²

Question 5.
Your garden is in the shape of a square of side 5 m. Each side is to be fenced with 2 rows of wire. Find how much amount is needed to fence the garden at ₹ 10 per metre.
Solution:
a = 5 m
The perimeter of the garden
= 4 a units
= 4 × 5 m
= 20 m
For 1 row
Amount needed to fence l m= Rs 10
Amount needed to fence 20 m
= Rs 10 × 20
= Rs 200
For 2 rows
Total amount needed = 2 × Rs 200 = Rs 400

Challenge Problems

Question 6.
A closed shape has 20 equal sides and one of its sides is 3 cm. Find its perimeter.
Solution:
Number of equal sides in the shape = 20
One of its side = 3 cm
Perimeter = length of one side × Number of equal sides
∴ Perimeter = (3 × 20) cm = 60 cm
∴ Perimeter = 60 cm

Question 7.
A rectangle has length 40 cm and breadth 20 cm. How many squares with side 10 cm can be formed from it.
Solution:
Area of rectangle = (length × breadth) units²
Length = 40 cm
Breadth = 20 cm
∴ Area = (40 × 20) cm² = 800 cm²
Area of rectangle = 800 cm²
Area of square = (side × side) units²
side = 10 cm
∴ Area of square = (10 × 10) cm² = 100 cm²
Required number of squares = \(\frac{\text { Area of Rectangle }}{\text { Area of } 1 \text { square }}=\frac{800 \mathrm{cm}^{2}}{100 \mathrm{cm}^{2}}\) = 8
8 squares can be formed.

Question 8.
The length of a rectangle is three times its breadth. If its perimeter is 64 cm, find the sides of the rectangle.
Solution:
Given perimeter of a rectangle = 64 cm
Also given length is three times its breadth.
Let the breadth of the rectangle = b cm
∴ Length = 3 × b cm
Perimeter = 64 m
i.e., 2 × (l + b) = 64 m
2 × (3b + b) = 64 m
2 × 4b = 64m
4b = \(\frac{64}{2}\) = 32 m
b = \(\frac{32}{4}\) = 8 m
l = 3 × b = 3 × 8 = 24 m
∴ Breadth of the rectangle = 8 m
Length of the rectangle = 24 m

Question 9.
How many different rectangles can be made with a 48 cm long string? Find the possible pairs of length and breadth of the rectangles.
Solution:
Length of the string to be made into rectangle = 48 cm
∴ Perimeter of the rectangle = 48 cm
2 × (l + b) = 48 cm
l + b = \(\frac{48}{2}\)
l + b = 24 cm
Possible pairs of length and breadth are (1, 23), (2, 22) (3, 21), (4, 20), (5, 19),
(6, 18), (7, 17), (8, 16), (9, 15), (10, 14), (11, 13), (12, 12)
Number of different rectangles = 12.

Question 10.
Draw a square B whose side is twice of the square A. Calculate the perimeters of the squares A and B.
Solution:

Perimeter of A = s + s + s + s units = 4 s units
Perimeter of B = (2s + 2s + 2s + 2s) units
= 8s units = 2 (4s) units.
∴ The perimeter of B is twice the perimeter of A

Question 11.
What will be the area of a new square formed if the side of a square is made one – fourth?
Solution:
Let the side of square is s units then area = (s × s) units²
If the side of the new square is made one fourth then side = \(\left(\frac{1 \times s}{4}\right)\) units
Then area = \(\left(\frac{1 \times s}{4} \times \frac{1 \times s}{4}\right)\) units² = \(\frac{s \times s}{16}=\frac{1}{16}\) (s × s) units²
Area of the new square is reduced to \(\frac{1}{16}\) times to that of original area.

Question 12.
Two plots have the same perimeter. One . is a square of side 10 m and another is a rectangle of breadth 8 m. Which plot has the greater area and by how much?
Solution:
a = 10 m, b = 8 m
Perimeter of the square plot
= 4 a units
= 4 × 10 m
= 40 m
Perimeter of the rectangular plot
40 = 2 (l + b) units
40 = 2 (l + 8) m
40 = 2 l + 16
2 l = 40 – 16
2 l = 24
l = \(\frac{24}{2}\)
l = 12 m
Area of the square plot
= a × a sq units
= 10 × 10 m²
= 100 m²
Area of the rectangular plot
= l × b sq units
= 8 × 12 m²
= 96 m²
Square plot has the greater area by 100 m² – 96 m² – 4 m²

Question 13.
Look at the picture of the house given and find the total area of the shaded portion.

Solution:
Total area of the shaded region = Area of a right triangle + Area of a rectangle
= (\(\frac{1}{2}\) × b × h) + (l × b) cm²
= [(\(\frac{1}{2}\) × 3 × 4) + (9 × 6)] cm²
= (6 + 54) cm² = 60 cm²

Question 14.
Find the approximate area of the flower in the given square grid.

Solution:
No of full squares = 11
No of half squares = 9
Area of 11 full squares
= 11 x 1 cm²
= 11 cm²
Area of 9 half squares
= 9 × \(\frac{1}{2}\) cm²
= 4.5 cm²
Area of the flower = (11 + 4.5) cm²
= 15.5 cm²

Students can download Maths Chapter 3 Perimeter and Area Ex 3.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 3 Perimeter and Area Ex 3.1

Question 1.
The table given below contains some measures of the rectangle. Find the unknown values.

Solution:

(i) Area of the rectangle = (length × breadth) sq unit.
Perimeter of a rectangle = 2(1 + b) units.
l = 5 cm
b = 8 cm
∴ p = 2 (l + b) cm = 2 (5 + 8) cm = 2 × 13 cm
p = 26 cm
Area = (l × b) cm² = (5 × 8) cm²
A = 40 cm²

(ii) l = 13 cm
p = 54 cm
Perimeter = 2 (l + b) units
54 = 2 (13 + b) cm
\(\frac{54}{2}\) = 13 + b
27 = 13 + b
b = 27 – 13
b = 14 cm
Area = l × b sq. unit = 13 × 14 cm²
A = 182 cm²

(iii) b = 15 cm
p = 60 cm
p = 2 (l + b) units
60 = 2 (l + 15) cm
\(\frac{60}{2}\) = l + 15
30 = l + 15
l = 30 – 15 .
l = 15 cm
Area = l × b unit² = 15 × 15 cm² = 225 cm²
A = 225 cm²

(iv) l = 10 m
Area = 120 sq metre
Area = l × b sq.m
120 = 10 × 6
b = \(\frac{120}{10}\)
b = 12 m
Perimeter =2 (l + b) units = 2(10 + 12) units = 2 × 22 m
A = 44 m

(v) b = 4 feet.
Area = 20 sq. feet
Area = l × b sq .feet
20 = l × 4
l = \(\frac{20}{4}\) feet
l = 5 feet
Perimeter = 2 (l + b) units.
p = 2 (5 + 4) feet = 2 × 9
p = 18 feet

Question 2.
The table given below contains some measures of the square. Find the unknown values.

Solution:
(i) 24 cm, 36 cm²
(ii) 25 m, 625 m²
(iii) 7 feet, 28 feet

Question 3.
The table given below contains some measures of the right angled triangle. Find the unknown values.

Solution:

Area of the right triangle = \(\frac{1}{2}\) × (base × height) unit²
(i) b = 20 cm
h = 40 cm
Area = \(\frac{1}{2}\) (b × h) cm² = \(\frac{1}{2}\) × 20 × 40 = 400 cm²
A = 400 cm²

(ii) b = 5 feet
Area = \(\frac{1}{2}\) × b × h unit²
= 20 = \(\frac{1}{2}\) × 5 × h sq. feet
\(\frac{20 \times 2}{5}\) = h
h = 8 feet

(iii) Area = \(\frac{1}{2}\) × (base × height) unit²
24 = \(\frac{1}{2}\) × b × 12 m²
base = \(\frac{24 \times 2}{12}\) m = 4 m
Base = 4m

Question 4.
The table given below contains some measures of the triangle. Find the unknown values.

Solution:
(i) 13 cm
(ii) 6 m
(iii) 8 feet

Question 5.
Fill in the blanks.
(i) 5 cm² = ______ mm²
(ii) 26 m² = ______ cm²
(iii) 8 km² = ______ m²
Solution:
(i) 500
(ii) 260000
(iii) 8000000

Question 6.
Find the perimeter and area of the following shapes.

Solution:
(i) Perimeter = (4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4)
= 48 cm
a = 4 cm
Area of 1 square = 4 × 4 cm²
= 16 cm²
Area of 5 squares = 5 × 16 cm²
= 80 cm²

(ii) Perimeter = (4 + 5 + 4 + 5 + 4 + 5 + 4 + 5)
= 36 cm
Area of 1 triangle = \(\frac{1}{2}\) × b × h sq units
= \(\frac{1}{2}\) × 4 × 5 cm²
= 10 cm²
Area of 4 triangles= 4 × 10 cm²
= 40 cm²
Area of the square = 3 × 3 cm²
= 9 cm²
Total area = (40 + 9) cm²
= 49 cm²

(iii) Perimeter = (15 + 50 + 12 + 13 + 10 + 10 + 40)
= 150 cm
Area of the square = 10 × 10 cm²
= 100 cm²
= 250 cm²
Area of the triangle = \(\frac{1}{2}\) × 12 × 5 cm²
= \(\frac{1}{2}\) × 12⁶ x 5 cm²
= 30 cm²
Total area = (100 + 250 + 30) cm²
= 380 cm²

Question 7.
Find the perimeter and the area of the rectangle whose length is 6 m and breadth is 4m?
Solution:
l = 6 m, b = 4 m Perimeter of the rectangle
= 2 (l + b) units
= 2 (6 + 4) m
= 2 (10) m
= 20 m
Area of the rectangle = l × b sq units
= 4 × 6 m²
= 24 m²

Question 8.
Find the perimeter and area of a square whose side is 8 cm.
Solution:
a = 8 cm
The perimeter of a square
= 4a units
= 4 × 8 cm
= 32 cm
Area of the square = a × a sq units
= 8 × 8 cm²
= 64 cm²

Question 9.
Find the perimeter and the area of right angled triangle whose sides are 6 feet, 8 feet and 10 feet.
Solution:
Perimeter of the triangle
= (a + b + c) units
= (6 + 8 + 10) feet
= 24 feet
Area of the triangle = \(\frac{1}{2}\) × b × h sq units
\(\frac{1}{2}\) × 6³× 8 feet square = 24 sq. feet

Question 10.
Find the perimeter of
(i) A scalene triangle with sides 7 m, 8 m, 10 m.
(ii) An isosceles triangle with equal sides 10 cm each and third side is 7 cm.
(iii) An equilateral triangle with a side of 6 cm.
Solution:
(i) Perimeter of the triangle
= (a + b + c) units
= (7 + 8 + 10) m
= 25

(ii) Perimeter of the triangle
= (10 + 10 + 7) cm
= 27 cm

(iii) Perimeter of the triangle
= (6 + 6 + 6) cm
= 18 cm

Question 11.
The area of a rectangular shaped photo is 820 sq. cm. and its width is 20 cm. What is its length? Also find its perimeter.
Solution:
Given Area = 820 cm²
Width = 20 cm
Area of the rectangle
= l × b sq. units
820 = l × 20
\(\frac{820}{20}\) = l
41 = l
length l = 41 cm
Perimeter = 2(l + b) units
= 2(41 + 20) cm
= 2(61) cm
= 122 cm

Question 12.
A square park has 40 m as its perimeter. What is the length of its side? Also find its area.
Solution:
perimeter = 40 m
4a = 40 m
a = \(\frac{40}{4}\)
Side a = 10 m
Area = a × a sq units
= 10 × 10 m²
= 100 m²

Question 13.
The scalene triangle has 40 cm as its perimeter and whose two sides are 13 cm and 15 cm, find the third side.
Solution:
Let the third side be C
perimeter = (a + b + c) units
40 = 13 + 15 + C
40 = 28 + C
C = 40 – 28
C = 12 units
C = 12 cm

Question 14.
A field is in the shape of a right angled triangle whose base is 25 m and height 20 m. Find the cost of levelling the field at the rate of Rs 45/- per sq.m²
Solution:
b = 25 m, h = 20 m
Area of the triangle = \(\frac{1}{2}\) × bh sq.units
= \(\frac{1}{2}\) × 25 × 20 m²
= 250 m²
Cost of levelling 1 m² = Rs 45
Cost of levelling 250 m² = Rs 45 × 250
= Rs. 11250

Question 15.
A square of side 2 cm is joined with a rectangle of length 15 cm and breadth 10 cm. Find the perimeter of the combined shape.
Solution:

Perimeter of the combined shape = Lengths of the outer boundaries
= (15 + 10 + 2 + 2 + 2 + 13 + 10) cm = 54 cm
Perimeter = 54 cm

Objective Type Questions

Question 16.
The following figures are of equal area. Which figure has the least perimeter?

Solution:
(b)

Question 17.
If two identical rectangles of perimeter 30 cm are joined together, then the perimeter of the new shape will be
(a) equal to 60 cm
(b) less than 60 cm
(c) greater than 60 cm
(d) equal to 45 cm
Solution:
(b) less than 60 cm

Question 18.
If every side of a rectangle is doubled, then its area becomes _____ times
(a) 2
(b) 3
(c) 4
(d) 6
Solution:
(c) 4
2l × 2b = 4l × b

Question 19.
The side of the square is 10 cm. If its side is tripled, then by how many times will its perimeter increase?
(a) 2 times
(b) 4 times
(c) 6 times
(d) 3 times
Solution:
(d) 3 times

Question 20.
The length and breadth of a rectangular sheet of paper are 15 cm and 12 cm respectively. A rectangular piece is cut from one of its corners. Which of the following statement is correct for the remaining sheet?
(a) Perimeter remains the same but the area changes
(b) Area remains the same but the perimeter changes
(c) There will be a change in both area and perimeter
(d) Both the area and perimeter remains the same.
Solution:
(a) Perimeter remains the same but the area changes

Students can download Maths Chapter 1 Numbers Ex 1.3 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 1 Numbers Ex 1.3

Miscellaneous Practice Problems

Question 1.
Every even number greater than 2 can be expressed as the sum of two prime numbers. Verify this statement for every even number upto 16.
Solution:
Even numbers greater then 2 upto 16 are 4, 6, 8, 10, 12, 14 and 16
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7 (or) 5 + 5
12 = 5 + 7
14 = 7 + 7 (or) 3 + 11
16 = 5 + 11 (or) 3 + 13

Question 2.
Is 173 a prime? Why?
Solution:
Yes, 173 is a prime. Because it has only 1 and itself as factors.

Question 3.
For which of the numbers, from n = 2 to 8.
Is 2n – 1 a prime?
Solution:
n = 2 ⇒ 2n – 1 = 2 × 2 – 1
= 4 – 1
= 3 (prime)
n = 3 ⇒ 2n – 1 = 2 × 3 – 1
= 6 – 1
= 5 (prime)
n = 4 ⇒ 2n – 1 = 2 × 4 – 1
= 8 – 1
= 7 (prime)
n = 5 ⇒ 2n – 1 = 2 × 5 – 1
= 10 – 1
= 9 (Not prime)
n = 6 ⇒ 2n – 1 = 2 × 6 – 1
= 12 – 1
= 11 (prime)
n = 7 ⇒ 2n – 1 = 2 × 7 – 1
= 14 – 1
= 13
n = 8 ⇒ 2n – 1 = 2 × 8 – 1
= 16 – 1
= 15 (Not prime)

Question 4.
Explain your answer with the reason for the following statements.
(a) A number is divisible by 9 if it is divisible by 3.
(b) A number is divisible by 6 if it is divisible by 12.
Solution:
(i) False, 42 is divisible by 3 but it is not divisible by 9
(ii) True, 36 is divisible by 12. Also divisible by 6.

Question 5.
Find A as required
(i) The greatest 2 digit number 9 A is divisible by 2.
(ii) The least number 567A is divisible by 3.
(iii) The greatest 3 digit number 9A6 is divisible by 6.
(iv) The number A08 is divisible by 4 and 9.
(v) The number 225A85 is divisible by 11.
Solution:
(i) 98 A = 8
(ii) 5670 A = 0
(iii) 996 A = 9
(iv) 108 A = 1
(v) 225885 A = 8

Question 6.
Numbers divisible by 4 and 6 are divisible by 24. Verify this statement and support your answer with an example.
Solution:
False 12 is divisible by both 4 and 6. But not divisible by 24

Question 7.
The sum of any two successive odd numbers is always divisible by 4. Justify this statement with an example.
Solution:
True 3 + 5 = 8 is divisible by 4.

Question 8.
Find the length of the longest rope that can be used to measure exactly the ropes of length 1 m 20cm, 3m 60 cm and 4 m.
Solution:
1 m 20 cm = 120 cm
3 m 60 cm = 360 cm
4 m = 400 cm
This is a HCF related problem. So, we need to find the HCF of 120,360 and 400.

120 = 2 × 2 × 2 × 3 × 5
360 = 2 × 2 × 2 × 3 × 3 × 5
400 = 2 × 2 × 2 × 2 × 5 × 5
HCF = 2 × 2 × 2 × 5 = 40
The length of the longest rope = 40 cm

Challenge Problems

Question 9.
The sum of three prime numbers is 80. The difference between the two of them is 4. Find the numbers.
Solution:
Given the sum of three prime numbers is 80
The numbers will be one or two-digit prime numbers. Also one of them is 2
Sum of the remaining 2 numbers = 78 [∵ one number must be even]
Also their difference = 4 (given) [Otherwise sum of three odd numbers is odd]
The numbers will be 37 and 41
The required numbers are 2, 37, 41

Question 10.
Find the sum of all the prime numbers between 10 and 20 and check whether that sum is divisible by all the single-digit numbers.
Solution:
Prime numbers between 10 and 20 are 11, 13, 17 and 19
Sum = 11 + 13 + 17 + 19 = 60
60 is divisible by 1, 2, 3, 4, 5 and 6.

Question 11.
Find the smallest number which is exactly divisible by all the numbers from 1 to 9.
Solution:
2520

Question 12.
The product of any three consecutive numbers is always divisible by 6. Justify this statement with an example.
Solution:
Yes. Because one of every two consecutive integers is even and so the product of three consecutive integers is even and divisible by 2.
Also one of every 3 consecutive integers is divisible by 3.
Product of any three consecutive integers is divisible by 6.
Example: 5 × 6 × 7

Question 13.
Malarvizhi, Karthiga, and Anjali are friends and natives of the same village. They work in different places. Malarvizhi comes to her home once in 5 days. Similarly, Karthiga and Anjali come to their homes once in 6 days and 10 days respectively, Assuming that they met each other on the 1st of October, when will all the three meet again?
Solution:
This is an LCM related problem. So, we need to find the LCM of 5, 6, and 10.

LCM = 5 × 2 × 1 × 3 × 1
= 30
All the three will meet again once in 30 days.

Question 14.
In an apartment consisting of 108 floors, two lifts A & B starting from the ground floor, stop at every 3rd and 5th floors respectively. On which floors, will both of them stop together?
Solution:
LCM of 3 and 5 = 3 × 5 = 15
The lifts stop together at floors 15, 30, 45, 60, 75, 90, and 105.

Question 15.
The product of 2 two-digit numbers is 300 and their HCF is 5. What are the numbers?
Solution:
15 × 20 = 300
HCF of 15 and 20 is 5
The numbers are 15 and 20

Question 16.
Find whether the number 564872 is divisible by 88. (use of the test of divisibility rule for 8 and 11 will help)
Solution:
564872 Divisibility by 8
564872 It is divisible by 8
Divisibility by 11
5 + 4 + 7 = 16
6 + 8 + 2 = 16
16 – 16 = 0
It is divisible by both 8 and 11 and hence divisible by 88.

Question 17.
Wilson, Mathan, and Guna can complete one round of a circular track in 10, 15, and 20 minutes respectively. If they start together from at the starting point of 7 am, at what time will they meet together again at the same starting point?
Solution:
This is an LCM related problem. So, we need to find the LCM of 10, 15, and 20.

LCM = 5 × 2 × 1 × 3 × 2 = 60 min
They will meet together again after 60 minutes.
ie. 7.am + 60 minutes = 8 am.