Category: Class 9

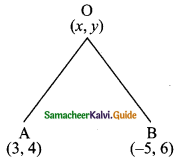
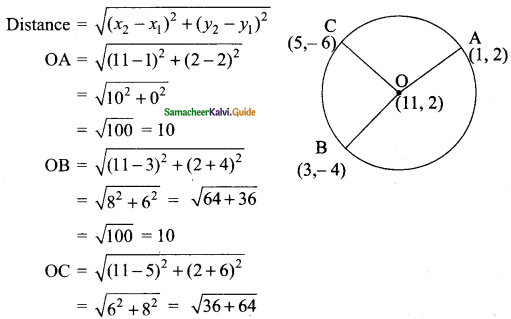
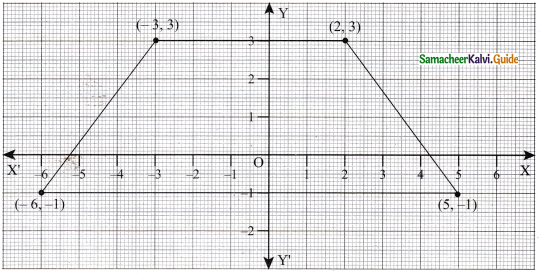
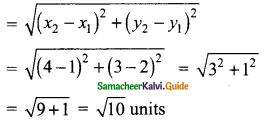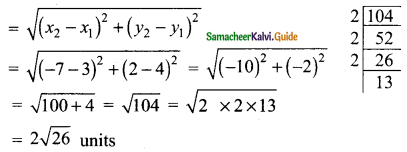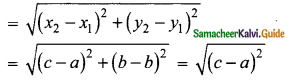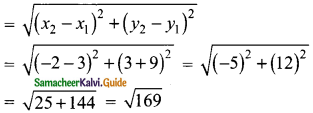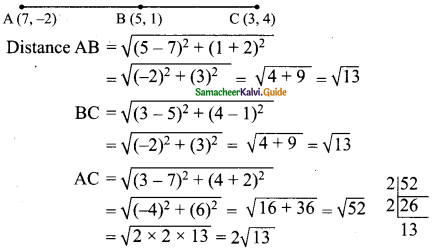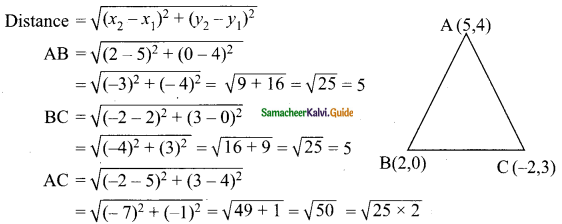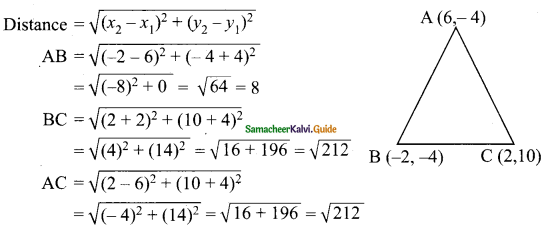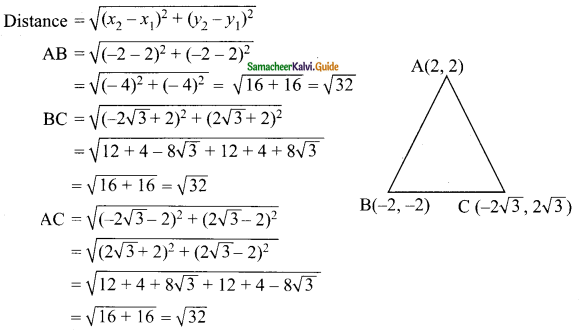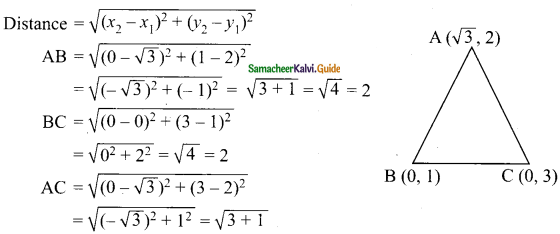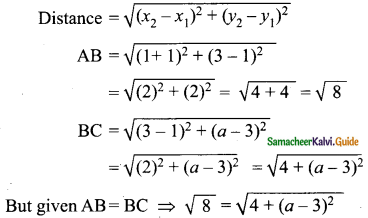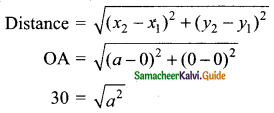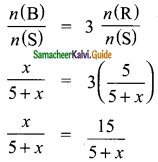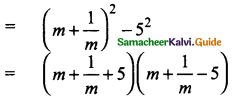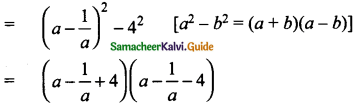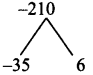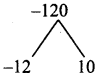Students can download Maths Chapter 5 Coordinate Geometry Ex 5.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.4

Question 1.
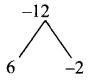
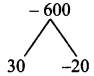
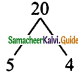
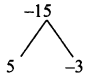
Find the coordinates of the point which divides the line segment joining the points A (4,-3) and B (9,7) in the ratio 3 : 2.
Solution:
A line divides internally in the ratio m : n

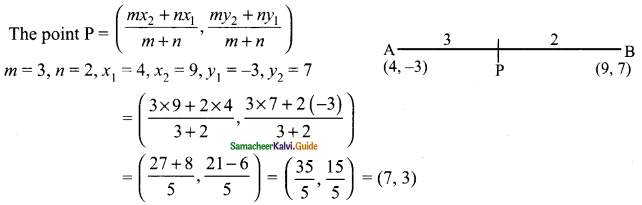
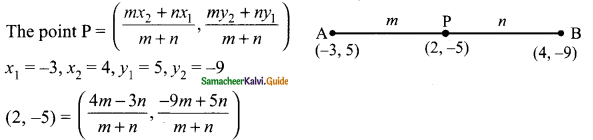
Question 2.
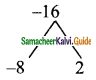
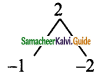
In what ratio does the point P(2, -5) divide the line segment joining A(-3, 5) and B(4, -9).
Solution:
A line divides internally in the ratio m : n

\(\frac{4m-3n}{m+n}\)
= 2
4m – 3n = 2m + 2n
4m – 2m = 3n + 2n
2m = 5n
\(\frac{m}{n}\) = \(\frac{5}{2}\)
m : n = 5 : 2
The ratio is 5 : 2.
and
\(\frac{-9m+5n}{m+n}\)
= -5
-9m + 5 n = -5(m + n)
-9m + 5 n = -5m – 5n
-9m + 5 m = -5n – 5n
-4m = -10
\(\frac{m}{n}\) = \(\frac{10}{4}\) ⇒ \(\frac{m}{n}\) = \(\frac{5}{2}\)
m : n = 5 : 2

Question 3.
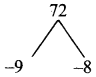
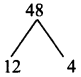
Find the coordinates of a point P on the line segment joining A(1, 2) and B(6, 7) in such a way that AP = \(\frac{2}{5}\) AB.
Solution:
Let the point A (1, 2) and B (6, 7)
AP = \(\frac{2}{5}\) AB
\(\frac{AP}{PB}\) = \(\frac{2}{5}\)
∴ AP = 2; PB = 5 – 2 = 3
A line divides internally in the ratio m : n

Question 4.
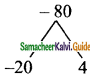
Find the coordinates of the points of trisection of the line segment joining the points A (-5, 6) and B (4, -3).
Solution:
Let P and Q be the point of trisection
so that AP = PB = QB

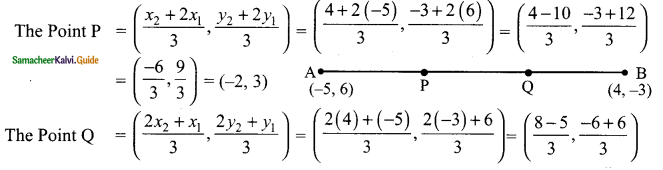
(\(\frac{3}{3}\), \(\frac{0}{3}\)) = (1, 0)
The Point P is (-2, 3), The Point Q is (1, 0)

Question 5.
The line segment joining A(6, 3) and B(-1, -4) is doubled in length by adding half of AB to each end. Find the coordinates of the new end points.
Solution:

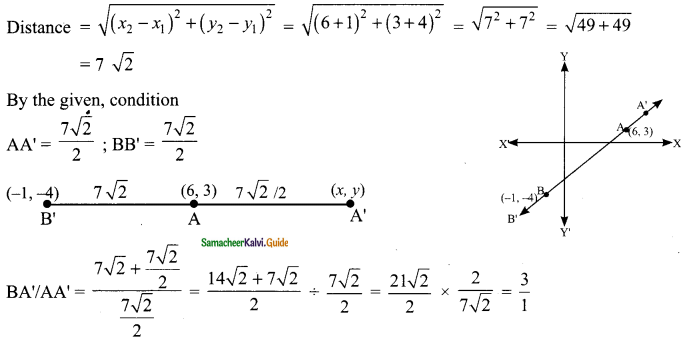
m : n = 3 : 1
A line divides externally in the ratio m : n

∴ BA’ divides in the ratio 2 : 1
A line divides internally in the ratio m : n the point is \(\frac{mx_{2}+nx_{1}}{m+n}, \frac{my_{2}+ny_{1}}{m+n}\)
Let the point A’ be (a, b)

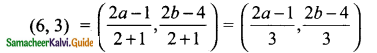
\(\frac{2a-1}{3}\) = 6
2a – 1 = 18
2a = 19
a = \(\frac{19}{2}\)
and
\(\frac{2b-4}{3}\) = 3
2b – 4 = 9
2b = 13
b = \(\frac{13}{2}\)

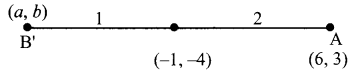
The point A’ is (\(\frac{19}{2}\), \(\frac{13}{2}\))
To find B’
Let B’ be (a, b)
AB = 7√2
BB’ = \(\frac{1}{2}\) × 7√2 = \(\frac{7√2}{2}\)
\(\frac{AB}{BB’}\) = 7√2 ÷ \(\frac{7√2}{2}\) = \(\frac{7√2×2}{7√2}\) = 2
AB’ divides in the ratio 2 : 1
(-1, -4) = \(\frac{2a+6}{3}\), \(\frac{2b+3}{3}\)
\(\frac{2a+6}{3}\) = -1
2a + 6 = -3
2a = -3 – 6
2a = -9
a = –\(\frac{9}{2}\)
and
\(\frac{2b+3}{3}\) = -4
2b + 3 = -12
2b = -12 – 3
2b = -15
b = –\(\frac{15}{2}\) = -1
The point B’ is (-\(\frac{9}{2}\), –\(\frac{15}{2}\))

Question 6.
Using section formula, show that the points A (7, -5), B (9, -3) and C (13, 1) are collinear.
Solution:
If three points are collinear, then one of the points divide the line segment joining the other points in the ratio r : 1. If P is between A and B and \(\frac{AP}{PB}\) = r

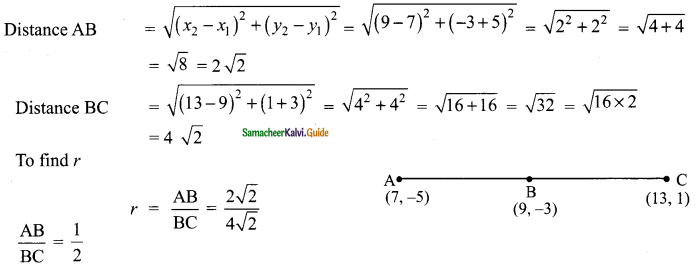
The line divides in the ratio 1 : 2
A line divides internally in the ratio m : n
The point P = (\(\frac{mx_{2}+nx_{1}}{m+n}\), \(\frac{my_{2}+ny_{1}}{m+n}\))
m = 1, n = 2, x₁ = 7, x₂ = 13, y₁ = – 5, y₂ = 1
By the given equation,
The Point B = (\(\frac{13+14}{3}\), \(\frac{1-10}{3}\))
= (\(\frac{27}{3}\), \(\frac{-9}{3}\))
= (9, -3)
∴ The three points A, B and C are collinear.

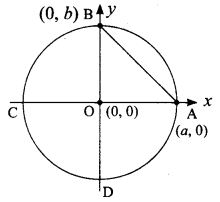
Question 7.
A line segment AB is increased along its length by 25% by producing it to C on the side of B. If A and B have the coordinates (-2, -3) and (2, 1) respectively, then find the coordinates of C.
Solution:
Let the point C be (a, b)

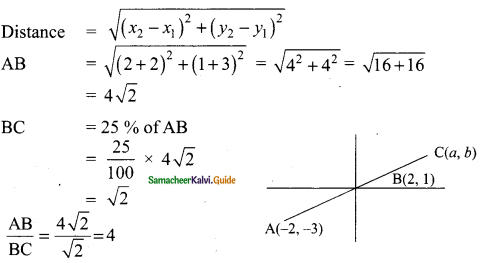
The ratio is 4 : 1 (m : n)
A line divides internally in the ratio m : n

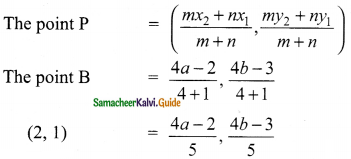
\(\frac{4a-2}{5}\) = 2
4a – 2 = 10
4a = 12
a = \(\frac{12}{4}\) = 3
and
\(\frac{4b-3}{5}\) = 1
4b – 3 = 5
4b = 8
b = \(\frac{8}{4}\) = 2
The co-ordinate of C is (3, 2)

Students can download Maths Chapter 5 Coordinate Geometry Ex 5.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.2

Question 1.
Find the distance between the following pairs of points.
(i) (1, 2) and (4, 3)
Solution:
Distance between the points (1, 2) and (4, 3)

(ii) (3, 4) and (-7, 2)
Solution:
Distance between the points (3,4) and (-7, 2)

(iii) (a, b) and (c, b)
Solution:
Distance between the two points (a, b) and (c, b)

= c – a units

(iv) (3,- 9) and (-2, 3)
Solution:
Distance between the two points (3, -9) and (-2, 3)

= 13 units

Question 2.
Determine whether the given set of points in each case are collinear or not.
(i) (7, -2), (5, 1), (3, 4)
Solution:
To prove that three points are collinear, sum of the distance between two pairs of points is equal to the third pair of points.

AB + BC = AC
\(\sqrt{13}\) + \(\sqrt{13}\) = 2\(\sqrt{13}\) ⇒ 2\(\sqrt{13}\) = 2\(\sqrt{13}\)
∴ The given three points are collinear.

(ii) (a, -2), (a, 3), (a, 0)
Solution:
A (a, -2) B (a, 3) C (a, 0)

√4
= 2
AC + BC = AB ⇒ 2 + 3 = 5
∴ The given three points are collinear.

Question 3.
Show that the following points taken in order to form an isosceles triangle.
(i) A (5, 4), B(2, 0), C (-2, 3)
Solution:

= 5√2
AB = BC = 5. (Two sides are equal)
∴ ABC is an isosceles triangle.

(ii) A (6, -1), B (-2, -4), C (2, 10)
Solution:

BC = AC = \(\sqrt{212}\) (TWO sides are equal)
∴ ABC is an isosceles triangle.

Question 4.
Show that the following points taken in order to form an equilateral triangle in each case.
(i) A(2, 2), B(-2, -2), C(-2√3, 2√3)
Solution:

AB = BC = AC (Three sides are equal)
∴ ABC is an equilateral triangle.

(ii) A(√3, 2), B (0, 1), C(0, 3)
Solution:

= √4
= 2
AB = BC = AC (Three sides are equal)
∴ ABC is an equilateral triangle.

Question 5.
Show that the following points taken in order to form the vertices of a parallelogram.
(i) A(-3, 1), B(-6, -7), C (3, -9) and D(6, -1)
Solution:

AB = CD = \(\sqrt{73}\) and BC = AD = \(\sqrt{85}\) (Opposite sides are equal)
∴ ABCD is a parallelogram.

(ii) A (-7, -3), B(5, 10), C(15, 8) and D(3, -5)
Solution:

AB = CD = \(\sqrt{313}\) and BC = AD = \(\sqrt{104}\) (Opposite sides are equal)
∴ ABCD is a parallelogram.

Question 6.
Verify that the following points taken in order to form the vertices of a rhombus.
(i) A(3, -2), B (7, 6),C (-1, 2) and D (-5, -6)
Solution:

AB = BC = CD = AD = \(\sqrt{80}\). All the four sides are equal.
∴ ABCD is a rhombus.

(ii) A (1, 1), B (2, 1),C (2, 2) and D (1, 2)
Solution:

AB = BC = CD = AD = 1. All the four sides are equal.
∴ ABCD is a rhombus.

Question 7.
A (-1, 1), B (1, 3) and C (3, a) are points and if AB = BC, then find ‘a’.
Solution:

4 + (a – 3)² = 8
(a – 3)² = 8 – 4
(a – 3)² = 4
a – 3 = √4
= ± 2
a – 3 = 2 (or) a – 3 = -2
a = 2 + 3 (or) a = 3 – 2
a = 5 (or) a = 1
∴ The value of a = 5 or a = 1.

Question 8.
The abscissa of a point A is equal to its ordinate, and its distance from the point B(1, 3) is 10 units, What are the coordinates of A?
Solution:
Let the point A be (a, a) B is (1, 3)
Distance AB = 10 (Given)
By distance formula \(\sqrt{(a – 1 )² + (a – 3)²}\) = 10
Simplifying 2a² – 8a + 10 = 100
a² – 4a – 45 = 0
(a – 9)(a + 5) = 0
⇒ a = – 5; A = (-5, -5)
a = 9; A = (9, 9)

Question 9.
The point (x, y) is equidistant from the points (3, 4) and (-5, 6). Find a relation between x and y.
Solution:
Let the point O be (x, y), A be (3, 4) and B be (-5, 6).

Distance = \(\sqrt{(x_{2} – x_{1})² + (y_{2} – y_{1})²}\)
Given ,OA = OB
\(\sqrt{(x – 3 )² + (y – 4)²}\) = \(\sqrt{(x + 5 )² + (y – 6)²}\)
Squaring on both sides
(x – 3)² + (y – 4)² = (x + 5)² + (y – 6)²
x² – 6x + 9 + y² – 8y + 16 = x² + 10x + 25 + y² – 12y + 36
x² + y² – 6x – 8y + 25 = x² + y² + 10x – 12y + 61
6x – 10x – 8y + 12y = 61 – 25 ⇒ -16x + 4y = 36
÷ 4 ⇒ -4x + y = 9
∴ The relation between x and y is y = 4x + 9

Question 10.
Let A(2,3) and B(2, -4) be two points. If P lies on the x-axis, such that AP = \(\frac{3}{7}\) AB, find the coordinates of P.
Solution:
Given points are A(2, 3) and B(2, -4)
The point P lies on the x-axis.
∴ The point P is (x, 0)

16x² – 64x + 208 = 9x² – 36x + 180
16x² – 9x² – 64x + 36x + 208 – 180 = 0
7x² – 28x + 28 = 0
x² – 4x + 4 = 0
(x – 2)² = 0
x – 2 = 0
x = 2
∴ The point P is (2, 0)

Question 11.
Show that the point (11, 2) is the centre of the circle passing through the points (1, 2), (3, -4) and (5, -6)
Solution:

\(\sqrt{100}\)
= 10
OA = OB = OC = 10
O is the centre of the circle passing through A, B and C.

Question 12.
The radius of a circle with centre at origin is 30 units. Write the coordinates of the points where the circle intersects the axes. Find the distance between any two such points.
Solution:

Radius of the circle = 30 units. The point O is (0, 0).
Let a intersect the x-axis and b intersect the y-axis.
∴ The point A is (a, 0) and B is (0, b)

Squaring on both sides
30² = a²
∴ a = 30
The point A is (30, 0)
OB = \(\sqrt{(0 – 0)² + (b – 0)²}\)
= \(\sqrt{0² + b²}\)
30 = \(\sqrt{b²}\)
Squaring on both sides
30² = b²
∴ b = 30
The point B is (0, 30)

= 30√2
∴ Distance between the two points = 30√2

Students can download Maths Chapter 5 Coordinate Geometry Ex 5.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.1

Question 1.
Plot the following points in the coordinate system and identify the quadrants P(-7, 6), Q(7, -2), R(-6, -7), S(3, 5) and T(3, 9)
Solution:

(i) P(-7, 6) lies in the II quadrant because the x-coordinate is negative and y-coordinate is positive.
(ii) Q(7, -2) lies in the IV quadrant because the x-coordinate is positive and y-coordinate is negative.
(iii) R(-6, -7) lies in the III quadrant because the x-coordinate is negative and y-coordinate is negative.
(iv) S(3, 5) lies in the I quadrant because the x-coordinate is positive and y-coordinate is also positive.
(v) T(3, 9) lies in the I quadrant because the x-coordinate is positive and y-coordinate is also positive.

Question 2.
Write down the abscissa and ordinate of the following.
(i) P
(ii) Q
(iii) R
(iv) S

Solution:
(i) P is (-4, 4) [-4 is abscissa and 4 is ordinate]
(ii) Q is (3, 3) [3 is abscissa and 3 is ordinate]
(iii) R is (4, -2) [4 is abscissa and -2 is ordinate]
(iv) S is (-5, -3) [-5 is abscissa and -3 is ordinate]

Question 3.
Plot the following points in the coordinate plane and join them. What is your conclusion about the resulting figure?
(i) (-5, 3) (-1, 3) (0, 3) (5, 3)
Solution:

Straight line parallel to x-axis.

(ii) (0, -4) (0, -2) (0, 4) (0, 5)
Solution:

The line is on the y-axis.

Question 4.
Plot the following points in the coordinate plane. Join them in order. What type of geometrical shape is formed?
(i) (0, 0) (-4, 0) (-4, -4) (0, -4)
Solution:

The geometrical shape of the figure is square.

(ii) (-3, 3) (2, 3) (-6, -1) (5, -1)
Solution:

The shape of the geometrical figure is Trapezium.

Students can download Maths Chapter 9 Probability Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 9 Probability Additional Questions

I. Choose the Correct Answer

Question 1.
Which of the following cannot be taken as probability of an event?
(a) 0
(b) 0.35
(c) \(\frac{7}{20}\)
(d) –\(\frac{7}{20}\)
Solution:
(d) –\(\frac{7}{20}\)

Question 2.
A letter is chosen at random from the word “MATHEMATICS” the probability of getting a vowel is ……..
(a) \(\frac{2}{11}\)
(b) \(\frac{3}{11}\)
(c) \(\frac{4}{11}\)
(d) \(\frac{5}{11}\)
Solution:
(c) \(\frac{4}{11}\)

Question 3.
If P(A) =\(\frac{1}{3}\) then P(A)’ is ………
(a) \(\frac{1}{3}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{3}{2}\)
(d) 1
Solution:
(b) \(\frac{2}{3}\)

Question 4.
An integer is chosen from the first twenty natural number, the probability that it is a prime number is ……..
(a) \(\frac{1}{5}\)
(b) \(\frac{2}{5}\)
(c) \(\frac{3}{5}\)
(d) \(\frac{4}{5}\)
Solution:
(b) \(\frac{2}{5}\)

Question 5.
From a well shuffled pack of 52 cards one card is drawn at random. The probability of getting not a king is ………
(a) \(\frac{12}{13}\)
(b) \(\frac{1}{13}\)
(c) \(\frac{4}{13}\)
(d) \(\frac{2}{13}\)
Solution:
(a) \(\frac{12}{13}\)

II. Answer the Following Questions

Question 6.
1500 families with 2 children were selected randomly and the following data were recorded.

Compute the probability of a family chosen at random having one girl.
Solution:
Total number of families = 1500
∴ n(S) = 1500
Let E be the event of getting one girl
n(E) = 814
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{814}{1500}\)
= \(\frac{407}{750}\)

Question 7.
The record of weather station shows that out of the part 250 consecutive days its whether forecast were correct 175 time. What is the probability that it was not correct on a given data?
Solution:
n(S) = 250
Let E be the event of getting whether forecast were correct
n(E) = 175
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{175}{250}\)
= \(\frac{7}{10}\)
Forecast was not correct on a given day = 1 – P(E)
= 1 – \(\frac{7}{10}\)
= \(\frac{10-7}{10}\)
= \(\frac{3}{10}\)

Question 8.
If A coin is tossed 200 times and is found that a tail comes up for 120 times. Find the probability of getting a tail.
Solution:
Number of trials = 200
n(S) = 200
Let E be the event of getting a tail
n(E) = 120
p(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{120}{200}\)
= \(\frac{12}{20}\)
= \(\frac{3}{5}\)

Question 9.
A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball from the bag is thrice that of drawing a red ball, then find the number of blue balls in the bag.
Solution:
Let the number of blue balls be “x”
Total number of balls = 5 + x
∴ n(S) = 5 + x
Let B be the event of drawing a blue ball and R be the event of drawing a red ball
Given P(B) = 3P(R)

∴ x = 15
Number of blue balls = 15

Question 10.
Find the probability that a non leap year selected at random will have 53 fridays.
Solution:
No. of days in a non leap year = 365 days
This year contain 52 weeks and one day
Sample space = {Sun, Mon, Tue, Wed, Thu, Fri, Sat}
n(S) = 7
Let A be the event of getting a friday
n(A) = 1
P(A) = \(\frac{n(A)}{n(S)}\)
= \(\frac{1}{7}\)

Students can download Maths Chapter 3 Algebra Ex 3.5 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.5

Question 1.
Factorise the following expressions:
(i) 2a² + 4a²b + 8a²c
(ii) ab – ac – mb + mc
Solution:
(i) 2a² + 4a²b + 8a²c = 2a²(1 + 2b + 4c)
(ii) ab – ac – mb + mc = a(b – c) – m(b – c)
= (b – c) (a – m)

Question 2.
Factorise the following expressions:
(i) x² + 4x + 4
(ii) 3a² – 24ab + 48b²
(iii) x⁵ – 16x
(iv) m² + \(\frac{1}{m^2}\) – 23
(v) 6 – 216x²
(vi) a² + \(\frac{1}{a^2}\) – 18
Solution:
(i) x² + 4x + 4 = x² + 2 × x × 2 + 2² [a² + 2ab+ b² = (a + b)²]
= (x + 2)²

(ii) 3a² – 24ab + 48b² = 3[a² – 8ab + 16b²]
= 3[a² – 2 × a × 4b + (4b)²]
= 3(a- 4b)² [a² – 2ab + b² = (a – b)²]

(iii) x⁵ – 16x = x[x⁴ – 16] [a² – b² = (a + b) (a – b)]
= x[(x²)² – 4²]
= x(x² + 4) (x² – 4)
= x(x² + 4) (x² – 2²)
= x(x²+ 4) (x + 2) (x – 2)

(iv) m² + \(\frac{1}{m^2}\) – 23 = [Add + 2 and – 2 to make -23 as -25]
= m² + \(\frac{1}{m^2}\) + 2 – 2 – 23 = m² + \(\frac{1}{m^2}\) + 2 – 25
= m² + \(\frac{1}{m^2}\) + 2 × m × \(\frac{1}{m}\) – 5²

(v) 6 – 216x² = 6[1 – 36x²]
= 6[1 – (6x)²] [a² – b² = (a + b)(a – b)]
= 6(1 + 6x) (1 – 6x)

(vi) a² + \(\frac{1}{a^2}\) – 18 = a² + \(\frac{1}{a^2}\) – 2 + 2 – 18
(add -2 and +2 to make 18 as 16)
= a² + \(\frac{1}{a^2}\) – 2 × a × \(\frac{1}{a}\) – 16 [a² + b² – 2ab = (a-b)(a- b)²]

Question 3.
Factorise the following expressions:
(i) 4x² + 9y² + 25z² + 12xy + 30yz + 20xz
Solution:
[a² + b² + c² + 2ab + 2bc + 2ac = (a + b + c)²]
= (2x)² + (3y)² + (5z)² + 2(2x) (3y) + 2(3y) (5z) + 2(5z) (2x)
= (2x + 3y + 5z)²

(ii) 25x² + 4y² + 9z² – 20xy + 12yz – 30xz
Solution:
= (5x)² + (2y)² + (3z)² + 2(5x) (-2y) + 2(-2y) (- 3z) + 2(-3z) (5x)
= (5x – 2y – 3z)²

Question 4.
Factorise the following expressions:
(i) 8x³ + 125y³
(ii) 27x³ – 8y³
(iii) a⁶ – 64
Solution:
(i) 8x³ + 125y³ = (2x)³ + (5y)³ [a³ + b³ = (a + b)(a² – ab + b²)
= (2x + 5y) [(2x)² – (2x) (5y) + (5y)²]
= (2x + 5y) (4x² – 10xy + 25y²)

(ii) 27x³ – 8y³ = (3x)³ – (2y)³ [a³ – b³ = (a – b)(a² + ab + b²)]
= (3x – 2y) [(3x)² + (3x) (2y) + (2y)²]
= (3x – 2y) (9x² + 6xy + Ay²)

(iii) a⁶ – 64 = a⁶ – 2⁶
= (a²)³ – (22)³ [a² – b³ = (a- b) + (a² + ab + b²)]
= (a² – 22) [(a²)² + (a²) (2²) + (2²)²]
= (a + 2) (a – 2) (a⁴ + 4a² + 16)
= (a + 2) (a – 2) [(a²)² + 4² + 8a² – 4a²]
= (a + 2)(a- 2) [(a² + 4)² – (2a)²] {a² – b² = (a + b) (a – b)}
= (a + 2) (a – 2) [(a² + 4 + 2a) (a² + 4 – 2a)
= (a + 2) (a – 2) (a² + 2a + 4) (a² – 2a + 4)

Question 5.
Factorize the following
(i) x³ + 8y³ + 6xy – 1
(ii) l³ – 8m³ – 27n³ – 18lmn
Using the formula [a³ + b³ + c³ – 3abc] = (a + b + c) (a² + b² + c² – ab – bc – ac)
Solution:
(i) x³ + 8y² + 6xy – 1 = -(-x³ – 8y³ – 6xy + 1)
= – (-x³ – 8y³ + 1 – 6xy)
= -[(-x)³ + (-2y)³ + 1 – 3(x) (2y) (1)]
= -[-x – 2y + 1] [(-x)² + (-2y)² + 1² – (-x) (-2y) – (-2y) (1) – (1) (-x)]
= (x + 2y – 1)(x² + 4y² + 1 – 2xy + 2y + x)

(ii) l³ – 8m³ – 27n³ – 18lmn
= l³ + (-2m)³ + (-3n)² – 3(l) (-2m) (-3n)
= (l – 2m – 3n) [l² + (-2m)² + (-3n)² -1 (-2m)] – (-2m)(-3n) – (-3n)(l)
= (l – 2m – 3n) (l² + 4m² + 9n² + 2lm – 6mn + 3ln)

Students can download Maths Chapter 1 Set Language Ex 1.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.4

Question 1.
If P = {1, 2, 5, 7, 9}, Q = {2, 3, 5, 9, 11}, R = {3, 4, 5, 7, 9} and S = {2, 3, 4, 5, 8} then find
(i) (P∪Q)∪R
(ii) (P∩Q)∩S
(m) (Q∩S)∩R
Solution:
P = {1, 2, 5, 7, 9}; Q = {2, 3, 5, 9, 11}; R = {3, 4, 5, 7, 9} and S = {2, 3, 4, 5, 8}
(i) P∪Q = {1, 2, 5, 7, 9} ∪ {2, 3, 5, 9, 11}
= {1, 2, 3, 5, 7, 9, 11}
(P∪Q)∪R = {1, 2, 3, 5, 7, 9, 11} ∪ {3, 4, 5, 7, 9}
= {1, 2, 3, 4, 5, 7, 9, 11}

(ii) P∩Q = {1, 2, 5, 7, 9} ∩ {2, 3, 5, 9, 11}
= {2, 5, 9}
(P∩Q)∩S = {2, 5, 9} ∩ {2, 3, 4, 5, 8}
= (2, 5}

(iii) Q∩S = {2, 3, 5, 9, 11} ∩ {2, 3, 4, 5, 8}
= {2, 3, 5}
(Q∩S)∩R = {2, 3, 5} ∩ {3, 4, 5, 7, 9}
= {3, 5}

Question 2.
Test for the commutative property of union and intersection of the sets
P = {x : x is a real number between 2 and 7} and
Q = {x : x is an irrational number between 2 and 7}
Solution:
P is a real number set
Q is a set of irrational number
∴ Q⊂P
P∪Q= Q∪P = P
∴ Union of sets is commutative.
P∩Q = Q∩P = Q
∴ Intersection of sets is commutative.

Question 3.
If A = {p, q, r, s}, B = {m, n, q, s, t} and C = {m, n, p, q, s}, then verify the associative property of union of sets.
Solution:
When union of sets is associative
A∪(B∪C) = (A∪B)∪C
(B∪C) = {m, n, q, s, t) ∪ {m, n, p, q, s}
= {m, n, p, q, s, t}
A∪(B∪C) = {p, q, r, s} ∪ {m, n, p, q, s, t}
= {m, n, p, q, r, s, t} ……..(1)
(A∪B) = {p, q, r, s} ∪ {m, n, q, s, t}
= {m, n, p, q, r, s, t}
(A∪B)∪C = {m, n, p, q, r, s, t} ∪ {m, n, p, q, s}
= {m, n, p, q, r, s, t} ……….(2)
From (1) and (2) it is verified that A∪(B∪C) = (A∪B)∪C

Question 4.
Verify the associative property of intersection of sets for A = {-11, √2, √5, 7},
B = {√3, √5, 6, 13} and C = {√2, √3, √5, 9}.
Solution:
When intersection of sets is associative
A∩(B∩C) = (A∩B)∩C
(B∩C) = {√3, √5, 6, 13} ∩ {√2, √3, √5, 9}
= {√3, √5}
A∩(B∩C) = {-11, √2, √5, 7} ∩ {√3, √5}
{√5} ………(i)
(A∩B) = {-11, √2, √5, 7} ∩ {√3, √5 ,6, 13}
= {√5}
(A∩B)∩C = {√5} n {√2, √3, √5, 9}
= {√5}……..(2)
From (1) and (2) it is verified that A∩(B∩C) = (A∩B)∩C

Question 5.
If A={ x : x = 2ⁿ, n ∈ W and n < 4}, B = {x : x = 2n, n ∈ N and n ≤ 4} and C = {0, 1, 2, 5, 6}, then verify the associative property of intersection of sets.
Solution:
A = {x : x = 2ⁿ, n ∈ W and n < 4}
A = {1, 2, 4, 8}
B = {x : x = 2n, n ∈ N and n ≤ 4}
B = {2, 4, 6, 8}
C ={0, 1, 2, 5, 6}
When intersection of sets is associative
A∩(B∩C) = (A∩B)∩C
(B∩C) = {2, 4, 6, 8} ∩ {0, 1, 2, 5, 6}
= {2, 6}
A∩(B∩C)= {1 ,2, 4, 8} ∩ {2, 6}
= {2}……….(1)
(A∩B) = {1, 2, 4, 8} ∩ {2, 4, 6, 8}
= {2, 4, 8}
(A∩B)∩c= {2, 4, 8} n {0, 1, 2, 5, 6}
= {2}………..(2)
From (1) and (2) we get A∩(B∩C) = (A∩B)∩C

Students can download Maths Chapter 1 Set Language Ex 1.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.3

Question 1.
Using the given venn diagram, write the elements of

(i) A
(ii) B
(iii) A∪B
(iv) A∩B
(v) A – B
(vi) B – A
(vii) A’
(viii) B’
(ix) U
Solution:
(i) A = {2, 4, 7, 8, 10}
(ii) B = {3, 4, 6, 7, 9, 11}
(iii) A∪B = {2, 3, 4, 6, 7, 8, 9, 10, 11}
(iv) A∩B = {4, 7}
(v) A – B = {2, 8, 10}
(vi) B – A = {3, 6, 9, 11}
(vii) A’ = {1, 3, 6, 9, 11, 12}
(viii) B’ = {1,2, 8, 10, 12}
(ix) U = {1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12}

Question 2.
Find A∪B, A∩B, A – B and B – A for the following sets
(i) A = {2, 6, 10, 14} and B = {2, 5, 14, 16}
Solution:
A∪B = {2, 6, 10, 14} ∪ {2, 5, 14, 16}
= {2, 5, 6, 10, 14, 16}
A∩B = {2, 6, 10, 14} ∩ {2, 5, 14, 16}
= {2, 14}
A – B = {2, 6, 10, 14} – {2, 5, 14, 16}
= {6, 10}
B – A = {2, 5, 14, 16} – {2, 6, 10, 14}
= {5, 16}

(ii) A = {a, b, c, e, u} and B = {a, e, i, o, u}
Solution:
A∪B = {a, b, c, e, u} ∪ {a, e, i, o, u}
= {a, b, c, e, i, o, u}
A∩B = {a, b, c, e, u} ∩ {a, e, i, o, u}
= {a, e, u}
A – B = {a, b, c, e, u} – {a, e, i, o, u}
= {b, c}
B – A = {a, e, i, o, u} – {a, b, c, e, u}
= {i, o}

(iii) A = {x : x ∈ N, x ≤ 10} and B = {x : x ∈ W, x < 6}
Solution:
A = {1, 2, 3, 4, 5, 6,7, 8, 9, 10} and B = {0, 1, 2, 3, 4, 5}
A∪B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ∪ {0, 1, 2, 3, 4, 5}
= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A∩B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ∩ {0, 1, 2, 3, 4, 5}
= {1, 2, 3, 4, 5}
A – B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – {0, 1, 2, 3, 4, 5}
= {6, 7, 8, 9, 10}
B – A = {0, 1, 2, 3, 4, 5} – {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
= {0}

(iv) A = Set of all letters in the word “mathematics” and B = Set of all letters in the word “geometry”
Solution:
A = {m, a, t, h, e, i, c, s}
B = {g, e, o, m, t, r, y}
A∪B = {m, a, t, h, e, i, c, s} ∪ {g, e, o, m, t, r, y}
= {a, c, e, g, h, i, m, o, r, s, t, y}
A∩B= {m, a, t, h, e, i, c, s} ∩ {g, e, o, m, t, r, y}
= {e, m, t}
A – B = {m, a, t, h, e, i, c, 5} – {g, e, o, m, t, r, y}
= {a, c, h, i, s}
B -A = {g, e, o, m, t, r, y} – {m, a, t, h, e, i, c, s}
= {g, o, r, y}

Question 3.
If U = {a, b, c, d, e, f, g, h), A = {b, d, f, h} and B = {a, d, e, h}, find the following sets.
(i) A’
Solution:
A’ = U – A
= {a, b, c, d, e, f, g, h} – {b, d, f, h)
= {a, c, e, g}

(ii) B’
Solution:
B’ = U – B
= {a, b, c, d, e, f, g, h} – {a, d, e, h}
= {b, c, f, g}

(iii) A’∪B’
Solution:
A’∪B’ = {a, c, e, g} ∪ {b, c,f, g}
= {a, b, c, e, f, g}

(iv) A’∩B’
Solution:
A’∩B’ = {a, c, e, g} ∩ {b, c, f, g}
= {c, g}

(v) (A∪B)’
Solution:
A∪B = {b, d, f, h} ∪ {a, d, e, h}
= {a, b, d, e, f, h}
(A∪B)’ = U – (A∪B)
= {a, b, c, d, e, f, g, h} – {a, b, d, e, f, h}
= {c, g}

(vi) (A∩B)’
Solution:
(A∩B) = {b, d, f, h) ∩ {a, d, e, h)
= {d, h}
(A∩B)’ = U – (A∩B)
= {a, b, c, d, e, f, g, h} – {d, h}
= {a, b, c, e, f, g}

(vii) (A’)’
Solution:
A’ = {a, c, e, g}
(A’)’ = U – A’
= {a, b, c, d, e, f, g, h} – {a, c, e, g}
= {b, d, f, h}

(viii) (B’)’
Solution:
B’ = {b, c, f, g}
(B’)’ = U – B’
= {a, b, c, d, e, f, g, h) – {b, c, f, g)
= {a, d, e, h}

Question 4.
Let U = {0, 1, 2, 3, 4, 5, 6, 7} A = {1, 3, 5, 7} and B = {0, 2, 3, 5, 7}, find the following sets.
(i) A’
Solution:
A’ = U – A
= {0, 1, 2, 3, 4, 5, 6, 7} – {1, 3, 5, 7}
= {0, 2, 4, 6}

(ii) B’ = U – B
Solution:
= {0, 1, 2, 3, 4, 5, 6, 7} – {0, 2, 3, 5, 7}
= {1, 4, 6}

(iii) A’∪B’
Solution:
A’∪B’ = {0, 2, 4, 6,}∪{1, 4, 6}
{0, 1, 2, 4, 6}

(iv) A’∩B’
Solution:
A’∩B’ = {0, 2, 4, 6,}∩{1, 4, 6}
{4, 6}

(v) (A∪B)’
Solution:
A∪B = {1, 3, 5, 7}∪{0, 2, 3, 5, 7}
= {0, 1, 2, 3, 5, 7}
(A∪B)’ = U – (A∪B)
{0, 1, 2, 3, 4, 5, 6, 7} – {0, 1, 2, 3, 5, 7}
{4, 6}

(vi) (A∩B)’
Solution:
(A∩B)= {1, 3, 5, 7}∩{0, 2, 3, 5, 7}
= {3, 5, 7}
(A∩B)’ = U – (A∩B)
= {0, 1, 2, 3, 4, 5, 6, 7} – {3, 5, 7}
= {0, 1, 2, 4, 6}

(vii) (A’)’
A’ = {0, 2, 4, 6}
(A’)’ = U – A’
= {0, 1, 2, 3, 4, 5, 6, 7} – {0, 2, 4, 6}
= {1, 3, 5, 7}

(viii) (B’)’
B’ = {1, 4, 6}
(B’)’ = {0, 1, 2, 3, 4, 5, 6, 7} – {1, 4, 6}
= {0, 2, 3, 5, 7}

Question 5.
Find the symmetric difference between the following sets.
(i) P = {2, 3, 5, 7, 11} and Q = {1, 3, 5, 11}
Solution:
Use anyone of the formula to find A & B
AΔB = (A – B)∪(B – A) or AΔB = (A∪B) – (A∩B)
P∪Q = {2, 3, 5, 7, 11} ∪ {1,3,5, 11}
= {1, 2, 3, 5, 7, 11}
P∩Q = {2, 3, 5, 7, 11}∩{1, 3, 5,11}
= {3, 5, 11}
PΔQ = (P∪Q) – (P∩Q)
= {1, 2, 3, 5, 7, 11} – {3, 5, 11}
= {1, 2, 7}
(OR)
P – Q = {2, 3, 5, 7, 11} – {1, 3, 5, 11}
= {2,7}
Q – P = {1, 3, 5, 11} – {2, 3, 5, 7, 11}
= {1}
PΔQ = (P – Q)∪(Q – P)
= {2, 7} ∪ {1}
= {1, 2, 7}

(ii) R = {l, m, n, o, p} and S = {j, l, n, q}
Solution:
R- S = {l, m, n, o, p} – {j, l, n, q}
= {m, o, p}
S – R = {j, l, n, q} – {l, m, n, o, p}
= {j, q}
RΔS = (R – S)∪(S – R)
= {m, o, p} – {j, q} = {j, m, o, p, q)
(OR)
R∪S = {l, m, n, o, p} ∪ {j,l,n,q}
= {l, m, n, o, p, j, q}
R∩S = {l, m, n, o,p} ∩ {j, l, n, q}
= {l, n}
RΔS = (R∪S) – (R∩S)
= {l, m, n, o, p, j, q} – { l, n}
= {m, o, p, j, q}

(iii) X = {5, 6, 7} and Y = {5, 7, 9, 10}
Solution:
X∪Y = {5, 6, 7} ∪ {5, 7, 9, 10}
= {5 ,6, 7, 9, 10}
X∩Y = {5, 6, 7} ∩ {5, 7, 9, 10}
= {5, 7}
XΔY = (X∪Y) – (X∩Y)
= {5, 6, 7, 9, 10} – {5, 7}
= {6, 9, 10}
OR
X – Y = {5, 6, 7} – {5, 7, 9, 10} = {6}
Y – X = {5, 7, 9, 10} – {5, 6, 7} = {9, 10}
XΔY = (X – Y) ∪ (Y – X)
= {6}∪{9, 10}
= {6, 9, 10}

Question 6.
Using the set symbols, write down the expressions for the shaded region in the following

Solution:

Question 7.
Let A and B be two overlapping sets and the universal set U. Draw appropriate Venn diagram for each of the following,
(i) A∪B
(ii) A∩B
(iii) (A∩B)’
(iv) (B – A)’
(v) A’∪B’
(Vi) A’∩B’
(vii) What do you observe from the Venn diagram (iii) and (v)?
Solution:
(i) A∪B

(ii) A∩B

(iii) (A∩B)’

(iv) (B – A)’

(v) A’∪B’

(Vi) A’∩B’

(vii) What do you observe from the diagram (iii) and (v)?
From the diagram (iii) and (v) we get (A∩B)’ = A’∪B’

Students can download Maths Chapter 3 Algebra Ex 3.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.3

Question 1.
Check whether p(x) is a multiple of g(x) or not.
(i) p(x) = x³ – 5x² + 4x – 3; g(x) = x – 2
Solution:
p(x) = x³ – 5x² + 4x – 3
P(2) = (2)³ – 5(2)² + 4(2) – 3
= 8 – 5(4) + 8 – 3
= 8 – 20 + 8 – 3
= 16 – 23
= -7
p{2) ≠ 0
∴ p(x) is not a multiple of g(x)

Question 2.
By remainder theorem, find the remainder when p(x) is divided by g(x) where,
(i) p(x) = x³ – 2x² – 4x – 1; g(x) = x + 1
Solution:
p(x) = x³ – 2x² – 4x – 1
p(-1) = (-1)³ – 2(-1)² – 4(-1) – 1
= 1 – 2 + 4 – 1
= 4 – 4 = 0
∴ The remainder = 0

(ii) p(x) = 4x³ – 12x² + 14x – 3; g(x) = 2x – 1
Solution:
p(x) = 4x³ – 12x² + 14x – 3

= 4 × \(\frac{1}{8}\) – 12 × \(\frac{1}{4}\) + 14 × \(\frac{1}{2}\) – 3
= \(\frac{1}{2}\) – 3 + 7 – 3
= \(\frac{1}{2}\) – 6 + 7
= \(\frac{1}{2}\) + 1
= \(\frac{3}{2}\)
∴ The reminder is \(\frac{3}{2}\)

(iii) p(x) = x³ – 3x² + 4x + 50; g(x) = x – 3
Solution:
p(x) = x³ – 3x² + 4x + 50
p(3) = 3³ – 3(3)² + 4(3) + 50
= 27 – 27 + 12 + 50
= 62
The remainder is 62.

Question 3.
Find the remainder when 3x³ – 4x² + 7x – 5 is divided by (x + 3)
Solution:
p(x) = 3x³ – 4x² + 7x – 5
When it is divided by x +3,
p(-3) = 3(-3)³ – 4(-3)² + 7(-3) – 5
= 3(-27) – 4(9) – 21 – 5
= -81 – 36 – 21 – 5
= -143
The remainder is -143.

Question 4.
What is the remainder when x²⁰¹⁸ + 2018 is divided by x – 1.
Solution:
p(x) = x²⁰¹⁸ + 2018
When it is divided by x – 1,
p(1) = 1²⁰¹⁸ + 2018
= 1 + 2018
= 2019
The remainder is 2019.

Question 5.
For what value of k is the polynomial
p(x) = 2x³ – kx² + 3x + 10 exactly divisible by x – 2
Solution:
p(x) = 2x³ – kx² + 3x + 10
When it is exactly divided by x – 2,
P(2) = 0
2(2)³ – k(2)² + 3(2) + 10 = 0
2(8) – k(4) + 6 + 10 = 0
16 – k(4) + 6 + 10 = 0
16 – 4k + 6 + 10 = 0
32 – 4k = 0
32 = 4k
∴ k = \(\frac{32}{4}\)
= 8
The value of k = 8

Question 6.
If two polynomials 2x³ + ax² + 4x – 12 and x³ + x² – 2x + a leave the same remainder when divided by (x – 3), find the value of a and also find the remainder.
Solution:
p(x₁) = 2x³ + ax² + 4x – 12
When it is divided by x – 3,
p(3) = 2(3)³ + a(3)² + 4(3) – 12
= 54 + 9a + 12 – 12
= 54 + 9a ……….(R₁)
p(x₂) = x³ + x² – 2x + a
When it is divided by x – 3,
p(3) = 3³ + 3² – 2(3) + a
= 27 + 9 – 6 + a
= 30 + a ………(R₂)
The given remainders are same (R₁ = R₂)
∴ 54 + 9a = 30 + a
9a – a = 30 – 54
8a = -24
∴ a = -24/8
= -3
Consider R₂,
Remainder = 30 – 3
= 27

Question 7.
Determine whether (x – 1) is a factor of the following polynomials:
(i) x³ + 5x² – 10x + 4
Solution:
p(x) = x³ + 5x² – 10x + 4
p(1) = 1³ + 5(1) – 10(1) + 4
= 1 + 5 – 10 + 4
= 10 – 10
= 0
∴ x – 1 is a factor of p(x)

(ii) x⁴ + 5x² – 5x + 1
Solution:
p(1) = 1⁴ + 5(1)² – 5(1) + 1
= 1 + 5 – 5 + 1
= 7 – 5
= 2
= 0
∴ x – 1 is not a factor of p(x)

Question 8.
Using factor theorem, show that (x – 5) is a factor of the polynomial
2x³ – 5x² – 28x + 15
Solution:
p(x) = 2x³ – 5x² – 28x + 15
x – 5 is a factor
p(5) = 2(5)³ – 5(5)² – 28(5) + 15
= 250 – 125 – 140 + 15
= 265 – 265
= 0
∴ x – 5 is a factor of p(x)

Question 9.
Determine the value of m, if (x + 3) is a factor of x³ – 3x² – mx + 24.
Solution:
p(x) = x³ – 3x² – mx + 24
when x + 3 is a factor
P(-3) = 0
(-3)³ – 3(-3)² – m(-3) + 24 = 0
-27 – 27 + 3m + 24 = 0
-54 + 24 + 3m = 0
-30 + 3m = 0
3m = 30
m = \(\frac{30}{3}\)
= 10
The value of m = 10

Question 10.
If both (x-2) and (x – \(\frac{1}{2}\)) are the factors of ax² + 5x + b, then show that a = b.
Solution:
p(x) = ax² + 5x + b
when (x-2) is a factor
P(2) = 0
a(2)² + 5(2) + b = 0
4a + 10 + b = 0
4a + b = -10 …….(1)
when (x – \(\frac{1}{2}\)) is a factor
p(\(\frac{1}{2}\)) = 0
a\((\frac{1}{2})^2\) + 5(\(\frac{1}{2}\)) + b = 0
Multiply by 4
a + 10 + 4b = 0
a + 46 = -10 …….(2)
From (1) and (2) we get
4a + b = a + 4b
4a – a = 4b – b
3a = 3b
a = b
Hence it is proved.

Question 11.
If (x – 1) divides the polynomial kx³ – 2x² + 25x – 26 without remainder, then find the value of k.
Solution:
p(x) = kx³ – 2x² + 25x – 26
When it is divided by x – 1
P(1) = 0
k(1)³ – 2(1)² + 25(1) – 26 = 0
k – 2 + 25 – 26 = 0
k + 25 – 28 = 0
k – 3 = 0
k = 3
The value of k = 3

Question 12.
Check if (x + 2) and (x – 4) are the sides of a rectangle whose area is x² – 2x – 8 by using factor theorem.
Solution:
Let the area of a rectangle be p(x)
p(x) = x² – 2x – 8
When x + 2 is the side of the rectangle
p(-2) = (-2)² – 2(-2) – 8
= 4 + 4 – 8
= 8 – 8
= 0
When x – 4 is the side of the rectangle.
P(4) = (4)² – 2(4) – 8
= 16 – 8 – 8
= 16 – 16
= 0
(x + 2) and (x – 4) are the sides of a rectangle

Students can download Maths Chapter 3 Algebra Ex 3.6 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.6

Question 1.
Factorise the following.
(i) x² + 10x + 24
Solution:
Product = 24, sum = 10

Split the middle term as 6x and 4x
x² + 10x + 24 = x² + 6x + 4x + 24
= x(x + 6) + 4 (x + 6)
= (x + 6) (x + 4)

(ii) z² + 4z – 12
Solution:
Product = -12, sum = 4

Split the middle term as 6z and -2z
z² + 4z – 12 = z² + 6z – 2z – 12
= z(z + 6) – 2 (z + 6)
= (z + 6) (z – 2)

(iii) p² – 6p – 16
Solution:
Product = -16, sum = -6

Split the middle term as – 8p and 2p
p² – 6p – 16 = p² – 8p + 2p – 16
= p(p – 8) + 2 (p – 8)
= (p – 8) (p + 2)

(iv) t² + 72 – 17t
Solution:
Product = +72, sum = -17

Split the middle term as -9t and -8t
t² – 17t + 72 = t² – 91 – 8t + 72
= t(t – 9) – 8 (l – 9)
= (t – 9) (t – 8)

(v) y² – 16y – 80
Solution:
Product = -80, sum = -16

Split the middle term as -20y and 4y
y² – 16y – 80 = y² – 20y + Ay – 80
= y(y – 20) + 4 (y – 20)
= (y – 20) (y + 4)

(vi) a² + 10a – 600
Solution:
Product = -600, sum =10

Split the middle term as 30a and -20a
a² + 10a – 600 = a² + 30a – 20a – 600
= a(a + 30) – 20 (a + 30)
= (a + 30) (a – 20)

Question 2.
Factorise the following.
(i) 2a² + 9a + 10
Solution:
Product = 2 × 10 = 20, sum = 9

Split the middle term as 5a and 4a
2a² + 9a + 10 = 2a² + 5a + 4a + 10
= a(2a + 5) + 2 (2a + 5)
= (2a+ 5) (a+ 2)

(ii) 5x² – 29xy – 42y²
Solution:
Product = 5 × -42 = -210, sum = -29

Split the middle term as -35x and 6x
5x² – 29xy – 42y² = 5x² – 35xy + 6xy – 42y²
= 5x (x – 7y) + 6y (x – 7y)
= (x – 7y) (5x + 6y)

(iii) 9 – 18x + 8x²
Solution:
Product = 9 × 8 = 72, sum = -18

Split the middle term as -12x and -6x
9 – 18x + 8x² = 8x² – 18x + 9
= 8x² – 12x – 6x + 9
= 4x (2x – 3) – 3 (2x – 3)
= (2x – 3) (4x – 3)

(iv) 6x² + 16xy + 8y²
Solution:
Product = 6 × 8 = 48, sum = 16

Split the middle term as 4xy and 12xy
6x² + 16xy + 8y² = 6x² + 12xy + 4xy + 8y²
= 6x (x + 2y) + 4y(x + 2y)
= (x + 2y) (6x + 4y)
= 2(x + 2y) (3x + 2y)

(v) 12x² + 36x²y + 27y²x²
Solution:
3x²2 [4 + 12y + 9y²]
= 3x² [9y² + 12y + 4]
Product = 9 x 4 = 36, sum =12

Split the middle term as 6y and 6y
12x² + 36x²y + 21y²x² = 3x² [9y² + 12y + 4]
= 3x² [9y² + 6y + 6y + 4]
= 3x² [3y(3y + 2) + 2(3y + 2)]
= 3x² (3y + 2) (3y + 2)
= 3x² (3y + 2)2

(vi) (a + b)² + 9 (a + b) + 18
Solution:
Let (a + b) = x
x² + 9x + 18
Product =18, sum = 9
Split the middle term as 6x and 3x
x² + 9x + 18 = x² + 6x + 3x + 18
= x (x + 6) + 3 (x + 6)
= (x + 6) (x + 3)
But x = a + b
(a + b)² + 9(a + b) + 18 = (a + b + 6) (a + b + 3)

Question 3.
Factorise the following.
(i) (p – q)² – 6(p – q) – 16
Solution:
Let (p – q) = x
(p – q)² – 6 (p – q) – 16 = x² – 6x – 16
Product = -16, sum = -6

Split the middle term as -8x and 2x
x² – 6x – 16 = x² – 8x + 2x – 16
= x(x – 8) + 2(x – 8)
= (x – 8) (x + 2)
(But x = p – q)
= (p – q – 8) (p – q + 2)

(ii) m² + 2mn – 24n²
Solution:
Product = -24, sum = 2

Split the middle term as 6mn and -4mn
m² + 2mn – 24m² = m² + 6mn – 4mn – 24n²
= m(m + 6n) – 4n (m + 6n)
= (m + 6n) (m – 4n)

(iii) √5 a² + 2a – 3√5?
Solution:
Product = √5 × – 3√5 = -15, sum = 2

Split the middle term as 5x and -3x
√5 a² + 2a – 3√5 = √5a² + 5a – 3a – 3√5
= √5 a(a + √5) – 3(a + √5)
= (a + √5) (√5a – 3)

(iv) a⁴ – 3a² + 2
Solution:
Let a² = x
a⁴ – 3a² + 2 = (a²)² – 3a² + 2
= x² – 3x + 2
Product = 2 and sum = -3

Split the middle term as -x and -2x
x² – 3x + 2 = x² – x – 2x + 2
= x(x – 1) – 2(x – 1)
= (x – 1) (x – 2)
a⁴ – 3a² + 2 = (a² – 1)(a² – 2) [But a² = x]
= (a + 1) (a – 1) (a² – 2)

(v) 8m³ – 2m²n – 15mn²
Solution:
8m³ – 2m²n – 15mn² = m(8m² – 2mn – 15n²)
Product = 8(-15) = -120 and sum = -2

Split the middle term as -12mn and 10mn
8m³ – 2m²n – 15mn² = m[8m² – 2mn – 15n²]
= m[8m²– 12mn + 10mn- 15n²]
= m[4m (2m – 3n) + 5n(2m – 3n)]
= m(2m – 3n) (4m + 5n)

(vi) \(\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{2}{x y}\)
Solution:

Students can download Maths Chapter 3 Algebra Ex 3.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.2

Question 1.
Find the value of the polynomial f(y) = 6y – 3y² + 3 at
(i) y = 1
(ii) y = -1
(iii) y = 0
Solution:
(i) When y = 1
f(y) = 6y – 3y² + 3
f(1) = 6(1) – 3(1)² + 3
= 6 – 3 + 3 = 6

(ii) When y = – 1
f(y) = 6y – 3y² + 3
f(-1) = 6(-1) – 3(-1)² + 3
= – 6 – 3 + 3
= – 6

(iii) When y = 0
f(y) = 6y – 3y² + 3
f(0) = 6(0) – 3(0)² + 3
= 0 – 0 + 3
= 3

Question 2.
If p(x) = x² – 2√2x + 1, find p(2√2).
Solution:
p(x) = x² – 2√2x + 1
p(2√2) = (2√2)² – 2√2 (2√2) + 1
= 8 – 8 + 1
= 0 + 1
= 1

Question 3.
Find the zeros of the polynomial in each of the following.
(i) P(x) = x – 3
Solution:
p( 3) = 3 – 3
= 0
p(3) is the zero of p(x)

(ii) p(x) = 2x + 5
Solution:

= -5 + 5
= 2(0)
= 0
Hence –\(\frac{5}{2}\) is the zero of p(x).

(iii) q(y) = 2y – 3
Solution:

= 2 × 0
= 0
Hence \(\frac{3}{2}\) is the zero of q(y).

(iv) f(z) = 8z
Solution:
f(0) = 8 × 0
= 0
Hence 0 is the zero of f(z)

(v) p(x) = ax when a ≠ 0
Solution:
p(0) = a(0)
= 0
Hence, 0 is the zero of p(x)

(vi) h(x) = ax + b, a ≠ 0, a, b∈R
Solution:

Hence –\(\frac{b}{a}\) is the zero of h(x).

Question 4.
Find the roots of the polynomial equations.
(i) 5x – 6 = 0
Solution:
5x = 6
x = \(\frac{6}{5}\)
\(\frac{6}{5}\) is the root of the polynomial.

(ii) x + 3 = 0
Solution:
x = -3
-3 is the root of the polynomial.

(iii) 10x + 9 = 0
Solution:
10x = -9
x = –\(\frac{9}{10}\)
–\(\frac{9}{10}\) is the root of the polynomial.

(iv) 9x – 4 = 0
Solution:
9x = 4
x = \(\frac{4}{9}\)
\(\frac{4}{9}\) is the root of the polynomial.

Question 5.
Verify whether the following are zeros of the polynomial, indicated against them,or not.
(i) p(x) = 2x – 1, x = \(\frac{1}{2}\)
Solution:
p (\(\frac{1}{2}\)) = 2(\(\frac{1}{2}\)) – 1
= 1 – 1
= 0
∴ \(\frac{1}{2}\) is the zero of the polynomial.

(ii) p(x) = x³ – 1, x = 1
Solution:
p(1) = 1³ – 1
= 1 – 1
= 0
∴ 1 is the zero of the polynomial

(iii) p(x) = ax + b, x = \(\frac{-b}{a}\)
Solution:
p(\(\frac{-b}{a}\)) = a(\(\frac{-b}{a}\)) + b
= -b + b
= 0
∴ \(\frac{-b}{a}\) is the zero of the polynomial. a

(iv) p(x) = (x + 3) (x – 4); x = -3, x = 4
Solution:
P(-3) = (-3 + 3) (-3 – 4)
= (0) (-7)
= 0
P( 4) = (4 + 3) (4 – 4)
= (7) (0)
= 0
∴ -3 and 4 are the zeros of the polynomial.

Question 6.
Find the number of zeros of the following polynomials represented by their graphs.

Solution:
(i) Number of zeros = 2 (The curve is intersecting the x-axis at 2 points)
(ii) Number of zeros = 3 (The curve is intersecting the x-axis at 3 points)
(iii) Number of zeros = 0 (The curve is not intersecting the x-axis)
(iv) Number of zeros = 1 (The curve is intersecting at the origin)
(v) Number of zeros = 1 (The curve is intersecting the x-axis at one point)