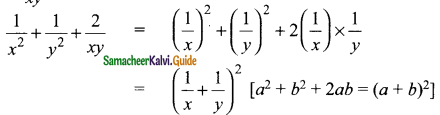Students can download Maths Chapter 3 Algebra Ex 3.6 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.6
Question 1.
Factorise the following.
(i) x² + 10x + 24
Solution:
Product = 24, sum = 10
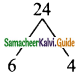
Split the middle term as 6x and 4x
x² + 10x + 24 = x² + 6x + 4x + 24
= x(x + 6) + 4 (x + 6)
= (x + 6) (x + 4)
(ii) z² + 4z – 12
Solution:
Product = -12, sum = 4
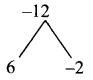
Split the middle term as 6z and -2z
z² + 4z – 12 = z² + 6z – 2z – 12
= z(z + 6) – 2 (z + 6)
= (z + 6) (z – 2)
![]()
(iii) p² – 6p – 16
Solution:
Product = -16, sum = -6
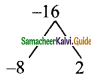
Split the middle term as – 8p and 2p
p² – 6p – 16 = p² – 8p + 2p – 16
= p(p – 8) + 2 (p – 8)
= (p – 8) (p + 2)
(iv) t² + 72 – 17t
Solution:
Product = +72, sum = -17
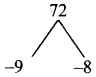
Split the middle term as -9t and -8t
t² – 17t + 72 = t² – 91 – 8t + 72
= t(t – 9) – 8 (l – 9)
= (t – 9) (t – 8)
(v) y² – 16y – 80
Solution:
Product = -80, sum = -16
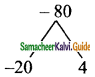
Split the middle term as -20y and 4y
y² – 16y – 80 = y² – 20y + Ay – 80
= y(y – 20) + 4 (y – 20)
= (y – 20) (y + 4)
(vi) a² + 10a – 600
Solution:
Product = -600, sum =10
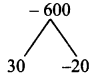
Split the middle term as 30a and -20a
a² + 10a – 600 = a² + 30a – 20a – 600
= a(a + 30) – 20 (a + 30)
= (a + 30) (a – 20)
![]()
Question 2.
Factorise the following.
(i) 2a² + 9a + 10
Solution:
Product = 2 × 10 = 20, sum = 9
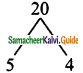
Split the middle term as 5a and 4a
2a² + 9a + 10 = 2a² + 5a + 4a + 10
= a(2a + 5) + 2 (2a + 5)
= (2a+ 5) (a+ 2)
(ii) 5x² – 29xy – 42y²
Solution:
Product = 5 × -42 = -210, sum = -29
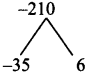
Split the middle term as -35x and 6x
5x² – 29xy – 42y² = 5x² – 35xy + 6xy – 42y²
= 5x (x – 7y) + 6y (x – 7y)
= (x – 7y) (5x + 6y)
(iii) 9 – 18x + 8x²
Solution:
Product = 9 × 8 = 72, sum = -18

Split the middle term as -12x and -6x
9 – 18x + 8x² = 8x² – 18x + 9
= 8x² – 12x – 6x + 9
= 4x (2x – 3) – 3 (2x – 3)
= (2x – 3) (4x – 3)
![]()
(iv) 6x² + 16xy + 8y²
Solution:
Product = 6 × 8 = 48, sum = 16
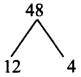
Split the middle term as 4xy and 12xy
6x² + 16xy + 8y² = 6x² + 12xy + 4xy + 8y²
= 6x (x + 2y) + 4y(x + 2y)
= (x + 2y) (6x + 4y)
= 2(x + 2y) (3x + 2y)
(v) 12x² + 36x²y + 27y²x²
Solution:
3x²2 [4 + 12y + 9y²]
= 3x² [9y² + 12y + 4]
Product = 9 x 4 = 36, sum =12

Split the middle term as 6y and 6y
12x² + 36x²y + 21y²x² = 3x² [9y² + 12y + 4]
= 3x² [9y² + 6y + 6y + 4]
= 3x² [3y(3y + 2) + 2(3y + 2)]
= 3x² (3y + 2) (3y + 2)
= 3x² (3y + 2)2
(vi) (a + b)² + 9 (a + b) + 18
Solution:
Let (a + b) = x
x² + 9x + 18
Product =18, sum = 9
Split the middle term as 6x and 3x
x² + 9x + 18 = x² + 6x + 3x + 18
= x (x + 6) + 3 (x + 6)
= (x + 6) (x + 3)
But x = a + b
(a + b)² + 9(a + b) + 18 = (a + b + 6) (a + b + 3)
![]()
Question 3.
Factorise the following.
(i) (p – q)² – 6(p – q) – 16
Solution:
Let (p – q) = x
(p – q)² – 6 (p – q) – 16 = x² – 6x – 16
Product = -16, sum = -6

Split the middle term as -8x and 2x
x² – 6x – 16 = x² – 8x + 2x – 16
= x(x – 8) + 2(x – 8)
= (x – 8) (x + 2)
(But x = p – q)
= (p – q – 8) (p – q + 2)
(ii) m² + 2mn – 24n²
Solution:
Product = -24, sum = 2

Split the middle term as 6mn and -4mn
m² + 2mn – 24m² = m² + 6mn – 4mn – 24n²
= m(m + 6n) – 4n (m + 6n)
= (m + 6n) (m – 4n)
![]()
(iii) √5 a² + 2a – 3√5?
Solution:
Product = √5 × – 3√5 = -15, sum = 2
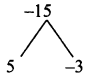
Split the middle term as 5x and -3x
√5 a² + 2a – 3√5 = √5a² + 5a – 3a – 3√5
= √5 a(a + √5) – 3(a + √5)
= (a + √5) (√5a – 3)
(iv) a4 – 3a² + 2
Solution:
Let a² = x
a4 – 3a² + 2 = (a²)² – 3a² + 2
= x² – 3x + 2
Product = 2 and sum = -3
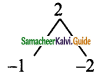
Split the middle term as -x and -2x
x² – 3x + 2 = x² – x – 2x + 2
= x(x – 1) – 2(x – 1)
= (x – 1) (x – 2)
a4 – 3a² + 2 = (a2 – 1)(a2 – 2) [But a2 = x]
= (a + 1) (a – 1) (a2 – 2)
![]()
(v) 8m3 – 2m2n – 15mn2
Solution:
8m3 – 2m2n – 15mn2 = m(8m2 – 2mn – 15n2)
Product = 8(-15) = -120 and sum = -2
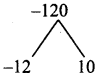
Split the middle term as -12mn and 10mn
8m3 – 2m2n – 15mn2 = m[8m2 – 2mn – 15n2]
= m[8m2– 12mn + 10mn- 15n2]
= m[4m (2m – 3n) + 5n(2m – 3n)]
= m(2m – 3n) (4m + 5n)
(vi) \(\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{2}{x y}\)
Solution: