Students can download Maths Chapter 5 Coordinate Geometry Ex 5.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.2
Question 1.
Find the distance between the following pairs of points.
(i) (1, 2) and (4, 3)
Solution:
Distance between the points (1, 2) and (4, 3)
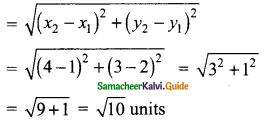
(ii) (3, 4) and (-7, 2)
Solution:
Distance between the points (3,4) and (-7, 2)
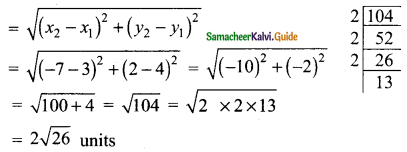
(iii) (a, b) and (c, b)
Solution:
Distance between the two points (a, b) and (c, b)
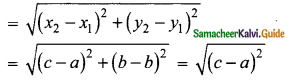
= c – a units
![]()
(iv) (3,- 9) and (-2, 3)
Solution:
Distance between the two points (3, -9) and (-2, 3)
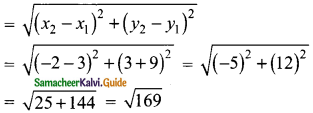
= 13 units
Question 2.
Determine whether the given set of points in each case are collinear or not.
(i) (7, -2), (5, 1), (3, 4)
Solution:
To prove that three points are collinear, sum of the distance between two pairs of points is equal to the third pair of points.
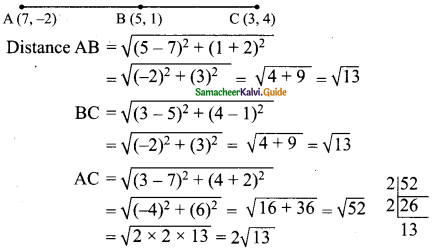
AB + BC = AC
\(\sqrt{13}\) + \(\sqrt{13}\) = 2\(\sqrt{13}\) ⇒ 2\(\sqrt{13}\) = 2\(\sqrt{13}\)
∴ The given three points are collinear.
(ii) (a, -2), (a, 3), (a, 0)
Solution:
A (a, -2) B (a, 3) C (a, 0)

√4
= 2
AC + BC = AB ⇒ 2 + 3 = 5
∴ The given three points are collinear.
![]()
Question 3.
Show that the following points taken in order to form an isosceles triangle.
(i) A (5, 4), B(2, 0), C (-2, 3)
Solution:
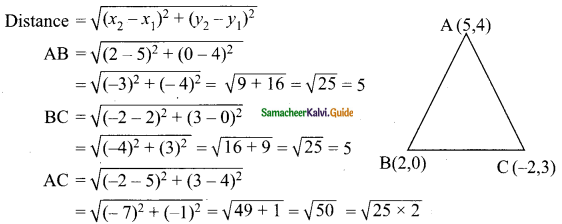
= 5√2
AB = BC = 5. (Two sides are equal)
∴ ABC is an isosceles triangle.
(ii) A (6, -1), B (-2, -4), C (2, 10)
Solution:
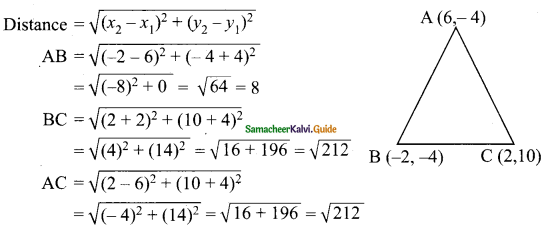
BC = AC = \(\sqrt{212}\) (TWO sides are equal)
∴ ABC is an isosceles triangle.
![]()
Question 4.
Show that the following points taken in order to form an equilateral triangle in each case.
(i) A(2, 2), B(-2, -2), C(-2√3, 2√3)
Solution:
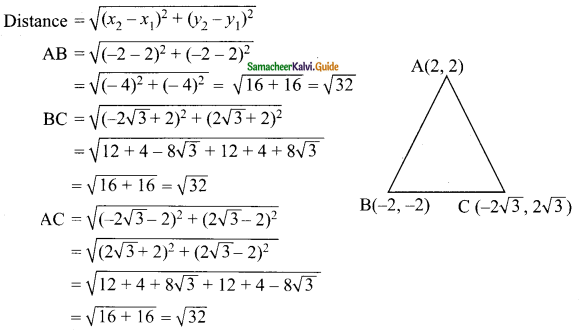
AB = BC = AC (Three sides are equal)
∴ ABC is an equilateral triangle.
(ii) A(√3, 2), B (0, 1), C(0, 3)
Solution:
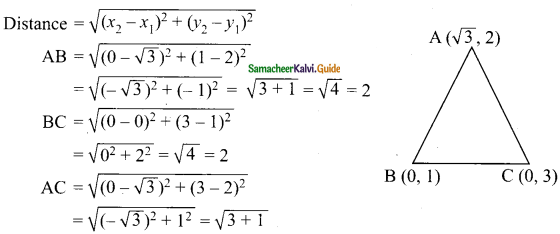
= √4
= 2
AB = BC = AC (Three sides are equal)
∴ ABC is an equilateral triangle.
![]()
Question 5.
Show that the following points taken in order to form the vertices of a parallelogram.
(i) A(-3, 1), B(-6, -7), C (3, -9) and D(6, -1)
Solution:

AB = CD = \(\sqrt{73}\) and BC = AD = \(\sqrt{85}\) (Opposite sides are equal)
∴ ABCD is a parallelogram.
(ii) A (-7, -3), B(5, 10), C(15, 8) and D(3, -5)
Solution:

AB = CD = \(\sqrt{313}\) and BC = AD = \(\sqrt{104}\) (Opposite sides are equal)
∴ ABCD is a parallelogram.
![]()
Question 6.
Verify that the following points taken in order to form the vertices of a rhombus.
(i) A(3, -2), B (7, 6),C (-1, 2) and D (-5, -6)
Solution:

AB = BC = CD = AD = \(\sqrt{80}\). All the four sides are equal.
∴ ABCD is a rhombus.
(ii) A (1, 1), B (2, 1),C (2, 2) and D (1, 2)
Solution:

AB = BC = CD = AD = 1. All the four sides are equal.
∴ ABCD is a rhombus.
Question 7.
A (-1, 1), B (1, 3) and C (3, a) are points and if AB = BC, then find ‘a’.
Solution:
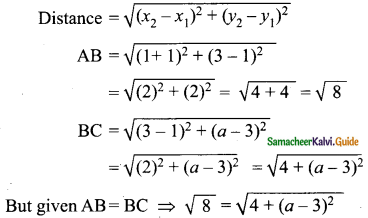
4 + (a – 3)² = 8
(a – 3)² = 8 – 4
(a – 3)² = 4
a – 3 = √4
= ± 2
a – 3 = 2 (or) a – 3 = -2
a = 2 + 3 (or) a = 3 – 2
a = 5 (or) a = 1
∴ The value of a = 5 or a = 1.
![]()
Question 8.
The abscissa of a point A is equal to its ordinate, and its distance from the point B(1, 3) is 10 units, What are the coordinates of A?
Solution:
Let the point A be (a, a) B is (1, 3)
Distance AB = 10 (Given)
By distance formula \(\sqrt{(a – 1 )² + (a – 3)²}\) = 10
Simplifying 2a² – 8a + 10 = 100
a² – 4a – 45 = 0
(a – 9)(a + 5) = 0
⇒ a = – 5; A = (-5, -5)
a = 9; A = (9, 9)
Question 9.
The point (x, y) is equidistant from the points (3, 4) and (-5, 6). Find a relation between x and y.
Solution:
Let the point O be (x, y), A be (3, 4) and B be (-5, 6).
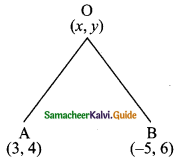
Distance = \(\sqrt{(x_{2} – x_{1})² + (y_{2} – y_{1})²}\)
Given ,OA = OB
\(\sqrt{(x – 3 )² + (y – 4)²}\) = \(\sqrt{(x + 5 )² + (y – 6)²}\)
Squaring on both sides
(x – 3)² + (y – 4)² = (x + 5)² + (y – 6)²
x² – 6x + 9 + y² – 8y + 16 = x² + 10x + 25 + y² – 12y + 36
x² + y² – 6x – 8y + 25 = x² + y² + 10x – 12y + 61
6x – 10x – 8y + 12y = 61 – 25 ⇒ -16x + 4y = 36
÷ 4 ⇒ -4x + y = 9
∴ The relation between x and y is y = 4x + 9
![]()
Question 10.
Let A(2,3) and B(2, -4) be two points. If P lies on the x-axis, such that AP = \(\frac{3}{7}\) AB, find the coordinates of P.
Solution:
Given points are A(2, 3) and B(2, -4)
The point P lies on the x-axis.
∴ The point P is (x, 0)

16x² – 64x + 208 = 9x² – 36x + 180
16x² – 9x² – 64x + 36x + 208 – 180 = 0
7x² – 28x + 28 = 0
x² – 4x + 4 = 0
(x – 2)² = 0
x – 2 = 0
x = 2
∴ The point P is (2, 0)
![]()
Question 11.
Show that the point (11, 2) is the centre of the circle passing through the points (1, 2), (3, -4) and (5, -6)
Solution:
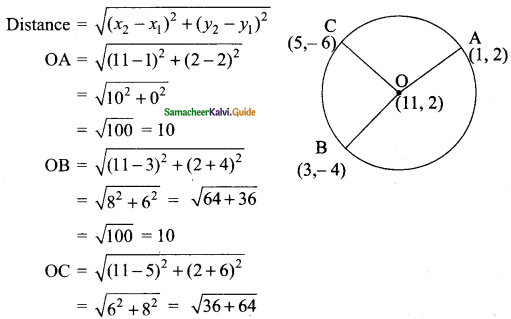
\(\sqrt{100}\)
= 10
OA = OB = OC = 10
O is the centre of the circle passing through A, B and C.
Question 12.
The radius of a circle with centre at origin is 30 units. Write the coordinates of the points where the circle intersects the axes. Find the distance between any two such points.
Solution:
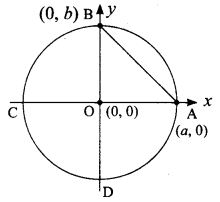
Radius of the circle = 30 units. The point O is (0, 0).
Let a intersect the x-axis and b intersect the y-axis.
∴ The point A is (a, 0) and B is (0, b)
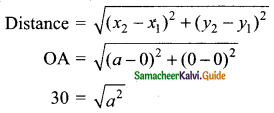
Squaring on both sides
30² = a²
∴ a = 30
The point A is (30, 0)
OB = \(\sqrt{(0 – 0)² + (b – 0)²}\)
= \(\sqrt{0² + b²}\)
30 = \(\sqrt{b²}\)
Squaring on both sides
30² = b²
∴ b = 30
The point B is (0, 30)
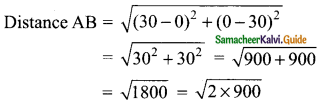
= 30√2
∴ Distance between the two points = 30√2
![]()