Category: Class 8

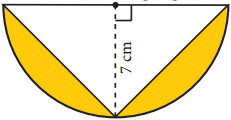
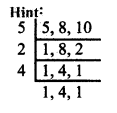
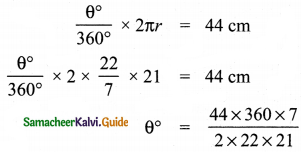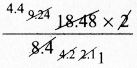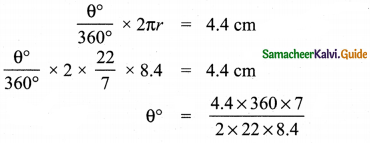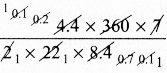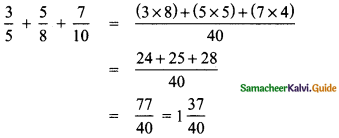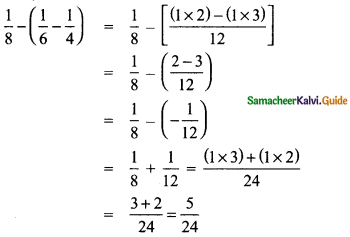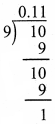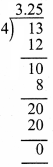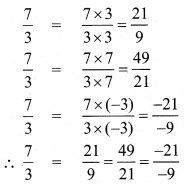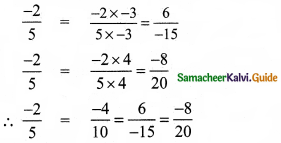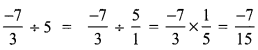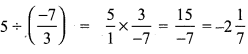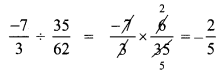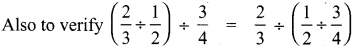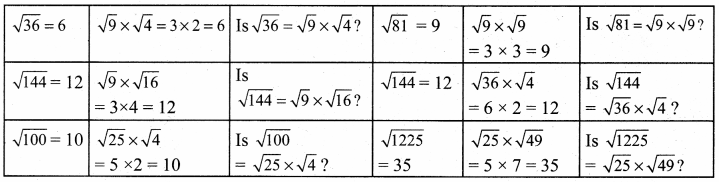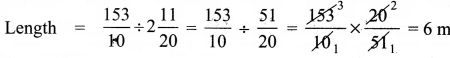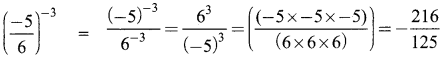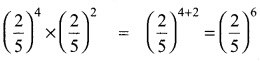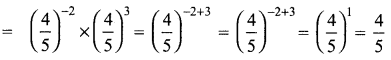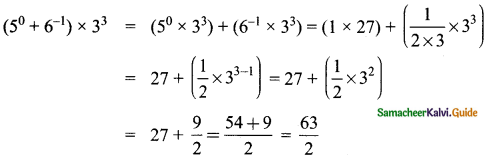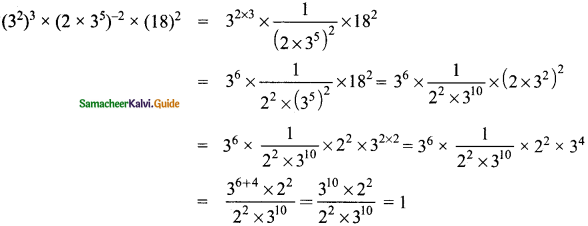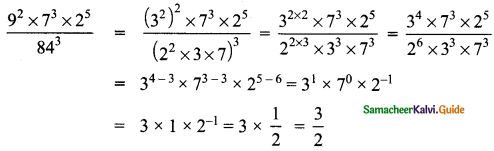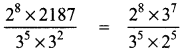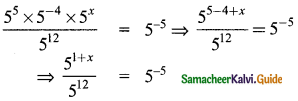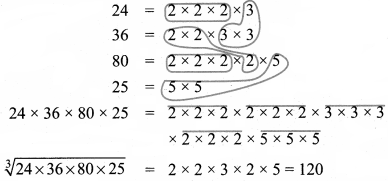Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.1

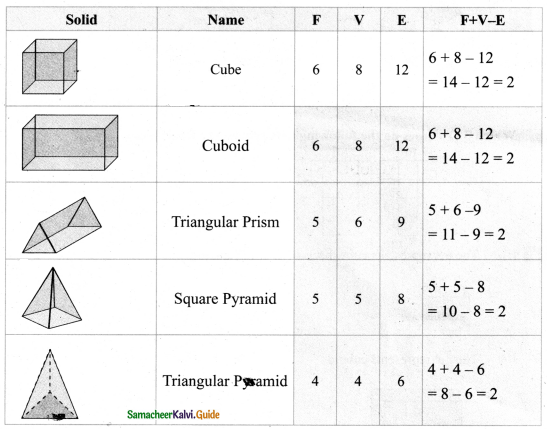
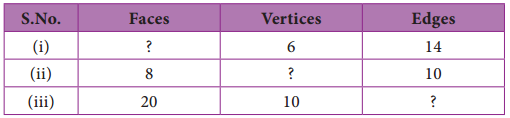
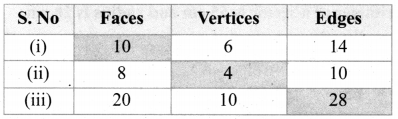
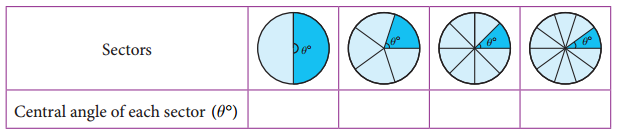
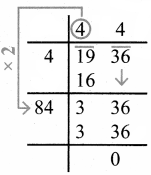
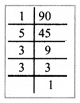
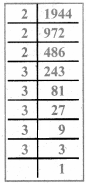
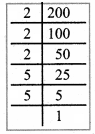
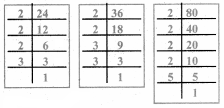
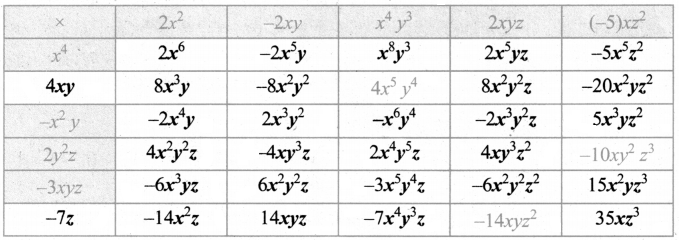
Question 1.
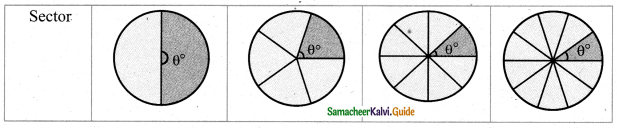
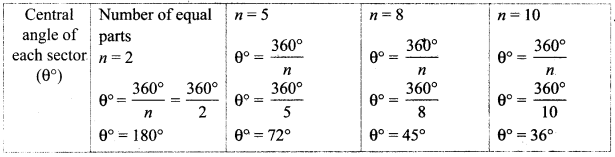
Complete the table.

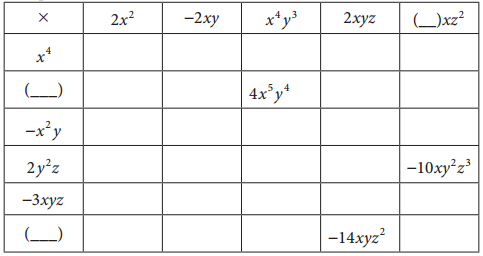
Answer:

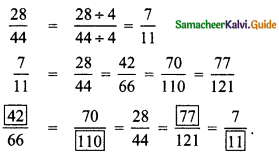
Question 2.
Find the product of the terms.
(i) -2mn, (2m)², -3mn
(ii) 3x²y , -3xy³, x²y²
Answer:
(i) (-2mn) × (2m)² × (-3mn) = (-2mn) × 2²m² × (-3mn) = (- 2mn) × 4m² × (- 3mn)
= (-) (+)(-) (2 × 4 × 3) (m × m² × m) (n × n)
= +24 m⁴ 4n²

(ii) (3x²y) × (-3xy³) × (x²y²) = (+) × (-) × (+) × (3 × 3 × 1)(x² × x × x²) × (y × y³ × y²)
= -9x⁵ y⁶

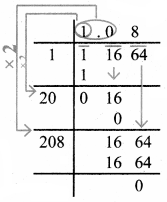
Question 3.
If l = 4pq², b = -3p²q h = 2p³q³ then, find the value of l × b × h.
Answer:
Given l = 4pq²
b = -3p²q
h = 2p³q³
l × b × h = (4pq²) × -3p²q × 2p³q³
= (+) (-) (+) (4 × 3 × 2) (p × p² × p³) (q × q² × q³)
= – 24p⁶q⁶

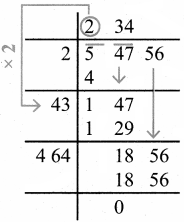
Question 4.
Expand
(i) 5x(2y – 3)
(ii) -2p(5p² – 3p + 7)
(iii) 3mn(m³n³ – 5m²n + 7mn²)
(iv) x²(x + y + z)+ y²(x+ y + z) + z²(x – y – z)
Answer:
(i) 5x(2y – 3)
5x(2y -.3) = (5x)(2y) – (5x)(3)
= (5 × 2) (x × y) – (5 × 3)x
= 10xy – 15x

(ii) -2p(5p² – 3p + 7)
-2p (5p² -3p + 7) = (-2p) (5p²) + (-2p) (-3p) + (-2p) (7)
= [(-) (+) (2 × 5) (p × p²)] + [(-) (-) (2 × 3) (p × p)] + (-)(+)(2 × 7)p
= -10p³ + 6p² – 14p

(iii) 3mn(m³n³ – 5m²n + 7mn²)
3mn(m³n³ – 5m²n + 7 mn²) = (3mn) (m³n³) + (3mn) (-5m³n) + (3mn)(7mn³)
= (3)(m ×m³) (n × n³) + (+)(-)(3 × 5)(m × m²)(n × n)+ (3 × 7) (m × m)(n × n²)
= 3m⁴n⁴ – 15m³n² + 21m²n³

(iv) x²(x + y + z)+ y²(x+ y + z) + z²(x – y – z)
x²(x + y + z) + y²(x + y + z) + z²(x – y – z) = (x² × x) + (x² × y) + (x² × z) + (y² × x) + (y² × y) + (y² × z) + (z² × x) + z² (-y) + z² (-z)
= x³ + x²y + x²z + xy² + y³ + y²z + xz² – yz² – z³
= x³ + y³ – z³ + x²y + x²z + xy² + zy² + xz² – yz²

Question 5.
Find the product of
(i) (2x + 3)(2x – 4)
(ii) (y² – 4)(2y² + 3y)
(iii) (m² – n)(5m²n² – n²)
(iv) 3(x – 5) × 2(x – 1)
Answer:
(i) (2x + 3)(2x – 4)
(2x + 3)(2x – 4) = (2x)(2x – 4) + 3(2x – 4)
= (2x × 2x) – 4(2x) – 3(2x) – 3(4)
= 4x² – 8x + 6x – 12
= 4x² + (- 8 + 6)x – 12
= 4x² – 2x – 12

(ii) (y² – 4)(2y² + 3y)
(y² – 4)(2y² + 3y) = y²(2y² + 3y) – 4(2y²) – 4(3y)
= y²(2y²) + y² (3y) – 4(2y²) – 4 (3y)
= 2y⁴ + 3y³ – 8y² – 12y

(iii) (m² – n)(5m²n² – n²)
(m² – n)(5m² n² – n²) = m² (5m²n² – n²) – n (5m²n² – n²)
= m² (5m²n²) + m² (-n²) – n (5m²n² ) + (-) (-) n (n²)
= 5m⁴n² – m²n² – 5m²n³ + n³

(iv) 3(x – 5) × 2(x – 1)
3(x – 5) × 2(x – 1) = (3 × 2) (x – 5) (x – 1)
= 6 × [x (x – 1) – 5 (x – 1)]
6 [x.x – x.1 – 5x + (-1)(-)5 1]
= 6[x² – x – 5x + 5] = 6[x² + (-1 – 5)x + 5]
= 6[x² – 6x + 5] = 6x² – 36 x + 30

Question 6.
Find the missing term.
(i) 6xy × ______ = -12x³y
Answer:
6xy × (-2x²) = -12x³y

(ii) ______ × (-15m²n³p) = 45m³n³p²
Answer:
-3mp × (-15m²n³p) = 45m³n³p²

(iii) 2y(5x²y – ____ + 3____ ) = 10x²y² – 2xy + 6y³
Answer:
2y(5x²y – x + 3y²) = 10x²y² – 2xy + 6y³

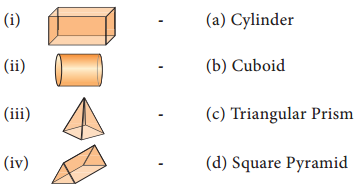
Question 7.
Match the following

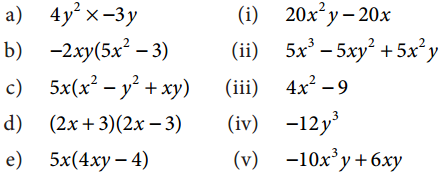
(A) iv, v, ii, i, iii
(B) v, iv, iii, ii, i
(C) iv, v, ii, iii, i
(D) iv, v, iii, ii, i
Answer:
(C) iv, v, ii, iii, i
a) – iv
b) – v
c) – ii
d) – iii
e) – i

Question 8.
A car moves at a uniform speed of (x + 30) km/hr. Find the distance covered by the car in (y + 2)hours. (Hint: distance = speed × time).
Answer:
Speed of the car = (x + 30) km/hr.
Time = (y + 2) hours
Distance = Speed × time
= (x + 30) (y + 2) = x(y + 2) + 30(y + 2)
= (x) (y) + (x) (2) + (30) (y) + (30) (2)
= xy + 2x + 30y + 60
Distance covered = (xy + 2x + 30y + 60) km

Objective Type Questions

Question 9.
The product of 7p³ and (2p²)² is
(A) 14p¹²
(B) 28p⁷
(C) 9p⁷
(D) 11p¹²
Answer:
(B) 28p⁷

Question 10.
The missing terms in the product -3m³n × 9(_) = _______ m⁴n³ are
(A) mn², 27
(B) m²n, 27
(C) m²n², – 27
(D) mn², – 27
Answer:
(A) mn², 27

Question 11.
If the area of a square is 36x⁴y² then, its side is _________ .
(A) 6x⁴y²
(B) 8x²y²
(C) 6x²y
(D) -6x²y
Answer:
(C) 6x²y

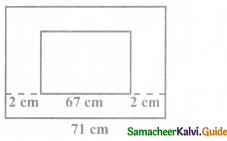
Question 12.
If the area of a rectangle is 48m²n³ and whose length is 8mn² then, its breadth is _____ .
(A) 6 mn
(B) 8m²n
(C) 7m²n²
(D) 6m²n²
Answer:
(A) 6 mn

Question 13.
If the area of a rectangular land is (a² – b²) sq.units whose breadth is(a – b) then, its length is_________
(A) a – b
(B) a + b
(C) a² – b
(D) (a + b)²
Answer:
(B) a + b

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 2 Measurements InText Questions Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 2 Measurements InText Questions

Think (Text Book Page No. 51)

Question 1.
\(\frac{22}{7}\) and 3.14 are rational numbers. Is ‘π’ a rational number? Why?
Answer:
\(\frac{22}{7}\) and 3.14 are rational numbers π has non-terminating and non-repoating decimal expansion. So it is not a rational number. it is an irrational number.

Question 2.
When is the’π’day celebrated? Why?
Answer:
March 14^th i.e. 3/14 every year. Approximately value of’ ‘π’ is 3.14.

Think (Text Book Page No. 53)

The given circular figure is di4dd into six equal parts. Can we call the parts as sectors? Why?

Answer:
No, the equal parts are not sectors. Because a sector is a plane surface that is enclosed between two radii and the circular arc of the circle. Here the boundaries are not radii.

Try These (Text Book Page No. 53)

Fill the central angle of the shaded sector (each circle is divided into equal sectors)

Answer:

Think (Text Book Page No. 54)

Question 1.
Instead of multiplying by \(\frac{1}{2}\), \(\frac{1}{3}\) and \(\frac{1}{4}\), we shall multiply by \(\frac{180^{\circ}}{360^{\circ}}\), \(\frac{120^{\circ}}{360^{\circ}}\) and \(\frac{90^{\circ}}{360^{\circ}}\) respectively. why?
Answer:
So, \(\frac{180^{\circ}}{360^{\circ}}\) = \(\frac{1}{2}\)
\(\frac{120^{\circ}}{360^{\circ}}\) = \(\frac{1}{3}\)
\(\frac{90^{\circ}}{360^{\circ}}\) = \(\frac{1}{4}\)

Think (Text Book Page No. 57)

If the radius of a circle is doubled, what will happen to the area of the new circle so formed?
Answer:
If r = 2r₁ ⇒ Area of the circle = πr² = π(2r₁)² = π4r₁²
Area = 4 × old area

Think (Text Book Page No. 61)

All the sides of a rhombus are equal. It is a regular polygon?
Answer:
For a regular polygon all sides and all the angles must be equal. But in a rhombus all the sides are equal. But all the angles are not equal
∴ It is not a regular polygon.

Try This (Text Book Page No. 64)

In the above example split the given mat into two trapeziums and verify your answer.
Answer:
Area of the mat = Area of I trapezium + Area of II trapezium
= [\(\frac { 1 }{ 2 }\) × h₁ × (a₁ + b₁)] + [\(\frac { 1 }{ 2 }\) × h₂ × (a₂ + b₂)] sq. units
= [\(\frac { 1 }{ 2 }\) × 2 × (7 + 5)] + \(\frac { 1 }{ 2 }\) × 2 × (9 + 7) sq.feet
= 12 + 16 = 28 sq.feet
∴ Cost per sq.feet = ₹ 20
Cost for 28sq. feet = ₹ 20 × 28 = ₹ 560
∴ Total cost for the entire mat = ₹ 560
Both the answers are the same.

Try This (Text Book Page No. 68)

Tabulate the number of faces (F), vertices (V) and edges (E) for the following polyhedrons. Also find F + V – E

What do you observe from the above table? We observe that, F + V – E = 2 in all the cases. This is true for any polyhedron and this relation F + V – E = 2 is known as Euler’s formula.
Answer:

From the table F + V – E = 2 for all the solid shapes.

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 2 Measurements Ex 2.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 2 Measurements Ex 2.4

Question 1.
Two gates are fitted at the entrance of a library. To open the gates easily, a wheel is fixed at 6 feet distance from the wall to which the gate is fixed. If one of the gates is opened to 90°, find the distance moved by the wheel (π = 3.14).

Amswer:
Let A be the position of the wall AC be the gate in initial position and AB be position when it is moved 90°.
Now the arc length BC gives the distance moved by the wheel.

Length of the arc = \(\frac{\theta}{360^{\circ}}\) × 2πr units
= \(\frac{90^{\circ}}{360^{\circ}}\) × 2 × 3.14 × 6 feets
= 3.14 × 3 feets
= 9.42 feets
∴ Distance moved by the wheel = 9.42 feets.

Question 2.
With his usual speed, if a person covers a circular track of radius 150 m in 9 minutes, find the distance that he covers in 3 minutes (π = 3.14).
Answer:
Radius of the circular track = 150m
Distance covers in 9 minutes = Perimeter of the circle = 2 × π × r units
Distance covered in 9 min = 2 × 3.14 × 150m
Distance covered in 1 min = \(\frac{2 \times 3.14 \times 150}{9} \mathrm{m}\)

Distance he covers in 3min = 314m

Question 3.
Find the area of the house drawing given in the figure.

Answer:
Area of the house = Area of a square of side 6 cm + Area of a rectangle with l = 8cm, b = 6 cm + Area of a ∆ with b = 6 cm and h = 4 cm + Area of a parallelogram with b = 8 cm, h = 4 cm
= (side × side) + (l × b) + (\(\frac { 1 }{ 2 }\) × b × h) + bh cm²
= (6 × 6) + (8 × 6) + (\(\frac { 1 }{ 2 }\) × 6 × 4) + (8 × 4) cm²
= 36 + 48 + 12 + 32 cm²
= 128 cm²
Required Area = 128 cm²

Question 4.
Draw the top, front and side view of the following solid shapes
(i)

Answer:
(a) Top view

(b) Front view

(c) Side view

(ii)

Answer:
(a) Top view

(b) Front view

(c) Side view

Challenging Problems

Question 5.
Guna has fixed a single door of width 3 feet in his room where as Nathan has fixed a double door, each of width 1 \(\frac { 1 }{ 2 }\) feet in his room. From the closed position, if each of the single and double doors can open up to 120°, whose door takes a minimum area?
Answer:
Width of the door that Guna fixed = 3 feet.
When the door is open the radius of the sector = 3 feet

Angle covered = 120°
∴ Area required to open the door

= 3π feet²

(b) Width of the double doors that Nathan fixed = 1 \(\frac { 1 }{ 2 }\) feet.
Angle described to open = 120°
Area required to open = 2 × Area of the sector
z
= \(\frac { 1 }{ 2 }\) (3π) feet²
∴ The double door requires the minimum area.

Question 6.
In a rectangular field which measures 15 m x 8m, cows are tied with a rope of length 3m at four corners of the field and also at the centre. Find the area of the field where none of the cow can graze. (π = 3.14).
Answer:
Area of the field where none of the cow can graze = Area of the rectangle – [Area of 4 quadrant circles] – Area of a circle

Area of the rectangle = l × b units²
= 15 × 8m² = 120m²
Area of 4 quadrant circles = 4 × \(\frac { 1 }{ 4 }\) πr² units
Radius ofthe circle = 3m
Area of 4 quadrant circles = 4 × \(\frac { 1 }{ 4 }\) × 3.14 × 3 × 3 = 28.26 m²
Area of the circle at the middle = πr² units
= 3.14 × 3 × 3m² = 28.26m²
∴ Area where none of the cows can graze
= [120 – 28.26 – 28.26]m² = 120 – 56.52 m² = 63.48 m²

Question 7.
Three identical coins, each of diameter 6 cm are placed as shown. Find the area of the shaded region between the coins. (π = 3.14) (√3 = 1.732)

Answer:
Given diameter of the coins = 6 cm
∴ Radius of the coins = \(\frac { 6 }{ 2 }\) = 3 cm
Area of the shaded region = Area of equilateral triangle – Area of 3 sectors of angle 60°

Area of the equilateral triangle = \(\frac{\sqrt{3}}{4}\) a² units² = \(\frac{\sqrt{3}}{4}\) × 6 × 6 cm²
= \(\frac{1.732}{4}\) × 6 × 6 cm² = 15.588 cm²
Area of 3 sectors = 3 × \(\frac{\theta}{360^{\circ}}\) × πr² sq.units
= 3 × \(\frac{60^{\circ}}{360^{\circ}}\) × 3.14 × 3 × 3 cm² = 1.458 cm²
∴ Area of the shaded region = 15.588 – 14.13 cm² = 1.458 cm²
Required area = 1.458 cm² (approximately)

Question 8.
Using Euler’s formula, find the unknowns.

Answer:
Euler’s formula is given by F + V – E = 2
(i) V = 6, E = 14
By Euler’s formula = F + 6 – 14 = 2
F = 2 + 14 – 6
F = 10

(ii) F = 8,E = 10
By Euler’s formula = 8 + V – 10 = 2
V = 2 – 8 + 10
V = 4

(iii) F = 20, V = 10
By Euler’s formula = 20 + 10 — E = 2
30 – E = 2
E = 30 – 2.
E = 28
Tabulating the required unknowns

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 2 Measurements Ex 2.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 2 Measurements Ex 2.3

Question 1.
Fill ini the blanks:

(i) The three dimensions of a cuboid are ______ , ______ and ______ .
Answer:
length, breadth, height

(ii) The meeting point of more than two edges in a polyhedron is called as ______ .
Answer:
Vertex

(iii) A cube has _________ faces.
Answer:
six

(iv) The cross section of a solid cylinder is ______ .
Answer:
circle

(v) If a net of a 3-D shape has six plane squares, then it is called ______ .
Answer:
cube

Question 2.
Match the following

Answer:
(i) – b
(ii) – a
(iii) – d
(iv) – c

Question 3.
Which 3 – D shapes do the following nets represents? Draw them.
(i)

Answer:
The net represents cube, because it has 6 squares.

(ii)

Answer:
The net represents cuboid

(iii)

Answer:
The net represents Triangular prism

(iv)

The net represents square pyramid

(v)

Answer:
Ine net represents cylinder

Question 4.
For each solid, three views are given. Identify for each solid, the corresponding Top, Front and Side (T, F and S) views.

Answer:

Question 5.
Verify Euler’s formula for the table given below.

Answer:
Euler’s formula is given by F + V – E = 2
(i) F = 4; V = 4; E = 6
F + V – E = 4 + 4 – 6 = 8 – 6
F + V – E = 2
∴ Euler’s formula is satisfied.

(ii) F = 10; V = 6; E = 12
F + V – E = 10 + 6 – 12 = 16 – 12 = 4 ≠ 2
∴ Euler’s formula is not satisfied.

(iii) F = 12; V = 20; E = 30
F + V – E = 12 + 20 – 30 = 32 – 30 = 2
∴Euler’s formula is satisfied.

(iv) F = 20; V = 13; E = 30
F + V – E = 20 + 13 – 30 = 33 – 30 = 3 ≠ 2
∴Euler’s formula is not satisfied.

(v) F = 32; V = 60; E = 90
F + V – E = 32 + 60 – 90 = 92 – 90 = 2
∴ Euler’s formula is satisfied.

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 2 Measurements Ex 2.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 2 Measurements Ex 2.2

Question 1.
Find the perimeter and area of the figures given below. (π = \(\frac{22}{7}\))
(i)

Answer:

Length of the arc of the semicircle = \(\frac{1}{2}\) × 2πr units
= \(\frac{22}{7} \times \frac{7}{2}\) m =11 m
∴ Perimeter = Sum of all lengths of sides that form the closed boundary
P = 11 + 10 + 7 + 10 m
Perimeter = 38 m
Area = Area of the rectangle – Area of semicircle
= (l × b) – \(\frac{1}{2}\) πr² sq. units

= 50.75 m² (approx)
Area of the figure = 50.75 m² approx.

(ii)

Answer:

Perimeter = sum of outside lengths
Length of the arc of quadrant circle = \(\frac{1}{4}\) × 2πr units
= \(\frac{1}{2} \times \frac{22}{7}\) × 3.5cm
= 11 × 0.5 cm = 5.5cm
∴ Length of arc of 2 sectors 2 × 5.5 cm
= 11 cm
∴ Perimeter P = 11 + 6 + 3.5 + 6 + 35 cm
P = 30 cm
Area Area of 2 quadrant circle + Area of a rectangle.
= 2 × \(\frac{1}{4}\)πr² + lb sq. units
= (\(\frac{1}{2} \times \frac{22}{7}\) × 3.5 × 3.5) + (6 × 3.5) cm²
= (11 × 3.5 × 0.5) + 21 cm²
= (19.25 + 21) cm² = 40.25 cm²
∴ Area = 40.25 cm² approx

Question 2.
Find the area of the shaded part in the following figures. (π = 3.14)
(i)

Answer:
Area of the shaded part = Area of 4 quadrant circles of radius \(\frac { 10 }{ 2 }\) cm
= 4 × \(\frac { 1 }{ 4 }\) × πr² = 3.14 × \(\frac { 10 }{ 2 }\) × \(\frac { 10 }{ 2 }\) cm²
= \(\frac { 314 }{ 4 }\) cm² = 78.5 cm²
Area of the shaded part = 78.5 cm²
Area of the unshaded part = Area of the square – Area of shaded part
= a² – 78.5 cm² = (10 × 10) – 78.5 cm²
= 100 – 78.5cm² = 21.5cm²
Area of the unshaded part = 21.5 cm² (approximately)

(ii)

Answer:
Area of the shaded part = Area of semicircle – Area of the triangle

= \(\frac { 1 }{ 2 }\) × 3.14 × 7 × 7 – \(\frac { 1 }{ 2 }\) × 14 × 7cm²
= \(\frac{153.86}{2}\) – 49 cm² = 76.93 – 49 cm²
= 27.3 cm²
∴ Area of the shaded part = 27.93 cm² (approximately)

Question 3.
Find the area of the combined figure given which is got by joining of two parallelograms

Answer:
Area of the figure = Area of 2 parallelograms with base 8 cm and height 3 cm
= 2 × (bh) sq. units
= 2 × 8 × 3cm² = 48 cm²
∴ Area of the given figure = 48 cm²

Question 4.
Find the area of the combined figure given, formed by joining a semicircle of diameter 6 cm with a triangle of base 6 cm and height 9 cm. (π = 3.14)

Answer:
Area of the figure = Area of the semicircle of radius 3 cm + 2 (Area of triangle with b = 9 cm and h = 3 cm)
= \(\left(\frac{1}{2} \pi r^{2}\right)+\left(2 \times \frac{1}{2} b h\right)\) sq. units
= \(\frac { 1 }{ 2 }\) × 3.14 × 3 × 3 + (2 × \(\frac { 1 }{ 2 }\) × 9 × 3)cm²
= \(\frac{28.26}{2}\) + 27 cm² = 14.13 + 27 cm² = 41.13 cm²
∴ Area of the figure = 41.13 cm² (approximately)

Question 5.
The door mat which is in a hexagonal shape has the following measures as given in the figure. Find its area.

Answer:
Area of the doormat = Area of 2 trapezium
Height of the trapezium h =\(\frac { 70 }{ 2 }\) cm: a = 90 cm; b = 70 cm
∴ Area of the trapezium = \(\frac { 1 }{ 2 }\) h (a + b) sq. units
Area of the door mat = 2 × \(\frac { 1 }{ 2 }\) × 35 (90 + 70)cm²
= 35 × 160 cm² = 5600 cm²
∴ Area of the door mat = 5600 cm²

Question 6.
A rocket drawing has the measures as given in the figure. Find its area.

Answer:
Area = Area of a rectangle + Area of a triangle + Area of a trapezium
For rectangle length l = 120 – 20 – 20 cm = 80 cm
Breadth b = 30 cm
For the triangle base = 30 cm
Height = 20 cm
For the trapezium height h = 20 cm
Parallel sided a = 50 cm
b = 30cm
∴ Area of the figure (l × b) + (\(\frac { 1 }{ 2 }\) × base × height) + \(\frac { 1 }{ 2 }\) × h × (a + b)sq. units
= (80 × 30) + (\(\frac { 1 }{ 2 }\) × 30 × 20) + \(\frac { 1 }{ 2 }\) × 20 × (50 + 30) cm²
= 2400 + 300 + 800 cm² = 3500 cm²
Area of the figure = 3500 cm²

Question 7.
Find the area of the irregular polygon shaped fields given below.

Answer:
Area of the field = Area of trapezium FBCH + Area of ∆DHC + Area of ∆EGD + Area of ∆EGA + Area of ∆BFA
Area of the triangle = \(\frac { 1 }{ 2 }\) bhsq.units
Area of the trapezium = \(\frac { 1 }{ 2 }\) × h × (a + b) sq.units
Area of the trapezium FBCH = \(\frac { 1 }{ 2 }\) × (10 + 8) × (8 + 3)m² = 9 × 11 = 99 m² ….. (1)
Area of the ∆DHC = \(\frac { 1 }{ 2 }\) × 8 × 5 m² = 20 m² ….. (2)
Area of ∆EGD = \(\frac { 1 }{ 2 }\) × 8 × 15m² = 60 m² …….. (3)
Area of ∆EGA = \(\frac { 1 }{ 2 }\) × 8 × (8 + 6)m² = 4 × 14 m²
= 56m²
Area of ∆BFA = \(\frac { 1 }{ 2 }\) × 3 × 6m² = 9 m²
∴ Area of the field = 99 + 20 + 60 + 56 + 9 m²
= 244 m²
Area of the field = 244 m²

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 2 Measurements Ex 2.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 2 Measurements Ex 2.1

Question 1.
Fill in the blanks:
(i) The ratio between the circumference and diameter of any circle is _______ .
Answer:
π

(ii) A line segment which joins any two points on a circle is a _______ .
Answer:
Chord

(iii) The longest chord of a circle is _______ .
Answer:
Diameter

(iv) The radius of a circle of diameter 24 cm is _______ .
Answer:
12 cm

(v) A part of circumference of a circle is called as _______ .
Answer:
an arc

Question 2.
Match the following

Answer:
(i) – c
(ii) – d
(iii) – e
(iv) – b
(v) – a

Question 3.
Find the central angle of the shaded sectors (each circle is divided into equal sectors).

Answer:

Question 4.
For the sectors with given measures, find the length of the arc, area and perimeter.
(π = 3. 14)
(i) central angle 45° r = 16 cm
Answer:
(i) central angle 45° r = 16 cm
Length of the arc l = \(\frac{\theta^{\circ}}{360^{\circ}}\) × 2πr units
l = \(\frac{45^{\circ}}{360^{\circ}}\) × 2 × 3.14 × 16 cm
l = \(\frac{1}{8}\) × 2 × 3.14 × 16 cm
l = 12.56 cm
Area of the sector = \(\frac{\theta^{\circ}}{360^{\circ}}\) × πr² sq. units
A = \(\frac{45^{\circ}}{360^{\circ}}\) × 3.14 × 16 × 16
A = 100.48 cm²
Perimeter of the sector P = l + 2r units
P = 12.56 + 2(16) cm
p = 44.56 cm

(ii) central angle 120°, d = 12.6 cm
Answer:
∴ r = \(\frac{12.6}{2}\) cm
r = 6.3cm
Length of the arc l = \(\frac{\theta^{\circ}}{360^{\circ}}\) × 2πr units
l = \(\frac{120^{\circ}}{360^{\circ}}\) × 2 × 3.14 × 63 cm
l = 13.188cm
I = 13.19cm
Area of the sector A = \(\frac{\theta^{\circ}}{360^{\circ}}\) × πr² sq. units
A = \(\frac{120^{\circ}}{360^{\circ}}\) × 3 14 × 6.3 × 6.3 cm²
A = 3.14 × 6.3 × 2.1 cm²
A = 41.54 cm²
Perimeter of the sector P = l + 2r cm
P = 13.19 + 2(6.3) cm
= 13.19 + 1.2.6 cm
P = 25.79 cm

Question 5.
From the measures given below, find the area of the sectors.
(i) Length of the arc = 48 m, r = 10 m
Answer:
Area of the sector A = \(\frac{l r}{2}\) sq. units
l = 48m
r = 10m
= \(\frac{48 \times 10}{2}\) m²
= 24 × 10m²
= 240 m²
Area of the sector = 240 m²

(ii) length of the arc = 50 cm, r = 13.5 cm
Answer:
Length of the arc l = 12.5 cm
Radius r = 6 cm
Area of the sector A = \(\frac{l r}{2}\) sq. units
A = \(\frac{12.5 \times 6}{2}\)
A = 12.5 × 3cm²
A = 37.5 cm²
Area of the sector A = 37.5 cm²

Question 6.
Find the central angle of each of the sectors whose measures are given below. (π = \(\frac{22}{7}\))
(i) area = 462 cm², r = 21 cm
Answer:
area = 462 cm², r = 21 cm
Radius of the Sector = 21 cm
Area of the sector = 462 cm²
\(\frac{l r}{2}\) = 462
\(\frac{l \times 21}{2}\) = 462
l = \(\frac{462 \times 2}{21}\)
l = 22 × 2
Length of the arc l = 44 cm

θ° = 120°
∴ Central angle of the sector = 120°

(ii) length of the arc = 44 m, r = 35 m
Answer:
Radius of the sector = 8.4cm
Area of the sector = 18.48 cm²
\(\frac{l r}{2}\) = 18.48
\(\frac{1 \times 8.4}{2}\) = 18.48
l = \(\frac{18.48 \times 2}{8.4}\)
Hint:

Length of the arc l = 4.4 cm

Hint:

θ° = 30°
Central angle = 30°

Question 7.
A circle of radius 120 m is divided into 8 equal sectors. Find the length of the arc of each of the sectors.
Answer:
Radius of the circle r = 120 m
Number of equal sectors = 8
∴ Central angle of each sector = \(\frac{360^{\circ}}{n}\)
θ° = \(\frac{360^{\circ}}{8}\)
θ° = 45°
Length of the arc l = \(\frac{\theta^{\circ}}{360^{\circ}}\) × 2πr units
= \(\frac{45^{\circ}}{360^{\circ}}\) × 2π × 120 m
Length of the arc = 30 × πm

Another method:
l = \(\frac{1}{n}\) × 2πr = \(\frac{1}{8}\) × 2 × π × 120 = 30 π m
Length of the arc = 30 π m

Question 8.
A circle of radius 70 cm is divided into 5 equal sectors. Find the area of each of the sectors.
Answer:
Radius of the sector r = 70 cm
Number of equal sectors = 5
∴ Central angle of each sector = \(\frac{360^{\circ}}{n}\)
θ° = 360°
θ° = 72°
Area of the sector = \(\frac{\theta^{\circ}}{360^{\circ}}\) × πr² sq.units
= \(\frac{72^{\circ}}{360^{\circ}}\) × π × 70 × 70cm²
Hint:

= 14 × 70 × πcm²
= 980 πcm²
Note: We can solve this problem using A = \(\frac{1}{n}\) πr² sq. units also.

Question 9.
Dhamu fixes a square tile of 30cm on the floor. The tile has a sector design on it as shown in the figure. Find the area of the sector. (π = 3.14).

Answer:
Side of the square = 30 cm
∴ Radius of the sector design = 30 cm
Given the design of a circular quadrant.
Area of the quadrant = \(\frac{1}{4}\) πr² sq.units
= \(\frac{1}{4}\) × 3.14 × 30 × 30cm²
= 3.14 × 15 × 15cm²
∴ Area of the sector design = 706.5 cm² (approximately)

Question 10.
A circle is formed with 8 equal granite stones as shown in the figure each of radius 56 cm and whose central angle is 45°. Find the area of each of the granite stones. (π = \(\frac { 22 }{ 7 }\))

Answer:
Number of equal sectors ‘n’ = 8
Radius of the sector ‘r’ = 56 cm
Area of each sector = \(\frac{1}{n}\) πr² sq. units
= \(\frac{1}{8} \times \frac{22}{7}\) × 56 × 56cm² =1232 cm²
Area of each sector = 1232 cm² (approximately)

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 1 Numbers InText Questions Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 1 Numbers InText Questions

Recap Exercise (Text Book Page No. 3)

Question 1.
The simplest form of \(\frac{125}{200}\) is
Answer:
\(\frac{125}{200}=\frac{125 \div 25}{200 \div 25}=\frac{5}{8}\)
= \(\frac{5}{8}\)

Question 2.
Which of the following is not an equivalent fraction of \(\frac{8}{12}\) ?
(A) \(\frac{2}{3}\)
(B) \(\frac{16}{24}\)
(C) \(\frac{32}{60}\)
(D) \(\frac{24}{36}\)
Answer:
(C) \(\frac{32}{60}\)
\(\frac{8}{12}=\frac{8+4}{12 \div 4}=\frac{2}{3}\)
\(\frac{8}{12}=\frac{8 \times 2}{12 \times 2}=\frac{16}{24}\)
\(\frac{8}{12}=\frac{8 \times 3}{12 \times 3}=\frac{24}{36}\)
But \(\frac{32}{60}=\frac{32 \div 5}{60 \div 5}=\frac{6.4}{12}\)
∴ \(\frac{32}{60}\) is not equivalent fraction of \(\frac{8}{12}\)

Question 3.
Which is bigger \(\frac{8}{9}\) or \(\frac{4}{5}\) ?
Answer:
LCM of 5 and 9 = 45

\(\frac{8}{9}\) is bigger than \(\frac{4}{5}\)

Question 4.
Add the fractions : \(\frac{3}{5}+\frac{5}{8}+\frac{7}{10}\).
Answer:
LCM of 5, 8, 10 = 5 × 2 × 4
= 40

Question 5.
Simplify: \(\frac{1}{8}-\left(\frac{1}{6}-\frac{1}{4}\right)\)
Answer:

Question 6.
Multiply: \(2 \frac{3}{5}\) and \(1 \frac{4}{7}\).
Answer:
\(2 \frac{3}{5} \times 1 \frac{4}{7}=\frac{13}{5} \times \frac{11}{7}=\frac{143}{35}=4 \frac{3}{35}\)

Question 7.
Divide \(\frac{7}{36}\) by \(\frac{35}{81}\).
Answer:
\(\frac{7}{36}+\frac{35}{81}=\frac{7}{36} \times \frac{81}{35}=\frac{9}{20}\)

Question 8.

Answer:

Question 9.
In a city \(\frac{7}{20}\) of the population are women and \(\frac{1}{4}\) are children. Find the fraction of the population of men.
Answer:
Let the total population = 1
Population of men = Total population – Women – Children

∴ Population of men = \(\frac{2}{5}\)

Question 10.
Represent \(\left(\frac{1}{2}+\frac{1}{4}\right)\) by a diagram.
Answer:

Try These (Text Book Page No. 3)

Question 1.
Is the number -7 a rational number? Why?
Answer:
A rational number, Because – 7 = \(\frac{-14}{2}=\frac{p}{q}\)

Question 2.
Write any 6 rational numbers between 0 and 1.
Answer:
\(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}, \frac{1}{7}\)

Try These (Text Book Page No. 4)

Write the decimal forms of the following rational numbers:

Question 1.
\(\frac{4}{5}\)
Answer:
\(\frac{4}{5}=\frac{4 \times 20}{5 \times 20}=\frac{80}{100}=0.80\)

Question 2.
\(\frac{6}{25}\)
Answer:
\(\frac{6}{25}=\frac{6 \times 4}{25 \times 4}=\frac{24}{100}=0.24\)

Question 3.
\(\frac{486}{1000}\)
Answer:
\(\frac{486}{1000}\) = 0.486

Question 4.
\(\frac{1}{9}\)
Answer:

\(\frac{1}{9}\) = 0.11….

Question 5.
\(3 \frac{1}{4}\)
Answer:

\(3 \frac{1}{4}\) = \(\frac{13}{4}\) = 3.25

Question 6.
\(-2 \frac{3}{5}\)
Answer:

\(-2 \frac{3}{5}\) = \(\frac{-13}{5}\) = -2.6

Try These (Text Book Page No. 6)

Question 1.
\(\frac{7}{3}=\frac{?}{9}=\frac{49}{?}=\frac{-21}{?}\)
Answer:

Question 2.
\(\frac{-2}{5}=\frac{?}{10}=\frac{6}{?}=\frac{-8}{?}\)
Answer:

Try These (Text Book Page No. 7)

Question 1.
Which of the following pairs represents equivalent rational numbers?
(i) \(\frac{-6}{4}, \frac{18}{-12}\)
(ii) \(\frac{-4}{-20}, \frac{1}{-5}\)
(iii) \(\frac{-12}{-17}, \frac{60}{85}\)
Answer:
(i) \(\frac{-6}{4}, \frac{18}{-12}\)
\(\frac{-6}{4}=\frac{-6 \times 3}{4 \times 3}=\frac{-18}{12}\)
∴ \(\frac{-6}{4}\) equivalent to \(\frac{-18}{12}\)

(ii) \(\frac{-4}{-20}, \frac{1}{-5}\)
\(\frac{-4}{-20}=\frac{-4 \div(-4)}{-20 \div(-4)}=\frac{1}{5} \neq-\frac{1}{5}\)
∴ \(\frac{-4}{-20}\) equivalent to \(\frac{1}{-5}\)

(iii) \(\frac{-12}{-17}, \frac{60}{85}\)
\(\frac{-12}{-17}=\frac{-12 x-5}{-17 x-5}=\frac{60}{85}\)
∴ \(\frac{-12}{-17}\) equivalent to \(\frac{60}{85}\)

Question 2.
Find the standard form of
(i) \(\frac{36}{-96}\)
(ii) \(\frac{-56}{-72}\)
(iii) \(\frac{27}{18}\)
Answer:
(i) \(\frac{36}{-96}\)
= \(\frac{-36 \div 12}{96 \div 12}=\frac{-3}{8}\)

(ii) \(\frac{-56}{-72}\)
= \(\frac{-56 \div(-8)}{-72 \div(-8)}=\frac{7}{9}\)

(iii) \(\frac{27}{18}\)
= \(1 \frac{9}{18}=1 \frac{1}{2}\)

Question 3.
Mark the following rational numbers on a number line.
(i) \(\frac{-2}{3}\)
Answer:
\(\frac{-2}{3}\) lies betveen 0 and -1.
T?ìe unit part between O and —lis divided into 3 equal parts and second part is taken.

(ii) \(\frac{-8}{-5}\)
Answer:
\(\frac{-8}{-5}\) = \(1 \frac{3}{5}\)
\(1 \frac{3}{5}\) lies between I and 2, The unit part between I and 2 is divided into 5 equal parts and the third part is taken.

(iii) \(\frac{5}{-4}\)
Answer:
\(\frac{5}{-4}\) = \(-\frac{5}{4}\) = \(-1 \frac{1}{4}\)
\(-1 \frac{1}{4}\) lies between -1 and -2. The unit part between -1 and -2 is divided into four equal parts and the first part is taken.

Think (Text Book Page No. 15)

Is zero a rational number? If so, what is its additive inverse
Answer:
Yes zero a rational number Additive inverse of zero is zero.

Think (Text Book Page No. 16)

What is the multiplicative inverse of 1 and -1?
Answer:
Multiplicative inverse of 1 is 1 and -1 is -1.

Try These (Text Book Page No. 16)

Divide
(i) \(\frac{-7}{3}\) by 5
(ii) 5 by \(\frac{-7}{3}\)
(iii) \(\frac{-7}{3}\) by \(\frac{35}{6}\)
Answer:
(i) \(\frac{-7}{3}\) by 5

(ii) 5 by \(\frac{-7}{3}\)

(iii) \(\frac{-7}{3}\) by \(\frac{35}{6}\)

Try These (Text Book Page No. 20)

The closure property on integers holds for subtraction and not for division. What about rational numbers? Verify.
Answer:
Let 0 and \(\frac{1}{2}\) te two rational numbers 0 – \(\frac{1}{2}\) = –\(\frac{1}{2}\) is a rational numter
∴ Closure property for subtraction holds for rational numbers.
But consider the two rational number \(\frac{5}{2}\) and 0.
\(\frac{5}{2}\) + 0 = \(\frac{5}{2 \times 0}=\frac{5}{0}\)
Here denominator = 0 and it is not a rational number.
∴ Closure property is not true for division of rational numbers.

Try These (Text Book Page No. 22)

(i) Is \(\frac{3}{5}-\frac{7}{8}=\frac{7}{8}-\frac{3}{5}\) ?
Answer:

LHS ≠ RHS
∴ \(\frac{3}{5} \div \frac{7}{8}\) ≠ \(\frac{7}{8}-\frac{3}{5}\)
∴ Subtraction of rational numbers is not commutative.

(ii) \(\frac{3}{5} \div \frac{7}{8}=\frac{7}{8} \div \frac{5}{3}\)? So, what do you conclude?
Answer:

LHS ≠ RHS
∴ \(\frac{3}{5} \div \frac{7}{8}\) ≠ \(\frac{7}{8} \div \frac{5}{3}\)
∴ Commutative property not hold good br division of rational numbers.

Try This (Text Book Page No. 22)

Check whether associative property holds for subtraction and division.
Answer:
Consider for rational numbers \(\frac{2}{3}, \frac{1}{2}\) and \(\frac{3}{4}\)

∴ Associative property not holds for subraction of rational numbers


∴ Associative property not holds for division of rational numbers

Try This (Text Book Page No. 25)

Question 1.
Observe that,
\(\frac{1}{1.2}+\frac{1}{2.3}=\frac{2}{3}\)
\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}=\frac{3}{4}\)
\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}=\frac{4}{5}\)
Use your reasoning skills, to find the sum of the first 7 numbers in the pattern given above.
Answer:

Think (Text Book Page No. 26)

Question 1.
Is the square of a prime number, prime?
Answer:
No, the square of a prime number ‘P’ has at Least 3 divisors 1, P and P². But a prime number is a number which has only two divisors, 1 and the number itself. So square of a prime number is not prime.

Question 2.
Will the sum of two perfect squares always be a perfect square? What about their difference and their product?
Answer:
The sum of two perfect squares, need not be always a perfect square. Also the difference of two perfect squares need not be always a perfect square. Bu the product of two perfect square is a perfect square.

Try These (Text Book Page No. 26)

Question 1.
Which among 256, 576, 960, 1025,4096 are perfect square numbers? (Hint: Try to extend the table of squares already seen).
Answer:
256 = 16²
576 = 24²
4096 = 64²
∴ 256, 576, and 4096 are perfect squares

Question 2.
One can judge just by look that each of the following numbers 82, 113, 1972, 2057, 8888, 24353 is not a perfect square. Explain why?
Answer:
Because the unit digit ola perfect square will be 0, 1,4, 5, 6, 9. But the given numbers have unit digits 2, 3, 7, 8. So they are not perfect squares.

Think (Text Book Page No. 27)

Consider the claim: “Between the squares of the consecutive numbers n and (n + 1), there are 2n non-square numbers’ Can it be true? FInd how many non-square numbers are there
(i) between 4 and 9 ?
(ii) between 49 and 64? and Verify the claim.
Answer:

Therefore we conclude that there are 2n non-square numbers between two consecutive square numbers.

Think (Text Book Page No. 30)

In this case, if we want to find the smallest factor with which we can multiply or divide 108 to get a square number, what should we do?
Answer:
108 = 2 × 2 × 3 × 3 = 2² × 3² × 3
If we multiply the factors by 2, then we get
2² × 3² × 3 × 3 = 2² × 3² × 3² = (2 × 3 × 3)²
Which is perfect square.
∴ Again if we divide by 3 then we get 2² × 3² ⇒ (2 × 3)², a perfect square.
∴ We have to multiply or divide 108 by 3 to get a perfect square.

Try These (Text Book Page No. 32)

Find the square root by long division method.
Question 1.
400
Answer:

√400 = 20

Question 2.
1764
Answer:

√1764 = 42

Question 3.
9801
Answer:

√9801 = 66

Try These (Text Book Page No. 32)

without calculating the square root, guess the number of digits in the square root of the following numbers:
Question 1.
14400
Answer:
\(\sqrt{14400}\) = \(\sqrt{144 \times 100}\)
= \(\sqrt{144} \times \sqrt{100}\)
= 12 × 10
= 120

Question 2.
390625
Answer:
\(\sqrt{390625}\) = \(\sqrt{25 \times 25 \times 25 \times 25}\)
= \(\sqrt{25 \times 25} \times \sqrt{25 \times 25}\)
= 25 × 25
= 625

Question 3.
100000000
Answer:
\(\sqrt{100000000}\) = \(\sqrt{10000 \times 10000}\)
= \(\sqrt{10000} \times \sqrt{10000}\)
= 100 × 100
= 10,000

Try These (Text Book Page No. 33)

Find the square root of
Question 1.
5.4756
Answer:

Question 2.
19.36
Answer:

Question 3.
116.64
Answer:

Think (Text Book Page No. 33)

Try to fill in the blanks using √ab = √a × √b

Answer:

Try These (Text Book Page No. 34)

Using this method, find the square root of the numbers 1.2321 and 11.9025.
Answer:
(i) 1.2321
√1.2321 = \(\sqrt{\frac{12321}{10000}}\)
= \(\frac{111}{100}\) = 1.11

(ii) 11.9025
√11.9025 = \(\frac{\sqrt{119025}}{\sqrt{10000}}\)
= \(\frac{345}{100}\) = 3.45

Try These (Text Book Page No. 34)

Write the numbers in ascending order.
Question 1.
4, √14, 5
Answer:
Squaring all the numbers we get 4², (√14)², 5² ⇒ 16, 14, 25
∴ Ascending order: 14, 16, 25
Ascending order: √14, 4, 5

Question 2.
7, √65, 8
Answer:
Squaring 7, √65 and 8 we get 7², (√65)², 8² ⇒ 49, 65, 64
Ascending order : 49, 64, 65
Ascending order: 7, 8, √65

Try These (Text Book Page No. 37)

Find the ones digit in the cubes of each of the following numbers.
(i) 12
(ii) 27
(iii) 38
(iv) 53
(v) 71
(vi) 84
Answer:
(i) 12
12 ends with 2, so its cube ends with 8 i.e. ones digit in 12³ is 8.

(ii) 27
27 ends with 7, so its cube end with 3. i.e., ones digit in 27³ is 3.

(iii) 38
38 ends with 8, so its cube ends with 2 i.e. ones digit in 38³ is 2.

(iv) 53
53 ends with 3, so its cube ends with 7. i.e, ones digit in 53³ is 7.

(v) 71
71 ends with 1, so its cube ends with 1. i.e. ones digit in 71³ is 1

(vi) 84
84 ends with 4, so its cube ends with 4. i.e, ones digit in 84³ is 4.

Try These (Text Book Page No. 41)

Expand the following numbers using exponents:
(i) 8120
(ii) 20,305
(iii) 3652.01
(iv) 9426.521
Answer:
(i) 8120
8120 = (8 × 1000) + (1 × 100) + (2 x×10) + 0 × 1
= (8 × 10³) + (1 × 10²) + (2 × 10¹)

(ii) 20,305
20305 = (2 × 10000) + (0 × 1000) + (3 × 100) + (0 × 10) + (5 × 1)
= (2 × 10⁴) + (3 × 10²) + 5

(iii) 3652.01
3652.01 = 3000 + 600 + 50 + 2 + \(\frac{0}{10}+\frac{1}{100}\)
= (3 × 1000) + (6 × 100) + (5 × 10) + (2 × 1) + (1 × \(\frac{1}{100}\))
= (3 × 10³) + (6 × 10²) + (5 × 10¹) + 2 + (1 × 10^-2)

(iv) 9426.521
= (9 × 1000) + (4 × 100) + (2 × 10) + (6 × 1) + \(\left(\frac{5}{10}\right)+\left(\frac{2}{100}\right)+\left(\frac{1}{1000}\right)\)
= (9 × 10³) + (4 × 10²) + (2 × 10¹) + 6 + (5 × 10^-1) + (2 × 10^-2) + (1 × 10^-3)

Try These (Text Book Page No. 42)

Verify the following rules (as we did above). Here, a,b are non-zero integers and are any integers.
1. Product of same powers to power of product rule: a^m × b^m = (ab)^m
2. Quotient of same powers to power of quotient rule: \(\frac{a^{m}}{b^{m}}=\left(\frac{a}{b}\right)^{m}\)
3. Zero exponent rule: a⁰ = 1.
Answer:
let a = 2; b = 3; m = 2
1. a^m × b^m = 2² × 3²
= 4 × 9 = 36 = (2 × 3)²

2. \(\frac{a^{m}}{b^{m}}=\frac{2^{2}}{3^{2}}=\frac{4}{9}=\left(\frac{2}{3}\right)^{2}\)

3. a⁰ = 2⁰ = 1.

Try These (Text Book Page No. 44)

Question 1.
Write in standard form: Mass of planet Uranus is 8.68 × 10²⁵ kg.
Answer:
Mass of Planet Uranus = 86800000000000000000000000 kg
[23 zeros after 88]

Question 2.
Write in scientific notation:
(i) 0.000012005
Answer:
0.000012005 = 1.2005 × 10^-5

(ii) 43 12.345
Answer:
43 12.345 = 4.312345 × 10³

(iii) 0.10524
Answer:
0.10524 = 1.0524 × 10^-1

(iv) The distance between the Sun and the planet Saturn 1.4335 × 10¹² miles.

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 1 Numbers Ex 1.7 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 1 Numbers Ex 1.7

Miscellaneous Practice Problems

Question 1.
If \(\frac{3}{4}\) of a box of apples weighs 3kg and 225 gm, how much does a full box of apples weigh?

Answer:
Let the total weight of a box of apple = x kg.
Weight of \(\frac{3}{4}\) of a box apples = 3 kg 225 gm.
= 3.225kg
\(\frac{3}{4}\) × x = 3225
x = \(\frac{3.225 \times 4}{3}\) kg
= 1.075 × 4kg = 4.3kg
= 4 kg 300 gm
Weight of the box of apples = 4 kg 300 gm.

Question 2.
Mangalam buys a water jug of capacity 3\(\frac{4}{5}\) litre. If she buys another jug which is 2\(\frac{2}{3}\) times as large as the smaller jug, how many litre can the larger one hold?
Answer:

Capacity of the small waterug = 3\(\frac{4}{5}\) litres.
Capacity of the big jug = \(2 \frac{2}{3}\) times the small one.
= \(2 \frac{2}{3} \times 3 \frac{4}{5}=\frac{8}{3} \times \frac{19}{5}=\frac{152}{15}\)
= \(\frac{2}{15}\) litres
Capacity of the large jug = \(\frac{2}{15}\) litres.

Question 3.
Ravi multiplied \(\frac { 25 }{ 8 }\) and \(\frac { 16 }{ 5 }\) to obtain \(\frac { 400 }{ 120 }\). He says that the simplest form of this product is \(\frac { 10 }{ 3 }\) and Chandru says the answer in the simplest form is \(3 \frac{1}{3}\). Who is correct? (or) Are they both correct? Explain.
Answer:

∴ The product is \(\frac{400}{120}\) and its simplest form improper fraction is \(\frac{10}{3}\)
And mixed fraction is \(3 \frac{1}{3}\)
∴ Both are correct

Question 4.
Find the length of a room whose area is \(\frac{153}{10}\) sq.m and whose breadth is \(2 \frac{11}{20}\)m.
Answer:
Length of the room × Breadth = Area of the room
Breadth of the room = \(2 \frac{11}{20}\) m
Area of the room = \(\frac{153}{10}\) sq.m
Length x \(2\frac{11}{20}\) = \(\frac{153}{10}\)

Length of the room = 6 m

Question 5.
There is a large square portrait of a leader that covers an area of 4489 cm². 1f each side has a 2 cm liner, what would be its area?
Answer:

Area of the square = 4489 cm²
(side)2 = 4489 cm²
(side)2 = 67 × 67
side = 67²
Length of a side = 67
Length of a side with liner = 67 + 2 + 2 cm
= 71 cm

Area of the larger square = 71 × 71 cm²
= 5041 cm²
Area of the liner = Area of big square – Area of small square
= (5041 – 4489) cm²
= 552 cm²

Question 6.
A greeting card has an area 90 cm². Between what two whole numbers is the length of its side?
Answer:

Area of the greeting card = 90 cm²
(side)² = 90 cm²
(side)² = 2 × 5 × 3 × 3 = 2 × 5 × 3²

Side = 3\(\sqrt{2 \times 5}\)
side = 3√10 cm
side = 3 × 3.2cm
side = 9.6 cm
∴ Side lies between the whole numbers 9 and 10.

Question 7.
225 square shaped mosaic tiles, each of area 1 square decimetre exactly cover a square shaped verandah. How long is each side of the square shaped verandah?
Answer:
Area of one tile = 1 sq.decimeter
Area of 225 tiles = 225 sq.decimeter
225 square tiles exactly covers the square shaped verandah.
∴ Area of 225 tiles = Area of the verandah
Area of the verandah = 225 sq.decimeter
side × side = 15 × 15 sq.decimeter
side = 15 decimeters
Length of each side of verandah = 15 decimeters.

Question 8.
If \(\sqrt[3]{1906624} \times \sqrt{x}\) = 31oo, find x.
Answer:

Question 9.
If 2^{m – 1} + 2^{m + 1} = 640, then find ‘m’.
Answer:
Given 2^{m – 1} + 2^{m + 1} = 640
2^{m – 1} + 2^{m + 1} = 128 + 512
2^{m – 1} + 2^{m + 1} – 2⁷ + 2⁹
m – 1 = 7
m = 7 + 1
m = 8
[consecutive powers of 2]

Powers of 2:
2, 4, 8, 16, 32, 64, 128, 256, 512,….

Question 10.
Give the answer in scientific notation:
A human heart beats at an average of 80 beats per minute. How many times does it beat in
i) an hour?
ii) a day?
iii) a year?
iv) 100 years?
Answer:
Heart beat per minute = 80 beats
(i) an hour
One hour = 60 minutes
Heart beat in an hour = 60 × 80
= 4800
= 4.8 × 10³

(ii) In a day
One day = 24 hours = 24 × 60 minutes
∴ Heart beat in one day = 24 × 60 × 80 = 24 × 4800 = 115200
= 1.152 × 10⁵

(iii) a year
One year = 365 days = 365 × 24 hours = 365 × 24 × 60 minutes
∴ Heart beats in a year = 365 × 24 × 60 × 80
= 42048000
= 4.2048 × 10⁷

(iv) 100 years
Heart beats in one year = 4.2048 × 10⁷
heart beats in 100 years = 4.2048 × 10⁷ × 100 = 4.2048 × 10⁷ × 10²
= 4.2048 × 10⁹

Challenging Problems:

Question 11.
In a map, if 1 inch refers to 120 km, then find the distance between two cities B and C which are \(4\frac{1}{6}\) inches and \(3\frac{1}{3}\) inches from the city A which lies between the cities B and C.
Answer:

1 inch = 120 km
Distance between A and B = \(4\frac{1}{6}\)
Distance between A and C = \(3\frac{1}{3}\)
∴ Distance between B and C = \(4 \frac{1}{6}+3 \frac{1}{3}\) inches

1 inch = 120km
∴ \(\frac{45}{6}\) inches = \(\frac{45}{6}\) × 120 km = 900 km
Distance between B and C = 900 km

Question 12.
Give an example and verify each of the following statements.
(i) The collection of all non-zero rational numbers is closed under division.
Answer:
let a = \(\frac{5}{6}\) and b = \(\frac{-4}{3}\) be two non zero rational numbers.

∴ Collection of non-zero rational numbers are closed under division.

(ii) Subtraction is not commutative for rational numbers.
Answer:
let a = \(\frac{1}{2}\) and b = \(-\frac{5}{6}\) be two rational numbers.

a – b ≠ b – a
∴ Subtraction is not commutative for rational numbers.

(iii) Division is not associative for rational numbers.
Answer:
Let a = \(\frac{2}{5}\), b = \(\frac{6}{5}\), c = \(\frac{3}{5}\) be three rational numbers.

a ÷ (b ÷ c) ≠ (a ÷ b) ÷ c
∴ Division is not associative for rational numbers.

(iv) Distributive property of multiplication over subtraction is true for rational numbers. That is, a (b – c) = ab – ac.
Answer:
Let a = \(\frac{2}{9}\), b = \(\frac{3}{6}\), c = \(\frac{1}{3}\) be three rational numbers.
To prove a × (b – c) = ab – bc

∴ From (1) and (2)
a × (b – c) = ab – bc
∴ Distributivity of multiplication over subtraction is true for rational numbers.

(v) The mean of two rational numbers is rational and lies between them.
Answer:
Let a = \(\frac{2}{11}\) and b = \(\frac{5}{6}\) be two rational numbers


∴ The mean lies between the given rational numbers \(\frac{2}{11}\) and \(\frac{5}{6}\)

Question 13.
If \(\frac { 1 }{ 4 }\) of a ragi adai weighs 120 grams, what will be the weight of \(\frac { 2 }{ 3 }\) of the same ragi adai ?
Answer:
Let the weight of 1 ragi adai = x grams
given \(\frac { 1 }{ 4 }\) of x = 120gm
\(\frac { 1 }{ 4 }\) × x = 120
x = 120 × 4
x = 480gm
∴ \(\frac { 2 }{ 3 }\) of the adai = \(\frac { 2 }{ 3 }\) × 480 gm = 2 × 160 gm = 320gm
\(\frac { 2 }{ 3 }\) of the weight of adai = 320gm

Question 14.
If p + 2q =18 and pq = 40, find \(\frac{2}{p}+\frac{1}{q}\)
Answer:
Given p + 2q = 18 ……… (1)
pq = 40 ……… (2)

Question 15.
Find x if \(5 \frac{x}{5} \times 3 \frac{3}{4}\) = 21.
Answer:

25 + x = 28
x = 28 – 25
x = 3

Question 16.

Answer:

Answer:

Question 17.
A group of 1536 cadets wanted to have a parade forming a square design. Is it possible? If it is not possible, how many more cadets would be required?
Answer:
Number of cadets to form square design


The numbers 2 and 3 are unpaired
∴ It is impossible to have the parade forming square design with 1536 cadets.

39 × 39 = 1521
Also 40 × 40 = 1600
∴ We have to add (1600 – 1536) = 64 to make 1536 a perfect square.
∴ 64 more cadets would be required to form the square design.

Question 18.
Evaluate: \(\sqrt{286225}\) and use it to compute \(\sqrt{2862.25}+\sqrt{28.6225}\)
Answer:

Question 19.
Simplify: (3.769 × 10⁵) + (4.21 × 10⁵)
Answer:
(3.769 × 10⁵) + (4.21 × 10⁵) = 3,76,900 + 4,21,000
= 7,97,000
= 7.979 × 10⁵

Question 20.
Order the following from the least to the greatest: 16²⁵, 8¹⁰⁰, 3⁵⁰⁰, 4⁴⁰⁰, 2⁶⁰⁰
Answer:
16²⁵ = (2⁴)²⁵ = 2¹⁰⁰
8¹⁰⁰ = (2³)¹⁰⁰ = 2³⁰⁰
4⁴⁰⁰ = (2²)⁴⁰⁰ = 2⁸⁰⁰
2⁶⁰⁰ = 2⁶⁰⁰
Comparing the powers we have.
2¹⁰⁰ < 2³⁰⁰ < 2⁶⁰⁰ < 2⁸⁰⁰
∴ The required order: 16²⁵, 8¹⁰⁰, 3⁵⁰⁰, 4⁴⁰⁰, 2⁶⁰⁰

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 1 Numbers Ex 1.6 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 1 Numbers Ex 1.6

Question 1.
Fill in the blanks.
(i) (-1)^{even integer} is __________ .
Answer:
1

(ii) For a ≠ 0, a⁰ is __________ .
Answer:
1

(iii) 4^-3 × 5^-3 = __________ .
Answer:
20^-3

(iv) (-2)^-7 is = __________ .
Answer:
\(\frac{-1}{128}\)

(v) \(\left(-\frac{1}{3}\right)^{-5}\) = _________ .
Answer:
– 243

Question 2.
Say True or False:
(i) If 8^x = \(\frac { 1 }{ 64 }\), the value of x is -2.
Answer:
True

(ii) The simplified form of \((256)^{\frac{-1}{4}} \times 4^{2}\) is \(\frac{1}{4}\).
Answer:
True

(iii) Using the power rule, \(\left(3^{7}\right)^{-2}\) = 3⁵
Answer:
True

(iv) The standard form of 2 × 10^-4 is 0.0002.
Answer:
False

(v) The scientific form of 123.456 is 1.23456 × 10^-2.
Answer:
True

Question 3.
Evaluate
(i) \(\left(\frac{1}{2}\right)^{3}\)
(ii) \(\left(\frac{1}{2}\right)^{-5}\)
(iii) \(\left(\frac{-5}{6}\right)^{-3}\)
(iv) (2^-5 × 2⁷) ÷ 2^-2
(v) (2^-1 × 3^-1) ÷ 6^-2
Answer:
(i) \(\left(\frac{1}{2}\right)^{3}\)

(ii) \(\left(\frac{1}{2}\right)^{-5}\)

(iii) \(\left(\frac{-5}{6}\right)^{-3}\)

(iv) (2^-5 × 2⁷) ÷ 2^-2
(2^-5 × 2⁷) ÷ 2^-2 = (2^{-5 + 7}) ÷ 2^-2
= 2² ÷ 2^-2
= 2²⁺²
= 2⁴
= 16

(v) (2^-1 × 3^-1) ÷ 6^-2
(2^-1 × 3^-1) ÷ 6^-2 = (2 × 3)^-1 ÷ 6^-2
= (6^-1) ÷ 6^-2
= 6^(-1)-(-2)
= 6¹
= 6

Question 4.
Evaluate
(i) \(\left(\frac{2}{5}\right)^{4} \times\left(\frac{5}{2}\right)^{-2}\)
(ii) \(\left(\frac{4}{5}\right)^{-2} \div\left(\frac{4}{5}\right)^{-3}\)
(iii) \(2^{7} \times\left(\frac{1}{2}\right)^{-3}\)
Answer:
(i) \(\left(\frac{2}{5}\right)^{4} \times\left(\frac{5}{2}\right)^{-2}\)

(ii) \(\left(\frac{4}{5}\right)^{-2} \div\left(\frac{4}{5}\right)^{-3}\)

(iii) \(2^{7} \times\left(\frac{1}{2}\right)^{-3}\)
= 2⁷ × 2³
= 2^{7 + 3}
= 2¹⁰

Question 5.
Evaluate:
(i) (5⁰ + 6^-1) × 3²
(ii) (2^-1 + 3^-1) ÷ 6^-1
(iii) (3^-1 + 4^-2 + 5^-3)⁰
Answer:
(i) (5⁰ + 6^-1) × 3²

(ii) (2^-1 + 3^-1) ÷ 6^-1
Answer:
(2^-1 + 3^-1) ÷ 6^-1 = \(\left(\frac{1}{2}+\frac{1}{3}\right)\) + 6^-1
= \(\left(\frac{3+2}{6}\right)\) + 6^-1 = \(\left(\frac{5}{6}\right)\) + 6^-1 = \(\frac{5}{6}\) × 6 = 5

(iii) (3^-1 + 4^-2 + 5^-3)⁰
Answer:
(3^-1 + 4^-2 + 5^-3)⁰ = 1
[∵ a⁰ = 1 where a ≠ 0]

Question 6.
Simplify
(i) (3²)³ × (2 × 3⁵)^-2 × (18)²
(ii) \(\frac{9^{2} \times 7^{3} \times 2^{5}}{84^{3}}\)
(iii) \(\frac{2^{8} \times 2187}{3^{5} \times 3^{2}}\)
Answer:
(i) (3²)³ × (2 × 3⁵)^-2 × (18)²

(ii) \(\frac{9^{2} \times 7^{3} \times 2^{5}}{84^{3}}\)

(iii) \(\frac{2^{8} \times 2187}{3^{5} \times 3^{2}}\)


= 2^8-5 × 3^7-5
= 2³ × 3²
= 8 × 9
= 72

Question 7.
Solve for x:
(i) \(\frac{2^{2 x-1}}{2^{x+2}}\) = 4
(ii) \(\frac{5^{5} \times 5^{-4} \times 5^{x}}{5^{12}}\) = 5^-5
Answer:
(i) \(\frac{2^{2 x-1}}{2^{x+2}}\) = 4
2^{2x – 1 – (x + 2)} = 2²
2^{2x – 1 – x – 2)} = 2²
2^{2x – 3} = 2²
Equating the powers of the same base 2.
x – 3 = 2
x – 3 + 3 = 2 + 3
x = 5

(ii) \(\frac{5^{5} \times 5^{-4} \times 5^{x}}{5^{12}}\) = 5^-5

⇒ 5^{1 + x – 12} = 5^-5
⇒ 5^{x – 11} = 5^-5
Equating the powers of same base 5.
x – 11 = – 5
x – 11 + 11 = – 5 + 11
x = 6

Question 8.
Expand using exponents:
(i) 6054.321
(ii) 897.14
Answer:
(i) 6054.321
6054.321 = (6 × 1000) + (0 × 100) + (5 × 10) + (4 × 10⁰) + \(\frac{3}{10}+\frac{2}{100}+\frac{1}{1000}\)
= (6 × 10³) + (5 × 10¹) + (4 × 10⁰) + \(\frac{3}{10}+\frac{2}{100}+\frac{1}{1000}\)
= (6 × 10³) + (5 × 10¹) + (4 × 10⁰) + (3 × 10^-1) + (2 × 10^-2) + (1 × 10^-3)

(ii) 897.14
= (8 × 100) + (9 × 10) + (7 × 10⁰) + \(\frac{1}{10}+\frac{4}{100}\)
= (8 × 1o²) +( 9 × 10¹) + (7 × 10⁰) + \(\left(1 \times \frac{1}{10}\right)+\left(4 \times \frac{1}{100}\right)\)
= (8 × 10³) + (9 × 10³) + (7 × 10⁰) + (1 × 10^-1) + (4 × 10^-2)

Question 9.
Find the number is standard form:
(i) 8 × 10⁴ + 7 × 10³ + 6 × 10² + 5 × 10¹ + 2 × 1 + 4 × 10^-2 + 7 × 10^-4
(ii) 5 × 10³ + 5 × 10¹ + 5 × 10^-1 + 5 × 10^-3
(iii) The radius of a hydrogen atom is 2.5 × 10^-11 m
Answer:
(i) 8 × 10⁴ + 7 × 10³ + 6 × 10² + 5 × 10¹ + 2 × 1 + 4 × 10^-2 + 7 × 10^-4
= 8 × 10⁴ + 7 × 10³ + 6 × 10² + 5 × 10¹ + 2 × 1 + 4 × 10^-2 + 7 × 10^-4
= 8 × 10000 + 7 × 1000 + 6 × 100 + 5 × 10 + 2 × 1 + 4 × \(\frac{1}{100}\) + 7 × \(\frac{1}{10000}\)
= 80000 + 7000 + 600 + 50 + 2 + \(\frac{4}{100}\) + \(\frac{7}{10000}\)
= 87652.0407

(ii) 5 × 10³ + 5 × 10¹ + 5 × 10^-1 + 5 × 10^-3
= 5 × 10³ + 5 × 10¹ + 5 × 10^-1 + 5 × 10^-3
= 5 × 1000 + 5 × 10 + 5 × \(\frac{1}{10}\) + 5 × \(\frac{1}{1000}\)
= 5000 + 50 + \(\frac{5}{10}+\frac{5}{1000}\) = 5050.505

(iii) The radius of a hydrogen atom is 2.5 10^-11 m
Radiys of a hydrogen atom = 2.5 × 10^-11 m
= \(2.5 \times \frac{1}{10^{11}} \mathrm{m}=\frac{2.5}{10^{11}} \mathrm{m}\)
= 0.000000000025 m

Question 10.
Write the following numbers in scientific notation:
(i) 467800000000
Answer:
467800000000 = 4.678 × 10¹¹

(ii) 0.000001972
Answer:
0.000001972 = 1.972 × 10^-6

(iii) 1642.398
Answer:
1642.398 = 1.642398 × 10³

(iv) Earth’s volume is about 1,083,000,000,000 cubic kilometres
Answer:
1,083,000,000,000
Earth’s volume = 1.083 110 × 10² cubic kilometres

(v) If you fill a bucket with dirt, the portion of the whole Earth that is in the bucket will be 0.00000000000000000000000 16 kg
Answer:
Portion of earth in the bucket = 0.00000000000000000000000 16 kg
= 1.6 10 × 10²⁴ kg.

Objective Type Questions

Question 11.
By what number should (-4)^-1 be multiplied so that the product becomes 10^-1?
(A) \(\frac{2}{3}\)
(B) \(\frac{-2}{5}\)
(C) \(\frac{5}{2}\)
(D) \(\frac{-5}{2}\)
Answer:
(B) \(\frac{-2}{5}\)
Hint:
(-4)^-1 = \(\left(-\frac{1}{4}\right)^{1}=\frac{-1}{4}\)

Question 12.
(-2)^-3 × (-2)^-2 = ___________.
(A) \(\frac{-1}{32}\)
(B) \(\frac{1}{32}\)
(C) 32
(D) -32
Answer:
(A) \(\frac{-1}{32}\)

Question 13.
Which is not correct?
(A) \(\left(\frac{-1}{4}\right)^{2}\) = 4^-2
(B) \(\left(\frac{-1}{4}\right)^{2}=\left(\frac{1}{2}\right)^{4}\)
(C) \(\left(\frac{-1}{4}\right)^{2}\) = 16^-1
(D) \(-\left(\frac{1}{4}\right)^{2}\) = 16^-1
Answer:
\(-\left(\frac{1}{4}\right)^{2}\) = 16^-1
Hint:
(-2) – 3 x (- 2) – 2 = (-2) – 3 – 2 = (-2) – 5 (\(-\frac { 1 }{ 2 }\))5 = \(-\frac { 1 }{ 32 }\)

Question 14.
If \(\frac{10^{x}}{10^{-3}}\) = 10⁹, then x is ___________ .
(A) 4
(B) 5
(C) 6
(D) 7

Question 15.
0.0000000002020 in scientific form is __________ .
(A) 2.02 × 10⁹
(B) 2.02 × 10^-9
(C) 2.02 × 10^-8
(D) 2.02 × 10^-10
Answer:
(D) 2.02 × 10^-10
Hint:
0.0000000002020

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 1 Numbers Ex 1.5 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 1 Numbers Ex 1.5

Question 1.
Fill in the blanks
(i) The ones digits in the cube of 73 is __________ .
Answer:
7

(ii) The maximum number of digits in the cube of a two digit number is __________ .
Answer:
6

(iii) The smallest number to be added to 3333 to make it a perfect cube is __________ .
Answer:
42

(iv) The cube root of 540×50 is __________ .
Answer:
30

(v) The cube root of 0.000004913 is __________ .
Answer:
0.017

Question 2.
Say True or False.
(i) The cube of 24 ends with the digit 4.
Answer:
True

(ii) Subtracting 103 from 1729 gives 93.
Answer:
True

(iii) The cube of 0.0012 is 0.000001728.
Answer:
False

(iv) 79570 is not a perfect cube.
Answer:
True

(v) The cube root of 250047 is 63.
Answer:
True

Question 3.
Show that 1944 is not a perfect cube.
Answer:

1944 = 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3

= 2³ × 3³ × 3 × 3
There are two triplets to make further triplets we need one more 3.
∴ 1944 is not a perfect cube.

Question 4.
Find the smallest number by which 10985 should be divided so that the quotient is a perfect cube.
Answer:

We have 10985 = 5 × 13 ×13 × 13
= 5 × 13 ×13 × 13
Here we have a triplet of 13 and we are left over with 5.
If we divide 10985 by 5, the new number will be a perfect cube.
∴ The required number is 5.

Question 5.
Find the smallest number by which 200 should be multiplied to make it a perfect cube.
Answer:


Grouping the prime factors of 200 as triplets, we are left with 5 × 5
We need one more 5 to make it a perfect cube.
So to make 200 a perfect cube multiply both sides by 5.

1000 = 2 × 2 × 2 × 5 × 5 × 5 × 5 × 5
Now 1000 is a perfect cube.
∴ The required number is 5.

Question 6.
Find the cube root 24 × 36 × 80 × 25.
Answer:

Question 7.
Find the cube root of 729 and 6859 prime factorisation.
Answer:
(i)


= 3 × 3
\(\sqrt[3]{729}\) = 9

(ii) \(\sqrt[3]{6859}\) = \(\sqrt[3]{19 \times 19 \times 19}\)
\(\sqrt[3]{6859}\) = 19

Question 8.
What is the square root of cube root of 46656?
Answer:

We have to find out \(\sqrt{(\sqrt[3]{46656})}\)
First we will find \(\sqrt[3]{46656}\)

∴ The required number is 6.

Question 9.
If the cube of a squared number is 729, find the square root of that number.
Answer:

(729)^1/3 = 3 × 3 = 9
∴ The cube of 9 is 729.
9 = 3 × 3 [ie 3 is squared to get 9]

We have to find out √3,
√3 = 1.732

Question 10.
Find two smallest perfect square numbers which when multiplied together gives a perfect cube number.
Answer:
Consider the numbers 2² and 4²
The numbers are 4 and 16.
Their procluct 4 × 16 = 64
64 = 4 × 4 × 4
∴ The required square numbers are 4 and 16