Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 2 Measurements Ex 2.2 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 2 Measurements Ex 2.2
Question 1.
Find the perimeter and area of the figures given below. (π = \(\frac{22}{7}\))
(i)
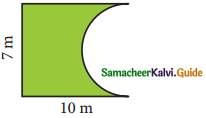
Answer:
Length of the arc of the semicircle = \(\frac{1}{2}\) × 2πr units
= \(\frac{22}{7} \times \frac{7}{2}\) m =11 m
∴ Perimeter = Sum of all lengths of sides that form the closed boundary
P = 11 + 10 + 7 + 10 m
Perimeter = 38 m
Area = Area of the rectangle – Area of semicircle
= (l × b) – \(\frac{1}{2}\) πr2 sq. units
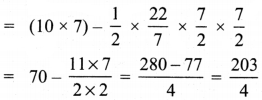
= 50.75 m2 (approx)
Area of the figure = 50.75 m2 approx.
![]()
(ii)
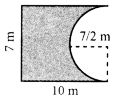
Answer:
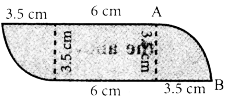
Perimeter = sum of outside lengths
Length of the arc of quadrant circle = \(\frac{1}{4}\) × 2πr units
= \(\frac{1}{2} \times \frac{22}{7}\) × 3.5cm
= 11 × 0.5 cm = 5.5cm
∴ Length of arc of 2 sectors 2 × 5.5 cm
= 11 cm
∴ Perimeter P = 11 + 6 + 3.5 + 6 + 35 cm
P = 30 cm
Area Area of 2 quadrant circle + Area of a rectangle.
= 2 × \(\frac{1}{4}\)πr2 + lb sq. units
= (\(\frac{1}{2} \times \frac{22}{7}\) × 3.5 × 3.5) + (6 × 3.5) cm2
= (11 × 3.5 × 0.5) + 21 cm2
= (19.25 + 21) cm2 = 40.25 cm2
∴ Area = 40.25 cm2 approx
![]()
Question 2.
Find the area of the shaded part in the following figures. (π = 3.14)
(i)
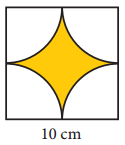
Answer:
Area of the shaded part = Area of 4 quadrant circles of radius \(\frac { 10 }{ 2 }\) cm
= 4 × \(\frac { 1 }{ 4 }\) × πr2 = 3.14 × \(\frac { 10 }{ 2 }\) × \(\frac { 10 }{ 2 }\) cm2
= \(\frac { 314 }{ 4 }\) cm2 = 78.5 cm2
Area of the shaded part = 78.5 cm2
Area of the unshaded part = Area of the square – Area of shaded part
= a2 – 78.5 cm2 = (10 × 10) – 78.5 cm2
= 100 – 78.5cm2 = 21.5cm2
Area of the unshaded part = 21.5 cm2 (approximately)
(ii)
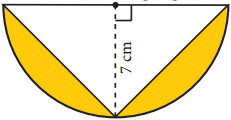
Answer:
Area of the shaded part = Area of semicircle – Area of the triangle
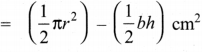
= \(\frac { 1 }{ 2 }\) × 3.14 × 7 × 7 – \(\frac { 1 }{ 2 }\) × 14 × 7cm2
= \(\frac{153.86}{2}\) – 49 cm2 = 76.93 – 49 cm2
= 27.3 cm2
∴ Area of the shaded part = 27.93 cm2 (approximately)
![]()
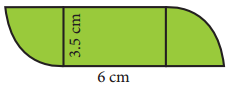
Question 3.
Find the area of the combined figure given which is got by joining of two parallelograms
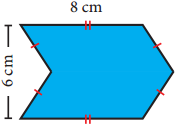
Answer:
Area of the figure = Area of 2 parallelograms with base 8 cm and height 3 cm
= 2 × (bh) sq. units
= 2 × 8 × 3cm2 = 48 cm2
∴ Area of the given figure = 48 cm2
Question 4.
Find the area of the combined figure given, formed by joining a semicircle of diameter 6 cm with a triangle of base 6 cm and height 9 cm. (π = 3.14)

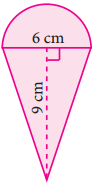
Answer:
Area of the figure = Area of the semicircle of radius 3 cm + 2 (Area of triangle with b = 9 cm and h = 3 cm)
= \(\left(\frac{1}{2} \pi r^{2}\right)+\left(2 \times \frac{1}{2} b h\right)\) sq. units
= \(\frac { 1 }{ 2 }\) × 3.14 × 3 × 3 + (2 × \(\frac { 1 }{ 2 }\) × 9 × 3)cm2
= \(\frac{28.26}{2}\) + 27 cm2 = 14.13 + 27 cm2 = 41.13 cm2
∴ Area of the figure = 41.13 cm2 (approximately)
![]()
Question 5.
The door mat which is in a hexagonal shape has the following measures as given in the figure. Find its area.
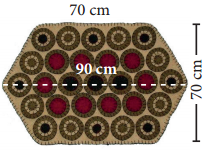
Answer:
Area of the doormat = Area of 2 trapezium
Height of the trapezium h =\(\frac { 70 }{ 2 }\) cm: a = 90 cm; b = 70 cm
∴ Area of the trapezium = \(\frac { 1 }{ 2 }\) h (a + b) sq. units
Area of the door mat = 2 × \(\frac { 1 }{ 2 }\) × 35 (90 + 70)cm2
= 35 × 160 cm2 = 5600 cm2
∴ Area of the door mat = 5600 cm2
Question 6.
A rocket drawing has the measures as given in the figure. Find its area.
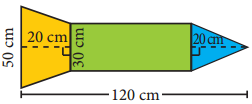
Answer:
Area = Area of a rectangle + Area of a triangle + Area of a trapezium
For rectangle length l = 120 – 20 – 20 cm = 80 cm
Breadth b = 30 cm
For the triangle base = 30 cm
Height = 20 cm
For the trapezium height h = 20 cm
Parallel sided a = 50 cm
b = 30cm
∴ Area of the figure (l × b) + (\(\frac { 1 }{ 2 }\) × base × height) + \(\frac { 1 }{ 2 }\) × h × (a + b)sq. units
= (80 × 30) + (\(\frac { 1 }{ 2 }\) × 30 × 20) + \(\frac { 1 }{ 2 }\) × 20 × (50 + 30) cm2
= 2400 + 300 + 800 cm2 = 3500 cm2
Area of the figure = 3500 cm2
![]()
Question 7.
Find the area of the irregular polygon shaped fields given below.
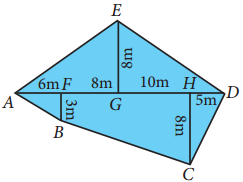
Answer:
Area of the field = Area of trapezium FBCH + Area of ∆DHC + Area of ∆EGD + Area of ∆EGA + Area of ∆BFA
Area of the triangle = \(\frac { 1 }{ 2 }\) bhsq.units
Area of the trapezium = \(\frac { 1 }{ 2 }\) × h × (a + b) sq.units
Area of the trapezium FBCH = \(\frac { 1 }{ 2 }\) × (10 + 8) × (8 + 3)m2 = 9 × 11 = 99 m2 ….. (1)
Area of the ∆DHC = \(\frac { 1 }{ 2 }\) × 8 × 5 m2 = 20 m2 ….. (2)
Area of ∆EGD = \(\frac { 1 }{ 2 }\) × 8 × 15m2 = 60 m2 …….. (3)
Area of ∆EGA = \(\frac { 1 }{ 2 }\) × 8 × (8 + 6)m2 = 4 × 14 m2
= 56m2
Area of ∆BFA = \(\frac { 1 }{ 2 }\) × 3 × 6m2 = 9 m2
∴ Area of the field = 99 + 20 + 60 + 56 + 9 m2
= 244 m2
Area of the field = 244 m2