Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 1 Numbers Ex 1.7 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 1 Numbers Ex 1.7
Miscellaneous Practice Problems
Question 1.
If \(\frac{3}{4}\) of a box of apples weighs 3kg and 225 gm, how much does a full box of apples weigh?

Answer:
Let the total weight of a box of apple = x kg.
Weight of \(\frac{3}{4}\) of a box apples = 3 kg 225 gm.
= 3.225kg
\(\frac{3}{4}\) × x = 3225
x = \(\frac{3.225 \times 4}{3}\) kg
= 1.075 × 4kg = 4.3kg
= 4 kg 300 gm
Weight of the box of apples = 4 kg 300 gm.
![]()
Question 2.
Mangalam buys a water jug of capacity 3\(\frac{4}{5}\) litre. If she buys another jug which is 2\(\frac{2}{3}\) times as large as the smaller jug, how many litre can the larger one hold?
Answer:

Capacity of the small waterug = 3\(\frac{4}{5}\) litres.
Capacity of the big jug = \(2 \frac{2}{3}\) times the small one.
= \(2 \frac{2}{3} \times 3 \frac{4}{5}=\frac{8}{3} \times \frac{19}{5}=\frac{152}{15}\)
= \(\frac{2}{15}\) litres
Capacity of the large jug = \(\frac{2}{15}\) litres.
Question 3.
Ravi multiplied \(\frac { 25 }{ 8 }\) and \(\frac { 16 }{ 5 }\) to obtain \(\frac { 400 }{ 120 }\). He says that the simplest form of this product is \(\frac { 10 }{ 3 }\) and Chandru says the answer in the simplest form is \(3 \frac{1}{3}\). Who is correct? (or) Are they both correct? Explain.
Answer:

∴ The product is \(\frac{400}{120}\) and its simplest form improper fraction is \(\frac{10}{3}\)
And mixed fraction is \(3 \frac{1}{3}\)
∴ Both are correct
![]()
Question 4.
Find the length of a room whose area is \(\frac{153}{10}\) sq.m and whose breadth is \(2 \frac{11}{20}\)m.
Answer:
Length of the room × Breadth = Area of the room
Breadth of the room = \(2 \frac{11}{20}\) m
Area of the room = \(\frac{153}{10}\) sq.m
Length x \(2\frac{11}{20}\) = \(\frac{153}{10}\)
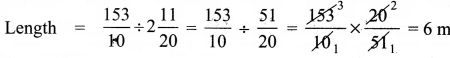
Length of the room = 6 m
Question 5.
There is a large square portrait of a leader that covers an area of 4489 cm2. 1f each side has a 2 cm liner, what would be its area?
Answer:
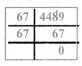
Area of the square = 4489 cm2
(side)2 = 4489 cm2
(side)2 = 67 × 67
side = 672
Length of a side = 67
Length of a side with liner = 67 + 2 + 2 cm
= 71 cm
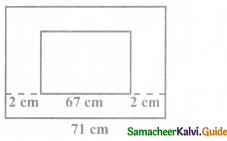
Area of the larger square = 71 × 71 cm2
= 5041 cm2
Area of the liner = Area of big square – Area of small square
= (5041 – 4489) cm2
= 552 cm2
![]()
Question 6.
A greeting card has an area 90 cm2. Between what two whole numbers is the length of its side?
Answer:
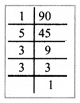
Area of the greeting card = 90 cm2
(side)2 = 90 cm2
(side)2 = 2 × 5 × 3 × 3 = 2 × 5 × 32
![]()
Side = 3\(\sqrt{2 \times 5}\)
side = 3√10 cm
side = 3 × 3.2cm
side = 9.6 cm
∴ Side lies between the whole numbers 9 and 10.
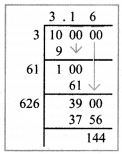
Question 7.
225 square shaped mosaic tiles, each of area 1 square decimetre exactly cover a square shaped verandah. How long is each side of the square shaped verandah?
Answer:
Area of one tile = 1 sq.decimeter
Area of 225 tiles = 225 sq.decimeter
225 square tiles exactly covers the square shaped verandah.
∴ Area of 225 tiles = Area of the verandah
Area of the verandah = 225 sq.decimeter
side × side = 15 × 15 sq.decimeter
side = 15 decimeters
Length of each side of verandah = 15 decimeters.
![]()
Question 8.
If \(\sqrt[3]{1906624} \times \sqrt{x}\) = 31oo, find x.
Answer:

Question 9.
If 2m – 1 + 2m + 1 = 640, then find ‘m’.
Answer:
Given 2m – 1 + 2m + 1 = 640
2m – 1 + 2m + 1 = 128 + 512
2m – 1 + 2m + 1 – 27 + 29
m – 1 = 7
m = 7 + 1
m = 8
[consecutive powers of 2]
Powers of 2:
2, 4, 8, 16, 32, 64, 128, 256, 512,….
![]()
Question 10.
Give the answer in scientific notation:
A human heart beats at an average of 80 beats per minute. How many times does it beat in
i) an hour?
ii) a day?
iii) a year?
iv) 100 years?
Answer:
Heart beat per minute = 80 beats
(i) an hour
One hour = 60 minutes
Heart beat in an hour = 60 × 80
= 4800
= 4.8 × 103
(ii) In a day
One day = 24 hours = 24 × 60 minutes
∴ Heart beat in one day = 24 × 60 × 80 = 24 × 4800 = 115200
= 1.152 × 105
(iii) a year
One year = 365 days = 365 × 24 hours = 365 × 24 × 60 minutes
∴ Heart beats in a year = 365 × 24 × 60 × 80
= 42048000
= 4.2048 × 107
![]()
(iv) 100 years
Heart beats in one year = 4.2048 × 107
heart beats in 100 years = 4.2048 × 107 × 100 = 4.2048 × 107 × 102
= 4.2048 × 109
Challenging Problems:
Question 11.
In a map, if 1 inch refers to 120 km, then find the distance between two cities B and C which are \(4\frac{1}{6}\) inches and \(3\frac{1}{3}\) inches from the city A which lies between the cities B and C.
Answer:
![]()
1 inch = 120 km
Distance between A and B = \(4\frac{1}{6}\)
Distance between A and C = \(3\frac{1}{3}\)
∴ Distance between B and C = \(4 \frac{1}{6}+3 \frac{1}{3}\) inches
![]()
1 inch = 120km
∴ \(\frac{45}{6}\) inches = \(\frac{45}{6}\) × 120 km = 900 km
Distance between B and C = 900 km
![]()
Question 12.
Give an example and verify each of the following statements.
(i) The collection of all non-zero rational numbers is closed under division.
Answer:
let a = \(\frac{5}{6}\) and b = \(\frac{-4}{3}\) be two non zero rational numbers.
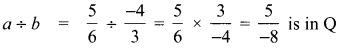
∴ Collection of non-zero rational numbers are closed under division.
(ii) Subtraction is not commutative for rational numbers.
Answer:
let a = \(\frac{1}{2}\) and b = \(-\frac{5}{6}\) be two rational numbers.
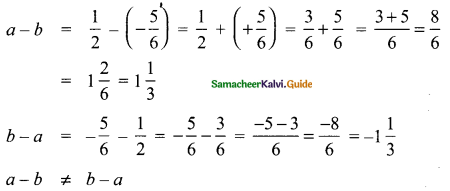
a – b ≠ b – a
∴ Subtraction is not commutative for rational numbers.
![]()
(iii) Division is not associative for rational numbers.
Answer:
Let a = \(\frac{2}{5}\), b = \(\frac{6}{5}\), c = \(\frac{3}{5}\) be three rational numbers.

a ÷ (b ÷ c) ≠ (a ÷ b) ÷ c
∴ Division is not associative for rational numbers.
(iv) Distributive property of multiplication over subtraction is true for rational numbers. That is, a (b – c) = ab – ac.
Answer:
Let a = \(\frac{2}{9}\), b = \(\frac{3}{6}\), c = \(\frac{1}{3}\) be three rational numbers.
To prove a × (b – c) = ab – bc
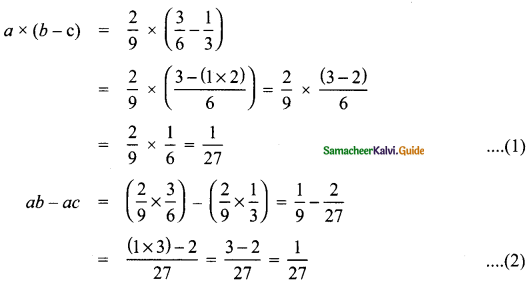
∴ From (1) and (2)
a × (b – c) = ab – bc
∴ Distributivity of multiplication over subtraction is true for rational numbers.
![]()
(v) The mean of two rational numbers is rational and lies between them.
Answer:
Let a = \(\frac{2}{11}\) and b = \(\frac{5}{6}\) be two rational numbers

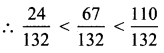
∴ The mean lies between the given rational numbers \(\frac{2}{11}\) and \(\frac{5}{6}\)
Question 13.
If \(\frac { 1 }{ 4 }\) of a ragi adai weighs 120 grams, what will be the weight of \(\frac { 2 }{ 3 }\) of the same ragi adai ?
Answer:
Let the weight of 1 ragi adai = x grams
given \(\frac { 1 }{ 4 }\) of x = 120gm
\(\frac { 1 }{ 4 }\) × x = 120
x = 120 × 4
x = 480gm
∴ \(\frac { 2 }{ 3 }\) of the adai = \(\frac { 2 }{ 3 }\) × 480 gm = 2 × 160 gm = 320gm
\(\frac { 2 }{ 3 }\) of the weight of adai = 320gm
![]()
Question 14.
If p + 2q =18 and pq = 40, find \(\frac{2}{p}+\frac{1}{q}\)
Answer:
Given p + 2q = 18 ……… (1)
pq = 40 ……… (2)
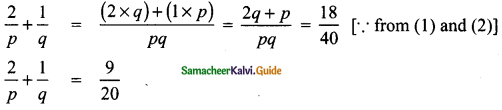
Question 15.
Find x if \(5 \frac{x}{5} \times 3 \frac{3}{4}\) = 21.
Answer:

25 + x = 28
x = 28 – 25
x = 3
![]()
Question 16.

Answer:
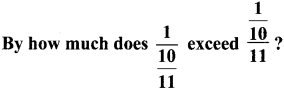
Answer:
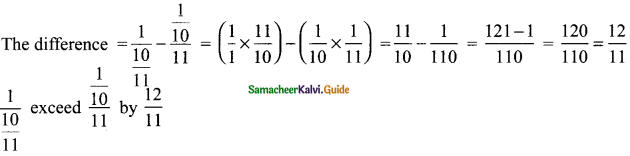
Question 17.
A group of 1536 cadets wanted to have a parade forming a square design. Is it possible? If it is not possible, how many more cadets would be required?
Answer:
Number of cadets to form square design
![]()

The numbers 2 and 3 are unpaired
∴ It is impossible to have the parade forming square design with 1536 cadets.
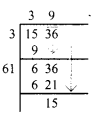
39 × 39 = 1521
Also 40 × 40 = 1600
∴ We have to add (1600 – 1536) = 64 to make 1536 a perfect square.
∴ 64 more cadets would be required to form the square design.
![]()
Question 18.
Evaluate: \(\sqrt{286225}\) and use it to compute \(\sqrt{2862.25}+\sqrt{28.6225}\)
Answer:

Question 19.
Simplify: (3.769 × 105) + (4.21 × 105)
Answer:
(3.769 × 105) + (4.21 × 105) = 3,76,900 + 4,21,000
= 7,97,000
= 7.979 × 105
![]()
Question 20.
Order the following from the least to the greatest: 1625, 8100, 3500, 4400, 2600
Answer:
1625 = (24)25 = 2100
8100 = (23)100 = 2300
4400 = (22)400 = 2800
2600 = 2600
Comparing the powers we have.
2100 < 2300 < 2600 < 2800
∴ The required order: 1625, 8100, 3500, 4400, 2600