Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 1 Numbers Ex 1.6 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 1 Numbers Ex 1.6
Question 1.
Fill in the blanks.
(i) (-1)even integer is __________ .
Answer:
1
(ii) For a ≠ 0, a0 is __________ .
Answer:
1
![]()
(iii) 4-3 × 5-3 = __________ .
Answer:
20-3
(iv) (-2)-7 is = __________ .
Answer:
\(\frac{-1}{128}\)
(v) \(\left(-\frac{1}{3}\right)^{-5}\) = _________ .
Answer:
– 243
Question 2.
Say True or False:
(i) If 8x = \(\frac { 1 }{ 64 }\), the value of x is -2.
Answer:
True
(ii) The simplified form of \((256)^{\frac{-1}{4}} \times 4^{2}\) is \(\frac{1}{4}\).
Answer:
True
![]()
(iii) Using the power rule, \(\left(3^{7}\right)^{-2}\) = 35
Answer:
True
(iv) The standard form of 2 × 10-4 is 0.0002.
Answer:
False
(v) The scientific form of 123.456 is 1.23456 × 10-2.
Answer:
True
Question 3.
Evaluate
(i) \(\left(\frac{1}{2}\right)^{3}\)
(ii) \(\left(\frac{1}{2}\right)^{-5}\)
(iii) \(\left(\frac{-5}{6}\right)^{-3}\)
(iv) (2-5 × 27) ÷ 2-2
(v) (2-1 × 3-1) ÷ 6-2
Answer:
(i) \(\left(\frac{1}{2}\right)^{3}\)
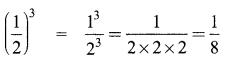
![]()
(ii) \(\left(\frac{1}{2}\right)^{-5}\)
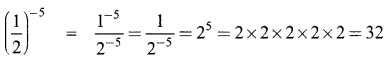
(iii) \(\left(\frac{-5}{6}\right)^{-3}\)
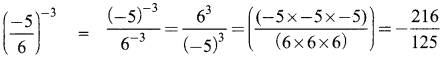
(iv) (2-5 × 27) ÷ 2-2
(2-5 × 27) ÷ 2-2 = (2-5 + 7) ÷ 2-2
= 22 ÷ 2-2
= 22+2
= 24
= 16
(v) (2-1 × 3-1) ÷ 6-2
(2-1 × 3-1) ÷ 6-2 = (2 × 3)-1 ÷ 6-2
= (6-1) ÷ 6-2
= 6(-1)-(-2)
= 61
= 6
![]()
Question 4.
Evaluate
(i) \(\left(\frac{2}{5}\right)^{4} \times\left(\frac{5}{2}\right)^{-2}\)
(ii) \(\left(\frac{4}{5}\right)^{-2} \div\left(\frac{4}{5}\right)^{-3}\)
(iii) \(2^{7} \times\left(\frac{1}{2}\right)^{-3}\)
Answer:
(i) \(\left(\frac{2}{5}\right)^{4} \times\left(\frac{5}{2}\right)^{-2}\)
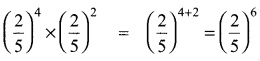
(ii) \(\left(\frac{4}{5}\right)^{-2} \div\left(\frac{4}{5}\right)^{-3}\)
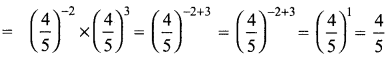
(iii) \(2^{7} \times\left(\frac{1}{2}\right)^{-3}\)
= 27 × 23
= 27 + 3
= 210
Question 5.
Evaluate:
(i) (50 + 6-1) × 32
(ii) (2-1 + 3-1) ÷ 6-1
(iii) (3-1 + 4-2 + 5-3)0
Answer:
(i) (50 + 6-1) × 32
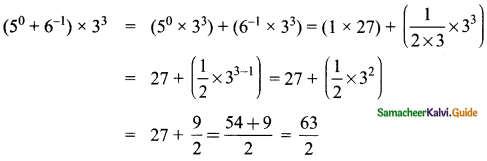
![]()
(ii) (2-1 + 3-1) ÷ 6-1
Answer:
(2-1 + 3-1) ÷ 6-1 = \(\left(\frac{1}{2}+\frac{1}{3}\right)\) + 6-1
= \(\left(\frac{3+2}{6}\right)\) + 6-1 = \(\left(\frac{5}{6}\right)\) + 6-1 = \(\frac{5}{6}\) × 6 = 5
(iii) (3-1 + 4-2 + 5-3)0
Answer:
(3-1 + 4-2 + 5-3)0 = 1
[∵ a0 = 1 where a ≠ 0]
Question 6.
Simplify
(i) (32)3 × (2 × 35)-2 × (18)2
(ii) \(\frac{9^{2} \times 7^{3} \times 2^{5}}{84^{3}}\)
(iii) \(\frac{2^{8} \times 2187}{3^{5} \times 3^{2}}\)
Answer:
(i) (32)3 × (2 × 35)-2 × (18)2
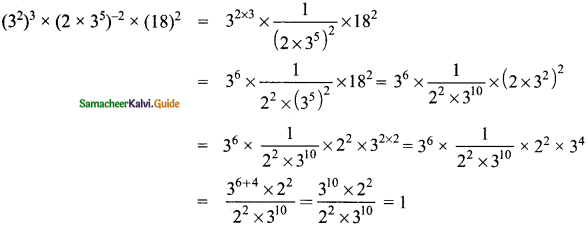
![]()
(ii) \(\frac{9^{2} \times 7^{3} \times 2^{5}}{84^{3}}\)
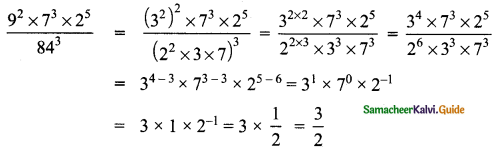
(iii) \(\frac{2^{8} \times 2187}{3^{5} \times 3^{2}}\)

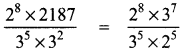
= 28-5 × 37-5
= 23 × 32
= 8 × 9
= 72
![]()
Question 7.
Solve for x:
(i) \(\frac{2^{2 x-1}}{2^{x+2}}\) = 4
(ii) \(\frac{5^{5} \times 5^{-4} \times 5^{x}}{5^{12}}\) = 5-5
Answer:
(i) \(\frac{2^{2 x-1}}{2^{x+2}}\) = 4
22x – 1 – (x + 2) = 22
22x – 1 – x – 2) = 22
22x – 3 = 22
Equating the powers of the same base 2.
x – 3 = 2
x – 3 + 3 = 2 + 3
x = 5
(ii) \(\frac{5^{5} \times 5^{-4} \times 5^{x}}{5^{12}}\) = 5-5
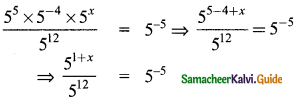
⇒ 51 + x – 12 = 5-5
⇒ 5x – 11 = 5-5
Equating the powers of same base 5.
x – 11 = – 5
x – 11 + 11 = – 5 + 11
x = 6
![]()
Question 8.
Expand using exponents:
(i) 6054.321
(ii) 897.14
Answer:
(i) 6054.321
6054.321 = (6 × 1000) + (0 × 100) + (5 × 10) + (4 × 100) + \(\frac{3}{10}+\frac{2}{100}+\frac{1}{1000}\)
= (6 × 103) + (5 × 101) + (4 × 100) + \(\frac{3}{10}+\frac{2}{100}+\frac{1}{1000}\)
= (6 × 103) + (5 × 101) + (4 × 100) + (3 × 10-1) + (2 × 10-2) + (1 × 10-3)
(ii) 897.14
= (8 × 100) + (9 × 10) + (7 × 100) + \(\frac{1}{10}+\frac{4}{100}\)
= (8 × 1o2) +( 9 × 101) + (7 × 100) + \(\left(1 \times \frac{1}{10}\right)+\left(4 \times \frac{1}{100}\right)\)
= (8 × 103) + (9 × 103) + (7 × 100) + (1 × 10-1) + (4 × 10-2)
Question 9.
Find the number is standard form:
(i) 8 × 104 + 7 × 103 + 6 × 102 + 5 × 101 + 2 × 1 + 4 × 10-2 + 7 × 10-4
(ii) 5 × 103 + 5 × 101 + 5 × 10-1 + 5 × 10-3
(iii) The radius of a hydrogen atom is 2.5 × 10-11 m
Answer:
(i) 8 × 104 + 7 × 103 + 6 × 102 + 5 × 101 + 2 × 1 + 4 × 10-2 + 7 × 10-4
= 8 × 104 + 7 × 103 + 6 × 102 + 5 × 101 + 2 × 1 + 4 × 10-2 + 7 × 10-4
= 8 × 10000 + 7 × 1000 + 6 × 100 + 5 × 10 + 2 × 1 + 4 × \(\frac{1}{100}\) + 7 × \(\frac{1}{10000}\)
= 80000 + 7000 + 600 + 50 + 2 + \(\frac{4}{100}\) + \(\frac{7}{10000}\)
= 87652.0407
![]()
(ii) 5 × 103 + 5 × 101 + 5 × 10-1 + 5 × 10-3
= 5 × 103 + 5 × 101 + 5 × 10-1 + 5 × 10-3
= 5 × 1000 + 5 × 10 + 5 × \(\frac{1}{10}\) + 5 × \(\frac{1}{1000}\)
= 5000 + 50 + \(\frac{5}{10}+\frac{5}{1000}\) = 5050.505
(iii) The radius of a hydrogen atom is 2.5 10-11 m
Radiys of a hydrogen atom = 2.5 × 10-11 m
= \(2.5 \times \frac{1}{10^{11}} \mathrm{m}=\frac{2.5}{10^{11}} \mathrm{m}\)
= 0.000000000025 m
Question 10.
Write the following numbers in scientific notation:
(i) 467800000000
Answer:
467800000000 = 4.678 × 1011
(ii) 0.000001972
Answer:
0.000001972 = 1.972 × 10-6
(iii) 1642.398
Answer:
1642.398 = 1.642398 × 103
![]()
(iv) Earth’s volume is about 1,083,000,000,000 cubic kilometres
Answer:
1,083,000,000,000
Earth’s volume = 1.083 110 × 102 cubic kilometres
(v) If you fill a bucket with dirt, the portion of the whole Earth that is in the bucket will be 0.00000000000000000000000 16 kg
Answer:
Portion of earth in the bucket = 0.00000000000000000000000 16 kg
= 1.6 10 × 1024 kg.
Objective Type Questions
Question 11.
By what number should (-4)-1 be multiplied so that the product becomes 10-1?
(A) \(\frac{2}{3}\)
(B) \(\frac{-2}{5}\)
(C) \(\frac{5}{2}\)
(D) \(\frac{-5}{2}\)
Answer:
(B) \(\frac{-2}{5}\)
Hint:
(-4)-1 = \(\left(-\frac{1}{4}\right)^{1}=\frac{-1}{4}\)

![]()
Question 12.
(-2)-3 × (-2)-2 = ___________.
(A) \(\frac{-1}{32}\)
(B) \(\frac{1}{32}\)
(C) 32
(D) -32
Answer:
(A) \(\frac{-1}{32}\)
Question 13.
Which is not correct?
(A) \(\left(\frac{-1}{4}\right)^{2}\) = 4-2
(B) \(\left(\frac{-1}{4}\right)^{2}=\left(\frac{1}{2}\right)^{4}\)
(C) \(\left(\frac{-1}{4}\right)^{2}\) = 16-1
(D) \(-\left(\frac{1}{4}\right)^{2}\) = 16-1
Answer:
\(-\left(\frac{1}{4}\right)^{2}\) = 16-1
Hint:
(-2) – 3 x (- 2) – 2 = (-2) – 3 – 2 = (-2) – 5 (\(-\frac { 1 }{ 2 }\))5 = \(-\frac { 1 }{ 32 }\)
Question 14.
If \(\frac{10^{x}}{10^{-3}}\) = 109, then x is ___________ .
(A) 4
(B) 5
(C) 6
(D) 7
![]()
Question 15.
0.0000000002020 in scientific form is __________ .
(A) 2.02 × 109
(B) 2.02 × 10-9
(C) 2.02 × 10-8
(D) 2.02 × 10-10
Answer:
(D) 2.02 × 10-10
Hint:
0.0000000002020