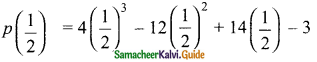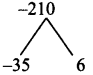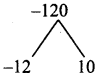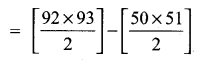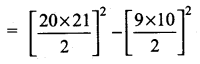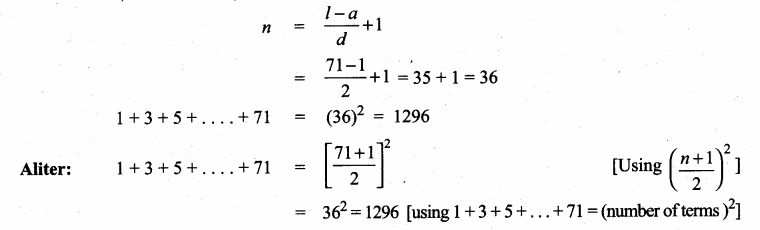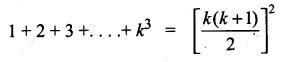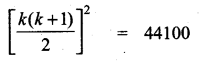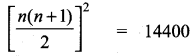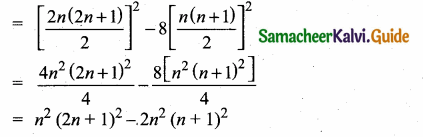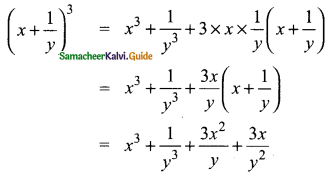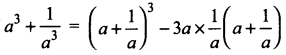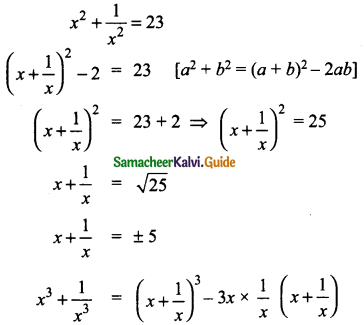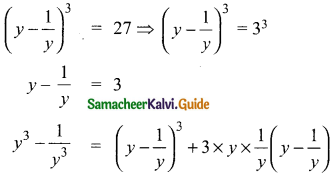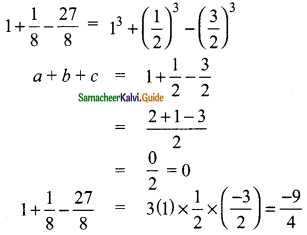Bhagya

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.10 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.10

Multiple choice questions:

Question 1.
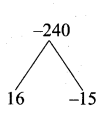
Euclid’s division lemma states that for positive integers a and b, there exist unique integers q and r such that a = bq + r, where r must satisfy ………………….
(1) 1 < r < b
(2) 0 < r < b
(3) 0 < r < 6
(4) 0 < r < b
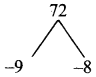
Ans.
(3) 0 < r < b

Question 2.
Using Euclid’s division lemma, if the cube of any positive integer is divided by 9 then the possible remainders are ………………….
(1) 0, 1, 8
(2) 1, 4, 8
(3) 0, 1, 3
(4) 1, 3, 5
Answer:
(1) 0, 1, 8
Hint: Let the +ve integer be 1, 2, 3, 4 …………
1³ = 1 when it is divided by 9 the remainder is 1.
2³ = 8 when it is divided by 9 the remainder is 8.
3³ = 27 when it is divided by 9 the remainder is 0.
4³ = 64 when it is divided by 9 the remainder is 1.
5³ = 125 when it is divided by 9 the remainder is 8.
The remainder 0, 1, 8 is repeated.

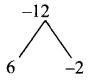
Question 3.
If the H.C.F of 65 and 117 is expressible in the form of 65m – 117 , then the value of m is
(1) 4
(2) 2
(3) 1
(4) 3
Answer:
(2) 2
Hint:
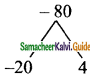
H.C.F. of 65 and 117
117 = 65 × 1 + 52
65 = 52 × 1 + 13
52 = 13 × 4 + 0
∴ 13 is the H.C.F. of 65 and 117.
65m – 117 = 65 × 2 – 117
130 – 117 = 13
∴ m = 2

Question 4.
The sum of the exponents of the prime factors in the prime factorization of 1729 is …………………….
(1) 1
(2) 2
(3) 3
(4) 4
Answer:
(3) 3
Hint: 1729 = 7 × 13 × 19
Sum of the exponents = 1 + 1 + 1
= 3

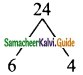
Question 5.
The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is
(1) 2025
(2) 5220
(3) 5025
(4) 2520
Answer:
(4) 2520
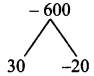
Hint:

L.C.M. = 2³ × 3² × 5 × 7
= 8 × 9 × 5 × 7
= 2520

Question 6.
7^4k ≡ ______ (mod 100)
(1) 1
(2) 2
(3) 3
(4) 4
Answer:
(1) 1
Hint:
7^4k ≡______ (mod 100)
y^4k ≡ y^{4 × 1} = 1 (mod 100)

Question 7.
Given F₁ = 1 , F₂ = 3 and F_n = F_n-1 + F_n-2 then F₅ is ………….
(1) 3
(2) 5
(3) 8
(4) 11
Answer:
(4) 11
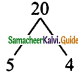
Hint:
F_n = F_n-1 + F_n-2
F₃ = F₂ + F₁ = 3 + 1 = 4
F₄ = F₃ + F₂ = 4 + 3 = 7
F₅ = F₄ + F₃ = 7 + 4 = 11

Question 8.
The first term of an arithmetic progression is unity and the common difference is 4. Which of the following will be a term of this A.P
(1) 4551
(2) 10091
(3) 7881
(4) 13531
Answer:
(3) 7881
Hint:
t₁ = 1
d = 4
t_n = a + (n – 1)d
= 1 + 4n – 4
4n – 3 = 4551
4n = 4554
n = will be a fraction
It is not possible.
4n – 3 = 10091
4n = 10091 + 3 = 10094
n = a fraction
4n – 3 = 7881
4n = 7881 + 3 = 7884
n = \(\frac{7884}{4}\), n is a whole number.
4n – 3 = 13531
4n = 13531 – 3 = 13534
n is a fraction.
∴ 7881 will be 1971st term of A.P.

Question 9.
If 6 times of 6^th term of an A.P is equal to 7 times the 7^th term, then the 13^th term of the A.P. is ………..
(1) 0
(2) 6
(3) 7
(4) 13
Answer:
(1) 0
Hint:
6 t₆ = 7 t₇
6(a + 5d) = 7 (a + 6d) ⇒ 6a + 30d = 7a + 42d
30 d – 42 d = 7a – 6a ⇒ -12d = a
t₁₃ = a + 12d (12d = -a)
= a – a = 0

Question 10.
An A.P consists of 31 terms. If its 16th term is m, then the sum of all the terms of this A.P. is
(1) 16 m
(2) 62 m
(3) 31 m
(4) \(\frac { 31 }{ 2 } \) m
Answer:
(3) 31 m
Hint:
t₁₆ = m
S₃₁ = \(\frac { 31 }{ 2 } \) (2a + 30d)
= \(\frac { 31 }{ 2 } \) (2(a + 15d))
(∵ t₁₆ = a + 15d)
= 31(t₁₆) = 31m

Question 11.
In an A.P., the first term is 1 and the common difference is 4. How many terms of the A.P must be taken for their sum to be equal to 120?
(1) 6
(2) 7
(3) 8
(4) 9
Answer:
(3) 8
Here a = 1, d = 4, S_n = 120
S_n = \(\frac { n }{ 2 } \)[2a + (n – 1)d]
120 = \(\frac { n }{ 2 } \) [2 + (n – 1)4] = \(\frac { n }{ 2 } \) [2 + 4n – 4)]
= \(\frac { n }{ 2 } \) [4n – 2)] = \(\frac { n }{ 2 } \) × 2 (2n – 1)
120 = 2n² – n
∴ 2n² – n – 120 = 0 ⇒ 2n² – 16n + 15n – 120 = 0
2n(n – 8) + 15 (n – 8) = 0 ⇒ (n – 8) (2n + 15) = 0
n = 8 or n = \(\frac { -15 }{ 2 } \) (omitted)
∴ n = 8

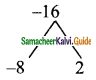
Question 12.
A = 2⁶⁵ and B = 2⁶⁴ + 2⁶³ + 2⁶² …. + 2⁰ which of the following is true?
(1) B is 2⁶⁴ more than A
(2) A and B are equal
(3) B is larger than A by 1
(4) A is larger than B by 1
Answer:
(4) A is larger than B by
A = 2⁶⁵
B = 2⁶⁴⁺⁶³ + 2⁶² + …….. + 2⁰
= 2
= 1 + 2² + 2² + ……. + 2⁶⁴
a = 1, r = 2, n = 65 it is in G.P.
S₆₅ = 1 (2⁶⁵ – 1) = 2⁶⁵ – 1
A = 2⁶⁵ is larger than B

Question 13.
The next term of the sequence \(\frac { 3 }{ 16 } \),\(\frac { 1 }{ 8 } \),\(\frac { 1 }{ 12 } \),\(\frac { 1 }{ 18 } \) is ………..
(1) \(\frac { 1 }{ 24 } \)
(2) \(\frac { 1 }{ 27 } \)
(3) \(\frac { 2 }{ 3 } \)
(4) \(\frac { 1 }{ 81 } \)
Answer:
(2) \(\frac { 1 }{ 27 } \)
Hint:
\(\frac { 3 }{ 16 } \),\(\frac { 1 }{ 8 } \),\(\frac { 1 }{ 12 } \),\(\frac { 1 }{ 18 } \)
a = \(\frac { 3 }{ 16 } \), r = \(\frac { 1 }{ 8 } \) ÷ \(\frac { 3 }{ 16 } \) = \(\frac { 1 }{ 8 } \) × \(\frac { 16 }{ 3 } \) = \(\frac { 2 }{ 3 } \)
The next term is = \(\frac { 1 }{ 18 } \) × \(\frac { 2 }{ 3 } \) = \(\frac { 1 }{ 27 } \)

Question 14.
If the sequence t₁,t₂,t₃ … are in A.P. then the sequence t₆,t₁₂,t₁₈ … is
(1) a Geometric Progression
(2) an Arithmetic Progression
(3) neither an Arithmetic Progression nor a Geometric Progression
(4) a constant sequence
Answer:
(2) an Arithmetic Progression
Hint:
If t₁, t₂, t₃, … is 1, 2, 3, …
If t₆ = 6, t₁₂ = 12, t₁₈ = 18 then 6, 12, 18 … is an arithmetic progression

Question 15.
The value of (1³ + 2³ + 3³ + ……. + 15³) – (1 + 2 + 3 + …….. + 15) is …………….
(1) 14400
(2) 14200
(3) 14280
(4) 14520
Answer:
(3) 14280
Hint:

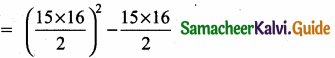
1202 – 120 = 120(120 – 1)
120 × 119 = 14280

Students can download Maths Chapter 1 Relations and Functions Ex 1.1 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Ex 1.1

1. Find A × B, A × A and B × A
(i) A = {2, -2, 3} and B = {1, -4}
(ii) A = B = {p, q}
(iii) A – {m, n} ; B = Φ
Answer:
(i) A = {2, -2, 3} and B = {1, -4}
A × B = {2,-2, 3} × {1,-4}
= {(2, 1), (2, -4)(-2, 1) (-2, -4) (3, 1) (3,-4)}
A × A = {2,-2, 3} × {2,-2, 3}
= {(2, 2)(2, -2)(2, 3)(-2, 2)
(-2, -2)(-2, 3X3,2) (3,-2) (3,3)}
B × A = {1,-4} × {2,-2, 3}
= {(1, 2)(1, -2)( 1, 3)(-4, 2) (-4,-2)(-4, 3)}

(ii) A = B = {p, q}
A × B = {p, q) × {p, q}
= {(p,p),(p,q)(q,p)(q,q)}
A × A = {p,q) × (p,q)
= {(p,p)(p,q)(q,p)(q,q)
B × A = {p,q} × {p,q}
= {(p,p)(p,q)(q,p)(q,q)

(iii) A = {m, n} × B = Φ
Note: B = Φ or {}
A × B = {m, n) × { }
= { )
A × A = {m, n) × (m, n)}
= {(m, m)(w, w)(n, m)(n, n)}
B × A = { } × {w, n}
= { }

Question 2.
Let A = {1, 2, 3} and B = {x | x is a prime number less than 10}. Find A × B and B × A.
Solution:
A = {1, 2, 3}, B = {2, 3, 5, 7}
A × B = {(1, 2), (1, 3), (1, 5), (1, 7), (2, 2), (2, 3) , (2, 5), (2, 7), (3, 2), (3, 3), (3, 5), (3, 7)}
B × A = {(2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3) , (5, 1), (5, 2), (5, 3), (7, 1), (7, 2) , (7, 3)}

Question 3.
If B × A = {(-2, 3),(-2, 4),(0, 3),(0, 4), (3,3) ,(3, 4)} find A and B.
Answer:
B × A = {(-2, 3)(-2, 4) (0, 3) (0, 4) (3, 3) (3,4)}
A = {3,4}
B = {-2,0,3}

Question 4.
If A ={5, 6}, B = {4, 5, 6} , C = {5, 6, 7}, Show that A × A = (B × B) ∩ (C × C).
Solution:
A = {5,6}, B = {4, 5, 6},C = {5, 6, 7}
A × A = {(5, 5), (5, 6), (6, 5), (6, 6)} ……….. (1)
B × B = {(4, 4), (4, 5), (4, 6), (5, 4),
(5, 5), (5, 6), (6, 4), (6, 5), (6, 6)} …(2)
C × C = {(5, 5), (5, 6), (5, 7), (6, 5), (6, 6),
(6, 7), (7, 5), (7, 6), (7, 7)} …(3)
(B × B) ∩ (C × C) = {(5, 5), (5,6), (6, 5), (6,6)} …(4)
(1) = (4)
A × A = (B × B) ∩ (C × C)
It is proved.

Question 5.
Given A = {1,2,3}, B = {2,3,5}, C = {3,4} and D = {1,3,5}, check if
(A ∩ C) × (B ∩ D) = (A × B) ∩ (C × D) is true?
Answer:
A = {1,2, 3}, B = {2, 3, 5}, C = {3,4} D = {1,3,5}
A ∩ c = {1,2,3} ∩ {3,4}
= (3}
B ∩ D = {2,3, 5} ∩ {1,3,5}
= {3,5}
(A ∩ C) × (B ∩ D) = {3} × {3,5}
= {(3, 3)(3, 5)} ….(1)
A × B = {1,2,3} × {2,3,5}
= {(1,2) (1,3) (1,5) (2, 2) (2, 3) (2, 5) (3, 2) (3, 3) (3, 5)}
C × D = {3,4} × {1,3,5}
= {(3,1) (3, 3) (3, 5) (4,1) (4, 3) (4, 5)}
(A × B) ∩ (C × D) = {(3, 3) (3, 5)} ….(2)
From (1) and (2) we get
(A ∩ C) × (B ∩ D) = (A × B) ∩ (C × D)
This is true.

Question 6.
Let A = {x ∈ W | x < 2}, B = {x ∈ N |1 < x < 4} and C = {3, 5}. Verify that
(i) A × (B ∪ C) = (A × B) ∪ (A × C)
(ii) A × (B ∩ C) = (A × B) ∩ (A × C)
(iii) (A ∪ B) × C = (A × C) ∪ (B × C)
(iv) A × (B ∪ C) = (A × B) ∪ (A × C)
Solution:
A = {x ∈ W|x < 2} = {0,1}
B = {x ∈ N |1 < x < 4} = {2,3,4}
C = {3,5}
LHS =A × (B ∪ C)
B ∪ C = {2, 3, 4} ∪ {3, 5}
= {2, 3, 4, 5}
A × (B ∪ C) = {(0, 2), (0, 3), (0,4), (0, 5), (1, 2) , (1, 3), (1, 4),(1, 5)} ………. (1)
RHS = (A × B) ∪ (A × C)
(A × B) = {(0, 2), (0, 3), (0, 4), (1, 2), (1, 3), (1, 4)}
(A × C) = {(0, 3), (0, 5), (1, 3), (1, 5)}
(A × B) ∪ (A × C)= {(0, 2), (0, 3), (0,4), (1, 2), (1, 3), (1, 4), (0, 5), (1, 5)} ….(2)
(1) = (2), LHS = RHS
Hence it is proved.

(ii) A × (B ∩ C) = (A × B) ∩ (A × C)
LHS = A × (B ∩ C)
(B ∩ C) = {3}
A × (B ∩ C) = {(0, 3), (1, 3)} …(1)
RHS = (A × B) ∩ (A × C)
(A × B) = {(0, 2), (0, 3), (0, 4), (1, 2), (1, 3), (1, 4)}
(A × C) = {(0, 3), (0, 5), (1, 3), (1, 5)}
(A × B) ∩ (A × C) = {(0, 3), (1, 3)} ……….. (2)
(1) = (2) ⇒ LHS = RHS.
Hence it is verified.

(iii) (A ∪ B) × C = (A × C) ∪ (B × C)
LHS = (A ∪ B) × C
A ∪ B = {0, 1, 2, 3, 4}
(A ∪ B) × C = {(0, 3), (0, 5), (1, 3), (1, 5), (2, 3), (2, 5), (3, 3), (3, 5), (4, 3), (4, 5)} …………. (1)
RHS = (A × C) ∪ (B × C)
(A × C) = {(0, 3), (0, 5), (1, 3), (1, 5)}
(B × C) = {(2, 3), (2, 5), (3, 3), (3, 5), (4, 3), (4, 5)}
(A × C) ∪ (B × C) = {(0, 3), (0, 5), (1, 3), (1, 5), (2, 3), (2, 5), (3, 3), (3, 5), (4, 3), (4, 5)} ………… (2)
(1) = (2)
∴ LHS = RHS. Hence it is verified.

Question 7.
Let A = The set of all natural numbers less than 8, B = The set of all prime numbers less than 8, C = The set of even prime number. Verify that
(i) (A ∩ B) × C = (A × c) ∩ (B × C)
(ii) A × (B – C) = (A × B) – (A × C)
Answer:
A = {1,2, 3, 4, 5,6, 7}
B = {2, 3, 5,7}
C = {2}

(i) (A ∩ B) × C = (A × C) ∩ (B × C)
A ∩ B = {1, 2, 3, 4, 5, 6, 7} ∩ {2, 3, 5, 7}
= {2, 3, 5, 7}
(A ∩ B) × C = {2, 3, 5, 7} × {2}
= {(2, 2) (3, 2) (5, 2) (7, 2)} ….(1)
A × C = {1,2, 3, 4, 5, 6, 7} × {2}
= {(1,2) (2, 2) (3, 2) (4, 2)
(5.2) (6, 2) (7, 2)}
B × C = {2, 3, 5, 7} × {2}
= {(2, 2) (3, 2) (5, 2) (7, 2)}
(A × C) ∩ (B × C) = {(2, 2) (3, 2) (5, 2) (7, 2)} ….(2)
From (1) and (2) we get
(A ∩ B) × C = (A × C) ∩ (B × C)

(ii) A × (B – C) = (A × B) – (A × C)
B – C = {2, 3, 5, 7} – {2}
= {3,5,7}
A × (B – C) = {1,2, 3, 4, 5, 6,7} × {3,5,7}
= {(1, 3) (1, 5) (1, 7) (2, 3) (2, 5)
(2, 7) (3, 3) (3, 5) (3, 7) (4, 3)
(4, 5) (4, 7) (5, 3) (5, 5) (5, 7)
(6, 3) (6, 5) (6, 7) (7, 3) (7, 5) (7, 7)} ………….(1)
A × B = {1,2, 3, 4, 5, 6, 7} × {2, 3, 5,7}
= {(1, 2) (1, 3) (1, 5) (1, 7) (2, 2) (2, 3)
(2, 5) (2, 7) (3, 2) (3, 3) (3, 5) (3, 7)
(4, 2) (4, 3) (4, 5) (4, 7) (5, 2) (5, 3) (5, 5)
(5, 7) (6, 2) (6, 3) (6, 5) (6, 7)
(7, 2) (7, 3) (7, 5) (7, 7)}
A × C = {1,2, 3,4, 5, 6, 7} × {2}
= {(1, 2) (2, 2) (3, 2) (4, 2) (5, 2) (6.2) (7,2)}
(A × B) – (A × C) = {(1, 3) (1, 5) (1, 7)
(2, 3) (2, 5) (2, 7) (3, 3) (3, 5)
(3, 7) (4, 3) (4, 5) (4, 7) (5, 3) (5, 5)
(5, 7) (6, 3) (6, 5) (6, 7) (7, 3) (7, 5) (7, 7)} ….(2)
From (1) and (2) we get
A × (B – C) = (A × B) – (A × C)

Relations
Let A and B be any two non-empty sets. A “relation” R from A to B is a subset of A × B satisfying some specified conditions.

Note:

1. The domain of the relations R = {x ∈ A/xRy, for some y ∈ B}
2. The co-domain of the relation R is B
3. The range of the ralation

R = (y ∈ B/xRy for some x ∈ A}

Students can download Maths Chapter 3 Algebra Ex 3.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.3

Question 1.
Check whether p(x) is a multiple of g(x) or not.
(i) p(x) = x³ – 5x² + 4x – 3; g(x) = x – 2
Solution:
p(x) = x³ – 5x² + 4x – 3
P(2) = (2)³ – 5(2)² + 4(2) – 3
= 8 – 5(4) + 8 – 3
= 8 – 20 + 8 – 3
= 16 – 23
= -7
p{2) ≠ 0
∴ p(x) is not a multiple of g(x)

Question 2.
By remainder theorem, find the remainder when p(x) is divided by g(x) where,
(i) p(x) = x³ – 2x² – 4x – 1; g(x) = x + 1
Solution:
p(x) = x³ – 2x² – 4x – 1
p(-1) = (-1)³ – 2(-1)² – 4(-1) – 1
= 1 – 2 + 4 – 1
= 4 – 4 = 0
∴ The remainder = 0

(ii) p(x) = 4x³ – 12x² + 14x – 3; g(x) = 2x – 1
Solution:
p(x) = 4x³ – 12x² + 14x – 3

= 4 × \(\frac{1}{8}\) – 12 × \(\frac{1}{4}\) + 14 × \(\frac{1}{2}\) – 3
= \(\frac{1}{2}\) – 3 + 7 – 3
= \(\frac{1}{2}\) – 6 + 7
= \(\frac{1}{2}\) + 1
= \(\frac{3}{2}\)
∴ The reminder is \(\frac{3}{2}\)

(iii) p(x) = x³ – 3x² + 4x + 50; g(x) = x – 3
Solution:
p(x) = x³ – 3x² + 4x + 50
p(3) = 3³ – 3(3)² + 4(3) + 50
= 27 – 27 + 12 + 50
= 62
The remainder is 62.

Question 3.
Find the remainder when 3x³ – 4x² + 7x – 5 is divided by (x + 3)
Solution:
p(x) = 3x³ – 4x² + 7x – 5
When it is divided by x +3,
p(-3) = 3(-3)³ – 4(-3)² + 7(-3) – 5
= 3(-27) – 4(9) – 21 – 5
= -81 – 36 – 21 – 5
= -143
The remainder is -143.

Question 4.
What is the remainder when x²⁰¹⁸ + 2018 is divided by x – 1.
Solution:
p(x) = x²⁰¹⁸ + 2018
When it is divided by x – 1,
p(1) = 1²⁰¹⁸ + 2018
= 1 + 2018
= 2019
The remainder is 2019.

Question 5.
For what value of k is the polynomial
p(x) = 2x³ – kx² + 3x + 10 exactly divisible by x – 2
Solution:
p(x) = 2x³ – kx² + 3x + 10
When it is exactly divided by x – 2,
P(2) = 0
2(2)³ – k(2)² + 3(2) + 10 = 0
2(8) – k(4) + 6 + 10 = 0
16 – k(4) + 6 + 10 = 0
16 – 4k + 6 + 10 = 0
32 – 4k = 0
32 = 4k
∴ k = \(\frac{32}{4}\)
= 8
The value of k = 8

Question 6.
If two polynomials 2x³ + ax² + 4x – 12 and x³ + x² – 2x + a leave the same remainder when divided by (x – 3), find the value of a and also find the remainder.
Solution:
p(x₁) = 2x³ + ax² + 4x – 12
When it is divided by x – 3,
p(3) = 2(3)³ + a(3)² + 4(3) – 12
= 54 + 9a + 12 – 12
= 54 + 9a ……….(R₁)
p(x₂) = x³ + x² – 2x + a
When it is divided by x – 3,
p(3) = 3³ + 3² – 2(3) + a
= 27 + 9 – 6 + a
= 30 + a ………(R₂)
The given remainders are same (R₁ = R₂)
∴ 54 + 9a = 30 + a
9a – a = 30 – 54
8a = -24
∴ a = -24/8
= -3
Consider R₂,
Remainder = 30 – 3
= 27

Question 7.
Determine whether (x – 1) is a factor of the following polynomials:
(i) x³ + 5x² – 10x + 4
Solution:
p(x) = x³ + 5x² – 10x + 4
p(1) = 1³ + 5(1) – 10(1) + 4
= 1 + 5 – 10 + 4
= 10 – 10
= 0
∴ x – 1 is a factor of p(x)

(ii) x⁴ + 5x² – 5x + 1
Solution:
p(1) = 1⁴ + 5(1)² – 5(1) + 1
= 1 + 5 – 5 + 1
= 7 – 5
= 2
= 0
∴ x – 1 is not a factor of p(x)

Question 8.
Using factor theorem, show that (x – 5) is a factor of the polynomial
2x³ – 5x² – 28x + 15
Solution:
p(x) = 2x³ – 5x² – 28x + 15
x – 5 is a factor
p(5) = 2(5)³ – 5(5)² – 28(5) + 15
= 250 – 125 – 140 + 15
= 265 – 265
= 0
∴ x – 5 is a factor of p(x)

Question 9.
Determine the value of m, if (x + 3) is a factor of x³ – 3x² – mx + 24.
Solution:
p(x) = x³ – 3x² – mx + 24
when x + 3 is a factor
P(-3) = 0
(-3)³ – 3(-3)² – m(-3) + 24 = 0
-27 – 27 + 3m + 24 = 0
-54 + 24 + 3m = 0
-30 + 3m = 0
3m = 30
m = \(\frac{30}{3}\)
= 10
The value of m = 10

Question 10.
If both (x-2) and (x – \(\frac{1}{2}\)) are the factors of ax² + 5x + b, then show that a = b.
Solution:
p(x) = ax² + 5x + b
when (x-2) is a factor
P(2) = 0
a(2)² + 5(2) + b = 0
4a + 10 + b = 0
4a + b = -10 …….(1)
when (x – \(\frac{1}{2}\)) is a factor
p(\(\frac{1}{2}\)) = 0
a\((\frac{1}{2})^2\) + 5(\(\frac{1}{2}\)) + b = 0
Multiply by 4
a + 10 + 4b = 0
a + 46 = -10 …….(2)
From (1) and (2) we get
4a + b = a + 4b
4a – a = 4b – b
3a = 3b
a = b
Hence it is proved.

Question 11.
If (x – 1) divides the polynomial kx³ – 2x² + 25x – 26 without remainder, then find the value of k.
Solution:
p(x) = kx³ – 2x² + 25x – 26
When it is divided by x – 1
P(1) = 0
k(1)³ – 2(1)² + 25(1) – 26 = 0
k – 2 + 25 – 26 = 0
k + 25 – 28 = 0
k – 3 = 0
k = 3
The value of k = 3

Question 12.
Check if (x + 2) and (x – 4) are the sides of a rectangle whose area is x² – 2x – 8 by using factor theorem.
Solution:
Let the area of a rectangle be p(x)
p(x) = x² – 2x – 8
When x + 2 is the side of the rectangle
p(-2) = (-2)² – 2(-2) – 8
= 4 + 4 – 8
= 8 – 8
= 0
When x – 4 is the side of the rectangle.
P(4) = (4)² – 2(4) – 8
= 16 – 8 – 8
= 16 – 16
= 0
(x + 2) and (x – 4) are the sides of a rectangle

Students can download Maths Chapter 3 Algebra Ex 3.6 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.6

Question 1.
Factorise the following.
(i) x² + 10x + 24
Solution:
Product = 24, sum = 10

Split the middle term as 6x and 4x
x² + 10x + 24 = x² + 6x + 4x + 24
= x(x + 6) + 4 (x + 6)
= (x + 6) (x + 4)

(ii) z² + 4z – 12
Solution:
Product = -12, sum = 4

Split the middle term as 6z and -2z
z² + 4z – 12 = z² + 6z – 2z – 12
= z(z + 6) – 2 (z + 6)
= (z + 6) (z – 2)

(iii) p² – 6p – 16
Solution:
Product = -16, sum = -6

Split the middle term as – 8p and 2p
p² – 6p – 16 = p² – 8p + 2p – 16
= p(p – 8) + 2 (p – 8)
= (p – 8) (p + 2)

(iv) t² + 72 – 17t
Solution:
Product = +72, sum = -17

Split the middle term as -9t and -8t
t² – 17t + 72 = t² – 91 – 8t + 72
= t(t – 9) – 8 (l – 9)
= (t – 9) (t – 8)

(v) y² – 16y – 80
Solution:
Product = -80, sum = -16

Split the middle term as -20y and 4y
y² – 16y – 80 = y² – 20y + Ay – 80
= y(y – 20) + 4 (y – 20)
= (y – 20) (y + 4)

(vi) a² + 10a – 600
Solution:
Product = -600, sum =10

Split the middle term as 30a and -20a
a² + 10a – 600 = a² + 30a – 20a – 600
= a(a + 30) – 20 (a + 30)
= (a + 30) (a – 20)

Question 2.
Factorise the following.
(i) 2a² + 9a + 10
Solution:
Product = 2 × 10 = 20, sum = 9

Split the middle term as 5a and 4a
2a² + 9a + 10 = 2a² + 5a + 4a + 10
= a(2a + 5) + 2 (2a + 5)
= (2a+ 5) (a+ 2)

(ii) 5x² – 29xy – 42y²
Solution:
Product = 5 × -42 = -210, sum = -29

Split the middle term as -35x and 6x
5x² – 29xy – 42y² = 5x² – 35xy + 6xy – 42y²
= 5x (x – 7y) + 6y (x – 7y)
= (x – 7y) (5x + 6y)

(iii) 9 – 18x + 8x²
Solution:
Product = 9 × 8 = 72, sum = -18

Split the middle term as -12x and -6x
9 – 18x + 8x² = 8x² – 18x + 9
= 8x² – 12x – 6x + 9
= 4x (2x – 3) – 3 (2x – 3)
= (2x – 3) (4x – 3)

(iv) 6x² + 16xy + 8y²
Solution:
Product = 6 × 8 = 48, sum = 16

Split the middle term as 4xy and 12xy
6x² + 16xy + 8y² = 6x² + 12xy + 4xy + 8y²
= 6x (x + 2y) + 4y(x + 2y)
= (x + 2y) (6x + 4y)
= 2(x + 2y) (3x + 2y)

(v) 12x² + 36x²y + 27y²x²
Solution:
3x²2 [4 + 12y + 9y²]
= 3x² [9y² + 12y + 4]
Product = 9 x 4 = 36, sum =12

Split the middle term as 6y and 6y
12x² + 36x²y + 21y²x² = 3x² [9y² + 12y + 4]
= 3x² [9y² + 6y + 6y + 4]
= 3x² [3y(3y + 2) + 2(3y + 2)]
= 3x² (3y + 2) (3y + 2)
= 3x² (3y + 2)2

(vi) (a + b)² + 9 (a + b) + 18
Solution:
Let (a + b) = x
x² + 9x + 18
Product =18, sum = 9
Split the middle term as 6x and 3x
x² + 9x + 18 = x² + 6x + 3x + 18
= x (x + 6) + 3 (x + 6)
= (x + 6) (x + 3)
But x = a + b
(a + b)² + 9(a + b) + 18 = (a + b + 6) (a + b + 3)

Question 3.
Factorise the following.
(i) (p – q)² – 6(p – q) – 16
Solution:
Let (p – q) = x
(p – q)² – 6 (p – q) – 16 = x² – 6x – 16
Product = -16, sum = -6

Split the middle term as -8x and 2x
x² – 6x – 16 = x² – 8x + 2x – 16
= x(x – 8) + 2(x – 8)
= (x – 8) (x + 2)
(But x = p – q)
= (p – q – 8) (p – q + 2)

(ii) m² + 2mn – 24n²
Solution:
Product = -24, sum = 2

Split the middle term as 6mn and -4mn
m² + 2mn – 24m² = m² + 6mn – 4mn – 24n²
= m(m + 6n) – 4n (m + 6n)
= (m + 6n) (m – 4n)

(iii) √5 a² + 2a – 3√5?
Solution:
Product = √5 × – 3√5 = -15, sum = 2

Split the middle term as 5x and -3x
√5 a² + 2a – 3√5 = √5a² + 5a – 3a – 3√5
= √5 a(a + √5) – 3(a + √5)
= (a + √5) (√5a – 3)

(iv) a⁴ – 3a² + 2
Solution:
Let a² = x
a⁴ – 3a² + 2 = (a²)² – 3a² + 2
= x² – 3x + 2
Product = 2 and sum = -3

Split the middle term as -x and -2x
x² – 3x + 2 = x² – x – 2x + 2
= x(x – 1) – 2(x – 1)
= (x – 1) (x – 2)
a⁴ – 3a² + 2 = (a² – 1)(a² – 2) [But a² = x]
= (a + 1) (a – 1) (a² – 2)

(v) 8m³ – 2m²n – 15mn²
Solution:
8m³ – 2m²n – 15mn² = m(8m² – 2mn – 15n²)
Product = 8(-15) = -120 and sum = -2

Split the middle term as -12mn and 10mn
8m³ – 2m²n – 15mn² = m[8m² – 2mn – 15n²]
= m[8m²– 12mn + 10mn- 15n²]
= m[4m (2m – 3n) + 5n(2m – 3n)]
= m(2m – 3n) (4m + 5n)

(vi) \(\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{2}{x y}\)
Solution:

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.9 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.9

Question 1.
Find the sum of the following series
(i) 1 + 2 + 3 + …….. + 60
(ii) 3 + 6 + 9 + …….. +96
(iii) 51 + 52 + 53 + …….. + 92
(iv) 1 + 4 + 9 + 16 + …….. + 225
(v) 6² + 7² + 8² + …….. + 21²
(vi) 10³ + 11³ + 12³ + …….. + 20³
(vii) 1 + 3 + 5 + …… + 71
Solution:
(i) 1 + 2 + 3 + …….. + 60 = \(\frac{60 \times 61}{2}\)
[Using \(\frac{n(n+1)}{2}\) formula]
= 1830

(ii) 3 + 6 + 9 + …….. + 96 = 3(1 + 2 + 3 + ……… + 32)
= \(\frac{3 \times 32 \times 33}{2}\)
= 1584

(iii) 51 + 52 + 53 + …….. + 92 = (1 + 2 + 3 + ……. + 92) – (1 + 2 + 3 + …… + 50)

= 4278 – 1275
= 3003

(iv) 1 + 4 + 9 + 16 + …….. + 225 = 1² + 2² + 3² + 4² + ………… + 15²
\(\frac{15 \times 16 \times 31}{6}\)
[using \(\frac{n(n+1)(2 n+1)}{6}\)] formula
= 1240

(v) 6² + 7² + 8² + …….. + 21² = 1 + 2² + 3² + 4² + ………… + 21² – (1 + 2² + ………… + 5²)
= \(\frac{21 \times 22 \times 43}{6}\) – \(\frac{5 \times 6 \times 11}{6}\)
= 3311 – 55
= 3256

(vi) 10³ = 11³ + 12³ + …….. + 20³ = 1³ + 2³+ 3³ + ………… + 20³ – (1³ + 2³ + 3³ + …………. + 9³)

[Using (\(\frac{n(n+1)}{2}\))² formula]
= 210² – 45² = 44100 – 2025
= 42075

(vii) 1 + 3 + 5+ … + 71
Here a = 1; d = 3 – 1 = 2; l = 71

Question 2.
If 1 + 2 + 3 + …. + k = 325 , then find 1³ + 2³ + 3³ + …………. + k³
Answer:
1 + 2 + 3 + …. + k = 325
\(\frac{k(k+1)}{2}\) = 325 ……(1)

= 325² (From 1)
= 105625

Question 3.
If 1³ + 2³ + 3³ + ………… + K³ = 44100 then find 1 + 2 + 3 + ……. + k
Answer:
1³ + 2³ + 3³ + ………….. + k³ = 44100

\(\frac{k(k+1)}{2}\) = \(\sqrt { 44100 }\) = 210
1 + 2 + 3 + …… + k = \(\frac{k(k+1)}{2}\)
= 210

Question 4.
How many terms of the series 1³ + 2³ + 3³ + …………… should be taken to get the sum 14400?
Answer:
1³ + 2³ + 3³ + ……. + n³ = 14400

\(\frac{n(n+1)}{2}\) = \(\sqrt { 14400 }\)
\(\frac{n(n+1)}{2}\) = 120 ⇒ n² + n = 240

n² + n – 240 = 0
(n + 16) (n – 15) = 0
(n + 16) = 0 or (n – 15) = 0
n = -16 or n = 15 (Negative will be omitted)
∴ The number of terms taken is 15

Question 5.
The sum of the squares of the first n natural numbers is 285, while the sum of their cubes is 2025. Find the value of n.
Answer:
1² + 2² + 3² + …. + n² = 285

Question 6.
Rekha has 15 square colour papers of sizes 10 cm, 11 cm, 12 cm, …, 24 cm. How much area can be decorated with these colour papers?
Answer:
Area of 15 square colour papers
= 10² + 11² + 12² + …. + 24²
= (1² + 2² + 3² + …. + 24²) – (1² + 2² + 9²)
= \(\frac{24 \times 25 \times 49}{6}-\frac{9 \times 10 \times 19}{6}\)
= 4 × 25 × 49 – 3 × 5 × 19
= 4900 – 285
= 4615
Area can be decorated is 4615 cm²

Question 7.
Find the sum of the series (2³ – 1)+(4³ – 3³) + (6³ – 15³) + …….. to
(i) n terms
(ii) 8 terms
Answer:
Sum of the series = (2³ – 1) + (4³ – 3³) + (6³ – 15³) + …. n terms
= 2³ + 4³ + 6³ + …. n terms – (1³ + 3³ + 5³ + …. n terms) …….(1)
2³ + 4³ + 6³ + …. n = ∑(2³ + 4³ + 6³ + ….(2n)³]
∑ 2³ (1³ + 2³ + 3³ + …. n³)
= 8 (\(\frac{n(n+1)}{2}\))²
= 2[n (n + 1)]²
1³ + 3³ + 5³ + ……….(2n – 1)³ [sum of first 2n cubes – sum of first n even cubes]

Substituting (2) and (3) in (1)
Sum of the series = 2n² (n + 1)² – n² (2n + 1)² + 2n²(n + 1)²
= 4n² (n + 1)² – n² (2n + 1)²
= n² [(4(n + 1)² – (2n + 1)²]
= n² [4n² + 4 + 8n – 4n² – 1 – 4n]
= n² [4n + 3]
= 4n³ + 3n²

(ii) when n = 8 = 4(8)³ + 3(8)²
= 4(512) + 3(64)
= 2240

Students can download Maths Chapter 3 Algebra Ex 3.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.2

Question 1.
Find the value of the polynomial f(y) = 6y – 3y² + 3 at
(i) y = 1
(ii) y = -1
(iii) y = 0
Solution:
(i) When y = 1
f(y) = 6y – 3y² + 3
f(1) = 6(1) – 3(1)² + 3
= 6 – 3 + 3 = 6

(ii) When y = – 1
f(y) = 6y – 3y² + 3
f(-1) = 6(-1) – 3(-1)² + 3
= – 6 – 3 + 3
= – 6

(iii) When y = 0
f(y) = 6y – 3y² + 3
f(0) = 6(0) – 3(0)² + 3
= 0 – 0 + 3
= 3

Question 2.
If p(x) = x² – 2√2x + 1, find p(2√2).
Solution:
p(x) = x² – 2√2x + 1
p(2√2) = (2√2)² – 2√2 (2√2) + 1
= 8 – 8 + 1
= 0 + 1
= 1

Question 3.
Find the zeros of the polynomial in each of the following.
(i) P(x) = x – 3
Solution:
p( 3) = 3 – 3
= 0
p(3) is the zero of p(x)

(ii) p(x) = 2x + 5
Solution:

= -5 + 5
= 2(0)
= 0
Hence –\(\frac{5}{2}\) is the zero of p(x).

(iii) q(y) = 2y – 3
Solution:

= 2 × 0
= 0
Hence \(\frac{3}{2}\) is the zero of q(y).

(iv) f(z) = 8z
Solution:
f(0) = 8 × 0
= 0
Hence 0 is the zero of f(z)

(v) p(x) = ax when a ≠ 0
Solution:
p(0) = a(0)
= 0
Hence, 0 is the zero of p(x)

(vi) h(x) = ax + b, a ≠ 0, a, b∈R
Solution:

Hence –\(\frac{b}{a}\) is the zero of h(x).

Question 4.
Find the roots of the polynomial equations.
(i) 5x – 6 = 0
Solution:
5x = 6
x = \(\frac{6}{5}\)
\(\frac{6}{5}\) is the root of the polynomial.

(ii) x + 3 = 0
Solution:
x = -3
-3 is the root of the polynomial.

(iii) 10x + 9 = 0
Solution:
10x = -9
x = –\(\frac{9}{10}\)
–\(\frac{9}{10}\) is the root of the polynomial.

(iv) 9x – 4 = 0
Solution:
9x = 4
x = \(\frac{4}{9}\)
\(\frac{4}{9}\) is the root of the polynomial.

Question 5.
Verify whether the following are zeros of the polynomial, indicated against them,or not.
(i) p(x) = 2x – 1, x = \(\frac{1}{2}\)
Solution:
p (\(\frac{1}{2}\)) = 2(\(\frac{1}{2}\)) – 1
= 1 – 1
= 0
∴ \(\frac{1}{2}\) is the zero of the polynomial.

(ii) p(x) = x³ – 1, x = 1
Solution:
p(1) = 1³ – 1
= 1 – 1
= 0
∴ 1 is the zero of the polynomial

(iii) p(x) = ax + b, x = \(\frac{-b}{a}\)
Solution:
p(\(\frac{-b}{a}\)) = a(\(\frac{-b}{a}\)) + b
= -b + b
= 0
∴ \(\frac{-b}{a}\) is the zero of the polynomial. a

(iv) p(x) = (x + 3) (x – 4); x = -3, x = 4
Solution:
P(-3) = (-3 + 3) (-3 – 4)
= (0) (-7)
= 0
P( 4) = (4 + 3) (4 – 4)
= (7) (0)
= 0
∴ -3 and 4 are the zeros of the polynomial.

Question 6.
Find the number of zeros of the following polynomials represented by their graphs.

Solution:
(i) Number of zeros = 2 (The curve is intersecting the x-axis at 2 points)
(ii) Number of zeros = 3 (The curve is intersecting the x-axis at 3 points)
(iii) Number of zeros = 0 (The curve is not intersecting the x-axis)
(iv) Number of zeros = 1 (The curve is intersecting at the origin)
(v) Number of zeros = 1 (The curve is intersecting the x-axis at one point)

Students can download Maths Chapter 3 Algebra Ex 3.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.4

Question 1.
Expand the following:
(i) (2x + 3y + 4z)²
(ii) (-p + 2q + 3r)²
(iii) (2p + 3) (2p – 4) (2p – 5)
(iv) (3a + 1) (3a – 2) (3a + 4)
Solution:
We know that (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac
(i) (2x + 3y + 4z)² = (2x)² + (3y)² + (4z)² + 2(2x) (3y) + 2(3y) (4z) + 2(4z) (2x)
= 4x² + 9y² + 16z² + 12xy + 24yz + 16xz

(ii) (-p + 2q + 3r)² = (-p)² + (2q)² + (3r)² + 2(-p) (2q) + 2(2q)(3r) + 2(3r) (- p)
= p²+ 4q² + 9r² – 4pq + 12qr – 6pr

(iii) (2p + 3) (2p – 4) (2p – 5)
[Here x = 2p, a = 3, b = -4 and c = -5]
= (2p)³ + (3 – 4 – 5) (2p)² + [(3)(-4) + (-4)(-5) + (3) (-5)] 2p + (3) (-4) (-5)
= 8p³ + (-6)(4p²) + (-12 + 20 – 15) 2p + 60
= 8p³ – 24p² – 14p + 60

(iv) (3a + 1) (3a – 2) (3a + 4)
[Here x = 3a, a = 1, b = -2 and c = 4]
= (3a)³ + (1 – 2 + 4) (3a)² + [(1)(-2) + (-2) (4) + (4) (1)] (3a) + (1) (-2) (4)
= 27a³ + 3(9a²) + (-2 – 8 + 4) (3a) – 8
= 27a³ + 27a² – 18a – 8

Question 2.
Using algebraic identity, find the coefficients of x², x and constant term without actual expansion.
(i) (x + 5)(x + 6)(x + 7)
Solution:
[Here x = x, a = 5, b = 6, c = 7]
(x + a) (x + b) (x + c) = x³ + (a + b + c)x² + (ab + bc + ac)x + abc
coefficient of x² = 5 + 6 + 7
= 18
coefficient of x = 30 + 42 + 35
= 107
constant term = (5) (6) (7)
= 210

(ii) (2x + 3)(2x – 5) (2x – 6)
Solution:
[Here x = 2x, a = 3, b = -5, c = -6]
(x + a) (x + b) (x + c) = x³ + (a + b + c)x² + (ab + bc + ac)x + abc
coefficient of x² = (3 – 5 – 6)4 [(2x)² = 4x²]
= (-8) (4)
= -32
coefficient of x = [(3)(-5) + (-5)(-6) + (-6)(3)](2)
= (-15 + 30-18) (2)
= (-3) (2)
= -6
constant term = (3) (-5) (-6)
= 90

Question 3.
If (x + a)(x + b)(x + c) = x³ + 14x² + 59x + 70, find the value of
(i) a + b + c
(ii) \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}\)
(iii) a² + b² + c²
(iv) \(\frac{a}{bc} + \frac{b}{ac} + \frac{c}{ab}\)
Solution:
(x + a) (x + b) (x + c) = x³ + 14x² + 59x + 70
x³ + (a + b + c)x² + (ab + bc + ac)x + abc = x³ + 14x² + 59x + 70
a + b + c = 14, ab + bc + ac = 59, abc = 70
(i) a + b + c = 14

(ii) \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}\) = \(\frac{bc+ac+ab}{abc}\)
= \(\frac{59}{70}\)

(iii) a² + b² + c² = (a + b + c)² – 2 (ab + bc + ac)
= (14)² – 2(59)
= 196 – 118
= 78

Question 4.
Expand:
(i) (3a – 4b)³
Solution:
(a – b)³ = a³ – b³ – 3ab (a – b)
(3a – 4b)³ = (3a)³ – (4b)³ – 3(3a)(4b)(3a – 4b)
= 27a³ – 64b³ – 36ab (3a – 4b)
= 27a³ – 64b³ – 108a²b + 144ab²

(ii) [x + \(\frac{1}{y}]^{3}\)
Solution:
(a + b)³ = a³ + b³ + 3ab (a + b)

Question 5.
Evaluate the following by using identities:
(i) 98³
Solution:
98³ = (100 – 2)³ [(a – b)³ = a³ – b³ – 3ab (a – b)]
= 100³ – (2)³ – 3(100) (2) (100 – 2)
= 1000000 – 8 – 600(98)
= 1000000 – 8 – 58800
= 1000000 – 58808
= 941192

(ii) 1001³
Solution:
(1001)³ = (1000 + 1)³
[(a + b)³ = a³ + b³ + 3ab (a + b)]
= (1000)³ + 1³ + 3(1000) (1) (1000 + 1)
= 1000000000 + 1 + 3000 (1001)
= 1000000001 + 3003000
= 1003003001

Question 6.
If (x + y + z) = 9 and (xy + yz + zx) = 26, then find the value of x² + y² + z².
Solution:
x + y + z = 9; xy + yz + zx = 26
x² + y² + z² = (x + y + z)² – 2xy – 2yz – 2xz
= (x + y + z)² – 2 (xy + yz + zx)
= 9² – 2(26)
= 81 – 52
= 29

Question 7.
Find 27a³ + 64b³, If 3a + 4b = 10 and ab = 2
Solution:
3a + Ab = 10, ab = 2
27a³ + 64b³ = (3a)³ + (4b)³
[a³ + b³ = (a + b)³ – 3 ab (a + b)]
= (3a + 4b)³ – 3 × 3a × 4b (3a + 4b)
= 103 – 36ab (10)
= 1000 – 36(2)(10)
= 1000 – 720
= 280

Question 8.
Find x³ – y³, if x – y = 5 and xy = 14.
Solution:
x – y = 5, xy = 14
x³ – y³  = (x – y)³ + 3xy (x – y)
= 5³ + 3(14) (5)
= 125 + 210
= 335

Question 9.
If a + \(\frac{1}{a}\) = 6, then find the value of a³ +\(\frac{1}{a^3}\)
Solution:
a + \(\frac{1}{a}\) = 6 [a³ + b³ = (a + b)³ – 3ab (a + b)]

= 6³ – 3(6)
= 216 – 18
= 198

Question 10.
If x² + \(\frac{1}{x^2}\) = 23, then find the value of x + \(\frac{1}{x}\) and x³ + \(\frac{1}{x^3}\)
Solution:

When x = 5 [a³ + b³ = (a + b)³ – 3ab (a + b)]
= (5)³ – 3(5)
= 125 – 15
= 110
when x = -5
x³ + \(\frac{1}{x^3}\) = (-5)³ – 3(-5)
= -125 + 15
= -110
∴ x³ + \(\frac{1}{x^3}\) = ±110

Question 11.
If (y – \(\frac{1}{y})^{3}\) = 27 then find the value of y³ – \(\frac{1}{y^3}\)
Solution:

= 3³ + 3(3)
= 27 + 9
= 36

Question 12.
Simplify:
(i) (2a + 3b + 4c) (4a² + 9b² + 16c² – 6ab – 12bc – 8ca)
(ii) (x – 2y + 3z) (x² + 4y² + 9z² + 2xy + 6yz – 3xz)
Solution:
x³ + y³ + z³ – 3xyz ≡ (x + y + z) (x² + y² + z² – xy – yz – zx)
(i) (2a + 3b + 4c) (4a² + 9b² + 16c² – 6ab – 12bc – 8ea)
= (2a)³ + (3b)³ + (4c)³ – 3 (2a) (3b) (4c)
= 8a³ + 27b³ + 64c³ – 72abc

(ii) (x – 2y + 3z) (x² + 4y² + 9z² + 2xy + 6yz – 3xz)
= x³ + (-2y)³ + (3z)³ – 3(x) (-2y) (3z)
= x³ – 8y³ + 27z³ + 18xyz

Question 13.
By using identity evaluate the following:
(i) 7³ – 10³ + 3³
Solution:
x³ + y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² – xy – yz – zx)
We know that a + b + c = 0 then a³ + b³ + c³ = 3ab
a + b + c = 7 + (-10) + 3
= 10 – 10
= 0
∴ 7³ – 10³ + 3³ = 3(7) (-10) (3)
= -630

(ii) 1 + \(\frac{1}{8}\) – \(\frac{27}{8}\)
Solution:
We know that a³ + b³ + c³ = 0 then a + b + c = 3abc

Question 14.
If 2x -3y – 4z = 0, then find 8x³ – 27y³ – 64z³.
Solution:
We know x³ +y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² – xy – yz – zx)
x³ + y³ + z³ = (x + y + z) (x² +y² + z² – xy – yz – zx) + 3xyz
8x³ – 27y³ – 64z³ = (2x)³ + (-3y)³ + (-4z)³
= (2x – 3y- 4z) [(2x)² + (-3y)² + (-4z)² – (2x)(-3y) – (-3y) (-4z) -(-4z)(2x)] + 3(2x)(-3y)(-4z)
= 0 (4x² + 9y² + 16z² + 6xy – 12yz + 8xz) + 72xyz
= 72xyz
8x³ – 27y³ – 64z³ = 72xyz

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.2 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.2

Question 1.
Find the rank of the following matrices by minor method:

Solution:

(i) A = \(\begin{bmatrix} 2 & -4 \\ -1 & 2 \end{bmatrix}\)
A is a matrix of order 2 × 2 and p(A) ≤ 2
Second order minor
|A| = \(\begin{bmatrix} 2 & -4 \\ -1 & 2 \end{bmatrix}\)
= 4 – 4 = 0
∴p(A) ≠ 2
First order minor is non vanishing
p(A) = 1

(ii) A = \(\left[\begin{array}{rr}
-1 & 3 \\
4 & -7 \\
3 & -4
\end{array}\right]\)
A is a matrix of order 3 × 2 and p(A) ≤ 2
Second order minor
\(\begin{bmatrix} -1 & 3 \\ 4 & -7 \end{bmatrix}\)
= 7 – 12 = -5 ≠ 0
∴ p(A) = 2

(iii) A = \(\left[\begin{array}{rrrr}
1 & -2 & -1 & 0 \\
3 & -6 & -3 & 1
\end{array}\right]\)
A is a matrix of order 2 × 4 and p(A) ≤ 2
Second order minor

= 1(-4 + 6) + 2(-2 + 30) + 3(2 – 20)
= 2 + 56 – 54 = 4 ≠ 0
∴p(A) = 3

Question 2.
Find the rank of the following matrices by row reduction method:

Solution:

The last equivalent matrix is in row echelon form. It has two non-zero rows.
∴ p(A) = 2

The last equivalent matrix is in row echelon form. It has three non-zero rows.
∴ p(A) = 3

The last equivalent matrix is in row echelon form. It has three non-zero rows.
∴ p(A) = 3

Question 3.
Find the inverse of each of the following by Gauss-Jordan method:

Solution:

Students can download Maths Chapter 1 Set Language Ex 1.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.2

Question 1.
Find the cardinal number of the following sets.
(i) M = {p, q, r, s, t, u}
(ii) P = {x : x = 3n + 2, n ∈ W and x < 15}
(iii) Q = {y : y = \(\frac{4}{3n}\), n ∈ N and 2 < n ≤ 5}
(iv) R = {x : x is an integer, x ∈ Z and – 5 ≤ x < 5}
(v) S = The set of all leap years between 1882 and 1906.
Solution:
(i) n (M) = 6
(ii) n (P) = 5 [n = {0, 1, 2, 3 . . . . 14}]
(iii) Since n = {3, 4, 5} ; n (Q) = 3
(iv) X = {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4} ∴ n (R) = 10
(v) S = {1884, 1888, 1892, 1896, 1904}; n (S) = 5

Question 2.
Identify the following sets as finite or infinite.
(i) X = The set of all districts in Tamilnadu.
(ii) Y = The set of all straight lines passing through a point.
(iii) A = {x : x ∈ Z and x < 5}
(iv) B = {x : x² – 5x + 6 = 0, x ∈ N}
Solution:
(i) Finite
(ii) Infinite set (many lines can be drawn from a point)
(iii) Infinite set {A = ……. -2, -1, 0, 1, 2, 3, 4}
(iv) Finite set [x² – 5x + 6 = 0 ⇒ (x – 3) (x – 2) = 0; x = 3 and 2]

Question 3.
Which of the following sets are equivalent or unequal or equal sets?
(i) A = The set of vowels in the English alphabets.
B = The set of all letters in the word “VOWEL”
(ii) C = {2, 3, 4, 5}
D = {x : x ∈ W, 1 < x < 5}
(iii) X = {x : x is a letter in the word “LIFE”}
Y = {F, I, L, E}
(iv) G = {x : x is a prime number and 3 < x < 23}
H = {x : x is a divisor of 18}
Solution:
(i) Equivalent set [n(A) = n(B) = 5] ∴ A ≈ B
(ii) Unequal sets [C = {2, 3, 4, 5}; D = {2, 3, 4}]
(iii) Equal sets [X = {L, I, F, E}; Y = {F, I, L, E} [n(X) = 4 = n(Y)] ∴ X ≈ Y
(iv) Equivalent sets [G = {5, 7, 11, 13, 17, 19}; H = {1, 2, 3, 6, 9, 18}]
[n(G) = n(H) = 6 ∴ G ≈ H)]

Question 4.
Identify the following sets as null set or singleton set.
(i) A = {x : x ∈ N, 1 < x < 2}
(ii) B = The set of all even natural numbers which are not divisible by 2
(iii) C = {0}.
(iv) D = The set of all triangles having four sides.
Solution:
(i) Null set [No natural numbers is in between 1 and 2]
(ii) Null set [All the even natural numbers are not divisible by 2]
(Hi) Singleton set [n (C) = 1]
(iv) Null set [All the triangles has 3 sides]

Question 5.
State which pairs of sets are disjoint or overlapping?
(i) A = {f, i, a, s} and B = {a, n, f, h, s}
A = {f, i, a, s} and B = {a, n, f, h, s}
A and B are overlapping sets

(ii) C = {x : x is a prime number, x > 2} and D = {x : x is an even prime number}
C= {3, 5, 7…….}
D = {2}
C and D are disjoint sets

(iii) E = {x : x is a factor of 24} and F = {x : x is a multiple of 3, x < 30}
E = {1, 2, 3, 4, 6, 8, 12, 24}
F = {3, 6, 9, 12, 15, 18, 21, 24, 27} [Hint: E ∩ F = {3, 6, 24, …….}]
E and F are overlapping sets

Question 6.
If S = {square, rectangle, circle, rhombus, triangle}. List the elements of the following subset of S.
(i) The set of shapes which have 4 equal sides.
(ii) The set of shapes which have radius.
(iii) The set of shapes in which the sum of all interior angles is 180°.
(iv) The set of shapes which have 5 sides.
Solution:
(i) Subset of S = {square, rhombus}
(ii) Subset of S = {circle}
(iii) Subset of S = {triangle}
(iv) Subset of S = { }

Question 7.
If A = {a,{a, b}}, write all the subsets of A.
Solution:
A = {a, {a, b}}
Subset of A are Ø, {a}, {a, b}, {a, {a, b}} (or) { }, {a}, {a,b, {a,{a,b}}
P(A) = {Ø, {a}, {a, b}, {a {a, b}} (or) {{ }, {a}, {a,b, {a,{a,b}}

Question 8.
Write down the power set of the following sets.
(i) A = {a, b}
(ii) B = {1, 2, 3}
(iii) D = {p, q, r, s}
(iv) E = Ø
Solution:
(i) A = {a, b)
P(A) = {{},{a},{b}, {a, b}}

(ii) B = {1, 2, 3}
P(B) = {{}, {1}, {2}, {3}, {1,2}, {2, 3}, {1,3}, {1,2,3}}

(iii) D = {p, q, r, s}
P(D) = {{},{p},{q},{r},{s},{p, q} {p, r} {p, s}
{q, r}, {q, s}, {r, s}, {p, q, r} {q, r, s}
{p, r, s} {p, q, s} {p, q, r, s}}

(iv) E = Ø
P(E) = {{}}
Note: (empty set is the subset of all the sets)

Question 9.
Find the number of subsets and the number of proper subsets of the following sets.
(i) W = {red, blue, yellow}
(ii) X = {x² : x ∈ N, x² ≤ 100}
Solution:
(i) W = {red, blue, yellow}
n (W) = 3
The number of subsets of W = n [P(W)] = 2^m
= 2³ = 8
Number of proper subsets of W = n[P(W)] – 1
= 8 – 1
= 7 (or)
Number of proper subsets of W = 2^m – 1
= 2³ – 1 = 8 – 1 = 7

(ii) X = {x² : x ∈ N, x² ≤ 100}.
X= {1,2, 3, 4, …. 10}
n(X) = 10
The number of subsets of X = n[P(X)]
= 2^m
= 2¹⁰ = 1024
Number of proper subsets of X = 2^m – 1
= 1024 – 1
= 1023

Question 10.
(i) If n(A) = 4, find n[P(A)]
(ii) If n(A) = 0, find n[P(A)]
(Hi) If n[P(A)] = 256, find n(A)
Solution:
(i) n (A) = 4
n [P(A)] = 2^m = 2⁴
= 16

(ii) n (A) = 0
n [P(A)] = 2^m = 2° = 1

(iii) n [P(A)] = 256

2^m = 2⁸
∴ n (A) = 8

శ్రీ సాయి దీక్షా విధానము

Students can download Maths Chapter 1 Set Language Ex 1.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.1

Question 1.
Which of the following are sets?
(i) The collection of prime numbers upto 100
(ii) The collection of rich people in India
(iii) The collection of all rivers in India
(iv) The collection of good hockey players
Solution:
(i) It is a set
(ii) It is not a set (The word “rich” is not well defined)
(iii) It is a set
(iv) It is not a set (The word “good” is not well defined)

Question 2.
List the set of letters of the following words in Roster form.
(i) INDIA
(ii) PARALLELOGRAM
(iii) MISSISSIPPI
(iv) CZECHOSLOVAKIA
Solution:
(i) A = {I, N, D, A}
(ii) B = {P, A, R, L , E, O, G, M}
(iii) C = {M, I, S, P}
(iv) D = {C, Z, E, H, O, S, L, V, A, K, I}

Question 3.
Consider the following sets A = {0, 3, 5, 8}, B = {2, 4, 6, 10} and C = {12, 14, 18, 20}.
(a) State whether True or False:
(i) 18 ∈ C
(if) 6 ∉ A
(iii) 14 ∉ C
(iv) 10 ∈ B
(v) 5 ∈ B
(vi) 0 ∈ B
Solution:
(i) True
(ii) True
(iii) False
(iv) True
(v) False
(vi) False

(b) Fill in the blanks:
(i) 3 ∈ …………
(ii) 14 ∈…………
(iii) 18 ……….. B
(iv) 4 ………. B
Solution:
(i) A
(ii) C
(iii) ∉
(iv) ∈

Question 4.
Represent the following sets in Roster form.
(i) A = The set of all even natural numbers less than 20.
(ii) B = {y : y = \(\frac{1}{2n}\), n∈N, n ≤ 5}
(iii) C = {x : x is perfect cube, 27 < x < 216}
(iv) D = {x : x ∈Z, – 5 < x ≤ 2}
Solution:
(i) A= {2, 4, 6, 8, 10, 12, 14, 16, 18}
(ii) B = {\(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{6}\), \(\frac{1}{8}\), \(\frac{1}{10}\)}
(iii) C = {64, 125}
(iv) D = {-4, -3, -2, -1, 0, 1, 2}

Question 5.
Represent the following sets in set builder form.
(i) B = The set of all cricket players in India who scored double centuries in one day internationals.
(ii) C = {\(\frac{1}{2}\), \(\frac{2}{3}\), \(\frac{3}{4}\), …….}
(iii) D = The set of all Tamil months in a year.
(iv) E = The set of odd Whole numbers less than 9.
Solution:
(i) B = {x : x is a set of all cricket players in India who scored double centuries in one day internationals}
(ii) C = {x : n ∈ N, x = \(\frac{n}{n + 1}\) }
(iii) D = {x : x ∈ set of all Tamil months in a year}
(iv) E = {x : x is an odd whole number and x < 9}

Question 6.
Represent the following sets in descriptive form.
(i) P = { January, June, July}
(ii) Q = {7, 11, 13, 17, 19, 23, 29}
(iii) R = {x : x∈N, x < 5}
(iv) S = {x : x is a consonant in English alphabets}
Solution:
(i) P = The set of all months beginning with the letter “J”
(ii) Q = The set of all prime numbers between 5 and 31
(iii) R = The set of natural numbers less than 5
(iv) S = The set of consonants in English alphabets

Read More:

ముకుందమాలా