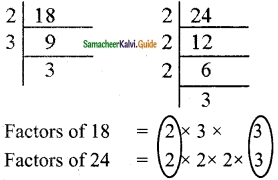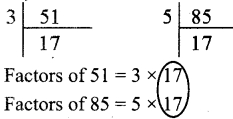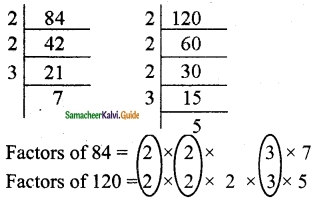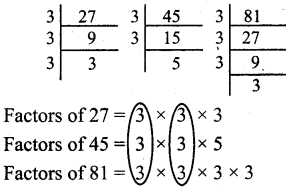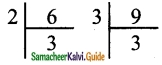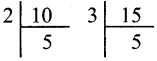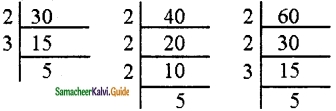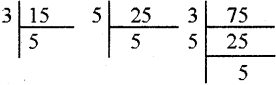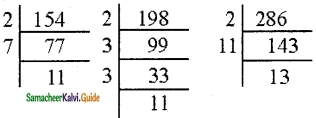Category: Class 6

Students can download Maths Chapter 1 Numbers Ex 1.3 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 1 Numbers Ex 1.3

Miscellaneous Practice Problems

Question 1.
Every even number greater than 2 can be expressed as the sum of two prime numbers. Verify this statement for every even number upto 16.
Solution:
Even numbers greater then 2 upto 16 are 4, 6, 8, 10, 12, 14 and 16
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7 (or) 5 + 5
12 = 5 + 7
14 = 7 + 7 (or) 3 + 11
16 = 5 + 11 (or) 3 + 13

Question 2.
Is 173 a prime? Why?
Solution:
Yes, 173 is a prime. Because it has only 1 and itself as factors.

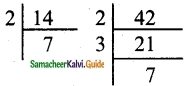
Question 3.
For which of the numbers, from n = 2 to 8.
Is 2n – 1 a prime?
Solution:
n = 2 ⇒ 2n – 1 = 2 × 2 – 1
= 4 – 1
= 3 (prime)
n = 3 ⇒ 2n – 1 = 2 × 3 – 1
= 6 – 1
= 5 (prime)
n = 4 ⇒ 2n – 1 = 2 × 4 – 1
= 8 – 1
= 7 (prime)
n = 5 ⇒ 2n – 1 = 2 × 5 – 1
= 10 – 1
= 9 (Not prime)
n = 6 ⇒ 2n – 1 = 2 × 6 – 1
= 12 – 1
= 11 (prime)
n = 7 ⇒ 2n – 1 = 2 × 7 – 1
= 14 – 1
= 13
n = 8 ⇒ 2n – 1 = 2 × 8 – 1
= 16 – 1
= 15 (Not prime)

Question 4.
Explain your answer with the reason for the following statements.
(a) A number is divisible by 9 if it is divisible by 3.
(b) A number is divisible by 6 if it is divisible by 12.
Solution:
(i) False, 42 is divisible by 3 but it is not divisible by 9
(ii) True, 36 is divisible by 12. Also divisible by 6.

Question 5.
Find A as required
(i) The greatest 2 digit number 9 A is divisible by 2.
(ii) The least number 567A is divisible by 3.
(iii) The greatest 3 digit number 9A6 is divisible by 6.
(iv) The number A08 is divisible by 4 and 9.
(v) The number 225A85 is divisible by 11.
Solution:
(i) 98 A = 8
(ii) 5670 A = 0
(iii) 996 A = 9
(iv) 108 A = 1
(v) 225885 A = 8

Question 6.
Numbers divisible by 4 and 6 are divisible by 24. Verify this statement and support your answer with an example.
Solution:
False 12 is divisible by both 4 and 6. But not divisible by 24

Question 7.
The sum of any two successive odd numbers is always divisible by 4. Justify this statement with an example.
Solution:
True 3 + 5 = 8 is divisible by 4.

Question 8.
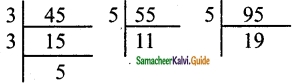
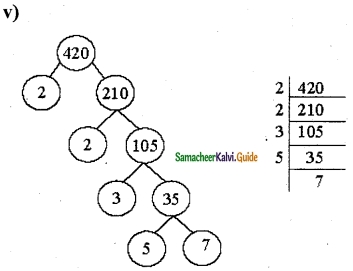
Find the length of the longest rope that can be used to measure exactly the ropes of length 1 m 20cm, 3m 60 cm and 4 m.
Solution:
1 m 20 cm = 120 cm
3 m 60 cm = 360 cm
4 m = 400 cm
This is a HCF related problem. So, we need to find the HCF of 120,360 and 400.

120 = 2 × 2 × 2 × 3 × 5
360 = 2 × 2 × 2 × 3 × 3 × 5
400 = 2 × 2 × 2 × 2 × 5 × 5
HCF = 2 × 2 × 2 × 5 = 40
The length of the longest rope = 40 cm

Challenge Problems

Question 9.
The sum of three prime numbers is 80. The difference between the two of them is 4. Find the numbers.
Solution:
Given the sum of three prime numbers is 80
The numbers will be one or two-digit prime numbers. Also one of them is 2
Sum of the remaining 2 numbers = 78 [∵ one number must be even]
Also their difference = 4 (given) [Otherwise sum of three odd numbers is odd]
The numbers will be 37 and 41
The required numbers are 2, 37, 41

Question 10.
Find the sum of all the prime numbers between 10 and 20 and check whether that sum is divisible by all the single-digit numbers.
Solution:
Prime numbers between 10 and 20 are 11, 13, 17 and 19
Sum = 11 + 13 + 17 + 19 = 60
60 is divisible by 1, 2, 3, 4, 5 and 6.

Question 11.
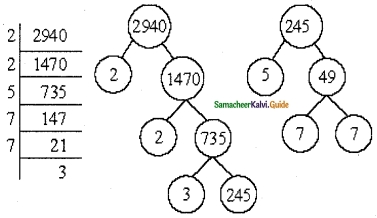
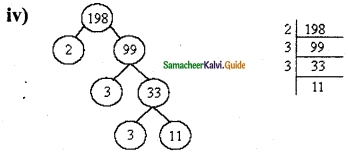
Find the smallest number which is exactly divisible by all the numbers from 1 to 9.
Solution:
2520

Question 12.
The product of any three consecutive numbers is always divisible by 6. Justify this statement with an example.
Solution:
Yes. Because one of every two consecutive integers is even and so the product of three consecutive integers is even and divisible by 2.
Also one of every 3 consecutive integers is divisible by 3.
Product of any three consecutive integers is divisible by 6.
Example: 5 × 6 × 7

Question 13.
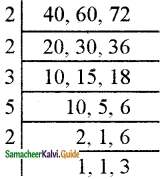
Malarvizhi, Karthiga, and Anjali are friends and natives of the same village. They work in different places. Malarvizhi comes to her home once in 5 days. Similarly, Karthiga and Anjali come to their homes once in 6 days and 10 days respectively, Assuming that they met each other on the 1st of October, when will all the three meet again?
Solution:
This is an LCM related problem. So, we need to find the LCM of 5, 6, and 10.

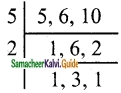
LCM = 5 × 2 × 1 × 3 × 1
= 30
All the three will meet again once in 30 days.

Question 14.
In an apartment consisting of 108 floors, two lifts A & B starting from the ground floor, stop at every 3rd and 5th floors respectively. On which floors, will both of them stop together?
Solution:
LCM of 3 and 5 = 3 × 5 = 15
The lifts stop together at floors 15, 30, 45, 60, 75, 90, and 105.

Question 15.
The product of 2 two-digit numbers is 300 and their HCF is 5. What are the numbers?
Solution:
15 × 20 = 300
HCF of 15 and 20 is 5
The numbers are 15 and 20

Question 16.
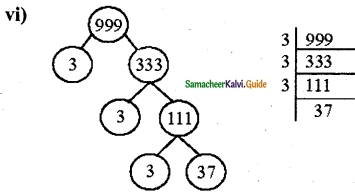
Find whether the number 564872 is divisible by 88. (use of the test of divisibility rule for 8 and 11 will help)
Solution:
564872 Divisibility by 8
564872 It is divisible by 8
Divisibility by 11
5 + 4 + 7 = 16
6 + 8 + 2 = 16
16 – 16 = 0
It is divisible by both 8 and 11 and hence divisible by 88.

Question 17.
Wilson, Mathan, and Guna can complete one round of a circular track in 10, 15, and 20 minutes respectively. If they start together from at the starting point of 7 am, at what time will they meet together again at the same starting point?
Solution:
This is an LCM related problem. So, we need to find the LCM of 10, 15, and 20.

LCM = 5 × 2 × 1 × 3 × 2 = 60 min
They will meet together again after 60 minutes.
ie. 7.am + 60 minutes = 8 am.

Students can download Maths Chapter 4 Geometry Ex 4.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.1

Question 1.
Fill in the blanks.
(a) Every triangle has at least _____ acute angles.
(b) A triangle in which none of the sides equal is called a _____.
(c) In an isosceles triangle ______ angles are equal.
(d) The sum of three angles of a triangle is ______.
(e) A right-angled triangle with two equal sides is called ______.
Solution:
(a) Two
(b) Scalene Triangle
(c) Two
(d) 180°
(e) Isosceles right-angled triangle

Question 2.
Match the following

Solution:
(i) Scalene triangle
(ii) Right-angled triangle
(iii) Obtuse angled triangle
(iv) Isosceles triangle
(v) Equilateral triangle

Question 3.
In ΔABC, name the

a) Three sides: ……….., ………., ……….
b) Three Angles: ………., ………, ……….
c) Three Vertices: ………., ………., ……….
Solution:
(a) \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CA}}\)
(b) ∠ABC, ∠BCA, ∠CAB or ∠A, ∠B, ∠C
(c) A, B, C

Question 4.
Classify the given triangles based on its sides as scalene, isosceles or equilateral.

Solution:
(i) Equilateral triangle
(ii) Scalene triangle
(iii) Isosceles triangle
(iv) Scalene triangle

Question 5.
Classify the given triangles based on their angles as acute-angled, right-angled, or obtuse-angled.

Solution:
(i) Acute angled triangle
(ii) Right-angled triangle
(iii) Obtuse angled triangle
(iv) Acute angled triangle

Question 6.
Classify the following triangles based on its sides and angles?

Solution:
(i) Isosceles Acute angled triangle
(ii) Scalene Right-angled triangle
(iii) Isosceles Obtuse angled triangle
(iv) Isosceles Right-angled triangle
(v) Equilateral Acute angled triangle
(vi) Scalene Obtuse angled triangle

Question 7.
Can a triangle be formed with the following sides? If yes, name the type of triangle.
(i) 8 cm, 6 cm, 4 cm
(ii) 10 cm, 8 cm, 5 cm
(iii) 6.2 cm, 1.3 cm, 3.5 cm
(iv) 6 cm, 6 cm, 4 cm
(v) 3.5 cm, 3.5 cm, 3.5 cm
(vi) 9 cm, 4 cm, 5 cm
Solution:
(i) Sum of two smaller sides of the triangle
= 6 + 4 = 10 cm > 8 cm
It is greater than the third side. So, a triangle can be formed a scalene triangle.

(ii) Sum of two smaller sides of the triangle
= 8 + 5 = 13 cm > 10 cm
It is greater than the third side. So, a triangle can be formed a scalene triangle.

(iii) Sum of two smaller sides of the triangle
= 1.3 + 3.5 = 4.8 cm < 6.2 cm
It is not greater than the third side. So, a triangle cannot be formed.

(iv) Two sides are equal.
So, a triangle can be formed. Isosceles triangle.

(v) Three sides are equal.
So, a triangle can be formed equilateral triangle.

(vi) Sum of two smaller sides of the triangle
= 4 + 5 = 9 cm = 9 cm
It is equal to the third side. No, a triangle cannot be formed.

Question 8.
Can a triangle be formed with the following angles? If yes, name the type of triangle.
(i) 60°, 60°, 60°
(ii) 60°, 40°, 42°
(iii) 90°, 55°, 35°
(iv) 60°, 90°, 90°
(v) 70°, 60°, 50°
(vi) 100°, 50°, 30°
Solution:
(i) 60°, 60°, 60°
Sum of the angles = 60°+ 60°+ 60° = 180°
A triangle can be formed as an acute-angled triangle.

(ii) 60°, 40°, 42°
Sum of the angles = 60° + 40° + 42° = 142°
A triangle cannot be formed.

(iii) 90°, 50°, 35°
Sum of the angles = 90° + 55° + 35° = 180°
A triangle can be formed Right-angled triangle.

(iv) 60°, 90°, 90°
No, a triangle can not be formed.
A triangle cannot have more than one right angle.

(v) 70°, 60°, 50°
Sum of the angles = 70° + 60° + 50° = 180°
A triangle can be formed as an acute-angled triangle.

(vi) 100°, 50°, 30°
Sum of the angles = 100° + 50° + 30° = 180°
A triangle can be formed as an obtuse-angled triangle.

Question 9.
Two angles of the triangles are given. Find the third angle
(i) 80°, 60°
(ii) 75°, 35°
(iii) 52°, 68°
(iv) 50°, 90°
(v) 120°, 30°
(vi) 55°, 85°
Solution:
(i) 80°, 60°
Let the third angle be x.
Sum of the angles = 180°
80° + 60° + x = 180°
140 + x = 180°
x = 180°- 140°
x = 40°
Third angle = 40°

(ii) 52°, 68°
Let the third angle be x.
Sum of the angles = 180°
52° + 68° + x = 180°
120 + x = 180°
180° – 120°
x = 60°
Third angle = 60°

(iii) 75°, 35°
Let the third angle be x.
Sum of the angles 180°
75° + 35° + x = 180°
110 + x = 180°
x = 180° – 110°
x = 70°
Third angle = 70°

(iv) 50°, 90°
Let the third angle be x. Sum of the angles = 180°
50° + 90° + x = 180°
140 + x = 180°
x = 180° – 140°
x = 40°
Third angle = 40°

(v) 120°, 30°
Let the third angle be x.
Sum of the angles = 180°
120° + 30° + x = 180°
150 + x = 180°
x = 180° – 150°
x = 30°
Third angle = 30°

(vi) 55°, 85°
Let the third angle be x.
Sum of the angles = 180°
55° + 85° + x = 180°
140 + x = 180°
x = 180° – 140°
x = 40°
Third angle = 40°

Question 10.
I am a closed figure with each of my three angles is 60°. Who am I?
Solution:
Equilateral triangle

Question 11.
Using the given information, write the type of triangle in the table given below.

Solution:
(ii) Acute angled triangle, Isosceles triangle
(iii) Right-angled triangle, Isosceles triangle
(iv) Acute angled triangle, Scalene triangle
(v) Acute angled triangle, Scalene triangle
(vi) Right-angled triangle. Scalene triangle
(vii) Obtuse angled triangle, Scalene triangle
(viii) Obtuse angled triangle, Isosceles triangle

Objective Type Questions

Question 12.
The given triangle is ……….

(a) a right-angled triangle
b) an equilateral triangle
(c) a scalene triangle
(d) an obtuse-angled triangle
Solution:
(b) an equilateral triangle

Question 13.
If all angles of a triangle are less than a right angle, then it is called _____.
(a) an obtuse-angled triangle
(b) a right-angled triangle
(c) an isosceles right-angled triangle
(d) an acute-angled triangle
Solution:
(d) an acute-angled triangle

Question 14.
If two sides of a triangle are 5 cm and 9 cm, then the third side is
(a) 5 cm
(b) 3 cm
(c) 4 cm
(d) 14 cm
Solution:
(a) 5 cm

Question 15.
The angles of a right-angled triangle are
(a) acute, acute, obtuse
(c) acute, right, right
(c) right, obtuse, acute
(d) acute, acute, right
Solution:
(d) acute, acute, right

Question 16.
An equilateral triangle is
(a) an obtuse-angled triangle
(b) a right-angled triangle
(c) an acute-angled triangle
(d) a scalene triangle
Solution:
(c) an acute-angled triangle

Students can download Maths Chapter 1 Numbers Ex 1.2 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 1 Numbers Ex 1.2

Question 1.
Fill in the blanks
(i) The HCF of 45 and 75 is …….
(ii) The HCF of two successive even numbers is …….
(iii) If the LCM of 3 and 9 is 9, then their HCF is ………
(iv) The LCM of 26, 39 and 52 is ……..
(v) The least number that should be added to 57 so that the sum is exactly divisible by 2, 3, 4 and 5 is ………
Solution:
(i) 15
(ii) 2
(iii) 3
(iv) 156
(v) 3

Question 2.
Say True or False
(i) The numbers 57 and 69 are co-primes.
(ii) The HCF of 17 and 18 is 1.
(iii) The LCM of two successive numbers is the product of the numbers.
(iv) The LCM of two co-primes is the sum of the numbers.
(v) The HCF of two numbers is always a factor of their LCM.
Solution:
(i) False
(ii) True
(iii) True
(iv) False
(v) True

Question 3.
Find the HCF of each set of numbers using the prime factorisation method.
(i) 18, 24
(ii) 51, 85
(iii) 61, 76
(iv) 84, 120
(v) 27, 45, 81
(vi) 45, 55, 95
Solution:
(i) 18, 24

HCF = 2 × 3 = 6

(ii) 51, 85

HCF = 17

(iii) 61, 76
61 = 1 × 61
For 61, 76, the common factor is 1
HCF = 1

(iv) 84, 120

HCF = 2 × 2 × 3 = 12

(v) 27, 45, 81

HCF = 3 × 3 = 9

(vi) 45, 55, 95

Factors of 55 = 5 × 11
Factors of 45 = 3 × 3 × 5
Factors of 95 = 5 × 19
HCF = 5

Question 4.
Find the LCM of each set of numbers using the prime factorisation method.
(i) 6, 9
(ii) 8, 12
(iii) 10, 15
(iv) 14, 42
(v) 30, 40, 60
(vi) 15, 25, 75
Solution:
(i) 6, 9

Factors of 6 = 2 × 3
Factors of 9 = 3 × 3
LCM of 6 and 9 = 3 × 2 × 3 = 18

(ii) 8, 12

(iii) 10, 15

Factors of 10 = 2 × 5
Factors of 15 = 3 × 5
LCM of 10 and 15 = 5 × 2 × 3 = 30

(iv) 14, 42

Factors of 14 = 2 × 7
Factors of 42 = 2 × 3 × 7
LCM of 14 and 42 = 7 × 2 × 3 = 42

(v) 30, 40, 60

Factors of 30 = 2 × 3 × 5
Factors of 40 = 2 × 2 × 2 × 5
Factors of 60 = 2 × 2 × 3 × 5
LCM of 30, 40, 60 = 2 × 5 × 3 × 2 × 2 = 120

(vi) 15, 25, 75

Factors of 15 = 3 × 5
Factors of 25 =5 × 5
Factors of 75 = 3 × 5 × 5
LCM of 15, 25, 75 = 5 × 3 × 5 = 75

Question 5.
Find the HCF and the LCM of the numbers 154, 198, 286
Solution:
HCF

Factors of 154 = 2 × 7 × 11
Factors of 198 = 2 × 3 × 3 × 11
Factors of 286 = 2 × 13 × 11
HCF of 154, 198, 286 = 11 × 2 = 22
LCM

LCM = 2 × 11 × 7 × 9 × 13
= 22 × 63 × 13
= 18018

Question 6.
What is the greatest possible volume of a vessel that can be used to measure exactly the volume of milk in cans (in full capacity) of 80 litres, 100 litres and 120 litres?
Solution:
This is an HCF related problem. So, we need to find the HCF of 80, 100, 120

80 = 2 × 2 × 2 × 2 × 5
100 = 2 × 2 × 5 × 5
120 = 2 × 2 × 2 × 3 × 5
HCF of 80, 100 and 120 = 2 × 2 × 5 = 20
Volume of the vessel = 20 litres

Question 7.
The traffic lights at three different road junctions change after every 40 seconds, 60 seconds, and 72 seconds respectively. If they changed simultaneously together at 8 a.m at the junctions, at what time will they simultaneously change together again?
Solution:
This is an LCM related problem. So, we need to find the LCM of 40, 60, 72

LCM of 40, 60 and 72
= 2 × 2 × 3 × 5 × 2 × 1 × 1 × 3
= 360 seconds
= 6 minutes
The traffic lights will change simultane¬ously again at 8 : 06 am.

Question 8.
The LCM of two numbers is 210 and their HCF is 14. How many such pairs are possible.
Solution:
Product of two numbers = LCM × HCF
x × y = 210 × 14
x × y = 2940
(12, 245), (20, 147)
Two pairs are possible.

Question 9.
The LCM of two numbers is 6 times their HCF. If the HCF is 12 and one of the numbers is 36, then find the other number.
Solution:
36x = 6 × 12 × 12
⇒ \(x=\frac{6 \times 12 \times 12}{36}=24\)

Objective Type Questions

Question 10.
Which of the following pairs is co-prime?
(a) 51, 63
(b) 52, 91
(c) 71, 81
(d) 81, 99
Solution:
(c) 71, 81

Question 11.
The greatest four-digit number which is exactly divisible by 8, 9, and 12 is
(a) 9999
(b) 9996
(c) 9696
(d) 9936
Solution:
(d) 9936

Question 12.
The HCF of two numbers is 2 and their LCM is 154. If the difference between the numbers is 8, then the sum is
(a) 26
(b) 36
(c) 46
(d) 56
Solution:
(b) 36

Question 13.
Which of the following cannot be the HCF of two numbers whose LCM is 120?
(a) 60
(b) 40
(c) 80
(d) 30
Solution:
(c) 80

Students can download Maths Chapter 3 Bill, Profit and Loss Ex 3.2 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 3 Bill, Profit and Loss Ex 3.2

Miscellaneous Practice Problems

Question 1.
A Shopkeeper buys three articles for Rs 325, Rs 450, and Rs 510. He is able to sell them for Rs 350, Rs 425, and Rs 525 respectively. Find the gain or loss to the shopkeeper on the whole.
Solution:
C.P of three articles = 325 + 450 + 510 = ₹ 1285
S.P of three articles = 350 + 425 + 525 = ₹ 1,300
Here S.P > C.P
Profit = S.P – C.P = 1,300 – 1285 = ₹ 15
The shopkeeper gained = ₹ 15

Question 2.
A stationery shop owner bought a scientific calculator for ₹ 750. He had put a battery worth ₹ 100 in it. He had spent ₹ 50 for its outer pouch. He was able to sell it at ₹ 850. Find his profit or loss.
Solution:
Cost of the scientific calculator = ₹ 750
Cost of its battery = ₹ 100
Cost of outer pouch = ₹ 50
Cost Price of the calculator = ₹ 750 + ₹ 100 + ₹ 50 = ₹ 900
S.P = ₹ 850
Here S.P > C.P
Loss = C.P – S.P = 900 – 850 = ₹ 50
Loss = ₹ 50

Question 3.
Nathan paid Rs 800 and bought 10 bottles of honey from a village vendor. He sold them in a gain for Rs 100 per bottle. Find his profit or loss.
Solution:
C.P of 10 bottles of honey = ₹ 800
C.P of 1 bottle honey = 800/10 = ₹ 80
S.P of a bottle honey = ₹ 100
Here S.P > C.P
Profit per bottle = ₹ 100 – ₹ 80 = ₹ 20
Profit for 10 bottles = 20 × 10 = ₹ 200
Profit = ₹ 200

Question 4.
A man bought 400 metres of cloth for ₹ 60,000 and sold it at the rate of ₹ 400 per metre. Find his profit or loss.
Solution:
C.P of 400 metres of cloth = ₹ 60,000
S.P per metre = ₹ 400
S.P of 400 metres of cloth = 400 × 400 = ₹ 1,60,000
Here S.P > C.P
Profit = C.P – S.P = 1,60,000 – 60,000 = ₹ 1,00,000

Challenge Problems

Question 5.
A fruit seller bought 2 dozen bananas at Rs 20 a dozen and sold them at Rs 3 per banana. Find his gain or loss.
Solution:
Cost of one dozen banana = ₹ 20
Cost of 2 dozen bananas = ₹ 20 × 2 = ₹ 40
C.P = ₹ 40
S.P per banana = ₹ 3
S.P for 2 dozen banana = ₹ 3 × 24 = ₹ 72
Here S.P > C.P
Profit = S.P – C.P = 72 – 40 = 32
Profit = ₹ 32

Question 6.
A store purchased pens at ₹ 216 per dozen. He paid ₹ 58 for conveyance and sold the pens at the discount of n per pen and made an overall profit of ₹ 50. Find the M.P of each pen.
Solution:
Cost of a dozen pens = ₹ 216
Paid for conveyance = ₹ 58
Cost price of 12 pens = 216 + 58 = ₹ 274 [∵ 1 dozen = 12]
Profit of 12 pens = ₹ 50
Profit = S.P – C.P
⇒ 50 = S.P – 274
⇒ S.P = 50 + 274 = ₹ 324
Also discount allowed per pen = ₹ 2
Discount for 12 pens = 2 × 12 = ₹ 24
S.P = M.P – Discount
⇒ 324 = M.P – 24
⇒ M.P = 324 + 24 = ₹ 348
Marked price for 12 pens = ₹ 348
M.P of a pen = \(\frac { 348 }{ 12 }\) = ₹ 29
M.P per pen = ₹ 29

Question 7.
A Vegetable vendor buys 10 kg of tomatoes per day at Rs 10 per kg, for the first three days of a week. 1 kg of tomatoes got smashed every day for those 3 days. For the remaining 4 days of the week, he buys 15 kg of tomatoes daily per kg. If for the entire week he sells tomatoes at Rs 20 per kg, then find his profit or loss for the week.
Solution:
Total tomatoes bought for 3 days = 3 × 10 = 30 kg
Cost of 1 kg = ₹ 10
Cost of 30kg tomatoes = 30 × 10 = ₹ 300
Total tomatoes bought for other 4 days = 4 × 15 = 60 kg
Cost of 1 kg = ₹ 8
Cost of 60 kg tomatoes = 60 × 8 = ₹ 480
Total cost of 90 kg tomatoes = 300 + 480 = ₹ 780
C.P = ₹ 780
Tomatoes smashed = 3 kg
Total kg of Tomatoes for sale = 90 – 3 = 87 kg
S.P of 1 kg tomatoes = ₹ 20
S.P of 87 kg tomatoes = 87 × 20 = ₹ 1740
Here S.P > C.P
Profit = S.P – C.P = 1740 – 780 = ₹ 960
Profit = ₹ 960

Question 8.
An electrician buys a used T.V for ₹ 12,000 and a used Fridge for ₹ 11,000. After spending ₹ 1000 on repairing the T.V and ₹ 1500 on painting the Fridge, he fixes up the M.P of T.V as ₹ 15,000 and that of the Fridge as ₹ 15,500. If he gives each ₹ 1000 discount oh each find his profit or loss.
Solution:
(i) Cost of a T.V = ₹ 12,000
Paid for repair = ₹ 1,000
C.P of the T.V = 12,000 + 1000 = ₹ 13,000
M.P of the T.V = ₹ 15,000
Discount on a TV = ₹ 1000
S.P = M.P – Discount = 15,000 – 1000 = ₹ 14,000
Here S.P > C.P
Profit = S.P – C.P = 14,000 – 13,000 = ₹ 1,000
Profit on the T.V = ₹ 1,000
(ii) Cost of the Fridge = ₹ 11,000
Painting charge = ₹ 1500
C.P of the Fridge = 11000 + 1500 = ₹ 12,500
M.P of the Fridge = ₹ 15,500
Discount allowed = ₹ 1000
S.P = M.P – Discount = ₹ 15,500 – ₹ 1000 = ₹ 14,500
Here also S.P > C.P
Profit = ₹ 14,500 – ₹ 12,500 = ₹ 2000
Total profit = Profit on T.V + Profit on Fridge = ₹ 1000 + ₹ 2000 = ₹ 3000
Profit = ₹ 3000

Students can download Maths Chapter 3 Bill, Profit and Loss Ex 3.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 3 Bill, Profit and Loss Ex 3.1

Question 1.
A School purchases some furniture and gets the following bill.

(i) What is the name of the store?
(ii) What is the serial number of the bill?
(iii) What is the cost of a black board?
(iv) How many sets of benches and desks does the school buy?
(v) Verify whether the total bill amount is correct.
Solution:
(i) Mullai Furniture mart
(ii) Serial No :: 728
(iii) Rs 3000
(iv) 50 sets
(v) Correct

Question 2.
Prepare a bill for the following books of biographies purchased from Maruthu Book Store, Chidambaram on 12.04.2018 bearing the bill number 507. 10 copies of Subramanya Bharathiar @ Rs 55 each, 15 copies of Thiruvalluvar @ Rs 75 each, 12 copies of Veeramamunivar @ Rs 60 each, and 12 copies of ThiruviKa @ Rs 70 each.
Solution:

Question 3.
Fill up the appropriate boxes in the following table.

Solution:
(i) CP = Rs 100
SP = Rs 120
CP < SP
Profit = SP – CP
= Rs 120 – Rs 100
= Rs 20

(ii) CP = Rs 110
SP = Rs 120
CP < SP
Profit = SP – CP
= Rs 120 – Rs 110
= Rs 10

(iii) CP = Rs 120
Profit = Rs 20
Profit = SP – CP
Rs 20 = SP – Rs 120
Rs 20 + Rs 120 = SP
SP = Rs 140

(iv) CP = Rs 100
SP = Rs 90
CP > SP
Loss = CP – SP
= Rs 100 – Rs 90
= Rs 10

(v) CP = Rs 120
Profit = Rs 25
Profit = SP – CP
Rs 25 = SP – Rs 120
Rs 25 + Rs 120 = SP
Rs 145 = SP
SP = Rs 145

Question 4.
Fill up the appropriate boxes in the following table.

Solution:
(i) CP = Rs 110
MP = Rs 130
Profit = SP – CP
= Rs 130 – Rs.110
= Rs 20
If there is no discount MP = SP
SP = Rs 130

(ii) CP = Rs 110 Profit
MP = 130
Discount = Rs 10
= SP – CP
= Rs 120 – Rs 110
= Rs 10
SP = MP – Discount
= Rs 130 – Rs 10
= Rs 120

(iii) CP = Rs 110
MP = Rs 130
Discount = Rs 30
Loss = CP – SP
= Rs 110 – Rs 100
= Rs 10
SP = Mp – Discount
= Rs 130 – Rs 30
= Rs 100

(iv) CP = Rs 110
MP = Rs 120
Loss = CP – SP
SP = CP – Loss
= Rs 110 – Rs 10
= Rs 100
Discount = MP – SP
= Rs 120 – Rs 100
= Rs 20

(v) MP = Rs 120
Discount = Rs 10
Profit = Rs 20
Loss = Rs 0
SP = MP – Discount
= Rs 120 – Rs 10
= Rs 110
Profit = Rs 20
= SP – CP
Rs 20 = Rs 110 – CP
CP = SP – Profit
= Rs 110 – Rs 20
= Rs 90

Question 5.
Rani bought a set of bangles for ₹ 310. Her neighbour liked it the most. So Rani sold it to her for ₹ 325. Find the profit or loss to Rani.
Solution:
CP = Rs 310
SP = Rs 325
Profit = SP – CP = Rs 325 – Rs 310 = Rs 15

Question 6.
Sugan bought a pair of jeans pant for Rs 750 not fit him. He sold it to his friend for Rs 710, Find the profit or loss to sugan.
Solution:
CP = Rs 750
SP = Rs 710
CP > SP
Loss = CP – SP
= Rs 750 – Rs 710
= Rs 40

Question 7.
Somu bought a second-hand bike for ₹ 28,000 and spent ₹ 2000 on its repair. He sold it for ₹ 30,000. Find his profit or loss. Solution:
CP = Rs 28,000 + Rs 2,000
CP = Rs 30,000
SP = Rs 30,000
CP = SP
No profit / Loss

Question 8.
Muthu has a car worth Rs 8,50,000 and he wants to sell it at a profit of Rs 25,000. What should be the selling price of the car?
Solution:
CP = Rs 8,50,000
Profit = Rs 25,000
SP = CP + Profit
= Rs 8,50,000 + Rs 25,000
= Rs 8,75,000

Question 9.
Valarmathi sold her pearl set for ₹ 30,000 at a profit of ₹ 5000. Find the cost price of the pearl set.
Solution:
SP = Rs 30,000
Profit = Rs 5,000
CP = SP – Profit
= Rs 30,000 – Rs 5,000
= Rs 25,000

Question 10.
If Guna marks his product to be sold for Rs 325 and gives a discount of Rs 30, then find the S.P.
Solution:
MP = Rs 325
Discount = Rs 30
SP = MP – Discount
= Rs 325 – Rs 30
= Rs 295

Question 11.
A man buys a chair for ₹ 1500. He wants to sell it at a profit of ₹ 250 after making a discount of ₹ 100. What is the M.P of the chair?
Solution:
CP = Rs 1,500
Profit = Rs 250
SP = CP + Profit
= Rs 1,500 + Rs 250
= Rs 1,750
Discount = Rs 100
SP = MP – Discount
MP = SP + Discount
= Rs 1,750 + Rs 100
= Rs 1,850

Question 12.
Amutha marked her home product of pickle as Rs 300 per pack. But she sold it for only Rs 275 per pack. What was the discount offered by her per pack?
Solution:
MP = Rs 300
SP = Rs 275
Discount = MP – SP
= Rs 300 – Rs 275
= Rs 25

Question 13.
Valavan bought 24 eggs for ₹ 96. Four of them were broken and also he had a loss of ₹ 36 on selling them. What is the selling price of one egg?
Solution:
Cost of 24 eggs = Rs 96
Since 4 of the eggs were broken, the number of remaining eggs = 24 – 4 = 20
Since the loss is Rs 36
The selling price of 20 eggs
SP = CP – Loss
= Rs 96 – Rs 36
= Rs 60
∴ Cost of 1 egg = Rs 60 / 20 = Rs. 3

Question 14.
Mangai bought a cell phone for Rs 12,585. It fell down. She spent Rs 500 on its repair. She sold it for Rs 7,500. Find her profit or loss.
Solution:
CP = Rs 12,585 + Rs 500
= Rs 13,085
SP = Rs 7,500
CP > SP
Loss = CP – SP
= Rs 13,085 – Rs 7,500
= Rs 5,585

Objective Type Questions

Question 15.
Discount is subtracted from ______ to get S.P.
(a) M.P
(b) C.P
(c) Loss
(d) Profit
Solution:
(a) M.P

Question 16.
Overhead expenses are always included in ………
(a) S.P
(b) C.P
(c) Profit
(d) Loss
Solution:
(b) C.P

Question 17.
There is no profit or loss when ______.
(a) C.P = S.P.
(b) C.P. > S.P
(c) C.P. < S.P
(d) M.P = Discount
Solution:
(a) cost price = selling price

Question 18.
Discount = M.P.
(a) Profit
(b) S.P
(c) Loss
(d) C.P
Solution:
(b) S.P

Students can download Maths Chapter 1 Numbers Ex 1.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 1 Numbers Ex 1.1

Question 1.
Fill in the blanks.
(i) The number of prime numbers between 11 and 60 is _______
(ii) The numbers 29 and _______ are twin primes.
(iii) 3753 is divisible by 9 and hence divisible by _______
(iv) The number of distinct prime factors of the smallest 4 digit number is______
(v) The sum of distinct prime factors of 30 is ________
Solution:
(i) 12
(ii) 31
(iii) 3
(iv) 2
(v) 10

Question 2.
Say True or False.
(i) The sum of any number of odd numbers is always even.
(ii) Every natural number is either prime or composite.
(iii) If a number is divisible by 6, then it must be divisible by 3.
(iv) 16254 is divisible by 2, 3, 6, and 9.
(v) The number of distinct prime factors of 105 is 3.
Solution:
(i) False
(ii) False
(iii) True
(iv) True
(v) True

Question 3.
Write the smallest and the biggest two-digit prime number.
Solution:
Smallest two-digit prime number – 11
Biggest two-digit prime number – 97.

Question 4.
Write the smallest and the biggest three-digit composite number.
Solution:
Smallest three-digit composite number – 100
Biggest three-digit composite number – 999

Question 5.
The sum of any three odd natural number is odd. Justify this statement with an example.
Solution:
True.
1 + 3 + 5 = 9 (Odd)

Question 6.
The digits of the prime number 13 can be reversed to get another prime number 31. Find if any such pair exists up to 100.
Solution:
(17, 71), (37, 73) and (79, 97)

Question 7.
Your friend says that every odd number is prime. Give an example to prove him/her wrong.
Solution:
False. 15 is an odd number. But not prime.

Question 8.
Each of the composite numbers has at least three factors. Justify this statement with an example.
Solution:
Factors of 4 are 1, 2, 4

Question 9.
Find the dates of any month in a calendar which are divisible by both 2 and 3.
Solution:
Every month the dates 6, 12, 18, 24, and 30 (excluding February) are divisible by both 2 and 3.

Question 10.
I am a two-digit prime number and the sum of my digits is 10.1 am also one of the factors of 57. Who am I?
Solution:
Two-digit prime numbers with a sum of digits 10 are 19, 37, 73.
of these factors of 57 is 19. the number is 19.

Question 11.
Find the prime factorisation of each number by factor tree method and division method.
(i) 60
(ii) 128
(iii) 144
(iv) 198
(v) 420
(vi) 999
Solution:

60 = 2 × 30 = 2 × 2 × 15
= 2 × 2 × 3 × 5

128 = 2 × 2 × 2 × 2 × 2 ×2 × 2
128 = 2 × 64 = 2 × 2 × 32
= 2 × 2 × 2 × 16
= 2 × 2 × 2 × 2 × 8
128 = 2 × 2 × 2 × 2 × 2 × 4
= 2 × 2 × 2 × 2 × 2 × 2 × 2

144 = 2 × 2 × 2 × 2 × 3 × 3
144 = 2 × 72 = 2 × 2 × 36
= 2 × 2 × 2 × 18 = 2 × 2 × 2 × 2 × 9
= 2 × 2 × 2 × 2 × 3 × 3

198 = 2 × 3 × 3 × 11
198 = 2 × 99 = 2 × 3 × 33 = 2 × 3 × 3 × 11

420 = 2 × 210
= 2 × 2 × 105
= 2 × 2 × 3 × 35 = 2 × 2 × 3 × 5 × 7

999 = 3 × 333 = 3 × 3 × 111
= 3 × 3 × 3 × 37

Question 12.
If there are 143 math books to be arranged in equal numbers in all the stacks, then find the number of books in each stack and also the number of stacks.
Solution:

143 = 11 × 13 (11, 13) or (13, 11)
143 = 11 × 13

Question 13.
The difference between two successive odd numbers is
(a) 1
(b) 2
(c) 3
(d) 0
Solution:
(b) 2

Question 14.
The only even prime number is
(a) 4
(b) 6
(c) 2
(d) 0
Solution:
(c) 2

Question 15.
Which of the following numbers is not a prime?
(a) 53
(b) 92
(c) 97
(d) 71
Solution:
(b) 92

Question 16.
The sum of the factors of 27 is
(a) 28
(b) 37
(c) 40
(d) 31
Solution:
(c) 40

Question 17.
The factors of the number are 1, 2, 4, 5, 8, 10, 16, 20, 40, and 80. What is the number?
(a) 80
(b) 100
(c) 128
(d) 160
Solution:
(a) 80

Question 18.
The prime factorisation of 60 is 2 × 2 × 3 × 5. Any other number which has the same prime factorisation as 60 is
(a) 30
(b) 120
(c) 90
(d) Impossible
Solution:
(d) Impossible

Question 19.
If the number 6354*97 is divisible by 9 then the value of * is
(a) 2
(b) 4
(c) 6
(d) 7
Solution:
(a) 2

Question 20.
The number 87846 is divisible by
(a) 2 only
(b) 3 only
(c) 11 only
(d) all of these
Solution:
(d) all of these

Students can download Maths Chapter 2 Measurements Ex 2.3 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 2 Measurements Ex 2.3

Miscellaneous practice problems

Question 1.
Two pipes whose lengths are 7 m 25 cm and 8 m 13 cm joined by welding and then a small piece 60 cm is cut from the whole. What is the remaining length of the pipe?
Solution:
Total length = 7 m 25 cm + 8 m 13 cm = 15 m 38 cm (or) 1538 cm
length detatched = 60 cm
Remaining length = 14 m 78 cm

Question 2.
The saplings are planted at a distance of 2 m 50 cm in the road of length 5 km by Saravanan. If he has 2560 saplings, how many saplings will be planted by him? how many saplings are left?
Solution:
Distance between two saplings = 2 m 50 cm = 250 cm
Total length of the road = 5000 m = 500000 cm

Question 3.
Put ✓ a mark in the circles which adds upto the given measure.

Solution:

Question 4.
Make a calendar for the month of February 2020. (Hint: January 1st, 2020 is Wednesday)
Solution:
February 2020 is a leap year

Question 5.
Observe and Collect the data for a minute

Solution:
Do your self.

Challenge Problems

Question 6.
A squirrel wants to eat the grains quickly. Help the Squirrel to find the shortest way to reach the grains. (Use your scale to measure the length of the line segments)

Solution:

The Shortest way to reach the grains is the AGFKE path.

Question 7.
A room has a door whose measures are 1 m wide and 2 m 50 cm high.
Can we make a bed of 2 m and 20 cm in length and 90 cm wide into the room?
Solution:
Measures of the door length 2 m 50 cm width and lm (100 cm)
(i) Measures of the bed 2 m 20 cm width and 90 cm
Measures of the bed < measures of the door
∴ Yes, we can take the bed into the room.

Question 8.
A post office functions from 10 a.m. to 5.45 p.m. with a lunch break of 1 hour. If the post office works for 6 days a week, find the total duration of working hours in a week.
Solution:
Working hours in a day = 6 hrs 45 min
= (6 × 60 min) + 45 min
= (360 + 45) min
= 405 min
Total duration of working hours in a week
= 6 × 405 min
= 2430 min
= \(\frac{2430}{60}\)
= \(\frac{810}{20}\)
= 40 \(\frac{1}{2}\)
= 40 hours 30 minutes

Question 9.
Seetha wakes up at 5.20 a.m. She spends 35 minutes to get ready and travels 15 minutes to reach the railway station. If the train departs exactly at 6.00 am, will Seetha catch the train?
Solution:
No, Seetha will not catch the train
Time at Seetha wakes up = 5.20 am
Time is taken for getting ready = 35 min
Travelling time to station = 15 min
Reporting time = 5.20 am + 50 min = 6.10 am
But, the train departs exactly at 6.00 am
So, Seetha will not catch the train.

Question 10.
A doctor advised Vairavan to take one tablet every 6 hours once on the 1st day and once every 8 hours on the 2nd and 3rd day. If he starts to take 9.30 am the first dose. Prepare a time chart to take the tablet in railway time.
Solution:

Students can download Maths Chapter 2 Measurements Ex 2.2 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 2 Measurements Ex 2.2

Question 1.
Say the time in two ways:

Solution:
(i) 10 : 15 hours; quarter past 10; 45 minutes to 11
(ii) 6 : 45 hours; quarter to 7; 45 minutes past 6
(iii) 4 : 10 hours; 10 minutes past 4; 50 minutes to 5
(iv) 3 : 30 hours; half-past 3; 30 minutes to 4
(v) 9 : 40 hours; 20 minutes to 10; 40 minutes past 9.

Question 2.
Match the following:

Solution:
(i) d
(ii) e
(iii) b
(iv) c
(v) a

Question 3.
Convert the following:
(i) 20 minutes into seconds
(ii) 5 hours 35 minutes 40 seconds into seconds
(iii) 3 ½ hours into minutes
(iv) 580 minutes into hours
(v) 25200 seconds into hours
Solution:
(i) 20 minutes into seconds:
1 min = 60 seconds
20 min = 20 × 60 seconds
= 1200 seconds

(ii) 5 hours 35 min 40 seconds into seconds
Solution:
1 hour = 60 min
1 min = 60 seconds
1 hour = 3600 seconds
5 hours = 5 × 3600 seconds
= 18000 seconds
35 min = 35 × 60 seconds
= 2100 seconds
5 hours 35 minutes 40 seconds
= (18000 + 2100 + 40) seconds
= 20140 seconds

(iii) 3 ½ hours into minutes
Solution:
1 hour = 60 minutes
3 ½ hours = 3 hours + 30 min
= (3 × 60 + 30) min
= (180 + 30)min
= 210 min

(iv) 580 minutes into hours
Solution:
1 hour = 60 min
580 min
= \(\frac{580}{60}\) hours
= \(\frac{290}{30}\) hours
= \(\frac{29}{3}\)
= 9 \(\frac{2}{3}\)
= 9 hours 40 min

(v) 25200 seconds into hours:
Solution:
25200 seconds = \(\frac{25200}{3600}\)
= \(\frac{126}{18}\) hours
= \(\frac{63}{9}\) hours
= 7 hours

Question 4.
The duration of electricity consumed by the farmer for his pump set on Monday and Tuesday was 7 hours 20 minutes 35 seconds and 3 hours 44 minutes 50 seconds respectively. Find the total duration of consumption of electricity.
Solution:
The total duration of electricity consumed on both days
= 7 hours 20 min 35 sec + 3 hours 44 min 50 sec
= (7 + 3) hours (20 + 44) min (35 + 50) sec
= 10 hours 64 min 85 seconds
= 11 hours 5 min 25 seconds

Question 5.
Subtract 10 hours 20 min 35 seconds from 12 hours 18 min 40 seconds.
Solution:
12 hours 18 min 40 seconds
= (12 × 3600) + (18 × 60) + 40 seconds
= 43200 + 1080 + 40 seconds
= 44320 seconds
10 hours 20 min 35 seconds
= (10 × 3600) + (20 × 60) + 35 seconds
= 36000 + 1200 + 35 seconds
= 37235 seconds
Difference:
44320 – 37235
= 7085
7085 seconds = (1 × 3600) + 3480 + 5 seconds
= 1 hour 58 minutes 5 seconds

Question 6.
Change the following into 12 hour format
(i) 02:00 hours
(ii) 08:45 hours
(iii) 21:10 hours
(iv) 11:20 hours
(v) 00:00 hours
Solution:
(i) 2 am
(ii) 08:45 am
(iii) 9:10 pm
(iv) 11:20 am
(v) 12 midrid

Question 7.
Change the following into 24-hour format.
(i) 3.15 am
( ii) 12.35 pm
(iii) 12.00 noon
(iv) 12.00 mid night
Solution:
(i) 03.15 hours
(ii) 12.35 hours
(iii) 12.00 hours
(iv) 24.00 hours

Question 8.
Calculate the duration of time
(i) from 5.30 am to 12.40 pm
(ii) from 1.30 pm to 10.25 pm
(iii) from 20.00 hours to 4.00 hours
(iv) from 17.00 hours to 5.15 hours
Solution:
(i) from 5.30 a.m. to 12 .40 p.m.
Duration of time from 5.30 a.m. to noon = 12 : 00 – 5 : 30 = 6 : 30 i.e 6 hours 30 minutes
From noon to 12.40 p.m the duration = 00 hours 40 minutes
Total duration = 6 hours 30 minutes + 00 hours 40 minutes
= 6 hours 70 minutes
= 6 hours + (60 + 10) minutes
= 6 hours + 1 hr 10 minutes
= 7 hours 10 minutes
∴ Duration of time from 5.30 am to 12.40 pm = 7 hours 10 minutes

(ii) From 1.30 pm to 10.25 pm
= (1.30 pm to 10.00 pm) + 25 min
= 8 hrs 30 min + 25 min
= 8 hrs 55 min

(iii) From 20.00 hours to 4.00 hours
= (20.00 hrs to 24.00 hrs) + (24.00 hrs to 4.00 hrs)
= 4 hrs + 4 hrs
= 8 hours

(iv) From 17.00 hrs to 5.15 hours
= (17.00 hrs to 05.00 hrs) + 15 min
= 12 hours + 15 min
= 12 hours 1.5 min

Question 9.
The departure and arrival timing of the Vaigai Superfast Express (No. 12635) from Chennai Egmore to Madurai Junction are given. Read the details and answer the following.

(i) At what time does the Vaigai Express start from Chennai and arrive at Madurai?
(ii) How many halts are there between Chennai and Madurai?
(iii) How long does the train halt at the Villupuram Junction?
(iv) At what time does the train come to Sholavandan?
(v) Find the journey time from Chennai Egmore to Madurai?
Solution:
(i) 13.40 hours – 21.20 hours
(ii) 8 halts
(iii) 5 minutes
(iv) 20.34 hours
(v) 7 hours 40 minutes

Question 10.
Manickam joined a chess class on 20.02.2017 and due to an exam, he left practice after 20 days. Again he continued to practice from 10.07.2017 to 31.03.2018. Calculate how many days did he practice?
Solution:
From the date of joining = 20 days From 10.07.2017 to 31.03.2018
July – 22
Aug – 31
Sep – 30
Oct – 31
Nov – 30
Dec – 31
Jan – 31
Feb – 28
Mar – 31
Total – 265
Total no of practice days = 265 + 20 = 285 days

Question 11.
A clock gains 3 minutes every hour. If the clock is set correctly at 5 am, find the time shown by the clock at 7 p.m?
Solution:
Time gained for 1 hour = 3 min
Time duration from 5 am to 7 pm = 14 hours
Time gained for 14 hours = 1 4 × 3 minutes
= 42 minutes
So, at 7 pm, the clock shows 7 hrs 42 minutes

Question 12.
Find the number of days between Republic day and Kalvi Valarchi Day in 2020.
Solution:
In 2020 Republic Day will be celebrated on 26th January and Kalvi Valarchi Day will be celebrated on 15th July.
Number of days between 26.01.2020 and 15.07.2020
January – 6 Days (from 26.01.2020)
February – 29 Days (2020 is a leap year)
March – 31 Days
April – 30 Days
May – 31 Days
June – 30 Days
July – 15 Days (upto 15.07.2020)
Total – 172 Days.
∴ Total number of days = 172

Question 13.
If the 11th of Jan 2018 is Thursday, what is the day on 20th July of the same year?
Solution:
Jan – 21
Feb – 28
Mar – 31
April – 30
May – 31
June – 30
July – 19
Total – 190 days
190 days = 27 weeks + 1 day
The required day is the first day after Thursday.
Therefore 20th July 2018 is Friday.

Question 14.
(i) Convert 480 days into years.
(ii) Convert 38 months into years
Solution:
(i) 480 days = \(\frac{480}{365}\)
= 1 year 115 days
= 1 year 3 months 25 days

(ii) 38 months = \(\frac{38}{12}\)
= 3 years 2 months

Question 15.
Calculate your age as on 01.06.2018
Solution:
My date of birth 20.11.1999
Convert in the format yyyy/mm/dd

My age is 18 yrs 6 months 11 days

Objective Type Questions

Question 16.
2 days = _____ hours.
(a) 38
(b) 48
(c) 28
(d) 40
Solution:
(b) 48

Question 17.
3 weeks = ……… days
(i) 21
(ii) 7
(iii) 14
(iv) 28
Solution:
(i) 21

Question 18.
The number of ordinary years between two consecutive leap years is _____.
(a) 4 years
(b) 2 years
(c) 1 year
(d) 3 years
Solution:
(d) 3 years

Question 19.
What time will it be 5 hours after 22:35 hours?
(i) 2:30 hours
(ii) 3:35 hours
(iii) 4:35 hours
(iv) 5:35 hours
Solution:
(ii) 3:35 hours

Question 20.
2\(\frac { 1 }{ 2 }\) years is equal to ______ months.
(a) 25
(b) 30
(c) 24
(d) 5
Solution:
(b) 30

Students can download Maths Chapter 2 Measurements Ex 2.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 2 Measurements Ex 2.1

Question 1.
Fill in the blanks.
(i) 250 ml + \(\frac{1}{2}\) ml = _____ l.
(ii) 150 kg 200 g + 55 kg 750 g = ____ kg ____ g.
(iii) 20 l – 1 l 500 ml = ____ l ___ ml
(iv) 450 ml × 5 = ____ l ____ ml.
(v) 50 Kg ÷ 100 g = ______
Solution:
(i) \(\frac{3}{4}\) l
(ii) 205 kg 950 g
(iii) 18 l 500 ml
(iv) 2l 250 ml
(v) 500

Question 2.
True or False.
(i) Pugazhenthi ate 100 g of nuts which is equal to 0.1 kg.
(ii) Meena bought 250 ml of buttermilk which is equal to 2.5 l.
(iii) Karkuzhali’s bag 1 kg 250 g and Poongkodi’s bag 2 kg 750 g. The total weight of their bags 4 kg.
(iv) Vanmathi bought 4 books each weighing 500 g. Total weight of 4 books is 2 kg.
(v) Gayathri bought 1 kg of birthday cake. She shared 450 g with her friends. The weight of cake remaining is 650 g.
Solution:
(i) True
(ii) False
(iii) True
(iv) True
(v) False

Question 3.
Convert into indicated units:
(i) 10 l and 50 ml into ml
(ii) 4 km and 300 m into m
(iii) 300 mg into g
Solution:
(i) 10 l and 50 ml
= 10 × 1000 ml + 50 ml
= (10000 + 50)ml
= 10050 ml

(ii) 4 km and 300 m
= 4 × 1000 + 300 m
= (4000 + 300) m
= 4300 m

(iii) 300 mg
= \(\frac{300}{1000}\)g
= 0.3 g

Question 4.
Convert into higher units:
(i) 13000 mm
(km, m, cm)
Solution:
13000 mm
= \(\frac{13000}{10}\) cm
= 1300 cm
= \(\frac{13000}{1000}\) m = 13000 mm
= 13 m
= \(\frac{13000}{1000000}\) km = 13000 mm
= 0.013 km

(ii) 8257 ml (kl, l)
Solution:
8257 ml
= \(\frac{8257}{1000}\) l
= 8.257 l
= 8257 ml
= \(\frac{8257}{1000000}\) kl
= 0.008257 kl

Question 5.
Convert into lower units:
(i) 15 km (m, cm, mm)
(ii) 12 kg (g, mg)
Solution:
(i) 15 km = 15 × 1000 m = 15000 m
15 km = 15 × 100000 cm
= 1500000 cm
15 km = 15 × 1000000 mm
= 15000000 mm

(ii) 12 kg (g, mg)
Solution:
12 kg = 12 × 1000 g
= 12000 g
12 kg = 12 × 1000000 mg
= 12000000 mg

Question 6.
Compare and put > or < or = in the following:
(i) 800 g + 150 g ____ 1 kg
(ii) 600 ml + 400 ml ____ 1 l
(iii) 6 m 25 cm ____ 600 cm + 25 cm
(iv) 88 cm ____ 8 m 8 cm
(v) 55 g ____ 550 mg
Solution:
(i) 800 g + 150g < 3kg
(ii) 600 ml + 400 ml = 1 l
(iii) 6 m 25 cm = 600 cm + 25 cm
(iv) 88 cm < 8 m 8 cm
(v) 55 g > 550 mg

Question 7.
Geetha brought 2 l and 250 ml of water in a bottle. Her friend drank 300 ml from it. How much of water is remaining in the bottle?
Solution:
Quantity of water Geetha brought = 2 l 250 ml
= 2 × 1000 + 250 ml
= 2000 + 250 ml
= 2,250 ml.
Quantity of water her friend drank = 300 ml
Remaining water = 2250 – 300 = 1950 ml. = 1 litre 950 ml.
Remaining water = 1 litre 950 ml.

Question 8.
Thenmozhi’s height is 1.25 m now she grows 5 cm every year. What would be her height after 6 years?
Solution:
Thenmozhi’s present height = 1.25 m
Rate of growth per year = 5 cm
Her growth in 6 years = 5 cm × 6 = 30 cm.
After 6 years her height = 1.25 m + 30 cm
= 1.25 × 100 + 30 cm
= 125 + 30 cm
= 155 cm.
∴ After 6 years Thenmozhi’s height will be 155 cm.

Question 9.
Priya bought 22\(\frac { 1 }{ 2 }\) kg of onion, Krishna bought 18\(\frac { 3 }{ 4 }\) kg of onion and Sethu bought 9 kg 250 g of onion. What is the total weight of onion did they buy?
Solution:
Priya’s weight = 22 kg 500 g
Krishna’s weight = 18 kg 750 g
Sethu’s weight = 9 kg 250 g
Total weight = 49 kg 1500 g = 49 kg + 1 kg 500 g = 50 kg + 500 g.
Their total weight = 50 kg 500 g.

Question 10.
Maran walks 1.5 km every day to reach the school while Mahizhan walks 1400 m. Who walks more distance and by how much?
Solution:
Distance which Maran walks = 1.5 km = 1.5 × 1000 m = 1500 m
The distance which Mahizhan walks = 1400 m.
Here 1500 > 1400
∴ Difference = 1500 – 1400 = 100 m.
∴ Maran walks more distance = 100 m.

Question 11.
In a JRC one day camp, 150 gm of rice and 15 ml oil are needed for a student. If there are 40 students to attend the camp how much rice and oil are needed?
Solution:
Rice needed for one student = 150 g
Rice needed for 40 students = 150 g × 40 = 6000 g. = \(\frac{6000}{1000}\) kg = 6 kg.
Oil needed for one student = 15 ml
Oil needed for 40 students = 15 ml × 40 = 600 ml. = \(\frac{600}{1000}\) l = 0.6 l
∴ For the camp 6 kg of rice and 0.6 l of oil needed.

Question 12.
In a school, 200 litres of lemon juice is prepared. If 250 ml lemon juice is given to each student, how many students get the juice?
Solution:
Total lemon juice prepared = 200 l = 200 × 1000 ml = 2,00,000 ml.
∴ Quantity of Lemon juice given to one student = 250 ml.
∴ Number of students can get = \(\frac{2,00,000}{250}\) = 800
∴ 800 students can get the lemon juice.

Question 13.
How many glasses of the given capacity will fill a 2 litre jug?
(i) 100 ml ___
(ii) 50 ml ____
(iii) 500 ml ____
(iv) 1 l ____
(v) 250 ml ____
Solution:
2 litre = 2 × 1000 ml = 2000 ml.
(i) 100 ml
\(\frac{2000}{100}=20\)
20 glasses of 100 ml.
(ii) 50 ml
\(\frac{2000}{50}=40\)
40 glasses of 50 ml
(iii) 500 ml
\(\frac{2000}{500}=4\)
4 glasses of 500 ml
(iv) 1 l
\(\frac{2 l}{1 l}=2\)
2 glasses of 1 l.
(v) 250 ml
\(\frac{2000}{250}=8\)
8 glasses of 250 ml can fill the jug.

Objective Type Questions

Question 14.
9 m 4 cm is equal to ……..
(i) 94 cm
(ii) 904 cm
(iii) 9.4 cm
(iv) 0.94 cm
Solution:
(ii) 904 cm

Question 15.
1006 g is equal to ____
(a) 1 kg 6 g
(b) 10 kg 6 g
(c) 100 kg 6 g
(d) 1 kg 600 g
Solution:
(a) 1 kg 6 g

Question 16.
Every day 150 l of water is sprayed in the garden. Water sprayed in a week is ……
(i) 700 l
(ii) 1000 l
(iii) 950 l
(iv) 1050 l
Solution:
(iv) 1050 l

Question 17.
Which is the greatest 0.007 g, 70 mg, 0.07 cg?
(a) 0.07 cg
(b) 0.007 g
(c) 70 mg
(d) all are equal
Solution:
(d) all are equal

Question 18.
7 km – 4200 m is equal to ……….
(i) 3 km 800 m
(ii) 2 km 800 m
(iii) 3 km 200 m
(iv) 2 km 200 m
Solution:
(ii) 2 km 800 m

Students can download Maths Chapter 3 Ratio and Proportion Ex 3.3 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 3 Ratio and Proportion Ex 3.3

Question 1.
Fill in the blanks.
(i) 3 : 5 :: …….. : 20
(ii) ……… : 24 :: 3 : 8
(iii) 5 : …….. :: 10 : 8 :: 15 : ………
(iv) 12 : ……… :: ………. :: 4 = 8 : 16
Solution:
(i) 12
Hint:
5x = 3 × 20 ⇒ x = 12
(ii) 9
8x = 24 × 3 ⇒ x = 9
(iii) 4, 12
Hint:
10x = 8 × 5 = 40 ⇒ x = 4
10y = 8 × 15 = 120 ⇒ y = 12
(iv) 24, 2
Hint:
16y = 8 × 4 ⇒ y = 2
12 × 4 = 2x ⇒ x = 24

Question 2.
Say True or False.
(i) 2 : 7 : : 14 : 4
(ii) 7 Persons are to 49 Persons as 11 kg is to 88 kg
(iii) 10 books are to 15 books as 3 books are to 15 books.
Solution:
(i) False
Hint:
7 × 14 ≠ 4 × 2
98 ≠ 8
(ii) False
Hint:
7 : 49 :: 11 : 48
49 × 11 ≠ 7 × 48
539 ≠ 336
(iii) False
Hint:
10 : 15 :: 3 : 5
\(\frac{10}{15}=\frac{5 \times 2}{5 \times 3}=\frac{2}{3} \Rightarrow \frac{3}{5}=\frac{3}{5}\)

Question 3.
Using the numbers 3, 9, 4, 12 write two ratios that are in proportion.
Solution:
(i) 3, 9, 4, 12
Here product of extremes = 3 × 12 = 36
Product of means = 9 × 4 = 36
3 : 9 : : 4 : 12

(ii) Also if we take 9, 3, 12, 4
Product of extremes = 9 × 4 = 36
Product of means = 3 × 12 = 36
9 : 3 : : 12 : 4

Question 4.
Find whether 12, 24,18, 36 are in order that can be expressed as two ratios that are in proportion.
Solution:
Yes, 12 : 24 : : 18 : 36
Because product of extremes 12 × 36 = 432
Product of means = 24 × 18 = 432
12 : 24 :: 18 : 36.

Question 5.
Write the mean and extreme terms in the following ratios and check whether they are in proportion.
(i) 78 liters is to 130 liters and 12 bottles are to 20 bottles
(ii) 400 gm is to 50 gm and 25 rupees is to 625 rupees
Solution:
(i) 78 : 130 :: 12 : 20
Extreme terms are 78 and 20.
Mean terms are 130 and 12.
Product of Extremes = 78 × 20 = 1560
Product of Means = 130 × 12 = 1560
Product of Extremes = Product of means
It is in proportion.

(ii) 400 : 50 : : 25 : 625
Product of extremes = 400 × 625 = 2,50,000
Product of means = 50 × 25 = 1250
Here product of extremes ≠ product of means
400 : 50 and 25 : 625 are not in proportion.

Question 6.
America’s famous Golden Gate bridge is 6480 ft long with 756 ft tall towers. A model of this bridge exhibited in a fair is 60 ft long with 7 ft tall towers. Is the model in proportion to the original bridge?

Solution:
6480 : 756, 60 : 7
Product of the means = 756 × 60 = 45360
Product of the extremes = 6480 × 7 = 45360
ad = bc
∴ They are in proportion

Objective Type Questions

Question 7.
Which of the following ratios are in proportion?
(a) 3 : 5, 6 : 11
(b) 2 : 3, 9 : 6
(c) 2 : 5, 10 : 25
(d) 3 : 1, 1 : 3
Solution:
(c) 2 : 5, 10 : 25
Hint:
2 × 25 = 5 × 10
⇒ 50 = 50

Question 8.
If the ratios formed using the numbers 2, 5, x, 20 in the same order are in proportion, then ‘x’ is
(a) 50
(b) 4
(c) 10
(d) 8
Solution:
(d) 8
5x = 2 × 20 ⇒ x = 8

Question 9.
If 7 : 5 is in proportion to x : 25, then ‘x’ is
(a) 27
(b) 49
(c) 35
(d) 14
Solution:
(c) 35
Hint:
5x = 7 × 25 ⇒ x = 35