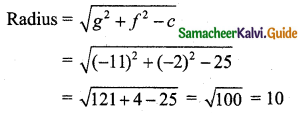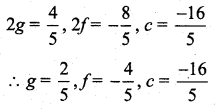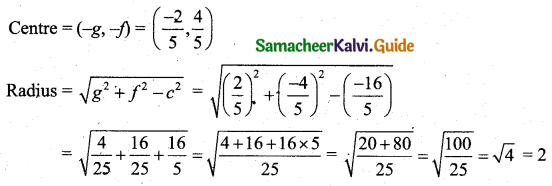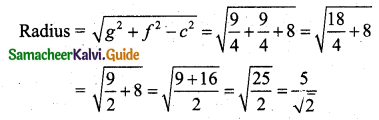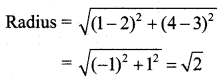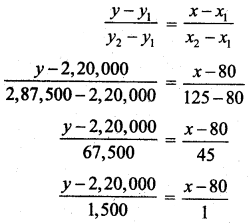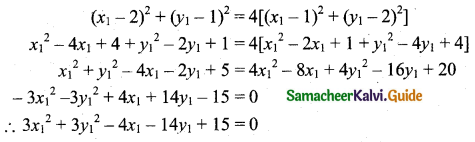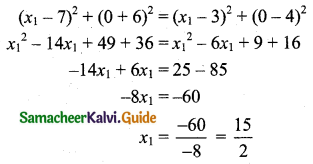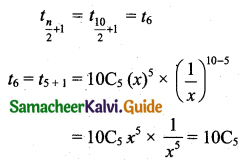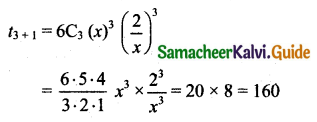Category: Class 11

Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.7 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.7

Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.7 Text Book Back Questions and Answers

Question 1.
If m₁ and m₂ are the slopes of the pair of lines given by ax² + 2hxy + by² = 0, then the value of m₁ + m₂ is:
(a) \(\frac{2 h}{b}\)
(b) \(-\frac{2 h}{b}\)
(c) \(\frac{2 h}{a}\)
(d) \(-\frac{2 h}{a}\)
Answer:
(b) \(-\frac{2 h}{b}\)

Question 2.
The angle between the pair of straight lines x² – 7xy + 4y² = 0 is:
(a) \(\tan ^{-1}\left(\frac{1}{3}\right)\)
(b) \(\tan ^{-1}\left(\frac{1}{2}\right)\)
(c) \(\tan ^{-1}\left(\frac{\sqrt{33}}{5}\right)\)
(d) \(\tan ^{-1}\left(\frac{5}{\sqrt{33}}\right)\)
Answer:
(c) \(\tan ^{-1}\left(\frac{\sqrt{33}}{5}\right)\)
Hint:
x² – 7xy + 4y² = 0
Here 2h = -7, a = 1, b = 4

Question 3.
If the lines 2x – 3y – 5 = 0 and 3x – 4y – 7 = 0 are the diameters of a circle, then its centre is:
(a) (-1, 1)
(b) (1, 1)
(c) ( 1, -1)
(d) (-1, -1)
Answer:
(c) ( 1, -1)
Hint:
To get centre we must solve the given equations
2x – 3y – 5 = 0 …….(1)
3x – 4y – 7 = 0 ………(2)
(1) × 3 ⇒ 6x – 9y = 15
(2) × 2 ⇒ 6x – 8y = 14
Subtracting, -y = 1 ⇒ y = -1
Using y = -1 in (1) we get
2x + 3 – 5 = 0
⇒ 2x = 2
⇒ x = 1

Question 4.
The x-intercept of the straight line 3x + 2y – 1 = 0 is
(a) 3
(b) 2
(c) \(\frac{1}{3}\)
(d) \(\frac{1}{2}\)
Answer:
(c) \(\frac{1}{3}\)
Hint:
To get x-intercept put y = 0 in 3x + 2y – 1 = 0 we get
3x – 1 = 0
x = \(\frac{1}{3}\)

Question 5.
The slope of the line 7x + 5y – 8 = 0 is:
(a) \(\frac{7}{5}\)
(b) \(-\frac{7}{5}\)
(c) \(\frac{5}{7}\)
(d) \(-\frac{5}{7}\)
Answer:
(b) \(-\frac{7}{5}\)
Hint:
Slope of 7x + 5y – 8 = 0 is = \(\frac{-x \text { coefficient }}{y \text { coefficient }}\) = \(-\frac{7}{5}\)

Question 6.
The locus of the point P which moves such that P is at equidistance from their coordinate axes is:
(a) y = \(\frac{1}{x}\)
(b) y = -x
(c) y = x
(d) y = \(\frac{-1}{x}\)
Answer:
(c) y = x
Hint:

Given PA = PB
y₁ = x₁
∴ Locus is y = x

Question 7.
The locus of the point P which moves such that P is always at equidistance from the line x + 2y + 7 = 0:
(a) x + 2y + 2 = 0
(b) x – 2y + 1 = 0
(c) 2x – y + 2 = 0
(d) 3x + y + 1 = 0
Answer:
(a) x + 2y + 2 = 0
Hint:
Locus is line parallel to line x + 2y + 7 = 0 which is x + 2y + 2 = 0

Question 8.
If kx² + 3xy – 2y² = 0 represent a pair of lines which are perpendicular then k is equal to:
(a) \(\frac{1}{2}\)
(b) \(-\frac{1}{2}\)
(c) 2
(d) -2
Answer:
(c) 2
Hint:
Here a = k, b = -2
Condition for perpendicular is
a + b = 0
⇒ k – 2 = 0
⇒ k = 2

Question 9.
(1, -2) is the centre of the circle x² + y² + ax + by – 4 = 0, then its radius:
(a) 3
(b) 2
(c) 4
(d) 1
Answer:
(a) 3
Hint:
Given centre (-g, -f) = (1, -2)
From the given equation c = -4
Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{1+4-(-4)}=\sqrt{9}\) = 3

Question 10.
The length of the tangent from (4, 5) to the circle x² + y² = 16 is:
(a) 4
(b) 5
(c) 16
(d) 25
Answer:
(b) 5
Hint:
Length of the tangent from (x₁, y₁) to the circle x² + y² = 16 is \(\sqrt{x_{1}^{2}+y_{1}^{2}-16}=5\)

Question 11.
The focus of the parabola x² = 16y is:
(a) (4 , 0)
(b) (-4, 0)
(c) (0, 4)
(d) (0, -4)
Answer:
(c) (0, 4)
Hint:
x² = 16y
Here 4a = 16 ⇒ a = 4
Focus is (0, a) = (0, 4)

Question 12.
Length of the latus rectum of the parabola y² = -25x:
(a) 25
(b) -5
(c) 5
(d) -25
Answer:
(a) 25
Hint:
y² = -25a
Here 4a = 25 which is the length of the latus rectum.

Question 13.
The centre of the circle x² + y² – 2x + 2y – 9 = 0 is:
(a) (1, 1)
(b) (-1, 1)
(c) (-1, 1)
(d) (1, -1)
Answer:
(d) (1, -1)
Hint:
2g = -2, 2f = 2
g = -1, f = 1
Centre = (-g, -f) = (1, -1)

Question 14.
The equation of the circle with centre on the x axis and passing through the origin is:
(a) x² – 2ax + y² = 0
(b) y² – 2ay + x² = 0
(c) x² + y² = a²
(d) x² – 2ay + y² = 0
Answer:
(a) x² – 2ax + y² = 0
Hint:
Let the centre on the x-axis as (a, 0).
This circle passing through the origin so the radius

Now centre (h, k) = (a, 0)
Radius = a
Equation of the circle is (x – a)² + (y – 0)² = a²
⇒ x² – 2ax + a² + y² = a²
⇒ x² – 2ax + y² = 0

Question 15.
If the centre of the circle is (-a, -b) and radius is \(\sqrt{a^{2}-b^{2}}\) then the equation of circle is:
(a) x² + y² + 2ax + 2by + 2b² = 0
(b) x² + y² + 2ax + 2by – 2b² = 0
(c) x² + y² – 2ax – 2by – 2b² = 0
(d) x² + y² – 2ax – 2by + 2b² = 0
Answer:
(a) x² + y² + 2ax + 2by + 2b² = 0
Hint:
Equation of the circle is (x – h)² + (y – k)² = r²
⇒ (x + a)² + (y + b)² = a² – b²
⇒ x² + y² + 2ax + 2by + a² + b² = a² – b²
⇒ x² + y² + 2ax + 2by + 2b² = 0

Question 16.
Combined equation of co-ordinate axes is:
(a) x² – y² = 0
(b) x² + y² = 0
(c) xy = c
(d) xy = 0
Answer:
(d) xy = 0
Hint:
Equation of x-axis is y = 0
Equation of y-axis is x = 0
Combine equation is xy = 0

Question 17.
ax² + 4xy + 2y² = 0 represents a pair of parallel lines then ‘a’ is:
(a) 2
(b) -2
(c) 4
(d) -4
Answer:
(a) 2
Hint:
Here a = 0, h = 2, b = 2
Condition for pair of parallel lines is b² – ab = 0
4 – a(2) = 0
⇒ -2a = -4
⇒ a = 2

Question 18.
In the equation of the circle x² + y² = 16 then v intercept is (are):
(a) 4
(b) 16
(c) ±4
(d) ±16
Answer:
(c) ±4
Hint:
To get y-intercept put x = 0 in the circle equation we get
0 + y² = 16
∴ y = ±4

Question 19.
If the perimeter of the circle is 8π units and centre is (2, 2) then the equation of the circle is:
(a) (x – 2)² + (y – 2)² = 4
(b) (x – 2)² + (y – 2)² = 16
(c) (x – 4)² + (y – 4)² = 16
(d) x² + y² = 4
Answer:
(c) (x – 2)² + (y – 2)² = 16
Hint:
Perimeter, 2πr = 8π
r = 4
Centre is (2, 2)
Equation of the circle is (x – 2)² + (y – 2)² = 4² = 16

Question 20.
The equation of the circle with centre (3, -4) and touches the x-axis is:
(a) (x – 3)² + (y – 4)² = 4
(b) (x – 3)² + (y + 4)² = 16
(c) (x – 3)² + (y – 4)² = 16
(d) x² + y² = 16
Answer:
(b) (x – 3)² + (y + 4)² = 16
Hint:
Centre (3, -4).
It touches the x-axis.
The absolute value of y-coordinate is the radius, i.e., radius = 4.
Equation is (x – 3)² + (y + 4)² = 16

Question 21.
If the circle touches the x-axis, y-axis, and the line x = 6 then the length of the diameter of the circle is:
(a) 6
(b) 3
(c) 12
(d) 4
Answer:
(a) 6
Hint:

Question 22.
The eccentricity of the parabola is:
(a) 3
(b) 2
(c) 0
(d) 1
Answer:
(d) 1

Question 23.
The double ordinate passing through the focus is:
(a) focal chord
(b) latus rectum
(c) directrix
(d) axis
Answer:
(b) latus rectum
Hint:

Question 24.
The distance between directrix and focus of a parabola y² = 4ax is:
(a) a
(b) 2a
(c) 4a
(d) 3a
Answer:
(b) 2a

Question 25.
The equation of directrix of the parabola y² = -x is:
(a) 4x + 1 = 0
(b) 4x – 1 = 0
(c) x – 1 = 0
(d) x + 4 = 0
Answer:
(b) 4x – 1 = 0
Hint:
y² = -x.
It is a parabola open leftwards.
Here 4a = 1 ⇒ a = \(\frac{1}{4}\)
Equation of directrix is x = a.
i.e., x = \(\frac{1}{4}\) (or) 4x – 1 = 0

Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.6 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.6

Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.6 Text Book Back Questions and Answers

Question 1.
Find the equation of the parabola whose focus is the point F(-1, -2) and the directrix is the line 4x – 3y + 2 = 0.
Solution:
F(-1, -2)
l : 4x – 3y + 2 = 0
Let P(x, y) be any point on the parabola.
FP = PM
⇒ FP² = PM²
⇒ (x + 1)² + (y + 2)² = \(\left[\frac{4 x-3 y+2}{\sqrt{4^{2}+(-3)^{2}}}\right]^{2}\)
⇒ x² + 2x + 1 + y² + 4y + 4 = \(\frac{16 x^{2}+9 y^{2}+4-24 x y+16 x-12 y}{(16+9)}\)
⇒ 25(x² + y² + 2x + 4y + 5) = 16x² + 9y² – 24xy + 16x – 12y + 4
⇒ (25 – 16)x² + (25 – 9)y² + 24xy + (50 – 16)x + (100 + 12)y + 125 – 4 = 0
⇒ 9x² + 16y² + 24xy + 34x + 112y + 121 = 0

Question 2.
The parabola y² = kx passes through the point (4, -2). Find its latus rectum and focus.
Solution:
y² = kx passes through (4, -2)
(-2)² = k(4)
⇒ 4 = 4k
⇒ k = 1
y² = x = 4(\(\frac{1}{4}\))x
a = \(\frac{1}{4}\)
Equation of LR is x = a or x – a = 0
i.e., x = \(\frac{1}{4}\)
⇒ 4x = 1
⇒ 4x – 1 = 0
Focus (a, 0) = (\(\frac{1}{4}\), 0)

Question 3.
Find the vertex, focus, axis, directrix, and the length of the latus rectum of the parabola y² – 8y – 8x + 24 = 0.
Solution:
y² – 8y – 8x + 24 = 0
⇒ y² – 8y – 4² = 8x – 24 + 4²
⇒ (y – 4)² = 8x – 8
⇒ (y – 4)² = 8(x – 1)
⇒ (y – 4)² = 4(2) (x – 1)
∴ a = 2
Y² = 4(2)X where X = x – 1 and Y = y – 4

Question 4.
Find the co-ordinates of the focus, vertex, equation of the directrix, axis and the length of latus rectum of the parabola (a) y² = 20x, (b) x² = 8y, (c) x² = -16y
Solution:
(a) y² = 20x
y² = 4(5)x
∴ a = 5

(b) x² = 8y = 4(2)y
∴ a = 2

(c) x² = -16y = -4(4)y
∴ a = 4

Question 5.
The average variable cost of the monthly output of x tonnes of a firm producing a valuable metal is ₹ \(\frac{1}{5}\) x² – 6x + 100. Show that the average variable cost curve is a parabola. Also, find the output and the average cost at the vertex of the parabola.
Solution:
Let output be x and average variable cost = y
y = \(\frac{1}{5}\) x² – 6x + 100
⇒ 5y = x² – 30x + 500
⇒ x² – 30x + 225 = 5y – 500 + 225
⇒ (x – 15)² = 5y – 275
⇒ (x – 15)² = 5(y – 55) which is of the form X² = 4(\(\frac{5}{4}\))Y
∴ Y average variable cost curve is a parabola
Vertex (0, 0)
x – 15 = 0; y – 55 = 0
x = 15; y = 55
At the vertex, output is 15 tonnes and average cost is ₹ 55.

Question 6.
The profit ₹ y accumulated in thousand in x months is given by y = -x² + 10x – 15. Find the best time to end the project.
Solution:
y = -x² + 10x – 15
⇒ y = -[x² – 10x + 5² – 5² + 15]
⇒ y = -[(x – 5)² – 10]
⇒ y = 10 – (x – 5)²
⇒ (x – 5)² = -(y – 10)
This is a parabola which is open downwards.
Vertex is the maximum point.
∴ Profit is maximum when x – 5 = 0 (or) x = 5 months.
After that profit gradually reduces.
∴ The best time to end the project is after 5 months.

Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.5 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.5

Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.5 Text Book Back Questions and Answers

Question 1.
Find the equation of the tangent to the circle x² + y² – 4x + 4y – 8 = 0 at (-2, -2).
Solution:
The equation of the tangent to the circle x² + y² – 4x + 4y – 8 = 0 at (x₁, y₁) is
xx₁ + yy₁ – 4\(\frac{\left(x+x_{1}\right)}{2}\) + 4\(\frac{\left(y+y_{1}\right)}{2}\) – 8 = 0
Here (x₁, y₁) = (-2, -2)
⇒ x(-2) + y(-2) – 2(x – 2) + 2(y – 2) – 8 = 0
⇒ -2x – 2y – 2x + 4 + 2y – 4 – 8 = 0
⇒ -4x – 8 = 0
⇒ x + 2 = 0

Question 2.
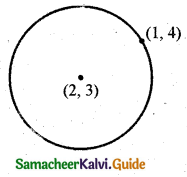
Determine whether the points P(1, 0), Q(2, 1) and R(2, 3) lie outside the circle, on the circle or inside the circle x² + y² – 4x – 6y + 9 = 0.
Solution:
The equation of the circle is x² + y² – 4x – 6y + 9 = 0
PT² = \(x_{1}^{2}+y_{1}^{2}\) – 4x₁ – 6y₁ + 9
At P(1, 0), PT² = 1 + 0 – 4 – 0 + 9 = 6 > 0
At Q(2, 1), PT² = 4 + 1 – 8 – 6 + 9 = 0
At R(2, 3), PT² = 4 + 9 – 8 – 18 + 9 = -4 < 0
The point P lies outside the circle.
The point Q lies on the circle.
The point R lies inside the circle.

Question 3.
Find the length of the tangent from (1, 2) to the circle x² + y² – 2x + 4y + 9 = 0.
Solution:
The length of the tangent from (x₁, y₁) to the circle x² + y² – 2x + 4y + 9 = 0 is \(\sqrt{x_{1}^{2}+y_{1}^{2}-2 x_{1}+4 y_{1}+9}\)
Length of the tangent from (1, 2) = \(\sqrt{1^{2}+2^{2}-2(1)+4(2)+9}\)
= \(\sqrt{1+4-2+8+9}\)
= \(\sqrt{20}\)
= \(\sqrt{4 \times 5}\)
= 2√5 units

Question 4.
Find the value of P if the line 3x + 4y – P = 0 is a tangent to the circle x² + y² = 16.
Solution:
The condition for a line y = mx + c to be a tangent to the circle x² + y² = a² is c² = a² (1 + m²)
Equation of the line is 3x + 4y – P = 0
Equation of the circle is x² + y² = 16
4y = -3x + P
y = \(\frac{-3}{4} x+\frac{P}{4}\)
∴ m = \(\frac{-3}{4}\), c = \(\frac{P}{4}\)
Equation of the circle is x² + y² = 16
∴ a² = 16
Condition for tangency we have c² = a²(1 + m²)
⇒ \(\left(\frac{P}{4}\right)^{2}=16\left(1+\frac{9}{16}\right)\)
⇒ \(\frac{P^{2}}{16}=16\left(\frac{25}{16}\right)\)
⇒ P² = 16 × 25
⇒ P = ±√16√25
⇒ P = ±4 × 5
⇒ P = ±20

Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.4 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.4

Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.4 Text Book Back Questions and Answers

Question 1.
Find the equation of the following circles having
(i) the centre (3, 5) and radius 5 units.
(ii) the centre (0, 0) and radius 2 units.
Solution:
(i) Equation of the circle is (x – h)² + (y – k)² = r²
Centre (h, k) = (3, 5) and radius r = 5
∴ Equation of the circle is (x – 3)² + (y – 5)² = 5²
⇒ x² – 6x + 9 + y² – 10y + 25 = 25
⇒ x² + y² – 6x – 10y + 9 = 0

(ii) Equation of the circle when centre origin (0, 0) and radius r is x² + y² = r²
⇒ x² + y² = 2²
⇒ x² + y² = 4
⇒ x² + y² – 4 = 0

Question 2.
Find the centre and radius of the circle
(i) x² + y² = 16
(ii) x² + y² – 22x – 4y + 25 = 0
(iii) 5x² + 5y²+ 4x – 8y – 16 = 0
(iv) (x + 2) (x – 5) + (y – 2) (y – 1) = 0
Solution:
(i) x² + y² = 16
⇒ x² + y² = 4²
This is a circle whose centre is origin (0, 0), radius 4.

(ii) Comparing x² + y² – 22x – 4y + 25 = 0 with general equation of circle x² + y² + 2gx + 2fy + c = 0
We get 2g = -22, 2f = -4, c = 25
g = -11, f = -2, c = 25
Centre = (-g, -f) = (11, 2)

(iii) 5x² + 5y² + 4x – 8y – 16 = 0
To make coefficient of x² unity, divide the equation by 5 we get,
\(x^{2}+y^{2}+\frac{4}{5} x-\frac{8}{5} y-\frac{16}{5}=0\)
Comparing the above equation with x² + y² + 2gx + 2fy + c = 0 we get,

(iv) Equation of the circle is (x + 2) (x – 5) + (y – 2) (y – 1) = 0
x² – 3x – 10 + y² – 3y + 2 = 0
x² + y² – 3x – 3y – 8 = 0
Comparing this with x² + y² + 2gx + 2fy + c = 0
We get 2g = -3, 2f = -3, c = -8
g = \(\frac{-3}{2}\), f = \(\frac{-3}{2}\), c = -8
Centre (-g, -f) = \(\left(\frac{3}{2}, \frac{3}{2}\right)\)

Question 3.
Find the equation of the circle whose centre is (-3, -2) and having circumference 16π.
Solution:
Circumference, 2πr = 16π
⇒ 2r = 16
⇒ r = 8
Equation of the circle when centre and radius are known is (x – h)² + (y – k)² = r²
⇒ (x + 3)² + (y + 2)² = 8²
⇒ x² + 6x + 9 + y² + 4y + 4 = 64
⇒ x² + y² + 6x + 4y + 13 = 64
⇒ x² + y² + 6x + 4y – 51 = 0

Question 4.
Find the equation of the circle whose centre is (2, 3) and which passes through (1, 4).
Solution:

Centre (h, k) = (2, 3)

Equation of the circle with centre (h, k) and radius r is (x – h)² + (y – k)² = r²
⇒ (x – 2)² + (y – 3)² = (√2)²
⇒ x² – 4x + 4 + y² – 6y + 9 = 2
⇒ x² + y² – 4x – 6y + 11 = 0

Question 5.
Find the equation of the circle passing through the points (0, 1), (4, 3) and (1, -1).
Solution:
Let the required of the circle be x² + y² + 2gx + 2fy + c = 0 ……… (1)
It passes through (0, 1)
0 + 1 + 2g(0) + 2f(1) + c = 0
1 + 2f + c = 0
2f + c = -1 …….. (2)
Again the circle (1) passes through (4, 3)
4² + 3² + 2g(4) + 2f(3) + c = 0
16 + 9 + 8g + 6f + c = 0
8g + 6f + c = -25 …….. (3)
Again the circle (1) passes through (1, -1)
1² + (-1)² + 2g(1) + 2f(-1) + c = 0
1 + 1 + 2g – 2f + c = 0
2g – 2f + c = -2 ……… (4)
8g + 6f + c = -25
(4) × 4 subtracting we get, 8g – 8f + 4c = -8
14f – 3c = -17 ………. (5)
14f – 3c = -17
(2) × 3 ⇒ 6f + 3c = -3
Adding we get 20f = -20
f = -1
Using f = -1 in (2) we get, 2(-1) + c = -1
c = -1 + 2
c = 1
Using f = -1, c = 1 in (3) we get
8g + 6(-1)+1 = -25
8g – 6 + 1 = -25
8g – 5 = -25
8g = -20
g = \(\frac{-20}{8}=\frac{-5}{2}\)
using g = \(\frac{-5}{2}\), f = -1, c = 1 in (1) we get the equation of the circle.
x² + y² + 2(\(\frac{-5}{2}\))x + 2(-1)y + 1 = 0
x² + y² – 5x – 2y + 1 = 0

Question 6.
Find the equation of the circle on the line joining the points (1, 0), (0, 1), and having its centre on the line x + y = 1.
Solution:

Let the equation of the circle be
x² + y² + 2gx + 2fy + c = 0 ……… (1)
The circle passes through (1, 0)
1² + 0² + 2g(1) + 2f(0) + c = 0
1 + 2g + c = 0
2g + c = 1 …….. (2)
Again the circle (1) passes through (0, 1)
0² + 1² + 2g(0) + 2f(1) + c = 0
1 + 2f + c = 0
2f + c = -1 ……. (3)
(2) – (3) gives 2g – 2f = 0 (or) g – f = 0 ………. (4)
Given that the centre of the circle (-g, -f) lies on the line x + y = 1
-g – f = 1 …….. (5)
(4) + (5) gives -2f = 1 ⇒ f = \(-\frac{1}{2}\)
Using f = \(-\frac{1}{2}\) in (5) we get
-g – (\(-\frac{1}{2}\)) = 1
-g = 1 – \(-\frac{1}{2}\) = \(\frac{1}{2}\)
g = \(-\frac{1}{2}\)
Using g = \(-\frac{1}{2}\) in (2) we get
2(\(-\frac{1}{2}\)) + c = -1
-1 + c = -1
c = 0
using g = \(-\frac{1}{2}\), f = \(-\frac{1}{2}\), c = 0 in (1) we get the equation of the circle,
x² + y² + 2(\(-\frac{1}{2}\))x + 2(\(-\frac{1}{2}\))y + 0 = 0
x² + y² – x – y = 0

Question 7.
If the lines x + y = 6 and x + 2y = 4 are diameters of the circle, and the circle passes through the point (2, 6) then find its equation.
Solution:
To get coordinates of centre we should solve the equations of the diameters x + y = 6, x + 2y = 4.
x + y = 6 ……. (1)
x + 2y = 4 ………. (2)
(1) – (2) ⇒ -y = 2
y = -2
Using y = -2 in (1) we get x – 2 = 6
x = 8
Centre is (8, -2) the circle passes through the point (2, 6).

Equation of the circle with centre (h, k) and radius r is (x – h)² + (y – k)² = r²
⇒ (x – 8)² + (y + 2)² = 10²
⇒ x² + y² – 16x + 4y + 64 + 4 = 100
⇒ x² + y² – 16x + 4y – 32 = 0

Question 8.
Find the equation of the circle having (4, 7) and (-2, 5) as the extremities of a diameter.
Solution:
The equation of the circle when entremities (x₁, y₁) and (x₂, y₂) are given is (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
⇒ (x – 4) (x + 2) + (y – 7) (y – 5) = 0
⇒ x² – 2x – 8 + y² – 12y + 35 = 0
⇒ x² + y² – 2x – 12y + 27 = 0

Question 9.
Find the Cartesian equation of the circle whose parametric equations are x = 3 cos θ, y = 3 sin θ, 0 ≤ θ ≤ 2π.
Solution:
Given x = 3 cos θ, y = 3 sin θ
Now x² + y² = 9 cos²θ + 9 sin²θ
x² + y² = 9 (cos²θ + sin²θ)
x² + y² = 9 which is the Cartesian equation of the required circle.

Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.3 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.3

Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.3 Text Book Back Questions and Answers

Question 1.
If the equation ax² + 5xy – 6y² + 12x + 5y + c = 0 represents a pair of perpendicular straight lines, find a and c.
Solution:
Comparing ax² + 5xy – 6y² + 12x + 5y + c = 0 with ax² + 2hxy + by² + 2gx + 2fy + c = 0
We get a = a, 2h = 5, (or) h = \(\frac{5}{2}\), b = -6, 2g = 12 (or) g = 6, 2f = 5 (or) f = \(\frac{5}{2}\), c = c
Condition for pair of straight lines to be perpendicular is a + b = 0
a + (-6) = 0
a = 6
Next to find c. Condition for the given equation to represent a pair of straight lines is

R₁ → R₁ – R₃
Expanding along first row we get 0 – 0 + (6 – c) [\(\frac{25}{4}\) + 36] = 0
(6-c) [\(\frac{25}{4}\) + 36] = 0
6 – c = 0
6 = c (or) c = 6

Question 2.
Show that the equation 12x² – 10xy + 2y² + 14x – 5y + 2 = 0 represents a pair of straight lines and also find the separate equations of the straight lines.
Solution:
Comparing 12x² – 10xy + 2y² + 14x – 5y + 2 = 0 with ax² + 2hxy + by² + 2gh + 2fy + c = 0
We get a = 12, 2h = -10, (or) h = -5, b = 2, 2g = 14 (or) g = 7, 2f = -5 (or) f = \(-\frac{5}{2}\), c = 2
Condition for the given equation to represent a pair of straight lines is \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=0\)
\(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{rrr}
12 & -5 & 7 \\
-5 & 2 & \frac{-5}{2} \\
7 & \frac{-5}{2} & 2
\end{array}\right|\)

= \(\frac{1}{4}\) [12(16 – 25) + 5(-40 + 70) + 7(50 – 56)]
= \(\frac{1}{4}\) [12(-9) + 5(30) + 7(-6)]
= \(\frac{1}{4}\) [-108 + 150 – 42]
= \(\frac{1}{4}\) [0]
= 0
∴ The given equation represents a pair of straight lines.
Consider 12x² – 10xy + 2y² = 2[6x² – 5xy + y²] = 2[(3x – y)(2x – y)] = (6x – 2y)(2x – y)
Let the separate equations be 6x – 2y + l = 0, 2x – y + m = 0
To find l, m
Let 12x² – 10xy + 2y² + 14x – 5y + 2 = (6x – 2y + l) (2x – y + m) ……. (1)
Equating coefficient of y on both sides of (1) we get
2l + 6m = 14 (or) l + 3m = 7 ………… (2)
Equating coefficient of x on both sides of (1) we get
-l – 2m = -5 ……… (3)
(2) + (3) ⇒ m = 2
Using m = 2 in (2) we get
l + 3(2) = 7
l = 7 – 6
l = 1
∴ The separate equations are 6x – 2y + 1 = 0, 2x – y + 2 = 0.

Question 3.
Show that the pair of straight lines 4x² + 12xy + 9y² – 6x – 9y + 2 = 0 represents two parallel straight lines and also find the separate equations of the straight lines.
Solution:
The given equation is 4x² + 12xy + 9y² – 6x – 9y + 2 = 0
Here a = 4, 2h = 12, (or) h = 6 and b = 9
h² – ab = 6² – 4 × 9 = 36 – 36 = 0
∴ The given equation represents a pair of parallel straight lines
Consider 4x² + 12xy + 9y² = (2x)² + 12xy + (3y)²
= (2x)² + 2(2x)(3y) + (3y)²
= (2x + 3y)²
Here we have repeated factors.
Now consider, 4x² + 12xy + 9y² – 6x – 9y + 2 = 0
(2x + 3y)² – 3(2x + 3y) + 2 = 0
t² – 3t + 2 = 0 where t = 2x + 3y
(t – 1)(t – 2) = 0
(2x + 3y – 1) (2x + 3y – 2) = 0
∴ Separate equations are 2x + 3y – 1 = 0, 2x + 3y – 2 = 0

Question 4.
Find the angle between the pair of straight lines 3x² – 5xy – 2y² + 17x + y + 10 = 0.
Solution:
The given equation is 3x² – 5xy – 2y² + 17x + y + 10 = 0
Here a = 3, 2h = -5, b = -2
If θ is the angle between the given straight lines then

Subject Matter Experts at SamacheerKalvi.Guide have created Samacheer Kalvi Tamil Nadu State Board Syllabus New Paper Pattern 11th Maths Model Question Papers 2020-2021 with Answers Pdf Free Download in English Medium and Tamil Medium of TN 11th Standard Maths Public Exam Question Papers Answer Key, New Paper Pattern of HSC 11th Class Maths Previous Year Question Papers, Plus One +1 Maths Model Sample Papers are part of Tamil Nadu 11th Model Question Papers.

Let us look at these Government of Tamil Nadu State Board 11th Maths Model Question Papers Tamil Medium with Answers 2020-21 Pdf. Students can view or download the Class 11th Maths New Model Question Papers 2021 Tamil Nadu English Medium Pdf for their upcoming Tamil Nadu HSC Board Exams. Students can also read Tamilnadu Samcheer Kalvi 11th Maths Guide.

TN State Board 11th Maths Model Question Papers 2020 2021 English Tamil Medium

Tamil Nadu 11th Maths Model Question Papers English Medium 2020-2021

• Tamil Nadu 11th Maths Model Question Paper 1 English Medium
• Tamil Nadu 11th Maths Model Question Paper 2 English Medium
• Tamil Nadu 11th Maths Model Question Paper 3 English Medium
• Tamil Nadu 11th Maths Model Question Paper 4 English Medium
• Tamil Nadu 11th Maths Model Question Paper 5 English Medium

Tamil Nadu 11th Maths Model Question Papers Tamil Medium 2019-2020

• Tamil Nadu 11th Maths Model Question Paper 1 Tamil Medium
• Tamil Nadu 11th Maths Model Question Paper 2 Tamil Medium
• Tamil Nadu 11th Maths Model Question Paper 3 Tamil Medium
• Tamil Nadu 11th Maths Model Question Paper 4 Tamil Medium
• Tamil Nadu 11th Maths Model Question Paper 5 Tamil Medium

11th Maths Model Question Paper Design 2020-2021 Tamil Nadu

Tamil Nadu 11th Maths Model Question Paper Weightage of Marks

It is necessary that students will understand the new pattern and style of Model Question Papers of 11th Standard Maths Tamilnadu State Board Syllabus according to the latest exam pattern. These Tamil Nadu Plus One 11th Maths Model Question Papers State Board Tamil Medium and English Medium are useful to understand the pattern of questions asked in the board exam. Know about the important concepts to be prepared for TN HSLC Board Exams and Score More marks.

We hope the given Samacheer Kalvi Tamil Nadu State Board Syllabus New Paper Pattern Class 11th Maths Model Question Papers 2020 2021 with Answers Pdf Free Download in English Medium and Tamil Medium will help you get through your subjective questions in the exam.

Let us know if you have any concerns regarding the Tamil Nadu Government 11th Maths State Board Model Question Papers with Answers 2020 21, TN 11th Std Maths Public Exam Question Papers with Answer Key, New Paper Pattern of HSC Class 11th Maths Previous Year Question Papers, Plus One +1 Maths Model Sample Papers, drop a comment below and we will get back to you as soon as possible.

Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.2 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.2

Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.2 Text Book Back Questions and Answers

Question 1.
Find the angle between the lines whose slopes are \(\frac{1}{2}\) and 3.
Solution:
Given that m₁ = \(\frac{1}{2}\) and m₂ = 3.
Let θ be the angle between the lines then

tan θ = 1
tan θ = tan 45°
∴ θ = 45°

Question 2.
Find the distance of the point (4, 1) from the line 3x – 4y + 12 = 0.
Solution:
The length of perpendicular from a point (x₁, y₁) to the line ax + by + c = 0 is d = \(\left|\frac{a x_{1}+b y_{1}+c}{\sqrt{a^{2}+b^{2}}}\right|\)
∴ The distance of the point (4, 1) to the line 3x – 4y + 12 = 0 is
[Here (x₁, y₁) = (4, 1), a = 3, b = -4, c = 12]

Question 3.
Show that the straight lines x + y – 4 = 0, 3x + 2 = 0 and 3x – 3y + 16 = 0 are concurrent.
Solution:
The lines a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0, a₃x + b₃y + c₃ = 0 are concurrent if
\(\left|\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|=0\)
The given lines x + y – 4 = 0, 3x + 0y + 2 = 0, 3x – 3y + 16 = 0
\(\left|\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|=\left|\begin{array}{rrr}
1 & 1 & -4 \\
3 & 0 & 2 \\
3 & -3 & 16
\end{array}\right|\)
= 1(0 + 6) – 1(48 – 6) – 4(-9 – 0)
= 6 – (42) + 36
= 42 – 42
= 0
The given lines are concurrent.

Question 4.
Find the value of ‘a’ for which the straight lines 3x + 4y = 13; 2x – 7y = -1 and ax – y – 14 = 0 are concurrent.
Solution:
The lines 3x + 4y = 13, 2x – 7y = -1 and ax – y – 14 = 0 are concurrent.
\(\left|\begin{array}{rrr}
3 & 4 & -13 \\
2 & -7 & 1 \\
a & -1 & -14
\end{array}\right|=0\)
⇒ 3(98 + 1) – 4(-28 – a) – 13(-2 + 7a) = 0
⇒ 3(99) + 112 + 4a + 26 – 91a = 0
⇒ 297 + 112 + 26 + 4a – 91a = 0
⇒ 435 – 87a = 0
⇒ -87a = -435
⇒ a = \(\frac{-435}{-87}\) = 5

Question 5.
A manufacturer produces 80 TV sets at a cost of ₹ 2,20,000 and 125 TV sets at a cost of ₹ 2,87,500. Assuming the cost curve to be linear, find the linear expression of the given information. Also, estimate the cost of 95 TV sets.
Solution:
Let x represent the TV sets, andy represent the cost.

The equation of straight line expressing the given information as a linear equation in x and y is

1(y – 2,20,000) = (x – 80)1500
y – 2,20,000 = 1500x – 80 × 1500
y = 1500x – 1,20,000 + 2,20,000
y = 1500x + 1,00,000 which is the required linear expression.
When x = 95,
y = 1,500 × 95 + 1,00,000
= 1,42,500 + 1,00,000
= 2,42,500
∴ The cost of 95 TV sets is ₹ 2,42,500.

Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.1 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.1

Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.1 Text Book Back Questions and Answers

Question 1.
Find the locus of a point which is equidistant from (1, 3) and x-axis.
Solution:

Let P(x₁, y₁) be any point on the locus.
Let A be the point (1, 3)
The distance from the x-axis on the moving pint P(x₁, y₁) is y₁.
Given that AP = y₁
AP² = \(y_{1}^{2}\)

∴ The locus of the point (x₁, y₁) is x² – 2x – 6y + 10 = 0

Question 2.
A point moves so that it is always at a distance of 4 units from the point (3, -2).
Solution:
Let P(x₁, y₁) be any point on the locus.
Let A be the point (3, -2)
Given that PA = 4
PA² = 16

∴ The locus of the point (x₁, y₁) is x² + y² – 6x + 4y – 3 = 0

Question 3.
If the distance of a point from the points (2, 1) and (1, 2) are in the ratio 2 : 1, then find the locus of the point.
Solution:
Let P(x₁, y₁) be any point on the locus.
Let A(2, 1) and B(1, 2) be the given point.
Given that PA : PB = 2 : 1
i.e., \(\frac{P A}{P B}=\frac{2}{1}\)
PA = 2PB
PA² = 4PB²

∴ The locus of the point (x₁, y₁) is 3x² + 3y² – 4x – 14y + 15 = 0

Question 4.
Find a point on the x-axis which is equidistant from the points (7, -6) and (3, 4).
Solution:
Let P(x₁, 0) be any point on the x-axis.
Let A(7, -6) and B(3, 4) be the given points.
Given that PA = PB
PA² = PB²

∴ The required point is \(\left(\frac{15}{2}, 0\right)\)

Question 5.
If A(-1, 1) and B(2, 3) are two fixed points, then find the locus of a point P so that the area of triangle APB = 8 sq.units.
Solution:
Let the point P(x₁, y₁).
Fixed points are A(-1, 1) and B(2, 3).
Given area (formed by these points) of the triangle APB = 8
⇒ \(\frac{1}{2}\) [x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] = 8
⇒ \(\frac{1}{2}\) [x₁(1 – 3) + (-1) (3 – y₁) + 2(y₁ – 1)] = 8
⇒ \(\frac{1}{2}\) [-2x₁ – 3 + y₁ + 2y₁ – 2] = 8
⇒ \(\frac{1}{2}\) [-2x₁ + 3y₁ – 5] = 8
⇒ -2x₁ + 3y₁ – 5 = 16
⇒ -2x₁ + 3y₁ – 21 = 0
⇒ 2x₁ – 3y₁ + 21 = 0
∴ The locus of the point P(x₁, y₁) is 2x – 3y + 21 = 0.