Tamil Nadu 11th Maths Model Question Paper 5 English Medium

Students can Download Tamil Nadu 11th Maths Model Question Paper 5 English Medium Pdf, Tamil Nadu 11th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

TN State Board 11th Maths Model Question Paper 5 English Medium

General Instructions:

1. The question paper comprises of four parts.
2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. All questions of Part I, II, III and IV are to be attempted separately.
4. Question numbers 1 to 20 in Part I are Multiple Choice Questions of one mark each.
   These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 21 to 30 in Part II are two-mark questions. These are to be answered in about one or two sentences.
6. Question numbers 31 to 40 in Part III are three-mark questions. These are to be answered in above three to five short sentences.
7. Question numbers 41 to 47 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.

Time: 2:30 Hours
Maximum Marks: 90

PART – I

I. Choose the correct answer. Answer all the questions. [20 × 1 = 20]

Question 1.
If n((A × B) ∩ (A × C)) = 8 and n(B ∩ C) = 2 then n(A) = …………………
(a) 6
(b) 4
(c) 8
(d) 16
Answer:
(b) 4

Question 2.
The value of log₃ \(\frac{1}{81}\) is ……………….
(a) -2
(b) -8
(c) -4
(d) -9
Answer:
(c) -4

Question 3.
The value of log₃ 11 log₁₁ 13 log₁₃ 15 log₁₅ 27 log₂₇ 81 is ……………………
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4

Question 4.
The value of sin(45° + θ) – cos (45° – θ) is …………………..
(a) 2 cos θ
(b) 1
(c) 0
(d) 2 sin θ
Answer:
(c) 0

Question 5.
If tanα and tan β are the roots of x² + ax + b = 0 then \(\frac{\sin (\alpha+\beta)}{\sin \alpha \sin \beta}\) is equal to ……………………..
(a) \(\frac{b}{a}\)
(b) \(\frac{a}{b}\)
(c) –\(\frac{a}{b}\)
(d) –\(\frac{b}{a}\)
Answer:
(c) –\(\frac{a}{b}\)

Question 6.
If a² – aC₂ = a² – aC₄ then the value of a is …………………….
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(b) 3

Question 7.
If ⁿP_r = 840, ⁿC_r= 35 then n = …………………..
(a) 1
(b) 6
(c) 5
(d) 4
Answer:
(a) 1

Question 8.
If 2x² + 3xy – cy² = 0 represents a pair of perpendicular lines then c = …………………….
(a) -2
(b) \(\frac{1}{2}\)
(c) – \(\frac{1}{2}\)
(d) 2
Answer:
(d) 2

Question 9.
The number of terms in the expansion of [(a + b)²]¹⁸ = …………………..
(a) 19
(b) 18
(c) 36
(d) 37
Answer:
(d) 37

Question 10.
The point on the line 2x – 3y = 5 is equidistance from (1, 2) and (3, 4) is …………………..
(a) (7, 3)
(b) (4, 1)
(c) (1,-1)
(d) (3, 4)
Answer:
(b) (4, 1)

Question 11.
Let A and B be two symmetric matrices of same order. Then which one of the following statement is not true?
(a) A + B is a symmetric matrix
(b) AB is a symmetric matrix
(c) (AB) = (BA)^T
(d) A^TB = AB^T
Answer:
(d) A^TB = AB^T

Question 12.
If [3 -1 2] B = [5, 6] then the order of B is ………………….
(a) 3 × 2
(b) 2 × 3
(c) 3 × 1
(d) 1 × 1
Answer:
(a) 3 × 2

Question 13.
1f \(\underset { x\rightarrow 0 }{ lim } \) \(\frac{sin px}{tan 3x}\) = 4 then the value of p is …………………….
(a) 6
(b) 9
(c) 12
(d) 4
Answer:
(c) 12

Question 14.
For \(\vec { a } \) = \(\vec { i } \) + \(\vec { j } \) – 2\(\vec { k } \), \(\vec { b } \) = \(\vec { i } \) + 2\(\vec { j } \) + \(\vec { k } \) and \(\vec { c } \) = \(\vec { i } \) – 2\(\vec { j } \) + 2\(\vec { k } \) the unit vector parallal to is \(\vec { a } \)
+ \(\vec { b } \) + \(\vec { c } \) is ……………………….
(a) \(\frac{\vec{i}+\vec{j}-\vec{k}}{\sqrt{3}}\)
(b) \(\frac{\vec{i}+\vec{j}+\vec{k}}{\sqrt{3}}\)
(c) \(\frac{\vec{i}+\vec{j}+\vec{k}}{3}\)
(d) \(\frac{\vec{i}-\vec{j}+\vec{k}}{\sqrt{6}}\)
Answer:
(b) \(\frac{\vec{i}+\vec{j}+\vec{k}}{\sqrt{3}}\)

Question 15.
The differential co-efficient of log₁₀ x with respect to log_x 10 is …………………….
(a) 1
(b) -(log₁₀x)²
(c) (log_x10)²
(d) \(\frac { x^{ 2 } }{ 100 } \)
Answer:
(b) -(log₁₀x)²

Question 16.
\(\frac{d}{dx}\)(e^x+5logx) is …………………..
(a) e^xx⁴(x + 5)
(b) e^xx(x + 5)
(c) e^x + \(\frac{5}{x}\)
(d) e^x – \(\frac{5}{x}\)
Answer:
(a) e^xx⁴(x + 5)

Question 17.
If f(x) = x tan^-1x thenf'(1) = ……………………..
(a) 1 + \(\frac { \pi }{ 4 } \)
(b) \(\frac{1}{2}\) + \(\frac { \pi }{ 4 } \)
(c) \(\frac{1}{2}\) – \(\frac { \pi }{ 4 } \)
(d) 2
Answer:
(b) \(\frac{1}{2}\) + \(\frac { \pi }{ 4 } \)

Question 18.
∫cosec xdx = …………………….
(a) log tan \(\frac{x}{2}\) + c
(b) -log (cosec x + cot x) + c
(c) log (cosecx – cot x) + c
(d) all of them
Answer:
(d) all of them

Question 19.
Ten coins are tossed; The probability of getting atleast 8 heads is …………………..
(a) \(\frac{7}{64}\)
(b) \(\frac{7}{32}\)
(c) \(\frac{7}{128}\)
(d) \(\frac{7}{16}\)
Answer:
(c) \(\frac{7}{128}\)

Question 20.
Two items are chosen from a lot containing twelve items of which four are defective. Then the probability that atleast one of the item is defective is …………………..
(a) \(\frac{19}{33}\)
(b) \(\frac{17}{33}\)
(c) \(\frac{23}{33}\)
(d) \(\frac{13}{34}\)
Answer:
(a) \(\frac{19}{33}\)

PART – II

II. Answer any seven questions. Question No. 30 is compulsory. [7 × 2 = 14]

Question 21.
For a set A, A × A contains 16 elements and two of its elements are (1, 3) and (0, 2). Find the elements of A?
Answer:
A × A = 16 elements = 4 × 4
⇒ A has 4 elements
∴ A = {0, 1, 2, 3}

Question 22.
Prove that \(\frac{\tan \theta+\sec \theta-1}{\tan \theta-\sec \theta+1}\) = \(\frac{1+sinθ}{cosθ}\)
Answer:

Question 23.
How many triangles can be formed by joining 15 points on the plane, in which no line joining any three points?
Answer:
No. of non-collincar points = 15
To draw a Triangle we need 3 points
∴ Selecting 3 from 15 points can be done in ¹⁵C₃ ways.
∴ No. of Tnangle formed ¹⁵C₃
= \(\frac{15 \times 14 \times 13}{3 \times 2 \times 1}\) = 455

Question 24.
Find the equation of the straight lines passing through (8, 3) and having intercepts whose sum is 1?
Answer:
Givc sum of the intercepts = 1
⇒ when x intercept a then y intercept = 1 – a
Equation of the line is \(\frac{x}{a}\) + \(\frac{y}{1-a}\) = 1
The line passes through (8, 3) ⇒ \(\frac{8}{a}\) + \(\frac{3}{1-a}\) = 1
(i.e) 8 (1 – a) + 3a = a(1 – a)
8 – 8a + 3a = a – a²
a² – 6a + 8 =0
(a – 2)(a – 4) = 0 ⇒a = 2 or 4
1. When a = 2 equation of the line is \(\frac{x}{2}\) + \(\frac{y}{-2}\) = 1 (i.e) \(\frac{x}{2}\) – y = 1 ⇒ x – 2y = 2
2.When a = 4 equation of the line is \(\frac{x}{4}\) + \(\frac{y}{1-4}\) = 1 (i.e) \(\frac{x}{4}\) – \(\frac{y}{3}\) = 1 ⇒ 3x – 4y = 12

Question 25.
Find the values of p, q, r, & s if \(\left[\begin{array}{ccc}
p^{2}-1 & 0 & -31-q^{3} \\
7 & r+1 & 9 \\
-2 & 8 & s-1
\end{array}\right]=\left[\begin{array}{rrr}
1 & 0 & -4 \\
7 & \frac{3}{2} & 9 \\
-2 & 8 & -\pi
\end{array}\right]\)
Answer:
When two matrices (of some order) are equal then their correspondings entries are equal.

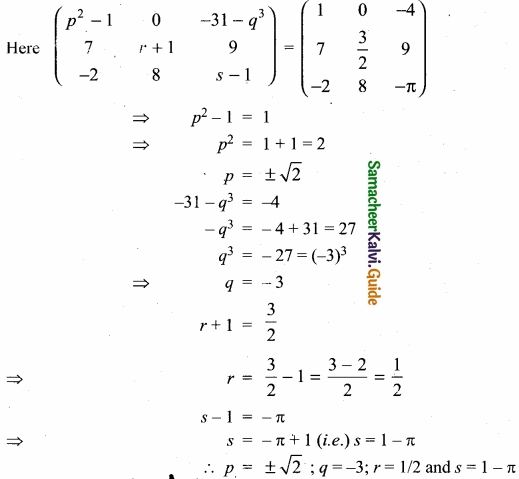
Question 26.
Find |\(\vec { a } \) × \(\vec { b } \)| where \(\vec { a } \) = 3\(\vec { i } \) + 4\(\vec { j } \) and \(\vec { b } \) = \(\vec { i } \) + \(\vec { j } \) + \(\vec { k } \)
Answer:

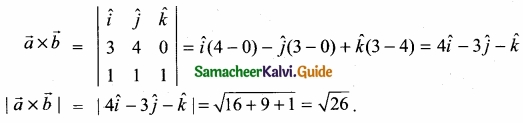
Question 27.
At the given point x₀ discover whether the given function is continous or discontinous citing the reasons for your answer?
Answer:

Question 28.
Evaluate y = xe^-x2
Answer:

Question 29.
Evaluate ∫\(\frac{1}{x logx}\) dx?
Answer:

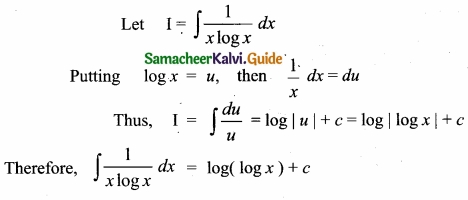
Question 30.
Evaluate [((256)^-1/2)^-1/4]³
Answer:

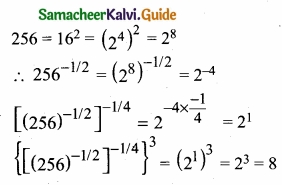
PART – III

III. Answer any seven questions. Question No. 40 Is compulsory. [7 × 3 = 21]

Question 31.
Find the largest possible domain for the real valued functionsf defined by f(x) = \(\sqrt { x^{ 2 }-5x+6 } \)

Question 32.
Show that tan 75° + cot 75° = 4?

Question 33.
There are 10 bulbs in a room. Each one of them can be operated independently. Find the number of ways in which the room can be illuminated?

Question 34.
Find the \(\sqrt [ 3 ]{ 126 } \) approximately to two decimal places?

Question 35.
Find the equation of the line passing through the point of intersection 2x + y = 5 and x + 3y + 8 = O and parallel to the line 3x + 4y = 7?

Question 36.
If \(\left|\begin{array}{ccc}
a & b & a \alpha+b \\
b & c & b \alpha+c \\
a \alpha+b & b \alpha+c & 0
\end{array}\right|\) = 0 prove that a, b, c are in G.P. or a is a root of ax² + 2bx + c =0

Question 37.
Evaluate \(\underset { x\rightarrow 3 }{ lim } \)\(\frac { x^{ 2 }-9 }{ x-3 } \) ¡f it exists by finding f(3^–) and f(3⁺)

Question 38.
Find the derivative of tan^-1 (1 + x²) with respect x² + x + 1?

Question 39.
Evaluate: ∫x⁵e^{x2 dx}

Question 40.
Prove that the line segment joining the mid points of the adjacent sides of a quadrilateral from parllelogram?

PART – IV

IV. Answer all the questions. [7 × 5 = 35]

Question 41.
(a) Graph the functions f(x) = x³ and g(x) = \(\sqrt [ 3 ]{ x } \) on the same coordinate plane. Find fog and graph it on the plane as well. Explain your results.

[OR]

(b) 1f x = -2 is one root of x³ – x² – 17x = 22 then find the other roots of the equation?

Question 42.
(a) lf A + B + C= it prove that cosA + cos B + cosC = 1 + 4 sin (\(\frac{A}{2}\)) sin (\(\frac{B}{2}\) sin (\(\frac{C}{2}\))

[OR]

(b) If A = \(\left[\begin{array}{lll}
1 & 2 & 2 \\
2 & 1 & 2 \\
2 & 2 & 1
\end{array}\right]\) show that A² – 4A – 5I = O

Question 43.
(a) If ⁿ⁺¹C₈ : ^(n-3)P₄ = 57 : 16, find the value of n?

[OR]

(b) If the letters of the word IITJEE arc permuted in all possible ways and the strings thus formed are arranged in the lexicographic order, find the rank of the word IITJEE?

Question 44.
(a) The line \(\frac{x}{a}\) + \(\frac{y}{b}\)= 1 moves in such a way that \(\frac { 1 }{ a^{ 2 } } \) + \(\frac { 1 }{ b^{ 2 } } \) = \(\frac { 1 }{ c^{ 2 } } \) where c is a constant. Find the locus of the foot of the perpendicular from the origin on the given line?

[OR]

(b) Show that the equation 4x² + 4xy + y² – 6x – 3y – 4 = 0 represents a pair of parallel lines. Find the distance between them?

Question 45 (a).
Prove that \(\left|\begin{array}{lll}
1 & x^{2} & x^{3} \\
1 & y^{2} & y^{3} \\
1 & z^{2} & z^{3}
\end{array}\right|\) = (x – y) (y – z) (z – x) (xy + yz + zx)

(b) Evaluate \(\underset { x\rightarrow \infty }{ lim } \) \(\frac{3}{x-2}\) – \(\frac{2 x+11}{x^{2}+x-6}\)

Question 46.
(a) Evaluate \(\frac{1}{6 x-7-x^{2}}\)

(b) Evaluate ∫e^tan-1x (\(\frac { 1+x+x^{ 2 } }{ 1+x^{ 2 } } \)) dx

Question 47 (a).
Suppose the chances of hitting a target by a person X is 3 times in 4 shots, by Y is 4 times in 5 shots, and by Z is 2 times in 3 shots. They fire simultaneously exactly one time. What is the probability that the target is damaged by exactly 2 hits?

[OR]

(b) Firm manufactures PVC pipes in three plants viz. X, Y and Z. The daily production volumes from the three firms X, Y and Z are respectively 2000 units, 3000 units and 5000 units. It is known from the past experience that 3% of the output from plant X, 4% from plant Y and 2% from plant Z are defective. A pipe is selected at random from a day’s total production,

1. find the probability that the selected pipe is a defective one.
2. if the selected pipe ¡s a defective, then what is the probability that it was produced by plant Y?