Category: Class 11

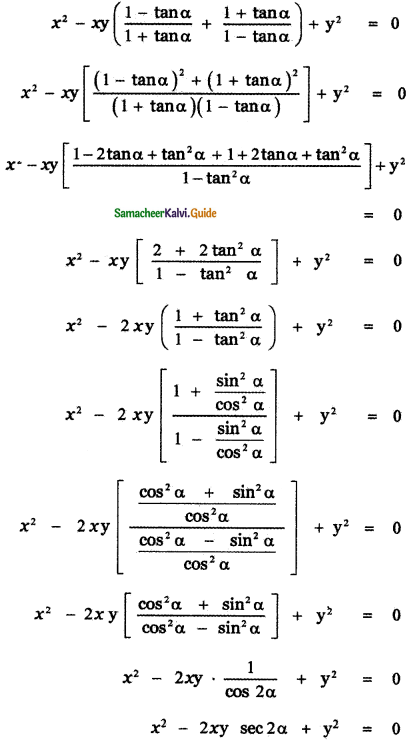
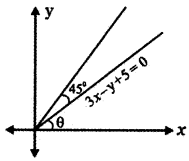
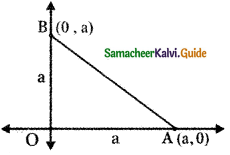
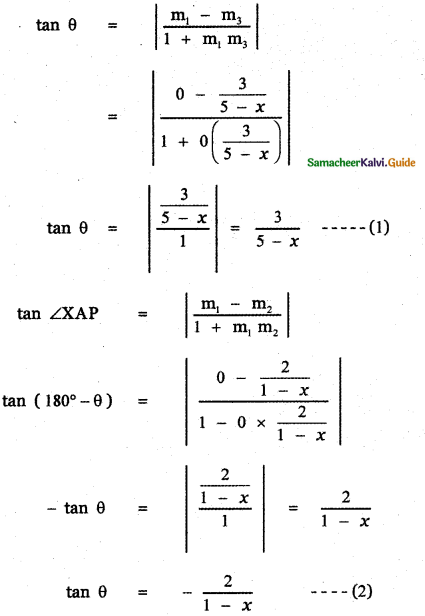
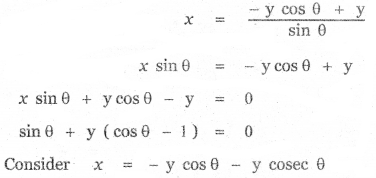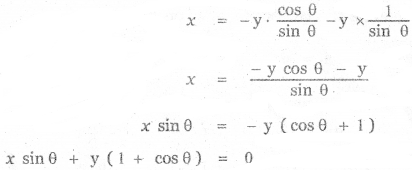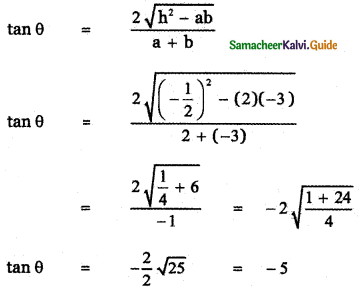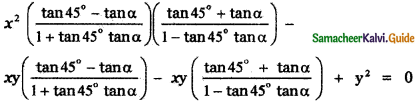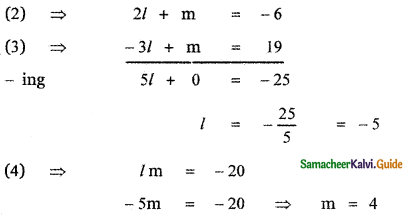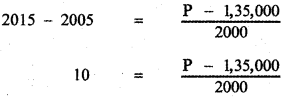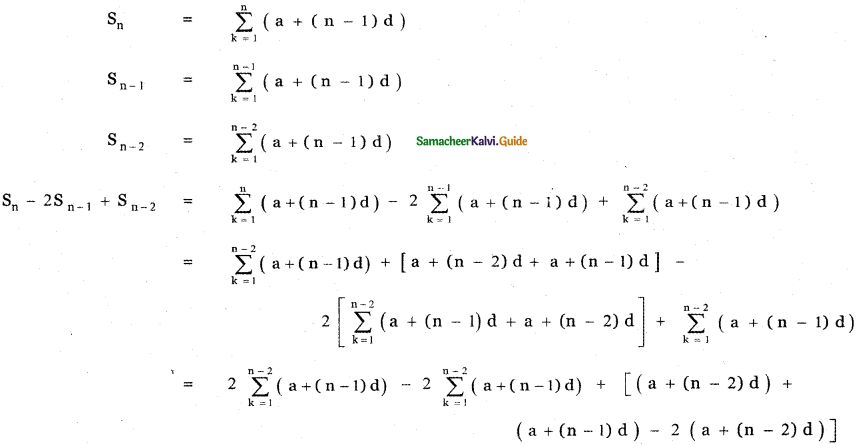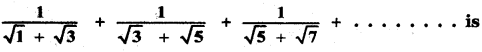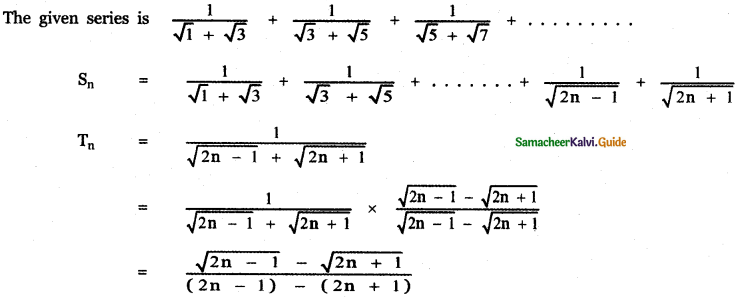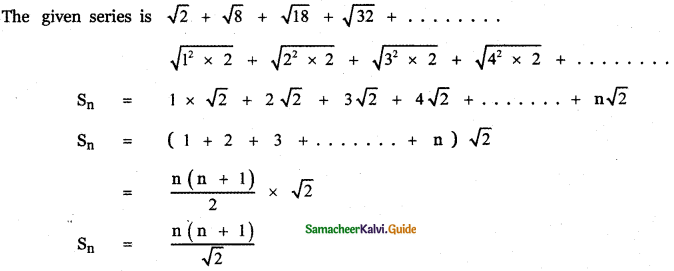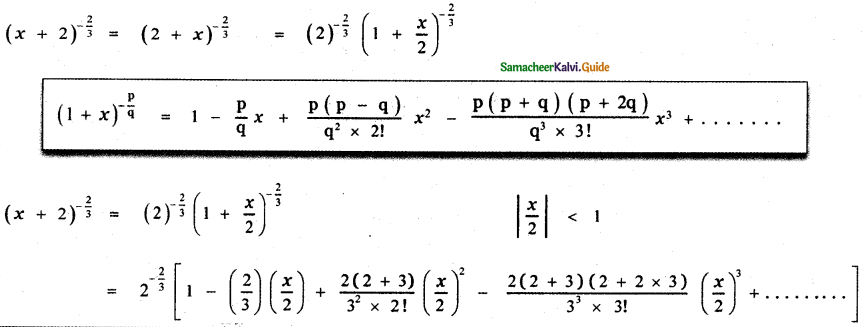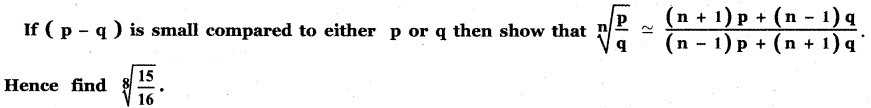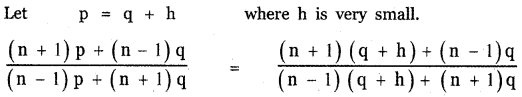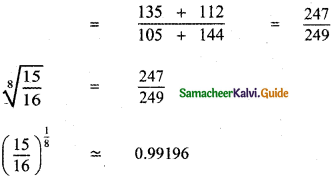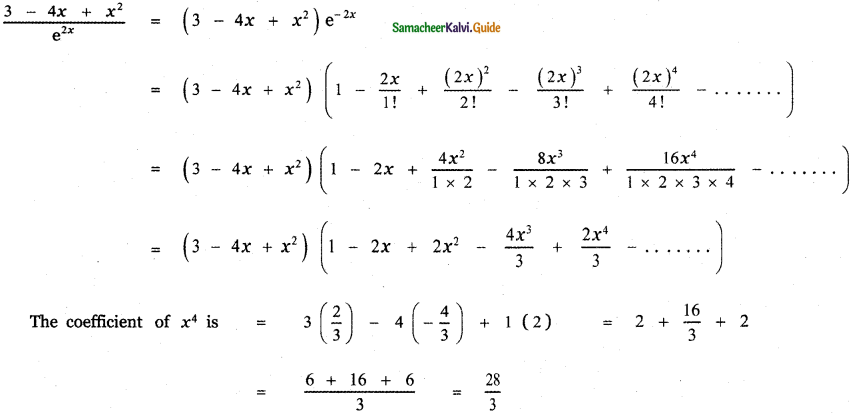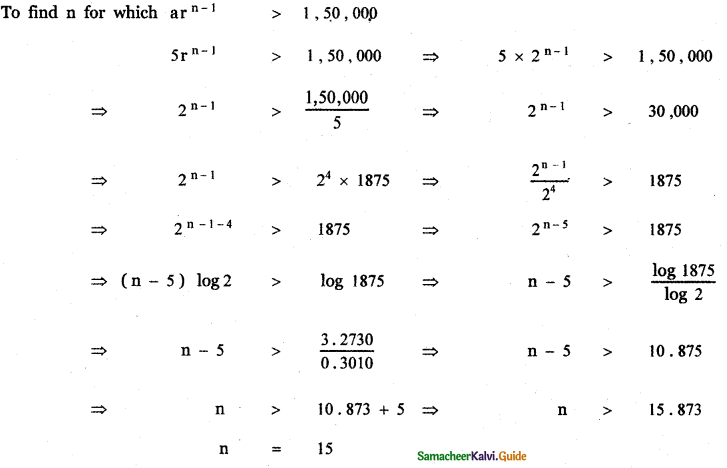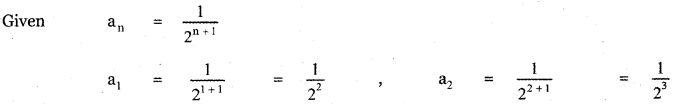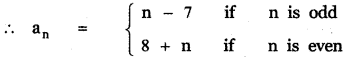Tamilnadu State Board New Syllabus Samacheer Kalvi 11th English Guide Pdf Prose Chapter 1 The Portrait of a Lady Text Book Back Questions and Answers, Summary, Notes.

Tamilnadu Samacheer Kalvi 11th English Solutions Prose Chapter 1 The Portrait of a Lady

11th English Guide The Portrait of a Lady Text Book Back Questions and Answers

Textual Questions:

1. Answer the following questions in one or two sentences based on your understanding of the story:

Question a.
Describe the grandfather as seen in the portrait.
Answer:
The author’s grandfather looked as if he were a hundred years old with lots of grandchildren. He had loose-fitting garments. He looked too old to have had a wife and children.

Question b.
Why was the author left with his grandmother in the village?
Answer:
The author’s parents went to the city to make a living. So he was left with his grandma till they settle well in the city.

Question c.
Where did the author study in his childhood?
Answer:
The author studied on the veranda of a village temple. He learned letters of the alphabet from the priest.

Question d.
Why did the grandmother accompany the author to school?
Answer:
The grandmother was pious. She accompanied the author to school as it was attached to the temple where she used to sit and read scriptures.

Question e.
What made the dogs follow the grandmother after school hours?
Answer:
Grandmother brought a bundle of stale chapattis with her to the temple. The village dogs followed her. On return, she went on throwing the chapattis to the dogs who growled and fought with each other to have a piece of chapatti.

Question f.
What was the happiest time of the day for their grandmother?
Answer:
The grandma spends half an hour in the afternoon feeding the sparrows. That was the happiest time of the day for grandma.

Question g.
Why didn’t the grandma feel sentimental when the author went abroad for higher education?
Answer:
Half an hour in the afternoon, grandma devoted her time to feeding sparrows. That half-an-hour was the happiest time of the day for grandmother.

2. Answer the following questions in three or four sentences each:

Question a.
Describe the author’s grandmother.
Answer:
The author s grandmother was short, fat, and slightly bent. She was like the winter landscape in the mountains, an expanse of pure white serenity breathing peace and contentment. She was religious, affectionate, and caring.

Question b.
What was the daily routine of the grandmother at home?
Answer:
Grandma started the mornings with a sing-song prayer. She woke up the author bathed and dressed him up and wanted him to learn the prayers by heart. Both would march to the school which was attached to a temple. She would stay inside chanting prayers and telling beads. In the evening, she would throw the stale chapattis to village dogs as they returned home.

Question c.
How is school education in the village different from that in the city?
Answer:
In the village school along with the teaching of subjects, there is the teaching of God and the scriptures, whereas city school concentrates more on western science and learning than with scriptures.

Question d.
The grandmother appreciated the value of education. Give instances in support of your answer.
Answer:
Grandma did have respect for education and that is why she personally monitored the village education of the author. She insisted on good manners and love for all living things. She demonstrated this by feeding village dogs and sparrows. She didn’t object to the author going abroad.

Question e.
The grandmother was strong-minded. Justify.
Answer:
When the author went abroad for his higher studies, She did not show her emotions. She had strong personal likes and dislikes. She was a woman of contentment.

Question f.
How did the grandmother spend the last few hours of her life?
Answer:
When she was in her death bed, she did not like to waste her time talking with the family members instead, She laid peacefully in bed praying and telling her beads.

3. Answer the following in a paragraph of 100 – 150 words each:

Question a.
The grandmother played a vital role in the author’s formative year. Give your own example of how elders have a positive influence on the younger generation. Include examples from the story also.
Answer:
The grandmother really played a vital role in moulding the author in his formative years. She was a good friend of the author during his childhood days. Like most other grandmothers she used to tell him many fables. She made the author get up early in the morning and listen to morning prayer. It was because of her the author inherited both moral and spiritual values.

Even in our day-to-day life, we have seen that there exist some basic differences in the character of children who are in a joint family with that of the children in a nuclear family. The elders in the joint family always have a positive influence over their grandchildren. There is no doubt that they act as the best guide and guardian of the younger generation.

Question b.
As young Khushwant Singh, write a letter to your parents describing your daily routine along with your thoughts and feelings about staying in the village.
Answer:
Dear dad,

I am fine. I feel extremely happy to share my thoughts and feelings of staying in the village with grandmother. First of all, I thank you so much for leaving me with grandma when you left for the city. Grandma is very affectionate towards me and I can’t leave her at any cost. She wakes me up early in the morning and makes me listen to her morning prayer. Though it is monotonous, I like listening to her voice. She makes me get ready for school and gives me chapattis for breakfast.

She accompanies me to school. On the way, we used to feed street dogs with stale chapattis which grandma carries with her daily. When we return from school those dogs follow us till we reach home. She also helps me in my studies. I am very much devoted to the love and affection which she shows to me. I like the atmosphere here and want to stay here for long. Hope you fulfill my wish.

Yours affectionately,
Khushwant Singh.

Question c.
Animals are capable of empathy. Substantiate this statement with examples from the story as well as your own experiences.
Answer:
Animals, which are considered not to have the sixth sense are far better than the human beings who have it. In fact the feeling of empathy is found more in animals than that in humans. In this story, we come to know that the grandmother develops a cordial relationship with the sparrows, whom she feeds daily with bread crumbs.

Those birds are also very affectionate towards her which we can understand by the way they sit on her shoulders, legs, and head. When grandmother died all the sparrows gathered there silently without any chirruping and they did not even touch the bread crumbs offered to them by the author’s mother.

When her corpse was taken away they all flew away silently. This clearly proves the fact that animals are really capable of empathy. The _ dogs which are tamed at home also possess the same feeling of empathy. We have heard of such incidents as where a dog dies just because it can’t tolerate the death of it’s owner.

Vocabulary:

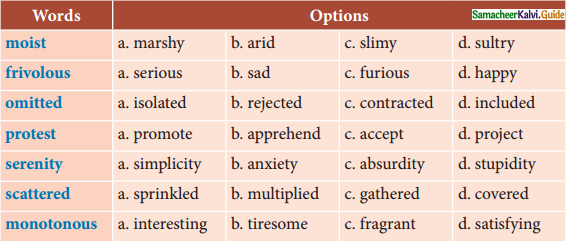
3a. Read the following words and choose the correct antonyms from the options given:

Question 1.
moist
(a) marshy
(b) arid
(c) slimy
(d) sultry
Answer:
(b. arid

Question 2.
frivolous
(a) serious
(b) sad
(c) furious
(d) happy
Answer:
(a) serious

Question 3.
omitted
(a) isolated
(b) rejected
(c) contracted
(d) included
Answer:
(d) included

Question 4.
protest
(a) promote
(b) apprehend
(c) accept
(d) project
Answer:
(c) accept

Question 5.
serenity
(a) simplicity
(b) anxiety
(c) absurdity
(d) stupidity
Answer:
(b) anxiety

Question 6.
scattered
(a) sprinkled
(b) multiplied
(c) gathered
(d) covered
Answer:
(c) gathered

Question 7.
monotonous
(a) interesting
(b) tiresome
(c) fragrant
(d) satisfying
Answer:
(a) interesting

Listening Activity:

Read the following statements and the given options. Now, listen to your teacher to read aloud a passage or play it on a recorder. You may listen to it again if required, to help you choose the right options:

Question i.
According to Napoleon ‘Good mothers make good ________.
a) housewives
b)jobs
c) nations
d)ideas
Answer:
c) nations

Question ii.
Mothers exhibit _______ love.
a) unauthorized
b) unapproved
c) unacceptable
d) unconditional
Answer:
d) unconditional

Question iii.
_______ mothers care much for their children.
a) Adapted
b) Adopted
c) Adoptive
d) Adaptable
Answer:
c) Adoptive

Question iv.
_______ is the most important thing in the world.
a) Wealth
b) Power
c) Love
d) Influence
Answer:
c) Love

Question v.
Love should be extended to _______ too.
a) friends
b) relatives
c) countrymen
d) creatures
Answer:
d) creatures

Reading:

Read the passage on ‘Laughter Therapy’ and answer the questions that follow:

1. Laughing is an excellent way to reduce stress in our lives; it can help you to cope with and survive a stressful life. Laughter provides full-scale support for your muscles and unleashes a rush of stress-busting endorphins. Since our body cannot distinguish between real and fake laughter, anything that makes you giggle will have a positive impact.

2. Laughter Therapy aims to get people laughing, in groups and individual sessions and can help reduce stress, make people and employees happier and more committed, as well as improve their interpersonal skills. This laughter comes from the body and not the mind.

3. Laughter Yoga (Hasya Yoga) is a practice involving prolonged voluntary laughter. It aims to get people laughing
in groups. It is practiced in the early mornings in open-parks. It has been made developed by Indian physician Madan Kataria, who writes about the practice in his 2002 book ‘Laugh for no reason. Laughter Yoga is based on the belief that voluntary laughter provides the same physiological as well as psychological benefits as spontaneous laughter.

4. Laughter yoga sessions may start with gentle warm-up techniques which include stretching, chanting, clapping, eye contact, and body movements to help break down inhibitions and encourage a sense of playfulness. Moreover, laughter is the best medicine. Breathing exercises are used to prepare the lungs for laughter followed by a series of laughter exercises that combine a method of acting and visualization techniques. Twenty minutes of laughter is sufficient to augment physiological development.

5. A handful of small scale scientific studies have indicated that laughter yoga has some medically beneficial effects, including cardiovascular health and mood. This therapy has proved to be good for depressed patients. Laughter therapy also plays a crucial role in social bonding.

Question a.
How does laughter help one to cope with stress?
Answer:
Laughter provides full-scale support for our muscles and unleashes a rush of stress-busting endorphins.

Question b.
Which word in the text (para 2) means the same as ‘dedicated’?
Answer:
Committed

Question c.
Why do you think voluntary laughter provides the same physiological as well as psychological benefits as spontaneous laughter?
Answer:
Our body cannot distinguish between real and fake laughter. Anything that makes us giggle will have a positive impact.

Question d.
‘Laughter is the best medicine’ explains.
Answer:
Laughter improves cardiovascular health and mood. It is also good for depressed patients.

Question e.
Given below is a set of activities. Which of these are followed in the ‘Laughter Yoga’ technique?

• sitting on the ground with legs crossed
• body movements
• clapping
• closed eyes
• breathing exercises
• chanting
• stretching of arms and legs
• bending backwards
• running/jogging
• eye contact

Answer:

• Clapping
• Breathing
• Exercises
• Bending backward
• Stretching of arms and legs

Question f.
‘Laughter therapy also plays a crucial role in social bonding How?
Answer:
When people sit together in laughter there develops a good or cordial relationship among them which improves their social bonding.

ஆசிரியரைப் பற்றி:

குஷ்வந்த் சிங் ஒரு இந்திய நாவலாசிரியர் மற்றும் வழக்கறிஞர். இவர் டெல்லியில் உள்ள புனித ஸ்டீஃபன்ஸ் கல்லூரியிலும் லண்டனில் உள்ள கிங்ஸ் கல்லூரியிலும் கல்வி பயின்றார். இவர் மத்திய அரசின் வெளியுறவுத்துறை பணியில் 1947ம் ஆண்டு சேர்ந்தார்.

இவர் சிறந்த எழுத்தாளராக சிறந்துவிளங்கியதோடு, மதச்சார்பின்மை , விமர்சனம் (நையாண்டி), கவிதை ஆகியவற்றால் புகழ் பெற்றார். 1974ல் இவருக்கு பத்ம விபூஷன் விருதும், 2007ல் சாகித்ய அகாடமி விருதும் இவரின் இலக்கிய பணிகளுக்காக வழங்கப்பட்டது, “விஷ்னுவின் அடையாளம்,” “சீக்கியர்களின் வரலாறு,” ”பாக்கிஸ்தானுக்குச்செல்லும் ரயில்” மேலும் பல இவரின் படைப்புகள் ஆகும்.

பாடத்தைப் பற்றி:

இந்த பாடத்தில் கொடுக்கப்பட்டுள்ள கதை ஆசிரியருக்கும் (குஷ்வன் சிங்) அவருடைய அன்பான பாட்டிக்கும் இடையிலான பாச பிணைப்பை வெளிக்காட்டுகிறது. வயதான பாட்டி சிறுவனாக இருக்கும் ஆசிரியரை உருவாக்குவதில் காட்டும் அக்கரையை எடுத்துக் காட்டுகிறது. பாட்டிக்கும் சிறுவனுக்கும் இடையில் உள்ள உறவை பார்க்கும் போது மெய்சிலிர்கிறது. பாட்டி முழுக்க முழுக்க பக்திமயமானவர். தன்னுடைய பேரனையும் பக்தியிலும், ஒழுக்கத்திலும் சிறந்தவனாக வளர்க்கிறார். பாட்டி அதிகம் படிக்கவில்லை என்றாலும் அவள் தன் பேரனுக்கு ஓர் சிறந்த ஆசிரியைதான்.

மனிதர்களுக்கு மட்டுமல்லாது விலங்குகளுக்கும் (நாய்), (சிட்டுக்குருவி) பறவைகளுக்கும் உணவழித்து மகிழ்கிறாள். இதைபோன்ற அன்புறவு நாம் நம் பாட்டிகளிடத்திலும் கண்டிருக்கலாம். ஆனால் இத்தலைமுறையினரிடம் இருக்கிறதா? என்றால் கேள்விக்குறிதான். பாட்டி இறக்கும் பொது கூறப்படும் செய்தியை நாம் வாசிக்கும் போது நம்மை அறியாமலே நமக்கு கண்ணீர் வருகிறது. இக்கதையை நாம் முழுமைாக படித்து பாட்டியின் அன்பை புரிந்து கொள்வோம்.

The Portrait of a Lady Summary in Tamil

எனது பாட்டி அனைவரது பாட்டியைப்போல் வயதான பெண்மணி. சுமார் இருபது ஆண்டுகளாய் முதிர்ந்த வயதுடையவளாகவும் சுருங்கிய கண்ணங்களோடும் அவளைப் பார்க்கிறேன். என் சுற்றத்தார் அனைவரும் என் பாட்டி இளமையில் அழகாகவும், (Pretty) இளமையாகவும், (Young) அவருக்கும் கணவர் இருந்தார் எனவும் கூறுவார்கள். அது எனக்கு வியப்பாக இருந்தது. எங்கள் வீட்டின் ஓவிய அறையின் (வரவேற்பு அறை) (Drawing room) மேலே என் தாத்தாவின் புகைப்படம் தொடங்கவிடப்பட்டிருந்தது. அதில் அவர் மிகப்பெரிய தலைப்பாகையும், தளர் ஆடையும் அணிந்திருந்தார்.

அவரின் நீளமான வெண்மை தாடி அவரின் மார்பகம் மறையும் அளவிற்கு இருந்தது, அவரை பார்பதற்கு மனைவி குழந்தைகள் இருப்பவராக மட்டமில்லாமல் அதிகமாக பேரன் பேத்திகளை கொண்டவர் போலும் காணப்பட்டார். எங்கள் பாட்டி அடிக்கடி தான் சிறுவயதில் விளையாடிய விளையாட்டைப் பற்றி எங்களிடம் கூறுவாள். அது அவள் மேல் அபத்தமான மற்றும் மதிப்பிழக்க (Undignified) செய்யும் அளவில் இருந்தாலும் அதை நாங்கள் இறைதூதர் (Prophets) சொல்லும் நீதிக்கதை (Fables) போல் எண்ணிக்கொள்வோம்.

அவள் குள்ளமாகவும் (Short) சாய்வாகவும் (Bent) நடப்பாள். அவள் முகத்தில் எங்கேயும் குறுக்குவெட்டுக் கோடுகளாலான (criss – cross) சுருக்கங்கள் இருக்கும். நாங்கள் அறிந்ததிலிருந்து முதுமை நிலையில், மிகவும் முதுமையான நிலையில் சுமார் இருபது ஆண்டுகள் இருக்கிறாள். அவள் அழகாக இல்லை என்றாலும் அவள் அழகு தான்.

ஒரு கையை கால்களுக்கு ஊன்றுகோளாகவும் மற்றொரு கையில் ஜெபமாலையும் வைத்துக்கொண்டு சிரமப்பட்டு நடப்பாள் (hobbled). வெள்ளியை போன்று முடிகள் அவளது சுருங்கிய முகத்தில் விழுந்து கிடக்கும், அவளது உதடுகள் மௌன ஜெபங்கள் பொழியும் (inaudible). ஆம் அவள் அழகுதான். பனிக்காலத்தில் தோன்றும் இயற்கை பரப்பரப்பு காட்சிபோல் விரிந்து (expanses) அமைதியான சமாதான மனநிறைவுடன் இருப்பாள்.

நானும் எனது பாட்டியும் நல்ல நண்பர்கள். என் பெற்றோர்கள் என்னை என் பாட்டியுடன் விட்டுவிட்டு நகர்ப்புறத்திற்கு சென்றார்கள். என்னை தினமும் காலையில் எழுப்பி பள்ளிக்கூடத்திற்கு புறப்பட செய்வாள். காலையில் என்னை குழிக்க வைக்கும் போதே மாறுபாடின்றி (monotonous) ஜெப கீதங்கள் படிப்பாள். அவை அனைத்தும் நான் என் இதயத்தால் அறிந்து உணர்வேன் என்ற நம்பிக்கையில் பாடுவாள். அவளின் இனிமையான குரலுக்கு நானும் அடிமை.

ஆனால் அவற்றை கற்க முற்கொள்ளமாட்டேன். பின் மரத்தாலான என்னுடைய சிலேட்டை (slate) நன்று துடைத்து அதனுடன் மஞ்சள் வண்ண எழுதுகோல், சிவப்பு பேனா அனைத்தையும் ஒரு கொத்தாக சேர்த்து என்னிடம் கொடுப்பாள். காய்ந்த ரொட்டியில் (சப்பாத்தி) வெண்ணை தடவி சர்க்கரையைத் தூவி காலை உணவை முடித்துவிட்டு நாங்கள் பள்ளிக்கு செல்வோம். அதிகமான காய்ந்த ரொட்டிகளை கிராமத்தில் உள்ள நாய்களுக்கு போட கையில் எடுத்துக் கொண்டு வருவாள்.

பள்ளிக்கூடத்திற்கு அருகே கோவில் இருப்பதால் என் பாட்டி என்னுடனே பள்ளிக்கு வருவாள். புரோகிதர் (பூசாரி – Priest) எங்களுக்கு காலை ஜெபங்கள் மற்றும் ஸ்லோகங்கள் சொல்லித் தருவார்.குழந்தைகள் வரிசையாக அமர்ந்து ஸ்லோகங்கள் சொல்லும்போது என் பாட்டி உள்ளே அமர்ந்து சமயத் திரு நூல்களை வாசிப்பாள்.

அனைத்து வேலைகளையும் முடித்தப் பிறகு இருவரும் சேர்ந்து வீட்டுக்கு செல்வோம். அந்த நேரத்தில் எங்கள் கிராமத்து நாய்க்குட்டிகள் நாங்கள் போட்ட ரொட்டிகைளை தின்றுக்கொண்டு எங்கள் பின்னால் சண்டைப் போட்டுக்கொண்டும், விளையாடிக் கொண்டும் வரும்.

எனது பெற்றோர் நகர்ப்புறத்தில் குடியேறியப் பிறகு எங்களையும் அழைத்துச் சென்றார்கள். அது எங்கள் தோழமைக்கு திருப்பு முனையாக இருந்தது. ஒரே அறையை நாங்கள் பகிர்ந்து கொண்டாலும், என்னுடன் என் பாட்டி பள்ளிக்கு வர இயலவில்லை. நானும் பள்ளிக்கு விசைப்பேருந்தில் (Motorbus) செல்வேன். தெருவில் நாய்களுக்கு உணவு அளிக்க முடியாததால் மொட்டை மாடியில் (Courtyard) குருவிகளுக்கு (Sparrows) உணவு அளிப்பாள்.

வருடங்கள் உருண்டோட நாங்கள் குறைவாக பார்த்துகொண்டோம். சில நேரம் என்னை பள்ளிக்கு புரப்படச்செய்வாள். நான் பள்ளியில் இருந்து வந்ததும் என் ஆசிரியர் எனக்கு கற்பித்த பாடத்தைக் கேட்பாள். நான் ஆங்கில வார்த்தைகள் மற்றும் மேற்கத்திய அறிவியல் பற்றிய படிப்புகள், புவிஈர்ப்புவிசை,அரித்மேட்டிஸ் கொள்கைகள், உலக உருண்டை, ஆகியவற்றைப் பற்றி கூறுவேன். ஆனால், அவை அவளுக்கு மகிழ்ச்சி அளிக்கவில்லை.

கடவுள் மற்றும் புனிதநூல்கள் பற்றி கற்றுத்தராததால் எங்கள் பள்ளியின் மேல் நம்பிக்கை வரவில்லை. ஒருநாள், எங்களுக்கு இசை வகுப்பு நடந்ததாக அவளிடம் கூறினேன். அவள் ஒன்றும் கூறவில்லை . ஆனால் அவளின் அமைதியே அவளின் விருப்பமின்மையைக் கூறியது. அதன்பிறகு என்னுடன் எப்போதாவது தான் பேசுவாள்.

நான் பல்கலைக்கழகத்துக்கு படிக்கச் சென்றபோது. எனக்கு தனி அறை வழங்கப்பட்டது. எங்களது பொது தோழமை முறியப்பட்டது (snapped). எனது பாட்டி தனிமையான (seclusion) இடத்தை ஏற்றுக்கொண்டார். யாருடனும் பேசுவதற்காக மட்டுமே எப்பொழுதாவது தான் சுழற்றும் கைராட்டையை நிறுத்துவாள். காலை தொடங்கி மாலை வரை சுழலும் சக்கரத்தில் அமர்ந்திருந்து பிராத்தனைகளை ஒப்புவிப்பாள்.

மதியவேளை மட்டும் சற்று நேரம் எழுந்து குருவிகளுக்கு உணவு அளிப்பாள். அவள் வீட்டின் தாழ்வாரத்தில் (முற்றத்தில்) அமர்ந்துக் கொண்டு ரொட்டி துண்டை சிறு துண்டுகளாக்கி பறவைகளுக்கு கொடுப்பாள். நூற்றுக்கணக்கான சிறு பறவைகள் அதை எடுத்து சாப்பிட்ட, மெய்யான கூச்சல் குழப்பம் கலகலப்பான ஒலி நிறைந்த இடமாக அது மாறும். சில பறவைகள் அவள் கால்களிலும் சில அவளின் தோள்களிலும் சில பறவைகள் தலையிலும் கூட அமர்ந்திருக்கும். அவற்றைப் பார்த்து சிரிப்பாளே தவிர அவற்றை விரட்டியது இல்லை. அந்த அரைமணி நேரம் அவளுக்கு மகிழ்ச்சியான நேரமாக இருக்கும்.

மேல்நிலைப்படிப்புக்காக நான் வெளிநாடு செல்ல முடிவெடுத்தபோது என் பாட்டி மனமுடைந்து (upset) போவாள் என்று எனக்குத் தெரியும். முதிர்ந்த வயதில் வெளியில் சொல்ல முடியாத வகையில் நான் ஐந்து ஆண்டுகள் அவரை விட்டு பிரிந்து இருந்தேன். அவர் என்னை ரயில் நிலையத்தில் விட்டுச் செல்லும் போது எந்த ஒரு வார்த்தையையும், உணர்வையும் வெளிக்காட்ட வில்லை.

அவளின் உதடுகள் மட்டும் ஜெபங்களை ஒப்பிவித்து கொண்டிருந்தன. அவரது விரல்கள் ஜெபமாலை முத்துக்களை எண்ணிக் கொண்டிருந்த வேலையில், என் நெற்றியில் மெதுவாக முத்தமிட்டாள். நான் அவளை விட்டு வரும்போது நேசத்துக்குரிய பாசம் தென்பட்டாலும் அது எங்களது கடைசி உடல்தொடர்பு என உணர்ந்தேன்.

ஆனால், அது அப்படி நடக்கவில்லை . ஐந்து ஆண்டுகள் கழித்து திரும்பி வந்து மறுபடியும் புகைவண்டி நிலையத்தில் நான் பாட்டியை சந்தித்தேன். அவளின் பழைய இயல்பை பார்க்கவில்லை. அவள் வாயில் வார்த்தைகள் இல்லை அவள் என்னை கட்டி அனைத்தாள். அப்போதும் அவள் ஒப்புவிக்கும் ஜெபத்தை நான் கேட்கமுடிந்தது. எனது முதல் நாளில் அவளின் மகிழ்ச்சியான தருணங்களாக நினைத்து, நீண்ட நாட்களாக உணவளித்த பறவைகளைக் கடிந்து கொண்டாள்.

மாலை நேரத்தில் அவளிடத்தில் ஒரு மாறுதல் தெரிந்தது. அவள் ஜெபங்கள் இப்போது செய்வதில்லை. பக்கத்து வீட்டில் உள்ள பெண்களை அழைத்து பழைய கொட்டு ஒன்றை வைத்துப் பாட்டு பாடுவாள். பல மணி நேரமாக பழமையான கொட்டை வைத்து (Dilapidated drum) (தாயகம்) வீடு திரும்பும் வீரர்களின் பாடலை பாடினாள். நாங்கள் அவளை கடுஞ்சோர்வு அடைந்துவிடக் கூடாது என்பதற்காக நிறுத்துவோம். அவள் ஜெபம் செய்யாமல் பார்ப்பது இதுவே முதல்முறை.

மறுநாள் காலையில் அவளுக்கு உடம்பு சரியில்லாமல் போய்விட்டது. மிதமான காய்ச்சல்தான். மருத்துவர் அது எளிதில் குணமாகிவிடும் என கூறினார். என் பாட்டி வேறுமாதிரி நினைத்தாள். என் வாழ்க்கையின் கடைசி அகராதியை (இறப்பு) முடிப்பதற்கே ஜெபங்கள் செய்வதை விலக்கி வைக்கிறேன் என்றும், எங்களோடு பேசி நேரத்தை வீணாக்க விரும்பவில்லை என்றும் கூறினாள்.நாங்கள் போராடினோம் (Protested).

ஆனால் அவள் எங்கள் போராட்டத்தை புறக்கணித்தாள் (Ignored). தனது படுக்கையில் அமைதியாக படுத்துகொண்டு ஜெபங்கள் மற்றும் மணிகள் சொல்லிக்கொண்டாள். நாங்கள் நினைப்பதற்க்குள் ஜெபமாலை அவளின் உயிரற்ற விரல்களில் இருந்து கீழே விழுந்தது. ஒரு அமைதியான வெளுப்பு நிறம் (Pallor) அவள் மேல் தோன்றியது. பின்பு அவள் இறந்தது எங்களுக்குத் தெரிந்தது.

நாங்கள் அவளை கட்டிலில் இருந்து கீழே இறக்கி வைத்து எங்களின் சம்பிரதாய முறைப்படி அவரின் உடலை சிவப்பு துணிகளால் சுற்றினோம். சற்று நேரம் அழுதுவிட்டு இறுதிச் சடங்கு (Funeral) ஏற்பாடு செய்ய சென்றோம். மாலை நேரத்தில் அவரது அறைக்கு சென்று stretcherல் எடுத்துக்கொண்டு அடக்கம் செய்ய சென்றோம். சூரியன் மறையும் போது அவரது அறையில் உள்ள விளக்கிலும் ஒளியை ஏற்றிவிட்டு சென்றோம். நாங்கள் பாதி வழியில் திண்ணையில் நின்றோம்.

என் பாட்டியின் அறை தாழ்வாரத்தில் (முற்றத்தில்); அவளை சுற்றி உள்ள துணிகளில் குருவிகள் நின்றுக் கொண்டிருந்தன. அங்கு மகிழ்ச்சி இல்லை. நாங்கள் அவற்றைப்பார்த்து வருந்தினோம். என் அம்மா அவற்றிற்கு சில ரொட்டி துண்டுகள் போட்டாள். ஆனால் அக்குருவிகள் அவற்றை பார்க்க கூட இல்லை. நாங்கள் என் பாட்டியின் பிணத்தை எடுத்துச் செல்லும் போது அவைகளும் மெதுவாக பறந்து சென்றன. அடுத்த நாள் தூய்மை செய்பவர் ரொட்டி துண்டுகளை கூட்டி குப்பைத் தொட்டியில் போட்டார்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 6 Two Dimensional Analytical Geometry Ex 6.5 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.5
Choose the correct or more suitable answer.

Question 1.
The equation of the locus of the point whose distance from y – axis is half the distance from origin is
(1) x² + 3y² = 0
(2) x² – 3y² = 0
(3) 3x + y² = 0
(4) 3x² – y² = 0
Answer:
(4) 3x² – y² = 0

Explaination:

Let the point be (h,k)
Equation of y axis is x = 0
Given the distance of the point from y – axis is
\(\frac{1}{2}\) × distance of the point from the origin Distance of the point (h, k) from the y- axis is
= \(\frac{\mathrm{h}}{\sqrt{1^{2}}}\) = h
The distance of the point P (h , k) from the origin

Squaring on both sides
4h² = h² + k²
4h² – h² – k² = 0
3h² – k² = o
The locus of ( h, k ) is 3x² – y² = 0

Question 2.
Which of the following equation is the locus of (at², 2at)
(1) \(\frac{x^{2}}{\mathbf{a}^{2}}-\frac{\mathbf{y}^{2}}{\mathbf{b}^{2}}\) = 1
(2) \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
(3) x² + y² = a²
(4) y² = 4ax
Answer:
(4) y² = 4ax

Explaination:
y² = 4ax ⇒ Equation that satisfies the given point (at², 2at)

Question 3.
Which of the following points lie on the locus of 3x² + 3y² – 8x – 12y + 17 = 0
(1) (0, 0)
(2) (-2, 3)
(3) (1, 2)
(4) (0, – 1)
Answer:
(3) (1, 2)

Explaination:
The point that satisfies the given equations (0, 0) ⇒ 17 ≠ 0
(-2, 3) ⇒ 3 (4) + 3 (9) + 16 – 36 + 17 ≠ 0
(1, 2) ⇒ 3 + 3 (4) – 8 (1) – 12 (2) + 17
32 – 32 = 0, 0 = 0

Question 4.
If the point (8, – 5) lies on the focus \(\frac{x^{2}}{16}-\frac{y^{2}}{25}\) = k, then the value of k is
(1) 0
(2) 1
(3) 2
(4) 3
Answer:
(4) 3

Explaination:
Given the point (8, – 5) lies on the locus

Question 5.
Straight line joining the points (2, 3) and (- 1, 4) passes through the point (α, β) if
(1) α + 2β = 7
(2) 3α + β = 9
(3) α + 3β = 11
(4) 3α + β = 11
Answer:
(3) α + 3β = 11

Explaination:
The equation of the straight line joining the points (2, 3) and (-1, 4) is

x – 2 = – 3(y – 3)
x – 2 = – 3y + 9
x + 3y – 2 – 9 = 0
x + 3y – 11 = 0
Given (α, P) lies on this line
α + 3β – 11 = 0

Question 6.
The slope of the line which males an angle 45°with the line 3x – y = – 5 are
(1) 1, – 1
(2) \(\frac{1}{2}\), – 2
(3) 1, \(\frac{1}{2}\)
(4) 2, –\(\frac{1}{2}\)
Answer:
(2) \(\frac{1}{2}\), – 2

Explaination:

The equation of the given line is
3x – y + 5 = 0 ………… (1)
the slope of the line (1) is m = tan θ

Angle made by the required line = θ + 45°
where tan θ = 3
Required slope m₁ = tan (θ + 45° )

Question 7.
Equation of the straight line that forms an isosceles triangle with coordinate axes in the
1-quadrant with perimeter 4 + 2√2 is
(1) x + y + 2 = 0
(2) x + y – 2 = 0
(3) x + y – √2 = 0
(4) x + y + √2 = 0
Answer:
(2) x + y – 2 = 0

Explaination:
Let OAB be the isosceles triangle formed in the first quadrant. Let OA = OB = a
In the right angle A OAB
AB² = OA² + OB²
AB² = a² + a² = 2a²
AB = √2a

Question 8.
The coordinates of the four vertices of a quadrilateral are (-2, 4), (-1, 2), (1, 2) and (2, 4) taken in order. The equation of the line passing through the vertex (-1, 2 ) and dividing the quadrilateral in the equal areas is
(1) x + 1 = 0
(2) x + y = 1
(3) x + y + 3 = 0
(4) x – y + 3 = 0
Answer:
(4) x – y + 3 = 0

Explaination:

ABCD is a quadrilateral in which the sides AD and BC are parallel. Draw AE and DF perpendicular to BC. ADFE is a square with sides
AD = AE = EF = DF = 2
Area of ADFE = 2 × 2 = 4
In ∆ AEB , BE = 1, AE = 2
∴ Area of ∆ AEB = \(\frac{1}{2}\) × 1 × 2 = 1
Similarly Area of ∆ DFC = 1
∆ Area of the quadrilateral A B C D = 4 + 1 + 1 = 6
Given the line through the vertex (- 1, 2 ) divides the quadrilateral ABCD into two half.
Let E (x , 4) is the point on the line BC such that the line DE divides the area of the quadrilateral ABCD into two half.
∴ Area of ∆ EDC = 3
\(\frac{1}{2}\) × EC × height = 3
\(\frac{1}{2}\) × (x + 2) × 2 = 3
x + 2 = 3 ⇒ x = 1
∴ The coordinates of E are (1, 4)
The equation of the line joining the points (- 1, 2) and (1, 4) is

x – 1 = y – 4
x – y + 3 = 0

Question 9.
The intercepts of the perpendicular bisector of the line segment joining (1,2) and (3,4) with coordinate axes are
(1) 5, – 5
(2) 5, 5
(3) 5, 3
(4) 5, – 4
Answer:
(2) 5, 5

Explaination:
Let the given points be A (1, 2) and B (3, 4) P( h,k )be a point in the plane such that PA = PB

Squaring on both the sides
(h – 1)² + (k – 2)² = (3 – h)² + (k – 4)²
h² – 2h + 1 + k² – 4k + 4 = 9 – 6h + h² + k² – 8k + 16
– 2h – 4k + 5 = – 6h – 8k + 25
6h + 8k – 2h – 4k + 5 – 25 = 0
4h + 4k – 20 = 0
h + k – 5 = 0
The locus of (h, k)is x + y – 5 = 0 which is the perpendicular bisector of A and B
x + y = 5
\(\frac{x}{5}+\frac{y}{5}\) = 1
x – intercept = 5 , y – intercept = 5

Question 10.
The equation of the line with slope 2 and the length of the perpendicular from the origin equal to √5 is
(1) x + 2y = √5
(2) 2x + y = √5
(3) 2x + y = 5
(4) x + 2y – 5 = 0
Answer:
Let the equation of the required line be
y = mx + c ……….. (1)
Given Slope m = 2
(1) ⇒ y = 2x + c
2x – y + c = 0 ……….. (2)
The length of the perpendicular from (0, 0) to line (2)

Substituting for c in equation (2), we have
2x – y + 5 = 0

Question 11.
If a line is perpendicular to the line Sx-y = 0 and forms a triangle with the coordinate axes of area 5 sq. units, then its equation is
(1) x + 5y ± 5√2 = 0
(2) x – 5y ± 5√2 = 0
(3) 5x + y ± 5√2 = 0
(4) 5x – y ± 5√2 = 0
Answer:
(1) x + 5y ± 5√2 = 0

Explaination:

The equation of the given line is 5x – y = 0 —— (1)
The equation of any perpendicular to line (1) is
-x – 5y + k = 0
x + 5y – k = 0 —– (2)
x + 5y = k

x- intercept = k , y – intercept = \(\frac{\mathrm{k}}{5}\)
The line (2) intersect the x-axis at A and y-axis at B
∴ A is (k, 0) and B is \(\left(0, \frac{k}{5}\right)\)
OA = k and OB = \(\frac{\mathrm{k}}{5}\)
Area of ∆ OBA = \(\frac{1}{2}\) × OA × OB

∴ The required equation is x + 5y = ± 5√2

Question 12.
Equation of the straight line perpendicular to the line x – y + 5 = 0 through the point of intersection y-axis and the given line
(1) x – y – 5 = 0
(2) x + y – 5 = 0
(3) x + y + 5 = 0
(4) x + y + 10 = 0
Answer:
(2) x + y – 5 = 0

Explaination:
The equation of the given line is
x – y + 5 = 0 ………. (1)
To find the point of intersection with y – axis, Put x = 0 in (1)
0 – y + 5 = 0 ⇒ y = 5
∴ The point of intersection is ( 0, 5)
The equation any line perpendicular to line (1) is
– x – y + k = 0
x + y – k = 0
This line passes through the point (0,5)
0 + 5 – k = 0 ⇒ k = 5
∴ The equation of the required line is
x + y – 5 = 0

Question 13.
If the equation of the base opposite to the vertex (2, 3) of an equilateral triangle is x + y = 2, then the length of a side is
(1) \(\frac{\sqrt{3}}{2}\)
(2) 6
(3) √6
(4) 3√2
Answer:
(3) √6

Explaination:
∆ ABC is an equilateral triangle. Vertex A is (2, 3)
Equation of the base BC is x + y = 2
Draw AD ⊥ BC. By the property of the equilateral triangle, D is the midpoint of BC
BD = DC
Let AB = a
AD = length of the perpendicular from A (2, 3) to the line x + y – 2 = 0

Question 14.
The line (p + 2q)x + (p – 3q)y = p – q for different values of p and q passes through the point
(1) \(\left(\frac{3}{2}, \frac{5}{2}\right)\)
(2) \(\left(\frac{2}{5}, \frac{2}{5}\right)\)
(3) \(\left(\frac{3}{5}, \frac{3}{5}\right)\)
(4) \(\left(\frac{2}{5}, \frac{3}{5}\right)\)
Answer:
(4) \(\left(\frac{2}{5}, \frac{3}{5}\right)\)

Explaination:
The equation of the given line is
(p + 2q)x + (p – 3q)y = p – q ……….. (1)

Question 15.
The point on the line 2x – 3y = 5 is equal distance from (1, 2), and (3, 4) is
(1) (7, 3)
(2) (4, 1)
(3) (1, – 1)
(4)(-2, 3)
Answer:
(2) (4, 1)

Explaination:
Let P (h, k) be a point on the line
2x – 3y – 5 = 0

Then 2h – 3k – 5 = 0 ……….. (1)
Let A (1, 2) and B ( 3, 4) be the given points such that PA = PB

Squaring on both sides
(h – 1)² + (k – 2)² = (h – 3)² + (k – 4)²
h² – 2h + 1 + k² – 4k + 4 = h² – 6h + 9 + k² – 8k + 16
-2h + 1 – 4k + 4 = – 6h + 9 – 8k + 16
-2h – 4k + 5 = – 6h – 8k + 25
6h – 2h + 8k – 4k + 5 – 25 = 0
4h + 4k – 20 = 0
h + k – 5 = 0 …………. (2)
To find P (h, k), Solve (1) and (2)

(2) ⇒ h + 1 – 5 = 0
h – 4 = 0 ⇒ h = 4
∴ The required point p(h, k) is (4, 1)

Question 16.
The image of the point (2, 3) in the line y = -x is
(1) (-3, -2)
(2) (-3, 2)
(3) (-2, -3)
(4) (3, 2)
Answer:
(1) (- 3, – 2)

Explaination:
The equation of the given line is y = -x
x + y = 0 ………… (1)
The coordinates of the image of the point (x₁, y₁) with respect to the line ax + by + c = 0 are given by

∴ The coordinates of the image of the point (2, 3) with respect to the line x + y = 0 are given by

x – 2 = y – 3 = – 5
x – 2 = -5 ⇒ x = -5 + 2 = -3
y – 3 = -5 ⇒ y = -5 + 3 = -2
∴ The required point is (-3, -2)

Question 17.
The length of perpendicular from the origin to the line \(\frac{x}{3}-\frac{y}{4}\) = is
(1) \(\frac{11}{5}\)
(2) \(\frac{5}{12}\)
(3) \(\frac{12}{5}\)
(4) –\(\frac{5}{12}\)
Answer:
(3) \(\frac{12}{5}\)

Explaination:
The equation of the given line is \(\frac{x}{3}-\frac{y}{4}\) = 1
\(\frac{4 x-3 y}{12}\) = 14x – 3y = 12
4x – 3y – 12 = 0
The length of the perpendicular from (0, 0) to the line 4x – 3y – 12 = 0 is

Question 18.
The y – intercept of the straight line passing through (1, 3) and perpendicular to 2x – 3y + 1 = 0 is
(1) \(\frac{3}{2}\)
(2) \(\frac{9}{2}\)
(3) \(\frac{2}{3}\)
(4) \(\frac{2}{9}\)
Answer:
(2) \(\frac{9}{2}\)

Explaination:
The equation of the given line is
2x – 3y + 1 = 0 …………. (1)
The equation of any line perpendicular to (1) is
-3x – 2y + k = 0
3x + 2y – k = 0 ………… (2)
This line passes through the point (1, 3)
∴ (2) ⇒ 3 × 1 + 2 × 3 – k = 0
3 + 6 – k = 0 ⇒ k = 9
∴ (2) ⇒ 3x + 2y – 9 = 0 ………. (3)
2y = – 3x + 9
y = \(-\frac{3}{2} x+\frac{9}{2}\)
∴ The required y – intercept is \(\frac{9}{2}\)

Question 19.
If the two straight lines x + (2k – 7)y + 3 = 0 and 3kx + 9y – 5 = 0 are perpendicular, then the value of k is
(1) k = 3
(2) k = \(\frac{1}{3}\)
(3) k = \(\frac{2}{3}\)
(4) k = \(\frac{3}{2}\)
Answer:
(1) k = 3

Explaination:
The equation of the given lines are
x + (2k – 7)y + 3 = 0 ……….. (1)
3kx + 9y – 5 = 0 …………. (2)
Slope of line (1), m₁ = \(-\frac{1}{2 k-7}\)
Slope of line (2), m₂ = \(-\frac{3 \mathbf{k}}{9}\)
Given that lines (1) and (2) are perpendicular
∴ m₁ m₂ = -1

k = -3(2k – 7)
k = -6k + 21
6k + k = 21
⇒ 7k = 21
k = \(\frac{21}{7}\) = 3

Question 20.
If a vertex of a square is at the origin and it’s one side lies along the line 4x + 3y – 20 = 0
then the area of the square is
(1) 20 sq. units
(2) 16 sq. units
(3) 25 sq. units
(4) 4 sq. units
Answer:
(2) 16 sq. units

Explanation:

OABC is a square in which the vertex O lies on the origin and the side AB along the line 4x + 3y – 20 = 0
OA = length of the perpendicular from (0, 0) to the line 4x + 3y – 20 = 0

∴ The length of the side of the square is 4 units.
∴ Area of the square = 4 × 4 = 16 sq. units

Question 21.
If the lines represented by the equation 6x² + 41xy – 7y² = 0 make angles α and β with x-axis then tan α . tan β =
(1) –\(\frac{6}{7}\)
(2) \(\frac{6}{7}\)
(3) –\(\frac{7}{6}\)
(4) \(\frac{7}{6}\)
Answer:
(1) –\(\frac{6}{7}\)

Explaination:
The equation of the given pair of lines is
6x² + 41xy – 7y² = 0 ……….. (1)
Let m₁, m₂ be slopes of the individual lines.
Given that the individual lines make angles α and β with x – axis.
∴ m₁ = tan α and m₂ = tan β
we have m₁ m₂ = \(\frac{a}{b}\) = \(\frac{6}{-7}\)
∴ tan α tan β = \(-\frac{6}{7}\)

Question 22.
The area of the triangle formed by the lines x² – 4y² = 0 and x = a is
(1) 2a²
(2) \(\frac{\sqrt{3}}{2}\)
(3) \(\frac{1}{2}\)
(4) \(\frac{2}{\sqrt{3}}\)
Answer:
(3) \(\frac{1}{2}\)

Explaination:

The equation of the given pair of straight lines is
x² – 4y² = 0
x² – 4y² = (x + 2y) (x – 2y)
∴ The separate equations of the straight lines are
x + 2y = 0 ………… (1)
x – 2y = 0 …………. (2)
The line x = a intersect the line (1) at A.
a + 2y = 0 ⇒ y = \(-\frac{a}{2}\)
∴ A is \(\left(a,-\frac{a}{2}\right)\)
The line x = a intersect the line (2) at B.

Question 23.
If one of the lines given by 6x² – xy – 4cy² = 0 is 3x + 4y = 0,then c equals to
(1) -3
(2) -1
(3) 3
(4) 1
Answer:
(1) -3

Explaination:
The given pair of straight lines is 6x² – xy – 4cy² = 0 ………. (1)
One of the separate equation is 3x + 4y = 0 ……… (2)
Let the separate equation of the other line be ax + by = 0 ………. (3)
∴ (ax + by) (3x + 4y) = 6x² – xy + 4cy²
3ax² + 4axy + 3bxy + 4by² = 6x² – xy + 4cy²
Equating the coefficient of y² on both sides
4b = 4c ⇒ c = b
Equating the coefficient of x² on both sides
3a = 6
⇒ a = \(\frac{6}{3}\) = 2
Equating the coefficient of xy both sides
4a + 3b = -1
4 × 2 + 3b = -1 ⇒ 3b = -1 – 8
b = \(-\frac{9}{3}\) = -3
∴ c = -3

Question 24.
θ is acute angle between the lines x² – xy – 6y² = 0 then \(\frac{2 \cos \theta+3 \sin \theta}{4 \cos \theta+5 \cos \theta}\) is
(1) 1
(2) \(-\frac{1}{9}\)
(3) \(\frac{5}{9}\)
(4) \(\frac{1}{9}\)
Answer:
(3) \(\frac{5}{9}\)

Explaination:
The equation of the given pair of lines is
x² -xy – 6y² = 0
a = 1, 2h = -1, b = -6
Given θ is the angle between the lines

Question 25.
The equation of one of the lines represented by the equation x² + 2xy cot θ – y² = 0 is
(I) x – y cot θ = 0
(2) x + y tan θ = 0
(3) x cos θ + y (sin θ + 1) = 0
(4) x sin θ + y(cos θ + 2) = 0
Answer:
(4) x sin θ + y(cos θ + 2) = 0

Explaination:
The equation of given pair of straight line is
x² + 2xy cot θ – y² = 0
x² + (2y cot θ)x + (-y²) = 0
This is a quadratic equation in x. Solving for x, we have

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 6 Two Dimensional Analytical Geometry Ex 6.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.4

Question 1.
Find the combined equation of the straight lines whose separate equations are x – 2y – 3 = 0 and x + y + 5 = 0.
Answer:
Separate equations are x – 2y – 3 = 0; x + y + 5 = 0
So the combined equation is (x – 2y – 3) (x + y + 5) = 0
x² + xy + 5x – 2y² – 2xy – 10y – 3x – 3y – 15 = 0
(i.e) x² – 2y² – xy + 2x – 13y – 15 = 0

Question 2.
Show that 4x² + 4xy + y² – 6x – 3y – 4 = 0 represents a pair of parallel lines.
Answer:
The equation of the given pair of straight lines is
4x² + 4xy + y² – 6x – 3y – 4 = 0 ………. (1)
Compare this equation with the equation
ax² + 2hxy + by² + 2gx + 2fy + c = 0 ………. (2)
a = 4, 2h = 4, b = 1, 2g = -6,
2f = -3, c = – 4
The condition for parallelism is
h² – ab = 0
2² – (4) (1) = 4 – 4 = 0
∴ The given pair of straight lines represents a pair of parallel straight lines.

Question 3.
Show that 2x² + 3xy – 2y² + 3x + y + 1 = 0 represents a pair of perpendicular straight lines.
Answer:
Comparing the given equation with the general form a = 2,h = 3/2, b = -2,g= 3/2, f = 1/2 and c = 1
Condition for two lines to be perpendicular is a + b = 0. Here a + b = 2 – 2 = 0
⇒ The given equation represents a pair of perpendicular lines.

Question 4.
Show that equation 2x² – xy – 3y² – 6x + 19y – 20 = 0 represents a pair of intersecting lines. Show further that the angle between them is tan^-1(5)
Answer:
The equation of the given pair of lines is
2x² – xy – 3y² – 6x + 19y – 20 = 0 —- (1)
Compare this equation with the equation
ax² + 2hxy + by² + 2gx + 2fy + c = 0 —- (2)
a = 2 , 2h = – 1, b = – 3, 2g = – 6, 2f = 19, c = – 20
h² – ab = \(\left(-\frac{1}{2}\right)^{2}\) – (2)(-3)
= \(\frac{1}{4}\) + 6 ≠ 0
∴ The given line (1) is not parallel.
∴ They are intersecting lines.
Let θ be the angle between the lines.

Taking the acute angle θ = tan^-1 (5)

Question 5.
Prove that the equation to the straight lines through the origin each of which makes an angle α with the straight line y = x is x² – 2xy sec 2α + y² = 0
Answer:

Let OP be the given line y = x having slope
m = 1 = tan 45°
Given that OA is the line making angle α with the line y = x.

Slope of the line OA = tan (45° – α)
The equation of OA is the equation of the line passing through the point (0, 0) having slope tan (45° – α).
y – 0 = tan(45°- α) (x – 0)
y = x tan (45°- α)
x tan (45° – α) – y = 0
Also given the line OB makes an angle α with the line y = x.

Slope of the line OB = tan(45° + α)
The equation of OB is the equation of the line passing through the point (0, 0) having slope tan(45° + α)
y – 0 = tan (45° + α) (x – 0)
y = x tan (45° + α)
x tan (45° + α) – y = 0 ………. (2)
The combined equation is
(x tan(45°- α) – y) (x tan(45°+ α) – y) = 0
x²tan(45° – α) tan(45° + α) – xy tan (45° – α) – xy tan(45° + α) + yz = 0

Question 6.
Find the equation of the pair of straight lines passing through the poInt (1,3) and
perpendicular to the lines 2x -3y + 1 = 0 and 5x + y – 3 = 0.
Answer:

Equation of a line perpendicular to 2x – 3y + 1 = 0 is of the form 3x + 2y + k = 0.
It passes through (1, 3) ⇒ 3 + 6 + k = 0 ⇒ k = – 9
So the line is 3x + 2y – 9 = 0
The equation of a line perpendicular to 5x + y – 3 = 0 will be of the form x – 5y + k = 0.
It passes through (1, 3) ⇒ 1 – 15 + k = 0 ⇒ k = 14
So the line is x – 5y + 14 = 0.
The equation of the lines is 3x + 2y – 9 = 0 and x – 5y + 14 = 0
Their combined equation is (3x + 2y – 9)(x – 5y + 14) = 0
(i.e) 3x² – 15xy + 42x + 2xy – 10y² + 28y – 9x + 45y – 126 = 0
(i.e) 3x² – 13xy – 10y² + 33x + 73y – 126 = 0

Question 7.
Find the separate equation of the following pair of straight lines.
(i) 3x² + 2xy – y² = 0
(ii) 6(x – 1)² + 5(x – 1) (y – 2) – 4(y – 3)² = 0
(iii) 2x² – xy – 3y² – 6x + 19y – 20 = 0
Answer:

(i) Factorising 3x² + 2xy – y² we get
3x² + 3xy – xy – y² = 3x (x + y) – y (x + y)
= (3 x – y)(x + y)
So 3x² + 2xy – y² = 0 ⇒ (3x – y) (x + y) = 0
⇒ 3x – y = 0 and x + y = 0

(ii) 6(x – 1)² + 5 ( x – 1) (y – 2) – 4(y – 3 )² = 0
Let X = x – 1 and Y = y – 2
∴ The given equation becomes
6X² + 5XY – 4Y² = 0
6X² + 8 XY – 3XY – 4Y² = 0
2X(3X + 4Y) – Y (3X + 4Y) = 0
(2X – Y) (3X + 4Y) = 0
2X – Y = 0 and 3X + 4Y = 0
Substituting for X and Y , we have
2X – Y = 0 ⇒ 2(x – 1) – (y – 2) = 0
⇒ 2x – 2 – y + 2 = 0
⇒ 2x – y = 0
3X + 4Y = 0 ⇒ 3 (x – 1) + 4 ( y – 2 ) = 0
⇒ 3x – 3 + 4y – 8 = 0
⇒ 3x + 4y – 11 = 0
∴ The separate equations are
2x – y = 0 and 3x + 4y – 11 = 0

(iii) 2x² – xy – 3y² – 6x + 19y – 20 = 0
The given equation is
2x² – xy – 3y² – 6x + 19y – 20 = 0 ……… (1)
2x² – xy – 3y² = 2x² – 3xy + 2xy – 3y²
= x (2x – 3y) + y (2x – 3y )
= (x + y) (2x – 3y)
Let the separate equation of the straight lines be
x + y + 1 = 0 and 2x – 3y + m = 0 …….. (A)
(1) ⇒ 2x² – xy – 3y² – 6x + 19y – 20 = (x + y + 1) (2x – 3y + m)
Equating the coeffident of x , y and constant term on both sides, we have
-6 = m + 2l ………. (2)
19 = m – 3l ………. (3)
lm = – 20 ………. (4)
Solving equations (2), (3) and (4) we have

Substituting the values of l and m in equation (A) the required separate equations of the lines are
x + y – 5 = 0 and 2x – 3y + 4 = 0

Question 8.
The slope of one of the straight lines ax² + 2hxy + by² = 0 is twice that of the other, show that 8h² = 9ab.
Answer:
The equation of the given straight line is
ax² + 2hxy + by² = 0 ………… (1)
Given that the slopes of the straight lines are m and 2m

Question 9.
The slope of one of the straight lines ax² + 2h xy + by² = 0 is three times the other, show that 3h² = 4ab.
Answer:
The equation of the given straight line is
ax² + 2hxy + by² = 0 ……….. (1)
Given that the slopes of the lines are m and 3m.

Question 10.
A ∆ OPQ is formed by the pair of straight lines x² – 4xy + y² = 0 and the line PQ. The equation of PQ is x + y – 2 = 0, Find the equation of the median of the triangle ∆ OPQ drawn from the origin O
Answer:

The equation of the given pair of lines is
x² – 4xy + y² = 0 ……….. (1)
The equation of the line PQ is
x + y – 2 = 0
y = 2 – x ……….. (2)
To find the coordinates of P and Q, .
Solve equations (1) and (2)
(1) ⇒ x² – 4x ( 2 – x) + ( 2 – x)² = 0
x² – 8x + 4x² + 4 – 4x + x² = 0
6x² – 12x + 4 = 0
3x² – 6x + 2 = 0

The midpoint of PQ is

The equation of the median drawn from 0 is the equation of the line joining 0 (0, 0) and D (1, 1)

∴ The required equation is x = y

Question 11.
Find p and q, if the following equation represents a pair of perpendicular lines
6x² + 5xy – py² + 7x + qy – 5 = 0
Answer:
The equation of the given pair of straight lines is
6x² + 5xy – py² + 7x + qy – 5 = 0 ……….. (1)
Given that equation (1) represents a pair of perpendicular straight lines.
∴ Coefficient of x² + coefficient of y² = 0
6 – p = 0 ⇒ p = 6
6x² + 5xy – 6y² = 6x² + 9xy – 4xy – 6y²
= 3x(2x + 3y) – 2y (2x + 3y)
= (2x + 3y) (3x – 2y)
Let the separate equation of the straight lines be
2x + 3y + 1 = 0 and 3x – 2y + m = 0
6x² + 5xy – 6y² + 7x + qy – 5
= (2x + 3y + 1)(3x – 2y + m)
Comparing the coefficients of x , y and constant terms on both sides
2m + 3l = 7 ………… (2)
3m – 2l = q ……….. (3)
lm = – 5 …….. (4)
Equation (4) ⇒ l = 1, m = – 5
or l = – 1, m = 5
When l = 1, m = – 5 , equation (2) does not satisfy.
∴ l = – 1 , m = 5
Substituting in equation (3)
3 (5) – 2(-1) = q ⇒ q = 17
∴ The required values are p = 6, q = 17

Question 12.
Find the value of k, if the following equation represents a pair of straight lines. Further, find whether these lines are parallel or intersecting
12x² + 7xy – 12y² – x +7y + k = 0
Answer:
The equation of the given pair of straight lines is
12x² + 7xy – 12y² – x + 7y + k = 0 ………. (1)
Compare this equation with the equation
ax² + 2hxy + by² + 2gx + 2f y + c = 0 ……….. (2)
a = 12, 2h = 7 , b = – 12 ,
2g = – 1, 2f = 7, k = c
a = 12, h = \(\frac{7}{2}\), b = – 12,
g = \(-\frac{1}{2}\), f = \(\frac{7}{2}\), c = k
The condition for a second degree equation in x and y to represent a pair of straight lines is
abc + 2fgh – af² – bg² – ch² = 0
Substituting the values


Coefficient of x² + coefficient of y² = 12 – 12 = 0
∴ The given pair of straight lines are perpendicular and hence they are intersecting lines.

Question 13.
For what values of k does the equation
12x² + 2kxy + 2y² +11x – 5y + 2 = 0 represent two straight lines.
Answer:
The given equation of the pair of straight line is
12x² + 2kxy + 2y² + 11x – 5y + 2 = 0 ……… (1)
Compare this equation with the equation
ax² + 2hxy + by² + 2gx + 2fy + c = 0 ………. (2)
a = 12, 2h = 2k, b = 2,
2g = 11, 2f = – 5 , c = 2 ,
a =12, h = k, b = 2,
g = \(\frac{11}{2}\), f = –\(\frac{5}{2}\), c = 2,
The condition for a second degree equation in x and y to represent a pair of straight lines is
abc + 2fgh – af² – bg² – ch² = 0

96 – 55k – 150 – 121 – 4k² = o
– 4k² – 55k – 175 = 0
4k² + 55k + 175 = 0

∴ The given equation represents a pair of straight lines when
k = – 5 and k = \(\frac{-35}{4}\)

Question 14.
Show that the equation 9x² – 24xy + 16y² – 12x + 16y – 12 = 0 represents a pair of parallel lines. Find the distance between them.
Answer:
The given equation of the pair of straight line is
9x² – 24xy + by² – 12x + 16y – 12 = 0 ………… (1)
9x² – 24xy + 16y² = 9x² – 12xy – 12xy + 16y²
= 3x (3x – 4y) – 4y (3x – 4y)
= (3x – 4y) (3x – 4y)
Let the separate equation of the straight lines be
3x – 4y + 1 = 0 and 3x – 4y + m = 0
9x² – 24xy + 16y² – 12x + 16y – 12
= (3x – 4y + l) ( 3x – 4y + m )
Comparing the coefficients of x , y and constant terms on both sides
3l + 3m = – 12
l + m = – 4 ……….. (2)
– 4l – 4m = 16
l + m = – 4 ………… (3)
lm = – 12 ……….. (4)
(l – m)² = (l + m)² – 4lm
= (- 4)² – 4 × – 12
= 16 + 48 = 64
l – m = √64 = 8
l – m = 8 ………… (5)
Solving equations (2) and (5 ), we have

(2) ⇒ 2 + m = – 4 ⇒ m = – 6
∴ l = 2 and m = – 6
∴ The separate equation of the straight lines are
3x – 4y – 6 = 0 and 3x – 4y + 2 = 0
The distance between the parallel lines is given by

∴ The given pair of straight lines are parallel and the distance between them is \(\frac{8}{5}\) units

Question 15.
Show that the equation 4x² + 4xy + y² – 6x – 3y – 4 = 0 represents a pair of parallel lines. Find the distance between them.
Answer:
The given equation of pair of straight lines is
4x² + 4xy + y² – 6x – 3y – 4 = 0 ………. (1)
4x² + 4xy + y² = (2x + y)²
Let the separate equation of the lines be
2x + y + l = 0 ……….. (2)
2x + y + m = 0 ………. (3)
4x² + 4xy + y² – 6x – 3y – 4 = (2x + y + l) (2x + y + m)
Comparing the coefficients of x , y and constant terms on both sides we have
2l + 2m = – 6
l + m = – 3 ……… (4)
l + m = – 3 ……… (5)
l m = – 4 ……… (6)
(l – m)² = (l + m)² – 4lm
(l – m )² = (- 3)² – 4 × – 4
(l – m)² = 9 + 16 = 25
l – m = 5 ………… (7)
Solving equations (4) and (7)

(4) ⇒ l + m = – 3 ⇒ m = – 4
∴ The separate equation of the straight lines are
2x + y + 1 =0 and 2x + y – 4 = 0
The distance between the parallel lines is

d = \(\frac{5}{\sqrt{5}}\) = \(\sqrt{5}\)
∴ The given equation represents a pair of parallel straight lines and the distance between the parallel lines is \(\sqrt{5}\) units.

Question 16.
Prove that one of the straight lines given by ax² + 2hxy + by² = 0 will bisect the angle between the coordinate axes if (a + b)² = 4h²
Answer:
The equation of the given pair of straight lines is
ax² + 2hxy + by² = 0 ……… (1)
Let m₁ and m₂, be the slopes of the separate straight lines.
Given that one of the straight lines of (1) bisects the angle between the coordinate axes.
∴ The angle made by that line with x-axis 45°.
Slope of that line m₁ = tan 45°
m₁ = 1

Squaring on both sides
(a + b)² = (- 2h)²
(a + b)² = 4h²

Question 17.
If the pair of straight lines x² – 2kxy – y² = 0 bisects the angle between the pair of straight lines x² – 2lxy – y² = 0. Show that the later pair also bisects the angle between the former.
Answer:
The equations of the given pair of straight lines are
x² – 2kxy – y² = 0 ………… (1)
x² – 2lxy – y² = 0 ………… (2)
Given that the pair x² – 2kxy – y² = 0 bisects the angle between the pair x² – 2lxy – y² = 0
∴ The equation of the bisector of the pair
x² – 2lxy – y² = 0 is the pair x² – 2kxy – y² = 0
The equation of the bisector of x² – 2lxy – y² = 0 is

Equation (3) and Equation (1) represents the same straight lines. ∴ The coefficients are proportional.

To show that the pair x² – 2lxy – y² = 0 bisects the angle between the pair x² – 2kxy – y² = 0, it is enough to prove the equation of the bisector of x² – 2kxy – y² = 0 is x² – 2lxy – y² = 0
The equation of the bisector of x² – 2kxy – y² = 0 is

x² – y² = 2lxy .
x² – 2lxy – y² = 0
∴ The pair x² – 2lxy – y² = 0 bisects the angle between the pair x² – 2kxy – y² = 0

Question 18.
Prove that the straight lines joining the origin to the points of intersection of 3x² + 5xy – 3y² + 2x + 3y = 0 and 3x – 2y – 1 = 0 are at right angle.
Answer:
Homogenizing the given equations 3x² + 5xy – 3y² + 2x + 3y = 0 and 3x – 2y – 1 = 0
(i.e) 3x – 2y = 1.
We get (3x² + 5xy – 3y²) + (2x + 3y)( 1) = 0
(i.e) (3x² + 5xy – 3y²) + (2x + 3y)(3x – 2y) = 0
3x² + 5xy – 3y² + bx² – 4xy + 9xy – 6y² = 0
9x² + 10xy – 9y² = 0
Coefficient of x² + coefficient of y² = 9 – 9 = 0
⇒ The pair of straight lines are at right angles.

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 6 Two Dimensional Analytical Geometry Ex 6.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.3

Question 1.
Show that the lines 3x + 2y + 9 = 0 and 12x + 8y – 15 = 0 are parallel lines.
Answer:
The equations of the given lines are
3x + 2y + 9 = 0 ——- (1)
12x + 8y – 15 = 0 ——- (2)

m₁ = m₂
∴ The given lines are parallel.

Question 2.
Find the equation of the straight line parallel to 5x – 4y + 3 = 0 and having x – intercept 3.
Answer:
The equation of any line parallel to 5x – 4y + 3 = 0 is
5x – 4y + k = 0 ……….. (1)
The x – intercept of line (I) is obtained by putting
y = 0 in the equation.
(1) ⇒ 5x – 4(0) + k = 0
5x = – k ⇒ x = \(-\frac{k}{5}\)
Given that the x – intercept in 3
∴ \(-\frac{k}{5}\) = 3 ⇒ k = – 15
∴ The equation of the required line is
5x – 4y – 15 = 0

Question 3.
Find the distance between the line 4x + 3y + 4 = 0 and a point
(i) (- 2, 4)
(ii) (7, – 3)
Answer:
(i) The distance between the line ax + by + c = 0 and the point (x₁, y₁) is d = \(\frac{a x_{1}+b y_{1}+c}{\sqrt{a^{2}+b^{2}}}\)
Here (x₁, y₁) = (- 2, 4) and the equation of the line is 4x + 3y + 4 = 0

(ii) Given point (x₁, y₁) = (7, – 3)
Given line 4x + 3y + 4 = 0

Question 4.
Write the equation of the lines through the point (1, – 1)
(i) Parallel to x + 3y – 4 = 0
(ii) Perpendicular to 3x + 4y = 6
Answer:
(i) Any line parallel to x + 3y – 4 = 0 will be of the form x + 3y + k = 0.
It passes through (1,-1) ⇒ 1 – 3 + k = 0 ⇒ k = 2
So the required line is x + 3y + 2 = 0

(ii) Any line perpendicular to 3x + 4y – 6 = 0 will be of the form 4x – 3y + k = 0.
It passes through (1, -1) ⇒ 4 + 3 + k = 0 ⇒ k = -7.
So the required line is 4x – 3y – 7 = 0

Question 5.
If (- 4, 7 ) is one vertex of a rhombus and if the equation of one diagonal is 5x – y + 7 = 0 then find the equation of another diagonal.
Answer:

In a rhombus, the diagonal cut at right angles.
The given diagonal is 5x – y + 7 = 0 and (- 4, 7) is not a point on the diagonal.
So it will be a point on the other diagonal which is perpendicular to 5x – y + 7 = 0.
The equation of a line perpendicular to 5x – y + 7 = 0 will be of the form x + 5y + k = 0.
It passes through (-4, 7) ⇒ -4 + 5(7) + k = 0 ⇒ k = -31
So the equation of the other diagonal is x + 5y – 31 = 0

Question 6.
Find the equation of the lines passing through the point of intersection of the lines 4x – y + 3 = 0 and 5x + 2y + 7 = 0 and
(i) through the point (-1,2)
(ii) parallel to x – y + 5 =0
(iii) perpendicular to x – 2y + 1 =0
Answer:
The equation of the straight line passing through the point of intersection of the lines.
4x – y + 3 = 0 and 5x + 2y + 7 = 0 is
( 4x – y + 3) + λ (5x + 2y + 7) = 0 ……… (1)

(i) Through the point (-1,2)
Given that line(1) passes through the point (-1, 2)
(1) ⇒ (4(-1) – 2 + 3) + λ (5(- 1) + 2(2) + 7) = 0
(-4 – 2 + 3) + λ (-5 + 4 + 7) = 0
– 3 + 6 λ = 0 ⇒ λ = \(\frac{3}{6}\) = \(\frac{1}{2}\)
∴ The equation of the required line is
(4x – y + 3) + \(\frac{1}{2}\) (5x + 2y + 7) = 0
2(4x – y + 3) + (5x + 2y + 7) = 0
8x – 2y + 6 + 5x + 2y + 7 = 0
13x +13 = 0 ⇒ x + 1 = 0

(ii) Equation of a line parallel to x – y + 5 = 0 will be of the form x – y + k = 0.
It passes through (-1, -1) ⇒ -1 + 1 + k = 0 ⇒ k = 0.
So the required line is x – y = 0 ⇒ x = y.

(iii) Perpendicular to x – 2y + 1 = 0
Given that the line (1) perpendicular to the line
x – 2y + 1 = 0 ………….. (3)
(1) ⇒ (4x – y + 3) + λ (5x + 2y + 7) = 0
4x – y + 3 + 5λx + 2λy + 7λ = 0
(4 + 5λ)x + (2λ – 1 )y + (3 + 7λ) = 0 ……….. (4)
Slope of this line (3) = \(-\frac{4+5 \lambda}{2 \lambda-1}\)
Slope of line (2) = \(-\frac{1}{-2}=\frac{1}{2}\)
Given that line (3) and line (4) are perpendicular

4 + 5λ = 2(2λ – 1 )
4 + 5λ = 4λ – 2
λ = – 6
Substituting the value of λ in equation (1) we have
(4x – y + 3) – 6 (5x + 2y + 7) = 0
4x – y + 3 – 30x – 12y – 42 = 0
-26x – 13y – 39 =0
2x + y + 3 = 0
which is the required equation.

Question 7.
Find the equations of two straight line which are parallel to the line 12x + 5y + 2 = 0 and at a unit distance from the point (1, – 1).
Answer:
The equation of the given line is
12x + 5y + 2 = 0 ……… (1)
Equation of any line parallel to the line (1) is
12x + 5y + k = 0 ………. (2)
Given that line (2) is at a unit distance from the point (1, – 1)

k = – 7 ± 13
k = -7 + 13 or k = – 7 – 13
k = 6 or k = – 20
∴ The equation of the required lines are
12x + 5y + 6 = 0 and 12x + 5y – 20 = 0

Question 8.
Find the equations of straight lines which are perpendicular to the line 3x + 4y – 6 = 0 and are at a distance of 4 units from (2, 1).
Answer:
The equation of the given line is
3x + 4y – 6 = 0 …………. (1)
The equation of any line perpendicular to line (1) is
4x – 3y + k = 0 …………. (2)
Given that this line is 4 units from the point (2, 1)

± 4 = \(\frac{5+k}{5}\)
5 + k = ± 20
k = ± 20 – 5
k = 20 – 5 or k = -20
k = 15 or k = -25
∴ The equation of the required lines are
4x – 3y + 15 = 0 and 4x – 3y – 25 = 0

Question 9.
Find the equation of a straight line parallel to 2x + 3y = 10 and which is such that the sum of its intercepts on the axes is 15.
Answer:
The equation of the given line is
2x + 3y = 10 ………….. (1)
The equation of any line parallel to (1) is
2x + 3y = k …………. (2)

Given that the sum of the intercepts of the line (2) on the axes is 15

∴ The equation of the required line is 2x + 3y = 18

Question 10.
Find the length of the perpendicular and the coordinates of the foot of the perpendicular from (-10, -2) to the line x + y – 2 = 0.
Answer:
The coordinate of the foot of the perpendicular from the point (x₁, y₁) on the line ax + by + c = 0 is

∴ The coordinate of the foot of the perpendicular from the point (- 10, – 2) on the line x + y – 2 = 0 is

x + 10 = y + 2 = \(\frac{14}{2}\)
x + 10 = y + 2 = 7
x + 10 = 7, y + 2 = 7
x = – 3, y = 5
∴ The required foot of the perpendicular is (- 3, 5).
Length of the perpendicular

Question 11.
If p₁ and p₂ are the lengths of the perpendiculars from the origin to the straight lines x sec θ + y cosec θ = 2a and x cos θ – y sin θ = a cos 2θ, then prove that p₁² + p₂² = a².
Answer:
Given P₁ is the length of the perpendicular from the origin to the straight line
x sec θ + y cosec θ – 2a = 0

Also given P₂ is the length of the perpendicular from the origin to the straight line
x cos θ – y sin θ – a cos 2θ = 0

Question 12.
Find the distance between the parallel lines
(i) 12x + 5y = 7 and 12x + 5y + 7 = 0
(ii) 3x – 4y + 5 = 0 and 6x – 8y – 15 = 0
Answer:
(i) 12x + 5y = 7 and 12x + 5y + 7 = 0
The equation of the given lines are
12x + 5y – 7 = 0 ……….. (1)
12x + 5y + 7 = 0 ……….. (2)
The distance between the parallel lines
ax + by + c₁ = 0 and ax + by + c₂ = 0 is
The equation of any line parallel to (1) is

The distance cannot be negative
∴ Required distance = \(\frac{14}{13}\)

(ii) 3x – 4y + 5 = 0 and 6x – 8y -15 = 0
The equation of the given lines are
3x – 4y + 5 = 0 ……….. (1)
6x – 8y – 15 = 0
3x – 4y – 1 = 0 ………… (2)
The distance between the parallel lines (1) and (2) is

Question 13.
Find the family of straight lines
(i) Perpendicular
(ii) Parallel to 3x + 4y – 12
Answer:
(i) Equation of lines perpendicular to 3x + 4y – 12 = 0 will be of the form 4x – 3y + k = 0, k ∈ R
(ii) Equation of lines parallel to 3x + 4y – 12 = 0 will be of the form 3x + 4y + k = 0, k ∈ R

Question 14.
If the line joining two points A (2, 0) and B (3, 1) is rotated about A in an anticlockwise direction through an angle of 15° , then find the equation of the line in the new position.
Answer:

Slope of the line AB
m = tan θ = \(\frac{1-0}{3-2}\)
tan θ = 1
θ = 45°
∴ The line AB makes an angle 45° with x-axis.
Given that the line AB is rotated through an angle of 15° about the point A in the anticlockwise direction.
∴ The angle made by the new line AB’ is 45° + 15° = 60°
Slope of the new line AB’ is m₁ = tan 60° = √3
∴ The equation of the new line AB’ is the equation of the straight line passing through the point A (2, 0) and having slope m₁ = √3
y – 0 = √3 (x – 2)
y = √3x – 2√3
√3x – y – 2√3 = 0

Question 15.
A ray of light coming from the point (1, 2) is reflected at a point A on the x – axis and it passes through the point (5, 3). Find the coordinates of point A.
Answer:

Let P(1, 2) and (5, 3) are the given points.
By the property of reflection,
∠XAB = ∠OAP = θ
(Angle of incidence = Angle of reflection)
Slope of the line OA (x – axis) m₁ = 0
Slope of the line joining the points P (1, 2) and A (x, 0)
Slope of AP, m₂ = \(\frac{2-0}{1-x}=\frac{2}{1-x}\)
Slope of the line joining the points B (5, 3 ) and A (x, 0)
Slope of AP, m₃ = \(\frac{3-0}{5-x}=\frac{3}{5-x}\)

From equations (1) and (2)
\(\frac{3}{5-x}\) = –\(\frac{2}{1-x}\)
3(1 – x) = – 2 (5 – x)
3 – 3x = – 10 + 2x
2x + 3x = 10 + 3
5x = 13 ⇒ x = \(\frac{13}{5}\)
∴ The required point A is \(\left(\frac{13}{5}, 0\right)\)

Question 16.
A line is drawn perpendicular to 5x = y + 7. Find the equation of the line if the area of the triangle formed by this line with co-ordinate axes is 10. sq. units.
Answer:

Let the given line be PQ whose equation is
5x = y + 7
5x – y – 7 = 0 ——- (1)
Let AB be the line perpendicular to the line PQ such that the area of the triangle OAB is 10 units.
The equation of the line AB is
– x – 5y + k = 0
x + 5y – k = 0
x + 5y = k ——- (2)

∴ A is (k, 0) and B is (0, \(\frac{\mathrm{k}}{5}\))
OA = k and OB = \(\frac{\mathrm{k}}{5}\)
Area of ∆OAB = \(\frac{1}{2}\) × OA × OB
= \(\frac{1}{2}\) × k × \(\frac{\mathrm{k}}{5}\)
Given area of ∆ OAB = 10
∴ \(\frac{\mathrm{k}^{2}}{10}\) = 10
k² = 100 ⇒ k = ±10
∴ The required equation of the straight line is
x + 5y = ±10

Question 17.
Find the image of the point (- 2, 3) about the line x + 2y – 9 = 0.
Answer:
The image of the point (x₁, y₁) about the line ax + by + c = 0 is

∴ The image of the point (- 2, 3) about the line x + 2y – 9 = 0 is

∴ The required point is (0, 7)

Question 18.
A photocopy store charges ₹ 1.50 per copy for the first 10 copies and ₹ 1.00 per copy after the 10^th copy. Let x be the number of copies, and y be the total cost of photo coping.
(i) Draw graph the cost as x goes from 0 to 50 copies
(ii) Find the cost of making 40 copies.
Answer:
(i) Draw graph of the cost as x goes from 0 to 50 copies:
Let x represent the number of copies and y represent the cost of photocopying.
Given photo copying charge for 1 copy is Rs. 1.50 for the first 10 copies and Rs. 1.00 per copy after the 10^th copy.
∴ The relation connecting the number of copies and cost of photocopying charge is given by
y = 1.50x, 0 ≤ x ≤ 10
y = 10(1.50) + (x – 10) (1)
y = 15 + x – 10
y = x + 5 ………… (1)

The graph for 0 to 50 copies:

When x = 10, y = 1.50 × x
⇒ y = 1.50 × 10 = 15
The corresponding point is (10 , 15)
When x = 20, y = x + 5
⇒ y = 20 + 5 = 25
The corresponding point is (20 , 25)
When x = 30, y = x + 5
⇒ y = 30 + 5 = 35
The corresponding point is (30, 35)
When x = 40, y = 40 + 5 = 45
The corresponding point is (40, 45 )
When x = 50, y = 50 + 5 = 55
The corresponding point is (50, 55 )
The cost of 40 copies is the value of y
When x = 40 , y = 40 + 5 = 45 rupees
Cost of 40 copies = 45 rupees

Question 19.
Find at least two equations of the straight lines in the family of file lines y = 5x + b for which b and the x – coordinate of the point of intersection of the lines with 3x – 4y = 6 are integers.
Answer:
The equations of the given straight lines are
y = 5x + b ……….. (1)
3x – 4y = 6 ……….. (2)
To find atleast two equations from the family y = 5x + b for which b is an integer and x – coordinate of the point of intersection of (1) and (2) is an integer. Solving (1)and (2) using equation (1) inequation (2) (2) ⇒ 3x – 4 (5x + b) = 6
3x – 20x – 4b = 6
-17x = 6 + 4b

The corresponding equation of the line is = 5x + 7
When b = – 10, we have x = \(\frac{6-40}{-17}\)
= \(\frac{-34}{-17}\) = 2
The corresponding equation of the line is y = 5x – 10
Thus y = 5x + 7 and y = 5x – 10 are the two straight lines belonging to the family such that b is an integer and the x – coordinate of the point of intersection with the line (2) is an integer.

Question 20.
Find all the equations of the straight lines in the family of the lines y = mx – 3 for which m and the x – coordinate of the point of intersection of the lines with x – y = 6 are integers.
Answer:
The equations of the given lines are
y = mx – 3 ………. (1)
x – y = 6 ………. (2)
Solving equations (1) and (2)
(2) ⇒ x – (mx – 3 ) = 6
x – mx + 3 = 6
x (1 – m) = 3
x = \(\frac{3}{1-\mathrm{m}}\) …….. (3)
From equation (3) let us find the values of x and m for which they are integers. The only values of m for which , x is an integer are m = 0, 2, -2
When m = 0, x = \(\frac{3}{1-0}\) = 3
The corresponding equation is
y = 0 . x – 3
y + 3 = 0

When m = 2, x = \(\frac{3}{1-2}\) = \(\frac{3}{-1}\) = – 3
The corresponding equation is y = -2x + 3
2x + y – 3 = 0

When m = – 2, x = \(\frac{3}{1+2}\) = \(\frac{3}{3}\) = 1
The corresponding equation is
y = – 2 x + 3
2x + y – 3 = 0
∴ The required equations of the lines are
y + 3 = 0 , 2x – y – 3 = 0 and
2x + y – 3 = 0

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 6 Two Dimensional Analytical Geometry Ex 6.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.2

Question 1.
Find the equation of the lines passing through the point (1, 1):
(i) with y – intercept – 4
(ii) with slope 3
(iii) and (-2, 3)
(iv) and the perpendicular from the origin makes an angle 60° with x – axis.
Answer:
(i) with y – intercept – 4
The equation the line with slope m and having y – intercept b is y = mx + b ——- (1)
Given b = – 4
∴ (1) ⇒ y = m x – 4
Given this line passes through the point (1, 1)
∴ 1 = m 1 – 4 ⇒ m = 5
∴ The required equation is y = 5x – 4

(ii) Slope m = 3, passing through (x₁, y₁) = (1, 1)
Equation of the line is y – y₁ = m(x – x₁)
(i.e) y- 1 = 3(x – 1) ⇒ y – 1 = 3x – 3 ⇒ 3x – y = 2

(iii) (-2, 3)
The equation of line joining the two points (x₁, y₁) and (x₂, y₂) is

Given (x₁, y₁) = (1, 1), (x₂, y₂) = (- 2, 3)
∴ The equation of the required line is

– 3 (y – 1) = 2 (x – 1)
– 3y + 3 = 2x – 2
2x + 3y – 2 – 3 = 0
2x + 3y – 5 = 0

(iv) The perpendicular from the origin makes an angle 60° with x – axis
The equation of the line in the normal form is x cos α + y sin α = p ——- (1)
Given α = 60°
∴ cos 60° = \(\frac{1}{2}\) , sin 60° = \(\frac{\sqrt{3}}{2}\)
(1) ⇒ x . \(\frac{1}{2}\) + y . \(\frac{\sqrt{3}}{2}\) = p
x + √3 = 2p —— (2)
This line passes through the point (1,1)
∴ 1 + √3 = 2p
Substituting for p in equation (2)
∴ The required equation is x + √3y = 1 + √3

Question 2.
If P (r, c) is mid point of a line segment between the axes then show that \(\frac{x}{\mathbf{r}}+\frac{\mathbf{y}}{\mathbf{c}}\) = 2
Answer:
Let AB be the line segment intercepted between the axes. Let A be (a, 0) and B be (0, b)

Given P (r, c) is the mid point of AB

The equation of the line AB having x-intercept a and y-intercept b is \(\frac{x}{a}+\frac{y}{b}\) = 1
Substituting for a, b in the above equation, we have

Question 3.
Find the equation of the line passing through the point (1, 5) and also divides the line segment between the coordinate axes in the ratio 3 : 10.
Answer:
Let the line divide the coordinate axis in the ratio 3 : 10.
∴ x-intercept = 3k
y-intercept = 10k
∴ The equation of the straight line is \(\frac{x}{3 k}+\frac{y}{10 k}\) = 1
This line passes through the point P (1, 5).

∴ The required equation is

Question 4.
If p is length of perpendicular from origin to the line whose intercepts on the axes are a and b, then show that \(\frac{1}{\mathbf{p}^{2}}=\frac{1}{\mathbf{a}^{2}}+\frac{1}{\mathbf{b}^{2}}\)
Answer:
The equation of the line with x – intercept a and y – intercept b is \(\frac{x}{a}+\frac{y}{b}\) = 1 ——- (1)
The length of the perpendicular from the origin (0, 0) to the line (1) is

Question 5.
The normal boiling point of water is 100° C or 212° F and the freezing point of water is 0° C or 32° F.
(i) Find the linear relationship between C and F. Find
(ii) the value of C for 98.6° F and
(iii) the value of F for 38° C.
Answer:
(i) Choose Celsius degree along the x-axis and Fahrenheit degree along the y-axis.
Given a Freezing point in Celsius = 0°C
The freezing point in Fahrenheit degree = 32° F
∴ The Freezing point is (0°, 32°)
Also given Boiling point in Celsius = 100°C
The boiling point in Fahrenheit = 212° F
∴ The Boding point is (100°, 212°)
Let C denote the Celsius degree and F denote the Fahrenheit degree.
The equation of the path connecting the freezing point (0°, 32°) and the boiling point (100°, 212° ) is

which is the required relation connecting C and F.

(ii) To find the value of C for 98.6° F
(1) For 98.6° F To find C.

(iii) To find the value of F for 38° C,
For 38° C To find F

Question 6.
An object was launched from a place P in constant speed to hit a target. At the 15^th second, it was 1400 m from the target, and at the 18^th second 800 m away. Find
(i) the distance between the place and the target
(ii) The distance covered by it in 15 seconds
(iii) time taken to hit the target.
Answer:
Let us take the time T along the x-axis and the Distance D along the y-axis.
Given when time T = 15 s , the distance D = 1400 m
The corresponding point is (15, 1400)
Also when time T = 18 s , the distance D = 800 m.
The corresponding point is (18, 800)

(i) The distance between the place and the target:
∴ The relation connecting T and D is the equation of the straight line joining the points (15, 1400) and (18, 800)

To find the distance between the target and the place, Put T = 0 in equation (1)

4400 – D = 0 ⇒ D = 4400 m.
Required distance = 4400 m.

(ii) The distance covered by it in 15 seconds:
Put T = 15 in the above equation
15 = \(\frac{1400-\mathrm{D}}{200}\) + 15
∴ \(\frac{1400-\mathrm{D}}{200}\) = 0 ⇒ D = 1400 m.

(iii) Time taken to hit the Target:
When the target is reached D = 0
∴ (1) ⇒ T = \(\frac{1400-0}{200}\) + 15
T = \(\frac{1400}{200}\) + 15
T = 7 + 15 = 22 seconds
∴ The time taken to hit the target is 22 seconds

Question 7.
The population of the city in the years 2005 and 2010 are 1, 35, 000 and 1, 45, 000 respectively. Find the approximate population in the year 2015. (assuming that the growth of population is constant).
Answer:
Let us choose the year along the x-axis and the population of the city along the y-axis.
Given In the year 2005 population is 1,35,000
The corresponding point is (2005, 1,35,000)
In the year 2010, population is 1,45,000
The corresponding point is (2010, 1,45,000)
Let Y denote the year and P denote the population.
The relation connecting Y and P is the equation of the straight line joining the points (2005, 1,35,000) and (2010, 1,45,000)

When y = 2015

P = 1,35,000 + 10 × 2,000
P = 1,35,000 + 20,000 = 1,55,000
∴ The population in the year 2015 is 1,55,000

Question 8.
Find the equation of the line if the perpendicular drawn from the origin makes an angle 30° with x – axis and its length is 12.
Answer:
Given length of the perpendicular p = 12
Angle made by the perpendicular α = 30°
The equation the straight line in the normal form is
x cos α + y sin α = p
∴ The required equation of the straight line is
x cos 30° + y sin 30° = 12
x\(\frac{\sqrt{3}}{2}\) + y × \(\frac{1}{2}\) = 12
√3x + y = 24

Question 9.
Find the equation of the straight lines passing through (8, 3) and having intercepts whose sum is 1.
Answer:
Let a and b be the x and y-intercepts of the line.
Given a + b = 1
b = 1 – a —— (1)
The equation of the straight line is

The line passes through the point (8, 3)

8(1 – a) + 3a = a(1 – a)
8 – 8a + 3a = a – a²
a² – 5a + 8 – a = 0
a² – 6a + 8 = 0
a² – 4a – 2a + 8 = 0
a(a – 4) – 2(a – 4) = 0
(a- 4) (a – 2) = 0
a = 4 or a = 2
When a = 2, b = 1 – 2 = – 1
When a = 4, b = 1 – 4 = – 3
∴ The equation of the straight lines are
x – 2y = 2 and 3x – 4y = 12

Question 10.
Show that the points (1, 3), (2, 1) and \(\left(\frac{1}{2}, 4\right)\) are collinear, by using
(i) concept of slope
(ii) using a straight line and
(iii) any other method.
Answer:
Let the given points be A (1 , 3), B (2 , 1) and \(\left(\frac{1}{2}, 4\right)\)

(i) Slope Method:
A (1 , 3 ), B (2 , 1 ), C\(\left(\frac{1}{2}, 4\right)\)

From equations (1) and (2)
Slope of AB = Slope of BC
∴ The given points A, B, C are collinear.

(ii) Using a straight line
A(1 , 3) , B(2 , 1) , C\(\left(\frac{1}{2}, 4\right)\)
The equation of the straight line joining the points
A( 1 , 3) , B(2 , 1) is

-2(x- 1) = y – 3
– 2x + 2 = y – 3
2x + y – 2 – 3 = 0
2x+ y – 5 = 0 ——- (2)
Substituting the third point C \(\left(\frac{1}{2}, 4\right)\) in equation (2)
we have 2\(\left(\frac{1}{2}\right)\) + 4 – 5 = 0
1 + 4 – 5 = 0
0 = 0
∴ The third point C\(\left(\frac{1}{2}, 4\right)\) lies on the straight line AB.
Hence the points A , B , C are collinear.

(iii) Distance method:
A(1 , 3) , B(2 , 1) , C\(\left(\frac{1}{2}, 4\right)\)


Thus BA + AC = BC
∴ The points A, B, C are collinear.

Question 11.
A straight line is passing through the point A (1, 2) with slope \(\frac{5}{12}\). Find the points on the line which are 13 units away from A.
Answer:
Slope of the line m = tan θ = \(\frac{5}{12}\)
sin θ = \(\frac{5}{13}\), cos θ = \(\frac{12}{13}\)

The parametric equation of the line passing through the point (1, 2) making angle θ with x – axis is

Any point on this line is

(1 + r cos θ, 2 + r sin θ) ……… (1)
where r is the distance of any point from A (1, 2) on the line.
To find the point which is 13 units away from A (1, 2) on the line.

Substitute r = ± 13, cos θ = \(\frac{12}{13}\), sin θ = \(\frac{5}{13}\) in equation (1)
Required point = \(\left(1 \pm 13\left(\frac{12}{13}\right), 2 \pm 13\left(\frac{5}{13}\right)\right)\)
= (1 ± 12, 2 ± 5)
= (1 + 12, 2 + 5)
= (1 + 12, 2 + 5) or (1 – 12, 2 – 5)
= (13, 7) or (- 11, – 3)

Question 12.
A 150 m long train is moving with a constant velocity of 12.5 m/s.
(i) The equation of motion of the train.
(ii) Time taken to cross a pole.
(iii) The time to cross the bridge of length 850m is?
Answer:
Length of the train = 150 m
Constant velocity of the train = 12.5 m/s

(i) The equation of motion of the train:
Take time in seconds along the x-axis and distance in meters along the y-axis.
Let the train be at the origin.
∴ Length of the train = 150 m is the negative y-intercept
b = -150
The slope of the motion of the train m = 12.5 m/s
The equation of the line with slope-intercept form is
y = mx + b
∴ y = 12.5x – 150
which is the required equation of motion of the train.

(ii) Time taken to cross a pole:
The equation of motion is y = 12.5 x – 150
To find the time taken to cross the pole, Put y = 0
0 = 12.5 x – 150 ⇒ 12.5 x = 150
⇒ x = \(\frac{150}{12.5}\) = 12 sec

(iii) The time taken to cross the bridge of length 850 m
The equation of motion is y = 12.5 x – 150
To find the time taken to cross the bridge of length 850 m, put y = 850
850 = 12.5 x – 150
12.5 x = 850 + 150 = 1000
x = \(\frac{1000}{12.5}=\frac{10000}{125}\) = 80 sec

Question 13.
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time shown in the following table.

(a) Draw a graph showing the results.
(b) Find the equation relating the length of the spring to the weight on it.
(c) What is the actual length of the spring?
(d) If the spring stretches to 9 cm long, how much weight should be added?
(e) How long will the spring be when 6 kilograms of weight on it?
Answer:
Choose the weight along the x-axis and Length along the y-axis.
(a)

(b) The points are(2, 3), (4, 4), (5, 4.5), (8, 6) The relation connecting weight and Length is the equation of the straight line joining the points (2, 3) and (4, 4)

x – 2 = 2(y – 3)
x – 2 = 2y – 6
x – 2y + 6 – 2 = 0
x – 2y + 4 = 0 —– (1)
which the required relation connecting weight and length.

(c) To find the actual length of the spring, put weight x = 0 in equation (1)
0 – 2y + 4 = 0 ⇒ 2y = 4 ⇒ y = 2
∴ The actual length of the spring is 2 cm.

(d) If the spring stretch to 9 cm long, To find the required weight, put y = 9, in equation (1)
(1) ⇒ x – 2 (9) + 4 = 0
x – 18 +4 = 0 ⇒ x = 14
Weight to be added is 14 kg.

(e) Next we find the length of the string when a weight of 6 kg is added.
Put x = 6 in equation (1)
6 – 2y + 4 = 0 ⇒ 2y = 10 ⇒ y = 5cm
∴ Required length is 5 cm.

Question 14.
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (Full weight 29.5 kg includes the empty cylinders tare weight of 15.3 kg.). If it is used at a constant rate, then it lasts for 24 days. Then the new cylinder is replaced
(i) Find the equation relating the quantity of gas in the cylinder to the days,
(ii) Draw the graph for the first 96 days.
Answer:
(i) Find the equation relating the quantity of gas in the cylinder to the days.
Given Total weight of cylinder = 29.5 kg
Weight of the gas inside the cylinder = 14.2 kg
Let x denote the number of days of consumption of the gas, y denote the quantity of gas inside a cylinder.
Initially x = 0 then y = 14.2
The corresponding point is (0, 14.2)
The gas inside the cylinder lasts for 24 days
∴ When x = 24, we have y = 0
The corresponding point is (24, 0)
∴ The linear relation between the quantity of gas in the cylinder to the number of days of consumption is the equation of the line joining the points (0, 14.2 ) and (24, 0).

which is the required relation

(ii) Draw the graph for the first 96 days:
The relation connecting the quantity of gas to the number of days of consumption is
y = –\(\frac{71}{120}\)x + 14.2
Let f(x) = –\(\frac{71}{120}\) x + 14.2
Here f(x) is a periodic function of period 24
∴ f(x + 24) = f(x)
When x = 0
f(0) = –\(\frac{71}{120}\) × 0 + 14.2 ⇒ y = 14.2
The corresponding point is (0, 14.2)

When x = 24
f(24) = –\(\frac{71}{120}\) × 0 + 14.2 ⇒ y = 14.2
⇒ f(24) = –\(\frac{71}{5}\) + 14.2
= – 14.2 + 14.2 = 0 ⇒ y = 0
Corresponding point is (24 , 0)

When x = 48
f(48) = f(24 + 24 + 0) = f(24 + 0)
= f(o) = o
Corresponding point is (48, 0)

When x = 72
f(72) = f(24 + 24 + 24 + 0)
= f(24 + 24 + 0) = f(24 + 0)
= f(0) = 0
Corresponding point is (72, 0)
The required graph is

Question 15.
In the shopping mall, there is a hall of cuboid shape with dimension 800 x 800 x 720 units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find
(i) the minimum total length of the escalator
(ii) the height at which the escalator changes its direction
(iii) the slopes of the escalator at the turning points.
Answer:
Give the dimension of the cube = 800 × 800 × 720

(i) Minimum total length of the escalator:

The path of the escalator is
from OA to AB to BC to CD
OE = 800, EA = \(\frac{1}{4}\) × height of the building
EA = \(\frac{1}{4}\) × 720 = 180
Since there are four steps for the escalator
∴ OA² = OE² + EA²
= 800² + 180²
= (40 × 20)² + (9 × 20)²
= 40² × 20² + 92 × 20²
= 20² (40² + 9²)
= 20² ( 1600 + 81)
= 20² × 1681
OA² = 20² × 41²
OA = \(\sqrt{20^{2} \times 41^{2}}\) = 20 × 41 = 820
Since ∆OAE ≡ ∆ ABB’ ≡ ∆ BCC ≡ ∆ CDD’
We have OA = AB = BC = CD
Total length of the escalator
= OA + AB + BC + CD
= 820 + 820 + 820 + 820
= 4 × 820
= 3280
Minimum length of the escalator = 3280 units

(ii) Lengths at which the escalator changes its direction:
The heights at which the escalator changes its direction
First step EA = \(\frac{1}{4}\) × 720 = 180 unis
Second step FB = \(\frac{1}{2}\) × 720 = 360 units
Third step GC = \(\frac{1}{3}\) × 720 = 540 units

(iii) The slopes of the escalator at the turning points.
In the right angle ∆ OAE
OE = 800, EA = 180
Let ∠ AOE = θ
The slope of the escalator OE 180

∴ Slope at each turning points is \(\frac{9}{40}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 6 Two Dimensional Analytical Geometry Ex 6.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.1

Question 1.
Find the locus of P, if for all values of a , the coordinates of a moving point P is
(i) (9 cos α, 9 sin α)
(ii) (9 cos α, 6 sin α)
Answer:
(i) (9 cos α, 9 sin α)
Let P (h , k) be any point on the required path. Then by the given data we have h = 9 cos α, k = 9 sin α

The locus of P (h , k) is obtained by replacing h by x and k by y.
∴ The required locus becomes x² + y² = 81

(ii) ( 9 cos α, 6 sin α)
Let P (h, k) be any point on the required path. Then by the given data we have h = 9 cos α, k = 6 sin α

The locus of p(h , k) is obtained by replacing h by x and k by y
∴ The required locus is \(\frac{x^{2}}{81}+\frac{y^{2}}{36}\) = 1

Question 2.
Find the locus of a point P that moves a constant distant of
(i) two units from the x-axis
(ii) three units from the y-axis.
Answer:
(i) Two units from x-axis:

Let P (h, k) be any point on the required path. From the given data, we have k = 2
The locus of P (h, k) is obtained by replacing h by x and k by y.
∴ The required locus is y = 2

(ii) Three units from y-axis:

Let (h, k) be any point on the required path. From the given data, we have h = 3.
The locus of P (h, k) is obtained by replacing h by x and k by y.
∴ The required locus is x = 3

Question 3.
If 6 is a parameter, find the equation of the locus of a moving point, whose coordinates are x = a cos³θ, y = a sin³θ.
Answer:
The given moving points is (a cos³θ, a sin³θ)

Question 4.
Find the values of k and b. If the points P(-3, 1) and Q (2, b) lie on the locus of x² – 5x + ky = 0
Answer:
Given P (-3, 1) lie on x² – 5x + ky = 0
⇒ (-3)² – 5(-3) + k(1) = 0
9 + 15 + k = 0 ⇒ k = -24
Q (2, b) lie on x² – 5x + ky = 0
(2)² – 5(2) + k(b) = 0 ⇒ 4 – 5(2) – 24b = 0

Question 5.
A straight rod of length 8 units slides with its ends A and B always on the x and y axes respectively, then find the locus of the midpoint of the line segment AB.
Answer:
Given A and B are the ends of the straight rod of length 8 unit on the x and y-axes. Let A be (a, 0) and B (0, b).

Let M (h, k) be the midpoint of AB (h,k) =

In the right-angled ∆ OAB
AB² = OA² + OB²
8² = a² + b²
64 = (2h)² + (2k)
64 = 4h² + 4k²
h² + k² = \(\frac{64}{4}\) = 16
The locus of M (h, k) is obtained by replacing h by x and k by y
∴ The required locus is x² + y² = 16

Question 6.
Find the equation of the locus of a point such that the sum of the squares of the distance from the points (3, 5), (1, -1) is equal to 20.
Answer:
Let P (h, k) be the moving point
Let the given point be A (3, 5) and B (1, -1)
We are given PA² + PB² = 20
⇒ (h – 3)² + (k – 5)² + (h – 1)² + (k + 1)² = 20
⇒ h² – 6h + 9 + k² – 10k + 25 + h² – 2h + 1 + k² + 2k + 1 = 20
(i.e.) 2h² + 2k² – 8h – 8k + 36 – 20 = 0
2h² + 2k² – 8h – 8k + 16 = 0
(÷ by 2 ) h² + k² – 4h – 4k + 8 = 0
So the locus of P is x² + y² – 4x – 4y + 8 = 0

Question 7.
Find the equation of the locus of the point P such that the line segment AB, joining the points A(1 ,-6) and B(4 , – 2) subtends a right angle at P.
Answer:

Given A (1, – 6) and B (4, – 2).
Let P (h, k) be a point such that the line segment AB subtends a right angle at P.
∴ ∆ APB is a right-angled triangle.
AB² = AP² + BP² ………… (1)
AB² = (4 – 1)² + (- 2 + 6)²
AB² = 3² + 4² = 9 + 16 = 25
AP² = (h – 1)² + (k + 6)²
BP² = (h – 4)² + (k + 2)²
(1) ⇒
25 = (h – 1)² + (k + 6)² + (h – 4)² + (k + 2)²
25 = h² – 2h + 1 + k² + 12k + 36 + h² – 8h + 16 + k² + 4k + 4
25 = 2h² + 2k² – 10h + 16k + 57
2h² + 2k² – 10h + 16k + 57 – 25 = 0
2h² + 2k² – 10h + 16k + 32 = 0
h² + k² – 5h + 8k + 16 =0
The locus of P (h , k) is obtained by replacing h by x and k by y.
∴ The required locus is x² + y² – 5x + 8y + 16 = 0

Question 8.
If O is origin and R is a variable point on y² = 4x, then find the equation of the locus of the mid-point of segment OR.
Answer:

Let the variable point R be (x, y). Let M (h, k) be the midpoint of R.

But R(x , y) is a point on y² = 4x
∴ (2k)² = 4(2h)
4k² = 8h
k² = 2h
The locus of M (h , k) is obtained by replacing h by x and k by y.
∴ The required locus is y² = 2x

Question 9.
The coordinates of a moving point P are (\(\frac{\mathbf{a}}{2}\) (cosec θ + sin θ), \(\frac{\mathbf{b}}{2}\) (cosec θ – sin θ) where θ is a variable parameter. Show that the equation of the locus P is b² x² – a² y² = a² b²
Answer:
Let the moving point P be (h, k)
By the given data we have


The locus of P ( h , k ) is obtained by replacing h by x and k by y
∴ The required locus is \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1
b² x² – a² y² = a² b²

Question 10.
If P (2, – 7) is given point and Q is a point on 2x² + 9y² = 18 then find the equations of the locus of the midpoint of PQ.
Answer:
Given P is (2, -7) and let Q be (x, y)
Given that Q is a point on 2x² + 9y² = 18
Let M (h, k) be the midpoint of PQ

2h = 2 + x ,                   2k = – 7 + y
x = 2h – 2,                     y = 2k + 7
But Q(x, y) is a point on 2x² + 9y² = 18
∴ 2 (2h – 2)² + 9 (2k + 7)² = 18
2 [4h² – 8h + 4] + 9 [4k² + 28k + 49] = 18
8h² – 16h + 8 + 36k² + 252k + 441 = 18
8h² + 36k² – 16h + 252k + 449 = 18
8h² + 36k² – 16h + 252k +431 =0
The locus of M ( h , k ) is obtained by replacing h by x and k by y.
∴ The required locus is
8x² + 36y² – 16x + 252y + 431 = 0

Question 11.
If R is any point on the x-axis and Q is any point on the y-axis and P is a variable point on RQ with RP = b, PQ = a, then find the equation of locus of P.
Answer:
Given R is any point on the x-axis and Q is any point on the y-axis.
Let R be (x, 0) and Q be (0, y)
Let P (h, k ) be the variable point on RQ such that RP = b and PQ = a

The point P ( h, k ) divides the line joining the points R(x, 0) and Q (0, y) in the ratio b : a


Substituting in equation (1), we have

The locus of P (h, k) is obtained by replacing h by x and k by y.
∴ The required locus is \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}\) = 1

Question 12.
If the points P (6, 2) and Q (- 2, 1 ) and R are the vertices of a ∆PQR and R is the point on the locus y = x² – 3x + 4 then find the equation of the locus of the centroid of ∆PQR.
Answer:
Given P (6, 2), Q (-2 , 1), R (a, b) are the vertices of ∆ PQR where R (a, b) lies on y = x² – 3x + 4
∴ b = a² – 3a + 4 (1)
Let the centroid of ∆ PQR be G (h, k)

Substituting in equation (1) we have
(1) ⇒ 3k – 3 = (3h – 4)² – 3(3h – 4) + 4
3k – 3 = 9h² – 24h + 16 – 9h + 12 + 4
9h² – 33h + 32 – 3k + 3 = 0
9h² – 33h – 3k + 35 = 0
The locus of G (h, k) is obtained by replacing h by x and k by y.
∴ The required locus is 9x² – 33x – 3y + 35 = 0

Question 13.
If Q is a point on the locus of x² + y² + 4x – 3y +7 = 0, then find the equation of locus of P which divides segment OQ externally in the ratio 3 :4 where O is origin.
Answer:
Let Q be (a, b) lying on the locus
x² + y² + 4x – 3y + 7 = 0
∴ a² + b² + 4a – 3b + 7 = 0
Let the movable point P be (h , k)
Given P divides OQ externally in the ratio 3 : 4

Substituting in equation (1) we have

h² + k² – 12h + 9k + 63 = 0
The locus of P(h, k) is obtained by replacing h by x and k by y.
∴ The required locus is
x² + y² – 12x + 9y + 63 = 0

Question 14.
Find the points on the locus of points that are 3 units from the x-axis and 5 units from the point (5, 1)
Answer:
Given that the required pointis3unitsfrom x-axis and 5 units from the point P (5, 1). Let Q (h, 3) and K (h,- 3) be the required points.

∴ PQ = 5
\(\sqrt{(5-\mathrm{h})^{2}+(1-3)^{2}}\) = 5
(5 – h)² + (- 2)² = 25
25 – 10h + h² + 4 = 25
h² – 10h + 29 – 25 = 0
h² – 10h + 4 = 0

PR = 5

(5 – k)² + 4² = 25
25 – 10k + k² + 16 = 25
k² – 10k + 16 = 0


∴ R (8, – 3), (2, – 3)
∴ Required points are
(5 + √21, 3), (5 – √21, 3), (8, – 3), (2, – 3)

Question 15.
The sum of the distance of a moving point from the points (4, 0) and (- 4, 0) is always 10 units. Find the equation to the locus of the moving point.
Answer:
Let A be (4, 0) and B be (-4, 0). Let the moving point be p(h, k)
Given PA + PB = 10

16h² + 200h + 625 = 25[h² + 8h + 16 + k²]
16h² + 200h + 625 = 25h² + 200h + 400 + 25k²
9h² + 26k² = 225

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 5 Binomial Theorem, Sequences and Series Ex 5.5 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.5

Choose the correct or the most suitable answer:

Question 1.
The value of 2 + 4 + 6 + …………… + 2n is
(1) \(\frac{n(n-1)}{2}\)
(2) \(\frac{n(n+1)}{2}\)
(3) \(\frac{2 n(2 n+1)}{2}\)
(4) n(n + 1)
Answer:
(4) n(n + 1)

Explaination:
2 + 4 + 6 + ……… + 2n = 2(1 + 2 + 3 + ………….. + n)
= 2 × \(\frac{n(n+1)}{2}\)
= n(n + 1)

Question 2.
The coefficient of x⁶ in (2 + 2x)¹⁰ is
(1) 10C₆
(2) 2₆
(3) 10C₆2⁶
(4) 10C₆2¹⁰
Answer:
(4) 10C₆2¹⁰

Explaination:

Question 3.
The coefficient of x⁸ y¹² in the expansion of (2x + 3y)²⁰ is
(1) 0
(2) 2⁸ 3¹²
(3) 2⁸ 3¹² + 2¹² 3⁸
(4) 20C₈ 2⁸ 3¹²
Answer:
(4) 20C₈ 2⁸ 3¹²

Explaination:

Question 4.
If nC₁₀ > nC_r for all possible r then a value of n is
(1) 10
(2) 21
(3) 19
(4) 20
Answer:
(4) 20

Explaination:
Out of ¹⁰C₁₀, ²¹C₁₀, ¹⁹C₁₀ and ²⁰C₁₀, ²⁰C₁₀ is larger.

Question 5.
If a is the Arithmetic mean and g is the Geometric mean of two numbers then
(1) a ≤ g
(2) a ≥ g
(3) a = g
(4) a > g
Answer:
(2) a ≥ g

Explaination:
Given Arithmetic mean = a,
Geometric mean = g
We have A. M ≥ G. M
∴ a ≥ g

Question 6.
If (1 + x²)² (1 + x)ⁿ = a₀ + a₁x + a₂x² + ………… + x^{n + 4} and if a₀, a₁, a₂ are in A. P then n is
(1) 1
(2) 2
(3) 3
(4) 4
Answer:
(3) 3

Explaination:

n² – 5n + 6 = 0
(n – 2) (n – 3) = 0
n = 2 or n = 3

Question 7.
If a, 8, b are in A .P , a, 4 , b are in G. P and if a, x ,b are in H . P then x is
(1) 2
(2) 1
(3) 4
(4) 16
Answer:
(1) 2

Explaination:
Given a, 8, b are in A. P ∴ 2 × 8 = a + b ⇒ a + b = 16 ——— (1)
Also a, 4, b are in G.P ∴ 4² = a . b ⇒ ab = 16 ——- (2)
Also a, x, b are in H.P. ∴ \(\frac{1}{a}, \frac{1}{x}, \frac{1}{b}\) are in A.P

Question 8.

(1) A. P
(2) G.P
(3) H.P
(4) AGP
Answer:
(3) H.P

Explaination:

Question 9.
The H.M of two positive numbers whose A.M and G.M are 16,8 respectively is
(1) 10
(2) 6
(3) 5
(4) 4
Answer:
(4) 4

Explaination:
Let a, b be the two numbers. Given A. M = \(\frac{a+b}{2}\) = 16
G.M = \(\sqrt{a b}\) = 8
a+b = 16 × 2 = 32
ab = 8² = 64
H.M = \(\frac{2 a b}{a+b}\)
= \(\frac{2 \times 64}{32}\) = 2 × 2 = 4

Question 10.
If S denote the sum of n terms of an A. P whose common difference is d, the value of S_n – 2S_{n- 1} + S_{n – 2} is
(1) d
(2) 2d
(3) 4d
(4) d²
Answer:
(1) d

Explaination:

= a + (n – 1) d – (a + (n – 2)d)
= a + (n – 1) d – a – (n – 2)d
= a + nd – d – a – nd + 2d = d

Question 11.
The remainder when 38¹⁵ is divided by 13 is
(1) 12
(2) 1
(3) 11
(4) 5
Answer:
(1) 12

Explaination:
38¹⁵ = (39 – 1)¹⁵ = 39¹⁵ – 15C₁ 39¹⁴(1) + 15C₂ (39)¹³(1)² – 15C₃ (39)¹²(1)³ ….. + 15C₁₄ (39)¹(1) – 15C₁₅(1)
Except -1 all other terms are divisible by 13.
∴ When 1 is added to it the number is divisible by 13. So the remainder is 13 – 1 = 12.

Question 12.
The nth term of the sequence 1, 2, 4, 7, 11, ………….. is
(1) n² + 3n² + 2n
(2) n³ – 3n² + 3n
(3) \(\frac{n(n+1)(n+2)}{3}\)
(4) \(\frac{n^{2}-n+2}{2}\)
Answer:
(4) \(\frac{n^{2}-n+2}{2}\)

Explaination:

Question 13.
The sum up to n terms of the series

(1) \(\sqrt{2 n+1}\)
(2) \(\frac{\sqrt{2 n+1}}{2}\)
(3) \(\sqrt{2 n+1}-1\)
(4) \(\frac{\sqrt{2 n+1}-1}{2}\)
Answer:
(4) \(\frac{\sqrt{2 n+1}-1}{2}\)

Explaination:

Question 14.
The n^th term of the sequence

(1) 2ⁿ – n – 1
(2) 1 – 2^-n
(3) 2^-n + n – 1
(4) 2^n-1
Answer:
(2) 1 – 2^-n

Explaination:

Question 15.
The sum up to n terms of the series

(1) \(\frac{\mathbf{n}(\mathbf{n}+1)}{2}\)
(2) 2n (n + 1)
(3) \(\frac{\mathbf{n}(\mathbf{n}+1)}{\sqrt{2}}\)
(4) 1
Answer:
(3) \(\frac{\mathbf{n}(\mathbf{n}+1)}{\sqrt{2}}\)

Explaination:

Question 16.
The value of the series

(1) 14
(2) 7
(3) 4
(4) 6
Answer:
(1) 14

Explaination:

Question 17.
The sum of an infinite G.P is 18. If the first term is 6 the common ratio is
(1) \(\frac{1}{3}\)
(2) \(\frac{2}{3}\)
(3) \(\frac{1}{6}\)
(4) \(\frac{3}{4}\)
Answer:
(2) \(\frac{2}{3}\)

Explaination:
Let the geometric series be a, ar, ar², …………… ar^n-1
Given a = 6, S_∞ = 18

Question 18.
The coefficient of x⁵ in the series e^-2x is
(1) \(\frac{2}{3}\)
(2) \(\frac{3}{2}\)
(3) \(-\frac{4}{15}\)
(4) \(\frac{4}{15}\)
Answer:
(3) \(-\frac{4}{15}\)

Explaination:

Question 19.
The value of

(1) \(\frac{e^{2}+1}{2 e}\)
(2) \(\frac{(e+1)^{2}}{2 e}\)
(3) \(\frac{(e-1)^{2}}{2 e}\)
(4) \(\frac{e^{2}+1}{2 e}\)
Answer:
(3) \(\frac{(e-1)^{2}}{2 e}\)

Explaination:

Question 20.
The value of

(1) log \(\left(\frac{5}{3}\right)\)
(2) \(\frac{3}{2}\) log \(\left(\frac{5}{3}\right)\)
(3) \(\frac{5}{3}\) log \(\left(\frac{5}{3}\right)\)
(4) \(\frac{2}{3}\) log \(\left(\frac{2}{3}\right)\)
Answer:
(2) \(\frac{3}{2}\) log \(\left(\frac{5}{3}\right)\)

Explaination:

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 5 Binomial Theorem, Sequences and Series Ex 5.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.4

Question 1.
Expand the following in ascending powers of x and find the condition on x for which the binomial expansion is valid.
(i) \(\frac{1}{5+x}\)
Answer:

(ii) \(\frac{2}{(3+4 x)^{2}}\)
Answer:

(iii) (5 + x²)^2/3
Answer:

(iv) \((x+2)^{-\frac{2}{3}}\)
Answer:

Question 2.
Find \(\sqrt[3]{1001}\) approximately. (two decimal places)
Answer:

Question 3.
Prove that \(\sqrt[3]{x^{3}+6}-\sqrt[3]{x^{3}+3}\) is approximately equal to \(\frac{1}{x^{2}}\) when x is sufficiently large.
Answer:

Question 4.
Prove that \(\sqrt{\frac{1-x}{1+x}}\) is approximately equal to 1 – x + \(\frac{x^{2}}{2}\) when x is very small.
Answer:

Question 5.
Write the first 6 terms of the exponential series
(i) e^5x
Answer:

(ii) e^-2x
Answer:

(iii) e^x/2
Answer:

Question 6.
Write the first 4 terms of the logarithmic series.
(i) log (1 + 4x)
(ii) log (1 – 2x)
(iii) log \(\left(\frac{1+3 x}{1-3 x}\right)\)
(iv) log \(\left(\frac{1-2 x}{1+2 x}\right)\)
Find the intervals on which the expansions are valid.
Answer:
(i) log ( 1 + 4x )

(ii) log (1 – 2x)

(iii) log \(\left(\frac{1+3 x}{1-3 x}\right)\)

(iv) log \(\left(\frac{1-2 x}{1+2 x}\right)\)

Question 7.

Answer:

Question 8.

Answer:

Question 9.
Find the coefficient of x⁴ in the expansion of \(\frac{3-4 x+x^{2}}{e^{2 x}}\)
Answer:

Question 10.
Find the value of
Answer:

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 5 Binomial Theorem, Sequences and Series Ex 5.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.3

Question 1.
Find the sum of the first 20 terms of the arithmetic progression having the sum of first 10 terms as 52 and the sum of the first 15 terms as 77 .
Answer:
Sum of the first n terms of an Arithmetic progression is S_n = \(\) [2a + (n – 1)d]
Given S₁₀ = 52
52 = \(\frac{10}{2}\) [ 2a + (10 – 1) d ]
52 = 5 [2a + 9d]
52 = 10a + 45d ……….. (1)
Also given S₁₅ = 77
77 = \(\frac{15}{2}\) [2a + (15 – 1)d]
77 = \(\frac{15}{2}\) [2a + 14d]
77 = 15 [a + 7d]
77 = 15a + 105d ………….. (2)

Substituting the value of d in (1)

Question 2.
Find the sum up to the 17^th term of the series
Answer:

Question 3.
Compute the sum of first n terms of the following series.
(i) 8 + 88 + 888 + 8888 + . . . . . . .
Answer:

(ii) 6 + 66 + 666 + 6666 + . . . . . . .
Answer:

Question 4.
Compute the sum of first n terms of 1 + (1 + 4) + (1 + 4 + 4²) + (1 + 4 + 4² + 4³) + …………..
Answer:
The given series is 1 + (1 + 4) + (1 + 4 + 4²) + (1 + 4 + 4² + 4³) + …………..
n^th term of the series is T_n = 1 + 4 + 4² + 4³ + ………………. + 4^n-1

Sum to n terms of the series
S_n = T₁ + T₂ + ………….. + T_n

Question 5.
Find the general terms and sum to n terms of the sequence 1, \(\frac{4}{3}\), \(\frac{7}{9}\), \(\frac{10}{27}\), ………….
Answer:
The given sequence as 1, \(\frac{4}{3}\), \(\frac{7}{9}\), \(\frac{10}{27}\), ………….
Consider the terms in the numerator 1, 4, 7, 10, ……………….. which is an Arithmetic progression
with first term a = 1, common difference d = 4 – 1 = 3
a_n = a + (n – 1)d = 1 + (n – 1)3 = 1 + 3n – 3 = 3n – 2
The given sequence can be written as 1, (1 + 3)\(\left(\frac{1}{3}\right)\), (1 + 2 × 3)\(\left(\frac{1}{3}\right)^{2}\) (1 + 3 × 3) \(\left(\frac{1}{3}\right)^{3}\), …………….
where \(1, \frac{1}{3}, \frac{1}{3^{2}}, \frac{1}{3^{3}}, \ldots \ldots\) is a G. P with first term a = 1 , common ratio r = \(\frac{1}{3}\)
∴ The given sequence is an Arithmetico – Geometric sequence.


which is an arithmetic – geometric sequence.
∴ The sum of first n terms of the arithmetico – geometric sequence is given by

Question 6.
Find the value of n if the sum to n terms of the series \(\sqrt{3}+\sqrt{75}+\sqrt{243}+\ldots \ldots . . . \text { is } 435 \sqrt{3}\)
Answer:

Question 7.
Show that the sum of ( m + n)^th and ( m – n)^th term of an A.P is equal to twice the m^th term.
Answer:
Let the A.P. be a, a + d, a + 2d, ……..
t_{m + n} = a + (m + n – 1)d
t_{m – n} = a + (m – n – 1)d
t_m = a + (m – 1)d
2t_m = 2[a + (m – 1)d]
To prove t_{m + n} + t_{m – n} = 2t_m
LHS t_{m + n} + t_{m – n} = a + (m + n – 1)d + a + (m – n – 1)d

= 2a + d [2m – 2]
= 2[a + (m – 1)d) = 2 t_m = RHS

Question 8.
A man repays an amount of Rs.3250 by paying Rs.20 in the first month and then increases the payment by Rs. 15 per month. How long will it take him to clear the amount?
Answer:
Amount of loan = 3250
Let n be the number of months taken to clear the loan
Amount paid in the first month a = 20
Increased payment in every month d = 15
∴ Amount paid in the second month = 20 + 15 = 35
Amount paid in the third month = 35 + 15 = 50
∴ The sequence of amount paid in every month is 20, 35, 50, …………. which is an A.P with first term a = 20 and common difference = 15
Given S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
S_n = 3250
3250 = \(\frac{n}{2}\) [2 × 20 + (n – 1) 15]
6500 = n[40 + 15n – 15]
6500 = n[25 + 15n]
6500 = 25n + 15n²
1300 = 5n + 3n²
3n² + 5n – 1300 = 0
3n² + 65n – 60n – 1300 = 0
n(3n + 65) – 20 (3n + 65) = 0
(n – 20) (3n + 65) = 0
n = 20 = 0 or 3n + 65 = 0
n = 20 or n = \(-\frac{65}{3}\)
n = \(-\frac{65}{3}\) is not possible ∴ n = 20
Thus, in 20 months the loan is cleared.

Question 9.
In a race, 20 balls are placed in a line at intervals of 4 meters with the first ball, 24 meters away from the starting point. A contestant is required to bring the balls back to the starting place one at a time. How far would the contestant run to bring back all balls?
Answer:
Number of balls placed in a line = 20
Let A be the starting point.
The distance of the first ball from A = 24 m
The distance of the second ball from the first ball = 4 m

A contestant starts from point A, travels a distance of 24 m and picks the first ball and brings it back to starting point A. This is continued for each ball.
Distance travelled by the contestant to bring the first ball = 24 + 24 = 2 × 24 = 48 m
Distance travelled to bring the second ball = 2 ( 24 + 4 ) = 2 × 28 = 56 m
Distance travelled to bring the third ball = 2 × (24 + 4 + 4) = 64 m

∴ The sequence of distances travelled are 48, 56, 64 ……………
This is an Arithmetic progression with first term a = 48 ,
common difference d = 56 – 48 = 8 ,
number of terms n = 20.
The sum of 20 terms of this A.P gives the total distance travelled by the contestant in bringing all balls to the starting place
S_n = \(\frac{\mathrm{n}}{2}\) [2a + (n – 1)d]
S₂₀ = \(\frac{\mathrm{20}}{2}\) [2 × 48 + (20 – 1)8] = 10 [96 + 19 × 8]
= 10 [ 96 + 152] = 10 × 248 = 2480
Total distance traveled = 2480 m

Question 10.
The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally how many bacteria will be present at the end of the 2nd hour, 4th hour, and nth hour?
Answer:
Number of bacteria at the beginning = 30
Number of bacteria after 1 hour = 30 × 2 = 60
Number of bacteria after 2 hours = 30 × 2² = 120
Number of bacteria after 4 hours = 30 × 24 = 30 × 16 = 480
∴ Number of bacteria after n^th hour = 30 × 2ⁿ

Question 11.
What will Rs. 500 amounts to in 10 years after its deposit in a bank which pays an annual interest rate of 10 % compounded annually?
Answer:

Question 12.
In a certain town, a viral disease caused severe health hazards, upon its people disturbing their normal life. It was found that on each day, the virus which caused the disease spread in Geometric Progression. The amount of infected virus particle gets doubled each day, being 5 particles on the first day. Find the day when the infections virus particles just grow over 1,50,000 units?
Answer:
The number of viruses present at the beginning = 5, Given virus, gets doubled each day
∴ The sequence of a number of viruses in each day is 5, 10, 20, 40, 80, ………………. which is a G. P with First-term a = 5, Common ratio r = \(\frac{10}{5}\) = 2
n^th term t_n = ar^n-1

∴ On the 15^th day, the infectious virus grows over 1,50,000 units.

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 5 Binomial Theorem, Sequences and Series Ex 5.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.2

Question 1.
Write the first 6 terms of the sequence whose nth terms are given below and classify them as Arithmetic progression Geometric progression, Arithmetic – geometric progression, Harmonic progression and none of them.
(i) \(\frac{1}{2^{n+1}}\)
Answer:

(ii)
Answer:

(iii) \(4\left(\frac{1}{2}\right)^{n}\)
Answer:

(iv) \(\frac{(-1)^{n}}{n}\)
Answer:

(v) \(\frac{2 n+3}{3 n+4}\)
Answer:

(vi) 2018
Answer:
The n^th term a_n = 2018
a₁ = 2018,
a₂ = 2018,
a₃ = 2018,
a₄ = 2018,
a₅ = 2018,
a₆ = 2018,
∴ The given sequence is 2018, 2018, 2018, 2018, 2018, 2018, ………….
This is a œnstant sequence which has same common ratio and common difference.
Hence this is an A. P, G . P and AGP.

(vii) \(\frac{3 n-2}{3^{n-1}}\)
Answer:

Question 2.
Write the first 6 terms of the sequences whose n^th term a_n is given below
(i)
n = 1, a_n = n + 1, a₁ = 1 + 1 = 2
n = 2, a_n = n, a₂ = 2
n = 3, a_n = n + 1, a₃ = 3 + 1 = 4
n = 4, a_n = n, a₄ = 4
n = 5, a_n = n + 1, a₅ = 5 + 1 = 6
n = 6, a_n = n, a₆ = 6
∴ The first six terms are 2, 2, 4, 4, 6, 6

(ii)
n = 1, a₁ = 1, n = 2, a₂ = 2
n = 3, a_n = a_n+1 + a_n-2, a₃ = a_{3 – 1} + a_{3 – 2} = a₂ + a₁ = 2 + 1 = 3

n = 4, a_n = a_n+1 + a_n-2, a₄ = a_{4 – 1} + a_{4 – 2} = a₃ + a₂ = 3 + 2 = 5

n = 5, a_n = a_n+1 + a_n-2, a₅ = a_{5 – 1} + a_{5 – 2} = a₄ + a₃ = 5 + 3 = 8

n = 6, a_n = a_n+1 + a_n-2, a₆ = a_{6 – 1} + a_{6 – 2} = a₅ + a₄ = 8 + 5 = 13
∴ The first six terms are 1, 2, 3, 5, 8, 13

(iii)
Answer:
n = 1, a_n = n, a₁ = 1
n = 2, a_n = n, a₂ = 1
n = 3, a_n = n, a₃ = 1

n = 4, a_n = a_n-1 + a_n-2 + a_n-3
a₄ = a_4-1 + a_4-2 + a_4-3
a₄ = a₃ + a₂ + a₁
a₄ = 3 + 2 + 1 = 6

n = 5, a_n = a_n-1 + a_n-2 + a_n-3
a₅ = a_5-1 + a_5-2 + a_5-3
a₅ = a₄ + a₃ + a₂
a₅ = 6 + 3 + 2 = 11

n = 6, a_n = a_n-1 + a_n-2 + a_n-3
a₆ = a_6-1 + a_6-2 + a_6-3
a₆ = a₅ + a₄ + a₃
a₆ = 11 + 6 + 3 = 20
∴ The first six terms are 1, 2, 3, 6, 11, 20

Question 3.
Write the n^th term of the following sequences.
(i) 2, 2, 4, 4, 6, 6, ……………..
Answer:
The odd terms are a₁ = 2, a₃ = 4, a₅ = 6
The even terms are a₂ = 2, a₄ = 4, a₆ = 6

(ii)
Answer:

The terms in the numerator are 1 , 2 , 3, 4
a = 1 , d = 2 – 1 = 1
a_n = a + (n – 1) d
a_n = 1 + (n – 1)(1) = 1 + n – 1 = n
a_n = n
The terms in the denominator are 2 , 3 , 4 , 5 , 6 .
a = 2, d = 3 – 2 = 1
a_n = a + (n – 1) d
a_n = 2 + (n – 1) (1) = 2 + n – 1 = n + 1
a_n = n + 1
∴ The n^th term of the given sequence is a_n = \(\frac{n}{n+1}\) for all n ∈ N

(iii)
Answer:

The terms in the numerator are 1, 3, 5, 7, 9, ………….
a = 1 , d = 3 – 1 = 2
a_n = a + (n – 1) d
a_n = 1 + (n – 1)2
a_n = 1 + 2n – 2 = 2n – 1
The terms in the denominator are 2, 4, 6, 8, 10, …………..
a = 2, d = 4 – 2 = 2
a_n = a + (n – 1) d
a_n = 2 + (n – 1)(2)
a_n = 2 + 2n – 2 = 2n
∴ The n^th term of the given sequence is a_n = \(\frac{2 n-1}{2 n}\) for all n ∈ N

(iv) 6, 10, 4, 12, 2, 14, 0, 16, – 2 …………………
Answer:
The given sequence is 6, 10, 4, 12, 2, 14, 0, 16, – 2 ……………..
The odd terms are a₁ = 6, a₃ = 4 , a₅ = 2 , a₇ = 0, a₉ = – 2
∴ a_n = n – 7, n is odd
The even terms are a₂ = 10, a₄ = 12 , a₆ = 14 , a₈ = 16
∴ a_n = 8 + n, n is even.

Question 4.
The product of three increasing numbers in a G.P is 5832 . If we add 6 to the second number and 9 to the third number, then resulting numbers form an A.P. Find the numbers in G.P.
Answer:
Let the increasing numbers in G.P be \(\), a, ar.
Given \(\frac{a}{r}\) × a × ar = 5832 ⇒ a³ = 5832 = 18³ ⇒ a = 18
Also given \(\frac{a}{r}\), a + 6, ar + 9 form an A.P.
∴ 2(a + b) = \(\frac{a}{r}\) + (ar + 9)
⇒ (a + 6) + (a + 6) = \(\frac{a}{r}\) + (ar + 9)
⇒ (a + 6) – \(\frac{a}{r}\) = (ar + 9) – (a + 6)
⇒ a + 6 – \(\frac{a}{r}\) = ar + 9 – a – 6
⇒ a + 6 – \(\frac{a}{r}\) = ar – a + 3
Substituting the value of a = 18, we get


39r = 18r² + 18
18r² – 39r + 18 = 0
(2r – 3)(3r -2) = 0
2r – 3 = 0 or 3r – 2 = 0
r = \(\frac{3}{2}\) or r = \(\frac{2}{3}\)

Case (i) When a = 18, r = \(\frac{3}{2}\) the numbers in G.P are

Case (ii) When a = 18, r = \(\frac{2}{3}\)

Question 5.
Write the n^th term of the sequence \(\frac{3}{1^{2} \cdot 2^{2}}, \frac{5}{2^{2} \cdot 3^{2}}, \frac{7}{3^{2} \cdot 4^{2}}\), …………….. as a difference of two terms.
Answer:

The terms in the numerator are 3,5, 7
which forms an A. P with first term a = 3 and common difference d = 5 – 3 = 2
n^th term t_n = a + (n – 1) d
= 3 + (n – 1)(2)
= 3 + 2n – 2 = 2n + 1
t_n = 2n + 1
The terms in the denominator are 1² . 2², 2² . 3², 3² . 4² ……………….
n^th term t_n = n² . (n + 1)²

Question 6.
If t_k is the k^th term of a G.P then show that t_{n – k}, t_k, t_{n + k} also form a G.F for any positive integer k.
Answer:
Given t^k is the k^th term of a G.P. We have n^th term of a G.P is t_n = ar^n-1

Question 7.
If a, b, c are in geometric progression and if a^1/x = b^1/y = c^1/z are in Arithmetic progression.
Answer:

Question 8.
The A.M of two numbers exceeds their G.M by 10 and H.M by 16. Find the numbers.
Answer:
Let the numbers be a and b

Question 9.
If the roots of the equation (q – r)x² + (r – p)x + (p – q) = 0 are equal then show that p , q and r are in A. P.
Answer:
The roots are equal ⇒ ∆ = 0
(i.e.) b² – 4ac = 0
Hence, a = q – r ; b = r – p ; c = p – q
b² – 4ac = 0
⇒ (r – p)² – 4(q – r)(p – q) = 0
r² + p² – 2pr – 4[qr – q² – pr + pq] = 0
r² + p² – 2pr – 4qr + 4q² + 4pr – 4pq = 0
(i.e.) p² + 4q² + r² – 4pq – 4qr + 2pr = 0
(i.e.) (p – 2q + r)² = 0
⇒ p – 2q + r = 0
⇒ p + r = 2q
⇒ p, q, r are in A.P.

Question 10.
If a , b , c are respectively the p^th, q^th and r^th terms of a G . P show that (q – r) log a + (r – p) log b + (p – q) log c = 0
Answer:
Let A be first term and R be the jmnon ratio of the G.P.
Given a = p^th term of the G.P
General term of a G. P with first term A and common ratio R is t_n = AR^{n – 1}
∴ a = t_p = AR^{P – 1}
log a = log AR^p-1 = log A + log R^p-1 = log A + (p – 1) log R

b = q^th term of the G.P
b = t_q = AR^q-1
log b = log AR^q-1 = log A + log R^q-1 = log A + (q – r)log R

c = r^th term of the G.P
c = t_r = AR^r-1
log c = log AR^r-1 = log A + log R^r-1 = log A + (r – 1) log R

(q – r) log a + (r – p) log b + (p – q) log c
= (q – r) [log A + (p – 1) log R] + (r – p) [ log A + (q – 1) log R ] + (P – q) [ log A + (r – 1) log R]
= (q – r) log A + (q – r) (p – 1 ) log R + (r – p) log A + (r – p) (q – 1) log R + (P – q) log A + (p – q) (r – 1 ) log R
= [ q – r + r – p + p – q ] log A + [ (q – r) (p – 1) + (r – p) (q – 1) + (p – q)(r – 1)] log R
= 0 × log A + [pq – q – rp + r + rq – r – pq + p + pr – p – rq + q] log R
= 0 × log R = 0
∴ (q – r) log a + (r – p) log b + (p – q) log c = 0