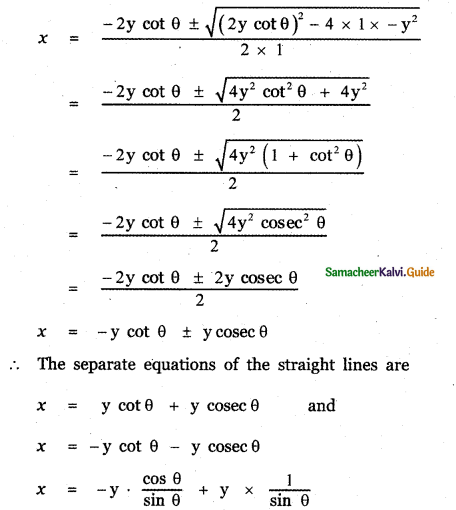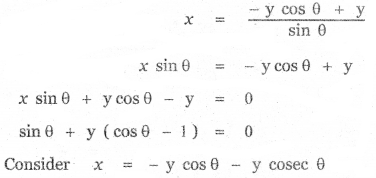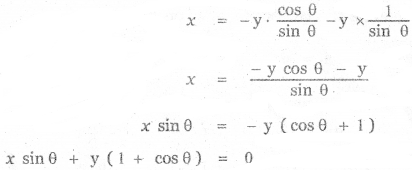Samacheer Kalvi 11th Maths Guide Chapter 6 Two Dimensional Analytical Geometry Ex 6.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 6 Two Dimensional Analytical Geometry Ex 6.5 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.5
Choose the correct or more suitable answer.

Question 1.
The equation of the locus of the point whose distance from y – axis is half the distance from origin is
(1) x² + 3y² = 0
(2) x² – 3y² = 0
(3) 3x + y² = 0
(4) 3x² – y² = 0
Answer:
(4) 3x² – y² = 0

Explaination:

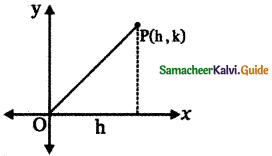
Let the point be (h,k)
Equation of y axis is x = 0
Given the distance of the point from y – axis is
\(\frac{1}{2}\) × distance of the point from the origin Distance of the point (h, k) from the y- axis is
= \(\frac{\mathrm{h}}{\sqrt{1^{2}}}\) = h
The distance of the point P (h , k) from the origin

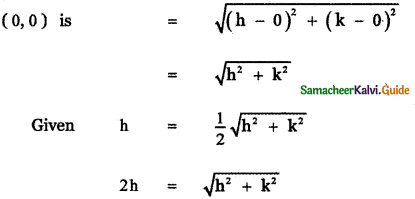
Squaring on both sides
4h² = h² + k²
4h² – h² – k² = 0
3h² – k² = o
The locus of ( h, k ) is 3x² – y² = 0

Question 2.
Which of the following equation is the locus of (at², 2at)
(1) \(\frac{x^{2}}{\mathbf{a}^{2}}-\frac{\mathbf{y}^{2}}{\mathbf{b}^{2}}\) = 1
(2) \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
(3) x² + y² = a²
(4) y² = 4ax
Answer:
(4) y² = 4ax

Explaination:
y² = 4ax ⇒ Equation that satisfies the given point (at², 2at)

Question 3.
Which of the following points lie on the locus of 3x² + 3y² – 8x – 12y + 17 = 0
(1) (0, 0)
(2) (-2, 3)
(3) (1, 2)
(4) (0, – 1)
Answer:
(3) (1, 2)

Explaination:
The point that satisfies the given equations (0, 0) ⇒ 17 ≠ 0
(-2, 3) ⇒ 3 (4) + 3 (9) + 16 – 36 + 17 ≠ 0
(1, 2) ⇒ 3 + 3 (4) – 8 (1) – 12 (2) + 17
32 – 32 = 0, 0 = 0

Question 4.
If the point (8, – 5) lies on the focus \(\frac{x^{2}}{16}-\frac{y^{2}}{25}\) = k, then the value of k is
(1) 0
(2) 1
(3) 2
(4) 3
Answer:
(4) 3

Explaination:
Given the point (8, – 5) lies on the locus

Question 5.
Straight line joining the points (2, 3) and (- 1, 4) passes through the point (α, β) if
(1) α + 2β = 7
(2) 3α + β = 9
(3) α + 3β = 11
(4) 3α + β = 11
Answer:
(3) α + 3β = 11

Explaination:
The equation of the straight line joining the points (2, 3) and (-1, 4) is

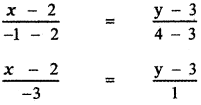
x – 2 = – 3(y – 3)
x – 2 = – 3y + 9
x + 3y – 2 – 9 = 0
x + 3y – 11 = 0
Given (α, P) lies on this line
α + 3β – 11 = 0

Question 6.
The slope of the line which males an angle 45°with the line 3x – y = – 5 are
(1) 1, – 1
(2) \(\frac{1}{2}\), – 2
(3) 1, \(\frac{1}{2}\)
(4) 2, –\(\frac{1}{2}\)
Answer:
(2) \(\frac{1}{2}\), – 2

Explaination:

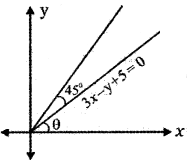
The equation of the given line is
3x – y + 5 = 0 ………… (1)
the slope of the line (1) is m = tan θ

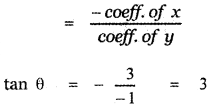
Angle made by the required line = θ + 45°
where tan θ = 3
Required slope m₁ = tan (θ + 45° )

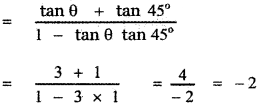
Question 7.
Equation of the straight line that forms an isosceles triangle with coordinate axes in the
1-quadrant with perimeter 4 + 2√2 is
(1) x + y + 2 = 0
(2) x + y – 2 = 0
(3) x + y – √2 = 0
(4) x + y + √2 = 0
Answer:
(2) x + y – 2 = 0

Explaination:
Let OAB be the isosceles triangle formed in the first quadrant. Let OA = OB = a
In the right angle A OAB
AB² = OA² + OB²
AB² = a² + a² = 2a²
AB = √2a

Question 8.
The coordinates of the four vertices of a quadrilateral are (-2, 4), (-1, 2), (1, 2) and (2, 4) taken in order. The equation of the line passing through the vertex (-1, 2 ) and dividing the quadrilateral in the equal areas is
(1) x + 1 = 0
(2) x + y = 1
(3) x + y + 3 = 0
(4) x – y + 3 = 0
Answer:
(4) x – y + 3 = 0

Explaination:

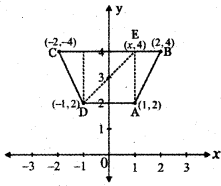
ABCD is a quadrilateral in which the sides AD and BC are parallel. Draw AE and DF perpendicular to BC. ADFE is a square with sides
AD = AE = EF = DF = 2
Area of ADFE = 2 × 2 = 4
In ∆ AEB , BE = 1, AE = 2
∴ Area of ∆ AEB = \(\frac{1}{2}\) × 1 × 2 = 1
Similarly Area of ∆ DFC = 1
∆ Area of the quadrilateral A B C D = 4 + 1 + 1 = 6
Given the line through the vertex (- 1, 2 ) divides the quadrilateral ABCD into two half.
Let E (x , 4) is the point on the line BC such that the line DE divides the area of the quadrilateral ABCD into two half.
∴ Area of ∆ EDC = 3
\(\frac{1}{2}\) × EC × height = 3
\(\frac{1}{2}\) × (x + 2) × 2 = 3
x + 2 = 3 ⇒ x = 1
∴ The coordinates of E are (1, 4)
The equation of the line joining the points (- 1, 2) and (1, 4) is

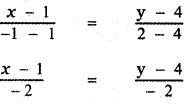
x – 1 = y – 4
x – y + 3 = 0

Question 9.
The intercepts of the perpendicular bisector of the line segment joining (1,2) and (3,4) with coordinate axes are
(1) 5, – 5
(2) 5, 5
(3) 5, 3
(4) 5, – 4
Answer:
(2) 5, 5

Explaination:
Let the given points be A (1, 2) and B (3, 4) P( h,k )be a point in the plane such that PA = PB

Squaring on both the sides
(h – 1)² + (k – 2)² = (3 – h)² + (k – 4)²
h² – 2h + 1 + k² – 4k + 4 = 9 – 6h + h² + k² – 8k + 16
– 2h – 4k + 5 = – 6h – 8k + 25
6h + 8k – 2h – 4k + 5 – 25 = 0
4h + 4k – 20 = 0
h + k – 5 = 0
The locus of (h, k)is x + y – 5 = 0 which is the perpendicular bisector of A and B
x + y = 5
\(\frac{x}{5}+\frac{y}{5}\) = 1
x – intercept = 5 , y – intercept = 5

Question 10.
The equation of the line with slope 2 and the length of the perpendicular from the origin equal to √5 is
(1) x + 2y = √5
(2) 2x + y = √5
(3) 2x + y = 5
(4) x + 2y – 5 = 0
Answer:
Let the equation of the required line be
y = mx + c ……….. (1)
Given Slope m = 2
(1) ⇒ y = 2x + c
2x – y + c = 0 ……….. (2)
The length of the perpendicular from (0, 0) to line (2)

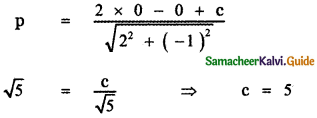
Substituting for c in equation (2), we have
2x – y + 5 = 0

Question 11.
If a line is perpendicular to the line Sx-y = 0 and forms a triangle with the coordinate axes of area 5 sq. units, then its equation is
(1) x + 5y ± 5√2 = 0
(2) x – 5y ± 5√2 = 0
(3) 5x + y ± 5√2 = 0
(4) 5x – y ± 5√2 = 0
Answer:
(1) x + 5y ± 5√2 = 0

Explaination:

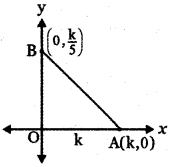
The equation of the given line is 5x – y = 0 —— (1)
The equation of any perpendicular to line (1) is
-x – 5y + k = 0
x + 5y – k = 0 —– (2)
x + 5y = k

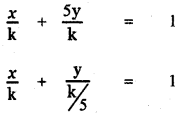
x- intercept = k , y – intercept = \(\frac{\mathrm{k}}{5}\)
The line (2) intersect the x-axis at A and y-axis at B
∴ A is (k, 0) and B is \(\left(0, \frac{k}{5}\right)\)
OA = k and OB = \(\frac{\mathrm{k}}{5}\)
Area of ∆ OBA = \(\frac{1}{2}\) × OA × OB

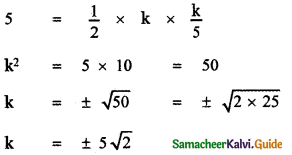
∴ The required equation is x + 5y = ± 5√2

Question 12.
Equation of the straight line perpendicular to the line x – y + 5 = 0 through the point of intersection y-axis and the given line
(1) x – y – 5 = 0
(2) x + y – 5 = 0
(3) x + y + 5 = 0
(4) x + y + 10 = 0
Answer:
(2) x + y – 5 = 0

Explaination:
The equation of the given line is
x – y + 5 = 0 ………. (1)
To find the point of intersection with y – axis, Put x = 0 in (1)
0 – y + 5 = 0 ⇒ y = 5
∴ The point of intersection is ( 0, 5)
The equation any line perpendicular to line (1) is
– x – y + k = 0
x + y – k = 0
This line passes through the point (0,5)
0 + 5 – k = 0 ⇒ k = 5
∴ The equation of the required line is
x + y – 5 = 0

Question 13.
If the equation of the base opposite to the vertex (2, 3) of an equilateral triangle is x + y = 2, then the length of a side is
(1) \(\frac{\sqrt{3}}{2}\)
(2) 6
(3) √6
(4) 3√2
Answer:
(3) √6

Explaination:
∆ ABC is an equilateral triangle. Vertex A is (2, 3)
Equation of the base BC is x + y = 2
Draw AD ⊥ BC. By the property of the equilateral triangle, D is the midpoint of BC
BD = DC
Let AB = a
AD = length of the perpendicular from A (2, 3) to the line x + y – 2 = 0

Question 14.
The line (p + 2q)x + (p – 3q)y = p – q for different values of p and q passes through the point
(1) \(\left(\frac{3}{2}, \frac{5}{2}\right)\)
(2) \(\left(\frac{2}{5}, \frac{2}{5}\right)\)
(3) \(\left(\frac{3}{5}, \frac{3}{5}\right)\)
(4) \(\left(\frac{2}{5}, \frac{3}{5}\right)\)
Answer:
(4) \(\left(\frac{2}{5}, \frac{3}{5}\right)\)

Explaination:
The equation of the given line is
(p + 2q)x + (p – 3q)y = p – q ……….. (1)

Question 15.
The point on the line 2x – 3y = 5 is equal distance from (1, 2), and (3, 4) is
(1) (7, 3)
(2) (4, 1)
(3) (1, – 1)
(4)(-2, 3)
Answer:
(2) (4, 1)

Explaination:
Let P (h, k) be a point on the line
2x – 3y – 5 = 0

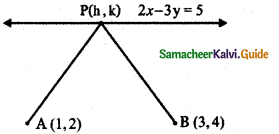
Then 2h – 3k – 5 = 0 ……….. (1)
Let A (1, 2) and B ( 3, 4) be the given points such that PA = PB

Squaring on both sides
(h – 1)² + (k – 2)² = (h – 3)² + (k – 4)²
h² – 2h + 1 + k² – 4k + 4 = h² – 6h + 9 + k² – 8k + 16
-2h + 1 – 4k + 4 = – 6h + 9 – 8k + 16
-2h – 4k + 5 = – 6h – 8k + 25
6h – 2h + 8k – 4k + 5 – 25 = 0
4h + 4k – 20 = 0
h + k – 5 = 0 …………. (2)
To find P (h, k), Solve (1) and (2)

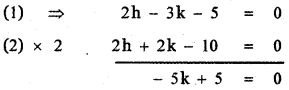
(2) ⇒ h + 1 – 5 = 0
h – 4 = 0 ⇒ h = 4
∴ The required point p(h, k) is (4, 1)

Question 16.
The image of the point (2, 3) in the line y = -x is
(1) (-3, -2)
(2) (-3, 2)
(3) (-2, -3)
(4) (3, 2)
Answer:
(1) (- 3, – 2)

Explaination:
The equation of the given line is y = -x
x + y = 0 ………… (1)
The coordinates of the image of the point (x₁, y₁) with respect to the line ax + by + c = 0 are given by

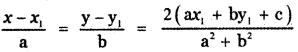
∴ The coordinates of the image of the point (2, 3) with respect to the line x + y = 0 are given by

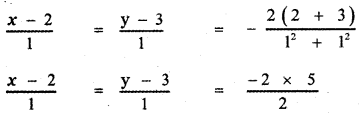
x – 2 = y – 3 = – 5
x – 2 = -5 ⇒ x = -5 + 2 = -3
y – 3 = -5 ⇒ y = -5 + 3 = -2
∴ The required point is (-3, -2)

Question 17.
The length of perpendicular from the origin to the line \(\frac{x}{3}-\frac{y}{4}\) = is
(1) \(\frac{11}{5}\)
(2) \(\frac{5}{12}\)
(3) \(\frac{12}{5}\)
(4) –\(\frac{5}{12}\)
Answer:
(3) \(\frac{12}{5}\)

Explaination:
The equation of the given line is \(\frac{x}{3}-\frac{y}{4}\) = 1
\(\frac{4 x-3 y}{12}\) = 14x – 3y = 12
4x – 3y – 12 = 0
The length of the perpendicular from (0, 0) to the line 4x – 3y – 12 = 0 is

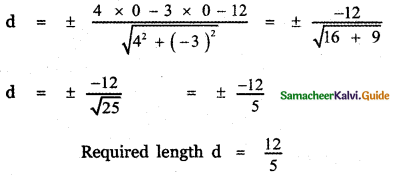
Question 18.
The y – intercept of the straight line passing through (1, 3) and perpendicular to 2x – 3y + 1 = 0 is
(1) \(\frac{3}{2}\)
(2) \(\frac{9}{2}\)
(3) \(\frac{2}{3}\)
(4) \(\frac{2}{9}\)
Answer:
(2) \(\frac{9}{2}\)

Explaination:
The equation of the given line is
2x – 3y + 1 = 0 …………. (1)
The equation of any line perpendicular to (1) is
-3x – 2y + k = 0
3x + 2y – k = 0 ………… (2)
This line passes through the point (1, 3)
∴ (2) ⇒ 3 × 1 + 2 × 3 – k = 0
3 + 6 – k = 0 ⇒ k = 9
∴ (2) ⇒ 3x + 2y – 9 = 0 ………. (3)
2y = – 3x + 9
y = \(-\frac{3}{2} x+\frac{9}{2}\)
∴ The required y – intercept is \(\frac{9}{2}\)

Question 19.
If the two straight lines x + (2k – 7)y + 3 = 0 and 3kx + 9y – 5 = 0 are perpendicular, then the value of k is
(1) k = 3
(2) k = \(\frac{1}{3}\)
(3) k = \(\frac{2}{3}\)
(4) k = \(\frac{3}{2}\)
Answer:
(1) k = 3

Explaination:
The equation of the given lines are
x + (2k – 7)y + 3 = 0 ……….. (1)
3kx + 9y – 5 = 0 …………. (2)
Slope of line (1), m₁ = \(-\frac{1}{2 k-7}\)
Slope of line (2), m₂ = \(-\frac{3 \mathbf{k}}{9}\)
Given that lines (1) and (2) are perpendicular
∴ m₁ m₂ = -1

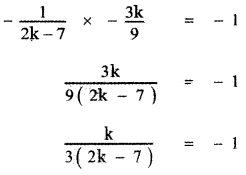
k = -3(2k – 7)
k = -6k + 21
6k + k = 21
⇒ 7k = 21
k = \(\frac{21}{7}\) = 3

Question 20.
If a vertex of a square is at the origin and it’s one side lies along the line 4x + 3y – 20 = 0
then the area of the square is
(1) 20 sq. units
(2) 16 sq. units
(3) 25 sq. units
(4) 4 sq. units
Answer:
(2) 16 sq. units

Explanation:

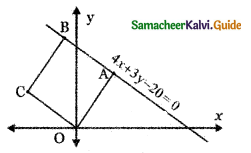
OABC is a square in which the vertex O lies on the origin and the side AB along the line 4x + 3y – 20 = 0
OA = length of the perpendicular from (0, 0) to the line 4x + 3y – 20 = 0

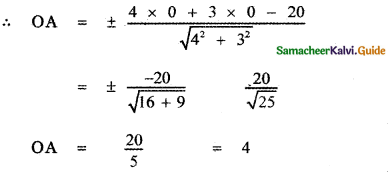
∴ The length of the side of the square is 4 units.
∴ Area of the square = 4 × 4 = 16 sq. units

Question 21.
If the lines represented by the equation 6x² + 41xy – 7y² = 0 make angles α and β with x-axis then tan α . tan β =
(1) –\(\frac{6}{7}\)
(2) \(\frac{6}{7}\)
(3) –\(\frac{7}{6}\)
(4) \(\frac{7}{6}\)
Answer:
(1) –\(\frac{6}{7}\)

Explaination:
The equation of the given pair of lines is
6x² + 41xy – 7y² = 0 ……….. (1)
Let m₁, m₂ be slopes of the individual lines.
Given that the individual lines make angles α and β with x – axis.
∴ m₁ = tan α and m₂ = tan β
we have m₁ m₂ = \(\frac{a}{b}\) = \(\frac{6}{-7}\)
∴ tan α tan β = \(-\frac{6}{7}\)

Question 22.
The area of the triangle formed by the lines x² – 4y² = 0 and x = a is
(1) 2a²
(2) \(\frac{\sqrt{3}}{2}\)
(3) \(\frac{1}{2}\)
(4) \(\frac{2}{\sqrt{3}}\)
Answer:
(3) \(\frac{1}{2}\)

Explaination:

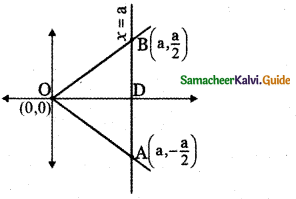
The equation of the given pair of straight lines is
x² – 4y² = 0
x² – 4y² = (x + 2y) (x – 2y)
∴ The separate equations of the straight lines are
x + 2y = 0 ………… (1)
x – 2y = 0 …………. (2)
The line x = a intersect the line (1) at A.
a + 2y = 0 ⇒ y = \(-\frac{a}{2}\)
∴ A is \(\left(a,-\frac{a}{2}\right)\)
The line x = a intersect the line (2) at B.

Question 23.
If one of the lines given by 6x² – xy – 4cy² = 0 is 3x + 4y = 0,then c equals to
(1) -3
(2) -1
(3) 3
(4) 1
Answer:
(1) -3

Explaination:
The given pair of straight lines is 6x² – xy – 4cy² = 0 ………. (1)
One of the separate equation is 3x + 4y = 0 ……… (2)
Let the separate equation of the other line be ax + by = 0 ………. (3)
∴ (ax + by) (3x + 4y) = 6x² – xy + 4cy²
3ax² + 4axy + 3bxy + 4by² = 6x² – xy + 4cy²
Equating the coefficient of y² on both sides
4b = 4c ⇒ c = b
Equating the coefficient of x² on both sides
3a = 6
⇒ a = \(\frac{6}{3}\) = 2
Equating the coefficient of xy both sides
4a + 3b = -1
4 × 2 + 3b = -1 ⇒ 3b = -1 – 8
b = \(-\frac{9}{3}\) = -3
∴ c = -3

Question 24.
θ is acute angle between the lines x² – xy – 6y² = 0 then \(\frac{2 \cos \theta+3 \sin \theta}{4 \cos \theta+5 \cos \theta}\) is
(1) 1
(2) \(-\frac{1}{9}\)
(3) \(\frac{5}{9}\)
(4) \(\frac{1}{9}\)
Answer:
(3) \(\frac{5}{9}\)

Explaination:
The equation of the given pair of lines is
x² -xy – 6y² = 0
a = 1, 2h = -1, b = -6
Given θ is the angle between the lines

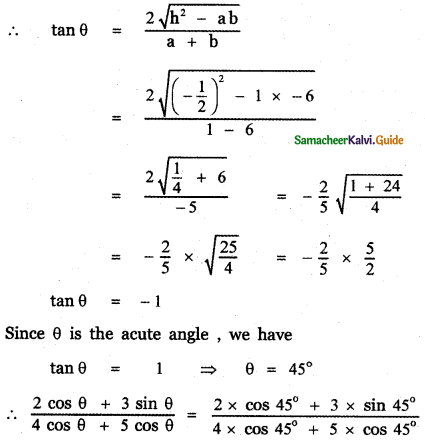
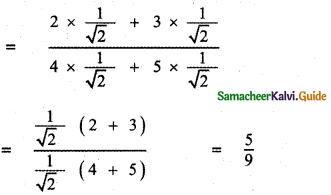
Question 25.
The equation of one of the lines represented by the equation x² + 2xy cot θ – y² = 0 is
(I) x – y cot θ = 0
(2) x + y tan θ = 0
(3) x cos θ + y (sin θ + 1) = 0
(4) x sin θ + y(cos θ + 2) = 0
Answer:
(4) x sin θ + y(cos θ + 2) = 0

Explaination:
The equation of given pair of straight line is
x² + 2xy cot θ – y² = 0
x² + (2y cot θ)x + (-y²) = 0
This is a quadratic equation in x. Solving for x, we have