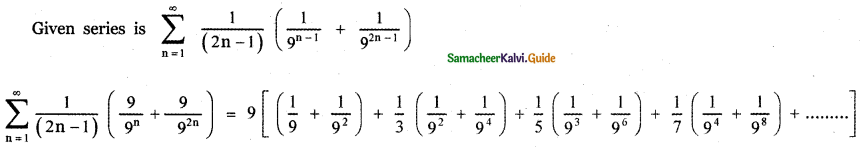Samacheer Kalvi 11th Maths Guide Chapter 5 Binomial Theorem, Sequences and Series Ex 5.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 5 Binomial Theorem, Sequences and Series Ex 5.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.4

Question 1.
Expand the following in ascending powers of x and find the condition on x for which the binomial expansion is valid.
(i) \(\frac{1}{5+x}\)
Answer:

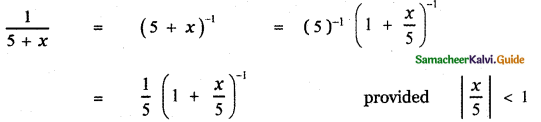
(ii) \(\frac{2}{(3+4 x)^{2}}\)
Answer:

(iii) (5 + x²)^2/3
Answer:

(iv) \((x+2)^{-\frac{2}{3}}\)
Answer:

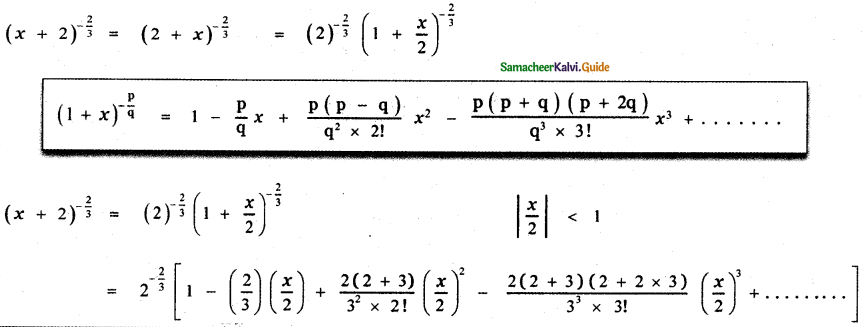
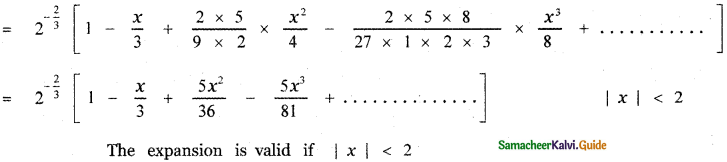
Question 2.
Find \(\sqrt[3]{1001}\) approximately. (two decimal places)
Answer:

Question 3.
Prove that \(\sqrt[3]{x^{3}+6}-\sqrt[3]{x^{3}+3}\) is approximately equal to \(\frac{1}{x^{2}}\) when x is sufficiently large.
Answer:

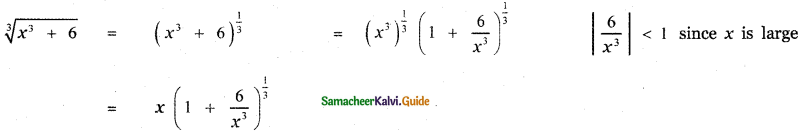
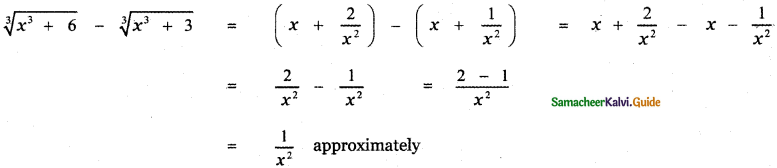
Question 4.
Prove that \(\sqrt{\frac{1-x}{1+x}}\) is approximately equal to 1 – x + \(\frac{x^{2}}{2}\) when x is very small.
Answer:

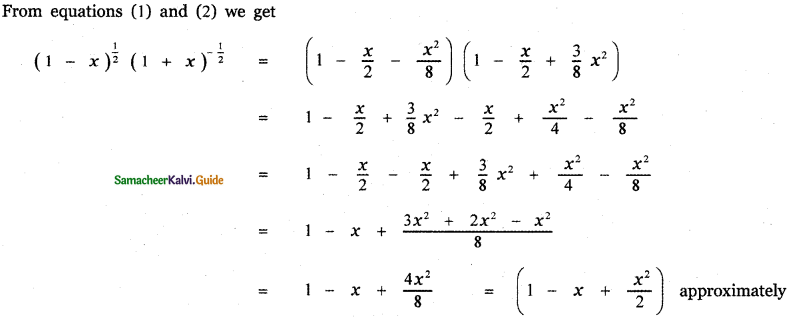
Question 5.
Write the first 6 terms of the exponential series
(i) e^5x
Answer:

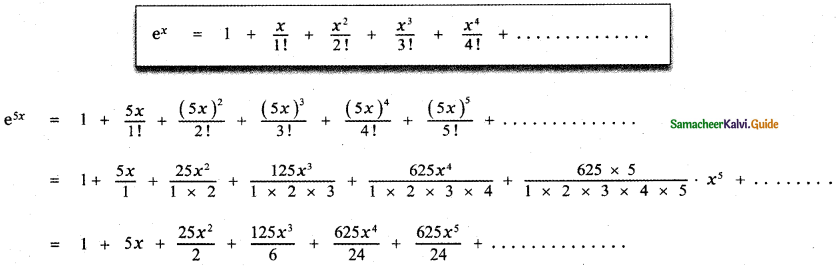
(ii) e^-2x
Answer:

(iii) e^x/2
Answer:

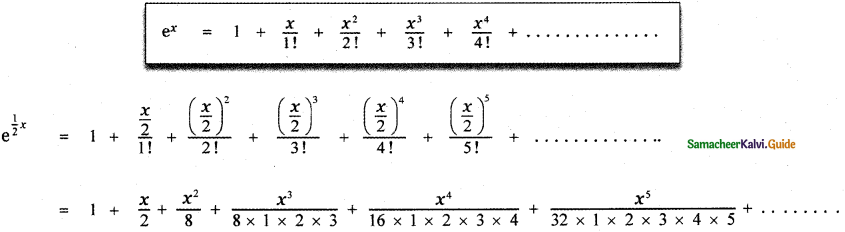
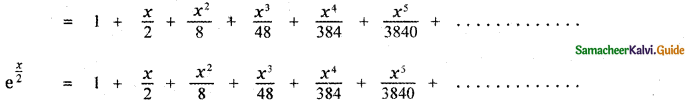
Question 6.
Write the first 4 terms of the logarithmic series.
(i) log (1 + 4x)
(ii) log (1 – 2x)
(iii) log \(\left(\frac{1+3 x}{1-3 x}\right)\)
(iv) log \(\left(\frac{1-2 x}{1+2 x}\right)\)
Find the intervals on which the expansions are valid.
Answer:
(i) log ( 1 + 4x )

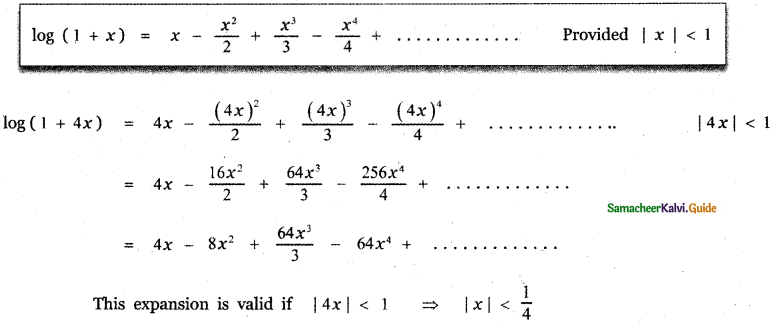
(ii) log (1 – 2x)

(iii) log \(\left(\frac{1+3 x}{1-3 x}\right)\)

(iv) log \(\left(\frac{1-2 x}{1+2 x}\right)\)

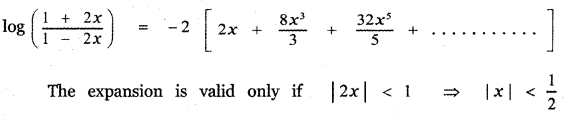
Question 7.

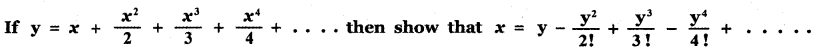
Answer:

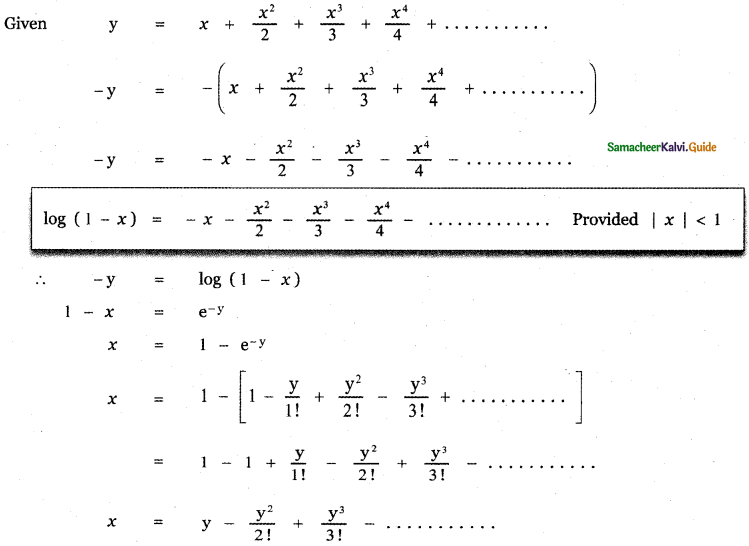
Question 8.

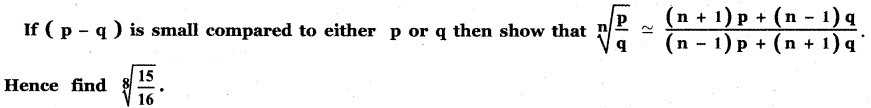
Answer:

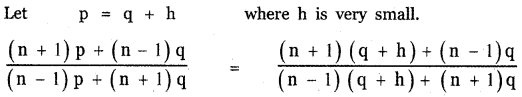
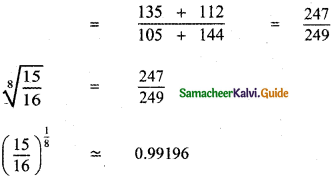
Question 9.
Find the coefficient of x⁴ in the expansion of \(\frac{3-4 x+x^{2}}{e^{2 x}}\)
Answer:

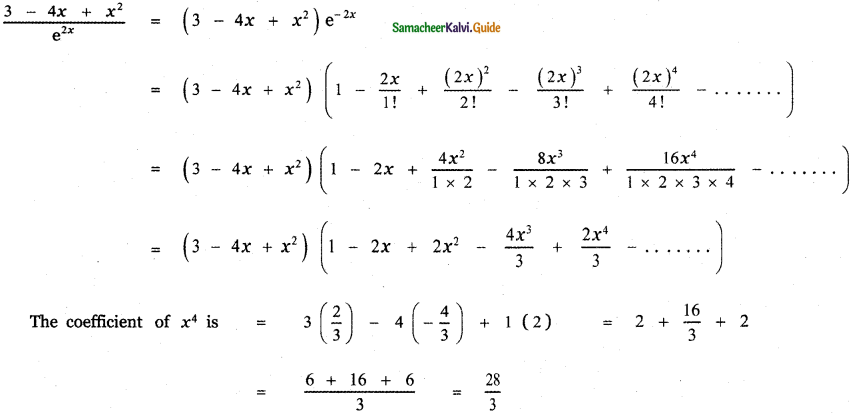
Question 10.
Find the value of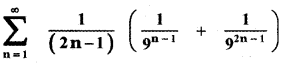
Answer: