Samacheer Kalvi 12th Business Maths Guide Chapter 9 Applied Statistics Miscellaneous Problems

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 9 Applied Statistics Miscellaneous Problems Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 9 Applied Statistics Miscellaneous Problems

Question 1.
Using three yearly moving averages, Determine the trend values from the following data.

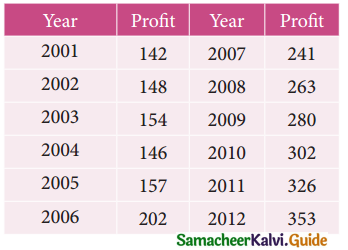
Solution:

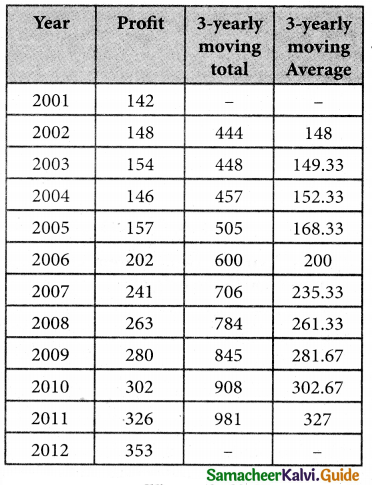
Question 2.
From the following data, calculate the trend values using fourly moving averages.

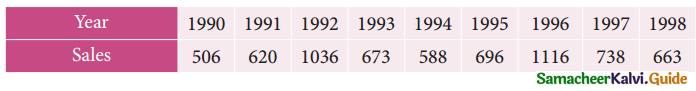
Solution:

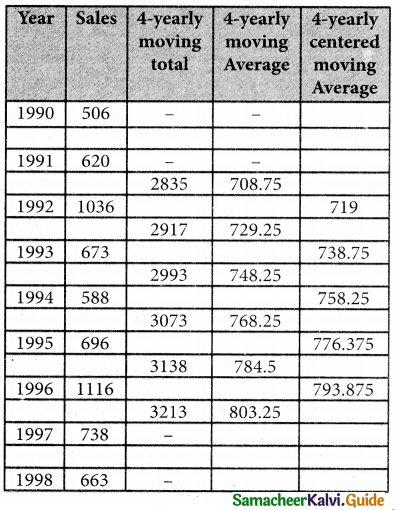
Question 3.
Fit a straight line trend by the method of least squares to the following data.

Solution:

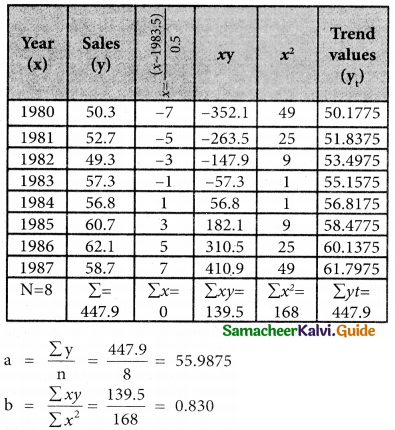
Therefore, the required equation of the straight line trend is given by
y = a + bx
y = 55.9875 + 0.830 x
⇒ y = 55.9875 + 0.83 (\(\frac { x-1983.5 }{0.5}\))
The trend values can be obtained by
When x = 1980
y = 55.9875 + 0.83 (\(\frac { 1980-1983.5 }{0.5}\))
= 55.9875 + 0.83 (-7)
= 55.9875 – 5.81
= 50.1775
When x = 1981
y = 55.9875 + 0.83 (\(\frac { 1981-1983.5 }{0.5}\))
= 55.9875 + 0.83 (-5)
= 55.9875 – 4.15
= 51.8375
When x = 1982
y = 55.9875 + 0.83 (\(\frac { 1981-1983.5 }{0.5}\))
= 55.9875 + 0.83 (-3)
= 55.9875 – 2.49
= 53.4975
When x = 1983
y = 55.9875 + 0.83 (\(\frac { 1983-1983.5 }{0.5}\))
= 55.9875 + 0.83 (-1)
= 55.9875 – 0.83
= 55.1575
When x = 1984
y = 55.9875 + 0.83 (\(\frac { 1984-1983.5 }{0.5}\))
55.9875 + 0.83 (1)
= 56.8175
when x = 1985
y = 55.9875 + 0.83 (\(\frac { 1985-1983.5 }{0.5}\))
= 55.9875 + 0.83 (3)
= 55.9875 + 2.49
= 58.4775
when x = 1986
y = 55.9875 + 0.83 (\(\frac { 1986-1983.5 }{0.5}\))
= 55.9875 + 0.83 (5)
= 55.9875 + 4.15
= 60.1375
when x = 1987
y = 55.9875 + 0.83 (\(\frac { 1987-1983.5 }{0.5}\))
= 55.9875 + 0.83 (7)
= 55.9875 + 5.81
= 61.7975

Question 4.
Fit a straight line trend by the method of least squares to the following data.

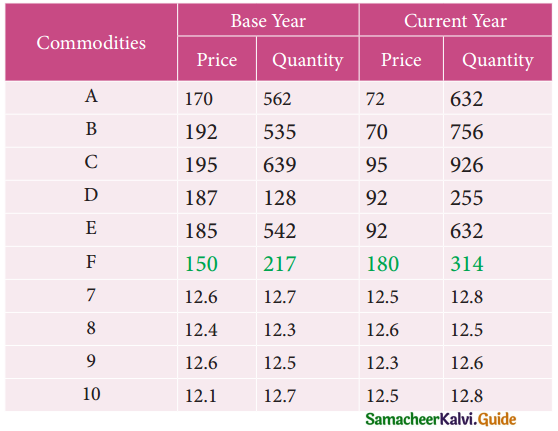
Solution:

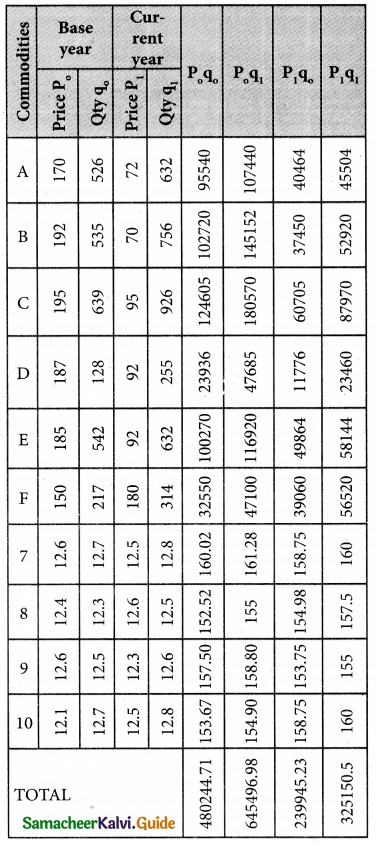
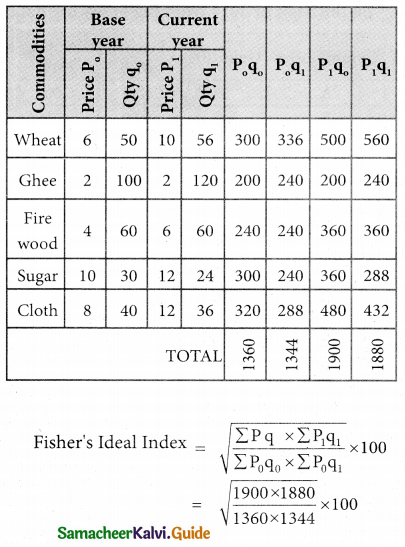
Lasperyre’s price Index number


Hence Fisher’s Ideal Index satisfies Time reversal test

Question 5.
Using the following data, construct Fisher’s Ideal Index Number and Show that it satisfies Factor Reversal Test and Time Reversal Test?

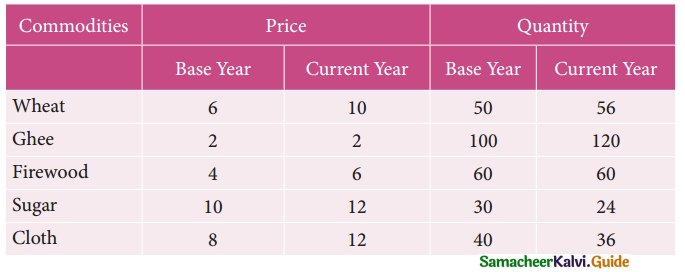
Solution:

Factor reversal test

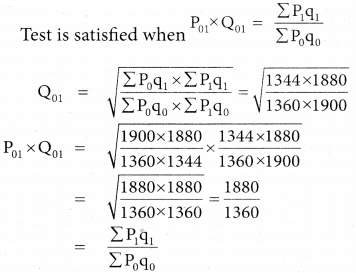
Hence Fisher’s Ideal Index satisfies Factor reversal test.

Question 6.
Compute the consumer price index for 2015 on the basis of 2014 from the following data.

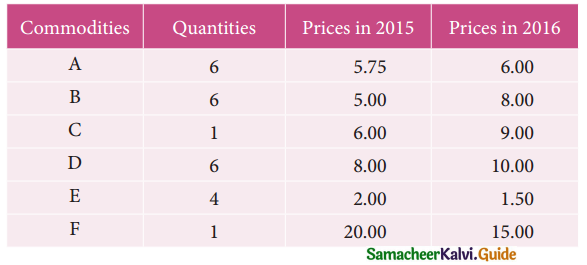
Solution:

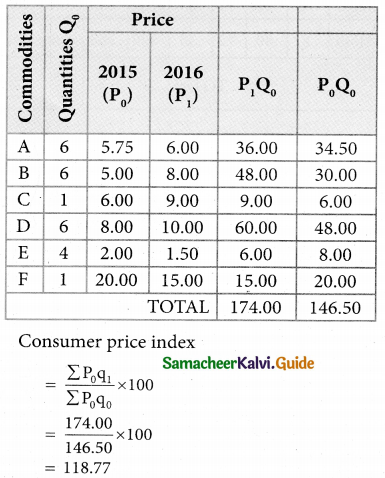
Question 7.
An Enquiry was made into the budgets of the middle class families in a city gave the following information.

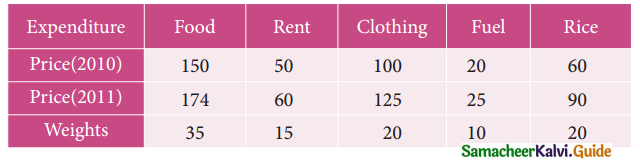
What changes in the cost of living have taken place in the middle class families of a city?
Solution:

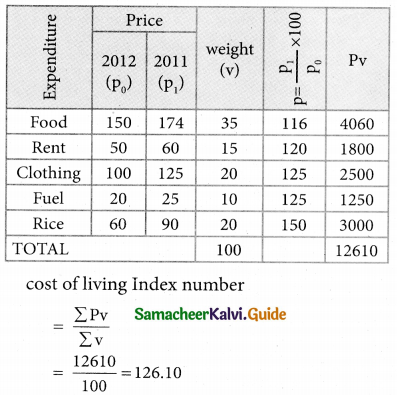
Conclusion:
The cost of living has increased up to 26.10% in 2011 as compared to 2010.

Question 8.
From the following data, calculate the control limits for the mean and range chart.

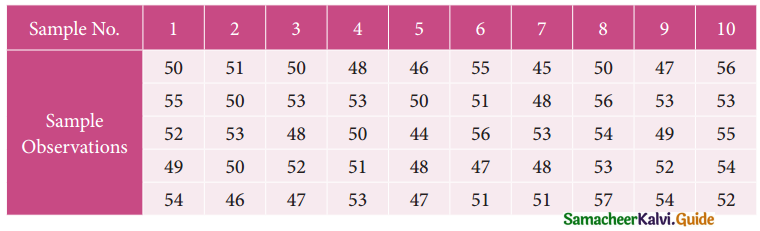
Solution:

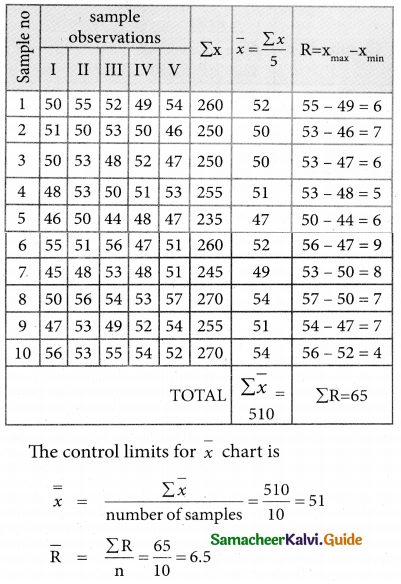
UCL = \(\bar { \bar x}\) + A₂\(\bar { R}\)
= 51 + 0.577(6.5)
= 51 + 3.7505
= 54.7505
= 54.75
CL = \(\bar { \bar x}\) = 51
UCL = \(\bar { \bar x}\) – A₂\(\bar { R}\)
= 51 – 0.577(6.5)
= 51 – 3.7505
= 47.2495
= 47.25
The control limits for Range chart is
UCL = D₄\(\bar { R}\)
= 2.114(6.5)
= 13.741
CL = \(\bar { R}\) = 6.5
LCL = D₃\(\bar { R}\) = 0(6.5) = 0

Question 9.
The following data gives the average life(in hours) and range of 12 samples of 5 lamps each. The data are

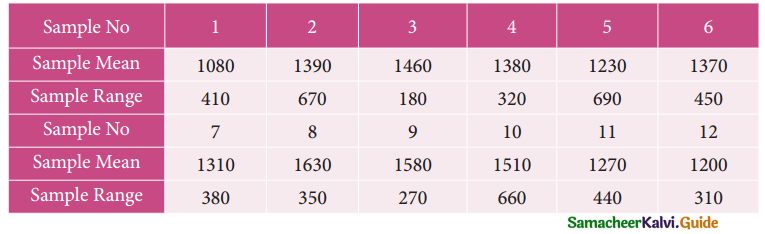
Construct control charts for mean and range Comment on the control limits.
Solution:

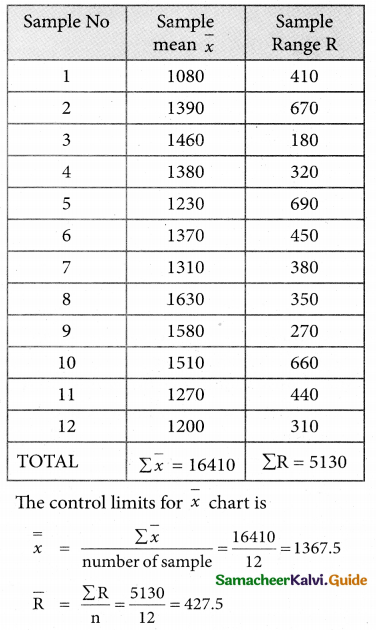
UCL = \(\bar { \bar x}\) + A₂\(\bar { R}\)
= 1367.5 + 0.577(427.5)
= 1367.5 + 246.6675
= 1614.1675
= 1614.17
CL = \(\bar { \bar x}\) = 1367.5
LCL = \(\bar { \bar x}\) + A₂\(\bar { R}\)
= 1367.5 – 0.577(427.5)
= 1367.5 – 246.6675
= 1120.8325
= 1120.83
The control limits for Range chart is
UCL = D₄\(\bar { R}\)
= 2.115(427.5)
= 904.1625
= 904.16
CL = \(\bar { R}\) = 427.5
LCL = D₃\(\bar { R}\)
= 0(427.5)
= 0

Question 10.
The following are the sample means and I ranges for 10 samples, each of size 5. Calculate ; the control limits for the mean chart and range chart and state whether the process is in control or not.

Solution:

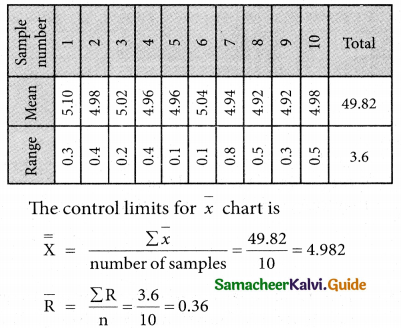
UCL = \(\bar { \bar x}\) + A₂\(\bar { R}\)
= 4.982 + 0.577(0.36)
= 4.982 + 0.20772
= 5.18972
= 5.19
CL = \(\bar { \bar x}\) = 4.982
LCL = \(\bar { \bar x}\) + A₂\(\bar { R}\)
= 4.982 – 0.577(0.36)
= 4.982 – 0.20772
= 4.77428
= 4.774
The control limits for range chart is
UCL = D₂\(\bar { R}\) = 2.115(3.6)
= 7.614
CL = \(\bar { R}\) = 3.6
LCL = D₃\(\bar { R}\)
= 0(0.36) = 0